It turns out that sometimes there may not be such a function. For
example, these functions arise frequently in applications:
e-x2 and sin(x)/x. Both of them have no
antiderivative which can be written in terms of familiar functions.
Most symbolic algebra programs can use all the techniques we will
see. BUT it is a very good idea to learn how the techniques
work and also the sorts of answers to expect. For example, we will see
that the antiderivative of a rational function (quotient of
polynomials) can certainly have an arctangent, but it should
not have an exponential. Also, sometimes the darn programs just
don't work, even when they should. My favorite example of this
in Maple (and I presume there are suitable examples with
other programs) is the following sequence of antiderivatives:
sqrt(1+sqrt(1+sqrt(x))) dx
Again, w=sqrt(1+sqrt(1+sqrt(x))) will change the problem into finding the
antiderivative of a polynomial. By the time the square roots get "nested" four deep,
Maple can't do the integral.
Mathematica can!
I tried my examples on Mathematica, and that program can keep
track of the nested square roots, and compute the antiderivative. On
the web, this web page
allows access to the Mathematica antidifferentiation
routine. But it can't handle Sqrt[1+Sqrt[1+Sqrt[1+Sqrt[x]]]] which the
program I used (Mathematica 4.1) can integrate. I have never
understood Wolfram's products.
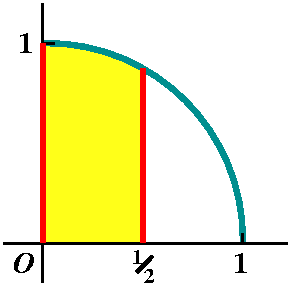
sqrt(1-x2) dx
Well, we know that
01sqrt(1-x2) dx
is Pi/4 since it is a quarter of a circle. What about
01/2sqrt(1-x2) dx?
Now maybe we need to come up with an antiderivaitve of
sqrt(1-x2). I will discuss this as I did in class, in spite
of the sneers and gibes which greeted my honest efforts
to disclose my thinking.
Word of the day gibe As a noun, this
can mean "a derisive remark".
If I want to get a substitution to make sqrt(1-x2) nice,
that means: x=? and then sqrt(1-?2)=! should also be
nice. But then 1-?2=!2, so we need two
functions, preferably familiar functions, so that
?2+!2=1. We get only one guess here: I will take
?=sin(theta). Then
sqrt(1-x2)=sqrt(1-sin(theta)2)=cos(theta) and
dx=d(sin(theta))=cos(theta) d(theta). The whole integral becomes
sqrt(1-x2) dx=(cos(theta))2d(theta).
Another way ...
We certainly can now use the reduction formula we've already derived. Let
me show you another way, which some people like. We know:
1 = (cos(theta))2+(sin(theta))2
cos(2theta) = (cos(theta))2-(sin(theta))2
Add these formulas, and get 1+cos(2theta)=2(cos(theta)2
size=+1>), so that
(cos(theta))2d(theta)=(1/2)(1+cos(2theta))d(theta). This I can antidifferentiate
almost easily (use the substitution u=2(theta) etc.). The result is:
(1/2)([sin(2theta)/2]+theta).
I should not plug in 0 and 1 here, because those are x-values. Let me show you
how to convert back to x-land from theta-land. Certainly, sin(2theta)=2sin(theta)cos(theta),
and we know that x=sin(theta) and sqrt(1-x2)=cos(theta). We chose the substitution
so that's correct. Also, since x=sin(theta), theta=arcsin(x). Therefore
(1/2)([sin(2theta)/2]+theta)
=(1/2)([2sin(theta)cos(theta)/2]+theta)
=(1/2)([x·sqrt(1-x2)+arcsin(x))
Fact sqrt(1-x2) dx=(1/2)([x·sqrt(1-x2)+arcsin(x))
If you don't believe this, you have the option to differentiate the
right-hand side and check that it is sqrt(1-x2). This is
possible.
Now, finally, 01/2sqrt(1-x2) dx=(1/2)([x·sqrt(1-x2)+arcsin(x))]01/2. The x=0 terms contribute nothing,
and the other terms give (1/2)(1/2)sqrt(1-(1/2)2)+arcsin(1/2).
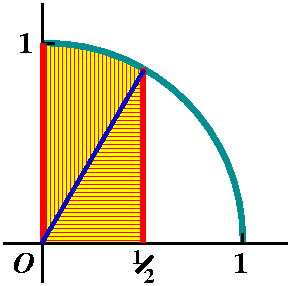
I knew this all the time ...
I do know arcsin(1/2) -- one of the few values of this function that I
"know".
So the answer is (1/2)(1/2)(sqrt(3)/2)+Pi/6. Well, look at the picture, darn it! The
horizontally striped triangle has "legs" of length 1/2 and sqrt(3)/2, so that gives
(1/2)(1/2)(sqrt(3)/2) area. The circular pie slice has area Pi/6.
It is almost never possible to check an integral computation using such neat
area facts. This is just a cute example.
1/sqrt(1+sqrt(1+x2) dx
Here I put ?=x so !=sqrt(1+?2) and we see that we need
functions which satisfy !2-?2=1. So we look
towards ... which is it? Ahhh ... sec(theta)=! so tan(theta)=!. And
since x=sec(theta), dx=sec(theta)tan(theta)d(theta).
The integral
1/sqrt(1+sqrt(1+x2) dx
becomes
1/tan(theta) sec(theta)tan(theta)d(theta)=sec(theta)d(theta). Look: it should not be surprising if
things turn out nice. The substitution is selected to make it all
work.
What is the antiderivative of secant?
Let's see: there's lots of history here. You can go to
Google and get some interesting references. But one
antiderivate of secant is ln(sec(theta)+tan(theta)). Why is this?
Well, differentiate. The chain rule gives
1 2
--------------------- (sec(theta)tan(theta)+sec(theta) )
sec(theta)+tan(theta)
and, wonders!, exactly the right stuff cancels and we get just
sec(theta). You can look up lots of clever derivations of
this. I just want to use it.
Now to go back to x-land. Since x=sec(theta) and
sqrt(1+x2)=tan(theta),
ln(sec(theta)+tan(theta))=ln(x+sqrt(1+x2). Therefore
img src="gifstuff/is6.gif"
width=6>1/sqrt(1+sqrt(1+x2) dx=ln(x+sqrt(1+x2)+C
I remarked in class that Maple gives the answer,
arcsinh(x) so maybe I should tell you about the hyperbolic
functions some time.
HOMEWORK
Read and do problems from 7.1, 7.2, and 7.3.
Thursday, September 15
We began by making sure that everyone was matched for the second set
of workshop problems. It was a ... pleasure ... (yes, that's how it is
spelled, not P-A-I-N).
Another great experience!
Of course Mr. Scheinberg did a terrific job answering questions. I am
happy.
x(x+1)1/3dx
I did this integral two different ways, just for fun. Sigh.
Substitution Take w=(x+1)1/3 because the
(x+1)1/3 is the center of the trouble (well, that's how my
head works, sorry). Then w3-1=x, so that
3w2dw=dx, and x(x+1)1/3dx=(w3-1)·w dw. But we can multiply out
(is "distribute" the correct word here?) and get
w4-w dw=(1/5)w5-(1/2)w2+C.
We can convert from w-land to x-land using w=(x+1)1/3 and the answer is
(1/5)(x+1)5/3-(1/2)(x+1)2/3+C.
Integrate by parts In x(x+1)1/3dx, good parts may not be immediately clear.
I am serious about this. But here is a choice that works.
u dv = uv - v du
u= x} {du=dx
dv=(x+1)1/3dx} {v=(3/4)(x+1)4/3
Therefore x(x+1)1/3dx=x((3/4)(x+1)4/3)-(3/4)(x+1)4/3dx=x((3/4)(x+1)4/3)+(3/4)(3/7)(x+1)7/3+C.
So the answer also is
x((3/4)(x+1)4/3)+(3/4)(3/7)(x+1)7/3+C!
Compare and contrast ...
It is not clear to me that the two answers are the same (well,
they both have "+C"!). This frequently happens when
antidifferentiating complicated functions. There can be more than one
algorithmic "route" to the answer and the appearance can be very
different. These answers actually are the same, but it takes
some algebra to verify the fact. Maple reports:
>int(x*(x+1)^(1/3),x);
4/3
3 (x + 1) (-3 + 4 x)
-----------------------
28
Does that help?
arctan(x) dx
Integrate by parts, with u=arctan(x) and dv=dx. Then du=[1/(1+x2)]dx and v=x.
And uv-v du is
x·arctan(x)-x/(1+x2) dx. The last
integral can be computed with the substitution w=1+x2. Then
x/(1+x2) dx becomes (1/2)dw/w which has antiderivative (1/2)ln(w)=(1/2)ln(1+x2). Putting it all together,
arctan(x) dx=x·arctan(x)-(1/2)ln(1+x2)+C.
QotD
What is ln(x) dx? This should follow the same pattern
as the previous antiderivative.
e3xsin(5x) dx
We will integrate by parts twice, in the correct order. But it turns
out that there is an easier way to do this that physicists and
engineers all know. We'll see it later.
Diary entry in progress! More to come
HOMEWORK
Just the second workshop
problems.
Wednesday, September 14
Wonderful student
presentations!
We had student presentations of most of the first set of "workshop
problems"
- Mr. Viernes discussed problem #1.
- Ms. Johnson discussed problem #2.
- No one discussed problem #3, since part b) seems to be totally
intractable! ("Difficult to manage or govern; stubborn.")
- Mr. Townley discussed problem #4.
- Ms. Van Saders gave a different solution to problem #4.
We all had a wonderful time.
I finally moved on and began to discuss integration by parts. In an
effort to further broaded student horizons ("liberal arts education"
indeed!) I messed up a quotation from a short story written by Arthur
C. Clarke, collected as one of his "Tales from the White Hart". Here's the correct quote:
"...But no-one expected he'd ever get very far, because I don't
suppose he could even integrate e to the x."
"Is such ignorance possible?" gasped someone.
"Maybe I exaggerate. Let's say x e to the x. ..."
|
The book has been reissued and is available. My copy is lost somewhere
in my attic.
Integration by parts is certainly the most important
antidifferentiation algorithm (o.k.: I guess more elementary and more
often used is substitution, but let me make the assertion). Now that
there are programs which can do lots of antiderivatives, we can still
see that integration by parts turns out to give lots of unexpected
information, and even insight. Let's get to it, finally:
The
product rule states that
(f·g)'(x)=f'(x)g(x)+f(x)g'(x). Therefore
f'(x)g(x)=(f·g)'(x)-f(x)g'(x). And let's integrate:
inxf'(x)g(x) dx=inx(f·g)'(x) dx-inxf(x)g'(x) dx. Now certainly inx(f·g)'(x) dx=f(x)g(x), because an antiderivative of a derivative is the original function. So we have:
Integration by parts
inxf'(x)g(x) dx=f(x)g(x)-inxf(x)g'(x) dx.
The only way you see why this is incredibly cute is by using
it. So let's do it, with the obvious first example.
What is inxxex dx?
We use the equation inxf'(x)g(x) dx=f(x)g(x)-inxf(x)g'(x) dx
to exchange what seems to be an intractable integral for what we hope is a better one.
Our template is f'(x)g(x) and we are given xex. What can we
select as f'(x) and what then must become g(x)? There are a few
choices but here let's try f'(x)=ex and g(x)=x. Then
f(x)=ex and g'(x)=1. So:
inxf'(x)g(x) dx=f(x)g(x)-inxf(x)g'(x) dx becomes
inx ex x dx= ex x -inxex1dx
We have "traded in" inxexx dx for the "nicer"
integral -inxex1dx with a "penalty" of exx.
Here the qualitative word "nicer" is just used in the sense of,
"Hey, an integral we can compute easily!" Of course,
-inxex1dx=-ex+C, so we get our final answer,
that
inxxex dx=exx-ex+C.
Of course if you don't believe the answer you can just
... differentiate. And, indeed, you will need the product rule, and
things will work out just fine.
How to really do the example
Most people I know will write the following template, if they think
that integration by parts will do them some good:
inxxex dx=
inx u dv = uv - inx v du
u= } {du=
dv= } { v=
and attempt to make a selection of u which then allows the other
spaces to be filled in. Here is what would happen in this case:
inxxex dx=xex-inxexdx
inx u dv = uv - inx v du
u=x } {du=dx
dv=exdx} { v=ex
and then we could merrily finish the computation by integrating
ex as before. There are certainly other ways of writing the
computation (such as "tabular integration"), but this way is what's
most familiar to me. I confess that sometimes I try to skip some
steps, and don't write the details. Then my "penalty" is that I
frequently have to do the computation again (and maybe even another
time) because I make mistakes. Sigh.
Another example
Let's try inxx2ex dx. Here we go:
inxx2ex dx=
inx u dv = uv - inx v du
u= } {du=
dv= } { v=
Now there are more possibilities for the parts u and dv. But if
we look ahead, if we try to anticipate a little bit, why then ...
let's use u=x2 and dv=exdx.
inxx2ex dx=x2ex-inxex2x dx
inx u dv = uv - inx v du
u=x2 } {du=2x dx
dv=exdx} { v=ex
Is this good? Well, we have made some progress. We have pushed "down"
the power of x and now we may recognize (if we pull out the constant
2) an integral we've already done. So:
inxx2ex dx=x2ex-2inxexx dx=x2ex-2(exx-ex)+C
Here already some characteristic problems show up: there are minus
signs to keep track of and parentheses to worry about. And what could
be +2C or -2C I just wrote as +C because it is just some constant. But we've "solved" the problem.
I could continue, and do x3ex and then
x4ex and even x5ex and ... but maybe there is a more systematic way to write things.
A first example of a reduction formula
Write inxxnexdx, where n is a positive integer,
in terms of stuff+an integral with an x term lower in degree. So:
inxxnex dx=
inx u dv = uv - inx v du
u= } {du=
dv= } { v=
(People who have written computer programs will recognize this as an
example of recursion.) What should we choose as u? To lower the
degree, I will choose u=xn. Then all the other entries can
be filled in rather easily, so:
inxxnex dx=xnex-inxexnxn-1dx
inx u dv = uv - inx v du
u=xn } {du=nxn-1dx
dv=exdx} { v=ex
And here is our desired reduction formula:
inxxnex dx=xnex-ninxexxn-1dx.
We can even make this a bit more interesting, by finding and stating a
reduction formula for inxxneax dx, for n, a
positive integer and a, some constant. There are a few little changes:
u=xn } {du=nxn-1dx
dv=eaxdx} { v=(1/a)eax
so the formula becomes:
inxxneax dx=(1/a)xneax-(n/a)inxexxn-1dx.
QotD
Well I asked for inx(x2-3)e5xdx but I really did
expect people to use the formulas I developed, not to attempt to
derive them again. Sigh. What a mess.
(x2-3)e5x=(x2e5-3e5x and then the first part becomes
(1/5)[x2e5-(2/5){(1/5)xe5-(1/52)}] etc. Sigh.
> int((x^2-3)*exp(5*x),x);
2
1/125 (-73 - 10 x + 25 x ) exp(5 x)
HOMEWORK
I reminded people to prepare for Mr. Scheinberg.
Monday, September 12
Homework issues
Mr. DOUGLAS A. SCHEINBERG, the peer
mentor for Math 192, will appear in class on Thursday. Mr. Scheinberg
will be happy to discuss the problems in sections 6.2, 6.3, 6.4, and
6.5. His e-mail address is cronodas@eden.rutgers.edu.
He is majoring in computer engineering.
Please try to look over the routine Math 152 problems assigned for
these sections, and discuss the problems with your classmates or me or
Mr. Scheinberg as necessary.
Another work problem
I tried to do problem #16 in section 6.4 (p.463):
A bucket that weighs 4 lbs and a rope of negligible weight are used to draw water from a well that is 80 ft deep. The bucket is filled with 40 lb of water and is pulled up at the rate of 2 ft/s, but the water leaks out of a hole in the bucket at a rate of 0.2 lb/s.
Find the work done in pulling the bucket to the top of the well.
Mr. J. Wolf, a smart physics major at Rutgers, read this problem,
thought for a bit, and remarked, "Oh yeah, you need to write the
bucket's weight as a function of the depth." Indeed, that's more or
less the whole point, but it took us a while to get there. Experience
helps a great deal in these problems.
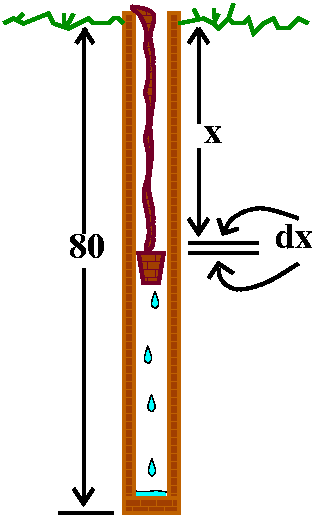We discussed the problem. The bucket takes 80/2=40 seconds to travel
to the top of the well. After t seconds (where 0<t<40), the
bucket weighs 44-.2t lbs. Well, but work is force·distance,
and time has nothing to do with it (in this physical approach). So
if we measure the depth of the well from the top of the well using
feet, and call x the distance, then x is between 0 and 80. The
bucket is at depth x when x=80-2t, so t=40-.5x, and the weight of
the bucket at that time is 44-.2(40-.5x)=36-(1/10)x. The weight
varies as a function of the height. Now if we pull the bucket
up dx feet (a really tiny length) when it is at a depth of x
feet, then we are doing [36-(1/10)x]dx work, a little bit of work,
which we could call, uhhh ... dw. The total work is the Sum of all the pieces of work, so that the
total work is 080[36-(1/10)x]dx. I believe I actually
evaluated this integral, and got 36(80)-(80)2/20 ft-lbs.
Is the answer correct? Well, if the bucket did not leak at all,
we would need 80(44) ft-lbs of work and this is less. And one clever
student (I've got to learn your names!) suggested that a
better estimate might be to take the bucket's weight at the middle
and multiply by 80, and this is close to the answer, also.
This problem is difficult for me. It has a lot of numbers in it, and
all of the numbers are needed. And the definition of work is needed
also. And ... and ... well, it just seems hard to me. I thought
doing this problem after "emptying the pool" last time would make an
interesting constrast. And I got to draw the well (lovely colors!).
Drawing a picture or diagram would have been the first thing I did
as I thought about the problem.
Average or mean value
Diary entry in progress! More to come
Mean value of an integral
Suppose the function f is defined on the interval The definiti
Diary entry in progress! More to come
Example
Uhhh ... it's gotta be the mean value of x2 on [0,1].
That mean value is [1/(1-0)]01x2dx=1/3.
QotD
The Question of the D was the
following:
Suppose we have a function whose mean value on the interval [1,4] is
7, and whose mean value on the interval [4,6] is 13. What is the mean
value of this function on the interval [1,6]?
Of course, this is a mean and nasty question. A very naive person
might think that the mean value was the average of the given mean
values, but that would ignore the differing lengths of the
intervals. So what's the solution? Well, I will copy what K. Waters wrote, which is correct, careful,
and complete:
7(3)+13(2) 21+26 47
---------- = ----- = --
5 5 5
14f(x) dx=21
46f(x) dx=26
16f(x) dx=47
1 47
---16f(x) dx=--
6-1 5
Multiply each average value by the length of the interval to find the
individual integrals. Combine the integrals to find the integral on
[1,6]. Divide this by (6-1) to find the average value on [1,6], which
is 47/5.
One fact
The mean value theorem for integrals: if a function f is continuous in the interval [a,b], then
there must be at
least one c in [a,b] with f(c)=[1/(b-a)]abf(x) dx.
This result is occasionally useful.
Counter(?)example
The following neat and simple not continuous function was
suggested: define f on the interval [-1,1] by f(x)=3 for x<0 and
f(x)=-3 for x>=0. Then the mean value of f on [-1,1] is
{1/[1-(-1)]}-11f(x) dx is 0, because the
positive and negative "areas" balance out. But the values of f are only -3 and 3, so there is no c with f(c)=0.
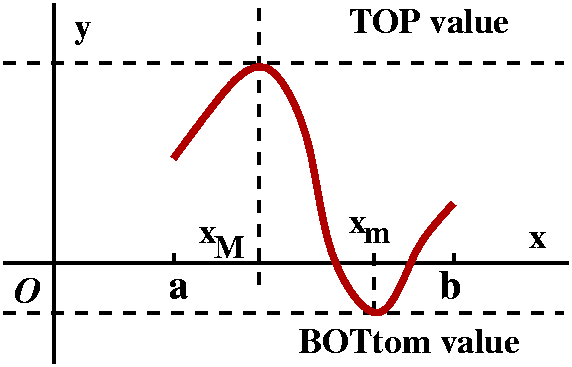Why is the result true?
The real reason to discuss this is so that I can cite several
important results from the first semester of calculus (heh, heh, heh
...).
If a function f is continuous on an interval [a,b], then the
function attains its TOP and BOTtom values. That is, there are values
of x (at least one of each, maybe more) in the interval so that:
f(xM)=TOP and f(xm)=BOT and for all x in [a,b],
f(xM)>=f(x)>=f(xm). This result is
sometimes called the Extreme Value Theorem and is not at all
obvious. For example, the function f(x)=x for x<1 and f(x)=x-1 for
x>=1 does not satisfy the Extreme Value Theorem (neither the
hypotheses nor the conclusion). I'm using xM because maybe
a capital M could mean "maximum", just as a small m could mean
"minimum".
So now I can integrate the inequality
f(xM)>=f(x)>=f(xm) from x=a to x=b. Notice
that the leftmost object is a constant (TOP) and the rightmost object
is also constant (BOT). Therefore I have the following inequality
(because I can integrate constants really well!):
f(xM)(b-a)>=abf(x) dx>=f(xm)(b-a)
Now divide by b-a, so that we look at:
f(xM)>=[1/(b-a)]abf(x) dx>=f(xm)
But, hey, now another of the major theoretical results about
continuous functions can be used: the Intermediate Value
Theorem: f is continuous on [a,b], and therefore every number
between any two values of f (here the two values are f(xM)
and f(xm) must be a value of f on [a,b]. This result is
also not obvious. The "in between" number I want to use here is
[1/(b-a)]abf(x) dx. So there must be at
least one c in [a,b] with f(c)=[1/(b-a)]abf(x) dx. And that's it.
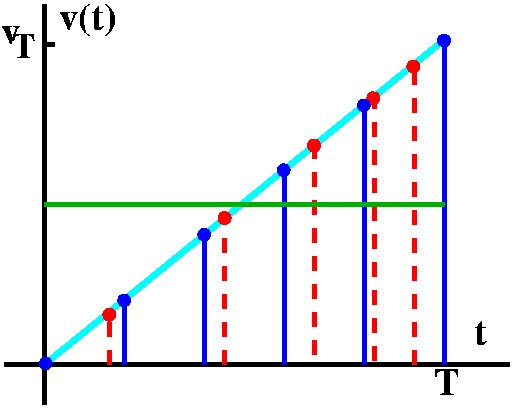
A puzzling textbook problem
Here's problem #20 in seciton 6.5, p.467:
If a freely falling body starts from rest, then its displacement is
given by s= {1/2}gt2. Let the velocity after a time $T$
be vT. Show that if we compute the average of the velocities with
respect to t we get vave={1/2}vT, but if we
compute the average of the velocities with respect to s we get
vave={2/3}vT.
This makes an excellent workshop problem, if one adds the extra
word/sentence, "Explain."
Diary entry in progress! More to come
Guessing an integral
Monte Carlo methods
Diary entry in progress! More to come
Wonderful quote
Anyone who attempts to generate random numbers by deterministic means is, of course, living in a state of sin.
John von Neumann
Diary entry in progress! More to come
An example?
Here is a chunk of Maple code:
> g:=evalf(rand(0..10^10-1)/10^10);
-9
g := 0.1000000000 10
(proc() (proc() option builtin; 391 end proc)(6, 10000000000, 34) end proc)
> seq(g(),j=1..10);
0.3223396161, 0.1434193644, 0.7012963252, 0.6771015081, 0.4121023379, 0.2645048018,
0.9236661736, 0.3118856733, 0.4762458159, 0.4987966881
> 10^(-4)*add(g()^2,j=1..10^4);
bytes used=8000368, alloc=4521156, time=0.25
0.3337136128
The first line creates a procedure (a Maple function) which
returns supposedly random numbers in the unit interval,
[0,1]. The second input line just displays the first 10 numbers
created using the function, and the third line finds the average of
the square of ten thousand of these numbers, a Monte Carlo
approximation to 01x2dx.
Further results
Below is a table of Monte Carlo approximations, using 10n
samples with n going from 1 to 7.
| Number of samples |
10 |
100 |
1,000 |
10,000 |
100,000 |
1,000,000 |
10,000,000 |
Resulting
approximation |
0.2290005751 |
0.3293312957 |
0.3561621917 |
0.3318810478 |
0.3330243211 |
0.3337357300 |
0.3333129117 |
The last two of these computations took a l-o-n-g time on my PC, since
Maple is an interpreted language rather than a compiled one.
Also there are problems with accuracy: for this many computations,
floating point errors are bound to accumulate. And there are problems
with randomness. The Maple "random number generator"
(rather, more precisely, a pseudo-random number generator) has some
serious defects. But, all this said, we've been luck. The accuracy of
the approximation has increased as the number of samples increased.
Diary entry in progress! More to come
Thursday, September 8
First, I indicated I would be following the Math
152 syllabus. I would be assigning occasional sets of challenging
problems, and would add and amplify certain topics. Right now, we will
be working through Chapter 6: today, indeed, finishing consideration
of 6.2 and 6.3, and beginning 6.4. Please look at the list of
suggested problems, and make sure that you can do them all. In this
case, what you probably should do is write solutions to a selection of
the easy and moderate problems, and definitely attempt the more
difficult ones. In standard textbook fashion, the problems generally
begin with rather simple exercises, and, as the problem numbers
increase, they get more difficult. We will have an opportunity to
discuss these problems next Thursday, so please try to work on them
this weekend and early this week.
An example that wasn't
Diary entry in progress! More to come
An example that is, and why
Look at y=x(x-1)4 for x between 0 and 1. This is a little
lump of area. (Look at the picture to the right!) Suppose we want to
"compute" the volume that this region sweeps out as it is revolved
around the y-axis. We can do this (almost) easily dx, using the shell
method. The integral will be the sum of 2Pi x multiplied by
x(x-1)4dx. This mess is a vertical slice, revolved around
the y-axis (radius x). Then add this up from 0 to 1, and the resulting
volume is
012Pi
x(x-1)4dx. A friend of mine whose life is generated
by atomic number 14 (silicon) tells me this is (1/[15]) Pi.
By the way, the Maple command for this is:
>int(2*Pi*x*(x-1)^4,x=0..1);
So what about doing this dy, with discs? Well then, we would need to
"solve" for x as a function of y in the equation y=x(x-1)4.
Here is a short history lesson.
Roots of polynomials
This is much more irritating than one would want. Of course, there are
formulas for the roots of quadratic polynomials (polynomials of degree
2). Now this is true also for cubic
polynomials (degree 3) and even for quartic (degree 4)
polynomials. The formulas are very complicated, and I have never
used them. Ir is possible to prove that in general there are no
formulas in terms of commonly known functions for the roots of a
random quintec (degree 5) polynomial. This is a bit distressing. Here it means we can't write "nice" functions for the left- and right-hand slices of the bump. So we can't "compute" the integral dy.
I guess this is an example of what can happen. I hope this commentary
helps.
The people who first proved statements
about the non-solvability of certain polynomials "in radicals" were
Abel and Galois. So:
the Norwegian mathematician, Abel, died at age 27, mostly of poverty. He was smart and original.
The French mathematician, Galois, died at age 21,
mostly of politics and passion, and more immediately, from an injury suffered during a duel.
Both Abel and Galois realized that most 5th (and higher)
degree equations can't generally be solved with a finite algebraic
formula. This was almost shocking at the time. A consequence is that
curve bounding the region shown above can't be solve for x in terms of
y neatly, using familiar functions. There are efficient techniques for
numerical approximation.
Torus, Torus, Torus
Diary entry in progress! More to come
With washers
Diary entry in progress! More to come
With shells
Diary entry in progress! More to come
With Pappus
Diary entry in progress! More to come
A variety of methods is good ...
Diary entry in progress! More to come
Work!
Diary entry in progress! More to come
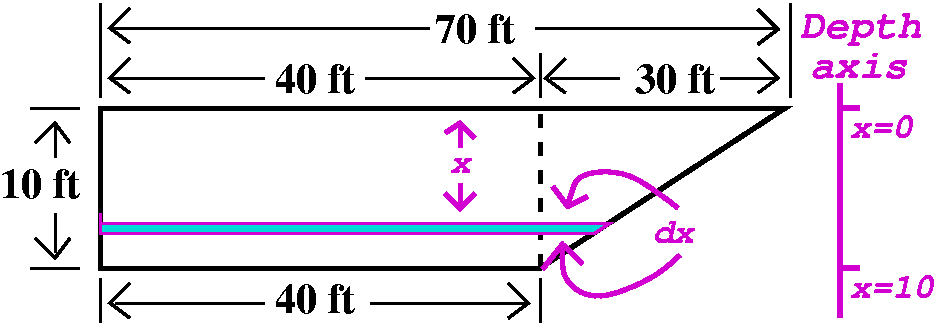
Emptying a swimming pool
|
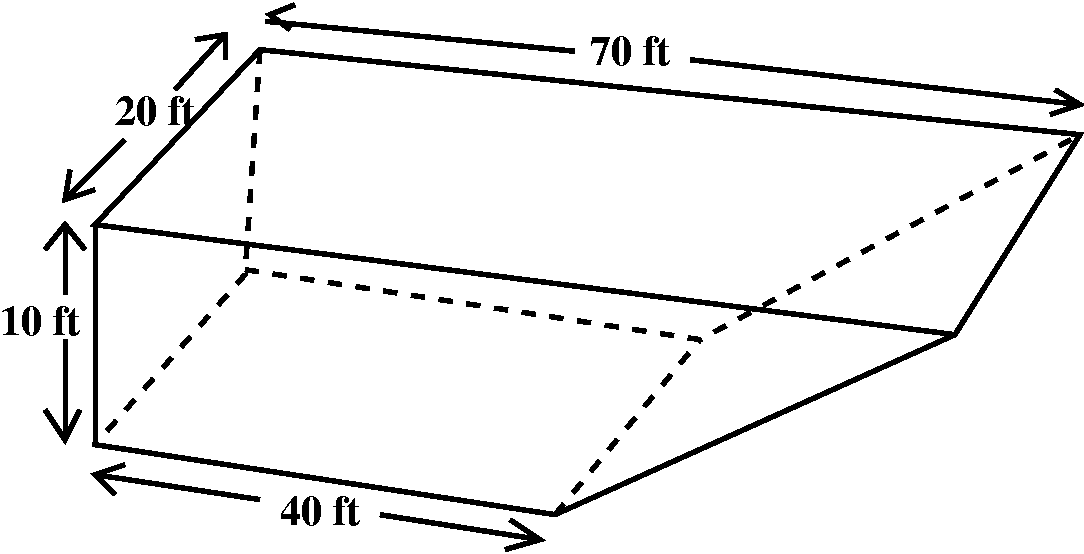
Here is a fact, which is probably true: one cubic foot
(ft3) of water weighs (approximately?) 62.42796 pounds
(lbs). To the right is a picture of "my swimming pool". The sides
(there are, including the top, six of them) are all flat. There's one
tilted side, as shown, and the others meet perpendicularly. I assume
that the pool is totally filled with water, and that I would like to
bring all the water to ground level (at the top) and empty the
pool. Since the pool is the same in the 20 ft direction, I think it
might be sensible to display it (and think about it!) sideways.
| 
|
|
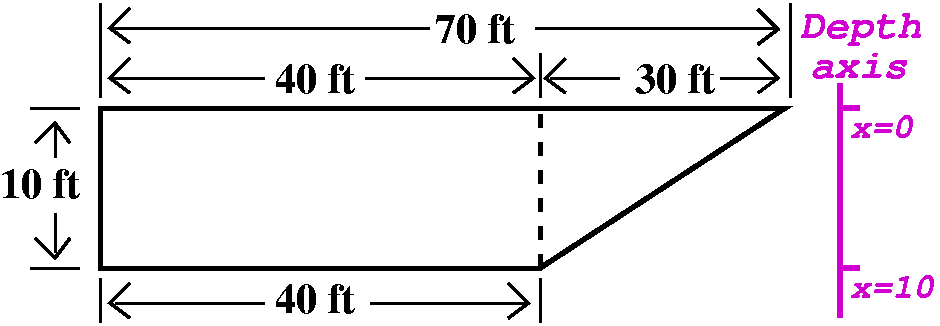
My "coordinate axis" will use the letter x and will measure positively
depth in the pool in ft. Ground level will be x=0 and the bottom of
the pool will be x=10. A piece of water weighing "blah" lbs at level x
in the pool will need blah·x ft-lbs of work to raise it to ground level.
|
|
|
Now take a very thin (dx!) slice (!!) of the pool water at depth
x. Look at the picture. The volume will be 20 ft times dx feet times
the horizontal width of the slice. The weight will be
62.43·20·(horizontal width)·dx. We will need
to lift this to ground level, a distance of x feet. So the work we
will need to do to lift this slice of pool water
is 62.43(20)x(hor. width) dx.
|
|
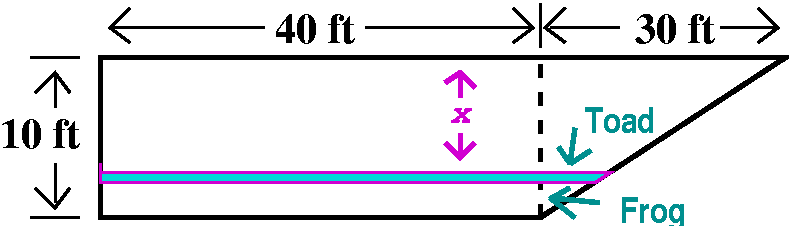
How long is the horizontal width?
Suppose we call Frog the distance 10-x, and Toad, the additional
length needed to make up the horizontal width (so, as shown, 40+Toad
is the horizontal width). Then Frog/Toad=10/30, so that
Toad=(30/10)Frog=3(10-x). I think a clever person (not me!) could have
predicted this. Look: Toad goes from 30 (at x=0) to 0 (at x=0), just
the way it should. So this horizontal width is
40+Toad, which is 40+3(10-x).
|
|
Now finally we can compute the work. It will be the sum of the work of
adding all the slices from x=0 to x=10. This is a definite integral.
It is 010
62.43(20)x[40+3(10-x)] dx. A silicon friend of my tells me that
this is about 3.1215·106 ft-lbs. And I could never
be a physicist or any kind of engineer, really, really, because I have
no feeling if this answer makes sense. Do you?
... psychology? ...
After class, as I was going home, I asked myself why I had
organized the pool computation the way I did. That is, why did I take
a horizontal slice of water? Why not a vertical slice? Why not an
oblique slice, maybe parallel to the "tilted" side? I don't
know. Certainly at the time the computation "made sense" the way I
organized it. I want to pull up lots of tiny chunks of water. The
major variation seemed (still seems!) the depth, to me. So I organized
the chunks of water to exploit that. Sigh. Does this help? It doesn't
help me. I still would like to understand how I think about these prob
lems.
HOMEWORK
Please look over the problems assigned for sections 6.2, 6.3, and 6.4
of the textbook. Write out solutions for an appropriate number of
them. Make sure you can do all of them.
Wednesday, September 7
I resolved to give calmer, more boring lectures. The latter would be
novel, and so here is a Math 152 lecture.
In the beginning of calculus, there seem to be these two basic
concepts, the derivative and the integral.
The derivative is flashy, and easy to explain.
The definite integral is more subtle and more difficult, but it is
where the big bucks (?) occur. Rather, to be more academic, it is
where the real applications and uses of calculus in engineering and
the physical sciences (as well as biology and economics) occur. The following concepts can be studied using definite integrals:
- Area
- Volume
- Work
- Arc length
- Surface Area
- Pressure
- And a plethora of others ...
The basic idea is to
- Slice
- Approximate
- Add up
- Take a limit
We end up with a definite integral. I'll present this with a series of
examples. I went over this material rather quickly, because I believed
that most students had seen it before.
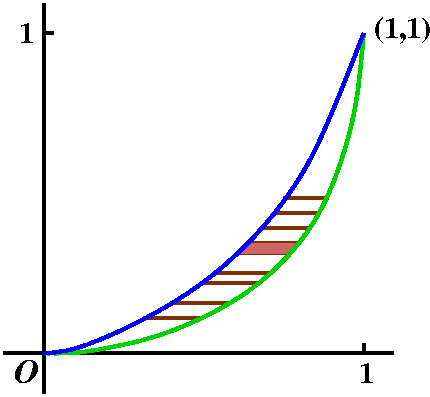
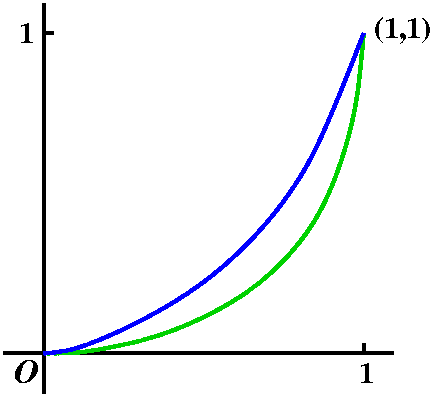Example 1 Consider y=x2 and y=x3 on the
interval [0,1]. These two curves form the boundary of a curvy
region. A drawing of this region is to the right.
Note As I mentioned in class, most examples I'll do with you
will be rather simple. I make enough mistakes with even simple
examples! If I find something interesting, I will probably give it to
you as a workshop problem! But even in the collection of simple
examples, this one (which I worked with for almost an hour!) is
perhaps a bit infelicitous (dictionary says:
"1. Inappropriate; ill-chosen 2. Not happy; unfortunate.") This is
because there are too many coincidences. The "corners" of the region
have coordinates which are equal: (0,0) and (1,1). This might lead to
confusion. I am sorry. Back to the example.
What is the area of the region enclosed?
The process
| First I'll slice up the area in the region with many,
many vertical lines. I'll drawn only a few (fear of carpal tunnel
syndrome!) but, please, you should imagine 1010 of them,
all arranged neatly, and very close together. I'll concentrate on just
one of these slices. I'll magnify it and analyze it. |
 |
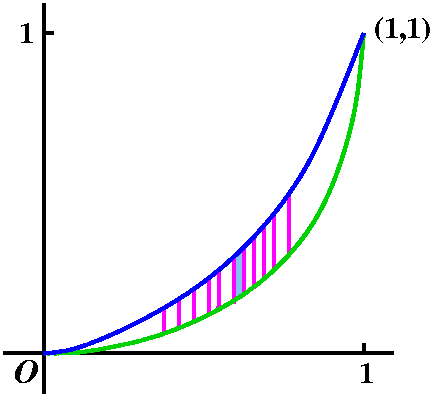| This is supposed to be a really narrow slice. It is so narrow that I can think of it as quite close in shape to a rectangle. The thickness is deltax, and the height is the difference in heights of the bottom curve, called Bottom(x), and the top curve, Top(x). So if this is nearly a rectangle, then the area is nearly the area of a rectangle whose dimensions are deltax and Top(x)-Bottom(x). The area of this slice is approximately
Top(x)-Bottom(x) deltax |
 |
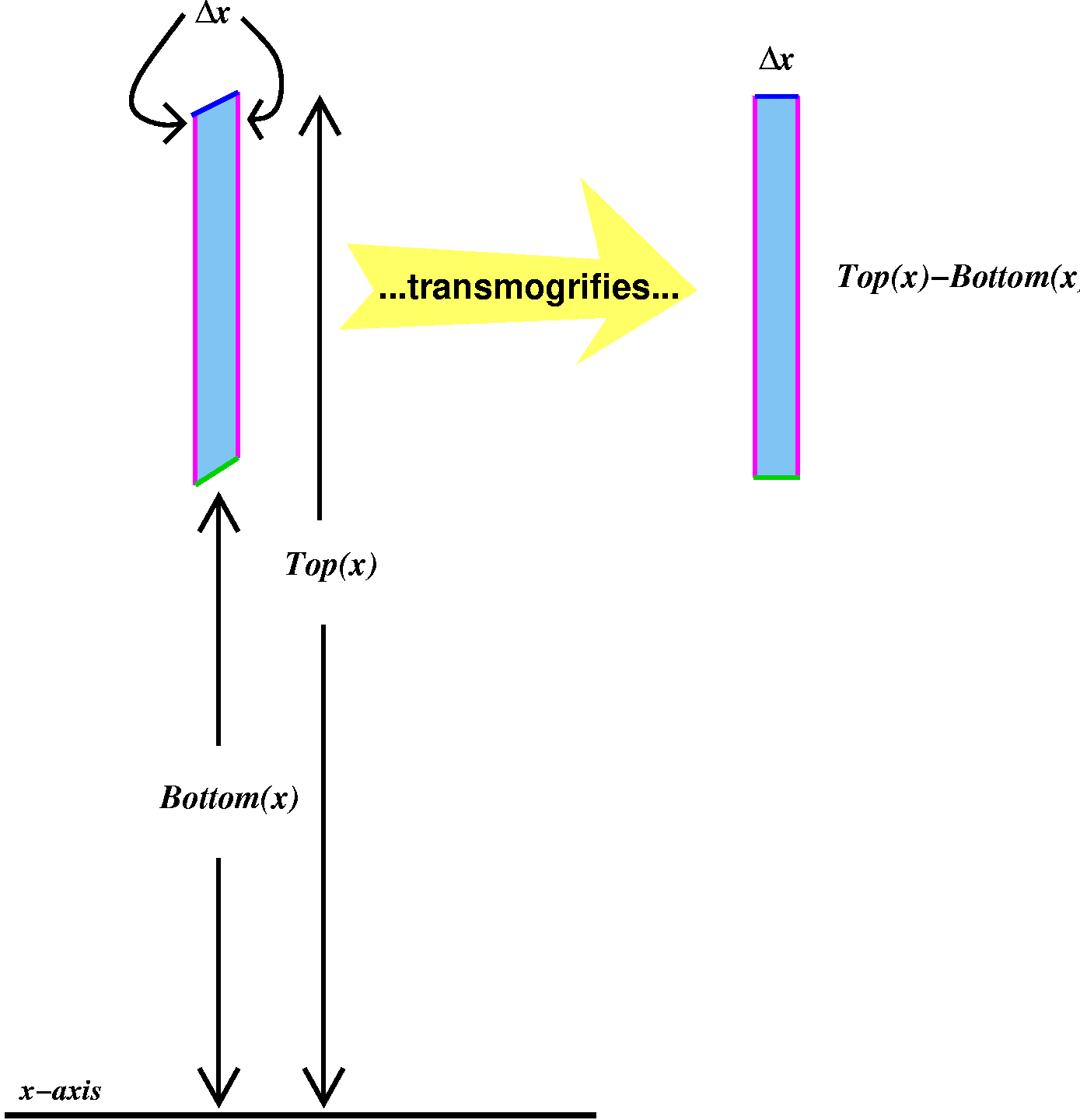Now we add up the approximations, from Left to Right, and take a limit of these sums. The result is a definite integral:
LeftRightTop(x)-Bottom(x) dx
In this specific case we have Top(x)=x2 and Bottom(x)=x3 and Left=0 and Right=1, and so we need to compute
01x2-x3 dx
We know antiderivatives of the functions involved, so we may use
FTC and get (1/3)x3-(1/4)x4|x=0x=1=(1/3)-(1/4).
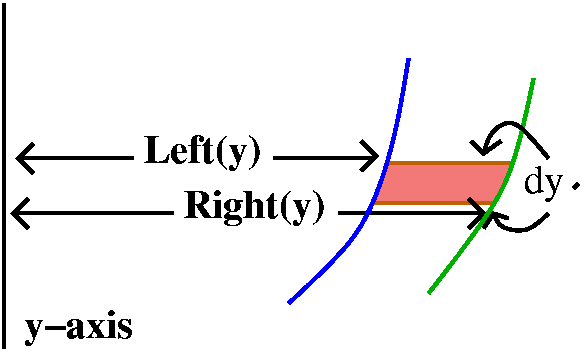
Example 1´ We could also slice horizontally. The
illustration to the right is an attempt to show the very thin slices.
We should really go through a description of this process similar to
what I wrote above, but the pictures actually take some time to
"draw". The result is again a definite integral, but here we are
adding up deltay (sigh, just dy) slices. And the horizontal
length of the rectangles will be a difference of a left length and the
right length, both depending on the value of y. We'll add these slices
up, from bottom to top:
BottomTopRight(y)-Left(y) dy
Here the boundary curves are given by y=x2 and
y=x3, and, in this specific case, it isn't too hard to find
the left curve, x=y1/2, and the right curve,
x=y1/3. Due to the dreadful coincidence mentioned earlier, top=1 and bottom=0. The area of the region will therefore be
01y1/3-y1/2 dy
and (my examples have easy functions!) we can use the FTC directly to get
(3/4)y4/3-(2/3)y3/2|y=0y=1=(3/4)-(2/3).
We have verified the amazing result obtained from equating the two
computations:
(3/4)-(2/3)=(1/3)-(1/4)
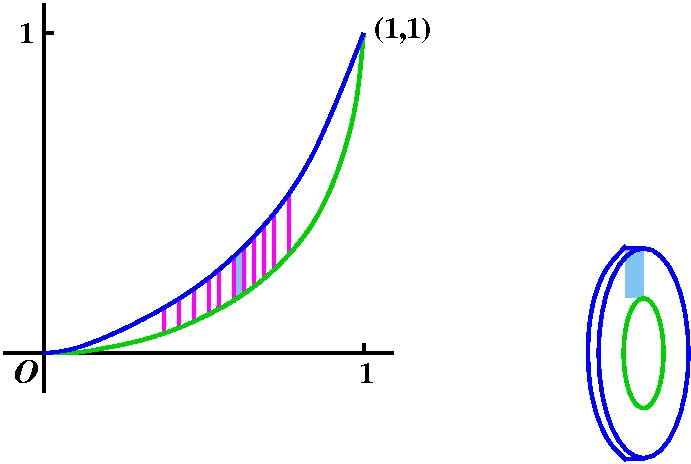Example 2 Revolve the region discussed around the x-axis and
find the volume. Here we use the method of washers (no, there doesn't
seem to be a method of dryers). We take one of the vertical slices
(with dx thickness) and rotate it around the x-axis. Here the
"transmogrification" or approximation is to imagine that the result is
a solid washer with the dx side flat, perpendicular to the vertical
side. The side area the difference in area of two circles. There is an
outer circle, with radius Outside(x), and an inner circle, with radius
Inside(x). The thickness is dx, and I think the chunk of volume, dV, for this is Pi(Outside(x)2-Inside(x)2) dx. The total volume is gotten by adding up all these dV's to get V (and taking a limit, of course, as the slices get very thin!). The result is a definite integral:
LeftRightPi(Outside(x)2-Inside(x)2) dx.
In this specific case, Left=0 and Right=1, of course. The Outside(x)
is what I previously called Top(x) and is x2. The Inside(x)
is the old Bottom(x) and is x3. So we need to compute
01Pi(x2)2-(x3)2) dx. This is
Pi01
x4-x6 dx=
(1/5)x5-(1/7)x7|x=0x=1=Pi[(1/5)-(1/7)].
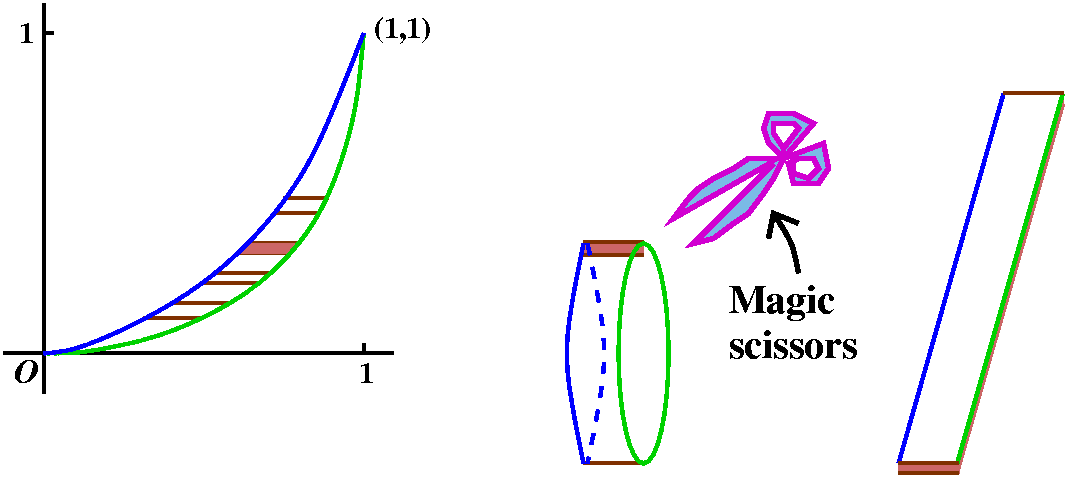Example 2´ We can also try to integrate dy to get the
volume when the region is revolved around the x-axis. This didn't seem
known to many people so certainly should have gone slower! (No one
really objected, but still ...) We take one of the dy strips, and
revolve it around the x-axis. Here everything should be written in
terms of y. The radius of the revolving circle is y (the strip is y
"up" from the x-axis) and the width of the strip is
Right(y)-Left(y). This idea is called the thin shell method. The next
step (at least in my mind!) is to think of magic scissors which cut
the thin shell or thin strip and then we flatten it out. The result is
pretty close to a rectangular solid (well, almost, maybe, sort of
...). The dimensions of the solid are dy and Right(y)-Left(y) and
2Pi y (the last is the circumference of a circle of radius y).
This is dV, a piece of the volume. Now we add these up, from bottom
to top to get the total volume, V. Therefore this formulation of the
volume of the solid of revolution is just
BottomTop2Pi y(Right(y)-Left(y)) dy.
Here we have Top: y=1 and Bottom: y=0, and Right(y)=y1/3
and Left(y)=y1/2. Therefore the volume should be
y=0y=12Pi y(y1/3-y1/2) dy. Again, because this is an example selected by the instructor, we can apply the FTC to it and evaluate:
First, the integral itself is
2Piy=0y=1(y4/3-y3/2 dy and this is
2Pi((3/7)y7/3-(2/5)y5/2)|y=0y=1=2Pi[(3/7)-(2/5)].
Hot news obtained from equating the two computations:
2[(3/7)-(2/5)]=(1/5)-(1/7)
I then asked students in the class to compute the volume when the
region is revolved around the y-axis, using both methods. We needed
some help, especially with the thin shell part (dx in this case).
Around the y-axis
dy: This uses washers. The inner radius is Left(y) and the outer
radius is Right(y), so the cross-sectional area of the washer is the
difference
in the area of two circles:
Pi[Right(y)2-Left(y)2]. The thickness of the
washer is dy. We add them up from bottom to top:
BottomTopPi[Right(y)2-Left(y)2] dy.
Here Bottom is 0 and Top is 1, while Left(y) is y1/2 and
Right(y) is y1/3. The answer, after applying FTC, is
Pi[(3/5)-(1/2)] (please check this!).
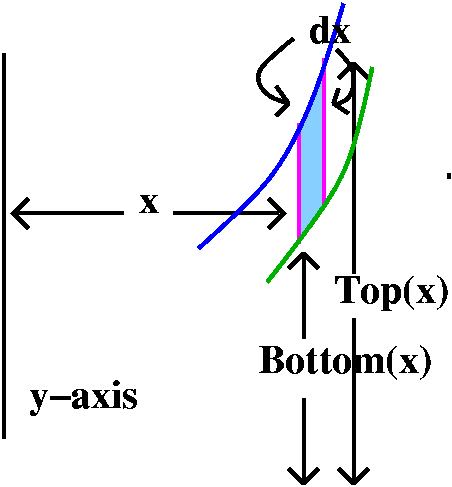Around the x-axis
dx: Thin shells. The height of the thin shell is Top(x)-Bottom(x), and
its thickness is dx. The thin rectangle is revolved around the
y-axis. Perhaps confusingly, the distance of a point (x,y) to the
y-axis is x, so the radius is x, and the thin rectangle travels a
distance of 2Pi x. Therefore, we add up and take limits, and the
result is:
LeftRight2Pi x[Top(x)-Bottom(x)] dy.
Since Left=0 and Right=1 and Top(x)=x2 and
Bottom(x)=x3, we need to compute
012Pi[x3-x4] dx,
and this is 2Pi[(1/4)-(1/5)].
Again, a new discovery, by comparing the results of the two
methods:
2[(1/4)-(1/5)]=(3/5)-(1/2)
I then asserted incorrectly that I could give an example where shells
could be computed but washers would be difficult. My example was
y=1/(1+x2) revolved around the y-axis, with x in the
interval from 0 to 1.
Well, I tried it dx: the thin shells give the following:
Here Left=0, Right=1, Top(x)=1/(1+x2) and Bottom(x)=0, and
radius=x as before. Then the integral becomes
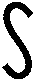012Pi x/(1+x2) dx.
We can use FTC on this with the substitution u=1+x2 and
du=2x dx and (1/2)du=x dx so that we need to compute
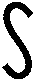(1/2)du/u, which is ln(u)+C. Going back to x-land, we have
(1/2)ln(1+x2)|x=0x=1, and this is
(1/2)ln(2).
But this can also be done dy, as I will show in the next class.
Pre-pre-example 14 I "computed"
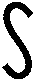-11sqrt(1-x2) dx by
realizing it was the area of half of the unit circle, and therefore
was Pi/2.
Pre-example 14 I revolved the semicircle of radius 1 (as given
above) around the x-axis. The volume of the resulting solid is given
by
Pi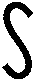-11(sqrt(1-x2)1/2dx,
and this is
Pi-11(1-x2)&nbps;dx (the square
of the square root of a non-negative number is that number). Now we
can use FTC and obtain Pi(x-(1/3)x3)|x=-1x=1 and this is
(4/3)Pi. In fact, the volume of a sphere of radius r is
(4/3)Pi r3.
All of this will be used in our next lovely computation, the volume of
a torus, shown to the right.
The torus is the official mathematical name for the volume of a
doughnut. Here we revolve a circle of radius r around a central
axis. The distance from the center of the circle to the axis is R, and
R>r. I'll finish this next time.
Thursday, September 1
Numbers
I described the number line as a geometric representation of
numbers, and then chose to associate decimal expansions with real
numbers. A decimal expansion had a finite number of digits to the
left of the decimal point, and an infinite string of digits to the
right. Conventionally, if the string of digits concludes with a string
of 0's, that string can be omitted. Also, if I had been precise (!) I
would have said that a decimal is prefixed by a sign, + or -. Actually
such a string really is just an address (?) to a point on the line,
and two addresses can lead to the same point. The simplest example is
that .9[repeating] addresses the same point as 1.0[repeating].
What kinds of numbers are there? There are integers, both positive and
negative. And then quotients of integers, ratiional numbers. It is
remarkable that real numbers which are rational numbers can be
characterized by their decimal expansions. Although this is an
elementary (!) I discussed it in some detail. First, any rational
number has a decimal expansion which eventually repeats. Why is this?
When we look at p/q and try to create the decimal expansion, there's
repreated long division, each time with a remainer integer less than q
(I am assuming that the + or - sign is handled outside of the division
process, so that p and q are positive integers). The remainder at each
stage is therefore an integer from the set {0,1,2,...,q-1}. The
division process proceeds through this finite set in a set way: if one
has a remainder of r, then the process always will give a remainder of
s (maybe the same as r!). Think of this as an arrow from r to s. Since
the set {0,1,2,...,q-1} is finite, I hope it is not hard to convince
yourself that eventually the process terminates in what's called a
cycle, a collection of remainders and arrows between them which are
circular. That provides the repetition observed in the decimal
expansion.
As I mentioned in class, the long-division algorithm is really quite
complicated. A complete analysis occupies pages 235 to 240 in Knuth's
The Art of Computer Programming: Volume 2, Seminumerical
Algorithms. The other algorithms of arithmetic (addition,
subtraction, and multiplicationn) just take up pages 229 to 234.
We also discussed how to go from a repeating decimal to a
representation as a quotient of integers. I showed this by taking the
sum of the geometric series which the decimal string represents.
There are numbers which are not rational. A number is
irrational if it is not equal to p/q, for any choice of
integers p and q. I then gave a non-routine proof that sqrt(2) is
irrational. The proof is very short, but has logical intricacies.
Here are two links to proofs that the square root of 2 is irrational:
http://www.cut-the-knot.org/proofs/sq_root.shtml
and
http://www.mathacademy.com/pr/prime/articles/irr2/index.asp.
Irrational numbers themselves can be subject to more analysis. (Name
everything! -- Isn't that a biblical injunction?) A number x is
algebraic if it is the root of a polynomial with integer
coefficients. Since x2-2=0 has sqrt(2) as a root, sqrt(2)
is algebra. So is a number like 171/3. The sum and product
of algebraic numbers is algebraic. This is not clear. I gave an
example, with sqrt(5)+sqrt(7). With the help of students, after
setting x=sqrt(5)+sqrt(7), we first squared to get
x2=5+2sqrt(5)sqrt(7)+7. Then (following suggestions from
students) x2-12=2sqrt(5)sqrt(7). And square again, to get
(x2-12)2=4·5·7. You can finish up,
but the result is actually a fourth degree polynomial which has
sqrt(5)+sqrt(7) as a root.
Well, now throw the rationals and the algebraic numbers at the real
line. Is that everything? What's not at all obvious to me is that
the answer is No!. And not only is the answer "No" but in fact,
in many ways, almost no numbers are algebraic or rational. The
left-out numbers are called transcendental.
First, can we exhibit at least one specific number which is
transcendental? Yes, we can. This was first done by Liouville a bit
more than a century ago. The only "theorem" needed is the Mean Value
Theorem. I wanted to present this result to you, but decided that I am
really supposed to teach calculus. Sigh. Here's a link to a discussion of Liouville numbers:
http://en.wikipedia.org/wiki/Liouville_number Take a look, if you
are interested. The numbers Pi and e which occur everywhere in
mathematics are transcendental. Verifying that they are transcendental
is difficult. Just seeing that they are irrational takes some effort.
Here is an exposition of Ivan Niven's brief and clever proof that Pi
is irrational:
http://www.lrz-muenchen.de/~hr/numb/pi-irr.html
and I don't
know how such a proof is invented. Here is a
discussion of the decimal representation of Pi, and here
is a discussion of the techniques involved in high-precision
computation of Pi. More than 1012 digits have been
computed. We will discuss some of these techniques later in the course.
A different, non-constructive approach, proves the existence of
transcendental numbers and also the rather shocking fact (to me, at
least!) that most numbers are transcendental. So if you take a
random string of digits, then that string is almost surely going to be
transcendental. The algebraic numbers are countable and the
collection of all real numbers is uncountable. These are
technical words and the initial discoveries were made by Cantor, again
a bit more than a century ago. There are many references to this
material on the web, or you can talk to me.
I then moved on to things more in the framework of a calculus
course. Specifically I discussed the Mean Value Theorem and how it can
be used to give a version of the Fundamental Theorem of Calculus, with
some error estimate comparing Riemann sums to the ideal, limiting
answer. I may have lost most of the students during this discussion. Here
are some
notes on the transition from MVT (Mean Value Theorem) to FTC
(Fundamental Theorem of Calculus) that may help.
HOMEWORK
Please do two of
the workshop problems (there's a hint for problem 3), learn Maple
by working with another student in the
course (please print out the second worksheet from here), and begin reading chapter 6 of the
textbook.
Maintained by
greenfie@math.rutgers.edu and last modified 9/11/2005.
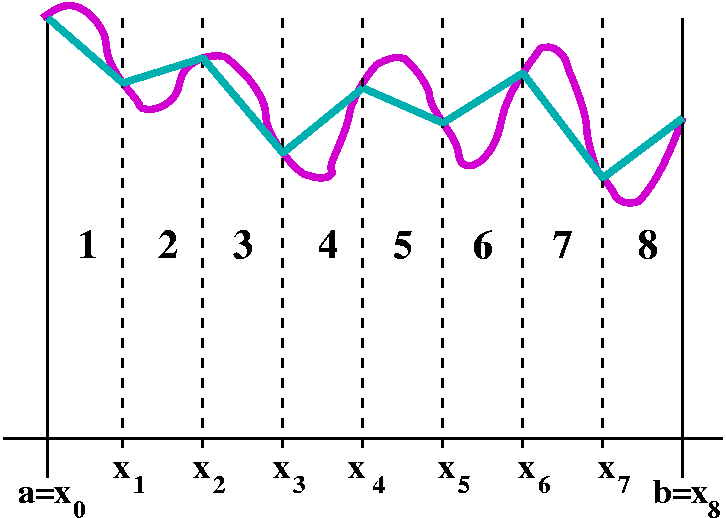So what's the formula?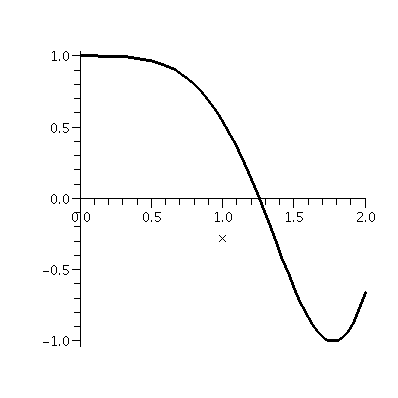
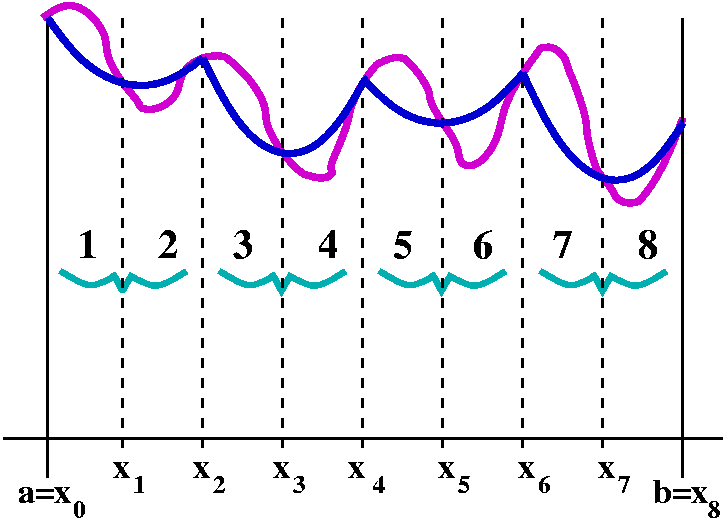The picture to the right is my attempt to show such
interpolation. Again we can ask
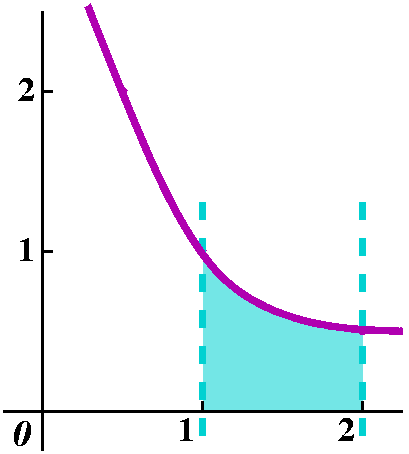What is ln(2)?
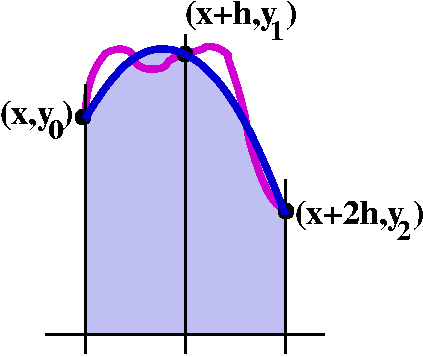
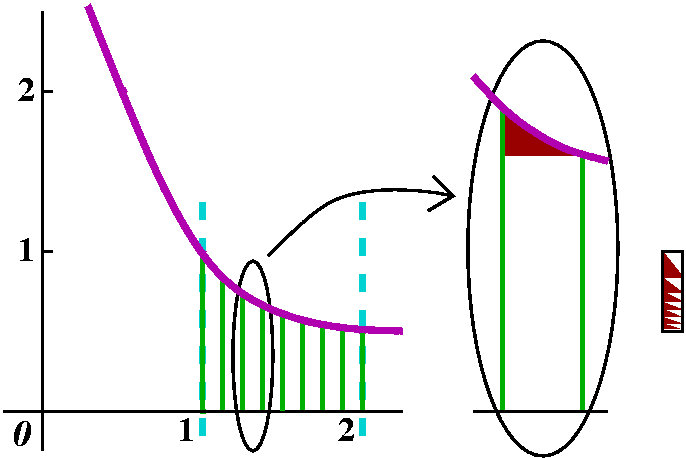Riemann sums and their error
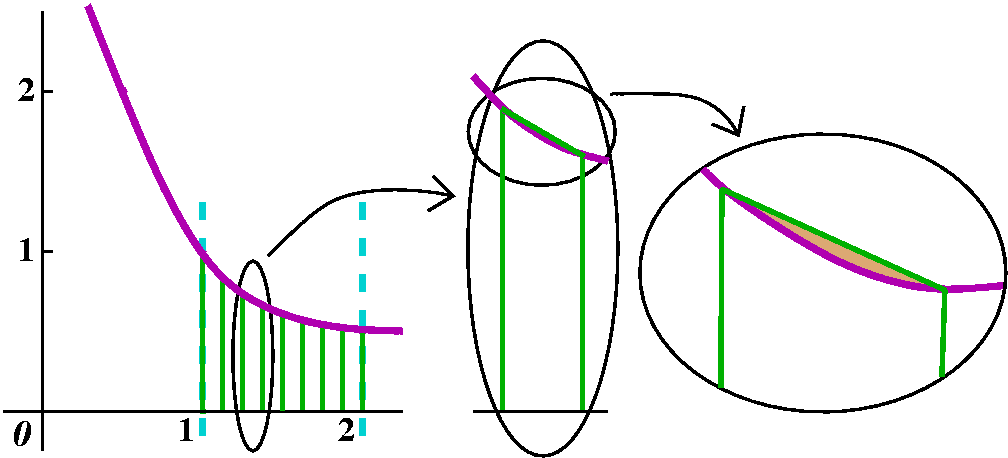Better integral approximations I: trapezoids
