Mathematical experiments
Almost every aspect of the practice of mathematics, both pure and
applied, has been improved and amplified in recent decades by the
widespread availability of "computer algebra systems", CAS. This
technology is much more than just algebra, of course. It is systematic
and powerful programs that permit algebraic manipulation
- What is the coefficient of
x6y4z2 in
(x+y+z)12?
13860
and numerical approximation
- What is an approximation to the only root of
3x+cos(2x2)=0?
-.3258460227
and graphing
-
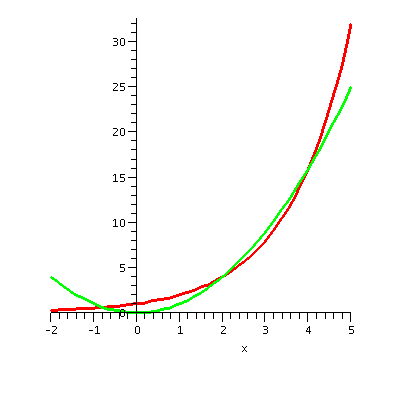
How often do the curves y=x2 and y=2x intersect?
The freedom to work with "exact" symbolic computation, with numerical
approximation (with specified accuracy) and with visual display of data
(human beings learn much more from pictures than from lists of
numbers!) is very useful.
Almost all of my teaching and research is
now improved by access to powerful programs which allow me to
experiment. I can get examples which are useful for
instruction. I've also used these programs to try to understand
complicated phenomena which I could not easily explain (further
explanation is available!).
Computer help
Many students have graphing calculators. These are useful, but are
limited by speed and memory size. Simple
errors may occur. There are large computer programs with powerful
numerical, symbolic, and graphical capabilities. These still may have
the potential for errors, but much effort has gone into their
programming. The most widely distributed programs are
Maple, Mathematica, and
Derive. In this course Maple will be favored,
since almost every large computer system at Rutgers has Maple
installed. These programs are not infallible but they can be
very helpful. Other programs available with special capabilities. For
example, Matlab, a program originally directed at problems of
linear algebra, is installed on systems of the Engineering School.
Also, I usually use Maple because I have a copy at
home. Students should learn how to use such programs.
Maple in Math 192
I think it would be useful to become familiar with Maple. It
will help in Math 192 (you can check your homework!). Maple is
not required, but ... it likely will
also be useful in other science and engineering courses. Even if you
later work with, say, Matlab, I think that familiarity with a
variety of programs is an asset.
The Maple exercises
If you work through these pages, I think you will have done enough
with Maple to at least understand when it is likely to be
helpful.
How to get those answers
The answers to the questions above were obtained with the following
Maple instructions. Please: this is not an effort to
impress you, but rather to show you how easy is is to get the answers.
- coeff(coeff(coeff((x+y+z)^12,x^6),y^4),z^2);
The command coeff(P,monomial) finds the coefficient of the
monomial in the expression P. Layering three repetitions of
coeff finds the desired coefficient.
- fsolve(3*x+cos(2*x^2)=0,x);
fsolve is a general "floating point" approximate equation
solver. Care must be used if there's more than one root. There are
also symbolic solvers, useful when there is a nice formula for the
solution.
- plot({2^x,x^2},x=-2..5,thickness=2)
The plotting programs are wonderful. In several variable calculus, the
three-dimensional plots will be very helpful.
Programming in Maple
Maple is also a programming environment. Maple
programs are known as procedures. The language has many
statements supporting program flow such as if ...then and
while and do etc., and also has a variety of data
types. There's no time in this course to teach this material, but
students should know that programmng is possible.
I have several books on Maple programming. My current
favorite is Maple A comprehensive introduction by Roy
Nicolaides and Noel Walkington, Cambridge University Press ($65, 484
pages, available for less in places on the web). There are also many
web pages which discuss programming in Maple. For example,
here's one
online tutorial. Warning: such pages are only for the enthusiast!
|