 What kinds of functions theory interlude #1
What kinds of functions theory interlude #1
The classical Laplace transform works with functions that have growth
no bigger than exponential growth. This means that a function f(t)
must satisfy some sort of estimate of the following type:
There are positive constants A and B so that |y(t)|<AeBt
for t>C, where C is some additional positive constant.
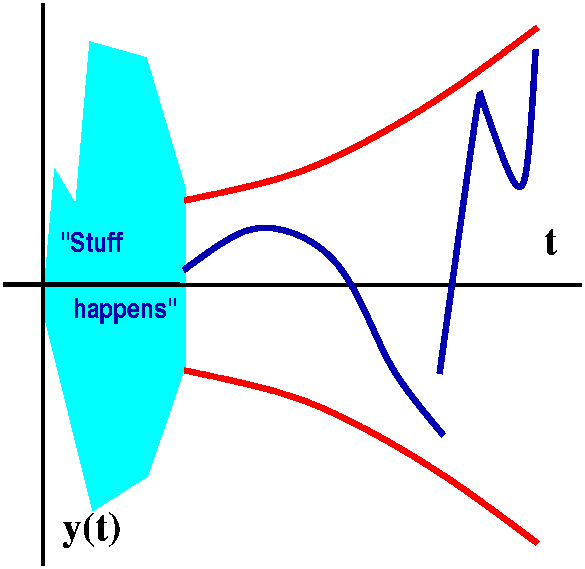
There's sort of a picture of the situation to the right. The "Stuff
happens" doesn't sort of matter. What matters is that for t large
enough (t>C), y(t) is "trapped" between AeBt and
-AeBt. The two curves occur because there are absolute
value signs around the y(t). If y(t) is trapped that way, then in the
integral that defines the Laplace transform, 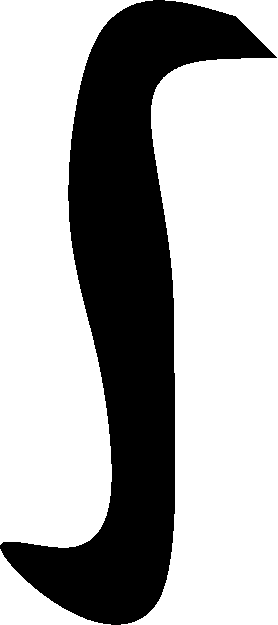 0infinitye-sty(t) dt,
when s>B, the integral is less than e(B-s)t in absolute
value, and since this is exponential decrease the integral must
converge.
0infinitye-sty(t) dt,
when s>B, the integral is less than e(B-s)t in absolute
value, and since this is exponential decrease the integral must
converge.
As I remarked, polynomials have exponential growth. Maybe that is
"clear" for t2, but not for, say, t216,000. In
fact, I bet that for t large enough positive, |t216,000| is
less than even .003e.000007t. We discussed this, and
decided that this could be verified with L'Hopital's rule. Look at the
quotient
t216,000/( .003e.000007t)
as
t-->infinity. Both the top and the bottom go to infinity. Use L'H lots
of times. If you use it 216,000 times, the result is
(Some huge constant)/[(Another stupid constant)e.000007t]
because the polynomial's powers go down to 0, and the bottom is still an exponential with positive exponent, and just "spits out" positive multiplicative constants upon differentiation. But the limit now, after 216,000 uses of L'H is 0, because the fraction is really just
CONSTANT/(exponential growth)
Therefore for large enough t, this is less than, say, 1.
Even something like t216,000e30003t has
exponential growth. It is bounded eventually by some multiple of
e30004t or even just e(30003.001)t.
Here is a candidate suggested by a student (who?) for a function which
does not have exponential growth:
tt=eln(t)·t.
Indeed, I agree: ln(t) can't be bounded by ANY POSITIVE CONSTANT,
so there's no B that will work.
What we're investigating here in Math 421 is the basic, classical
Laplace transform. It has been fiddled with in many ways. So actually
there are ways that functions with faster growth can be used. And
there are ways that, say, difference equations (a discrete analog of
differential equations) can be solved with similar tools. But let's
learn the classical case well enough so that you will be able to use
and understand the variant methods.
Inverse Laplace transforms theory interlude #2
Well, here in the board (I said, motioning to the side blackboard) is
a table of Laplace transforms. It turns out that it is also, more or
less, sort of, almost, also a table of inverse Laplace
transforms. Here in a wonderfully logical 640 subject course what
do the words "more or less, sort of, almost ..." mean?
 Well, I considered the following example. Certainly our table tells us
that the Laplace transform of t2 is 2/s2. Let's
call t2 by the name, h(t), and let's further define the
function g(t) by the stipulations that g(t) is -1 when t=3 and g(t) is
40 when t=6 and otherwise g(t)=t2. I know the darn picture
is not drawn to scale, but the poetic truth is there. So, anyway,
certainly h and g are distinct functions. But they have the same Laplace transform. Look,
the formula for the Laplace transform of y(t) is
Well, I considered the following example. Certainly our table tells us
that the Laplace transform of t2 is 2/s2. Let's
call t2 by the name, h(t), and let's further define the
function g(t) by the stipulations that g(t) is -1 when t=3 and g(t) is
40 when t=6 and otherwise g(t)=t2. I know the darn picture
is not drawn to scale, but the poetic truth is there. So, anyway,
certainly h and g are distinct functions. But they have the same Laplace transform. Look,
the formula for the Laplace transform of y(t) is 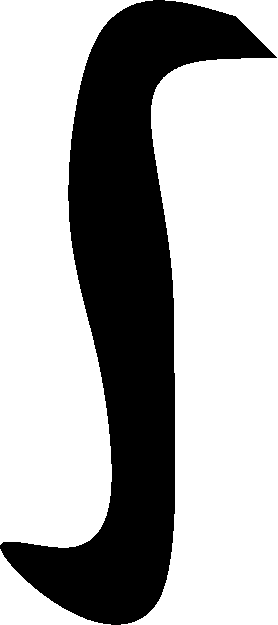 0infinitye-sty(t) dt. And
the integral doesn't even notice if you change the values of
the integrand (the function that's being integrated) at a couple of
points. (Look at the darn definition of the integral, if you don't
believe it, and take a Riemann sum with very, very narrow width around
the jump places.) So there can be two functions whose Laplace
transforms are exactly the same. Well, but for all practical
purposes if you are in a physical situation, you won't notice that
change at a point. And it turns out, more or less, that this is the
only kind of problem you'll face.
0infinitye-sty(t) dt. And
the integral doesn't even notice if you change the values of
the integrand (the function that's being integrated) at a couple of
points. (Look at the darn definition of the integral, if you don't
believe it, and take a Riemann sum with very, very narrow width around
the jump places.) So there can be two functions whose Laplace
transforms are exactly the same. Well, but for all practical
purposes if you are in a physical situation, you won't notice that
change at a point. And it turns out, more or less, that this is the
only kind of problem you'll face.
Lerch's Theorem (I'm sorry but I like the name.)
If two functions have the same Laplace transform, then they differ only on a collection of values that the integral doesn't notice.
Yeah, this can be more precise, but that's all I want to say. But, you
may ask, what if we are supposed to find an inverse Laplace transform?
For example, the inverse Laplace transform of 2/s3? Well,
yeah again, you do have to choose between h(t) and g(t). What everyone
chooses is a function that is as continuous as possible. So if the
left and right-hand limits agree at a point, that's the value the
inverse Laplace transform should have at the point. And the algorithms
in symbolic algebra packages are designed to make such a choice. And
also, there is an inverse Laplace transform with an integral formula,
called Bromwich's integral, which "automatically" gives you the
most continuous (there's a phrase!) inverse Laplace transform. All
these things can be implemented symbolically and numerically.
You can find lots
of references to this stuff on the web.
Our major present goal is to expand our table of Laplace transforms
(and, therefore, inverse Laplace transforms). The two shifting or
translation theorems are very important in accomplishing this.
The first {shifting|translation} theorem
If F(s) is the Laplace transform of f(t), then the Laplace transform
of eatf(t) is F(s-a).
This is correct because the Laplace transform of eatf(t) is
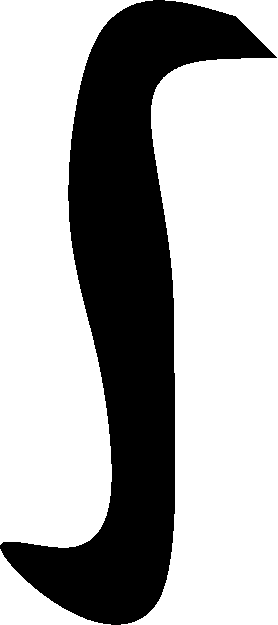 0infinitye-steatf(t) dt
which is the same as
0infinitye-steatf(t) dt
which is the same as
 0infinitye-st+atf(t) dt
which is the same as
0infinitye-st+atf(t) dt
which is the same as  0infinitye-(s-a)tf(t) dt
and that is exactly the Laplace transform of f(t) evaluated at
s-a, or F(s-a).
0infinitye-(s-a)tf(t) dt
and that is exactly the Laplace transform of f(t) evaluated at
s-a, or F(s-a).
Easy examples
Uhhh, can we find the Laplace transform of e5tsin(3t)? The
table stated that the transform of sin(3t) is 3/(s2+9). But
(take a=5) the Laplace transform of e5tsin(3t) must then be 3/((s-5)2+9).
More ofter we'll need to apply this result backwards. Can we find a
function whose Laplace transform is 5/(s+7)14? We look at
the table and see that this seemed to be Constant/s14
shifted. So this should be related to the Laplace transform of
t13. We needed to fix up the multiplicative constant so
that we would get 5. And therefore we multiply t13 by 5 and
divided it by 13! so that the Laplace transform of
(5/(13!)t13 is 5/s14. Now we need to shift by
-7, and conclude that the Laplace transform of
e-7t(5/(13!)t13 is 5/(s+7)14.
Isn't this cool!
The Heaviside function
I defined the Heaviside or unit step function, called
U(t) in your text (actually with a calligraphic U). Oliver
Heaviside was a brilliant English engineer whose life was,
overall, rather sad. U is the function which is 0 for t<0
and is 1 for t>=0. There's a jump of 1 at 0, and otherwise the
function's graph consists of two half lines.
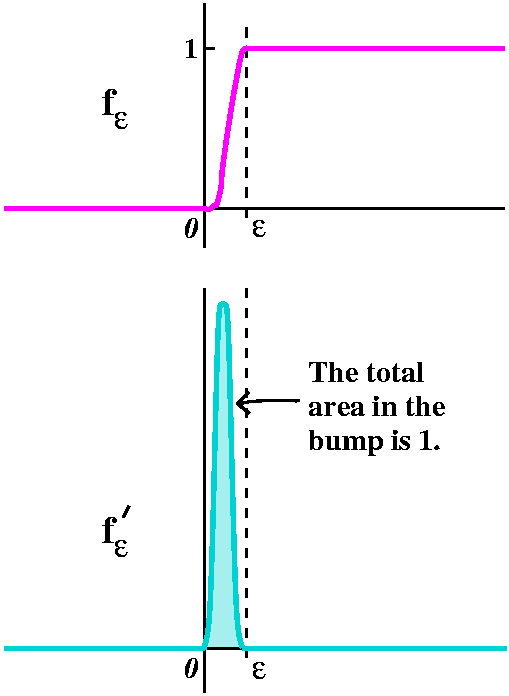 Another thought about delta
Another thought about delta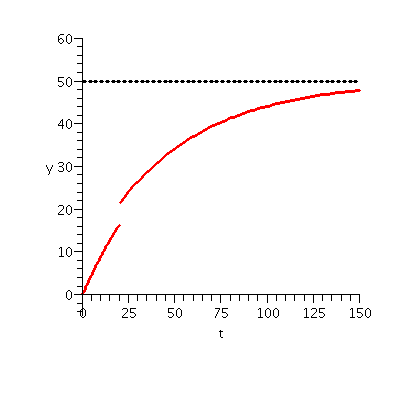
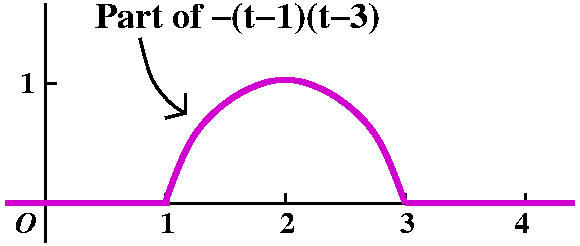 Ms. Jones kindly put her solution on
the board. The given information was a mixture of geometric and
algebraic. The graph of a function was drawn. It was 0 for t<1 and
t>3, and was -(t-1)(t-3) for t between 1 and 3. I asked for the
Laplace transform of this function. I emphasized that it would
probably be easier to begin by describing the function using the
Heaviside function.
Ms. Jones kindly put her solution on
the board. The given information was a mixture of geometric and
algebraic. The graph of a function was drawn. It was 0 for t<1 and
t>3, and was -(t-1)(t-3) for t between 1 and 3. I asked for the
Laplace transform of this function. I emphasized that it would
probably be easier to begin by describing the function using the
Heaviside function.
 Here is an intricate example copied from Counterexamples in
Analysis by Gelbaum and Olmstead, showing that "differentiation
under the integral" is not always valid. Knowing the details of this
example is definitely not part of Math 421, certainly, but I
include it here so that near maniacs can verify there may be some
problems with interchanging differentiation and integration.
Here is an intricate example copied from Counterexamples in
Analysis by Gelbaum and Olmstead, showing that "differentiation
under the integral" is not always valid. Knowing the details of this
example is definitely not part of Math 421, certainly, but I
include it here so that near maniacs can verify there may be some
problems with interchanging differentiation and integration. What kinds of functions theory interlude #1
What kinds of functions theory interlude #1 Well, I considered the following example. Certainly our table tells us
that the Laplace transform of t2 is 2/s2. Let's
call t2 by the name, h(t), and let's further define the
function g(t) by the stipulations that g(t) is -1 when t=3 and g(t) is
40 when t=6 and otherwise g(t)=t2. I know the darn picture
is not drawn to scale, but the poetic truth is there. So, anyway,
certainly h and g are distinct functions. But they have the same Laplace transform. Look,
the formula for the Laplace transform of y(t) is
Well, I considered the following example. Certainly our table tells us
that the Laplace transform of t2 is 2/s2. Let's
call t2 by the name, h(t), and let's further define the
function g(t) by the stipulations that g(t) is -1 when t=3 and g(t) is
40 when t=6 and otherwise g(t)=t2. I know the darn picture
is not drawn to scale, but the poetic truth is there. So, anyway,
certainly h and g are distinct functions. But they have the same Laplace transform. Look,
the formula for the Laplace transform of y(t) is 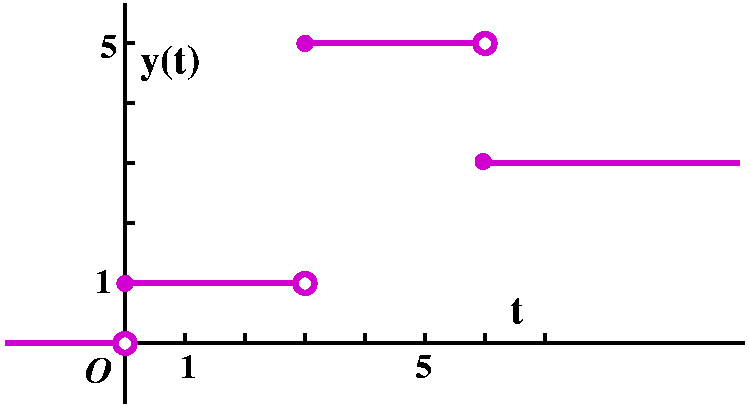
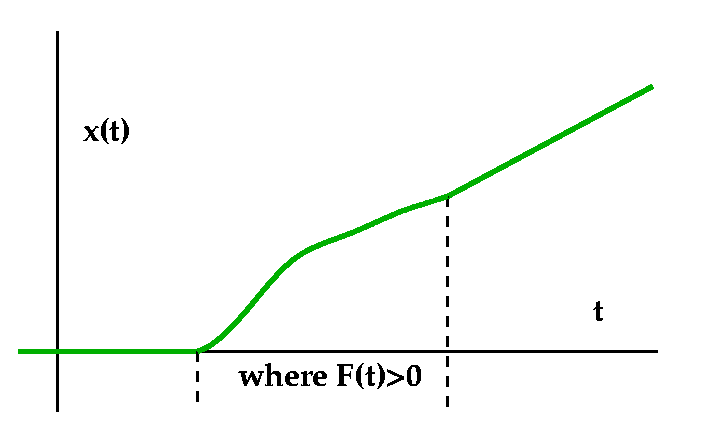
 Suppose y(t) is
the function which is 0 for t<0, is t2 for t in the
interval [0,1], is 1 in between 1 and 3, is (t-4)2 in the interval [3,4], and is 0 for "later" t. I hope I've drawn a picture of y(t) to the left.
Suppose y(t) is
the function which is 0 for t<0, is t2 for t in the
interval [0,1], is 1 in between 1 and 3, is (t-4)2 in the interval [3,4], and is 0 for "later" t. I hope I've drawn a picture of y(t) to the left. 
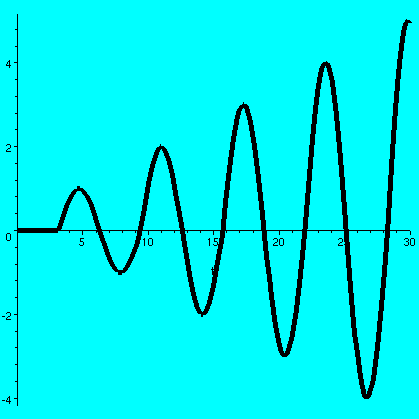
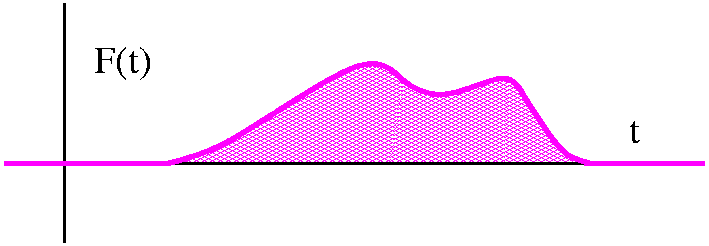
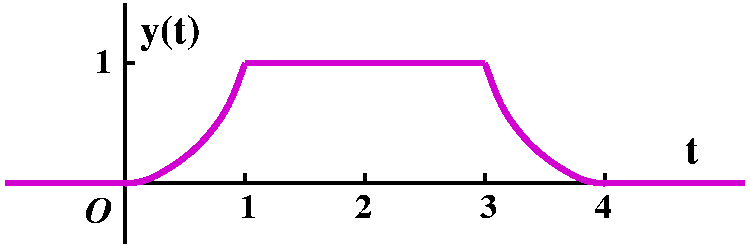
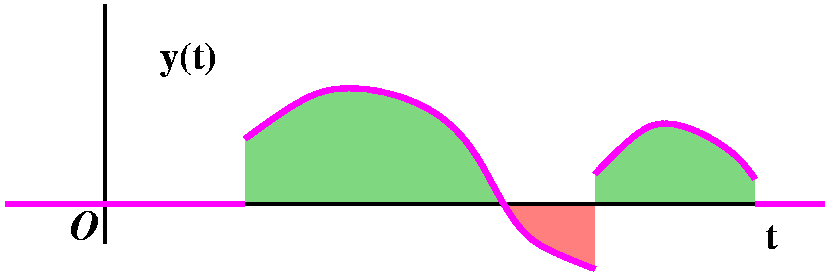 Suppose our y(t) is some sort of collection of lumps and bumps, sort
of as shown. Well, the Laplace transform formula multiplies this by
e-st, and integrates dt. We will only consider positive s,
so the exponential is always decreasing. When s gets larger and larger
positive, the exponential decreases more and more rapidly to 0. Yes,
it stays at 1 when t=0, but the dropoff gets very rapid indeed. The
product of the exponential with y(t) will be some collection
{l|b}umps, but the amplitude, the height, will surely -->0. So
for the functions we are considering, Y(s)-->0 as s-->infinity.
Suppose our y(t) is some sort of collection of lumps and bumps, sort
of as shown. Well, the Laplace transform formula multiplies this by
e-st, and integrates dt. We will only consider positive s,
so the exponential is always decreasing. When s gets larger and larger
positive, the exponential decreases more and more rapidly to 0. Yes,
it stays at 1 when t=0, but the dropoff gets very rapid indeed. The
product of the exponential with y(t) will be some collection
{l|b}umps, but the amplitude, the height, will surely -->0. So
for the functions we are considering, Y(s)-->0 as s-->infinity.
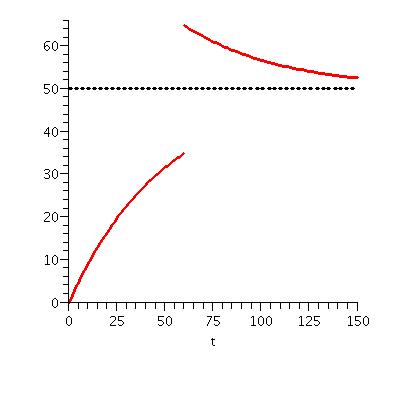
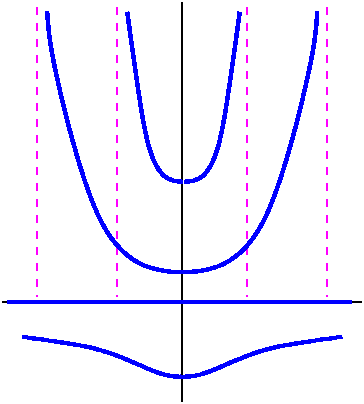 Let's look at some specific solutions. The solution satisfying the IC
(0,100) has C=2/100, so y=2/(.01-t2). The natural domain of
this function is (-1/10,1/10). As t-->1/10-, y-->infinity:
the solution explodes. If the IC is (0,2·104) the solution is
y=2/(.0001-t2) and it has domain (-1/100,1/100). There is
one special case (you need to look critically at the separation of
variables process to spot what goes wrong) but if the initial
condition is (0,0), the solution is y=0 for all t.
Let's look at some specific solutions. The solution satisfying the IC
(0,100) has C=2/100, so y=2/(.01-t2). The natural domain of
this function is (-1/10,1/10). As t-->1/10-, y-->infinity:
the solution explodes. If the IC is (0,2·104) the solution is
y=2/(.0001-t2) and it has domain (-1/100,1/100). There is
one special case (you need to look critically at the separation of
variables process to spot what goes wrong) but if the initial
condition is (0,0), the solution is y=0 for all t.