Silly example:
xn=7Pi for 1<=n<=10,000
xn=0 for 10,001<=n<=20,000
xn=1+(1/n) for 20,001<=n
Does this sequence converge? If it does, what is its limit?
It certainly does, and its limit is 1.
Why?
Maybe a less silly example:
Look at the beginning of this sequence which is defined by quite a
simple formula (computations done by Maple):
1.367879478, 0.6353353374, 0.3831204465, 0.2683156682, 0.2067379638,
0.1691454278, 0.1437690293, 0.1253354648, 0.1112345219, 0.1000454004
It surely looks "good", controlled, maybe convergent, etc. Here is the
100th term:
0.01000000000
and the 1,000th term:
0.0001000000000
and now the 1,000,000th term:
-5
0.1000000000 10
This is a sort of tiny number.
But here is the 100,000,000th term:
390865034
0.5163291506 10
which is quite a large number.
What is going on? This is the formula I had Maple use:
xn=(1/n)+e-n+.0000001n2. The ".0000001"
in the exponent makes it clear that the "effect" of the n2
won't be "felt" for "a while". But an n2 in the exponent
will dominate surely for large enough n, and the darn sequence will
definitely explode: it will not
converge.
This tail gets too big.
Interlude: geometry, axioms, logic, truth, beauty ...
http://mathworld.wolfram.com/ParallelPostulate.html
Diary entry in progress! More to come
Calculators, graphs, etc., with rational numbers only
The Intermediate Value Theorem fails: our eyes deceive us!
Diary entry in progress! More to come
The additional assumption
Diary entry in progress! More to come
An iteration
Consider the function f(x)=sqrt(4x+73). This is a fairly simple
function. We will use it to define a sequence recursively:
x1=1
xn+1=f(xn)
Here are the first ten terms of the sequence:
1.000000000, 8.774964387, 10.39710814, 10.70459867, 10.76189550,
10.77253833, 10.77451406, 10.77488080, 10.77494887, 10.77496151
This sure looks (and smells?) like a convergent sequence. But you
can't really tell. Only the infinite tail matters, and I can't
directly "access" the infinite tail.
Analysis of this sequence
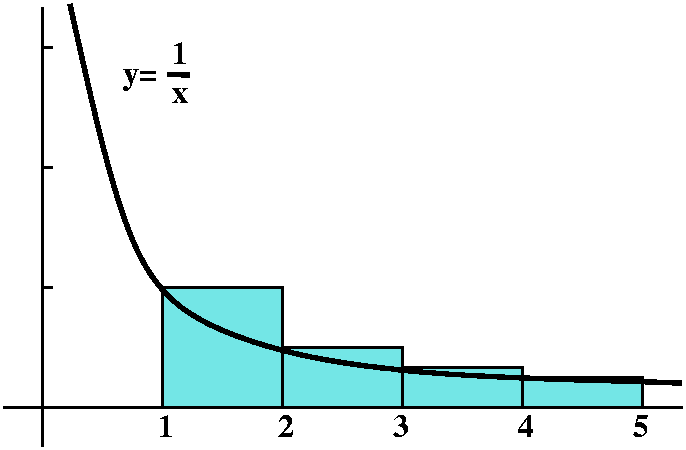 The harmonic numbers revisited
The harmonic numbers revisited
The numbers, {Hn}, were previously
defined. Here is another way to analyze them, by comparing them
to areas under the curve y=1/x.
Diary entry in progress! More to come
Dichotomy of monotone sequences
Our word, dichotomy, has as its first definition,
a division into two, esp[ecially]. a sharply defined one.
That's certainly what I want here. Remember that a monotone sequence
is a sequence which is either increasing or decreasing. So the
sequence {(-1)n} which alternates between +1 and -1 is not
monotone.
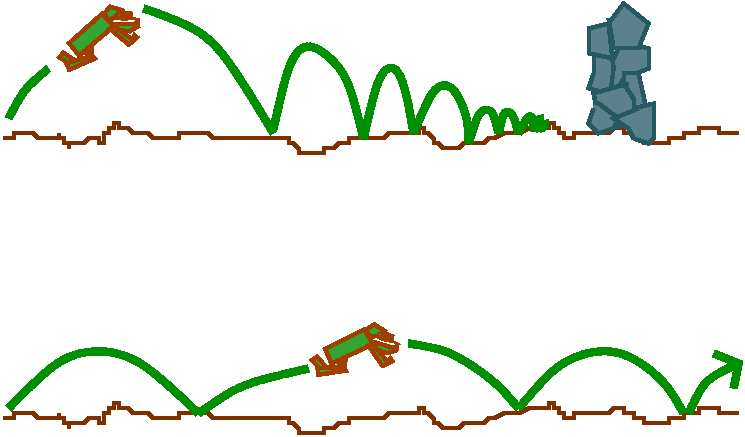
Either a monotone sequence is bounded and converges
or it is unbounded and diverges.
Diary entry in progress! More to come
Monday, October 24
Definition of sequence
A sequence is a function whose domain is the positive integers (that's
1 and 2 and 3 and 4 and ...). It will sometimes be convenient to have
sequences starting at 0, so their domain will be the non-negative
integers (0 and 1 and 2 and 3 and 4 and 5 and ...).
Example (trap rule approximations)
Suppose I was (unfortunately) interested in computing something like
 02cos(x7)/(1+x4) dx. No
one knows an antiderivative of this function in terms of familiar
functions. I could define a sequence in the following way:
02cos(x7)/(1+x4) dx. No
one knows an antiderivative of this function in terms of familiar
functions. I could define a sequence in the following way:
Tn is the result of using the trapezoid rule approximation
for the function cos(x7)/(1+x4) on
the interval [0,2], when the interval is divided into n equal parts.
I certainly wouldn't want to compute this, but I (or my silicon
pals) could do it, if necessary. In addition, due to the
extravagant work we did earlier this semester, I know that if I had
to, I could find a number Q so that (if the letter I represents the
true value of the integral), then
|Tn-I|<Q/n2. It wouldn't be fun to compute a
value of Q but we could do it.
I bet that the sequence {Tn} converges and that the limit
of this sequence is the value of I.
Example (decimal approximations to sqrt(2)
12 is less than 2 and 22 is greater than 2. So I'll start with 1.
1.42 is less than 2 and 1.52 is greater than
2. So my next term will be 1.4.
1.412 is less than 2 and 1.422 is greater than
2. So my next term will be 1.41.
1.4142 is less than 2 and 1.4152 is greater than
2. So my next term will be 1.414.
1.41422 is less than 2 and 1.41432 is greater
than 2. So my next term will be 1.4142.
Etc. (Etc. here means, uhhh, it is probably difficult to describe the
whole process exactly.) But I bet if qn is the
nth term in this sequence,
|qn-sqrt(2)|<10-n+1. (I think I wrote
10-n in class but isn't that wrong?)
I bet that the sequence {qn} converges and that the limit
of this sequence is sqrt(2).
Convergence
A sequence converges (roughly) if there is a number that it gets close
to and stays close to. That number is called the limit of the
sequence. A precise definition is near the bottom of p.703 of the
text.
Sequences don't have to converge
Just look at {(-1)n} which flips back and forth from +1 to
-1. It does not get close and stay close to any one number, so this
sequence does not converge.
Facts about limits of sequences
There are a bunch of facts about limits and sequences which you should
know. All of these facts can be proved, and none require any advanced
techniques besides a great deal of concentration and patience. We
usually verify these facts in Math
311 which some of you may want to take. But right now, I'd just
like you to agree that they are probably true.
Algebraic facts
Sandwich or squeeze result If {an} and
{bn}and {cn} are three sequences, and I know
that an<=bn<=cn for all n, and
I know that
{an} and {cn} both converge to the same limit,
then the middle sequence, {bn} also converges to that limit.
Warning! Subtlety coming!!!
There's one more limit fact that I will recite next time which is
somewhat more subtle than all of these.
Sequences can be defined by formulas
This is probably the most familiar way.
rn
Suppose r is between 0 and 1. Then {rn converges, and the
limit of this sequence is 0.
Why? Well, rn=en ln(r). Now ln(r) is
a negative number since r is between 0 and 1. Multiplying this
negative number by n as n-->infinity makes it more negative. In fact,
n ln(r)-->-infinity. But then
en ln(r)-->e-infinity and that's 0 (if you
have a picture of y=ex in your head!).
a1/n
Suppose a is a positive number. Then the sequence {a1/n}
converges, and its limit is always 1.
Why? Well, a1/n=e(1/n)ln(a) and I know
that (1/n)ln(a)-->0 as n-->infinity. So
a1/n-->e0=1 as n-->infinity.
Comment I really don't think this is totally obvious. Here
are the 1/nth powers of 2 as n goes from 1 to 10:
2.000000000, 1.414213562, 1.259921050, 1.189207115, 1.148698355,
1.122462048, 1.104089514, 1.090507733, 1.080059739, 1.071773463
These numbers go down to 1.
I really don't think this is totally obvious. Here
are the 1/nth powers of 1/3 as n goes from 1 to 10:
0.3333333333, 0.5773502692, 0.6933612743, 0.7598356856, 0.8027415617,
0.8326831776, 0.8547513999, 0.8716855429, 0.8850881521, 0.8959584598
These numbers go up to 1.
n1/n
Huh: the n's in the base grow and the 1/nth powers
push things down. I don't think the "winner" is clear, even though most students did. Here are the first 20 terms:
1.000000000, 1.414213562, 1.442249570, 1.414213562, 1.379729661,
1.348006155, 1.320469248, 1.296839555, 1.276518007, 1.258925412,
1.243575228, 1.230075506, 1.218114044, 1.207442027, 1.197860058,
1.189207115, 1.181352075, 1.174187253, 1.167623484, 1.161586350
and maybe even now this isn't totally "clear". But, in fact,
{n1/n} does converge, and its limit is 1.
Why? Well, n1/n=eln(n)/n, and from our
extended holidy with l'H we know that:
ln(n)/n, as n-->infinity, is of the form infinity/infinity, so that it
is eligible for l'H. Thus we must study, instead of ln(n)/n, the quotient
(1/n)/1, and this limit is surely 0. Therefore ln(n)/n-->0 and
eln(n)/n-->e0=1. Indeed.
By the way, 10001/1000 is approximately 1.006931669.
(3n+7n)1/n
I asked if this sequence converged. Here's some numerical evidence, the first 10 terms:
10.00000000, 7.615773106, 7.179054352, 7.058305379, 7.020125508,
7.007210537, 7.002652582, 7.000995354, 7.000379289, 7.000146315
So I guess that this sequence converges and the limit is 7. Well,
that's true. Why? I will use the Squeeze result carefully.
Certainly
7n<=3n+7n<=7n+7n=2·7n.
That means
(7n)1/n<=(3n+7n)1/n<=(2·7n)1/n=21/n(7n)1/n.
So
7<=(3n+7n)1/n<=21/n7.
But 21/n-->1 as n-->infinity, so that
(3n+7n)1/n is sandwiched between two
sequences which have limit=7, and therefore it must also converge and
have limit=7.
Sequences can be defined recursively
Many sequences of great importance in science and engineering are
defined recursively. This means that terms of the sequence are
defined interms of previous terms of the sequence. Let me discuss some
examples.
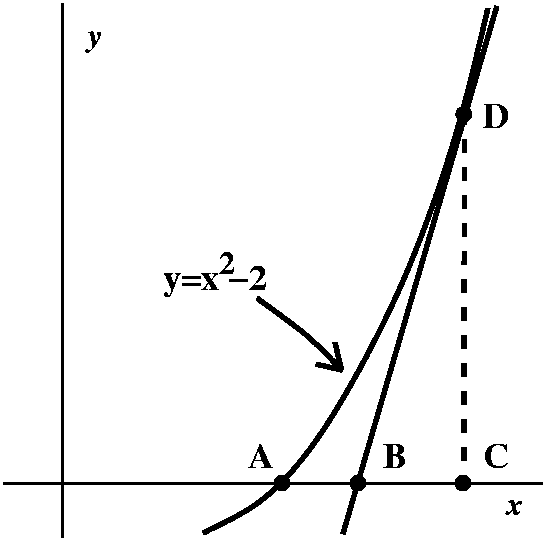 Sqrt(2) by Newton's method
Sqrt(2) by Newton's method
Newton's method is a way of replacing a guess at a solution of f(x)=0
by an improved guess, obtained by "sliding down" a tangent line. It is
discussed in section 4.9 of the textbook. Here let me show a way to
approximate sqrt(2). I'll take f(x)=x2-2. Then sqrt(2) is
the postive root of this function. The iteration or recursion step
describes how to go from a guess, xn, to a new guess,
xn+1. Let me tell you what the coordinates of the points in
the picture to the right are. First, A is the point (sqrt(2),0). C has
coordinates (xn,0) (the old guess, which is to be
improved). D is the point (xn,xn2-2)
on the curve y=f(x). The line tangent to the curve will have slope
f'(xn)=2xn. Therefore, since the slope
represents the tangent of the angle CBD, it must be the ratio of the
geoemetric lengths DC/BC. But DC is xn2-2, and
so 2xn=(xn2-2)/BC, and the length of
BC is (xn2-2)/(2xn). The coordinates
of the point B are supposed to be (xn+1,0), and
xn+1 is the improved guess. So xn+1 will be
xn with the length of BC subtracted from xn: the guess moves backwards. Therefore
xn+1=xn-((xn2-2)/(2xn))
The reason I'm going through this is that this specific formula
simplifies in a remarkable way.
x n2-2 2xn2-(2xn2-2) 2xn2+2 1 ( 2 )
xn- -------- = ------------- = -------- = - (xn+--)
2xn 2xn 2xn 2 ( xn)
So we replace xn by the average of xn and
2/xn.
I'll define a sequence by
x1=1
xn+1=(1/2)(xn+2/xn)
Uhhhh .... Maple calculated the first few elements of this sequence:
x2=3/2
17
x3=--
12
577
x4=---
408
665857
x5=------
470832
886731088897
x6=------------
627013566048
1572584048032918633353217
x7=-------------------------
1111984844349868137938112
You should understand that the values quoted are exact values. A decimal approximation of the last number is
1.414213562, which happens to agree with Maple's 10 digit approximation to sqrt(2).
History
There is evidence that this averaging idea was known to "ancient
civilizations" (Egypt, India) and was used to improve approximations
to square roots. But I don't think that a non-recursive (formula!)
method for defining the sequence is known.
Look at the recursion:
xn+1=(1/2)(xn+2/xn)
If xn--> a limit, L, then surely
xn+1--> the same limit, L, because xn+1 is just
the same sequence, moved one step further on. But then the recursion
xn+1=(1/2)(xn+2/xn) becomes )(as n-->infinity)
L=(1/2)(L+2/L) and this is 2L=L+2/L which is L=2/L which is L2=2
which is L=+/-sqrt(2). In fact, the limit should be +sqrt(2)
since we started at x1=1>0, and the averaging process
keeps all terms positive.
Therefore ...
Have we proved that the sequence converges to sqrt(2)?
Actually, no. We showed (the logic is important!) that if the
sequence converges, then its limit is sqrt(2). Theory and
practical application are full of examples where the "if" part is
missing or untrue. Students should recognize this.
Another recursive sequence
We could define the sequence by
x1=1
xn+1=(n+1)xn
Well, since x1=1, x2=(2)(1)=2,
x3=3(2)=6, x4=4(6)=24, etc. In fact,
xn=n!, but the notation is really a description, not
a formula. I don't know any nice "formula" for n! (except for itself).
Yet another recursive sequence
Try
x1=1
xn+1=(n+1)+xn
Here the sequence looks like 1, 1+2=3, 1+2+3=6, 1+2+3+4=10, etc. In
this case, a formula can be guessed. It seems that xn
should be (n{n+1})/2. I will call yn=(n{n+1})/2. If
you plug in n+1 and n=2 and n=3 and n=4, you'll get the numbers
y1=1 and y2=3 and y3=6 and
y4=10. But why should x10,000 be equal to
y10,000? Why should all of the infinitely many
equations xn=yn be true?
A proof strategy
We could think of a very long row of dominos standing on their narrow
end. The dominos are close enough together so that if one falls, the next one falls
over. I bet that if the first one
is pushed
then they will all fall over.
the first one is pushed ...
This is just the observation that
x1=1 and y1=1.
|
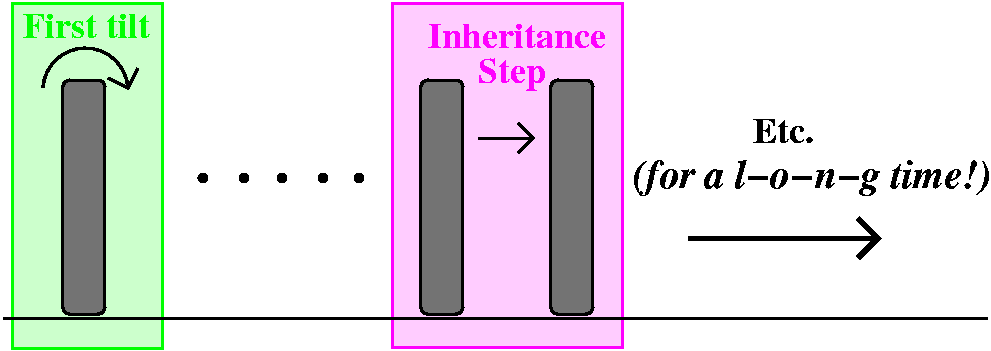 |
if one falls, the next one falls
over.
Suppose xn=yn. Then yn+1=(using the formula!) ([n+1]{n+1 +1})/2=([n+1]{n+2})/2=
([n+1]{n}+[n+1]2)/2=([n+1]{n})/2 + ([n+1]2)/2= yn+[n+1]. But we assumed that
xn=yn so this means
yn+1=xn+[n+1]=xn+1.
|
 The domino
theory was a part of U.S. foreign policy for a long time (it still
might be). Here, my dominos represent a proof technique called
mathematical induction. I just used the technique to try to
convince you that for all n, xn=yn. I hope that
you appreciate the almost paradoxical strength of this: a finite
amount of writing has proved an infinite number of statements!
The domino
theory was a part of U.S. foreign policy for a long time (it still
might be). Here, my dominos represent a proof technique called
mathematical induction. I just used the technique to try to
convince you that for all n, xn=yn. I hope that
you appreciate the almost paradoxical strength of this: a finite
amount of writing has proved an infinite number of statements!
Much of this sort of verification can now be done by computer. One of
the world leaders in this endeavor is Professor Doron
Zeilberger, a faculty member at Rutgers. He is very approachable,
and he is really smart.
The harmonic numbers
Here is a sequence which occurs in many applications. The
nth harmonic number is the sum 1+1/2+1/3+1/4+...+1/n. This
can be abbreviated by SUMk=1n1/k. Here k
is called the index of summation, and I can't see k
(logically!) outside of the SUM sign. It is logically just as
inaccessible as the integration variable in  1x1/t dt=
1x1/t dt= 1x1/q dq=
1x1/q dq= 1x1/w dw.
1x1/w dw.
Maybe you might find the harmonic numbers more appealing if I wrote
the definition recursively:
H1=1
Hn+1=[1/(n+1)]+Hn
The text Concrete Mathematics: A Foundation for Computer
Science by Graham, Knuth, and Patashnik shows that the harmonic
numbers are related to stacking books over an edge. Please see the
pictures displayed here
and a more complete explanation, while available in the text cited, is
also here.
What can one say about the harmonic numbers? Do they converge?
Here are the first 20:
1.000000000, 1.500000000, 1.833333333, 2.083333333, 2.283333333,
2.450000000, 2.592857143, 2.717857143, 2.828968254, 2.928968254,
3.019877345, 3.103210678, 3.180133755, 3.251562326, 3.318228993,
3.380728993, 3.439552522, 3.495108078, 3.547739657, 3.597739657
I can't see anything clearly from this. But look at H8:
Break up into pieces:
1 +1/2 +1/3+1/4 +1/5+1/6+1/7+1/8
Underestimate each piece:
1 +1/2 +1/4+1/4 +1/8+1/8+1/8+1/8
Sum:
1 +1/2 2(1/4)=1/2 4(1/8)=1/2
So that H8>=1+3(1/2). I hope this persuades you (a proof
can be done by mathematical induction, or I'll show you another way
next time) that
H2m>=1+m(1/2). First this shows that the
sequence of harmonic numbers grows without any upper bound so that
it can't converge. And, wow, this estimate grows very slowly. For example,
to be sure that a harmonic number is greater than 100 using this estimate,
I would need to look at H2198: that is, I'd need
to add up about 1060 terms! That's a lot of terms.
I will investigate this more Wednesday.
Thursday, October 20
{ Perpendicular | Orthogonal | Normal }
In many areas of math and science and engineering, these words are
intended to mean the same thing.
Lines
Well, C=y/x2 also describes these curves. The reason
for isolating the C is because I want to differentiate, and the C will
go away. I'd like to get some differential equation describing this
family of curves. Let me d/dx the equation C=y/x2. The
result is:
0 (of course!) = stuff from the quotient rule.
What is the "stuff from the quotient rule"? It is:
(dy/dx)x2-2xy
-------------
(x2)2
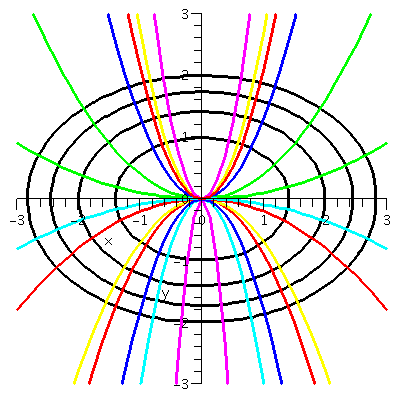 This should be 0, so (if we multiply by x4), we get
dy/dx(x2)-2xy=0, and then
dy/dx=2y/x. Now if we want curves which are orthogonal to these
curves, we need dy/dx to be the negative reciprocal of this. The
orthogonal curves must satisfy the differential equation
dy/dx=-x/2y.
This should be 0, so (if we multiply by x4), we get
dy/dx(x2)-2xy=0, and then
dy/dx=2y/x. Now if we want curves which are orthogonal to these
curves, we need dy/dx to be the negative reciprocal of this. The
orthogonal curves must satisfy the differential equation
dy/dx=-x/2y.
This is a separable equation, and not so hard. Therefore we can solve
it:
Separate: dy/dx=-x/2y gives 2y dy=-x dx
Integrate: which gives  2y dy=
2y dy= -x dx
-x dx
And we know that the equation
(1/2)x2+y2=Constant describes a family of curves
orthogonal to the original parabolas. These new curves are a
collection of ellipses with center at the origin and with major axis
on the x-axis and minor axis, 1/sqrt(2) as long, on the y-axis.
Some of the original parabolas are shown in the accompanying picture,
along with some of the ellipses of the family of curves orthogonal to
them.
Another way to get the differential equation of the family of
parabolas
If y=Cx2, then dy/dx=2Cx. But
C=y/x2, so that dy/dx=2Cx=2[y/x2]x
and therefore dy/dx=2y/x, just as we had above.
And we ended by ...
breaking up into small groups and working on the limit problems. It
was fun!!!
HOMEWORK
I'd like to make
sure that we are all up to speed on methods of evaluating
limits, because this will be very useful in the remaining part of the
course. So please hand in these problems
on Monday.
Here are pieces of the 152 syllabus which I'd like you to look at, and
I hope that Mr. Scheinberg will be able
to answer questions about them on Thursday.
Arc length,
surface area |
8.1: 3, 8, 11, 34
8.2: 1, 4, 5, 6, 14, 31 |
Differential equations,
direction fields |
9.1: 1, 3, 4, 6, 9, 10
9.2: 1, 3, 4, 5, 6, 9, 11 |
Separable equations;
exponential growth |
9.3: 1, 4, 19, 20, 21, 37, 39
9.4: 3, 4, 5, 9, 10, 14 |
Wednesday, October 19
I reviewed where we were: discussing solving differential equations. I
mentioned the examples we had: the vibrating spring, exponential
growth and decay, and separable differential equations. Each of these
examples had families of solutions, and a function in the family of
solutions was specified by some constants that I referred to as
initial conditions. I asserted that everything is included in the following wonderful
Basic Theorem about solutions of differential equations
If f(x,y) is a differentiable function of x and y and if
(x0,y0) is in the domain of f(x,y), then the
initial value problem y´=f(x,y) satisfying
y(x0)=y0 has exactly one solution.
Beloved question BC4 (free response question #4 on the 2005 AP
calculus BC exam) dealt with f(x,y)=2x-y and asked questions about the
slope field and Euler's method.
When I first learned of the Basic
Theorem, as I call it above, I thought that it sort of handled all
possible difficulties related to differential equations. I couldn't
really understand the complexities of trying to actually use
mathematics in real applications. The proof of this result
could probably be explained to you by the end of this course. For
example, one way to get the solution mentioned is by using Euler's
method (that's a rather slow way, but it works). What kinds of
reasonable questions are not answered by this theorem? Let me show
you.
Example 1 Suppose I know that
y´(x)=e(x2). Well, here is the
solution which is guaranteed by the theorem:
F(x)= 0xe(w2)dw+C. The
Fundamental Theorem of Calculus says that
F'(x)=e(x2) and the "+C" allows adjustment for
an initial condition. In fact, we've just rewritten the differential
equation and transferred the computational "responsibility" to the
definite integral. As I mentioned back when we were first starting
methods of antidifferentiation, there's no way to find an
explicit antiderivative of this function in terms of standard
functions. Evaluation must be done through an approximation
technique. So learning about the solution (that it exists, that there
is exactly one) has not helped at all.
0xe(w2)dw+C. The
Fundamental Theorem of Calculus says that
F'(x)=e(x2) and the "+C" allows adjustment for
an initial condition. In fact, we've just rewritten the differential
equation and transferred the computational "responsibility" to the
definite integral. As I mentioned back when we were first starting
methods of antidifferentiation, there's no way to find an
explicit antiderivative of this function in terms of standard
functions. Evaluation must be done through an approximation
technique. So learning about the solution (that it exists, that there
is exactly one) has not helped at all.
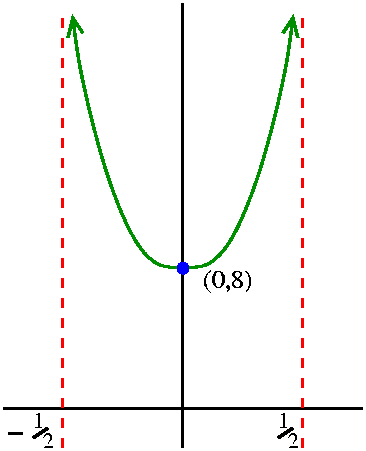 Example 2 I think this equation has more subtle aspects. Let's
look at y´(x)=xy2. This equation looks "easy". It is
certainly separable, and the f(x,y) seems rather simple. We separate
variables and integrate: so dy/y2=x dx and then
-1/y=(1/2)x2+C and we can even solve for y in terms of x:
y=1/(C-{1/2}x2). (I renamed C.) Now suppose we want the
solution to satisfy the initial condition: when x=0, y=8. Then C
should be 1/8, and the solution looks like
y=1/({1/8}-{1/2}x2). This is o.k., a nice function. A
picture is to the right (with units on the horizontal and vertical
axes are rather different). We get into some trouble when we think
about the solution curve. Suppose the curve represents the growth of
"something" (I think I suggested "wahoonies" in class). Usually x
represents the "independent" variable, say, time. What happens to the
growth of the wahoonies? Look at {1/8}-{1/2}x2 from x=0
(where it is 1/8) up to ... well, this should not be 0 because it is
in the denominator. It will be 0 when x=1/2 (also, of course,
-1/2). The growth gets larger and large, and, finally, explodes (!?)
at 1/2 (also, of course, backwards at -1/2). We can't predict the
population of wahoonies on further than 1/2 or further backwards than
-1/2. This disaster is, to me, unforseen in the nice function
xy2. Things are actually worse than this.
Example 2 I think this equation has more subtle aspects. Let's
look at y´(x)=xy2. This equation looks "easy". It is
certainly separable, and the f(x,y) seems rather simple. We separate
variables and integrate: so dy/y2=x dx and then
-1/y=(1/2)x2+C and we can even solve for y in terms of x:
y=1/(C-{1/2}x2). (I renamed C.) Now suppose we want the
solution to satisfy the initial condition: when x=0, y=8. Then C
should be 1/8, and the solution looks like
y=1/({1/8}-{1/2}x2). This is o.k., a nice function. A
picture is to the right (with units on the horizontal and vertical
axes are rather different). We get into some trouble when we think
about the solution curve. Suppose the curve represents the growth of
"something" (I think I suggested "wahoonies" in class). Usually x
represents the "independent" variable, say, time. What happens to the
growth of the wahoonies? Look at {1/8}-{1/2}x2 from x=0
(where it is 1/8) up to ... well, this should not be 0 because it is
in the denominator. It will be 0 when x=1/2 (also, of course,
-1/2). The growth gets larger and large, and, finally, explodes (!?)
at 1/2 (also, of course, backwards at -1/2). We can't predict the
population of wahoonies on further than 1/2 or further backwards than
-1/2. This disaster is, to me, unforseen in the nice function
xy2. Things are actually worse than this.
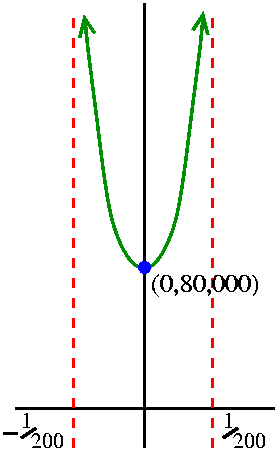 If we change the
initial condition to, say, (0,1/80,000), then the unique solution is
y=1/({1/80,000}-{1/2}x2) and the domain of this function is
only (-1/200,+1/200): the wahoonie explosion is even closer in
time. Another picture is shown, with even more distorted axes, but the
idea is, I hope, clear: a narrower steeper curve with a higher up
initial condition. As the initial number of wahoonies grows, the
explosion comes closer and closer in time.
If we change the
initial condition to, say, (0,1/80,000), then the unique solution is
y=1/({1/80,000}-{1/2}x2) and the domain of this function is
only (-1/200,+1/200): the wahoonie explosion is even closer in
time. Another picture is shown, with even more distorted axes, but the
idea is, I hope, clear: a narrower steeper curve with a higher up
initial condition. As the initial number of wahoonies grows, the
explosion comes closer and closer in time.
How to "solve" ODE's
What these two examples, and others, can tell you about the famous
Existence and Uniqueness Theorem for ODE's (a version is quoted
above as the "Basic Theorem") is not that the theorem is wrong or a
fraud, but more that it declares only what is there. I know that I've
had a tendency to "read into" the theorem a heck of a lot more than it
contains. The two examples I showed are an effort to convince me
(again!) and maybe you that solutions may not be effectively
computable, and that the solutions are guaranteed only to "live" for a
short time, and more than that cannot be assumed.
Solving ODE's can occur on various levels.
- We could ask for solutions which
are nice formulas written in terms of familiar functions. Let me call
this the algebraic level.
- We could ask for numerical approximations which are guaranteed to
be close to the real solutions. This is certainly possible, but more
difficult than one might initially imagine: how could we numerically
analyze the explosion in the wahoonies? How does one numerically
analyze the behavior of space/time near black holes? I'll call this
the numerical level.
- We could ask for asymptotic information. Such things might include
ideas about rates of growth, limit behavior, and dependence on initial
conditions ("chaotic behavior"). I'll call this the qualitative
level.
People interested in differential equations usually want to exploit
all of these methods to get information and it's not a good idea to
neglect any of them. The qualitative level may be a bit new to you, so
let me contrast it with the algebraic level in one example (a logistic
equation). I'll totally neglect the numerical level in this course,
but I know that you've seen Euler's method, which is a rather slow
numerical approximation technique.
Exact solution of a logistic equation
Here I'll look at y'(t)=y(1-y). We're supposed to think that the rate
of change is directly proportional to the population y(t) at time
time, but is also limited by the amount of resources available. Here
the resource limit (carrying capacity?) is 1. Of course I have made
the numbers simple so that someone essentially even more simple can
analyze the equation easily. To solve this equation (in the
sense of the first level above) I recognize it as a separable equation
and write
dy
------ = dx
y(1-y)
and then (partial fractions!) recognize that
1/[y(1-y)]={1/y}+{1/(1-y)} where the advantage is that I can
antidifferentiate the pieces. So ln(y)-ln(1-y)=x+C (I forgot
the minus sign one when I was analyzing this in preparation for the
lecture!) so that ln(y/(1-y))=x+C and (renaming K=eC)
y/(1-y)=Ket so that
y=(1-y)Ket=Ket-Ket and
y+Ket=Ket and
(1+Ket)y=Ket. Finally,
y=Ket/(1+Ket).
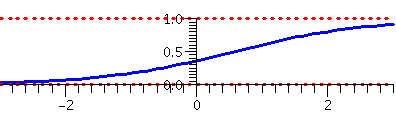 Well, how can we use this formula? I can try to match an initial
condition, and then I can look at a solution curve. In class I used
(0,3/4) (so K was "clearly" 3) but let me be more adventurous
here. When t=0 in Ket/(1+Ket) we get K/(1+K).
If we want K/(1+K) to be .37, and approximate value of K is .587 (yes,
a silicon pal helped me here). And my same pal graphed the solution
curve shown to the right. It sure looks like the curve is an
increasing function of time, and to the right it approaches +1 and to
the left it approaches 0. You can check these limits using the
algebraic formula:
Well, how can we use this formula? I can try to match an initial
condition, and then I can look at a solution curve. In class I used
(0,3/4) (so K was "clearly" 3) but let me be more adventurous
here. When t=0 in Ket/(1+Ket) we get K/(1+K).
If we want K/(1+K) to be .37, and approximate value of K is .587 (yes,
a silicon pal helped me here). And my same pal graphed the solution
curve shown to the right. It sure looks like the curve is an
increasing function of time, and to the right it approaches +1 and to
the left it approaches 0. You can check these limits using the
algebraic formula:
y=.587et/(1+.587et)
As t-->+infinity, the quotient is always less than 1 (the bottom is
larger than the top!) but the 1 becomes less and less significant,
because ex-->infinity. If you would like a bit more
algebra, consider that (factor out the exp!)
.587et/(1+.587et)=1/([1/.587]e-t+1)
as e-t-->0 as t-->+infinity.
Similarly, et-->0 as t-->-infinity, so that
y-->0 then.
One problem is that in real applications, we seldom know exact
initial conditions, and one thing that differential equations "teach"
is there may be what's called sensitivity to initial conditions. What
happens if I change the initial condition from .37 to .38? How certain
is it that y(t) will still-->1 as t-->infinity? A qualitative study
may give such information easily.
| | | |
Slope field analysis of a logistic
equation
| |
|
|
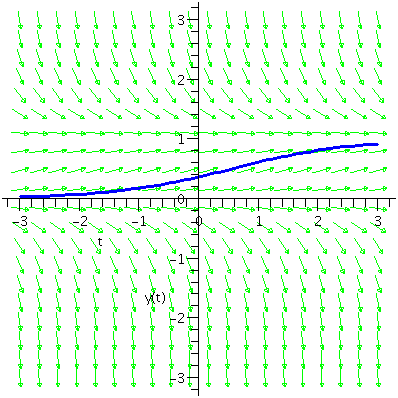
Look at the differential equation: y'(t)=y(1-y). If a solution curve of
this equation passes through the point (2,3), then the slope of the
curve must be (3)(-2)=-6. The curve must be tangent to a line of slope
-6 passing through (2,3). We could therefore {think|hope} that the
curve will look a bit like that line near (2,3): we can draw a short
line segment of slope -6 through the point (2,3). We can try to draw
lots of these little line segments. This is called a direction field
(textbook) or a slope field (what I will call it
here). Maple's command, dfieldplot (included in the
package DETools) produced the collection of green arrows
here. I am not too familiar with the plethora (!) of options of
dfieldplot, so I took the default settings, which produce "line field"
elements with arrow heads. I superimposed the solution curve we know
already. I hope you can see that it is tangent to the slope field
elements shown.
|
|
|
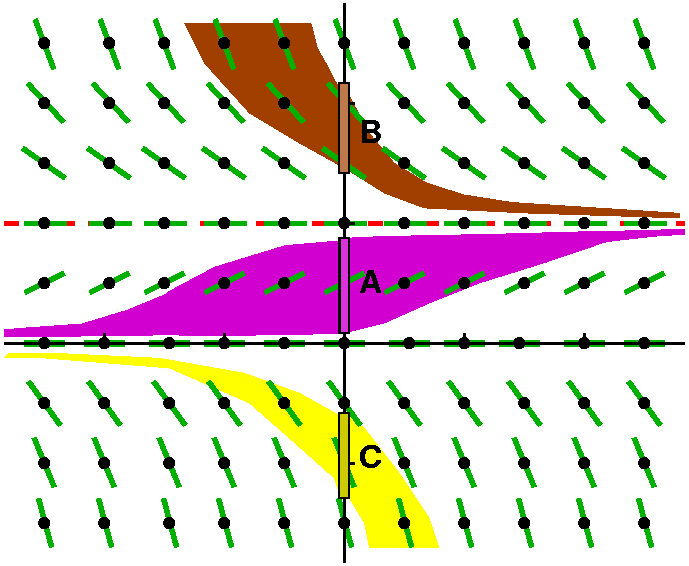
Here's a picture with more of a qualitative point of view. I drew the
slope field at integers and half-integers froom -3 to -3 in both the
horizontal and vertical directions. Then I tried to understand and
sketch what would happen with various initial conditions at time
0. There are two special solution curves which happen when
y(1-y)=0. The two constants identified, 0 and 1, are graphs of
horizontal lines which satisfy the differential equation. These
constants make the right-hand signs equal to 0, and, since the
functions are constants, the derivatives of the functions are 0. These
are called equilibrium solutions of the differential equation.
|
 |
|
The initial conditions |
|
The initial conditions in interval A on the
y-axis are in magenta. Forward evolution pulls the
corresponding solution curves all towards the equilibrium condition
y=1. Backwards, they seem to approach y=0.
|
The initial conditions in region B seem to evolve
as t-->+infinity towards again the equilibrium solution y=1. As time
goes backwards, these solutions explode out (the wahoonies are
exploding again). The solution y=1 is a special kind of equilibrium,
called a stable equilibrium. Small disturbances in initial
conditions near this equilibrium lead to solutions which all approach
it as t-->+infinity. |
(I tried this color but it was too darn hard to
read!)Here in region C the instability of the
equilibrium solution y=0 is shown. If you do perturb the solution up
or down, eventually solution curves push away from the
equilibrium. Region C's initial conditions lead to negative infinity
type of explosions, as shown.
|
Comment One thing which makes drawing the slope field and
undertanding it easier is that the differential equation y'(t)=y(1-y)
is autonomous: there is no mention of the independent variable,
t, on the right-hand side. The word autonomous has the
following (perhaps more common) dictionary meanings:
- Not controlled by others or by outside forces; independent: an
autonomous judiciary; an autonomous division of a corporate
conglomerate.
- Independent in mind or judgment; self-directed.
I think this is very nice, but of course one loses some precision with
the qualitative point of view. For example, a solution curve between
y=0 is concave up for a while and then is concave down.It has one
inflection point. The algebraic solution allows (in principle!)
finding the inflection point exactly. The geometry justs sorts of
waves at it. But maybe that's enough?
How are human brains built? (Maybe -- a limited
comment!)
I've been told that the human brain has a terrific amount of its
capacity directed towards interpretation of visual data. Certainly I
find the slope field pictures much more convincing than looking at the
formula of the algebraic solution. And more numbers would not
necessarily help that much: I find a bunch of numbers difficult to
interpret. So that's why people like visual displays of information.
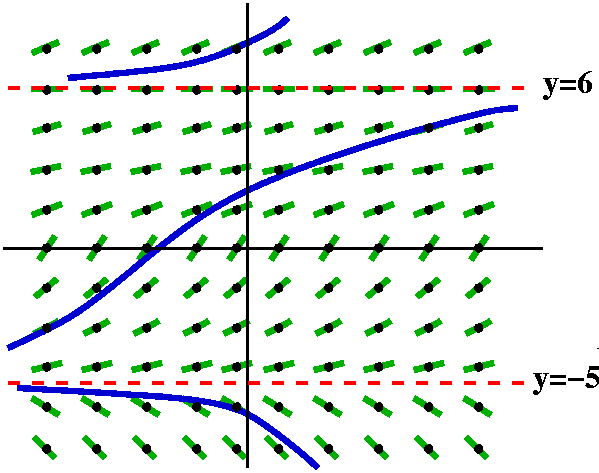 And another automomous equation
And another automomous equation
I think I looked at something like
y´(t)=(y-6)4(y+5)7. Certainly I don't think
I could explicitly solve and get an algebra solution. But I could
easily (well, almost easily!) sketch a slope field for this
equation. It is also autonomous so I can move the slope field elements
left and right after I sketch them on one vertical line. The lines
y=-5 and y=6 represent equilibrium solutions. y=-5 is an unstable
equilibrium. Perturbations of it move up to 6 or out to -infinity.
y=6 is a more complicated situation.
Limit manipulations
I'd like students to do these problems
and hand them in on Monday. That way I will have a firmer expectation
that we'll be able to cope with future limit problems (which will
occur!) in the course.
Return of exam
I returned the exam and asserted that everyone in the class should
stay in the class. Further remarks will be made on Thursday.
Thursday, October 13
Valiant Mr. Scheinberg answered
questions about the remainder of the sections of chapter 7.
Another differential equation
Here's a simpler differential equation than the one we looked at last
time: y'(t)=Ky(t), where K is some fixed constant.
What it might mean
What are the solutions
All the solutions?
Another way to solve it
Separable equations
A modification of growth, with a carrying capacity
The logistic equation
Diary entry in progress! More to come
Wednesday, October 12
Galileo
is reported to have declared, "Nature's great book is written in
mathematics." If that is so, then ever since Newton's
efforts to mathematicize physics, the chief mathematical dialect in
which this book is written is the language of differential equations.
An initial situation is specified mathematically, and then "things"
evolve or change according to some well-specified "laws" relating
their interaction. Efforts of scientists and engineers were based upon
this approach for several centuries. Although the approach is not
sufficient to handle everything, and sometimes is not easy, it had
major successes in both theoretical and practical aspects of science
and engineering. In today's discussion, we will look at a
very idealized model of a physical situation which might make subsequent
consideration of theory easier. We will consider an ideal vibrating
spring with no damping. This isn't the simplest differential
equation. Some important differential equations are simpler --
certainly the equations describing the motion of a rock dropping under
gravity, widely considered in early study of calculus, are easier. But
what happens in this example is much more characteristic of how
differential equations are used than most simpler examples.
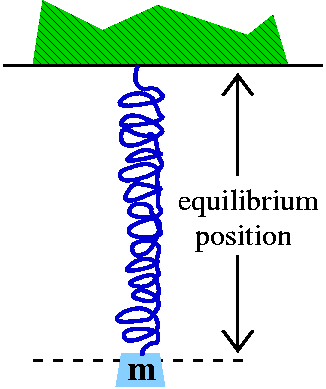 What we need to know
What we need to know
We need F=ma: the force on an object is directly proportional to the
rate of change of the rate of change of the position of the object:
the acceleration. The constant of proportionality is called mass. We
will discuss the an ideal spring, without damping or dissipation of
energy. One should think that the spring is floating in space, in
fact, it is alone in the universe. There's no gravity, no air
resistance, no ... anyway, the spring has a mass attached to it. If we
attached the mass very gently and at the correct length (in
equilibrium) the spring would not appear to move. However if we
push or pull the mass, or attach the mass at a position other than
equilibrium, a force seems to act on the mass. Hooke's
law states that the spring exerts a force on the object whose
direction is opposite to the object's displacement from equilibrium
and whose magnitude is directly proportional to the magnitude of the
displacement. So if x(t) is the displacement from equilibrium at time
t, the spring exerts a force of -kx(t) on the object. Since also F=ma,
and a is x´´(t), the acceleration, we have the law of motion for an
undamped spring: mx´´(t)=-kx(t). By the way, Hooke's law has been
experimentally verified under many conditions, as look at the spring
is not stretched or squeezed too much (don't take a rubber band
and stretch it 20 feet, for example).
The double game
I will try to play two sorts of intellectual game: I will try
to use physical "intuition" to determine what to expect about spring
motion, and I will also investigate what purely mathematical
deductions can be made. Well, first I want to make my life a little
bit easier. I'll assume that my "units" are chosen so that m=1 and
k=1. Remarks at the end will cover what happens if we don't assume
this. Now I want to solve the equation mx´´(t)=-kx(t). Well,
what does "solve" the equation mean? I know if I study the polynomial
2B3-4B-8=0 that a solution is B=2. When I substitute 2 into
the polynomial the equation becomes true. Here I have what's called a
second-order (the unknown function appears with a maximum of two
derivatives) ordinary differential equation. The word "ordinary" is
sometimes used, because there are other sorts of differential
equations, such as partial differential equations. A solution would be
a function which could be substituted into the equation, and for which
the equation would be true for all appropriate values of t (say, t in
the domain of x(t), for example). We could try some x(t)'s. For
example, functions like x(t)=-16t2+9t-5 occur when we drop
rocks. Then x´´(x)=-32, and there are very few t's for which
-32=-(-16t2+9t-5). So this x(t) is not a solution. But we
should try to use our physical intuition. The motion of a spring
should be back and forth, so certainly likely candidates should be
bounded. But, in fact, the function -16t2+9t-5 gets
arbitrarily large in magnitude. What should we try? Well, sin(t) was
suggested, and that works: if x(t)=sin(t), then
x´´(t)=-sin(t)=-x(t). And so does cos(t). Wait: so does
cos(t)+sin(t). Indeed, lots of other suggestions work:
x(t)=Acos(t)+Bsin(t) works if A and B are any constants. The equation
x´´(t)=-x(t) is structurally rather nice. The sum of two solutions is
a solution, and a constant multiplying a solution is a solution. (This
is called, in mathspeak, linearity, and in engineeringspeak, the
principle of superposition). Well, mathematically A and B are
nice. But what do they say about the physics of the situation?
Initial conditions
If x(t)=Acos(t)+Bsin(t), then A=x(0) and B=x´(0). Therefore A
represents the initial position (really, displacement from
equilibrium) and B represents the initial velocity of the mass. What
do cos(t) and sin(t) represent? Since cos(0)=1 and cos´(0)=-sin(0)=0,
somehow cos(t) in this situation represents and initial position
solution to x´´(t)=-x(t): we could call it xpos(t). And
sin(t) has sin(0)=0 and sin´(0)=cos(0)=1, an initial chunk of
velocity. And so maybe in this situtation we could call cos(t) the
solution xvel(t), an initial velocity solution. If we
needed to do lots of solutions to x´´(t)=-x(t) with many varied
initial positions and velocities, the formula
Axpos(t)+Bxvel(t) might be useful.
Algebraic digression: simple harmonic motion
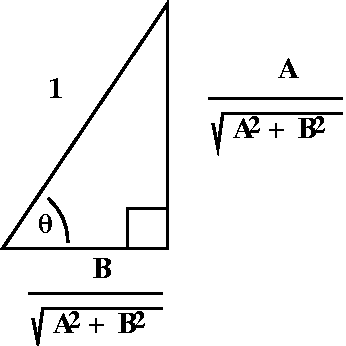 I didn't do this in class, mainly because I find algebra
painful. The algebra following is really motivated by physical
considerations, so maybe that excuses it.
I didn't do this in class, mainly because I find algebra
painful. The algebra following is really motivated by physical
considerations, so maybe that excuses it.
Look at Acos(t)+Bsin(t). I can rewrite this in a way which some people
find more appealing. I'll multiply and divide by
sqrt(A2+B2). The result is
A B
sqrt(A2+B2)[----------·cos(t)+ ------------·sin(t)]
sqrt(A2+B2) sqrt(A2+B2)
There are some funny numbers appearing:
A/sqrt(sqrt(A2+B2)) and
B/sqrt(A2+B2). These numbers have squares which
sum to 1, and therefore there is a right triangle with hypoteneuse of
length=1 which has them as legs. Also therefore there is an angle,
theta, so that sin(theta)=A/sqrt(A2+B2) and
cos(theta)=B/sqrt(A2+B2). This is "just" from
triangle geometry. Look at the picture. Then
x(t)=sqrt(A2+B2)[sin(theta)cos(t)+cos(theta)sin(t)]=sqrt(A2+B2)sin(t+theta).
We have rewritten x(t) as a magnitude,
sqrt(A2+B2), multiplied by sin(t+theta). This is
a sine "wave" with a phase angle, theta, retarding it. So the motion,
x(t), goes up and down, and the largest deviation from equilibrium is
sqrt(A2+B2) and the phase angle is arctan(A/B).
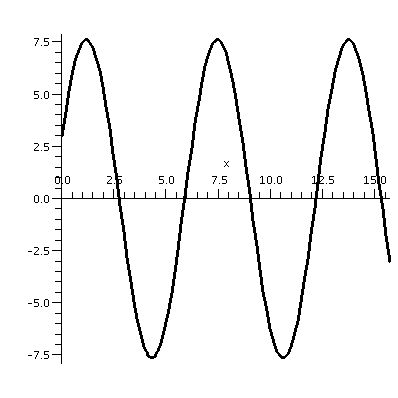
I gave Maple A=3 and B=7, and the result, 3sin(t)+7cos(t), is
plotted here. To me the fact that simple harmonic motion is the result
is not totally obvious. The magnitude,
sqrt(A2+B2), is about 7.62, and the phase angle,
arctan(A/B), is about .40.
Other solutions?
I told students that I knew another solution to x´´(t)=-x(t) besides
Acos(t)+Bsin(t). Being clever rascals (RASCAL: "One that is playfully
mischievous") they refused to believe me. I said, I have a secret
solution, W(t), which satisfies W´´(t)=-W(t) and W(0)=3 and
W´(0)=-4. They asserted that this W(t) would have to be
3cos(t)-4sin(t). So we compared them. Here is one way to
compare: form a function by taking the difference, and then look at
this difference. So we defined:
C(t)=W(t)-(3cos(t)-4sin(t)). What do we know about C(t)? Well,
C´´(t)=-C(t). This is not entirely obvious, but it comes from
subtracting the equations
W´´(t)=-W(t) and (3cos(t)-4sin(t))''=-(3cos(t)-4sin(t)).
These equations are true because both functions are solutions of the
spring motion equation. What else do we know?
C(0)=W(0)-(3cos(0)-4sin(0)). I assumed that W(0)=3, so C(0)=0.
Also, C´(t)=W´(t)-(3cos(t)-4sin(t))´ so C´(0)=0.
This shouldn't be so strange since we created C(t) to compare
solutions with the same initial velocity and position. Now C(t) is
supposed to describe the motion of a spring when the initial
displacement and the initial velocity is 0. I believe that
under those conditions the ideal spring will not move, and will not
move even forever. Why, either from the physical or
mathematical points of view, should this be so?
Conserved quantities
 I know that the kinetic
energy of a mass, m, (recall, m=1 here) is
(1/2)mv2. Therefore the kinetic energy of the mass on the
spring is (1/2)x´(t)2. The potential
energy is equal to the amount of work which must be done to
get something into a position. Now to push the mass into a
displacement of x(t) from equilibrium, we must push against the
Hooke's law force of -kx(t). But that force varies with distance. We
did some problems like this when we discussed work. What you do is
multiply kx(t) by dx, a tiny distance in which the force hardly
varies, sum, take limits, and, hey, we end up with
I know that the kinetic
energy of a mass, m, (recall, m=1 here) is
(1/2)mv2. Therefore the kinetic energy of the mass on the
spring is (1/2)x´(t)2. The potential
energy is equal to the amount of work which must be done to
get something into a position. Now to push the mass into a
displacement of x(t) from equilibrium, we must push against the
Hooke's law force of -kx(t). But that force varies with distance. We
did some problems like this when we discussed work. What you do is
multiply kx(t) by dx, a tiny distance in which the force hardly
varies, sum, take limits, and, hey, we end up with  0x(t)kx dx
and this is (1/2)kx(t)2. Also, k should be 1. Also we lost
the minus sign because we are pushing against the spring. Wow!
0x(t)kx dx
and this is (1/2)kx(t)2. Also, k should be 1. Also we lost
the minus sign because we are pushing against the spring. Wow!
The total energy of this ideal and isolated spring is the sum of the
potential and kinetic energies, so it is
TE(t)=(1/2)x´(t)2+(1/2)x(t)2. I wonder if this
energy changes over time?
The picture is supposed to show you the kinetic energy and the
potential energy separately. Indeed, it turns out that the total
is a constant. Read on!
The math person takes the energy and runs ...
Now forget the previous paragraph, and consider the TE(t) associated
with the function C(t) which has these properties:
C´´(t)=-C(t) and C(0)=0 and C´(0)=0.
Take d/dt of TE(t)=(1/2)C´(t)2+(1/2)C(t)2, and
get (minding the Chain Rule!)
TE´(t)=(1/2)2C´(t)C´´(t)+(1/2)2C(t)C´(t). More than one student
noticed that this is the same as TE´(t)=C´(t)[C´´(t)+C(t)]. But the quantity
inside the []'s is 0 since the spring equation is satisfied. Therefore
TE´(t)=0 for all t (this is a version of conservation of
energy). That means TE(t) is constant. But
TE(t)=(1/2)C´(0)2+(1/2)C(0)2, so (using the
initial conditions we have) TE(0)=0 so that TE(t) is always 0. Hey,
that means C(t)2 is always 0, so C(t)=0 always, so
W(t)-(3cos(t)-4sin(t))=0 for all t so W(t)=3cos(t)-4sin(t) and I must
have been mistaken: the W(t) I thought was different is exactly the
same as the solutions I knew before.
Therefore ...
In some sense we have a perfect Newtonian description of this very
simple system. The initial conditions of position and velocity
determine the motion of the spring for all time, using the
differential equation to describe how the spring "evolves" through
time. The key to realizing that we had all solutions and therefore had
described all of the legal motions of the system was examination of
the total energy of the system.
If I had not set k and m equal to 1 I think I would have needed to
look at cos(sqrt{m/k}t) and sin(sqrt{m/k}t) as solutions of
mx´´(t)=-kx(t).
I also asked what would happen if we changed x´´(t)=-x(t) to
x´´(t)=x(t). Some suggestions were made. And, actually, et
and e-t are solutions. And, indeed, if A and B are
constants, then Aet+Be-t are solutions. I asked
what the initial position and velocity solutions were. That is, can we
find A and B so that if x(t)=Aet+Be-t, then
x(0)=1 and x´(0)=0. With some thought, we got A=1/2 and
B=1/2. Huh. The initial velocity solution, with x(0)=0 and x´(0)=1,
has A=1/2 and B=-1/2. Indeed. So: for this equation, x´´(t)=x(t),
xpos(t)=(1/2)(et+e-t). This is the
hyperbolic cosine, called cosh(t) ("kosh of t"). And
xvel(t)=(1/2)(et-e-t). This is the
hyperbolic sine, called sinh(t) ("cinch of t").
Diary entry in progress! More to come
HOMEWORK
Material related to
what is discusssed today is in chapter 9 of the textbook, but I hope
you will be ready tomorrow to discuss any questions you may have about
problems from the remainder of chapter 7.
Monday, October 10
Exam news
Today's class
Two formulas, one for arc length and one for (lateral) surface area. I
covered this material in a very cursory fashion, because I
don't think I really have much to add to what any textbook says.
Word of the day cursory
hasty, hurried.
Diary entry in progress! More to come
The definite integral computes ...
Cut apart, approximate, sum, take limits.
Diary entry in progress! More to come
A formula for arc length
Diary entry in progress! More to come
Testing the formula
- Straight line segment
- Circular arc
- Parabolic arc
Diary entry in progress! More to come
Computational defects of the arc length formula
- A random example
- A textbook example
What's going on?
Diary entry in progress! More to come
(Lateral) surface area
Diary entry in progress! More to come
Testing the formula
- The cone
- The sphere
- The torus (with a check from Pappus!)
Diary entry in progress! More to come
Similar defects
Quote a textbook example. General comment.
Diary entry in progress! More to come
Reality?
Here is a volume which can be filled with paint but which
can't be painted.
What does this mean?
Diary entry in progress! More to come
HOMEWORK
Please be ready tomorrow to discuss any questions you may have about
problems from the remainder of chapter
7. You may wish to read about the material we discussed today in
sections 8.1 and 8.2 of the textbook.
Thursday, October 6
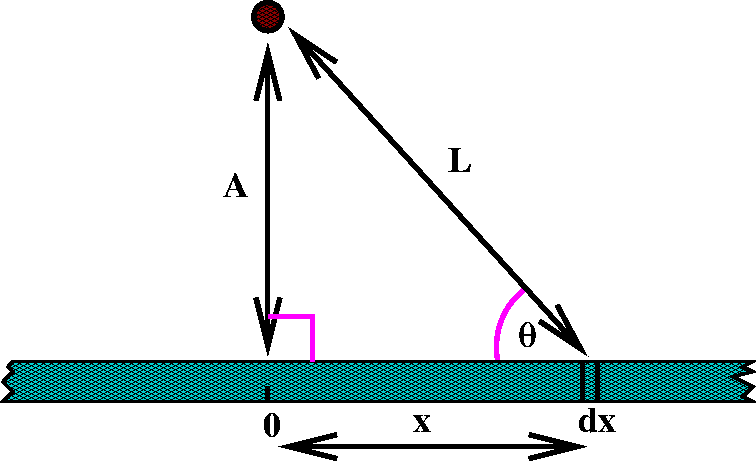 Gravity and the infinite wire
Gravity and the infinite wire
So suppose I have a small mass, m, and a straight line: a homogeneous
infinite wire, of constant density. What is the gravitational
attraction between the wire and the mass?
Shouldn't the force be infinite since the wire has infinite mass?
Well, no, because the wire's effects begin to fade with distance. But
let us be more precise.
Put a coordinate system on
the wire, whose origin will be the closest point to the external
mass. The distance between the wire and the mass will be called A. Cut
up the wire into thin dx-long pieces. Assume the density of the wire
is K. Then the dx-slab of wire has mass Kdx, and the attraction
between the mass and the wire is GmK dx/L2, where L is the
distance between the piece of wire and the mass. Notice that force's
direction is along the hyponteneuse of the triangle. We only need the
component "up", because the left/right part of the force is exactly
canceled by a symmetric piece of wire on the other side of 0. We
should multiply the magnitude by the sine of theta to get that
component: notice that this sine is A/L. So the component of the force
is [GmK dx/L2]·(A/L) which is
(GmKA/L3) dx. Since
L=sqrt(x2+A2), and we should add up all the
pieces of the force (?) the actual total force is
 -infinityinfinity(GmKA/(x2+A2)3/2) dx.
-infinityinfinity(GmKA/(x2+A2)3/2) dx.
Computing the force
It was recognized in class (note the passive voice!) that this
integral can be
computed with a trig substitution. But first we used the substitution Ax=t
so A dx=dt and
(x2+A2)3/2)=A3(t2+1)3/2.
The limits amazingly stay the same: as x goes from -infinity to
+infinity so does t (this is one nice thing about the improper
integral). The force is (another A cancels out due to the top part of
the sine fraction) (GmK/A) -infinityinfinity(1/(t2+1)3/2) dt.
-infinityinfinity(1/(t2+1)3/2) dt.
Now finish by computing  -infinityinfinity(1/(t2+1)3/2) dt
(which I don't need -- you may not notice but the point of the
computation is already done!). So take t=tan(w), then -infinity=t and
+infinity=t become w=-Pi/2 and w=Pi/2 and dt=(sec(w))2dw
and (1/(t2+1)3/2) becomes 1/(sec(w))3
and the integral becomes
-infinityinfinity(1/(t2+1)3/2) dt
(which I don't need -- you may not notice but the point of the
computation is already done!). So take t=tan(w), then -infinity=t and
+infinity=t become w=-Pi/2 and w=Pi/2 and dt=(sec(w))2dw
and (1/(t2+1)3/2) becomes 1/(sec(w))3
and the integral becomes  -Pi/2Pi/2cos(w) dw which is 2. The
force is then (2GmK/A).
-Pi/2Pi/2cos(w) dw which is 2. The
force is then (2GmK/A).
The wonderful fact is that the force between the wire and the external
mass is now inverse first power, starting from an inverse
square law of attraction. This is very neat to me. The reason why I
claimed earlier that the "point of the computation is already done" is
that I wanted to show the force was inverse first power. The
particular constant of proportionality is not as interesting to me
here.
Angstroms and molecules
Any inverse square law works the same. So if one has a tiny molecule
maybe
attracted by some force (charge, for example) to a big molecule which
is sort of straight, the computation shows that the attraction should
be approximately inverse first power. The improper integral does
closely approximate the real thing, because the "edges" (far away from
x=0) don't usually matter very much. Neat, neat, neat.
Back to Pi
My exposition of the famous Gaussian
integral is here. This integral is connected to the Central Limit
Theorem, one of the most remarkable results in probability and
statistics. Please look up this result on the web. There are many
animations demonstrating it.
The other kind of improper integral
We have been looking at improper integrals where there is a
defect in the range: the range is infinite. There are also
improper integrals where the defect is in the domain. Please remember
these integrals:
 56201[1/x5] dx=-1/(4x4)]56201=-1/(4{201}4)+1/(4{56}4)
56201[1/x5] dx=-1/(4x4)]56201=-1/(4{201}4)+1/(4{56}4)
 56201[1/x1/5] dx=(5/4)x4/5)]56201=(5/4){201}4/5)-(5/4){56}4/5)
56201[1/x1/5] dx=(5/4)x4/5)]56201=(5/4){201}4/5)-(5/4){56}4/5)
Now change 56 to B, where B is a positive number less than 201.
 B201[1/x5] dx=-1/(4x4)]B201=-1/(4{201}4)+1/(4{B}4)
B201[1/x5] dx=-1/(4x4)]B201=-1/(4{201}4)+1/(4{B}4)
 B201[1/x1/5] dx=(5/4)x4/5)]B201=(5/4){201}4/5)-(5/4){B}4/5)
B201[1/x1/5] dx=(5/4)x4/5)]B201=(5/4){201}4/5)-(5/4){B}4/5)
Now investigate what happens as B-->0+. The first integral, with
1/x5 as integrand, goes to +infinity. So we will say that
The improper integral
 0201[1/x5] dx diverges.
0201[1/x5] dx diverges.
As B-->+infinity, the value of the second integral with integrand 1/x1/5, approaches (5/4){201}4/5). So we will say that
The improper integral
 0201[1/x1/5] dx converges and its value is (5/4){201}4/5).
0201[1/x1/5] dx converges and its value is (5/4){201}4/5).
A failure of physical theory?
The repulsion between two protons is inverse square. So how much work
would be required to "push" two protons together to form another atom
with two protons in its nucleus? If we compute this work using the
improper integral that simple theory would require, then we'd have
something like  0someplace[1/x2] dx and
this integral would diverge: an infinite amount of work would be
required. So maybe we need to change theories. Maybe the neutrons
"mediate" in some way, or maybe the inverse square law of attraction
breaks down at really small (nuclear) dimensions, or maybesome other
sort of theory is needed. I don't know.
0someplace[1/x2] dx and
this integral would diverge: an infinite amount of work would be
required. So maybe we need to change theories. Maybe the neutrons
"mediate" in some way, or maybe the inverse square law of attraction
breaks down at really small (nuclear) dimensions, or maybesome other
sort of theory is needed. I don't know.
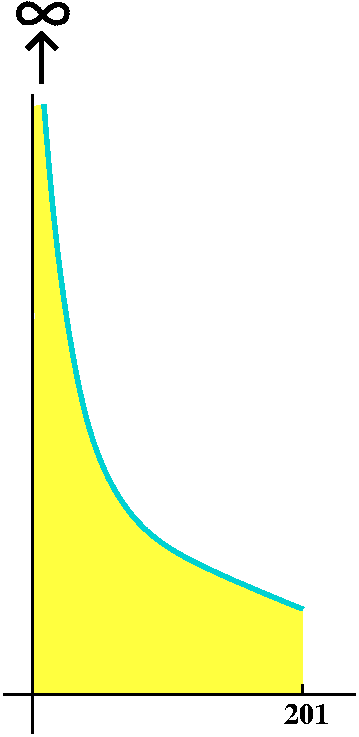
Inverse powers
We considered which integrals of the form  0201[1/xSTUFF] dx
would converge and which would diverge. Here were the conclusions we
reached:
0201[1/xSTUFF] dx
would converge and which would diverge. Here were the conclusions we
reached:
If STUFF<1, then the integral would converge.
If STUFF>1, then the integral would diverge.
When STUFF=1 we had to consider the integral separately,
because the antiderivative was no longer a simple power of x, but was
ln(x). We concluded that
If STUFF=1, then the integral would diverge.
This is exactly the reverse (except for the borderline case of 1) of
what happened in the other case. Also here is a picture. The picture doesn't help me much at all. Oh well. I like pictures.
Just one more integral
Let's look at  01ln(x) dx. I know that ln(x)-->-infinity
as x-->0+. Is there a finite amount of "area" enclosed
between the y-axis, the x-axis, and this curve?
01ln(x) dx. I know that ln(x)-->-infinity
as x-->0+. Is there a finite amount of "area" enclosed
between the y-axis, the x-axis, and this curve?
Let's integrate by parts.
u=ln(x) du=(1/x)dx
dv=dx v=x
Suppose B is positive and close to 0. Then
So  B1ln(x) dx=x·ln(x)]B1-
B1ln(x) dx=x·ln(x)]B1- B11 dx=x·ln(x)-x]B1. When x=1 we get just -l since ln(10=0. What about B·ln(B)-B? As B-->0+, the -B term -->0.
But ln(B)-->-infinity, and B-->0. Which one "wins" in the
B·ln(B) computation? Well, just as exponentials go faster, logs go slower.
To see that the limit of B·ln(B)-->0 as B-->0+,
I will need to rearrange things as a fraction so that we can take advantage,
again, of L'Hopital's rule. So:
B11 dx=x·ln(x)-x]B1. When x=1 we get just -l since ln(10=0. What about B·ln(B)-B? As B-->0+, the -B term -->0.
But ln(B)-->-infinity, and B-->0. Which one "wins" in the
B·ln(B) computation? Well, just as exponentials go faster, logs go slower.
To see that the limit of B·ln(B)-->0 as B-->0+,
I will need to rearrange things as a fraction so that we can take advantage,
again, of L'Hopital's rule. So:
ln(B)
B·ln(B)= -----
1/B
As B-->0+ this has the infinity/infinity form, so its limit (by L'H)
will be the same as the limit of (1/B)/[-1/B2]=B2/B=B.
But that's 0. So  01ln(x) dx converges and its value is
-1.
01ln(x) dx converges and its value is
-1.
This is not too surprising since  0infinitye-x dx was
computed earlier and its value was +1, and the geometric areas are the
same, just flipped over y=x.
0infinitye-x dx was
computed earlier and its value was +1, and the geometric areas are the
same, just flipped over y=x.
Exam news
Next Thursday
I hope that Mr. Scheinberg will discuss problems from
sections 7.4, 7.5, 7.7 and 7.8. progress!
HOMEWORK
Please do problems from the remainder of chapter 7.
Wednesday, October 5
I'm starting another section of the diary because the file is large
and taking too long to load. Oh well. This lecture introduced the idea
of improper integrals. I began in a characteristically
lackadaisical fashion.
Word of the day lackadaisical
- Lacking spirit, liveliness, or interest; languid.
- idle or indolent especially in a dreamy way.
I asked for the computation of two integrals.
Integral #1
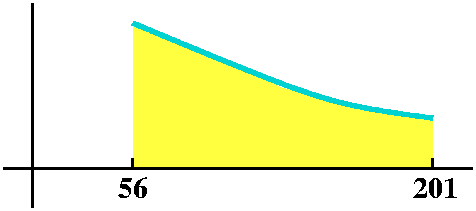
 56201[1/x5] dx=-1/(4x4)]56201=-1/(4{201}4)+1/(4{56}4)
56201[1/x5] dx=-1/(4x4)]56201=-1/(4{201}4)+1/(4{56}4)
Please notice that this integral is positive, as it should be. I have
attempted to give a rough qualitative sketch of a region in the plane
whose area is computed by the integral.
Integral #2

 56201[1/x1/5] dx=(5/4)x4/5)]56201=(5/4){201}4/5)-(5/4){56}4/5)
56201[1/x1/5] dx=(5/4)x4/5)]56201=(5/4){201}4/5)-(5/4){56}4/5)
Please notice that this integral is positive, as it should be. I have
attempted to give a rough qualitative sketch of a region in the plane
whose area is computed by the integral.
Nasty comment department
Well, yeah, the two pictures are the same, but I emphasized
that the drawing was just a tiny qualitative help to us. Why, Ms. Johnson agreed that I accidentally
left off any marks on the vertical axis so of course both pictures are
valid.
Integral #1, again
Suppose A is a large positive number. Then
 56A[1/x5] dx=-1/(4x4)]56A=-1/(4{A}4)+1/(4{56}4)
56A[1/x5] dx=-1/(4x4)]56A=-1/(4{A}4)+1/(4{56}4)
Now as A-->infinity, this "area" seems to approach a limit. The value
of that limit is 1/(4{56}4). We will say that  56infinity[1/x5] dx
converges and that the value of this improper integral is
1/(4{56}4).
Please notice that this integral is positive, as it should be. I have
attempted to give a rough qualitative sketch of a region in the plane
whose area is computed by the integral.
56infinity[1/x5] dx
converges and that the value of this improper integral is
1/(4{56}4).
Please notice that this integral is positive, as it should be. I have
attempted to give a rough qualitative sketch of a region in the plane
whose area is computed by the integral.
Integral #2, again
Suppose A is a large positive number. Then
 56A[1/x1/5] dx=(5/4)x4/5)]56A=(5/4){A}4/5)-(5/4){56}4/5)
56A[1/x1/5] dx=(5/4)x4/5)]56A=(5/4){A}4/5)-(5/4){56}4/5)
Now as A-->infinity, this "area" seems to get larger. It certainly does not approach a finite limit. We will say that  56infinity[1/x1/5] dx diverges (or does not converge).
56infinity[1/x1/5] dx diverges (or does not converge).

Huh?
Both of the regions from 56 "out to infinity" look maybe something
like what I've drawn. Although I love pictures, I can't tell by
looking that one of these regions "has" finite area, and the other one
does not. The phenomenon seems to be subtle.
We discussed the {con|di}vergence of the following integrals (or
something like them):
 56infinity236/x5 dx:
even though this is "larger" than the convergent integral, it also
converges, and its value is 238 times the value of the convergent
integral.
56infinity236/x5 dx:
even though this is "larger" than the convergent integral, it also
converges, and its value is 238 times the value of the convergent
integral.
 56infinity1/(x5+44x2) dx. This
integral also converges. The region is smaller than the region we
analyzed before, because the 44x2 in the denominator
(bottom, darn it!) makes the height lower, but still positive. The value of this integral might be difficult to determine, but I think the value of the integral is positive, and less than 1/(4{56}4).
56infinity1/(x5+44x2) dx. This
integral also converges. The region is smaller than the region we
analyzed before, because the 44x2 in the denominator
(bottom, darn it!) makes the height lower, but still positive. The value of this integral might be difficult to determine, but I think the value of the integral is positive, and less than 1/(4{56}4).
Well, this all seems slightly silly. But it isn't because improper
integrals arise frequently in applications and sometimes are much
easier and more important to compute than standard definite
integrals.
Escape ..
 When I was very young, I read a science fiction novel by Robert
Heinlein which stated "... the escape velocity from the Earth is 7
miles per second ..." and now I would like to sort of verify this
using only well-known (?) facts and some big ideas of physics.
When I was very young, I read a science fiction novel by Robert
Heinlein which stated "... the escape velocity from the Earth is 7
miles per second ..." and now I would like to sort of verify this
using only well-known (?) facts and some big ideas of physics.
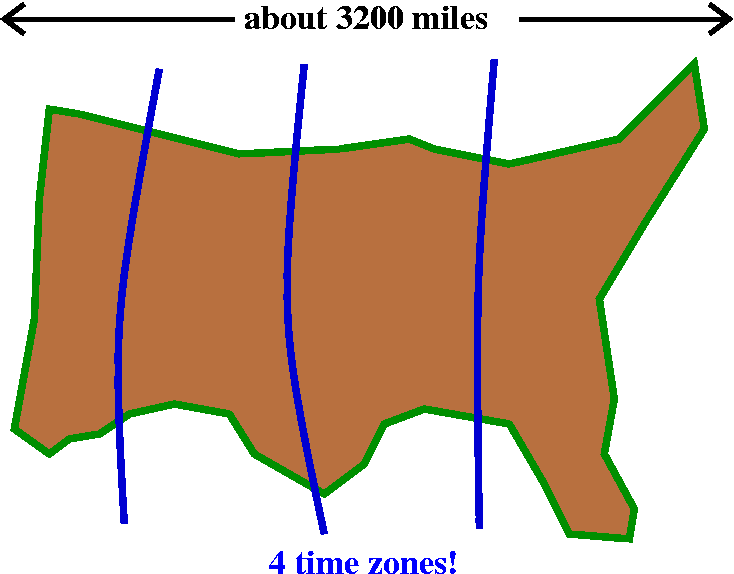
The radius of the earth
Well, a sketch of the (continental)
United States is shown to the right. There are 4 time zones. The
U.S. is about 3000+ (maybe 3200?) miles wide. Therefore one time zone
is about 1000 miles wide (I think the Pacific time zone actually slops
a bit into the ocean), and since there are 24 time zones around the
world, the circumference of the world is ... uhh ... about 25,000
miles. Or so. And therefore the radius of the earth is that divided by
2Pi, and therefore the radius of the earth is about 4,000 miles.
Newton and gravitation
Two masses attract each other with a force
whose magnitude is proportional to the product of the masses and
inversely proportional to the square of the distance between
them. Therefore, if I have a mass, m, and if the Earth has mass M, the
magnitude of the force of gravity is GmM/r2. G is a
constant.
Work lifting up
Suppose we want to lift a mass m from the surface
of the earth to a distance R, where R is very large. Then the work
done is force multiplied by distance. The force needed to act against
gravity certainly changes with distance. So I will compute the work
with calculus. If x is some distance between 4,000 and R, then the
force is GmM/x2. If the distance is a little bit, say, dx,
then the work dW needed is GmM/x2 dx. The total work,
W, is  x=4,000RGmM/x2 dx which
I can compute readily as -GmM/x]4,000R=GmM({1/4,000}-1/R). I
think I did the minus signs correctly. Notice that as R-->infinity,
this work -->GmM/4,000: this is the most work you can do, to get
anywhere in the universe (assuming the universe is empty except for
the mass m and the earth, of course).
Kinetic energy
x=4,000RGmM/x2 dx which
I can compute readily as -GmM/x]4,000R=GmM({1/4,000}-1/R). I
think I did the minus signs correctly. Notice that as R-->infinity,
this work -->GmM/4,000: this is the most work you can do, to get
anywhere in the universe (assuming the universe is empty except for
the mass m and the earth, of course).
Kinetic energy
How much kinetic energy would we need to supply
to the mass m so that it would equal the potential energy the mass
would have if it were lifted out to anywhere in the universe?
Well, kinetic energy is (1/2)mv2 and that potential energy
we already computed is GmM/4,000. So (1/2)mv2=GmM/4,000,
and thus v2=2GM/4,000. But what is GM?
But F=ma
On the earth, a, the acceleration of gravity, is 32
ft/(sec)2. Yes, this is an archaic system of measurement,
but that's part of the fun. But also F=GmM/(4,000)2. So
GmM/(4,000)2=32m. Therefore
GM=(4,000)2·32.
And the answer is
...
v2=2GM/4,000=2[(4,000)2·32]/4,000=8,000·32=
(256,000)/(5,280)=(approximately)50. The 5,280 came from converting
feet to miles. Therefore v, the escape velocity, is about 7. I think
this computation is so silly that it is cool.
Inverse powers
We considered which integrals of the form  56infinity[1/xSTUFF] dx
would converge and which would diverge. Here were the conclusions we
reached:
56infinity[1/xSTUFF] dx
would converge and which would diverge. Here were the conclusions we
reached:
If STUFF>1, then the integral would converge.
If STUFF<1, then the integral would diverge.
When STUFF=1 we had to consider the integral separately,
because the antiderivative was no longer a simple power of x, but was
ln(x). We concluded that
If STUFF=1, then the integral would diverge.
Exponential decay versus polynomial growth
I asked which other improper integrals might converge. Well,
exponential decay was suggested. So, of course  0infinitye-xdx converges. We
computed this as the limit of
0infinitye-xdx converges. We
computed this as the limit of  0Ae-xdx as A-->infinity, and
we got 1 as the answer. I wondered if, say,
0Ae-xdx as A-->infinity, and
we got 1 as the answer. I wondered if, say,  0infinityx56e-xdx
converged?
0infinityx56e-xdx
converged?
Thinking about how
x56e-x behaves when x gets large leads to the question:
which of x56 and ex gets bigger faster? So I
answer this:
lim x56 lim 56x55 [ After ] lim const
x-->inf ---- =(L'hop) x-->inf ---- = [ several ]= x-->inf ----
ex ex [uses of L'H] ex
So this limit must be 0.
This is important. For example, consider
the function f(x)=x3,124e-.00002x. Here there is
an enormous power of x, multiplied by a very slightly (?)
decreasing exponential. Let me call upon something that can
compute better than I can:
> f:=x->x^3124*exp(-.00002*x);
3124
f := x -> x exp(-0.00002 x)
> f(10);
3124
0.9998000200 10
> f(100);
6248
0.9980019987 10
> f(10^10);
-55618
0.1269460960 10
So f(10) is large, and f(100) is even larger. And f(1010)
is very, very, very small, indeed. In many applications, exponential
growth and decay occur, and they eventually "win" over what
might seem huge competition.
Some more improper integrals
We had already computed  0infinitye-xdx=1. Now I
computed
0infinitye-xdx=1. Now I
computed  0infinityxe-xdx. I used (of
course) integration by parts. Here the parts were:
0infinityxe-xdx. I used (of
course) integration by parts. Here the parts were:
u = x du=dx
dv = e-xdx v=-e-x
The boundary term is (x)(-e-x)]0A (as A-->infinity).
When x=0 this "disappears" because of the first factor. And
Ae-A-->0 because exponential decay is faster
than any polynomial growth. The minus signs cancel, and we
seem to see that
 0infinityxe-xdx converges and
its value is 1.
0infinityxe-xdx converges and
its value is 1.
I wonder what  0infinityxne-xdx
is? Are all of the values equal to 1? What's the pattern?
0infinityxne-xdx
is? Are all of the values equal to 1? What's the pattern?
Go whole hog
"To engage in something without reservation or constraint"
"If you go the whole hog, you do something completely or to its
limits."
"To carry out or do something completely."
I will do all of these computations at the same time. Suppose n is a
positive integer. Define In to be
 0infinityxne-xdx,
which will be a convergent improper integral. What is its value? So I
will integrate by parts.
0infinityxne-xdx,
which will be a convergent improper integral. What is its value? So I
will integrate by parts.
u = xn du=nxn-1dx
dv = e-xdx v=-e-x
The boundary term here is
(xn)(-e-x)]0A (as A-->infinity).
When x=0 this "disappears" (for n positive integer!) because of
the first factor. And
Ane-A-->0 because exponential decay is faster
than any polynomial growth. The minus signs cancel, and we see that
knowing that the integral In-1 converges implies that the
integral In converges, and In=n·In-1
So these integrals are ... (!!!)
We know these facts. If In= 0infinityxne-xdx,
then
0infinityxne-xdx,
then
I1=1
In=n·In-1
Well, I happen to know some other numbers which obey these rules: they
are the factorials. Therefore In=n! for all n.
Officially this is a proof by a technique
called
mathematical induction.
Maple knows these integrals. Look, 120 is 5!:
> int(x^5*exp(-x),x=0..infinity);
120
And therefore one-half factorial is ...
So the integral expression  0infinityxne-xdx
can be used to define n! for n's different from positive integer
n.
0infinityxne-xdx
can be used to define n! for n's different from positive integer
n.
> int(sqrt(x)*exp(-x),x=0..infinity);
1/2
Pi
-----
2
So (1/2)! is sqrt(Pi)/2.
Not clearly!!!!
Maintained by
greenfie@math.rutgers.edu and last modified 9/11/2005.
![]() STARTING THETAENDING THETA(1/2)r2 dtheta
STARTING THETAENDING THETA(1/2)r2 dtheta I applied this to find the equation of a line tangent to my favorite
curve, x=t^3-t, y=1/(1+t^2), when t=2. I found a point on the curve
and I found the slope of the tangent line, and then found the line. It
sloped slightly down, just as the picture suggested. Then I found the
angle between the parts of the curve at the "self-intersection", when
t=+/-1. This involved some work with geometry and with finding the
slopes of the appropriate tangent lines. The best we could do is with
some numerical approximations to the angles.
I applied this to find the equation of a line tangent to my favorite
curve, x=t^3-t, y=1/(1+t^2), when t=2. I found a point on the curve
and I found the slope of the tangent line, and then found the line. It
sloped slightly down, just as the picture suggested. Then I found the
angle between the parts of the curve at the "self-intersection", when
t=+/-1. This involved some work with geometry and with finding the
slopes of the appropriate tangent lines. The best we could do is with
some numerical approximations to the angles.
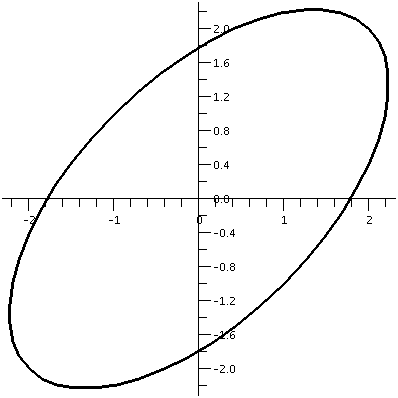 I asked people what the curve x=sin(t)+2cos(t), y=2cos(t)-sin(t),
looked like. We decided it was bounded because sine and cosine are
always between -1 and +1, so the points of the curve must be in the
box -3
I asked people what the curve x=sin(t)+2cos(t), y=2cos(t)-sin(t),
looked like. We decided it was bounded because sine and cosine are
always between -1 and +1, so the points of the curve must be in the
box -3![]() STARTENDsqrt(f'(t)^2+g'(t)^2) dt. The
integrand (the function integrated) is frequently called the speed:
sqrt(f'(t)^2+g'(t)^2).
STARTENDsqrt(f'(t)^2+g'(t)^2) dt. The
integrand (the function integrated) is frequently called the speed:
sqrt(f'(t)^2+g'(t)^2).
 I tried to describe the parametric description of a cycloid. This is done
with a slightly different explanation in section 10.1 of the
text.
I tried to describe the parametric description of a cycloid. This is done
with a slightly different explanation in section 10.1 of the
text.
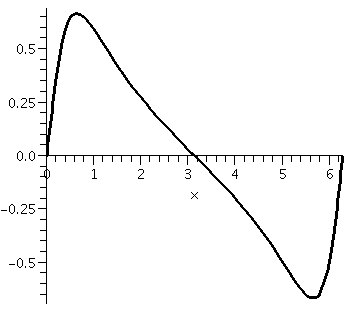
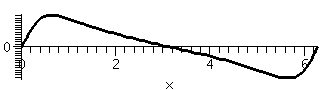
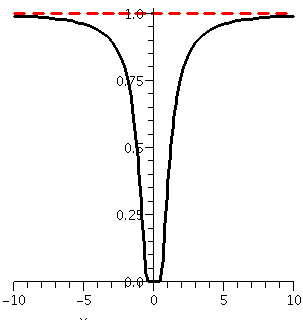 A horrible function
A horrible function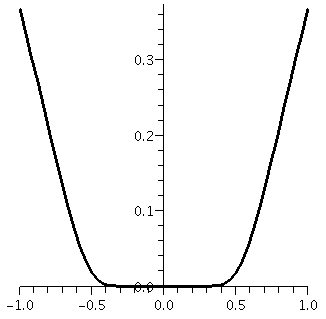 The most interesting aspect of this function is its behavior near 0
which doesn't show up much in the picture above. So here is a
picture with x between -.1 and .1, again distorted to fill a square.
This function's graph is flat near 0. In fact, most people who
think about this function state that it is infinitely flat near
0.
The most interesting aspect of this function is its behavior near 0
which doesn't show up much in the picture above. So here is a
picture with x between -.1 and .1, again distorted to fill a square.
This function's graph is flat near 0. In fact, most people who
think about this function state that it is infinitely flat near
0.
![]() ABS(x) dx=
ABS(x) dx=![]() ABSUMn=0infinitycn(x-a)n dx=SUMn=0infinitycn((B-a)n-(A-a)n) if both A and B are inside the interval of
convergence.
ABSUMn=0infinitycn(x-a)n dx=SUMn=0infinitycn((B-a)n-(A-a)n) if both A and B are inside the interval of
convergence.
![]() 01cos(x3) dx as the sum
of a series. How many terms are needed to get accuracy up to
10-10?
01cos(x3) dx as the sum
of a series. How many terms are needed to get accuracy up to
10-10?
 If |x|<=1/2, I split the series (for no good reason) into two
pieces:
If |x|<=1/2, I split the series (for no good reason) into two
pieces:![]() 121/(x2+t) dx=
121/(x2+t) dx=![]() 12limt-->0[1/(x2+t)] dx
12limt-->0[1/(x2+t)] dx![]() 01A2(1-x)xAdx=1
but
01A2(1-x)xAdx=1
but
![]() 01limA-->infinity[A2(1-x)xA]dx=0.
01limA-->infinity[A2(1-x)xA]dx=0. The instructor shows a device with the help of "a student"
(Mr. Townley)
The instructor shows a device with the help of "a student"
(Mr. Townley)![]() anywhereinfinityf(x) dx both converge and diverge together.
anywhereinfinityf(x) dx both converge and diverge together.
 The harmonic numbers revisited
The harmonic numbers revisited
![]() 02cos(x7)/(1+x4) dx. No
one knows an antiderivative of this function in terms of familiar
functions. I could define a sequence in the following way:
02cos(x7)/(1+x4) dx. No
one knows an antiderivative of this function in terms of familiar
functions. I could define a sequence in the following way: Sqrt(2) by Newton's method
Sqrt(2) by Newton's method

 The domino
theory was a part of U.S. foreign policy for a long time (it still
might be). Here, my dominos represent a proof technique called
mathematical induction. I just used the technique to try to
convince you that for all n, xn=yn. I hope that
you appreciate the almost paradoxical strength of this: a finite
amount of writing has proved an infinite number of statements!
The domino
theory was a part of U.S. foreign policy for a long time (it still
might be). Here, my dominos represent a proof technique called
mathematical induction. I just used the technique to try to
convince you that for all n, xn=yn. I hope that
you appreciate the almost paradoxical strength of this: a finite
amount of writing has proved an infinite number of statements!
![]() 1x1/t dt=
1x1/t dt=![]() 1x1/q dq=
1x1/q dq=![]() 1x1/w dw.
1x1/w dw.
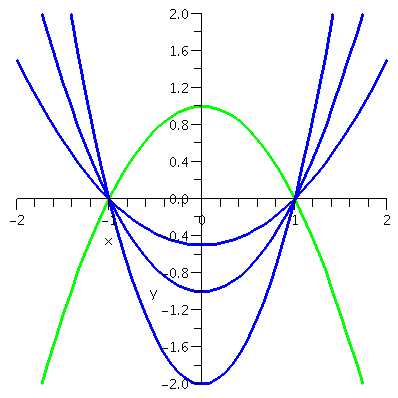
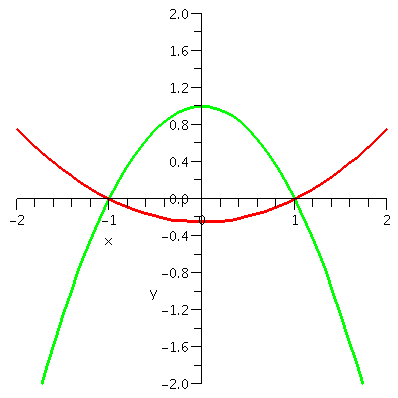
 A very dilute bit of physics: heating a thin metal plate
A very dilute bit of physics: heating a thin metal plate Suppose I give you a heat distribution on the edge of the plate, as
shown. The red stuff is supposed to be flames, and the blue stuff is
supposed to be ice cubes. If I let time pass and keep the ice cubes
and flames on the edge, maybe you can see that eventually the
temperature distribution inside the plate will stabilize, and we will
get a steady state temperature distribution. Maybe you can see the
heat flow curves ("flux") and the isothermals. It is not
obvious that these families of curves are orthogonal, but this
actually is true!
Suppose I give you a heat distribution on the edge of the plate, as
shown. The red stuff is supposed to be flames, and the blue stuff is
supposed to be ice cubes. If I let time pass and keep the ice cubes
and flames on the edge, maybe you can see that eventually the
temperature distribution inside the plate will stabilize, and we will
get a steady state temperature distribution. Maybe you can see the
heat flow curves ("flux") and the isothermals. It is not
obvious that these families of curves are orthogonal, but this
actually is true!
 This should be 0, so (if we multiply by x4), we get
dy/dx(x2)-2xy=0, and then
dy/dx=2y/x. Now if we want curves which are orthogonal to these
curves, we need dy/dx to be the negative reciprocal of this. The
orthogonal curves must satisfy the differential equation
dy/dx=-x/2y.
This should be 0, so (if we multiply by x4), we get
dy/dx(x2)-2xy=0, and then
dy/dx=2y/x. Now if we want curves which are orthogonal to these
curves, we need dy/dx to be the negative reciprocal of this. The
orthogonal curves must satisfy the differential equation
dy/dx=-x/2y.![]() 2y dy=
2y dy=![]() -x dx
-x dx![]() 0xe(w2)dw+C. The
Fundamental Theorem of Calculus says that
F'(x)=e(x2) and the "+C" allows adjustment for
an initial condition. In fact, we've just rewritten the differential
equation and transferred the computational "responsibility" to the
definite integral. As I mentioned back when we were first starting
methods of antidifferentiation, there's no way to find an
explicit antiderivative of this function in terms of standard
functions. Evaluation must be done through an approximation
technique. So learning about the solution (that it exists, that there
is exactly one) has not helped at all.
0xe(w2)dw+C. The
Fundamental Theorem of Calculus says that
F'(x)=e(x2) and the "+C" allows adjustment for
an initial condition. In fact, we've just rewritten the differential
equation and transferred the computational "responsibility" to the
definite integral. As I mentioned back when we were first starting
methods of antidifferentiation, there's no way to find an
explicit antiderivative of this function in terms of standard
functions. Evaluation must be done through an approximation
technique. So learning about the solution (that it exists, that there
is exactly one) has not helped at all.
 Example 2 I think this equation has more subtle aspects. Let's
look at y´(x)=xy2. This equation looks "easy". It is
certainly separable, and the f(x,y) seems rather simple. We separate
variables and integrate: so dy/y2=x dx and then
-1/y=(1/2)x2+C and we can even solve for y in terms of x:
y=1/(C-{1/2}x2). (I renamed C.) Now suppose we want the
solution to satisfy the initial condition: when x=0, y=8. Then C
should be 1/8, and the solution looks like
y=1/({1/8}-{1/2}x2). This is o.k., a nice function. A
picture is to the right (with units on the horizontal and vertical
axes are rather different). We get into some trouble when we think
about the solution curve. Suppose the curve represents the growth of
"something" (I think I suggested "wahoonies" in class). Usually x
represents the "independent" variable, say, time. What happens to the
growth of the wahoonies? Look at {1/8}-{1/2}x2 from x=0
(where it is 1/8) up to ... well, this should not be 0 because it is
in the denominator. It will be 0 when x=1/2 (also, of course,
-1/2). The growth gets larger and large, and, finally, explodes (!?)
at 1/2 (also, of course, backwards at -1/2). We can't predict the
population of wahoonies on further than 1/2 or further backwards than
-1/2. This disaster is, to me, unforseen in the nice function
xy2. Things are actually worse than this.
Example 2 I think this equation has more subtle aspects. Let's
look at y´(x)=xy2. This equation looks "easy". It is
certainly separable, and the f(x,y) seems rather simple. We separate
variables and integrate: so dy/y2=x dx and then
-1/y=(1/2)x2+C and we can even solve for y in terms of x:
y=1/(C-{1/2}x2). (I renamed C.) Now suppose we want the
solution to satisfy the initial condition: when x=0, y=8. Then C
should be 1/8, and the solution looks like
y=1/({1/8}-{1/2}x2). This is o.k., a nice function. A
picture is to the right (with units on the horizontal and vertical
axes are rather different). We get into some trouble when we think
about the solution curve. Suppose the curve represents the growth of
"something" (I think I suggested "wahoonies" in class). Usually x
represents the "independent" variable, say, time. What happens to the
growth of the wahoonies? Look at {1/8}-{1/2}x2 from x=0
(where it is 1/8) up to ... well, this should not be 0 because it is
in the denominator. It will be 0 when x=1/2 (also, of course,
-1/2). The growth gets larger and large, and, finally, explodes (!?)
at 1/2 (also, of course, backwards at -1/2). We can't predict the
population of wahoonies on further than 1/2 or further backwards than
-1/2. This disaster is, to me, unforseen in the nice function
xy2. Things are actually worse than this. If we change the
initial condition to, say, (0,1/80,000), then the unique solution is
y=1/({1/80,000}-{1/2}x2) and the domain of this function is
only (-1/200,+1/200): the wahoonie explosion is even closer in
time. Another picture is shown, with even more distorted axes, but the
idea is, I hope, clear: a narrower steeper curve with a higher up
initial condition. As the initial number of wahoonies grows, the
explosion comes closer and closer in time.
If we change the
initial condition to, say, (0,1/80,000), then the unique solution is
y=1/({1/80,000}-{1/2}x2) and the domain of this function is
only (-1/200,+1/200): the wahoonie explosion is even closer in
time. Another picture is shown, with even more distorted axes, but the
idea is, I hope, clear: a narrower steeper curve with a higher up
initial condition. As the initial number of wahoonies grows, the
explosion comes closer and closer in time.
 Well, how can we use this formula? I can try to match an initial
condition, and then I can look at a solution curve. In class I used
(0,3/4) (so K was "clearly" 3) but let me be more adventurous
here. When t=0 in Ket/(1+Ket) we get K/(1+K).
If we want K/(1+K) to be .37, and approximate value of K is .587 (yes,
a silicon pal helped me here). And my same pal graphed the solution
curve shown to the right. It sure looks like the curve is an
increasing function of time, and to the right it approaches +1 and to
the left it approaches 0. You can check these limits using the
algebraic formula:
Well, how can we use this formula? I can try to match an initial
condition, and then I can look at a solution curve. In class I used
(0,3/4) (so K was "clearly" 3) but let me be more adventurous
here. When t=0 in Ket/(1+Ket) we get K/(1+K).
If we want K/(1+K) to be .37, and approximate value of K is .587 (yes,
a silicon pal helped me here). And my same pal graphed the solution
curve shown to the right. It sure looks like the curve is an
increasing function of time, and to the right it approaches +1 and to
the left it approaches 0. You can check these limits using the
algebraic formula:

 And another automomous equation
And another automomous equation What we need to know
What we need to know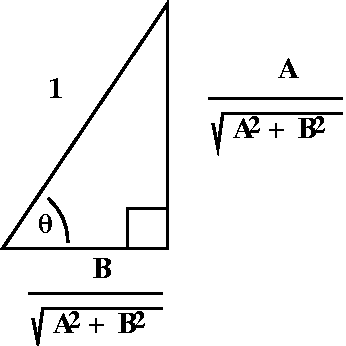 I didn't do this in class, mainly because I find algebra
painful. The algebra following is really motivated by physical
considerations, so maybe that excuses it.
I didn't do this in class, mainly because I find algebra
painful. The algebra following is really motivated by physical
considerations, so maybe that excuses it.
 I know that the kinetic
energy of a mass, m, (recall, m=1 here) is
(1/2)mv2. Therefore the kinetic energy of the mass on the
spring is (1/2)x´(t)2. The potential
energy is equal to the amount of work which must be done to
get something into a position. Now to push the mass into a
displacement of x(t) from equilibrium, we must push against the
Hooke's law force of -kx(t). But that force varies with distance. We
did some problems like this when we discussed work. What you do is
multiply kx(t) by dx, a tiny distance in which the force hardly
varies, sum, take limits, and, hey, we end up with
I know that the kinetic
energy of a mass, m, (recall, m=1 here) is
(1/2)mv2. Therefore the kinetic energy of the mass on the
spring is (1/2)x´(t)2. The potential
energy is equal to the amount of work which must be done to
get something into a position. Now to push the mass into a
displacement of x(t) from equilibrium, we must push against the
Hooke's law force of -kx(t). But that force varies with distance. We
did some problems like this when we discussed work. What you do is
multiply kx(t) by dx, a tiny distance in which the force hardly
varies, sum, take limits, and, hey, we end up with ![]() 0x(t)kx dx
and this is (1/2)kx(t)2. Also, k should be 1. Also we lost
the minus sign because we are pushing against the spring. Wow!
0x(t)kx dx
and this is (1/2)kx(t)2. Also, k should be 1. Also we lost
the minus sign because we are pushing against the spring. Wow! Gravity and the infinite wire
Gravity and the infinite wire![]() -infinityinfinity(GmKA/(x2+A2)3/2) dx.
-infinityinfinity(GmKA/(x2+A2)3/2) dx.
![]() -infinityinfinity(1/(t2+1)3/2) dt.
-infinityinfinity(1/(t2+1)3/2) dt.
![]() -infinityinfinity(1/(t2+1)3/2) dt
(which I don't need -- you may not notice but the point of the
computation is already done!). So take t=tan(w), then -infinity=t and
+infinity=t become w=-Pi/2 and w=Pi/2 and dt=(sec(w))2dw
and (1/(t2+1)3/2) becomes 1/(sec(w))3
and the integral becomes
-infinityinfinity(1/(t2+1)3/2) dt
(which I don't need -- you may not notice but the point of the
computation is already done!). So take t=tan(w), then -infinity=t and
+infinity=t become w=-Pi/2 and w=Pi/2 and dt=(sec(w))2dw
and (1/(t2+1)3/2) becomes 1/(sec(w))3
and the integral becomes ![]() -Pi/2Pi/2cos(w) dw which is 2. The
force is then (2GmK/A).
-Pi/2Pi/2cos(w) dw which is 2. The
force is then (2GmK/A). ![]() 56201[1/x5] dx=-1/(4x4)]56201=-1/(4{201}4)+1/(4{56}4)
56201[1/x5] dx=-1/(4x4)]56201=-1/(4{201}4)+1/(4{56}4)![]() 56201[1/x1/5] dx=(5/4)x4/5)]56201=(5/4){201}4/5)-(5/4){56}4/5)
56201[1/x1/5] dx=(5/4)x4/5)]56201=(5/4){201}4/5)-(5/4){56}4/5)![]() B201[1/x5] dx=-1/(4x4)]B201=-1/(4{201}4)+1/(4{B}4)
B201[1/x5] dx=-1/(4x4)]B201=-1/(4{201}4)+1/(4{B}4)![]() B201[1/x1/5] dx=(5/4)x4/5)]B201=(5/4){201}4/5)-(5/4){B}4/5)
B201[1/x1/5] dx=(5/4)x4/5)]B201=(5/4){201}4/5)-(5/4){B}4/5)![]() 0201[1/x5] dx diverges.
0201[1/x5] dx diverges. ![]() 0201[1/x1/5] dx converges and its value is (5/4){201}4/5).
0201[1/x1/5] dx converges and its value is (5/4){201}4/5).
![]() 0someplace[1/x2] dx and
this integral would diverge: an infinite amount of work would be
required. So maybe we need to change theories. Maybe the neutrons
"mediate" in some way, or maybe the inverse square law of attraction
breaks down at really small (nuclear) dimensions, or maybesome other
sort of theory is needed. I don't know.
0someplace[1/x2] dx and
this integral would diverge: an infinite amount of work would be
required. So maybe we need to change theories. Maybe the neutrons
"mediate" in some way, or maybe the inverse square law of attraction
breaks down at really small (nuclear) dimensions, or maybesome other
sort of theory is needed. I don't know.

![]() 0201[1/xSTUFF] dx
would converge and which would diverge. Here were the conclusions we
reached:
0201[1/xSTUFF] dx
would converge and which would diverge. Here were the conclusions we
reached:![]() 01ln(x) dx. I know that ln(x)-->-infinity
as x-->0+. Is there a finite amount of "area" enclosed
between the y-axis, the x-axis, and this curve?
01ln(x) dx. I know that ln(x)-->-infinity
as x-->0+. Is there a finite amount of "area" enclosed
between the y-axis, the x-axis, and this curve?
![]() B1ln(x) dx=x·ln(x)]B1-
B1ln(x) dx=x·ln(x)]B1-![]() B11 dx=x·ln(x)-x]B1. When x=1 we get just -l since ln(10=0. What about B·ln(B)-B? As B-->0+, the -B term -->0.
But ln(B)-->-infinity, and B-->0. Which one "wins" in the
B·ln(B) computation? Well, just as exponentials go faster, logs go slower.
To see that the limit of B·ln(B)-->0 as B-->0+,
I will need to rearrange things as a fraction so that we can take advantage,
again, of L'Hopital's rule. So:
B11 dx=x·ln(x)-x]B1. When x=1 we get just -l since ln(10=0. What about B·ln(B)-B? As B-->0+, the -B term -->0.
But ln(B)-->-infinity, and B-->0. Which one "wins" in the
B·ln(B) computation? Well, just as exponentials go faster, logs go slower.
To see that the limit of B·ln(B)-->0 as B-->0+,
I will need to rearrange things as a fraction so that we can take advantage,
again, of L'Hopital's rule. So:![]() 01ln(x) dx converges and its value is
-1.
01ln(x) dx converges and its value is
-1.![]() 0infinitye-x dx was
computed earlier and its value was +1, and the geometric areas are the
same, just flipped over y=x.
0infinitye-x dx was
computed earlier and its value was +1, and the geometric areas are the
same, just flipped over y=x.

![]() 56201[1/x5] dx=-1/(4x4)]56201=-1/(4{201}4)+1/(4{56}4)
56201[1/x5] dx=-1/(4x4)]56201=-1/(4{201}4)+1/(4{56}4)

![]() 56201[1/x1/5] dx=(5/4)x4/5)]56201=(5/4){201}4/5)-(5/4){56}4/5)
56201[1/x1/5] dx=(5/4)x4/5)]56201=(5/4){201}4/5)-(5/4){56}4/5)
![]() 56A[1/x5] dx=-1/(4x4)]56A=-1/(4{A}4)+1/(4{56}4)
56A[1/x5] dx=-1/(4x4)]56A=-1/(4{A}4)+1/(4{56}4)
![]() 56infinity[1/x5] dx
converges and that the value of this improper integral is
1/(4{56}4).
Please notice that this integral is positive, as it should be. I have
attempted to give a rough qualitative sketch of a region in the plane
whose area is computed by the integral.
56infinity[1/x5] dx
converges and that the value of this improper integral is
1/(4{56}4).
Please notice that this integral is positive, as it should be. I have
attempted to give a rough qualitative sketch of a region in the plane
whose area is computed by the integral.
![]() 56A[1/x1/5] dx=(5/4)x4/5)]56A=(5/4){A}4/5)-(5/4){56}4/5)
56A[1/x1/5] dx=(5/4)x4/5)]56A=(5/4){A}4/5)-(5/4){56}4/5)
![]() 56infinity[1/x1/5] dx diverges (or does not converge).
56infinity[1/x1/5] dx diverges (or does not converge).

![]() 56infinity236/x5 dx:
even though this is "larger" than the convergent integral, it also
converges, and its value is 238 times the value of the convergent
integral.
56infinity236/x5 dx:
even though this is "larger" than the convergent integral, it also
converges, and its value is 238 times the value of the convergent
integral.
![]() 56infinity1/(x5+44x2) dx. This
integral also converges. The region is smaller than the region we
analyzed before, because the 44x2 in the denominator
(bottom, darn it!) makes the height lower, but still positive. The value of this integral might be difficult to determine, but I think the value of the integral is positive, and less than 1/(4{56}4).
56infinity1/(x5+44x2) dx. This
integral also converges. The region is smaller than the region we
analyzed before, because the 44x2 in the denominator
(bottom, darn it!) makes the height lower, but still positive. The value of this integral might be difficult to determine, but I think the value of the integral is positive, and less than 1/(4{56}4).
 When I was very young, I read a science fiction novel by Robert
Heinlein which stated "... the escape velocity from the Earth is 7
miles per second ..." and now I would like to sort of verify this
using only well-known (?) facts and some big ideas of physics.
When I was very young, I read a science fiction novel by Robert
Heinlein which stated "... the escape velocity from the Earth is 7
miles per second ..." and now I would like to sort of verify this
using only well-known (?) facts and some big ideas of physics.
![]() x=4,000RGmM/x2 dx which
I can compute readily as -GmM/x]4,000R=GmM({1/4,000}-1/R). I
think I did the minus signs correctly. Notice that as R-->infinity,
this work -->GmM/4,000: this is the most work you can do, to get
anywhere in the universe (assuming the universe is empty except for
the mass m and the earth, of course).
x=4,000RGmM/x2 dx which
I can compute readily as -GmM/x]4,000R=GmM({1/4,000}-1/R). I
think I did the minus signs correctly. Notice that as R-->infinity,
this work -->GmM/4,000: this is the most work you can do, to get
anywhere in the universe (assuming the universe is empty except for
the mass m and the earth, of course).
![]() 56infinity[1/xSTUFF] dx
would converge and which would diverge. Here were the conclusions we
reached:
56infinity[1/xSTUFF] dx
would converge and which would diverge. Here were the conclusions we
reached:![]() 0infinitye-xdx converges. We
computed this as the limit of
0infinitye-xdx converges. We
computed this as the limit of ![]() 0Ae-xdx as A-->infinity, and
we got 1 as the answer. I wondered if, say,
0Ae-xdx as A-->infinity, and
we got 1 as the answer. I wondered if, say, ![]() 0infinityx56e-xdx
converged?
0infinityx56e-xdx
converged?
![]() 0infinitye-xdx=1. Now I
computed
0infinitye-xdx=1. Now I
computed ![]() 0infinityxe-xdx. I used (of
course) integration by parts. Here the parts were:
0infinityxe-xdx. I used (of
course) integration by parts. Here the parts were:![]() 0infinityxe-xdx converges and
its value is 1.
0infinityxe-xdx converges and
its value is 1.
![]() 0infinityxne-xdx
is? Are all of the values equal to 1? What's the pattern?
0infinityxne-xdx
is? Are all of the values equal to 1? What's the pattern?
![]() 0infinityxne-xdx,
which will be a convergent improper integral. What is its value? So I
will integrate by parts.
0infinityxne-xdx,
which will be a convergent improper integral. What is its value? So I
will integrate by parts.![]() 0infinityxne-xdx,
then
0infinityxne-xdx,
then![]() 0infinityxne-xdx
can be used to define n! for n's different from positive integer
n.
0infinityxne-xdx
can be used to define n! for n's different from positive integer
n.