Past, current and future research topics include:
Optimal bounds and optimal microstructures for multiphase composites
Eshelby inclusion problems
Predictive modeling of multifunctional composites
Dynamic modeling of heterogeneous structures/media
Variational inequalities and their applications in designs
Superconductive composites and modeling
Surface energy and elasticity
Thermoelectric materials, modeling, design and energy harvesting
Continuum theory for multiferroic materials
Multiscale analysis: homogenization theory and theories for lower dimensional bodies
Optimal bounds and optimal microstructures for multiphase composites
A central problem in the study of composite materials is to characterize the effective properties of a composite based on the observed microstructure of the constituent phases. The effective properties, however, depend on the detailed microstructure, and finding the effective properties of a composite requires solutions to partial differential equations which are generally impractical for realistic microstructures.
This problem can be addressed by a classic method of first deriving microstructure-independent bounds and then constructing microstructures for composites. The best-known rigorous bounds are obtained by Hashin-Shtrikman bounds in 1960's. It is also known that Hashin-Shtrikman bounds are attainable for two-phase composites, at least for some effective modulus, e.g., conductivity and bulk modulus. On the other hand, Hashin-Shtrikman bounds are not optimal for three or more phase composite, not even for the conductivity, and hencforth cannot be used to completely characterize the possible effective behaivors of composites of more than two constituent phases.
Improving against Hashin-Shtrikman bounds appears to be extremely difficult for multiphase composites, not to mention the optimality. Nevertheless, there are other mathematically and physically interesting problems in this area as follows.
1. Characterizing the optimality of Hashin-Shtrikman bounds for multiphase composites. An easier problem than improving Hashin-Shtrikman bounds is to find precisely when the Hashin-Shtrikman bounds are attainable and when they are unattainable. This problem can be solved for three-phase conductivity problem and partially solved for four and more-phase composites. The necessary conditions for attainability follows from the a property of Null Lagrangian and the Maximum principle; the sufficient condition follows from a new type of microstructure:three-phase coated spheres with variable effective properties on the shell, as illustrated below
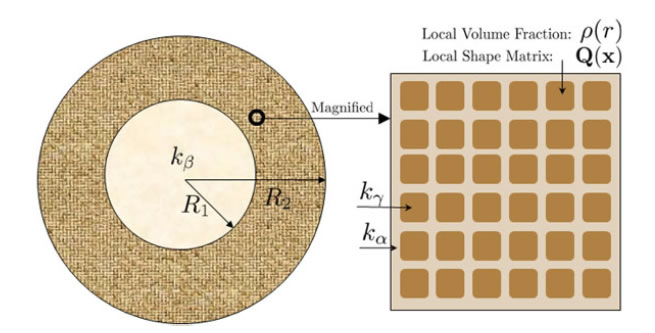
Figure 1. A three-phase coated sphere: the core sphere is occupied by phase-alpha; the shell is occupied by two-phase composites of phases beta and gamma. The microstructure of the composite is a periodic E-inclusion with local shape matrix Q(x) and local volume fraction rho(r).
Figure 2. The assembled composites (Hashin's construction) by three-phase coated sphere.
Upon combining the necessary condition and sufficient condition, we can plot the attainable, unattainalbe and unknown regions of the Hashin-Shtrikman bounds in the parameters space which are typically chosen as the volume fractions of contituent phases. As an example, in the following figure we show the attainable, unattainalbe and unknown regions for four-phase composites.
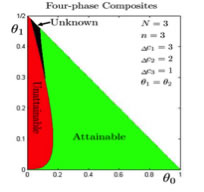
Figure 3. The attainability of the lower HS bounds for four-phase composites. Various parameters are specified on the top-right of each panel; all intermediate phases have the same volume fraction. The horizontal axis represents the volume fraction of worst conductor whereas the vertical axis represents the volume fraction of best conductor. The plane is divided into three regions of Hashin-Shtrikman bounds: attainable (green), unattainable (red) and unknown (black).
The details for the above results are presented in our publications: LiuMultiphase2010, LiuAttainability2011.
Along the above line of argument, on-going or open project problems include:
a) Characterizing the G-closure for multiphase composites;
b) Attainability of shear modulus bounds for two or more phase composites.
2. Improving the Hashin-Shtrikman bounds for multiphase composites. As mentioned above, this problem is difficult but still worth being examed from time to time.
3. An easier but practically important problem is to derive and improve microstructure-dependent bounds. Of course, the additional microstructure information used in deriving bounds shall be judiciously chosen so that the bounds are informative and simple.
Eshelby inclusion problems have played a pivotal role in many micromechanical models including composites, fracture mechanics, dislocations, phase transformations, etc. The original problem for most models, e.g., composites and fracture, is the inhomogeneous Eshelby inclusion problem. However, the inhomogeneous inclusion problem is difficult to solve, particular from an analytical view point. The simplified problem, i.e., homogeneous Eshelby inclusion problems can be conveniently handled by the powerful methods of Green's function and Fourier method. In addition, as shown in the classic paper of Eshelby (1957), the solution to the homogeneous inclusion problem solves precisely the inhomogeneous inclusion problem for ellipsoidal inclusions since ellipsoids enjoy the remarkable uniformity property --- the induced strain or stress inside the inclusion is uniform for given uniform eigenstrain on the inclusion.
The explicit closed-form solutions of Eshelby for ellipsoidal inclusions are extremely useful in models of mechanics and materials, as evident in the classic textbook of Mura (1987). However, the Eshelby's framework and subsequent analysis based on the Eshelby's solutions suffer from one severe limitation, i.e., only one inclusion may appear in the models and the solution strategy cannot be applied situations when interactions between inhomogeneities (e.g., voids, cracks, precipitates, dislocations) are important. Therefore, strictly speaking, analysis based the Eshelby's solution can only be applied to composites in the dilute limit. Nevertheless, there is a nice intuitive way to get around this limitation. The Mori-Tanaka theory assumes that, in the non-dilute senarios, the field in inclusions, though no longer uniform, may still be estimated from the Eshelby's solutions upon introducing the concept of average Eshelby tensor. This approximation scheme often gives satisfactory results for composites and is closely related with the Hashin-Shtrikman bounds.
We seek to extend the Eshelby's approach in a different direction. Since multiple ellipsoids together no long enjoy the uniformity property, we raise the question whether there exist some special shapes that do enjoy the Eshelby uniformity property. The answer turns out to be "Yes". In fact we can construct infinite many shapes/domains with different topology, volume/volume fractions, aspect ratios, etc such that uniform dilatational eigenstrain induces uniform stress/strain (not necessarily dilatational) on the inclusions. We name these new shapes E-inclusion, after Eshelby, Ellipsoids and many Extremal properties they enjoy. Examples of 2D and 3D E-inclusions are shown in the following figures.
Figure 1. Two-dimensional E-inclusion with three components.
Figure 2. Two-dimensional E-inclusion with five components.
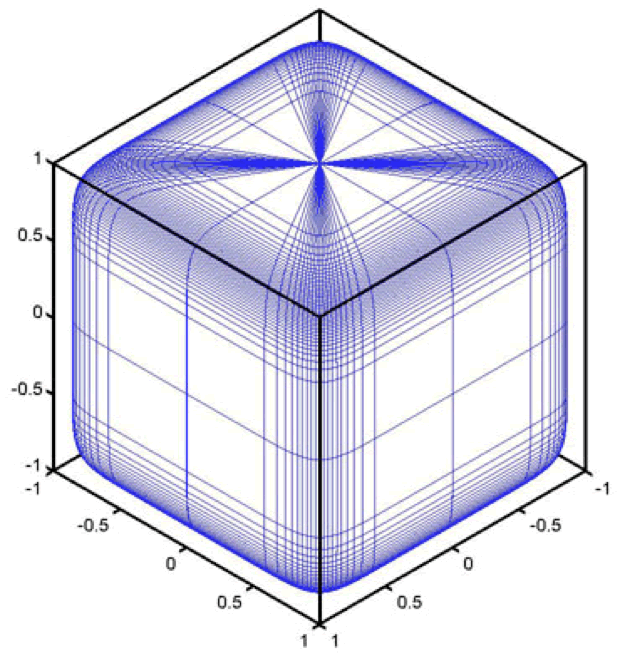
Figure 3. Three-dimensional periodic E-inclusion with volume fraction of 0.7 in a cubic unit cell and equal aspect ratio.
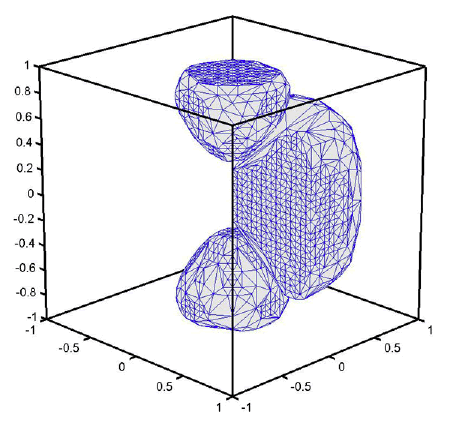
Figure 4. Three-dimensional periodic E-inclusion with three components. Note that only one fourth of the middle component is plotted in the figure.
As a generalization of ellipsoids, analysis based on Eshelby's solutions may also be applied to media with (periodic) E-inclusions as the microstruture. Further, we can show that (periodic) E-inclusions actually optimal microstructures for minimizing/maximizing effective conductivities or bulk elastic modulus for multiphase composites and for minimizing stress concentration. Therefore, it is anticipated that (periodic) E-inclusions will be useful for models in mechanics and materials as much as ellipsoids. Details of calculations and additional examples can be found in our publications: LJL2007, LJLARMA, and LiuEshelbyConjecture.
We shall also remark that in 2D, single-component periodic E-inclusions are first found by Vigdergauz in 1980's when studying "equal-strength" holes in a plate and is subsequently referred to as "Vigdergauz microstructure".
In spite of the above progresses in Eshelby inclusions problems, there are still research issues of both practical and scientific significance as follows.
1. Weak Eshelby conjecture
Eshelby (1961) conjectured that ellipsoids are the only "closed surface with this convenient (i.e., uniformity) properties", which is subsequently referred to the Eshelby conjecture. However, we may take this statement in two ways as explained in Kang and Milton (2008) and Liu (2008). The strong version can be proved, that is, if any uniform eigenstrains on the inclusion induce uniform stress on the inclusion and the inclusion is connnected (with Lipschitz boundary), then the inclusion must be an ellipsoid. The premise of the weak version are weakened, requiring only that uniform induced stress hold for one nonzero eigenstrain. For an artificial elasticity tensor (but still strongly elliptic), it is known the weak Eshelby conjecture fails, as shown in Liu (2008).
It would be interesting to prove or disprove the weak Eshelby conjecture for a realistic elasticity tensor.
2. Homogeneous periodic Eshelby inclusion problems
The classic Eshelby inclusion problem assume the matrix is infinite and henceforth the results suffer the same limitation as the Eshelby's solutions, and henceforth they cannot, at least strickly speaking, be used to account for interactions between inhomogeneities. To address this limitation, we may consider periodic Eshelby inclusion problem, for which the volume fraction of inclusion can be finite (instead of infinitesimal) and the interactions between inclusions are taken care of by the periodic boundary conditions. The Fourier analysis for periodic problem has little difference than the classic probem. However, for analytical solutions, it would be convenient to have an explicit Green's function for periodic problems. This can be done in two dimension, as shown in our work LiuPeriodicInclusion2010. The main difficulty in this problem is to correctly modify the Green's function for entire space suitable such that the summation over the periodic lattice converges uniformly away from the sigularities.
It would be interesting to find the explicit Green's function for periodic problems in 3D and the explicit parametrization for special shapes such as periodic E-inclusions.
3. Inhomogeneous periodic Eshelby inclusion problems
As mentioned above, modelsl for materials often requires solutions to the inhomogeneous inclusion problems instead of the homogeneous inclusion problems. Therefore, it is of interest to establish the relation between two problems. A classic result asserts that one can always expand the solutions to inhomogeneous problem in terms of solutions to homogeneous problems where the difference between materials properties play the role of small parameters. Based on this expansion, much can be said concerning the effective behavior or energy of the inhomogeneous problem, e.g., microstructure-dependent bounds. These on-going calculations will be wrapped up soon.
Predictive modeling of multifunctional composites
Multifunctional materials can be stimulated by and response to multiple external fields and serve several functions. For example, conformal antennas on an airplane use multifunctional materials of sufficient structural strength, ultra-light weight as well as desirable electromagnetic properties; biomedical devices such as stents require fatigue resistance, bio-compatibility and the ability to perform an actuation task, such as supporting weak points in arteries. They are now indispensable in modern industrial and military systems for their efficient multi-actuating, multi-sensing, self-adaptivity, etc.
We are currently developing predictive models for various functional composites and investigating how to engineer microstructures to realized desired functionalities.
Dynamic modeling of heterogeneous structures/media
It may sound surprising that it is still unknown whether free surface waves exist for any anisotropic media, though Barnett and Lothe in 1970's have resolved the existence of subsonic free surface waves. The technical difficulty lies in characterizing whether the stable solutions to an algebraic Riccati equation overlaps a fixed subspace when a real parameter v (phase-speed of the surface wave) varies from zero to the largest bulk wave phase speed.
However, by energy method we can show the existence of free surfaces in periodic heterogeneous media. The argument is to first derive a lower bound on the continuous spectrum, and then construct a test function with Rayleigh quotient smaller than this bound. This method can only be used to prove the existence of subsonic waves, as explained in HuLiuBhatt2011.
Another dynamic problem we have work on concerned sandwich plates for their applications in naval structures. The lowest branch wave modes changes significantly as wavelength decreases (or frequency increases) as illustrated in the following figure and explained in LiuBhatta2009.
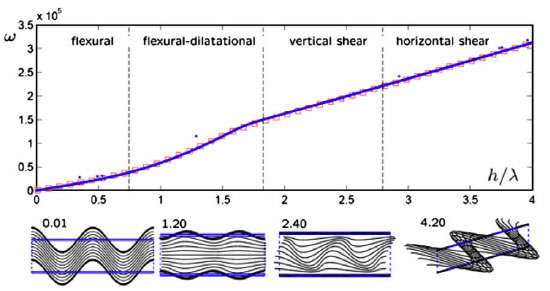
Figure 1. The top figure shows the lowest branch of the dispersion relation of the sandwich structure. The horizontal axis is roughly divided into four regimes labeled by ''flexural", ''flexural-dilatational", ''vertical shear" and ''horizontal shear". The corresponding typical mode shapes are shown in the bottom.
Variational inequalities and their applications in designs
The mathematical theory of varational inequalities has by and large been established in the last century, see e.g., textbook of Kinderlehrer and Stampacchia (1980) and Friedman (1982). The latest applications of variational inequalities in solid mechanics is (i) to construct optimal microstructures for composites, and (ii) to construct structures for any desirable physically possible fields. Moreover, it enables us to systematically define or construct special geometries which we name as "polynomial inclusions". Polynomial inclusions of degree two are precisely ellipsoids and an example of polynomial inlcusions of degree three is illustrated below.
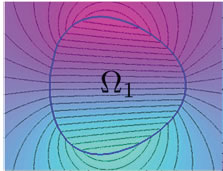
Figure 1. A polynomial inclusion of degree three.
We can use polynomial inclusions to construct structures generating any desirable local fields. For example, upon overlapping two polynomial inclusions of degree three, we obtain a perfect quadrupole field in the bore region, as shown below.
Figure 2. The blue regions has magnetization point up and red regions point down. The magnetic field inside the bore area is a perfect quadrupole field.
Applications of variational inequalities in designing arbrary magnetic field is presented in our publication Liumagnetdesign2011. Current project in this direction is to use currents as sources and to design magnets with desirable field so as to manipulate nanoparticles or for imaging in MRI applications.
Superconductive composites and modeling
The large-scale applications of superconductors in energy transmission, energy storage, and large field (above 20T) magnets, etc still remain as a long-term vision since the discovery of high temperature superconductors by Bednorz and Muller in 1986. The main issue arises from the low critical current density-Jc of these new ceramic superconductors, e.g., YBCO, in spite of their significantly improved critical transition temperature-Tc. Most of the critical-current-density improvement strategies are to introduce oriented pinning centers into superconductors. The pinning centers, essentially some kind of defects, break the translational symmetry of the underlying vortex lattice; an external force and hence a transport current is required to push the vortex lattice. Therefore, to increase critical current density, we need to increase the "friction" between vortex lattice and defects so that the vortex lattice remains remains immobile and non-dissipative. In particular, defects shall pin vortex collectively rather than randomly.
We are therefore motivated to consider heterogeneous structure as illustrated below.
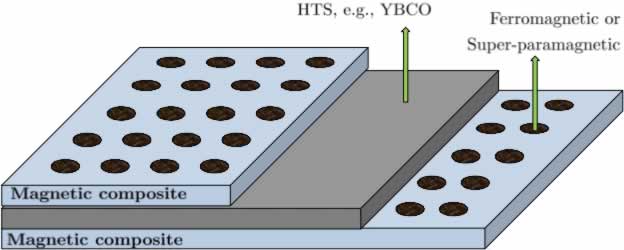
Figure 1. Heterogeous structure of superconductor film, magnetic composites with periodic ferromagnetic columnar inclusions.
It is hoped that the magnetic interaction between the two face magnetic composite film can pin vortex lattice (i.e., increase the "friction") and increase the critical currents of the superconducting film.
We are currently investigating the designs of magnetic composite film based on the Grinzburg-Landau theory.
As microelectronics are miniaturized, the applicablilty of classic continuum mechanics which takes into account only the bulk phenomena are in question. A more accurate theory shall account for surface/interface energy. The continuum theory including surface/interface energy has been established by Gurtin and Murdoch in 1970s-1980s. The question we are now faced with is to establish a seamless pathway from an atomistic model to the Gurti-Murdoch's theory and give an answer to questions such as: How to calculate the macroscopic surface elasticity properties from the underlying atomistic model? Are there some intrinsic realtions between bulk elastic properties and surface elastic properties? Does the stability of free surface place some restrictions on the possible interactions between atoms? Are there simple experimental techniques to measure surface elastic properties?
There project is currently investigated by Ph.D. student Mr. Lixin Hu.
Thermoelectric materials, modeling, design and energy harvesting
Thermoelectric (TE) materials directly convert heat into electric energy, and can be used for power generation and refrigeration. Being all solid state and without moving parts, thermoelectric devices have the unique advantage of portability, silence, scalability, durability and reliability in extreme environment. Also, they are readily customized and embedded into a large system to provide independent power or refrigeration and improve the realiability of the system. Additional applications of thermoelectric devices include temperature and thermal energy sensors for precise temperature and thermal flux control, hybrid photovoltaic-thermoelectric energy systems which have an improved solar power conversion efficiency, etc. However, thermoelectric devices suffer from a critical disadvantage of low efficiency. Nevertheless, thermoelectric materials show serious potential of coping with the energy crisis in 21st century for the abundence of thermal energy in nature.
For designing thermoelectric materials with balanced efficiency (figure of merit) and power factor, a continuum theory is systematically developed in our paper. In addition, we predict how figure of merits and power factors depend on the microstructures: volume fraction and aspect ratio, as shown in the following figures.
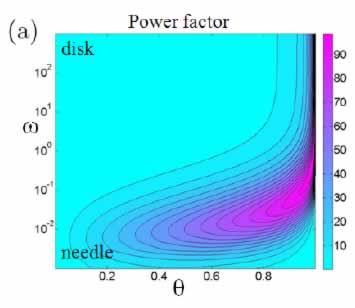
Figure 1. Contours of normalized effective ective power factors where the horizontal and vertical axes represent volume fraction and aspect ratio of the particles, respectively.
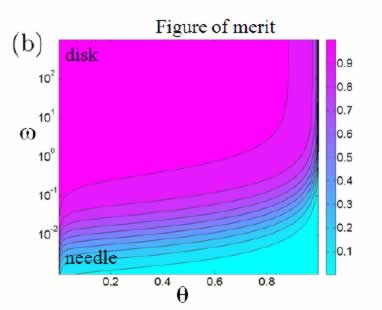
Figure 2. Contours of normalized figure of merits where the horizontal and vertical axes represent volume fraction and aspect ratio of the particles, respectively.
The on-going research in this area concerns designing thermoelectric engines which can use thermal energy in nature which cannot be utilized before with energy price comparable with conventional power plant.
Continuum theory for multiferroic materials
The coexistence of magnetic, electric and elastic ordering in ferroic materials have stimulated considerable scientific and technological interest. The classic theories addressing long-range ordering include the Landau-Lifshitz theory of micromagnetics (1935), the Landau-Ginzburg-Devonshire theory of ferroelectrics (1949, 1954), and the theory of martensitic shape memory alloys. These theories have focused on individual ferroic phenomenon and achieved great success in the study of the corresponding materials. The literature is, however, lack of a systematic treatment of multiferroism, in spite of recent elevated interest in multiferroic materials. The term multiferroism was coined by Schmid (1994) to describe the coexistence of spontaneous magnetization, polarization and strain in one material and has attracted many researchers in attempts to realize ever better multifunctionalities.
To develop a continuum theory for multiferroic bodies, we will follow the classic framework of continuum mechanics, in particular, nonlinear elasticity: the constitutive law will be provided by postulating an internal energy density function; restriction on the internal density function will be found based on the fundamental laws of thermodynamics and material symmetries; the corresponding linearized theory will be derived and stability will be analyzed; material constants will be inferred from simple benchmark experiments. Combined together, this approach is anticipated to furnish a solvable, predictive and realistic theory for multiferroic materials, regardless of the microscopic mechanisms of multiferroism (which is precisely the advantage of a continuum theory).
This project is on-going and it is hoped that the constructed theory can guide the design of multiferroic materials for as-yet unrealizable multifunctionalities.
Multiscale analysis: homogenization theory and theories for lower dimensional bodies
Under construction.
