Eshelby inclusion problems

Eshelby inclusion problems have played a pivotal role in many micromechanical models including composites, fracture mechanics, dislocations, phase transformations, etc. The original problem for most models, e.g., composites and fracture, is the inhomogeneous Eshelby inclusion problem. However, the inhomogeneous inclusion problem is difficult to solve, particular from an analytical view point. The simplified problem, i.e., homogeneous Eshelby inclusion problems can be conveniently handled by the powerful methods of Green's function and Fourier method. In addition, as shown in the classic paper of Eshelby (1957), the solution to the homogeneous inclusion problem solves precisely the inhomogeneous inclusion problem for ellipsoidal inclusions since ellipsoids enjoy the remarkable uniformity property --- the induced strain or stress inside the inclusion is uniform for given uniform eigenstrain on the inclusion.

The explicit closed-form solutions of Eshelby for ellipsoidal inclusions are extremely useful in models of mechanics and materials, as evident in the classic textbook of Mura (1987). However, the Eshelby's framework and subsequent analysis based on the Eshelby's solutions suffer from one severe limitation, i.e., only one inclusion may appear in the models and the solution strategy cannot be applied situations when interactions between inhomogeneities (e.g., voids, cracks, precipitates, dislocations) are important. Therefore, strictly speaking, analysis based the Eshelby's solution can only be applied to composites in the dilute limit. Nevertheless, there is a nice intuitive way to get around this limitation. The Mori-Tanaka theory assumes that, in the non-dilute senarios, the field in inclusions, though no longer uniform, may still be estimated from the Eshelby's solutions upon introducing the concept of average Eshelby tensor. This approximation scheme often gives satisfactory results for composites and is closely related with the Hashin-Shtrikman bounds.

We seek to extend the Eshelby's approach in a different direction. Since multiple ellipsoids together no long enjoy the uniformity property, we raise the question whether there exist some special shapes that do enjoy the Eshelby uniformity property. The answer turns out to be "Yes". In fact we can construct infinite many shapes/domains with different topology, volume/volume fractions, aspect ratios, etc such that uniform dilatational eigenstrain induces uniform stress/strain (not necessarily dilatational) on the inclusions. We name these new shapes E-inclusion, after Eshelby, Ellipsoids and many Extremal properties they enjoy. Examples of 2D and 3D E-inclusions are shown in the following figures.

Figure 1. Two-dimensional E-inclusion with three components.

Figure 2. Two-dimensional E-inclusion with five components.

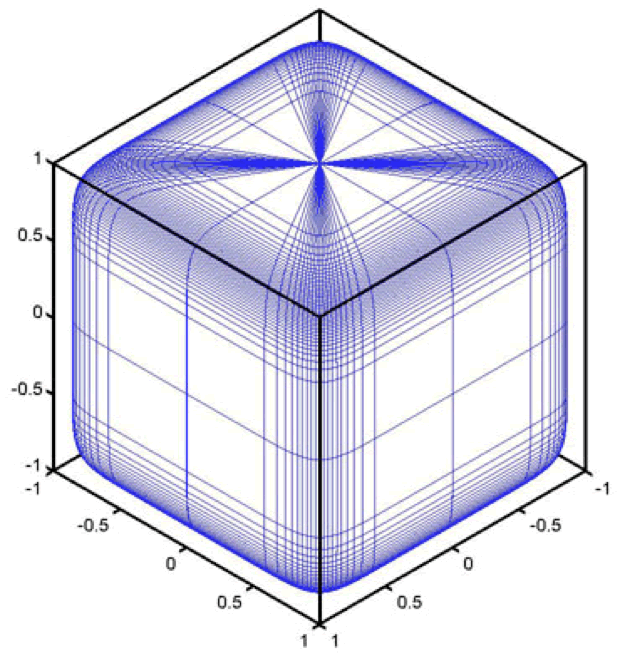
Figure 3. Three-dimensional periodic E-inclusion with volume fraction of 0.7 in a cubic unit cell and equal aspect ratio.

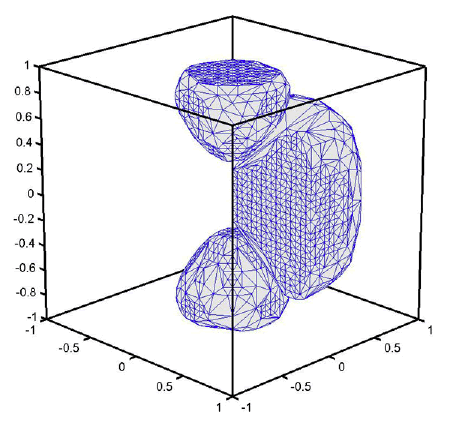
Figure 4. Three-dimensional periodic E-inclusion with three components. Note that only one fourth of the middle component is plotted in the figure.

As a generalization of ellipsoids, analysis based on Eshelby's solutions may also be applied to media with (periodic) E-inclusions as the microstruture. Further, we can show that (periodic) E-inclusions actually optimal microstructures for minimizing/maximizing effective conductivities or bulk elastic modulus for multiphase composites and for minimizing stress concentration. Therefore, it is anticipated that (periodic) E-inclusions will be useful for models in mechanics and materials as much as ellipsoids. Details of calculations and additional examples can be found in our publications: LJL2007, LJLARMA, and LiuEshelbyConjecture.

We shall also remark that in 2D, single-component periodic E-inclusions are first found by Vigdergauz in 1980's when studying "equal-strength" holes in a plate and is subsequently referred to as "Vigdergauz microstructure".

In spite of the above progresses in Eshelby inclusions problems, there are still research issues of both practical and scientific significance as follows.

1. Weak Eshelby conjecture

Eshelby (1961) conjectured that ellipsoids are the only "closed surface with this convenient (i.e., uniformity) properties", which is subsequently referred to the Eshelby conjecture. However, we may take this statement in two ways as explained in Kang and Milton (2008) and Liu (2008). The strong version can be proved, that is, if any uniform eigenstrains on the inclusion induce uniform stress on the inclusion and the inclusion is connnected (with Lipschitz boundary), then the inclusion must be an ellipsoid. The premise of the weak version are weakened, requiring only that uniform induced stress hold for one nonzero eigenstrain. For an artificial elasticity tensor (but still strongly elliptic), it is known the weak Eshelby conjecture fails, as shown in Liu (2008).

It would be interesting to prove or disprove the weak Eshelby conjecture for a realistic elasticity tensor.

2. Homogeneous periodic Eshelby inclusion problems

The classic Eshelby inclusion problem assume the matrix is infinite and henceforth the results suffer the same limitation as the Eshelby's solutions, and henceforth they cannot, at least strickly speaking, be used to account for interactions between inhomogeneities. To address this limitation, we may consider periodic Eshelby inclusion problem, for which the volume fraction of inclusion can be finite (instead of infinitesimal) and the interactions between inclusions are taken care of by the periodic boundary conditions. The Fourier analysis for periodic problem has little difference than the classic probem. However, for analytical solutions, it would be convenient to have an explicit Green's function for periodic problems. This can be done in two dimension, as shown in our work LiuPeriodicInclusion2010. The main difficulty in this problem is to correctly modify the Green's function for entire space suitable such that the summation over the periodic lattice converges uniformly away from the sigularities.

It would be interesting to find the explicit Green's function for periodic problems in 3D and the explicit parametrization for special shapes such as periodic E-inclusions.

3. Inhomogeneous periodic Eshelby inclusion problems

As mentioned above, modelsl for materials often requires solutions to the inhomogeneous inclusion problems instead of the homogeneous inclusion problems. Therefore, it is of interest to establish the relation between two problems. A classic result asserts that one can always expand the solutions to inhomogeneous problem in terms of solutions to homogeneous problems where the difference between materials properties play the role of small parameters. Based on this expansion, much can be said concerning the effective behavior or energy of the inhomogeneous problem, e.g., microstructure-dependent bounds. These on-going calculations will be wrapped up soon.