Research Interests
Mathematics helps to situate us in a particular realm of possibility. For example, the Poincare-Bendixson theorem tells us that chaos is impossible in a planar flow; moreover the long term behavior of any initial condition limits to either a fixed point, periodic orbit, or a collection of connecting orbits. Invariant sets such as these are of great importance in a dynamical system, as their topology will remain the same under small perturbations, or at least until the system bifurcates.
In specific systems, identifying these objects requires specialized calculations, and intuition is often gained through linear approximations and numerical simulations. A natural question to ask is: When is my approximation good enough?
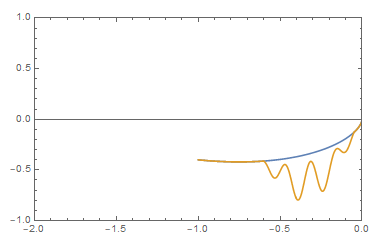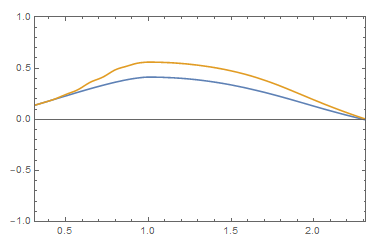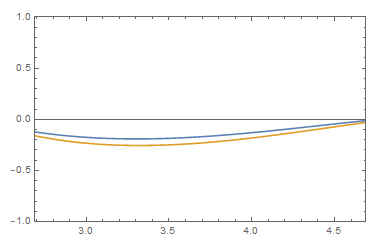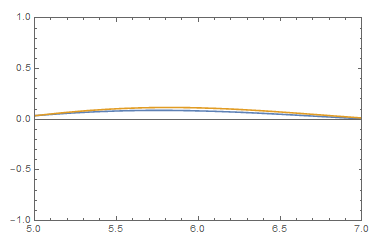A simulation of the delay differential equation known as Wright's equation
Broadly speaking, my research aims to answer this question by developing constructive methods to study dynamical systems and differential equations. In my thesis I resolve longstanding conjectures regarding the scalar delay differential equation known as Wright's equation.
Download Full Research Statement