The vector field <0,0,z2> is not the curl of another vector field, because 0+0+2z is not always 0.
When is a vector field a gradient?
Several weeks ago we asked when a vector field could be a gradient
vector field. That is, given F=Pi+Qj+Rk,
when is there φ so that ∇φ=F? Although we can
integrate and compare the various descriptions, integration is
frequently tedious and difficult. I mentioned that a quick check can
be gotten by looking at the "cross second derivatives". The resulting
equations are also callled "compatibility conditions". Here is a
way of encoding this idea.
The curl
If F(x,y,z)=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k,
then the curl of F is another vector field, ∇xF. It is a cross-product, and can be
evaluated by taking the determinant:
( i j k )
det ( ∂/∂x ∂/∂y ∂/∂z )
( P(x,y,z) Q(x,y,z) R(x,y,z) )
It turns out this is equal to (if I don't foul up the signs!) the
following vector field:
If a vector field is a gradient, its curl is 0
A way of testing if a vector field is a gradient vector field: take
the curl: the result should be 0. Hamilton would want you to remember
this by writing ∇x∇f=0 since a vector crossed with
itself is 0.
The formula for curl is horrible, and difficult to remember but the
notation (especially the cross product and ∇) is supposed to
help. Suppose we ∂/∂x the i component of curl
F, ∂/∂y the
j component, and ∂/∂z the k component. Here in
this 21st century (!) math course, I may be doing this for
fun. The people who actually invented these results had the
computations forced on them (really!) because they wanted
descriptions of certain aspects of reality involving fluid flow and
electromagnetism. These are the three results we get for the
differentiations:
(Ryx–Qzx) –(Rxy–Pzy) (Qxz–Pyz).
A number of students observed that if we added these results, the
result would be 0! This is weird and wonderful (or weird and
remarkable, a phrase which might be used either positively or
negatively about many parts of this course).
If a vector field is a curl, its divergence is 0
Our conclusion is that a vector field G for which
∇·G is not 0 cannot be the curl of another
vector field. This is a "compatibility condition" for being a curl.
Example (from a textbook problem)
The vector field <0,0,z2> is not the curl of
another vector field, because 0+0+2z is not always 0.

What is the curl?
curl F is a complicated object. If F represents a fluid
flow, then each component of the curl of F is supposed to
represent the amount the fluid flow rotates around the corresponding
i or j or k. For example, a few
weeks ago we looked at the vortex flow, which was <–y,x,0>,
and has P=–y, Q=x. and R=0. Then
(Ry–Qz)i–(Rx–Pz)j+(Qx–Py)k
turns out to be (we computed it!) 0i+0j+2k: the
fluid "swirls" around the k axis at a uniform speed.
The darn curl is so complicated because analyzing the motion of a fluid is quite complicated and difficult, and the tools are correspondingly intricate.
The ingredients for Stokes' Theorem
Stokes' Theorem was developed in response to ideas of electromagnetism
and fluid dynamics. Just like Green, Stokes was interested in both
mathematics and physics, and he attempted to construct mathematical
models for rapidly evolving fields of physics. I will attempt to list
the ingredients for a (relatively!) straightforward version of Stokes'
Theorem.
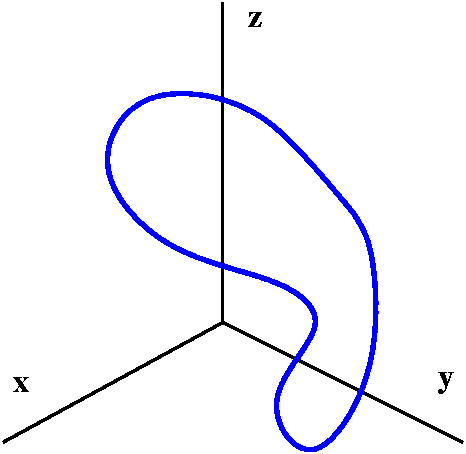
So this is a curve in space (R3) with START=END and which has no other self-intersections. |
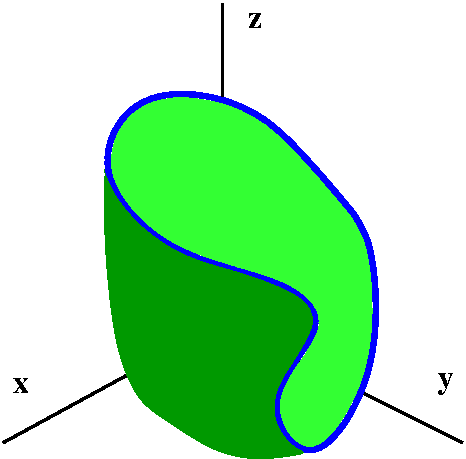 This should be a piece of a surface, all of whose boundary is the
curve mentioned above. As several students remarked, specifying the
boundary curve does not mean there's only one surface. In fact,
there are many really neat and clever computations which depend on
changing the surfaces involved. I'll show you one of these in a few
minutes.
This should be a piece of a surface, all of whose boundary is the
curve mentioned above. As several students remarked, specifying the
boundary curve does not mean there's only one surface. In fact,
there are many really neat and clever computations which depend on
changing the surfaces involved. I'll show you one of these in a few
minutes.
|
|
Stokes' Theorem connects the work of a vector field around a closed curve with the flux of a related vector field over a surface. So this means that we need to have a direction on the curve (how we push things around) and we also need to make a selection of normal vector on the surface. These choices need to be made together. The textbook interprets the work in the fluid dynamics sense, as a circulation. We didn't have enough time in class to consider circulation. There is discussion of this in sections 17.1 (on page 1010) and 17.2 (see page 1025). |
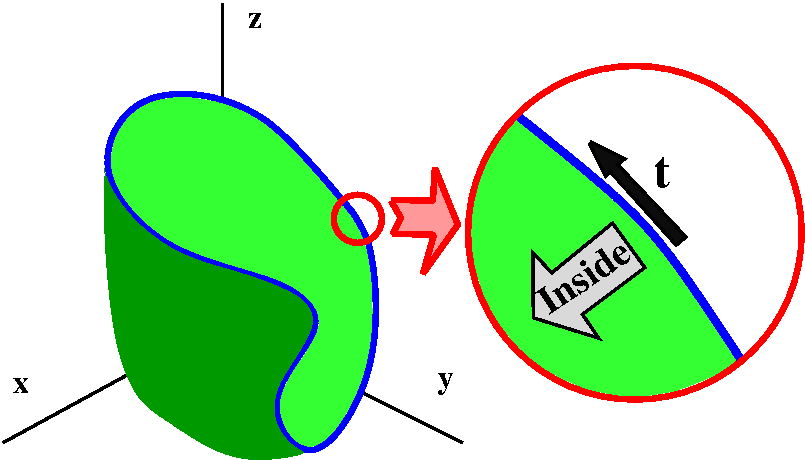 • How the surface and curve interact (by their orientations)
• How the surface and curve interact (by their orientations)
The word "orientation" here means how to select t, the unit
tangent vector on the boundary curve, and N, the unit normal on
the surface. The boundary curve will be a parameterized curve. It has
a unit tangent vector, t, pointing in the direction of
increasing parameter value. If we "walk" along the boundary curve in
this direction, the surface should be to our left. Now we have
t and a direction to the left. Complete this to a right-handed
coordinate system. The selection of N, the unit normal vector
to the surface, is made so N points in the direction of the
last entry of a right-handed coordinate system which begins with
t and the inside surface direction. I think in the accompanying
picture to the right, the N would point "out" of the page, and
towards the "inside" of the cup-shaped surface.
Under these conditions, then the Stokes Theorem Equation is true:
∫The boundary curveF·t ds=∫∫The surfacecurl F·N dS
The textbook writes this in a slightly different way as
∫The boundary curveF·ds=∫∫The surfacecurl F·dS
So the work or circulation of F around the boundary is equal to the flux through the surface of the curl F. This is a well-known complicated theorem. If the curve is in R2 and the surface is the inside of the curve, then the result is "just" Green's Theorem, which is already quite complicated. I'd like to spend most of the time in this lecture just checking both sides of the Stokes' Theorem equation, and getting some familiarity with it that way.
A textbook problem
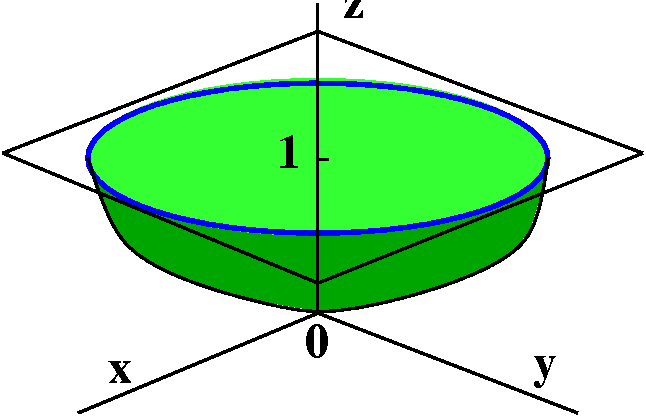 Here is a problem from a calculus textbook:
Here is a problem from a calculus textbook:
Verify that Stokes' Theorem is true for the vector field
F(x,y,z)=y2i+xj+z2k
and the surface is the part of the paraboloid
z=x2+y2 that lies below the plane z=1, oriented
upward.
Some discussion
The plane z=1 intersects the paraboloid in a circle. This is a circle
of radius 1 centered at (0,0,1). The paraboloid "overlays" a region
inside a circle of radius 1 centered at the origin in the xy-plane. We
will compute both integrals in Stokes' Theorem and (I hope!) get the
same answers. If the paraboloid is "oriented upward" then I presume
that the N points up. Going around the blue circle in the
standard (counterclockwise/positive) direction will orient the
boundary curve "compatibly": the t, the leftish piece of
surface next to the boundary curve, and the up N form a
right-handed triple. This took some time to see in class.
The work integral
So I need to compute ∫The curvey2dx+x dy+z2dz.
The curve is a circle, and can be parameterized as:
x=1cos(t) dx=–sin(t)dt y=1sin(t) dy=cos(t)dt z=1 dz=0and the parameterization interval for the whole circle is [0,2Π]. Then ∫The curvey2dx+x dy+z2dz becomes
The surface integral
Now we need to compute
∫∫The paraboloidcurl F·N dS.
The curl
This is ∇xF, so:
( i j k ) det( ∂/∂x ∂/∂y ∂/∂z )=0i–0j+(1–2y)k ( y2 x z2 )Parameterizing the surface, etc.
( i j k ) det( 1 0 2u )=–2ui–2vk+1k ( 0 1 2v )We discussed the magical cancellation a few lectures ago. V·N dS became V·(ruxrv) dAu,v. curl F here is (1–2y)k=(1–2v)k so that curl F·N dS=(1–2v)k·(–2ui–2vk+1k)dAu,v=(1–2v)dAu,v.
Computation of the surface integral
We need to identify the domain in the uv-plane which parameterizes our
little cup. The uv-plane is the xy-plane in different clothing, but
the cup is the graph over the region inside the unit circle:
u2+v2≤1. So we need
∫∫Inside the unit circle(1–2v)dAu,v
But the 2v integrates to 0, since the region is symmetric in v and 2v is "odd" (the + and – cancels totally). The 1 in the integrand just gives the area, and the area inside the unit circle is Π(12), and this is Π.
This instantiation (?) of Stokes' Theorem is verified: Π=Π.
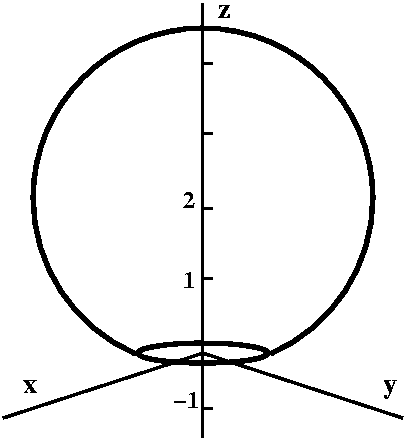 Another textbook problem
Another textbook problemHere is a slightly more vicious (viscous?) problem from the Stokes' Theorem section of a calculus text by Robert A. Adams: Find ∫∫The surfacecurl F·N dS where the surface is that part of the sphere x2+y2+(z–2)2=8 which lies above the xy-plane, and N is the outward unit normal on the surface, and F is y2cos(xz)i+x3eyzj–e–xyzk. Since the problem occurs in the Stokes' Theorem section of the text we should probably use Stokes' Theorem. The region of the sphere is shown to the right. The sphere is centered at (0,0,2) and its radius is sqrt(8)=2sqrt(2). So a portion of the sphere extends below the xy-plane. 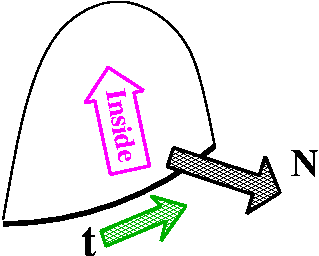 The boundary of the top portion occurs if z=0 in the equation
x2+y2+(z–2)2=8. This becomes
x2+y2+(–2)2=8 so
x2+y2=4. This is a circle of radius 2 centered
at the origin in the xy-plane. We should establish the orientation of
this circle. If we look closely at a small piece of the surface near
the boundary curve, the outward unit normal points slightly down. We
must "walk" along the curve so that the surface is to the left. The
t direction is the standard counterclockwise direction on the
boundary circle. I hope the local picture to the right helps to
convince you of that. Again, the problem of deciding the resulting
orientation of one chunk (surface, boundary curve) from the other
(boundary curve, surface) has frequently seemed to me to be the most
complicated qualitative aspect of this problem.
The boundary of the top portion occurs if z=0 in the equation
x2+y2+(z–2)2=8. This becomes
x2+y2+(–2)2=8 so
x2+y2=4. This is a circle of radius 2 centered
at the origin in the xy-plane. We should establish the orientation of
this circle. If we look closely at a small piece of the surface near
the boundary curve, the outward unit normal points slightly down. We
must "walk" along the curve so that the surface is to the left. The
t direction is the standard counterclockwise direction on the
boundary circle. I hope the local picture to the right helps to
convince you of that. Again, the problem of deciding the resulting
orientation of one chunk (surface, boundary curve) from the other
(boundary curve, surface) has frequently seemed to me to be the most
complicated qualitative aspect of this problem.
Now Stokes' Theorem applies: ( i j k )
det ( ∂/∂x ∂/∂y ∂/∂z )=Blah!i–Blah, blah!j+[3x2eyz–2ycos(xz)]k
( y2cos(xz) x3eyz –e–xyz)
A further simplification occurs. We're on the xy-plane, where z=0. So
the k component, 3x2eyz–2ycos(xz), becomes
3x2–2y because cos(0)=1 and e0=1.
So we need ∫∫The disc3x2–2y dAu,v. Just as in the previous problem, the –2y integral over the disc is 0, because there is cancellation of the positive and negative contributions of y. I see no clever way to compute the 3x2 integral and will do this using polar coordinates (with x=rcos(θ)): ∫∫The disc3x2dAu,v=3∫θ=0θ=2Π∫r=0r=2r2[cos(θ)]2r dr dθ= 3∫θ=0θ=2Π[cos(θ)]2dθ∫r=0r=2r3dr. The θ integral is Π (a trick used before) and the r integral is 16/4. So the flux is 12Π.
Comment Also since the divergence of a curl is 0, the flux of a curl vector field on a closed surface must be 0 (the Divergence Theorem) so again the previous result is verified.
FTC through the ages ...
In the first half of the twentieth century, people began to understand
what's going on more systematically. All of these big
"Theorems" actually turn out to be special cases of a result that,
after the language is understood, is wonderful to contemplate. Here is an
appropriate Wikipedia link.
|
Here is a quote from a web page entitled Earliest Uses of Symbols of Calculus:
|
The vector differential operator, now written as an upside-down delta, ∇, and called nabla or del, was introduced by William Rowan Hamilton (1805-1865). |
So "del" is given by: ∇=(∂/∂x)i+(∂/∂y)j+(∂/∂z)k. Here are some uses:
In fluid dynamics, div F represents the source rate of the fluid (more fluid if positive, less fluid if negative) at a point.
The following result is used in modeling and understanding many natural phenomena. For example, it is used to go from the PDE (partial differential equation) statements of Maxwell's equations to their integral statements (these equations are vital for analysis of electromagnetism). The result is also used to deduce the heat equation, which is a PDE descfribing heat flow. The result is also important in understanding how gases and liquids flow and mix (in atmospheric science, oceanography, etc.).
Statement of the Divergence Theorem
Suppose E is a solid bounded region in space (R3) and S is
the boundary of E, with N the outward pointing unit normal on
S. Suppose also that F is a vector field with differentiable
coefficients. Then:
∫∫SF·N dS=∫∫∫Ediv F dV.
The ingredients
Here S divides up space, R3, into two pieces (examples
follow). One of the pieces is a bounded region, E. The surface S is
always oriented in this "scenario" to have its N pointing
outward, which means away from the bounded region E.
The vector field, F(x,y,z), will be
P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k where P, Q, and R
are differentiable functions. The divergence of F is a
function, ∇·F:
(∂P/∂x)+(∂Q/∂y)+(∂R/∂z).
Fluids and the Divergence Theorem equation
The equation ∫∫SF·N dS=∫∫∫Ediv F dV
itself has meaning in fluid dynamics. The left-hand side is the net
flow(flux) in/out of region E (in fact, if the region is a cube, it is
commonly called a flow box in that field). If you
believe the interpretation mentioned above (that the divergence
of a vector field is its "local source rate" -- this needs to be
justified at length in a fluid dynamics course!) then the equation
declares that to the net flow through the boundary of the object is
equal to the "sum" (the triple integral adds up the local rates) of
the local sources. This should almost make physaical sense to
you. Perhaps I hope
Simple examples of regions and surfaces Most "concrete" computations with the Divergence Theorem will likely involve fairly simple shapes.
|

|
| |
|
 Proving the Divergence Theorem for the unit cube
Proving the Divergence Theorem for the unit cube
I wanted to "demystify" the Divergence Theorem by explaining why it is
true for the unit cube in R3.
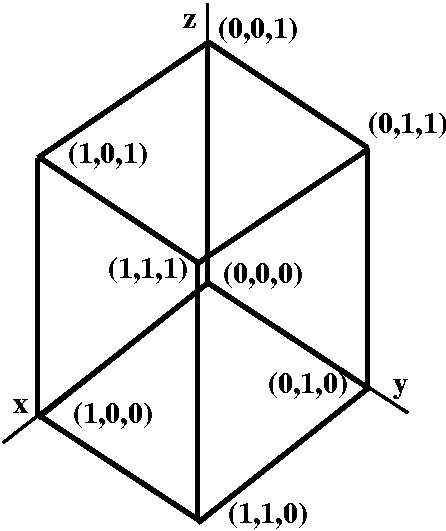
The unit cube is a parallelopiped whose vertices (corners) have entries 0 or 1. There are 8 vertices: (0,0,0), (1,0,0), (0,1,0), (0,0,1), (1,1,0), (1,0,1), (0,1,1), and (1,1,1). There are 12 edges. Edges join at two vertices whose coordinates differ by one entry. There are 6 faces, each obtained by holding one coordinate equal either to 0 or to 1. By the way, the unit cube and its generalizations in higher dimensions turn out to be very interesting. One reason is the existence of Gray codes.
Now the triple integral side of the Divergence Theorem is ∫∫∫The cube(∂P/∂x)+(∂Q/∂y)+(∂R/∂z) dV. I will split this into three separate integrals, and analyze each part.
|
I hope that some students will notice what we should do. We shold look
at
∫∫∫The cube(∂Q/∂y) dV.
We decided to write dV here as dy dAx,z. The reason
for this is that the integration with respect to y will "undo" the
∂/∂y.
The innermost integral is then ∫y=0y=1(∂Q/∂y) dy. The Fundamental Theorem of Calculus immediately applies and we get Q(x,y,z)]y=0y=1=Q(x,1,z)–Q(x,0,z). We then integrate both of these: ∫∫x,z between 0&1Q(x,1,z) dAx,z–∫∫x,z between 0&1Q(x,0,z) dAx,z Now look at the surface. The (x,1,z) part of the surface integral has j as normal, and the (x,0,z) part of the surface has –j as normal. The surface integral of F·n will be –Q(x,0,z) and will be +Q(x,1,z). In both cases, x and z will range from 0 to 1. The Fundamental Theorem of Calculus yields a minus sign when "stuff" is at the lower end of the integral. Geometrically, we get a minus sign on part of the boundary because the normals are directed outward. |
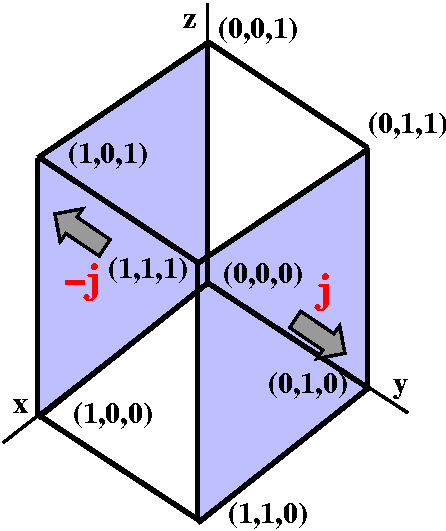
|
|
Let's look at ∫∫∫The cube(∂R/∂z) dV. I would write dV as dz dAx,y. The
Fundamental Theorem of Calculus would apply to the innermost
integral: ∫z=0z=1(∂R/∂z) dz=Q(x,y,z)]z=0z=1=Q(x,y,1)–Q(x,y,0). Again integrate both of these: ∫∫x,y between 0&1Q(x,y,1) dAx,y–∫∫x,y between 0&1Q(x,y,0) dAx,z The minus sign comes from the Fundamental Theorem of Calculus and it comes from the +/–orientation of the normals. |
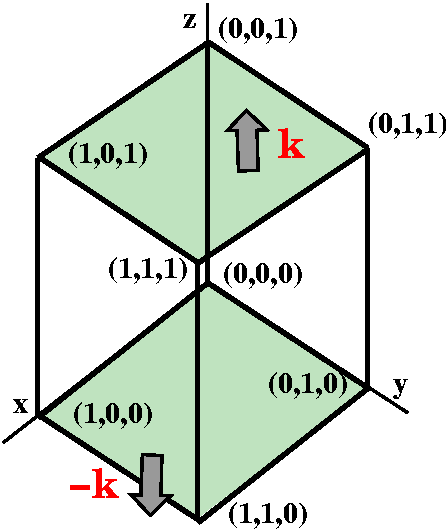
|
|
Finally the last term is ∫∫∫The cube(∂P/∂x) dV. I hope that you see dV here should be written as
dx dAy,z. Then the Fundamental Theorem of Calculus
applies and we've got this: ∫x=0x=1(∂P/∂x) dx=P(x,y,z)]x=0x=1=P(1,y,z)–Q(1,y,z). Each of these terms needs to be integrated with respect to y and z from 0 to 1. The + part (that is, at (1,y,z) in the cube) has a normal vector of i and the – part (that is, at (0,y,z) in the cube) has a normal vector of –i. So this part of the triple integral, after using the Fundamental Theorem of Calculus, gives the flux over the two indicated pieces of the boundary of the cube. |
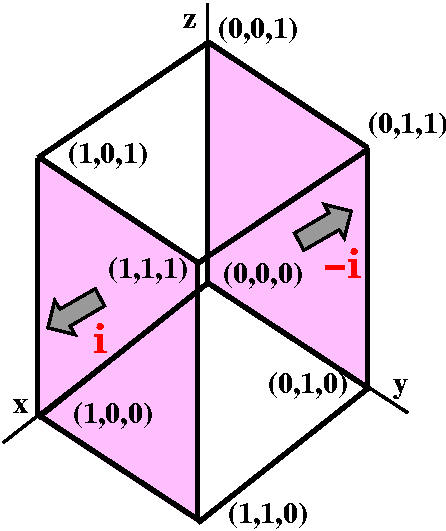
|
If now we add up the three pieces of the triple integral we will get the surface integral of F·N over the boundary of the cube with the "correct" (outward) orientation. I wanted to tell you that the Divergence Theorem is a version of the Fundamental Theorem of Calculus, and that the signs checked. Algebraically, the signs occur because of FTC and ]. Geometrically, they come from the outward choices.
Two old computations redone
We introducted flux computations in the previous class. The first
example I gave was:
Suppose our vector field is F=<xy,z2,3>. What is the total outward flux of F through the surface of the unit cube, 0≤x≤1, 0≤y≤1, and 0≤z≤1?Our answer was: "... the total flux is 1/2." The computation was not difficult but it was a bit tedious. Now let's do it using the Divergence Theorem. Well, div F=y+0+0, not too difficult. And then the triple integral were supposed to compute is ∫∫∫The cubey dV. If we order the d's as, say, dy dx dz, then dy gives us y2/2 and the limits give us 1/2. This "integrates" to 1/2 dx from 0 to 1, and then 1/2 again dz. The answer is indeed 1/2, and with a tiny effort you could even do the computation "in your head".
Here is the other example we considered then.
If F(x,y,z)= x2i+yzj–4zk, and the surface is the sphere of radius 5 centered at the origin, what is the total flux of F through this sphere (directed outwards)?Please look at what we did earlier. The computation was a good deal of work. We can also use the Divergence Theorem on this problem.
A textbook problem
Here is a standard textbook problem in the Divergence Theorem section
of a U.S. calculus book. The reasoning needed for this problem
resembles some of the problems we handled with Green's Theorem. Here
the vector field is
F(x,y,z)=z arctan(y2)i+z3ln(x2+1)j+zk.
We need to find the flux of F across the part of the paraboloid
x2+y2+z=2 which lies above the plane z=1 and is
oriented upward.
Discussion and solution
The divergence of F is 0+0+1: we've gotten rid of a great deal
of mess! In fact, it is the presence of the ludicrous (?) functions
arctan(y2) and ln(x2+1) which sort of signals
me, declaring that I'd better try to compute the desired quantity
indirectly. Of course, it doesn't also hurt (!) that the problem
occurs at the end of the section discussing the Divergence Theorem!
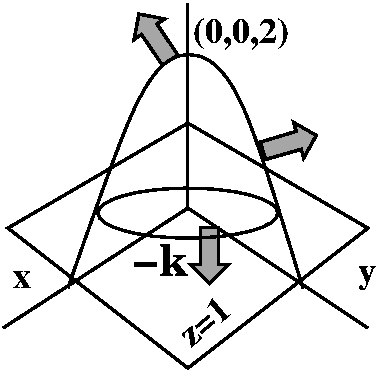
The paraboloid is z=2–x2–y2: it "opens" down. The vertex or top is at (0,0,2). The normals to the paraboloid vary a great deal. While it might be possible to compute the flux directly, the Divergence Theorem states that the integral of 1 (that's div F) over the solid region above z=1 and below z=2–x2–y2 will equal the flux through the parabolic cap plus the flux through the disc on the plane z=1. That disc has radius 1, centered at the origin, since the boundary is 1=2–x2–y2 or x2+y2=1. Also the outward normal on the disc is constant because the disc is flat, and the outward normal is –k.
Let's compute the triple integral: ∫∫∫The cup1 dV. Probably this is
simplest to compute with cylindrical coordinates. θ will go from 0
to 2Π, and r will go from 0 to 1. That's a polar description of the
base of the solid. What's the height? The bottom is at z=1, and the
top is at z=2–x2–y2, or (in "polar")
z=2–r2. So we compute
∫θ=0θ=2Π∫r=0r=1∫z=1z=2–r21 dz r dr dθ=∫θ=0θ=2Π∫r=0r=1(2–r2–1)r dr dθ=
∫θ=0θ=2Π∫r=0r=1(r–r3)dr dθ=
∫θ=0θ=2Π(r2/2–r4/4)]r=0r=1dθ=∫θ=0θ=2Π(1/4)dθ=Π/2.
Now the surface integral over the "bottom" disc. F·N is (z arctan(y2)i+z3ln(x2+1)j+zk)·(–k) which is –z. But z=1 on this disc, so we need to integrate –1 over a disc bounded by a circle of radius 1: the answer is –Π, –1 multiplied by the area of the area.
We now have: Π/2 (the divergence integral) is equal to the flux over the paraboloid plus –Π (the flux over the disc). Therefore the flux over the paraboloid must be (3Π)/2. (This almost resembles a use of integration by parts -- the boundary term over the parabolic cap is exchanged for the boundary term over the disc, with a penalty paid: the triple integral over the inside.
|
Other uses While textbook problems are (sometimes) nice, more interesting uses of the Divergence Theorem include a discussion of heat transfer and Gauss's Law for electric charges. We have no time, but I just want to remark that the results are remarkable and really interesting. Gauss's Law is discussed in many physics books. Also you can look at pages 1037 and 1038 of the textbook. The heat equation, which tries to describe heat transfer, is discussed in lots of engineering courses and in several math courses, including Math 421 and Math 423 which many of the students in this class likely will take. |
From last time ...
If r takes R2 to R3, then the image of a very
small du-by-dv rectangle is supposed to be
||ruxrv|| du dv.
Surface integrals
If we believe a piece of surface in R3 could be a
mathematical model of a thin curved plate, then the plate could have
varying density. We could add up the density multiplied by the area to
get mass. This is a surface integral:
∫∫Region in (u,v)(Density) dS.
 Textbook example
Textbook example
Let me try an artificial (textbook!) example. Here is
problem 22 of section 16.4. It asks us to calculate
∫∫Rectf(x,y,z) dS if the surface is given by
r(u,v)=<u cos(v),u sin(v),v>, Rect is the
rectangle in u and v where 0≤u≤1 and 0≤v≤2π, and
f(x,y,z)=sqrt(x2+y2).
This whole example is arranged so that things will work out "well".
The surface is called a helicoid.
If we hold v constant, then
the curves with u varying are straight line segments of length
1, at height v (a number between 0 and 2π), radiating out from the
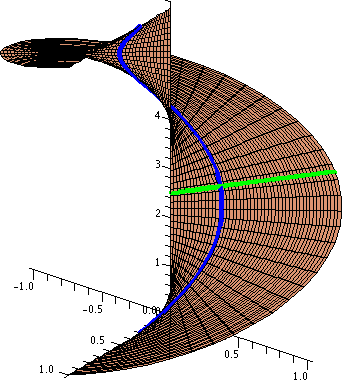
z-axis. The curve drawn in green shown in the
picture to the right is what happens when v=2.5. So it is the curve
(cos(2.5)u,sin(2.5)u,2.5) for u between 0 and 1.
If we hold u constant, then the curve is actually a helix wrapping
around the z-axis. The curve drawn in blue shown in
the picture to the right is what happens when u=.3. So it is the curve
(.3cos(v),.3sin(v),v) for v between 0 and 2π.
Computation
Since
r(u,v)=<u cos(v),u sin(v),v>, we have
ru=<cos(v),sin(v),0>
rv=<–u sin(v),u cos(v),1>
The cross product: ( i j k )
ruxrv=det( cos(v) sin(v) 0 )
( –u sin(v) u cos(v) 1 )
So this is sin(v)i–(cos(v))j+(u(cos(v))+u(sin(v))2)k=sin(v)i–cos(v)j+uk. The
magnitude of this vector is sqrt(1+u2). So here
dS=sqrt(1+u2) du dv.
The function or "density" is sqrt(x2+y2) but in the helicoid parameterization, x=u cos(v) and y=u sin(v). So sqrt(x2+y2) accidentally (!) turns out to be u because again cos2+sin2=1.
The integral ∫∫Rectf(x,y,z) dS is also accidentally ∫v=0v=2Π∫u=0u=1u sqrt(1+u2) du dv. By total coincidence, we can compute this exactly. It is 2Π(sqrt(2)/3–1/3). Wow. Wowie. I guess this is terrific (and all totally arranged, of course).
Non-textbook example
What's the surface integral of x3+y2+z of that
part of the graph z=3x2+5y4 which is over the
unit square, 0≤x≤1 and 0≤y≤1? The parameterization is the
straightforward
r(u,v)=ui+vj+(3u2+5v4)k
so that ru=1i+6uk and
ru=1j+20v3k and the
cross-product ruxrv is
–6ui–20v3j+1k. (I did this
in class. If you weren't there [your loss, about 35 to 40 dollars
worth] please check the result!). Therefore dS is
sqrt(1+36u2+400v6) du dv (not so
agreeable, huh?).
And x3+y2+z changes to
u3+v2+3u2+5v4. So we just need to compute
∫v=0v=1∫u=0u=1(u3+v2+3u2+5v4)sqrt(1+36u2+400v6) dv du
Maple knows a lot more about antidifferentiation than I do, and it can't "do" this computation exactly, although on my home PC about a second passes before Maple admits this. With evalf, we get 26.484 as an approximate numerical value in less than a tenth of a second.
Most surface integrals can't be evaluated exactly.
This is a pity, since flux, an important physical quantity, is defined to be a surface integral. So we need to discuss flux, and, just as before, "Strangely enough , it all turns out well."
Flux
The horrible factor ||ruxrv|| makes a "random" surface integral almost
impossible to compute in terms of antidifferentiations involving
familiar functions. It is very nice that the surface integrals of most
interest in physical and engineering problems are not "random" but
result from computations of flux, and it turns out that the horrible
factor disappears for such computations.
 Suppose we have a vector field, F in R3. We could
imagine a surface in R3, and then try to see how the flow
of the vector field interacts with the surface. The picture to the
right is quite imaginary. I've never seen the arrows of a vector
field, and I want the surface, sort of like a net, not to give any
resistance to the imaginary arrows. It is, of course, an imaginary
surface.
Suppose we have a vector field, F in R3. We could
imagine a surface in R3, and then try to see how the flow
of the vector field interacts with the surface. The picture to the
right is quite imaginary. I've never seen the arrows of a vector
field, and I want the surface, sort of like a net, not to give any
resistance to the imaginary arrows. It is, of course, an imaginary
surface.
The flux is the net flow through the surface.
What do these words mean?
net
The direction the fluid flows means something. It is possible that at
some points the fluid crosses the surface in different directions. We
should have some way of giving a sign to the flow, left to right/right
to left, inward/outward, and then totaling the different
contributions, with signs, to see whether the net flow is
positive or negative.
through
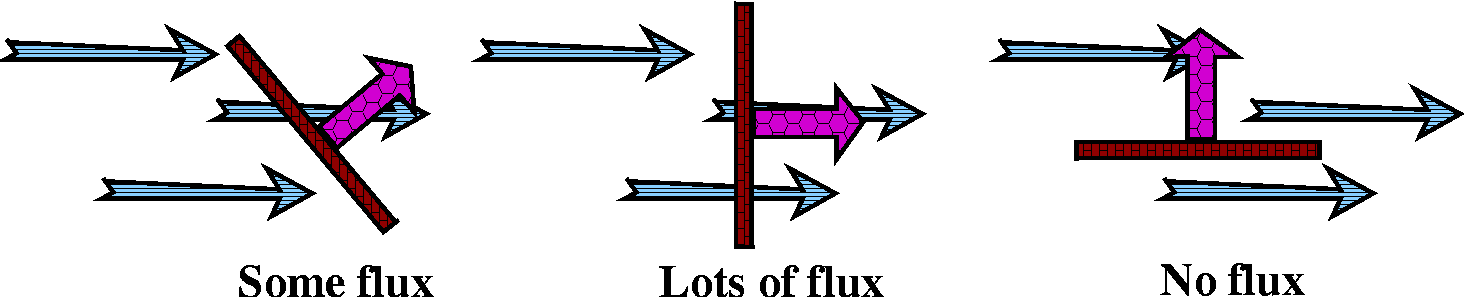 The flow through the surface is important. The same piece of surface
("dS") can have different flux, even if the vector field is constant
-- always the same direction and magnitude. What can then change is
the angle of the dS piece relative to the flow. If it is perpendicular
to the flow, there will be the most flux. If the dS is parallel to the
flow, there will be no flux. In between, there will be some "in
between" amount. In fact, if you think about this, the amount of flux
will depend on the cosine of the angle the surface makes with the
vector field. We can compute this with F·N where N is a unit vector normal or
perpendicular to the surface. Notice that the choice of N is
important. –N is also a unit normal, and using that choice will
change the sign of the flux.
The flow through the surface is important. The same piece of surface
("dS") can have different flux, even if the vector field is constant
-- always the same direction and magnitude. What can then change is
the angle of the dS piece relative to the flow. If it is perpendicular
to the flow, there will be the most flux. If the dS is parallel to the
flow, there will be no flux. In between, there will be some "in
between" amount. In fact, if you think about this, the amount of flux
will depend on the cosine of the angle the surface makes with the
vector field. We can compute this with F·N where N is a unit vector normal or
perpendicular to the surface. Notice that the choice of N is
important. –N is also a unit normal, and using that choice will
change the sign of the flux.
The pictures above are supposed to be cross-sectional so they cut the
surface perpendicularly. The flux is the normal component, and
the work is the tangential component. So in this lecture and
also in the last two, we will be studying the normal component.
 The whole
surface
The whole
surface
If we want to compute the net flux through the whole surface, then we
will need to assign unit normal vectors at every point of the
surface. There are some surfaces which can't accept such
assignments. The simplest example is the Mobius strip
(take a long rectangle, make a half-twist in the long direction, and
attach the short edges together). If you give an N at any one
point, and then follow around the assignment continuously, when you
get back to the point, you'll discover that you have reversed the
normal! So there will be no nice way to define and compute flux
through surfaces which don't permit nice "assignments" of normals. I
will assume such a problem will not occur in the remainder of this
course (hey, it doesn't for planes and spheres and toruses and
... almost anything you will encounter in applications).
The specific technical words used are at the beginning of section
16.5: our surfaces will be oriented surfaces, where it is
possible to specify a choice of normal continuously at every point of
the surface. So the Mobius strip is not an oriented surface.
An example on a cube
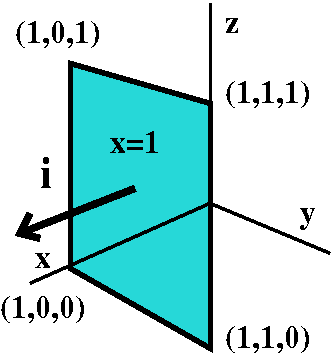 Suppose our vector field is F=<xy,z2,3> and
the surface we're interested in is the surface of the cube defined by
0≤x≤1, 0≤y≤1, and 0≤z≤1. It is not an accident that
this surface is an example of a closed surface which divides
all of space, R3, into two pieces, points inside and points
outside the surface. This is similar to a closed curve in
R2. Such surfaces are important in physical
applications. We will choose the normal to be the outward-pointing
unit normal, so flows out are positive. I would like to compute the
total flux of F through the surface of this cube. There are a
total of 6 faces. I'll do one face carefully, and then the others more
rapidly.
Suppose our vector field is F=<xy,z2,3> and
the surface we're interested in is the surface of the cube defined by
0≤x≤1, 0≤y≤1, and 0≤z≤1. It is not an accident that
this surface is an example of a closed surface which divides
all of space, R3, into two pieces, points inside and points
outside the surface. This is similar to a closed curve in
R2. Such surfaces are important in physical
applications. We will choose the normal to be the outward-pointing
unit normal, so flows out are positive. I would like to compute the
total flux of F through the surface of this cube. There are a
total of 6 faces. I'll do one face carefully, and then the others more
rapidly.
Magical cancellation!
If our surface is parameterized there is a natural way to get a
unit normal. Just take ru and rv:
these are velocity vectors for curves on the surface, and are tangent
to the surface. Their cross-product will be perpendicular to the
surface. If we then normalize (divide by the magnitude) we'll get an
acceptable N. So we can take N to be
ruxrv
divided by the scalar ||ruxrv||. If Flux=∫∫The surfaceF·N dS this will be the same as
∫∫The surface[F·(ruxrv)/||ruxrv||] ||ruxrv|| dAuv
Look at the marvelous cancellation (much the same as what occurred in
the line integral case).
Therefore the flux integral is
∫∫The surfaceF·(ruxrv) dAuv.
While a "plain" surface integral needs to be very carefully prepared
to be "computable" (as the two examples considered earlier show), the
cancellation here means no horrible square root terms, and many flux
integrals should be computable. Let me now compute another flux over a
closed surface.
An example on the sphere
Suppose F is x2i+yzj–4zk and I
would like to know the flux through the sphere of radius 5 centered at
the origin. We considered this surface before and
there we learned
ruxrv=–25cos(u)[sin(v)]2i–25sin(u)[sin(v)]2j–25sin(v)cos(v)k.
Is this the inward or outward pointing normal? Look at v=Π/2 and
u=0. Then (substitute -- we did this in class!) the point on the
surface is (5,0,0) and the vector we just computed is
<–25,0,0>. This points inward and we are therefore
considering flow in to be positive. This is different from the
previous cube example, and that's o.k. as long as we realize what we
are doing!
|
Also, the parameterization itself was x(u,v)=5cos(u)sin(v); y(u,v)=5sin(u)sin(v); z(u,v)=5cos(v). This means that F described in (u,v) terms becomes 25sin(u)2sin(v)2i+25sin(u)sin(v)cos(v)j–20cos(v)k
We need to integrate F·N dS,
but this, because of the cancellation of the horrible factor ||ruxrv|| becomes just F·(ruxrv) dAu,v. Let
me match up the components and get the integrand:
Problem 18 in section 16.5
|
And, oh yes,
An intellectual simile unless it is a
metaphor
Let's see: here is a useful "ratio":
Line integrals and work are to
Green's Theorem
as
Surface integrals and flux are
to Stokes' Theorem and the Divergence
Theorem
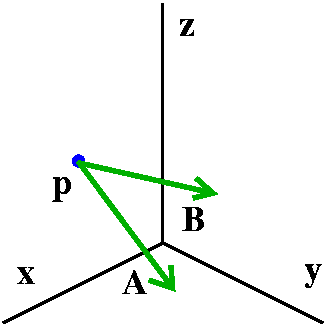
How to describe a plane
Suppose I give you a point, p=(3,1,2), and two vectors,
A=<4,–1,3> and B=<1,5,2>. I would like to
describe algebraically the plane which contains the point p in the
direction of the vectors A and B. Here is how we did
this problem earlier in the course.
An implicit description of the plane
Compute the cross-product of A and B: ( i j k )
det( 4 –1 3 )=–17i–5j+21k.
( 1 5 2 )
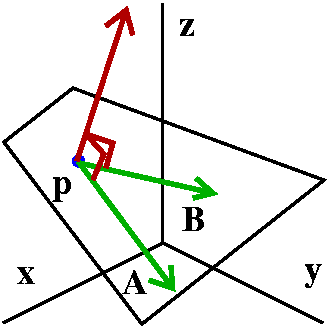 It is easy to check (I just did with some dot products) that the
resulting vector is perpendicular to both A and B and is
a normal vector to the plane we'd like to describe. A point with
coordinates (x,y,z) is on this plane if
It is easy to check (I just did with some dot products) that the
resulting vector is perpendicular to both A and B and is
a normal vector to the plane we'd like to describe. A point with
coordinates (x,y,z) is on this plane if
–17(x–3)–5(y–1)+21(z–2)=0.
This implicit description, using a normal vector, was very convenient
for parts of the course since the gradient always gives a vector
normal to a level surface, and therefore normal to a plane which is
tangent to that level surface. But there's another way to describe the
plane.
An explicit description
Change the point p=(3,1,2) to a position vector,
P=<3,1,2>. Then every point on this plane has a unique
description as P plus some multiple of A plus some
(possibly other) multiple of B. Your text calls these
multiplies u and v, so I will also. So the plane is anything which can
be written as P+uA+vB. We can write this with
more details:
<3,1,2>+u<4,–1,3>+v<1,5,2>=<3+4u+1v,1–u+5v,2+3u+2v>. The
textbook writes this as a vector position function:
r(u,v)=(3+4u+1v)i+(1–u+5v)j+(2+3u+2v)j
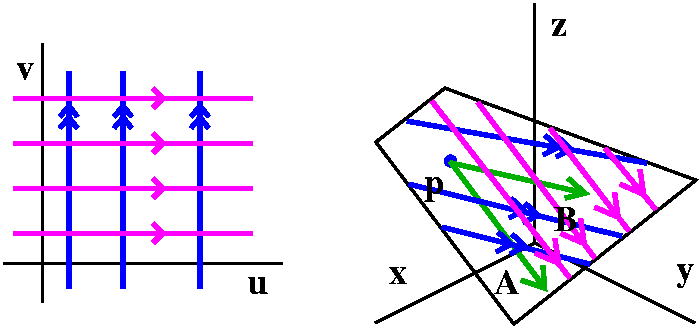
Notation comment
The textbook uses Φ(u,v) for the vector-valued position
function.
I am going to write r(u,v) instead, since I have trouble with
capital Greek letters.
The i component is called x(u,v), the j component is
called y(u,v), and the k component is called z(u,v), Each point
on the plane has a unique "address" in terms of the pair of numbers
(u,v). This is like the central Manhattan street grid: streets and
avenues. So 3rd Avenue and 47th Street is a
unique point, and every intersection has a unique address.
 A sphere
A sphere
Creating a "mapping" from a piece of the (u,v) plane to a surface in
R3 is frequently called a coordinate chart (although
not in your book, where it is called a
parameterization). Getting a coordinate chart for a plane is
not difficult. Getting (useful!) coordinate charts for curved surfaces
can be much harder. Here's an example which is only moderately
difficult because we have studied spherical coordinates: a sphere of
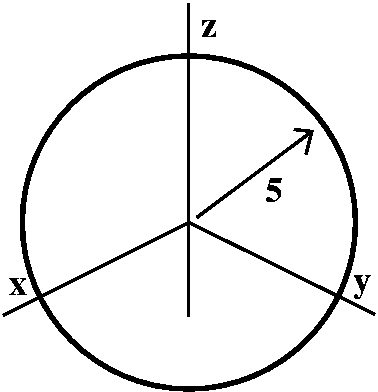
radius 5 centered at the origin in R3.
Now let's use spherical coordinates, with ρ fixed at 5. We see that
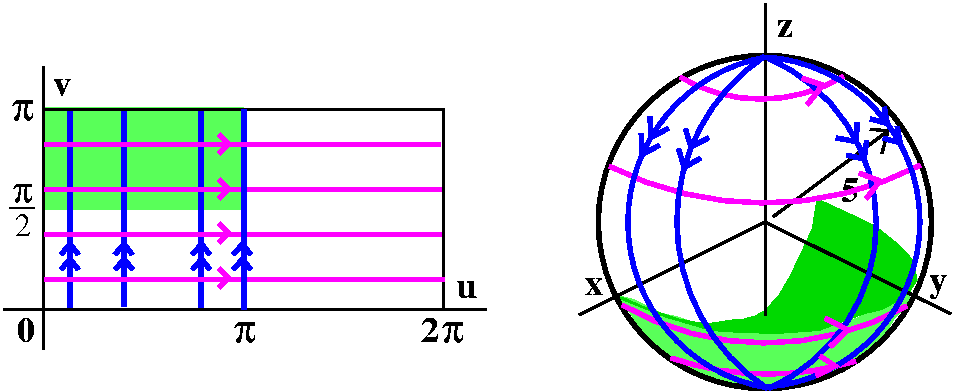
a point on the sphere will be described by (I use u for θ and v for φ):
x(u,v)=5cos(u)sin(v); y(u,v)=5sin(u)sin(v); z(u,v)=5cos(v).
I want points on the sphere to have unique (u,v) addresses, and the conventional choice for restriction of the (u,v) domain is 0≤u≤2Π and 0≤v≤Π.
Horizontal lines in the (u,v) domain become circles parallel to the
xy-plane on the sphere (latitudes?). Vertical lines in the (u,v)
domain, where v varies and u is fixed, become half great circles on
the sphere, going from the "North Pole" to the "South Pole". The
region in the (u,v) domain where 0≤u≤Π and Π/2≤v≤Π
becomes the lower (z≤0) and "forward" (y≥0) quarter sphere.
|
A torus I'll try now to give a parametric description of a torus. So the torus (the surface of a doughnut) will be a surface which is gotten when a circle perpendicular to the xy-plane, and radially oriented, is revolved around the z-axis. One view of what I'm trying to describe is to the right. The center of the circle to be revolved around the z-axis is moved so that it describes a circle in the xy-plane centered at the origin. There are two more views below of the surface. One is from "above", looked down the z-axis. The other is from the "side", looking along the y-axis. | 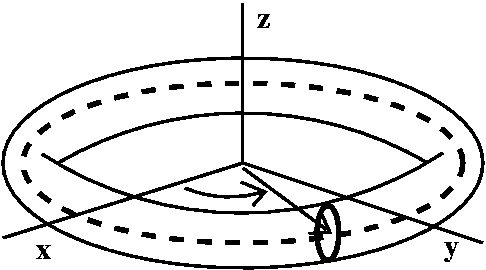 |
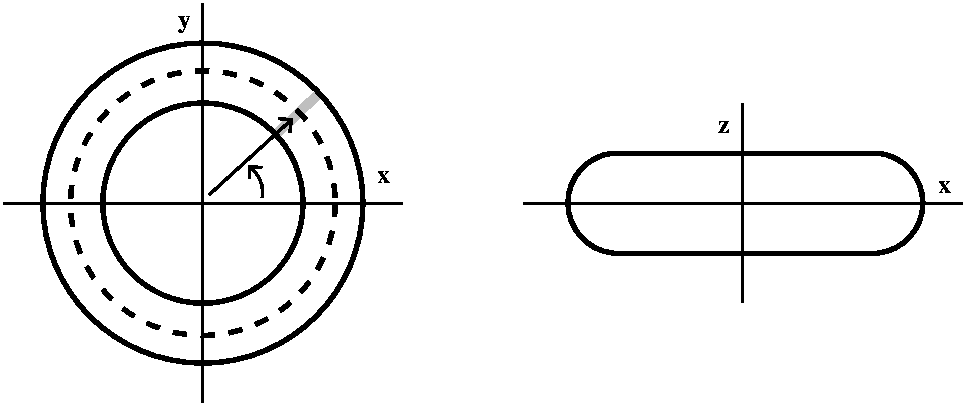
I can give points on the torus a unique "address" in terms of two numbers. These two numbers will represent angles. One angle will be θ, but I'll call it u to agree with the text. I'll make this specific torus more definite: the length of the vector from the z-axis to the center of the circle will be 4, and the radius of the circle being revolved around the z-axis will be 2. The left picture below shows the angle u. The right picture shows a slice perpendicular to the xy-plane, through the vector of length 4. I will specify a point on the torus by letting v be the angle made by a line from the point on the torus to the center of the circle compared to the xy-plane itself. 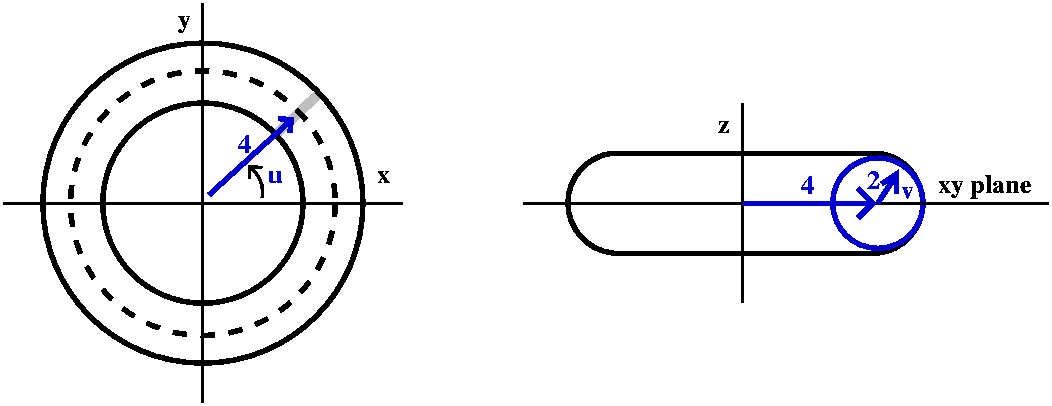 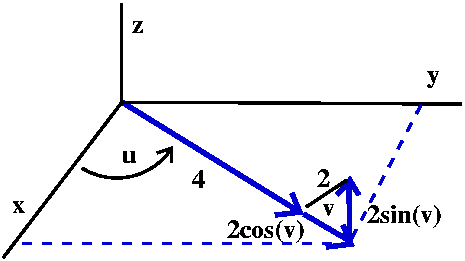 The z coordinate of the point only involves v. The z coordinate is the
"opposite" side of a right triangle with acute angle v and hypotenuse
2. So z=2sin(v). The vector from the origin to the center of the
circle has length 4. The angle v adds on another 2cos(v) to that
length. But then we use this total length, 4=2cos(v), along with the
angle u (secretly, θ) to get the x and y coordinates. So
x=(4+2cos(v))cos(u) and y=(4+2cos(v))sin(u).
The z coordinate of the point only involves v. The z coordinate is the
"opposite" side of a right triangle with acute angle v and hypotenuse
2. So z=2sin(v). The vector from the origin to the center of the
circle has length 4. The angle v adds on another 2cos(v) to that
length. But then we use this total length, 4=2cos(v), along with the
angle u (secretly, θ) to get the x and y coordinates. So
x=(4+2cos(v))cos(u) and y=(4+2cos(v))sin(u).
Therefore the torus will be given by the following vector-valued function: In the 21st century I can check using a picture what I've just written. Here is a Maple command and its output. I should remark, if you've never been in my office watching me try to use Maple, that typing this command and looking at its output took 5 attempts before I was successful. Such wonderful efforts may explain why I wouldn't trust myself to use Maple in class while people watched and giggled, and we all wasted time. plot3d([4+2*cos(v))*cos(u),4+2*cos(v))*sin(u),2*sin(v)], u=0..2*Pi,v=0..2*Pi, scaling=constrained,axes=normal);
Finally, we can consider horizontal lines across the domain of the
coordinate chart, r(u,v), and ask what kinds of curves these
create on the torus. These lines, where u changes and v is unchanged,
become circles around the z-axis. Similarly, the vertical lines in the
domain of r become lines "around" the torus, for fixed u=θ.
Surface area
The surface area of the sphere
( i j k )
ruxrv=det(–5sin(u)sin(v) 5cos(u)sin(v) 0 )
( 5cos(u)cos(v) 5sin(u)cos(v) –5sin(v) )
The i component is just –25cos(u)[sin(v)]2 and the
j component is –25sin(u)[sin(v)]2 and the k
component is
–25[sin(u)]2sin(v)cos(v)–25[cos(u)]2sin(v)cos(v). The
last component simplifies (sin(u)2+cos(u)2=1) and the
result isruxrv=–25cos(u)[sin(v)]2i–25sin(u)[sin(v)]2j–25sin(v)cos(v)k Now for the magnitude of this vector: the square root of the sum of the squares of the components. There's a common factor of 252[sin(v)]2 when everything is squared, so I'll take that out of the square root (sin(v) is positive when v is between 0 and Π as it is here). So we must multiply 25sin(v) by {cos(u)sin(v)]2+[sin(u)sin(v)]2+[cos(v)]2. Now look at this: one use of sin(u)2+cos(u)2=1 turns this into sin(v)2+cos(v)2 and that's 1 also! So therefore we square root things and see that |ruxrv|=25sin(v). We get the whole sphere when the coordinate patch is 0≤u≤2Π and 0≤v≤pi, so the whole surface area is ∫0Π∫02Π25sin(v) du dv. This integral can be computed, and its value is 100Π. The surface area of a sphere of radius r is supposed to be 4Π r2 (four "great circles") so when r=5 this is the textbook answer.
Please try to read section 16.4 and do a few problems.
Tuesday, November 23, sections 12-14 and sections 15-17, lecture #24Theorem Suppose V=<F1,F2,F3> is a vector field. These conditions are logically equivalent:
This result has turned out to be very influential in many areas of science and technology, even when it is not directly applicable. For example, a number of complicated computer algorithms are designed around the idea of a potential (even though there's nothing involving vector fields in the algorithm) and evaluating results using the difference of the potential's values. Today I'll discuss Green's Theorem (section 17.1 of the text) before completing chapter 16 in the next few lectures. I want to show you another thing wonderful and mysterious. I basically know three ways to evaluate line integrals:
About George Green
Silly example
Proofy paragraph 1
Proofy paragraph 2
Connection with the previous lecture
So ∫Sy dx+x2dy=∫Sy dx+x2dy+∫Ly dx+x2dy=∫S+Ly dx+x2dy, and the curve S+L, which is S followed by L, encloses the upper half of the area inside a circle of radius 3 centered at the origin: a semidisc (great word!). I'll call it Q.
Then a version of Green's Theorem allows us to replace ∫S+Ly dx+x2dy by ∫∫Q∂(x2)/∂x–∂y/∂y dA. The
integrand is 2x–1, and we need to integrate it over Q. I would agree that this is an awkward, even ludicrous way of evaluating the line integral. (But it is slick!) I went through it because in a week we'll be trying computations like this in three dimensions and maybe things there won't be as clear.
The text's version of Green's Theorem
Definitions of terms
Information transported from the boundary to the inside People designed interesting mechanical linkages to compute areas based on such results. These instruments are called planimeters. People can be very clever. Analogous results in higher dimensions (R3) would allow some knowledge of the heart based upon electrical readings on the skin (EKG's?). Or the results can be used to try to deduce the presence of cracks inside structures (steel beams?) as a result of measurements on the outside. Detect conditions inside an object using surface measurements, so there is no need for invasive procedures.
Another example, somewhat paradoxical
But but but ... the integrand on the "other side" of Green's Theorem is Qx–Py and we computed that to be 0. A circle certainly is a simple closed curve, positively oriented, etc. We haven't made any errors. Maybe it is true that 2π=0?
Technicalities matter.
Thursday, November 18, sections 12-14, and Friday, November 19, sections 15-17, lecture #23Before teaching the Friday lecture, a colleague asked me what I would talk about. I answered (including some enthusiastic comments about how wonderful this stuff is) and was asked, "When did you [me] understand how important these ideas were?" My reply was (and this is true) that understanding the importance of the ideas (and the computations) took about 5 to 7 years. Yes, I could push around the symbols, but really seeing what what going on took quite a while longer. I need lots of time with new ideas.
An example
Computing some work
Another work computation
Different?
Path independence is a very strong property. Let me be more precise about it. Take any two points p and q. Take any path connecting p to q. Then the work done will depend only on p and q, and not on the choice of path.
Which vector fields are conservative?
So I want to write the line integral of F1(x,y,z) dx+F2(x,y,z) dy+F3(x,y,z) dz over these three line segments. Here we go, but watch carefully, because the details are quite important. Here y is changing and x and z do not change. So a simple parameterization is x=–2,y=t,z=3, and then dx=0 dt, dy=1 dt, and dz=0 dt. The integral becomes ∫6yF2(–2,t,3) dt. Here x is changing and y and z do not change. So a simple parameterization is x=t,y=y (a constant!),z=3, and then dx=1 dt, dy=0 dt, and dz=0 dt. The integral becomes ∫–2xF1(t,y,3) dt. Here z is changing and x and y do not change. So a simple parameterization is x=x (a constant),y=y (a constant),z=t, and then dx=0 dt, dy=0 dt, and dz=1 dt. The integral becomes ∫3zF3(x,y,t) dt.
The total integral which is g(x,y,z) is therefore the sum of all three of these.
Look at this mess. Actually, it isn't a mess, but it is somewhat complicated. How many y's are there in the formula? If you count carefully, there are 3. And there are two x's. But there is only one z. So let me try to understand how g(x,y,z) depends on z. What if I ∂/∂z this formula for g(x,y,z)? The first two integrals have no z at all in them. So from the z point of view they are constants. Therefore the result of ∂/∂z of those integrals is 0. The last integral has z in the upper bound of the integral. This is a first semester calculus exercise. The Fundamental Theorem of Calculus says that the way to differentiate a function defined by a definite integral with a variable upper bound is to plug that variable into the integrand. Here the integrand is F3(x,y,t) and we are integrating with respect to t. Therefore ∂g/∂z=F3(x,y,z). We could have picked other orders of the variables from the list of x and y and z, and written similar straight line segment paths going from (–2,6,3) to (x,y,z). The value of g(x,y,z) would be the same because of path independence. If, say, y were the last variable picked, then I would ∂/∂y the result. The y path would have as integrand F2. The result would be ∂g/∂y=F2(x,y,z). And if we picked an order where the last named variable was x, and did a similar computation, the result would be ∂g/∂x=F1(x,y,z).
A conclusion That is, ∇g=F and F is a gradient vector field, with g as one potential. The effect, by the way, of picking another ground state, is just to alter g by an additive constant. getting a different potential. You can see this by realizing that a path from the "new" ground state to (x,y,z) is a path from the new ground state to the old ground state and then to (x,y,z): the line integral values would differ by the constant amount of the line integral from the new ground state to the old ground state. If a vector field is conservative, then it is a gradient vector field. Just differentiate the upper value of the integral.
If F is a conservative vector field, then F is a gradient vector field.
The other way!
So dx=(dx/dt) dt, dy=(dy/dt) dt, and dz=(dz/dt) dt. We
need to "plug in" the parameterization to the components of
F. So the line integral, ∫CF·Tds, becomes
"Strangely enough , it all turns out well." Well, it is not too
strange if you realize that 150 years of effort have gone into what
I'm showing you today. Several students recognized that the integrand, The work done is the value of the potential at the End minus its value at the Start.. This is such a marvelous fact that I want to use it immediately.
One way to compute the work is to use the parameterization, substitute things. etc. But since I know that F=∇g, I can take advantage of the result we just discovered, and find the values of g at the End and Start and subtract them.
Start
End The value of the line integral is g(End)–g(Start)=(1,500&pi+5)–(–250&pi+5)=1,750π. This seems much easier to me than working the with parameterization, differentiating, substituting, integrating, and evaluating. Your opinion may be different but I think you'd be wrong!
And, of course, after all this, a number of students saw the answer immediately. Of course I wanted all of the drama to myself, but I was just as happy that they did see it. The important fact here is that Start=End, so that g(End)–g(Start)=0. I don't need to do any computation at all!
Wednesday, November 17, sections 12-14 and sections 15-17, lecture #22I began with might have seemed some irrelevant observations, but these "observations" were an effort to get students to expect that certain kinds of integrals would be useful in investigating vector fields.
How to get from the gradient back to a
potential?
Combining the descriptions of φ
We need to think and compare definitions. Any part of φ involving
both x and y must appear in both descriptions, and that here is just
sin(x2y). Any y alone function must appear in the y
description and any x alone function must appear in the x
description. Anything else is truly just a constant -- it can't in any
way depend on either x or y. So combining the descriptions we get this
as our answer, a complete description of all potentials of the
given vector field:
Try again ...
How about 3 dimensions not just 2?
Segue
Line integrals
Suppose I cut the wire up into lots of little chunks. How little?
Well, the length of each chunk will be ds, a tiny piece of arc length
(we discussed this in several lectures given late January, long, long
ago). If I assume that the density D(x,y) varies only a small amount
because the chunk of the wire is very small, then dm, the mass of this
piece, is nearly D(x,y) ds (remember I made the cross-sectional
area equal to 1). Further, I can add up these pieces of mass to get
the total mass. I can take the limit as the number of pieces gets
large and the length of the pieces gets small. The result is that the mass
of the wire should be given by
∫The wireD(x,y) ds.
This is a totally insignificant, physically unrealistic (to me) computation. The only thing I had fun with is drawing the picture, which with its varying colors is supposed to suggest the increasing density of the wire as y increases. There is one very important fact which should be mentioned now:
Independence of parameterization
Random example
ds is the obstacle Cognitive dissonance arises from conflicting cognitions. Cognitive dissonance is the perception of incompatibility between two cognitions, which for the purpose of cognitive dissonance theory can be defined as any element of knowledge, attitude, emotion, belief or value, as well as a goal, plan, or an interest. In brief, the theory of cognitive dissonance holds that contradicting cognitions serve as a driving force that compels the mind to acquire or invent new thoughts or beliefs, or to modify existing beliefs, so as to minimize the amount of dissonance (conflict) between cognitions.
Work with a varying vector field along a curve
A computation
ds
As before, the speed becomes
F
T The unit tangent vector, T, is a vector in the direction of the curve. The position vector of the curve is <t,t4> so that the velocity vector is <1,4t3>. But we need a unit vector to get the projection of F in the direction of the curve. Divide by the magnitude of <1,4t3>. Therefore, T=<1,4t3>/sqrt(1+16t6).
Assembling the work integral
What happens?
Using the notation to help
Problem statement
A solution
A possible QotD
Thursday, November 11, sections 12-14, and Friday, November 12, sections 15-17, lecture #21About 70% of the course has gone by. Much of what we've done will be very useful for many of the students, but, perhaps, some of what we've done will be neeeded less often (I am trying to be "diplomatic"). The last portion of the course, about what is frequently called Vector Calculus, can help students understand and model many complicated phenomena they will likely encounter. For example, consider a big "chunk" of "stuff". Look at the heat in the chunk. Sometimes some of the heat might originate inside the object, and sometimes there might be cooling. And there are also boundary effects. If there's something really hot near part of the boundary, heat will flow in around that part, and, similarly, there might be cool things (?) near some other part of the boundary, and heat will flow out that part of the boundary. This is all very complicated. Somehow, there should be some way of balancing the heat sources and sinks inside the region, and the boundary flow of heat, and expressing this in a neat way. The tools we develop in this last portion of the course will allow us to create a model of this situation.
The Fundamental Theorem of Calculus is this:
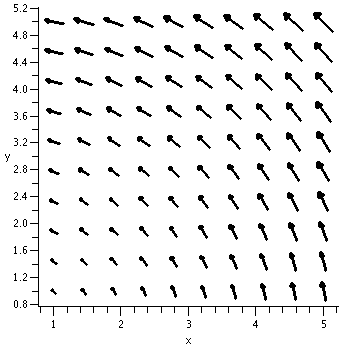
Vector fields
Models? The force field (gravity, electromagnetism, etc.) might be the simplest. The "arrow" at every point denotes the presence of a "force" which can act on the proper kind of object (gravitation: an object with mass, magnetism, an object with magnetic "stuff", etc.). In Newton's law of gravitation, we could think of a powerful mass, M, (the sun?) at the center of the universe, and other very small masses, m's, scattered around. Ignore interactions between the m's. Each m will be attracted to the M with a force of magnitude GmM/(dist)2 where "dist" is the distance from m to M. The direction of the attraction is from m to M. To get a vector field, just sketch an arrow in the direction of the force, with a length proportional to the magnitude of the force. Then to complete the creation (?) of the force field, just remove all the little m's and leave the arrows. This is quite an idea, really a big leap of imagination. I have never seen any of these arrows, but imagining them is sometimes quite helpful. A quote (New York Times, March 19, 1940) from Albert Einstein describing radio may be appropriate here: You see, wire telegraph is a kind of a very, very long cat. You pull his tail in New York and his head is meowing in Los Angeles. Do you understand this? And radio operates exactly the same way: you send signals here, they receive them there. The only difference is that there is no cat.
Associated to a fluid flow are streamlines, which would describe how a fluid actually flows (the velocity vector field only would give what's called the "instantaneous" flow). Such streamlines are investigated and can sometimes be described exactly by solving differential equations.
Vector fields
The simplest ways students discover vector fields in their studies
is:
Gradient vector fields
In general ...
How many potentials?
Then I asked a harder question: could we list all possible
potentials of the vector field 2xi+2yj? Well, there
was a bit of discussion, and then I wrote
x2+y2+Constant, where "Constant" means any
possible constant. Why is this true? Well, if two functions have the
same gradient, then their difference will
have gradient equal to 0. Now the question is: why would a function,
let's call it g(x,y), with ∂g/∂x=0 always and
∂g/∂y=0 always have to be constant?
Is the vortex flow a gradient vector field? ∂/∂y
φx= –y → φxy= –1
∂/∂x
φy= x → φyx= 1
But "mixed" partial derivatives are supposed to be equal (that is, if
some hypotheses are satisfied, but these are all very reasonable
functions and nothing weird happens). Since –1 is not equal to 1 we
know that the vortex flow is not a gradient vector field. I
don't think this is an obvious fact.
Please look at the textbook, which also discusses and shows some 3-dimensional vector fields.
Maintained by greenfie@math.rutgers.edu and last modified 11/12/2010. | ||||||||||||||||||||||||||||||||||