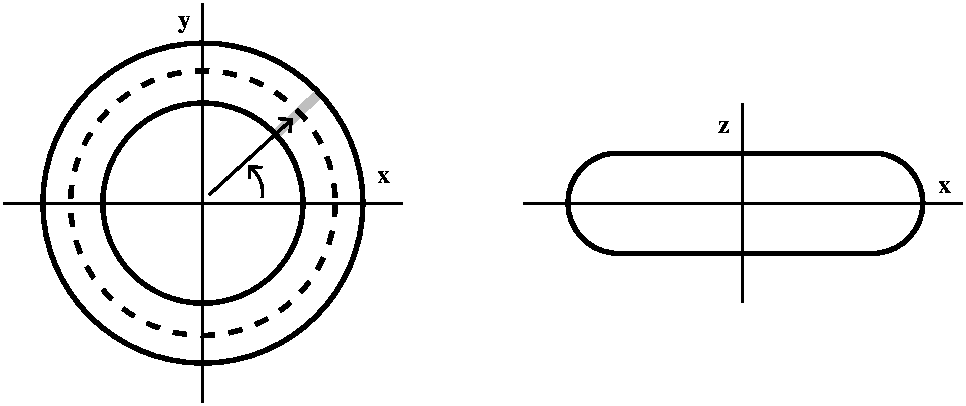
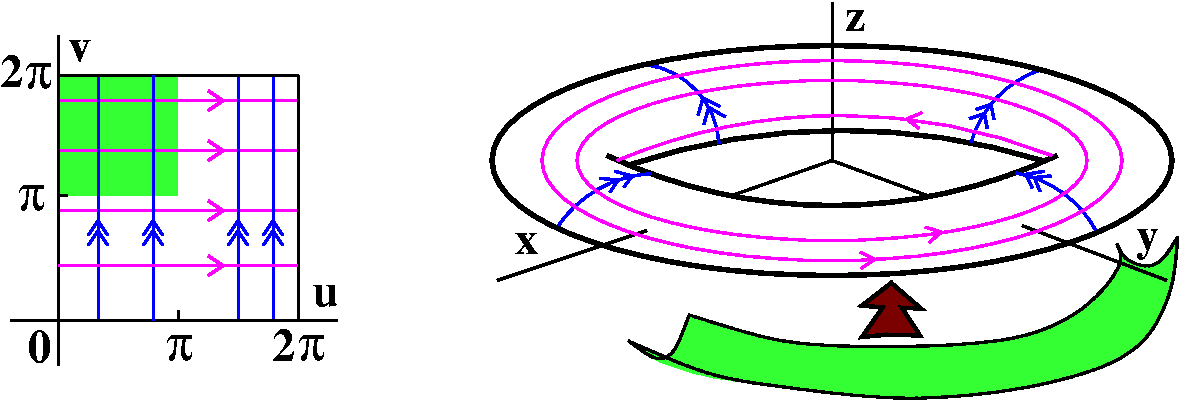
I can give points on the torus a unique "address" in terms of two
numbers. These two numbers will represent angles. One angle will be
θ, but I'll call it u to agree with the text.
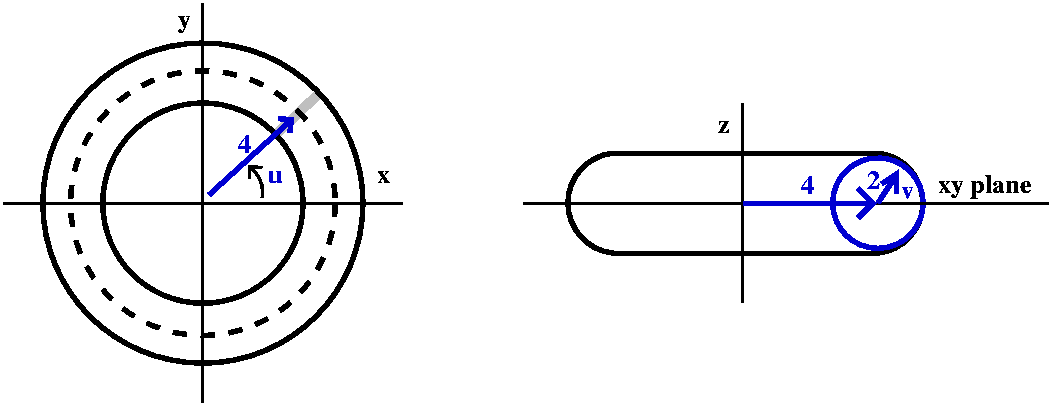
I'll make this specific torus more definite: the length of the vector
from the z-axis to the center of the circle will be 4, and the radius
of the circle being revolved around the z-axis will be 2. The left
picture below shows the angle u. The right picture shows a slice
perpendicular to the xy-plane, through the vector of length 4. I will
specify a point on the torus by letting v be the angle made by a line
from the point on the torus to the center of the circle compared to
the xy-plane itself.
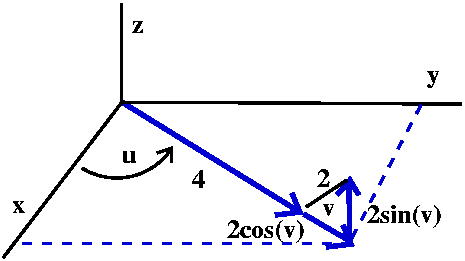 The z coordinate of the point only involves v. The z coordinate is the
"opposite" side of a right triangle with acute angle v and hypotenuse
2. So z=2sin(v). The vector from the origin to the center of the
circle has length 4. The angle v adds on another 2cos(v) to that
length. But then we use this total length, 4=2cos(v), along with the
angle u (secretly, θ) to get the x and y coordinates. So
x=(4+2cos(v))cos(u) and y=(4+2cos(v))sin(u).
The z coordinate of the point only involves v. The z coordinate is the
"opposite" side of a right triangle with acute angle v and hypotenuse
2. So z=2sin(v). The vector from the origin to the center of the
circle has length 4. The angle v adds on another 2cos(v) to that
length. But then we use this total length, 4=2cos(v), along with the
angle u (secretly, θ) to get the x and y coordinates. So
x=(4+2cos(v))cos(u) and y=(4+2cos(v))sin(u).
Therefore the torus will be given by the following vector-valued function:
r(u,v)=x(u,v)i+y(u,v)j+z(u,v)k with
x(u,v)=(4+2cos(v))cos(u) and
y(u,v)=(4+2cos(v))sin(u) and z(u,v)=2sin(v).
The domain of the coordinate chart which will give each point on the
torus surface a unique (u,v) address is 0≤u≤2Π and
0≤u≤2Π.
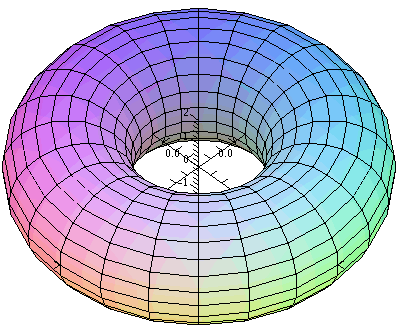
In the 21st century I can check using a picture what I've just
written. Here is a Maple command and its output. I should
remark, if you've never been in my office watching me try to
use Maple, that typing this command and looking at its output
took 5 attempts before I was successful. Such wonderful effort may
explain why I wouldn't trust myself to use Maple in class
while people watched and giggled, and we all wasted time.
plot3d([4+2*cos(v))*cos(u),4+2*cos(v))*sin(u),2*sin(v)], u=0..2*Pi,v=0..2*Pi, scaling=constrained,axes=normal);
Finally, we can consider horizontal lines across the domain of the
coordinate chart, r(u,v), and ask what kinds of curves these
create on the torus. These lines, where u changes and v is unchanged,
become circles around the z-axis. Similarly, the vertical lines in the
domain of r become lines "around" the torus, for fixed u=θ.
If we restrict to region where 0≤u≤Π and Π≤v≤2Π,
then the part of the torus which results is "forward" of the xz-plane
(where y≥0) and below the xy-plane (where z<=0). This is a
quarter of the torus.
A graph
Here I considered a rather simple surface given by a graph:
z=3x2+5y4. Certainly all I expected people to
see and say was this this surface is (vaguely) cup-shaped, and its
lowest point is at (0,0,0). There's a really simple way to
parameterize such surfaces: just use x and y. So
r(u,v)=ui+vj+(3u2+5v4)k. The
parameterization geometrically consists of pushing up a grid from the
xy-plane until it hits the graph.
|
 |
Surface area
Here once again was used the wonderful integral calculus mantra:
Cut up, approximate, sum, limit
Small rectangles in the uv domain, of dimension Δu by Δv
were changed to approximate parallelograms. The curve with u varying
and v fixed has a tangent vector, and that tangent vector is
ru, that is, ∂r/∂u (take the
partial derivative of the component functions with respect to u). The
text calls this Tu but I think we have lots of T's
in this course. The tangent vector along the curve with v varying and
u fixed is rv. The resulting area of the approximate
parallelogram is obtained by taking a cross product (you need to
remember a much earlier result, which is that the area of a
parallelogram is the magnitude of the cross product of vectors forming
adjacent sides), and we get ||ruxrv||ΔuΔv. Then add these up and take
the limit. The surface area for a part of the surface which is
parameterized by a domain, D, in the uv-plane turns out to be
∫∫D||ruxrv|| du dv. The
textbook calls ||ruxrv|| du dv by the
name, dS, for a piece of surface area. It will also be useful to
realize that ruxrv, a cross-product of two
vectors tangent to the u- and v- coordinate curves on the surface, is
a vector normal to the surface.
 Jacobians?
Jacobians?
I don't think my discussion of the surface area was good enough, but
Ms. Lee remarked that it reminded her
of Jacobians and I had to agree. Let me briefly explain. It is
possible that the surface we are parameterizing has z(u,v)=0. This is
perhaps a bit silly, but this means that the surface is just a piece
of the xy-plane, and we are putting coordinates on that. So the
function r(u,v) is really <x(u,v),y(u,v),0>. The area
magnification factor is ||ruxrv||ΔuΔv and in this case that's the
Jacobian of the transformation taking (u,v) to (x,y). So the
discussion here is a generalization of the previous computations
involving change of variables from (u,v) to (x,y).
|
The surface area of the sphere
Here
r(u,v)=5cos(u)sin(v)i+5sin(u)sin(v)j+5cos(v)k
Therefore
ru=–5sin(u)sin(v)i+5cos(u)sin(v)j+0k
and
rv=5cos(u)cos(v)i+5sin(u)cos(v)j–5sin(v)k
( i j k )
ruxrv=det(–5sin(u)sin(v) 5cos(u)sin(v) 0 )
( 5cos(u)cos(v) 5sin(u)cos(v) –5sin(v) )
The i component is just –25cos(u)[sin(v)]2 and the
j component is –25sin(u)[sin(v)]2 and the k
component is
–25[sin(u)]2sin(v)cos(v)–25[cos(u)]2sin(v)cos(v). The
last component simplifies (sin(u)2+cos(u)2=1) and the
result is
ruxrv=–25cos(u)[sin(v)]2i–25sin(u)[sin(v)]2j–25sin(v)cos(v)k
Now for the magnitude of this vector: the square root of the sum of
the squares of the components. There's a common factor of
252[sin(v)]2 when everything is squared, so I'll
take that out of the square root (sin(v) is positive when v is between
0 and Π as it is here). So we must multiply 25sin(v) by
{cos(u)sin(v)]2+[sin(u)sin(v)]2+[cos(v)]2. Now
look at this: one use of sin(u)2+cos(u)2=1 turns
this into sin(v)2+cos(v)2 and that's 1 also! So
therefore we square root things and see that |ruxrv|=25sin(v). We get the whole sphere when the
coordinate patch is 0≤u≤2Π and 0≤v≤pi, so the whole
surface area is
∫0Π∫02Π25sin(v) du dv.
This integral can be computed, and its value is 100Π. The surface
area of a sphere of radius r is supposed to be
4Π r2 (four "great circles") so when r=5 this is
the textbook answer.
The surface area of the torus
Please try this yourself
first. PLEASE do this!!!
The answer is
32Π2, and a detailed explanation is below.
Let's try this:
r(u,v)=(4+2cos(v))cos(u)i+(4+2cos(v))sin(u)j+2sin(v)k.
Then
ru=–(4+2cos(v))sin(u)i+(4+2cos(v))cos(u)j+0k
and
rv=(–2sin(v))cos(u)i+(–2sin(v))sin(u)j+2cos(v)k
so that ( i j k )
ruxrv=det(–(4+2cos(v))sin(u) (4+2cos(v))cos(u) 0 )
( –2sin(v)cos(u) –2sin(v)sin(u) 2cos(v) )
The i component is
8cos(v)cos(u)+4cos(v)2cos(u)=4cos(v)(2cos(u)+cos(v)cos(u)). This
is 4cos(v)cos(u)(2+cos(v)).
The j component is
8cos(v)sin(u)+4[cos(v)]2sin(u)=4cos(v)(2sin(u)+cos(v)sin(u)). This
is 4cos(v)sin(u)(2+cos(v)).
The k component is
8[sin(u)]2sin(v)+4[sin(u)]2cos(v)sin(v)+8sin(v)[cos(u)]2+4[cos(u)]2sin(v)cos(v). This
simplifies (again with sin2+cos2) to
8sin(v)+4sin(v)cos(v)=4sin(v)(2+cos(v)).
I have never done this computation before, but I hope it will work out. Now let us square and add the components:
42cos(v)2cos(u)2(2+cos(v))2+
42cos(v)2sin(u)2(2+cos(v))2+
42sin(v)2(2+cos(v))2
Again sin2+cos2 is used, and we get:
42cos(v)2(2+cos(v))2+
42sin(v)2(2+cos(v))2
One last time, sin2+cos2, and this becomes:
42(2+cos(v))2.
This is ||ruxrv||2, so we take the square root and
get 4(2+cos(v)) (notice that 2+cos(v) is always non-negative so the
square root of its square is itself). Now to get the area of the whole
torus we need to integrate this over the uv-square which is [0,2Π]
by [0,2Π]. So the area is
∫02Π∫02Π4(2+cos(v)) du dv. The
answer is 32Π2.
This answer is correct. A torus is such a symmetric figure that
its surface area can be determined using a (sort of) calculus-free
method called the Theorem
of Pappus.
The surface area of a piece of the graph
Here the integral turns out to be
∫01∫01sqrt(1+36x2+400y6) dx dy. Maple can't "do" this integral, and gives the
approximate value 6.8005 when asked. Most surface areas can't be
computed explicitly in terms of values of familiar functions.
|
Please try to read section 16.4 and do a few problems.
Monday, April 19, lecture #24
Today I'll deviate significantly from order of the text. The reason
is that I'd like to discuss a result called Green's Theorem before we
develop yet another kind of integral in the course. This is section
17.1. I will return with the concluding sections of chapter 16 and
discuss the other parts of chapter 17 in the last part of the course.
Evaluating line integrals
I basically know three ways to evaluate line integrals:
- Parameterize them, and hope that the Fundamental Theorem of
Calculus can handle the resulting definite integral.
- Hope that the integrand results from a gradient vector field, and
try to create a potential. Then the value of the line integral is the
difference of the values of the potential at the End minus its value at the Start.
- Green's Theorem, which tells how to compute line integrals on
closed curves.
Green's Theorem will look at first rather special but the uses are
really remarkable. I should emphasize that although this is not a
course on physics or on engineering applications, Green's Theorem was
actually developed in the 19th century to handle certain
problems about electricity and magnetism, and then also about fluid
flow. The result was not "invented" in some abstract situation, but
really did follow from attempts to understand how to describe real
world problems.
About George Green
George Green, whose name is attached to this result (and to others in
mathematical physics), lived from 1793 to 1841. Biographical
information is available here and here.
Some aspects of his adult life were quite unconventional, but perhaps
more interesting is that (quoted from the first link), "The younger
Green only had about one year of formal schooling as a child, between
the ages of 8 and 9." Later, in 1832, nearly 40 years old (!), he
"went to college" (Cambridge). A version of his original 1828
publication, An Essay on the Application of mathematical Analysis
to the theories of Electricity and Magnetism. (83 pages), is
available here if you
have the curiosity and courage to look at it. Almost every page is
dominated by physical discussions. The essay was written before
his college attendance.
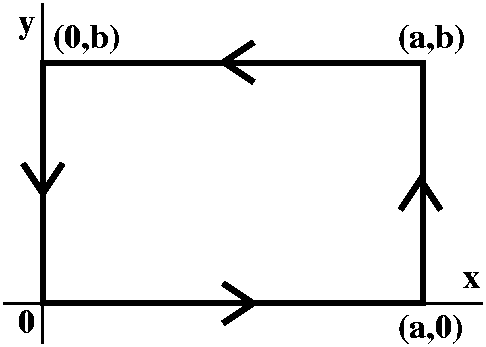 Rectangular Green's Theorem
Rectangular Green's Theorem
I stated a result called Green's Theorem for a rectangle with
corners at (0,0), (a,0), (a,b), and (0,b).
The result was the following:
∫Rectangular bdryP(x,y)dx+Q(x,y)dy=∫∫Inside of rect∂Q(x,y)/∂x–∂P(x,y)/∂y dA.
Silly example
I first tried a rather silly example which was something like the
following. I think I took a=3 and b=2, and specified that
P(x,y)=5y+Junk1(x) and
Q(x,y)=x2+Junk1(y). Here the
Junk functions were some absurd formulas:
arctan(y3) or ecos(x). I wanted to compute the
line integral of P(x,y)dx+Q(x,y)dy around the boundary of the
rectangle. Of course I used the version of Green's Theorem stated
above, and the two Junk terms disappeared after the partial
differentiations, and the double integral had integrand 2x–5, which is
rather simple to compute over a rectangle.
Since this is a math course, I decided I should give some
deductive "reason" that Green's Theorem is true. I tried to verify
∫rectangle bdryP(x,y)dx=∫∫rectangle–(∂P/∂y) dA.
The verification amounted to some juggling with the
Fundamental Theorem of Calculus. I only discussed the Green's Theorem
equation with P(x,y). The verification for Q(x,y) is quite similar. I
started with
∫∫rectangle–(∂P/∂y) dA. A
student suggested dy dx, so the
double integral became the iterated integral
∫x=0x=a∫y=0y=b–(∂P/∂y) dy dx.
Let's look at the inside. The dy and ∂/∂y "cancel". I
really mean that FTC (the Fundamental Theorem of Calculus applied to
the y variable) can be applied. So
∫y=0y=b–(∂P/∂y) dy=P(x,y)|y=by=0=–P(x,b)+P(x,0).
Now we are supposed to integrate this result from 0 to a with respect
to x. We worked hard and realized that P(x,0) integrated dx from
0 to a was the lower horizontal side of the line integral, and
–P(x,b) integrated from 0 to a dx was the upper
horizontal side of the line integral -- the minus sign corresponds
to integrating on that segment from right to left. What about the up
and down parts of that line integral? Well, P(x,y)dx on the up and
down parts is 0 because x does not change on those parts
of the line integral, so the result is 0. We therefore have verified
Green's Theorem for P(x,y)dx. The Q part works in the same way, and
Green's Theorem is really mathematically true for a rectangle.
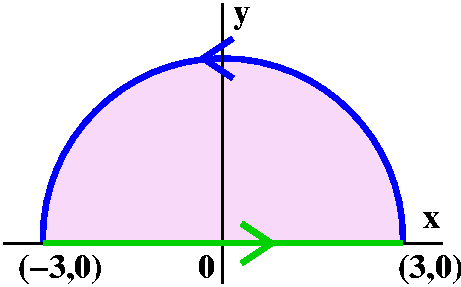 Computation on a semicircle
Computation on a semicircle
This is another example created for the classroom, but it is more
complex, and more resembles some real uses of Green's Theorem. Here I
considered the line integral ∫Sy dx+x2dy
where S represents the upper half of the
circle of radius 3 centered at the origin. I think this integral
certainly can be computed straightforwardly by a parameterization but
I'd like to show another technique. First, what is the value of ∫Ly dx+x2dy where L is the line segment along the x-axis stretching
from (–3,0) to (3,0)? Since y doesn't change on L, dy=0. Also notice that y=0 on all of L. Therefore y dx+x2dy is 0 on all
of L.
So ∫Sy dx+x2dy=∫Sy dx+x2dy+∫Ly dx+x2dy=∫S+Ly dx+x2dy, and the
curve S+L, which is S
followed by L, encloses the upper half
of the area inside a circle of radius 3 centered at the origin: a
semidisc (great word!). I'll call it Q.
Then a version of Green's Theorem allows us to replace ∫S+Ly dx+x2dy by ∫∫Q∂(x2)/∂x–∂y/∂y dA. The
integrand is 2x–1, and we need to integrate it over Q.
The integral ∫∫Q2x dA is actually 0, because
the region Q is symmetric with
respect to the y-axis, and 2x takes equally positive and negative
values on this region. So the values cancel. And the integral
∫∫Q–1 dA is
minus one-half the area of a circle of radius 3. Therefore the
original line integral, ∫Sy dx+x2dy, has the
value –9π/2.
I would agree that this is an awkward, even ludicrous way of
evaluating the line integral. (But it is slick!) I went through
it because in a week we'll be trying computations like this in three
dimensions and maybe things there won't be as clear.
The text's version of Green's Theorem
Suppose C is a positively (counterclockwise) oriented piecewise smooth
simple closed curve, and D is the region bounded by C. Suppose that
P(x,y) and Q(x,y) are functions with continuous first partial
derivatives in D. Then:
∫CP(x,y)dx+Q(x,y)dy=∫∫D∂Q(x,y)/∂x–∂P(x,y)/∂y dA.
Definitions of terms
The statement above is complicated, and I think many of the words need
some explanation.
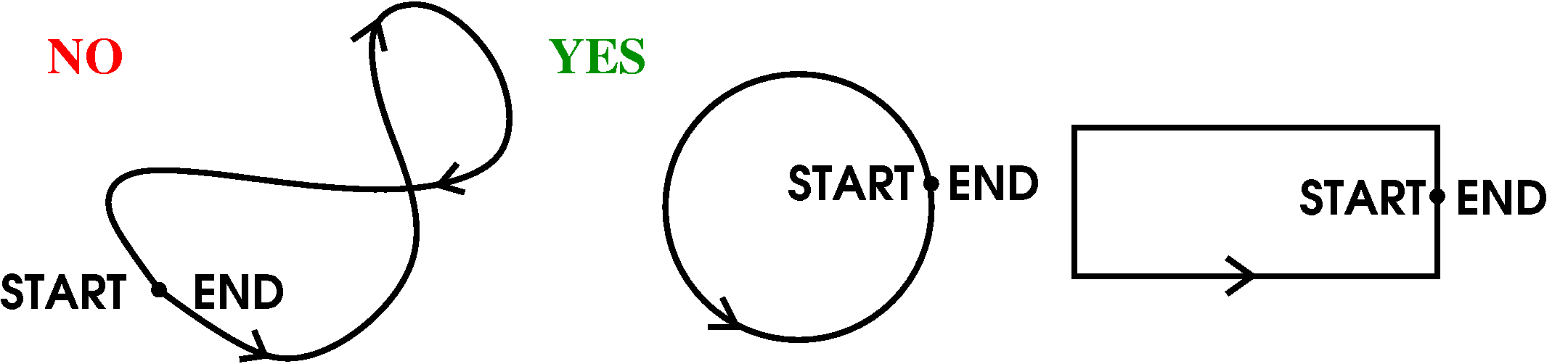
- Closed curve
We have encountered this phrase before. A closed curve is a
parameterized curve which has an initial point (START) equal
to its terminal point (END).

- Simple closed curve
A simple closed curve is a curve with no self-intersections
(crossings) except for the START=END.
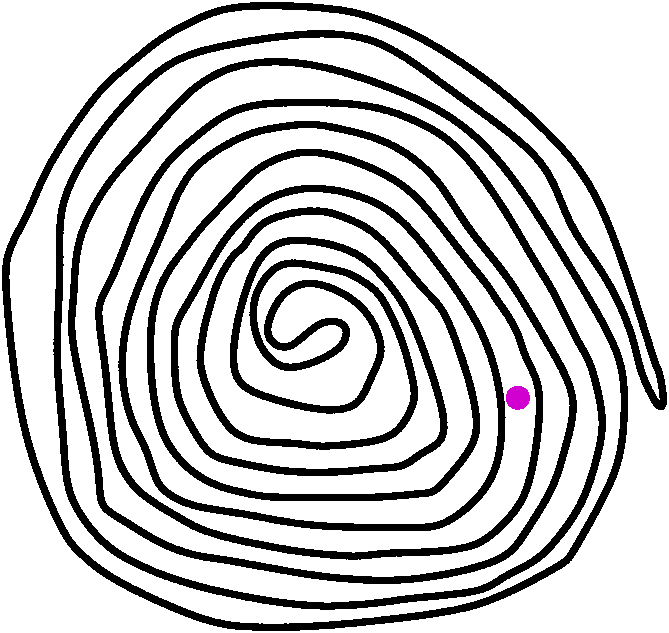 One additional remark, please: simple closed curves don't have to be
so "simple" in the non-technical meaning of the word. I sketched
something like what is shown to the right. It may not even be clear
whether the point indicated in magenta
(purple?) is inside or outside the curve (but count the number
of crossings from the point to the outside and find the parity
[odd/even]). So things can really get complicated if you want to do
curves more complicated than circles or rectangles.
One additional remark, please: simple closed curves don't have to be
so "simple" in the non-technical meaning of the word. I sketched
something like what is shown to the right. It may not even be clear
whether the point indicated in magenta
(purple?) is inside or outside the curve (but count the number
of crossings from the point to the outside and find the parity
[odd/even]). So things can really get complicated if you want to do
curves more complicated than circles or rectangles.
- Positively (counterclockwise) oriented
This is more subtle. The boundary curve C is parameterized. You can
think of the parameter as time: it describes walking along the
curve. And the phrase positively oriented here means that as
the parameter describing C increases, the neighboring region D
should be to the left. Finally, a victory for left-handed folks!
In this case, we (the whole world!) has made a choice about the sign
of these integrals. You should not disagree, unless you are extremely
persuasive (such an activity would not be part of Math 251). I
mentioned the experiment
by Millikan to determine the amount of charge, but perhaps not the
sign of the charge, of the electron. It turns out that the "decision"
to give the electron a negative charge (which always confused
me) may not have been his.
Below are two "local" pictures of how D should look in relation to
increasing values of the parameter on C. The arrows are pointing in
the direction of increasing values of the parameter.
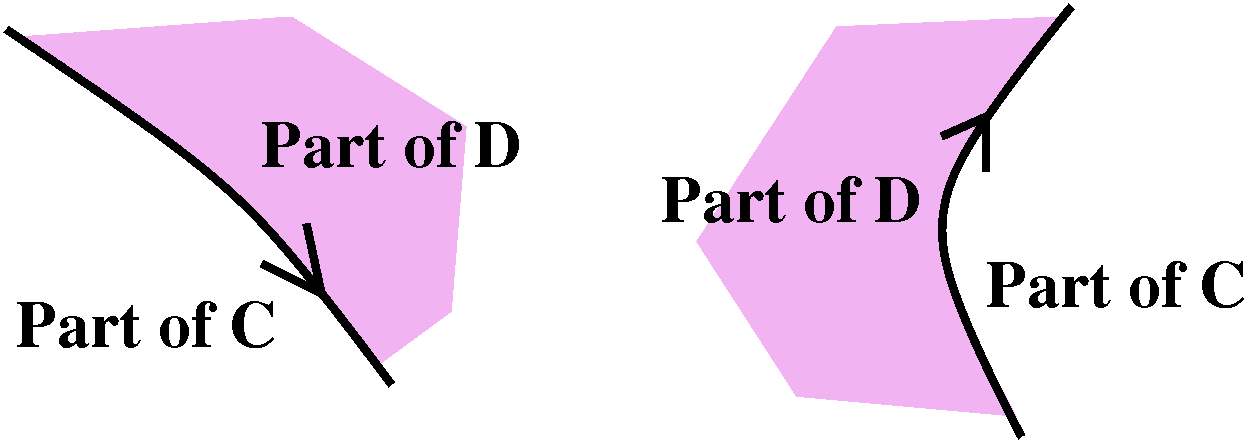 Look back at the rectangle picture. You should see, I hope, that the
boundary is a simple closed curve, which is positively oriented with
respect to the interior. And look again at the semidisc (can't be a
word!). The inside of the semidisc is to the left of the boundary as
the parameter increases.
Look back at the rectangle picture. You should see, I hope, that the
boundary is a simple closed curve, which is positively oriented with
respect to the interior. And look again at the semidisc (can't be a
word!). The inside of the semidisc is to the left of the boundary as
the parameter increases.
- Piecewise smooth
This means that the functions parameterizing the boundary should be
differentiable, or that they should be a finite "sum" of
differentiable functions. For example, a rectangle is a "sum" of four
smooth boundary parameterizations. Here the sum is understood to be in
the sense of curves, where one curve followed by another is thought of
as adding the curves.
Information transported from the boundary to the inside
Suppose P(x,y)=–(1/2)y and Q(x,y)=(1/2)x. Then
∂Q(x,y)/∂x–∂P(x,y)/∂y just "happens" to be 1 (the
P and Q were selected carefully!). And the double integral of 1 over
the region is equal to its area. So apparently
∫C–(1/2)y dx+(1/2)x dy is the area of D. Let
me help you understand this result, which I consider rather
remarkable. The curve C should be parameterized. So x=x(t) and y=y(t)
for t between a and b. The line integral gets translated into the
following Riemann integral:
∫t=at=b–(1/2)y(t)x´(t)+(1/2)x(t)y´(t) dt.
So suppose you are in a race car, driving around a "closed
course". Your position could be measured with a GPS device, so you
would know <x(t),y(t)> (the position vector). You could also
imagine that you have some idea of your velocity:
<x´(t),y´(t)>. You could approximate this, after all,
but doing arithmetic on successive position vectors over a small time
interval. So from this "boundary data" you could
compute (at least approximately) the integral
∫t=at=b–(1/2)y(t)x´(t)+(1/2)x(t)y´(t) dt
and this must be the area of enclosed by the race track. This is
astonishing to me.
People designed interesting mechanical linkages to compute areas based
on such results. These instruments are called planimeters. People can be very clever.
Analogous results in higher dimensions (R3) would allow
some knowledge of the heart based upon electrical readings on the skin
(EKG's?). Or the results can be used to try to deduce the presence of
cracks inside structures (steel beams?) as a result of measurements on
the outside. Detect conditions inside an object using surface
measurements, so there is no need for invasive procedures.
Another example, somewhat paradoxical
Here I will tell again you what P(x,y) and Q(x,y) should be. These are
certainly not randomly chosen but are specific functions which are
used to model important physical phenomena.
P(x,y)=–y/(x2+y2) and
Q(x,y)=x/(x2+y2)
It just happens (!!) that:
∂P/∂y=[–(x2+y2)+y(2y)]/(x2+y2)2=[y2–x2]/(x2+y2)2
and
∂Q/∂x=[(x2+y2)–2x(x)]/(x2+y2)2=[y2–x2]/(x2+y2)2.
Therefore in this case, Py=Qx so that
Qx–Py is 0.
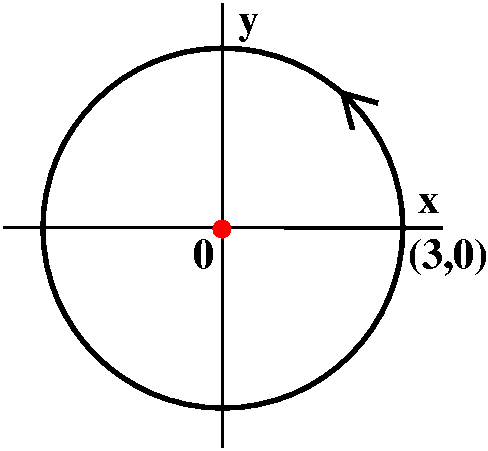 Now let me compute the line integral ∫CP(x,y)dx+Q(x,y)dy, where C is, say, the circle of
radius 3 centered at (0,0). The first parameterization you should
consider is this: x=3cos(t) and y=3sin(t) so that dx=–3sin(t) dt
and dy=3cos(t) dt. Then x2+y2=32
because sin2+cos2=1. Thus
Now let me compute the line integral ∫CP(x,y)dx+Q(x,y)dy, where C is, say, the circle of
radius 3 centered at (0,0). The first parameterization you should
consider is this: x=3cos(t) and y=3sin(t) so that dx=–3sin(t) dt
and dy=3cos(t) dt. Then x2+y2=32
because sin2+cos2=1. Thus
∫C–y/(x2+y2)dx+x/(x2+y2)dy
becomes ∫t=0t=2π([–3sin(t)/32](–3sin(t))+[3cos(t)/32]3cos(t))dt. If the arithmetic is done correctly we need to
integrate 1 from 0 to 2π (almost everything cancels!) and the result
is 2π.
But but but ... the integrand on the "other side" of Green's Theorem
is Qx–Py and we computed that to be 0. A circle
certainly is a simple closed curve, positively oriented, etc. We
haven't made any errors. Maybe it is true that 2π=0? No! That is not true.
Technicalities matter.
I've ignored the requirements on P(x,y) and Q(x,y). Here the
requirements definitely are relevant. Both P(x,y) and Q(x,y), and
their first partial derivatives, are quotients of polynomials, and
have x2+y2 in the denominator (the bottom of the
fraction). That expression is 0 at the origin, (0,0). In fact, P(x,y)
and Q(x,y) and their first partial derivatives are not
continuous at (0,0), which I will call the "bad point". This bad point
is inside the circle. The example shows that even if the hypothesis
"P(x,y) and Q(x,y) are functions with continuous first partial
derivatives" fails at just one point of D, the equality predicted by
Green's Theorem can fail very very emphatically (I think "zero equals
something non-zero" is a fairly emphatic failure).
Information transported from one curve to another, using what's in
between (!?)
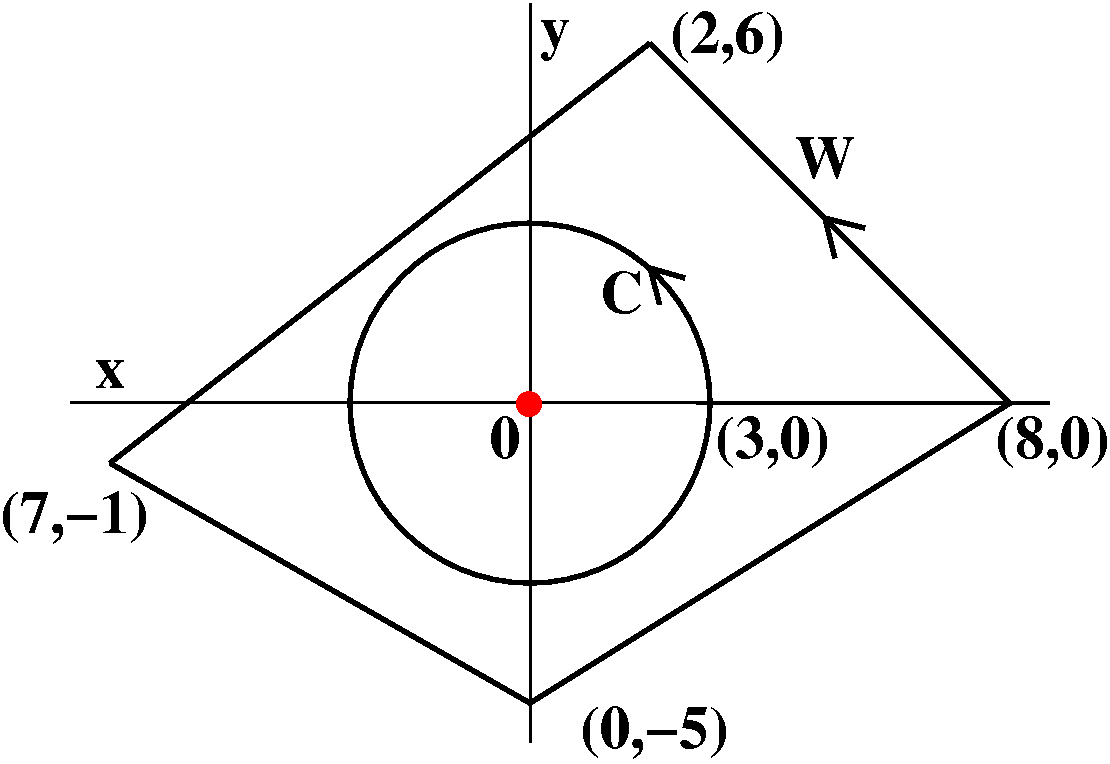 The example considered is, however, very important in practice. Let me
show why. Let's consider another path, W, which is a quadrilateral. W
is a simple closed curve made of four straight line segments. It
starts at (8,0), goes to (2,6), then to (7,–1), then to (0,–5), and
finally back to (8,0). I would like to compute ∫W–y/(x2+y2)dx+x/(x2+y2)dy. Here
I am not so sure I could "easily" compute the integrals which would
come out of parameterizing the four line segments, and changing the
x,y language to t language. At least the task would be lengthy. So let
me show you another way. Again, I can't just apply Green's Theorem to
W and the region inside W, since W encloses the same bad point. But I
can do something very clever using Green's Theorem.
The example considered is, however, very important in practice. Let me
show why. Let's consider another path, W, which is a quadrilateral. W
is a simple closed curve made of four straight line segments. It
starts at (8,0), goes to (2,6), then to (7,–1), then to (0,–5), and
finally back to (8,0). I would like to compute ∫W–y/(x2+y2)dx+x/(x2+y2)dy. Here
I am not so sure I could "easily" compute the integrals which would
come out of parameterizing the four line segments, and changing the
x,y language to t language. At least the task would be lengthy. So let
me show you another way. Again, I can't just apply Green's Theorem to
W and the region inside W, since W encloses the same bad point. But I
can do something very clever using Green's Theorem.
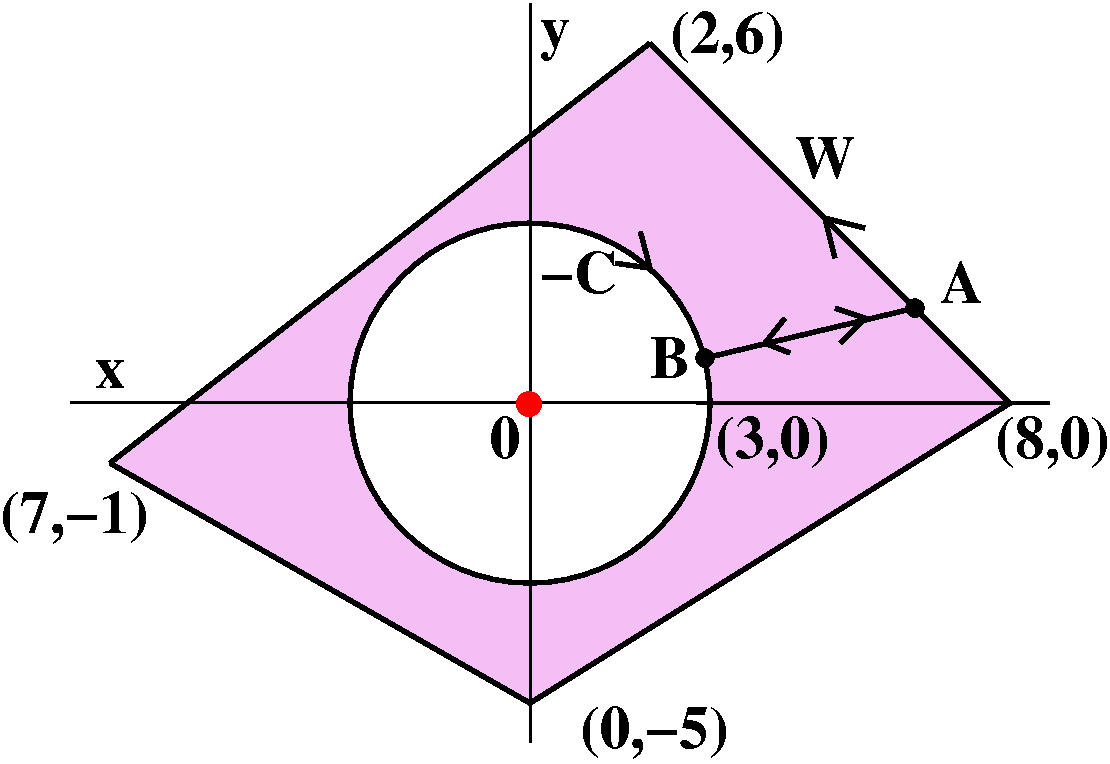
Crosscut
Let me select a point A on W and a point B on C and join them by a
line segment. Now I want to describe a closed curve in the plane, and
this is very very clever. I'll go first from (8,0) on W to A. Then I
will go from A to B on the crosscut. Then around C in reverse (note
that the picture now has the arrowhead on C reversed and the label
states "–C"). Then I go from B to A, and finally, I follow the
remainder of W around to (8,0). What about the integral of
P(x,y)dx+Q(x,y)dy along this path? The integrals on the crosscut line
segments cancel, and the integral on –C is minus the integral along C,
and the remainder is the integral on W. So the result is the integral along W minus the integral along C.
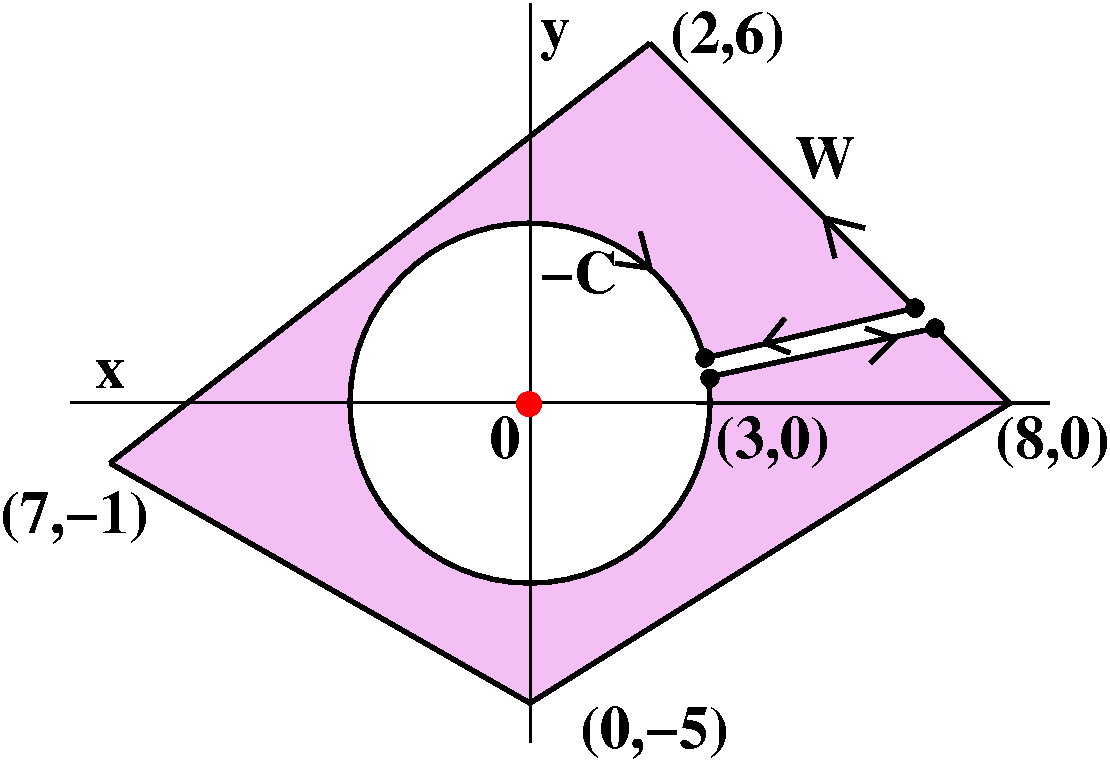
Now let me split up the crosscut into two distinct line segments, one
directed from W to C and one directed backwards. The points A and B
become doubled, and each pair is slightly separated. Now the closed
curve is a simple closed curve. The region this simple closed
curve bounds does not include the origin, the bad point. Inside
the region, Py=Qx and therefore the double
integral side of the Green's Theorem equation is 0. The line integral
side is also 0. This will work for any separation, no matter how
small. Now the line integral will vary continuously as the
separation →0. And therefore, when the separation=0, the line
integral will still be 0. And so, clearly the integral along W
minus the integral along C is 0 (because the crosscuts cancel!) so the
integral along W is the same as the integral along C: it must be 2π!
That clearly may be the worst
clearly in the course. I don't think an accusation of excessive
rigor (too much proving: "the quality of being logically valid") would
be correct in Math 251, and the statement I am asserting as clear
needs proof. What I am asserting is that if one path is close to
another, and if P(x,y) and Q(x,y) are, say, at least continuous, then
the work along the two paths will be close. To me this is physically
reasonable. I hope it is to you.
This crosscutting technique is so familiar to people who use it that
it is rarely discussed in detail. In fact, any curve which goes around
the origin exactly once will have the line integral of our
P(x,y)dx+Q(x,y)dy equal to 2π for similar reasons.
A physical model?
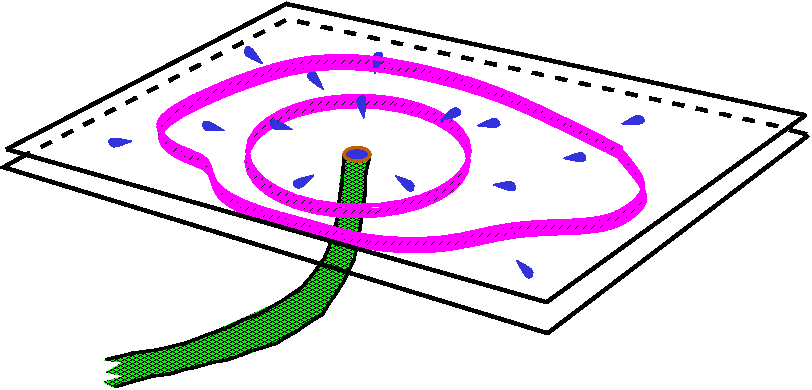 I think the computations I've just done are difficult to
understand. Here is another physical model. Line integrals can also be
thought of as measuring flux, the net flow through the
curve. We will investigate this situation in R3 soon. But
consider the following physical setup: two parallel planes of plastic,
and a hose inserted through one of the planes, pumping water in at a
steady rate (the blue things in the picture are not minnows, they are
water drops!). If we surround this source with some sort of
circular detection "fence" then we can look at how the water goes
through the fence, and from that deduce the rate at which water is
being pumped in. But we could also install another detection fence. If
we do the same computations for that fence, the source rate should be
the same, because the hose is pumping water in steadily: its rate is
not varying. The mathematical computation with the crosscuts above is
a version of this physical situation. When
Py–Qx=0, away from the hose (at the origin) the
source rate is 0. Any comprehensive measurement of flow surrounding
the origin will get the same answer.
I think the computations I've just done are difficult to
understand. Here is another physical model. Line integrals can also be
thought of as measuring flux, the net flow through the
curve. We will investigate this situation in R3 soon. But
consider the following physical setup: two parallel planes of plastic,
and a hose inserted through one of the planes, pumping water in at a
steady rate (the blue things in the picture are not minnows, they are
water drops!). If we surround this source with some sort of
circular detection "fence" then we can look at how the water goes
through the fence, and from that deduce the rate at which water is
being pumped in. But we could also install another detection fence. If
we do the same computations for that fence, the source rate should be
the same, because the hose is pumping water in steadily: its rate is
not varying. The mathematical computation with the crosscuts above is
a version of this physical situation. When
Py–Qx=0, away from the hose (at the origin) the
source rate is 0. Any comprehensive measurement of flow surrounding
the origin will get the same answer.
Another physical setup which this P and Q model is an isolated point
charge. There the work done in moving around the charge will always be
the same. We will encounter this in three dimensions soon, and maybe
there it will be easier to understand.
Another application (important!) of Green's Theorem
I did not get a chance to discuss this in class. When is a vector
field P(x,y)i+Q(x,y)j conservative? Certainly when it is
a gradient vector field: so there is a potential function, f(x,y),
with ∂f/∂x=P(x,y) and ∂f/∂y=Q(x,y). We can try to find f(x,y) by integrating and
matching the descriptions. But this can be difficult and
lengthy. Differentiation is easier, and certainly if
there is a potential, f(x,y), then ∂P/∂y=∂Q/∂x by Clairaut's Theorem. But the example above (the isolated
electric charge or the fluid flow point source) shows that we can have
∂P/∂y=∂Q/∂x without having a
potential. Why? If we had a potential then the integral around closed
curves would be 0, but we saw that such an integral for our example
may not be 0. If we had no bad points, then the integral around closed
curves would be 0 using Green's Theorem. So any region where
there are no bad points has the converse true:
If ∂P/∂y=∂Q/∂x and there are no
"bad points" for P or Q, then there is a potential.
This can sometimes be very useful because differentiation is
... easier! So people have given a name to regions which have no
holes. A region is simply connected if it has no
holes. In such a region, if the condition
∂P/∂y=∂Q/∂x is correct at all points, then there
is a potential, so the vector field is conservative. A disc (the
inside of a circle) is simply connected. But if you remove a point,
the result is not simply connected.
|
Exams returned
 I returned exams to students who were in class today. The problem
whose answers were most interesting and frustrating to read was
probably the second one, about Lagrange multipliers. The non-zero
solutions to the system of equations give only one value of the
objective function, so if you believe that value is both max and min,
the function must be constant, which is certainly incorrect. There are
other solutions where some of the variables are 0, and they must be
considered.
I returned exams to students who were in class today. The problem
whose answers were most interesting and frustrating to read was
probably the second one, about Lagrange multipliers. The non-zero
solutions to the system of equations give only one value of the
objective function, so if you believe that value is both max and min,
the function must be constant, which is certainly incorrect. There are
other solutions where some of the variables are 0, and they must be
considered.
Here is a version of the
exam, and here are answers. A
discussion of the grading is here.
There's some effort involved in prompt and accurate grading of exams,
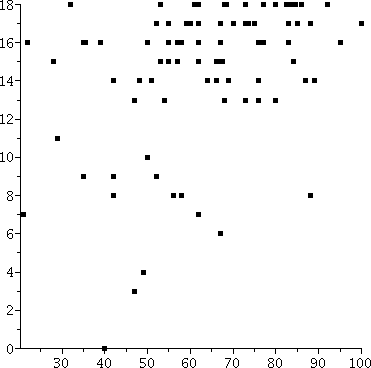
but I believe that such grading is important so I try to do it. 84
students took the exam. 16 were not present to pick up their exam
(about 20% of the class). The mean grade of the exams not picked up
was 48.36, and the mean grade of all exams was 63.68. 15 points is
about 1 standard deviation on the total exam score.
Thursday, April 15, lecture #23
An exam was given.
Monday, April 12, lecture #22
Today's vocabulary word: effrontery. It means
"shameless or impudent boldness; barefaced audacity". It was published
in English as early as 1715.
Today finally we will begin to get what I think of as significant payoffs from 251. There are some
remarkable results which I'll begin telling you about today which have
had great influence on the interaction of math with science and
technology. In particular, I really know only a few ways to evaluate
line integrals. So far, we've seen "Parameterize and use the
definition." Today we'll see a distinctly different method, one which
has great physical significance.
An example
The examples I've been giving in class (and here) have almost all
concerned 2-dimensional vector fields. I'll discuss one more such
example, and then the remaining part of the discussion in this lecture
will have 3-dimensional examples, even though 2-dimensional ones could
be give. 2 is good, but so is 3. Please get used to both of them. And
4 ... and 5 ... and ...
Computing some work
Let's consider integrating
xy dx+y2dy from (1,2) to (3,10). If you wish you could
think that this involves computing the work against the force field
xyi+y2j.
 One work computation
One work computation
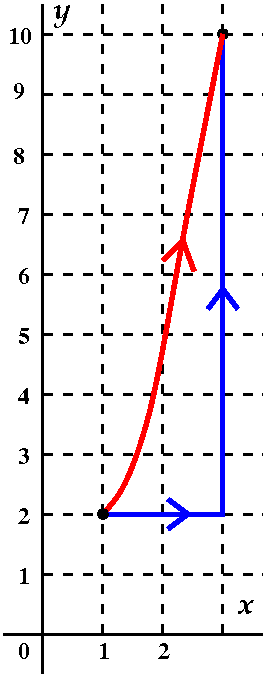
Let's move from (1,2) to (3,2) along a straight line segment (y=2),
and then from (3,2) to (3,10) along another straight line segment
(x=3). I'll use a parameterization for each of the two pieces.
From (1,2) to (3,2): x=t, y=2, 1≤t≤3, dx=dt, and
dy=0dt. Then xy dx+y2dy integrated on this
horizontal line segment becomes
∫13t(2) dt=t2]t=1t=3=9–1=8.
From (3,2) to (3,10): x=3, y=t, 2≤t≤10, dx=0dt, and
dy=dt. Then xy dx+y2dy integrated on this
vertical line segment becomes
∫210t2dt=(1/3)t3]t=2t=10=(1,000–8)/3=992/3.
So the total work is (992/3)+8=1,016/3.
Another work computation
We could move from (1,2) to (3,11) along y=x2+1. For this
path, we can choose x=t, so y=t2+1, 1≤t≤3, dx=dt, and
dy=2t dt. Then xy dx+y2dy integrated on this
parabola becomes
∫13t(t2+1)(1)+(t2+1)2(2t) dt=
∫13t3+t+(t2+1)2(2t) dt=
∫132t5+5t3+3t dt=
(2/6)t6+(5/4)t4+(3/2)t2]t=1t=3=
(2/6)36+(5/4)34+(3/2)32–(2/6)16+(5/4)14+(3/2)12)
(1/4)34+(1/2)32+(1/3)(32+1)3
–(1/4)14–(1/2)12+(1/3)(12+1)3=1,064/3.
You may be amused to know when I did this by myself,
unwatched, and then checked the computation with
Maple I had, of course, made
several mistakes. Oh well.
Different?
So the integral of xy dx+y2dy along two paths joining
(1,3) and (2,11) is different. Why should we expect the values
to be the same, anyway? Maybe the math models a situation where we are
moving a pebble along a sort of flat area, and there is more friction
or the path is bumpier in part of the area. Sometimes, though, the
values are always the same. It turns out this is true for some models
of physical reality and some forces that people have measured. Such a
integral, or rather, a force, is called path dependent.
 What if the integrals are the same?
What if the integrals are the same?
This is called path independence or, a physics word,
conservative. It turns out that gravity is a conservative
vector field, and so is a point charge's electric field, and so are
magnetic fields. (Not totally obvious -- I will check it later).
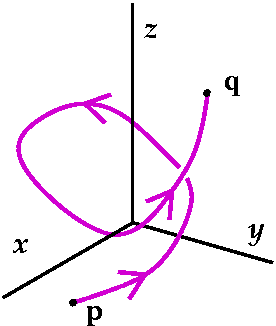
Path independence is a very strong property. Let me be more precise
about it. Take any two points p and
q. Take any path connecting p to q. Then
the work done will depend only on p and q,
and not on the choice of path.
Which vector fields are conservative?
Now let me consider what happens in R3 and try to
understand conservative vector fields. This is such an absurdly strong
property that you shouldn't be surprised if remarkable things
happen. Suppose
F=<F1,F2,F3> is
conservative in R3. What can we do then? Let me show you
some very clever things.
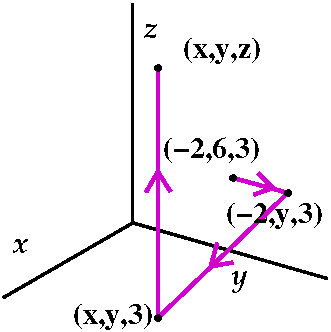 We could pick a point at random, say (–2,6,3). Such a "random" point
was picked by a student in the class. This is called the ground
state physically. Then we could consider the function g(x,y,z),
the total work, which results from taking any path from (–2,6,3) to
(x,y,z). Since all paths result in the same work, this does define a
function. What can we say about g(x,y,z)? Well, select an order from
x and y and z. An order of the variables was picked by various
students in the class, I think the order was y to x to z. Then I will
show you that something neat happens. If we want to move from (–2,6,3)
to (x,y,z), then we could move in pieces, each by a line segment, and
only changing one variable at a time. We've done this repeatedly in
251. Changing lots of variables at once is difficult, so try to change
one at a time -- maybe things will be easier.
We could pick a point at random, say (–2,6,3). Such a "random" point
was picked by a student in the class. This is called the ground
state physically. Then we could consider the function g(x,y,z),
the total work, which results from taking any path from (–2,6,3) to
(x,y,z). Since all paths result in the same work, this does define a
function. What can we say about g(x,y,z)? Well, select an order from
x and y and z. An order of the variables was picked by various
students in the class, I think the order was y to x to z. Then I will
show you that something neat happens. If we want to move from (–2,6,3)
to (x,y,z), then we could move in pieces, each by a line segment, and
only changing one variable at a time. We've done this repeatedly in
251. Changing lots of variables at once is difficult, so try to change
one at a time -- maybe things will be easier.
So I want to write the line integral of
F1(x,y,z) dx+F2(x,y,z) dy+F3(x,y,z) dz
over these three line segments. Here we go, but watch carefully,
because the details are quite important.
First segment
Here y is changing and x and z do not
change. So a simple parameterization is x=–2,y=t,z=3, and then dx=0 dt,
dy=1 dt, and dz=0 dt. The integral becomes
∫6yF2(–2,t,3) dt.
Second segment
Here x is changing and y and z do not
change. So a simple parameterization is x=t,y=y (a constant!),z=3, and then dx=1 dt,
dy=0 dt, and dz=0 dt. The integral becomes
∫–2xF1(t,y,3) dt.
Third segment
Here z is changing and x and y do not
change. So a simple parameterization is x=x (a constant),y=y (a
constant),z=t, and then dx=0 dt, dy=0 dt, and
dz=1 dt. The integral becomes
∫3zF3(x,y,t) dt.
The total integral which is g(x,y,z) is therefore the sum of all three of these.
g(x,y,z)=∫6yF2(–2,t,3) dt+∫–2xF1(t,y,3) dt+∫3zF3(x,y,t) dt.
Look at this mess. Actually, it isn't a mess, but it is somewhat
complicated. How many y's are there in the formula? If you count
carefully, there are 3. And there are two x's. But there is only one
z. So let me try to understand how g(x,y,z) depends on z. What if I
∂/∂z this formula for g(x,y,z)? The first two integrals have
no z at all in them. So from the z point of view they are
constants. Therefore the result of ∂/∂z of those integrals
is 0. The last integral has z in the upper bound of the integral. This
is a first semester calculus exercise. The Fundamental Theorem of
Calculus says that the way to differentiate a function defined by a
definite integral with a variable upper bound is to plug that variable
into the integrand. Here the integrand is F3(x,y,t) and we
are integrating with respect to t. Therefore
∂g/∂z=F3(x,y,z).
We could have picked other orders of the variables from the list of x
and y and z, and written similar straight line segment paths going
from (–2,6,3) to (x,y,z). The value of g(x,y,z) would be the same
because of path independence. If, say, y were the last variable
picked, then I would ∂/∂y the result. The y path would have
as integrand F2. The result would be
∂g/∂y=F2(x,y,z).
And if we picked an order where the last named variable was x, and did
a similar computation, the result would be
∂g/∂x=F1(x,y,z).
A conclusion
Suppose F=<F1,F2,F3> is
path independent. If g(x,y,z) is the work function resulting from
picking a ground state and integrating from there to (x,y,z), then
∂g/∂x=F1(x,y,z); ∂g/∂y=F2(x,y,z); ∂g/∂z=F3(x,y,z).
That is, ∇g=F and F is a gradient vector field,
with g as one potential. The effect, by the way, of picking another
ground state, is just to alter g by an additive constant, and getting
a different potential. You can see this by realizing that a path from
the "new" ground state to (x,y,z) is a path from the new ground state
to the old ground state and then to (x,y,z): the line integral values
would differ by the consistent amount of the line integral from the
new ground state to the old ground state.
If a vector field is conservative, then it is a gradient vector
field. Just differentiate the upper value of the integral.
If F is a conservative vector field, then
F is a gradient vector field.
The other way!
It happens that the converse of
the preceding statement is true. That is, any gradient vector field
must be conservative. Let me show you why, because the why here
is not an irrelevant verification, but shows a remarkably useful
computational shortcut.
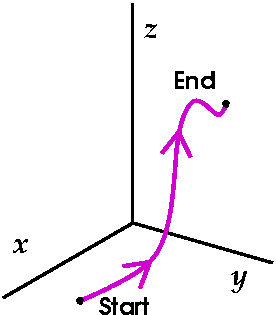 So let me now assume that
F=<F1,F2,F3> and that I
happen to know a function g so that
∂g/∂x=F1(x,y,z),
∂g/∂y=F2(x,y,z), and
∂g/∂z=F3(x,y,z). I would like to compute the line
integral of
F1(x,y,z) dx+F2(x,y,z) dy+F3(x,y,z) dz
along a curve going from p where t=Start to q where t=End. So we have a parameterization,
(x(t),y(t),z(t)) of the
curve.
So let me now assume that
F=<F1,F2,F3> and that I
happen to know a function g so that
∂g/∂x=F1(x,y,z),
∂g/∂y=F2(x,y,z), and
∂g/∂z=F3(x,y,z). I would like to compute the line
integral of
F1(x,y,z) dx+F2(x,y,z) dy+F3(x,y,z) dz
along a curve going from p where t=Start to q where t=End. So we have a parameterization,
(x(t),y(t),z(t)) of the
curve.
So dx=(dx/dt) dt, dy=(dy/dt) dt, and dz=(dz/dt) dt. We
need to "plug in" the parameterization to the components of
F. So the line integral, ∫CF·Tds, becomes
∫StartEnd(F1(x(t),y(t),z(t))(dx/dt)+F2(x(t),y(t),z(t))(dy/dt)+F3(x(t),y(t),z(t))(dz/dt)) dt.
"Strangely enough , it all turns out well." Well, it is not too
strange if you realize that 150 years of effort have gone into what
I'm showing you today. Several students recognized that the integrand,
F1(x(t),y(t),z(t))(dx/dt)+F2(x(t),y(t),z(t))(dy/dt)+F3(x(t),y(t),z(t))(dz/dt)
the whole thing, is the derivative with respect to t of
g(x(t),y(t),z(t)). This is exactly because F1 is
∂g/∂x, F2 is ∂g/∂y, and F3
is ∂g/∂z and we are multiplying each of these by the
appropriate dx/dt, dy/dt, and dz/dt. This is a consequence of the
several variable Chain Rule (actually, this is the most important use
of the Chain Rule in the course). So what we have is
∫StartEndd/dt(g(x(t),y(t),z(t))dt. Another use
of FTC is that the integral of a derivative can be evaluated by just
forgetting the derivative, and taking the value of the original
function at the top limit minus its value at the bottom limit. Well,
if you do that, the result is
The work done is the value of the potential at the End minus its value at the
Start..
This is such a marvelous fact that I want to use it immediately.
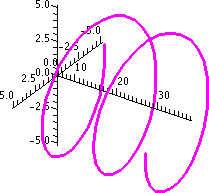 Example
Example
Suppose g(x,y,z)=x3y+xz2+5. Then ∇g is
(3x2+z2)i+x3j+2xzk. I'll
call this F. Now consider the helix with position vector
C(t)=<5cos(2t),4t,5sin(2t)>. Let's compute the work done
against F from t=π/2 to t=3π on the helix. A Maple picture of this helix is shown to the
right. Its axis of symmetry is the y-axis, and it spins around that
axis in the x and z directions as y increases.
One way to compute the work is to use the parameterization, substitute
things. etc. But since I know that F=∇g, I can take
advantage of the result we just discovered, and find the values of g
at the End and Start and subtract them.
Start
This is when t=π/2. So
we plug this into the curve and get the starting position. So we need
<5cos(2[π/2]),4[π/2],5sin(2[π/2])>=<–5,2π,0)>. Now
we need to compute g at this point: g(–5,2π,0)=
(–5)3(2π)+(–5)02+5=–250&pi+5.
End
This is when t=3π. So
we plug this into the curve and get the ending position. So we need
<5cos(2[3π]),4[3π],5sin(2[3π])>=<5,12π,0)>. Now
we need to compute g at this point: g(5,12π,0)=
(5)3(12π)+(5)02+5=1,500&pi+5.
The value of the line integral is g(End)–g(Start)=(1,500&pi+5)–(–250&pi+5)=1,750π.
This seems much easier to me than working the with parameterization,
differentiating, substituting, integrating, and evaluating. Your
opinion may be different but I think you'd be wrong!
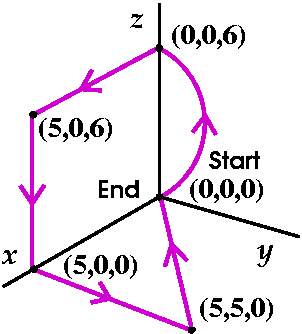 Continue with this vector field and compute another example
Continue with this vector field and compute another example
This one might seem extremely weird to you. The "curve" will need some
description. I want to begin at (0,0,0), the origin. The first piece
will be a semicircle in the yz plane whose other end will be
(0,0,6). I want to follow that with a line segment from (0,0,6) to
(5,0,6). Then a line segment from (5,0,6) down to (5,0,0) on the
x-axis. And then a line segment from (5,0,0) to (5,5,0). And finally,
we will finish up with a line segment from (5,5,0) to (0,0,0). A
attempt at drawing this is shown to the right. This is all C. I would
like to compute
∫C(3x2+z2)dx+x3dy+2xzdz.
And, of course, after all this, a number of students saw the answer
immediately. Of course I wanted all of the drama to myself, but
I was just as happy that they did see it. The important fact here is
that Start=End, so that g(End)–g(Start)=0. I don't need to do
any computation at all!
Another definition
A closed curve is one where Start=End.
Big result, allowing easy computation of many line integrals
These three statements are logically equivalent:
- F=<F1,F2,F3> is
path independent (or, if you prefer, conservative).
- If
F=<F1,F2,F3>=∇g, and
C is any curve, then ∫CF·Tds=∫CF1(x,y,z)dx+F2(x,y,z)dy+F3(x,y,z)dz=g(End)–g(Start).
- If C is any closed curve, then
∫CF1(x,y,z)dx+F2(x,y,z)dy+F3(x,y,z)dz=0.
An important physical example
We looked at inverse square vector fields in R2. A three
dimensional version is not too difficult to exhibit:
[–x/(x2+y2+z2)3/2]i+[–y/(x2+y2+z2)3/2]j+[–z/(x2+y2+z2)3/2]k
This vector field points from (x,y,z) to (0,0,0) because
it is a positive multiple of –xi–yj–zk. The
reason for the (initially) strange scaling factor of
(x2+y2+z2)–3/2 is that
when you compute the length, you will see it is exactly (distance from (x,y,z) to (0,0,0))–2: inverse square.
Now "notice" that ∂/∂x of
–(x2+y2+z2)–1/2 is
–x/(x2+y2+z2)3/2], the
i component of the inverse square vector field. Also
∂/∂y and ∂/∂z applied to the same function give
the j and k components. So the inverse square vector
field is a gradient vector field! Therefore work computations are path
independent and the results will be the difference of the
gravitational potential. Just verifying the derivatives, just these
very basic computations, allows us now to conclude many things about
work for this vector field. I think this is remarkable.
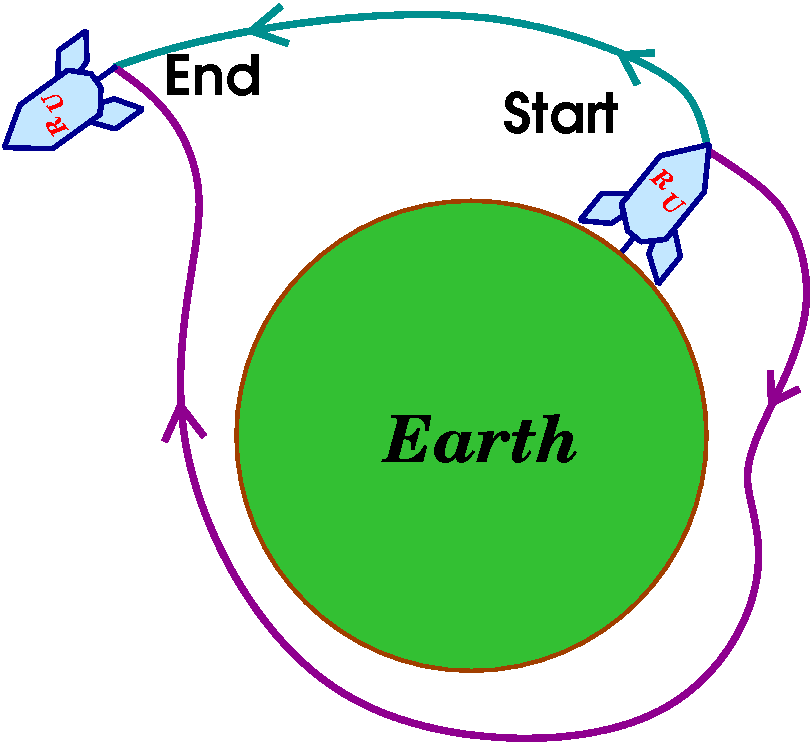
One physical result
What does this mean? Well, if you could
imagine a rocket making two trips from a Start somewhere on the surface of the
Earth to an End at the same
point in space, then (ideally, ignoring all sorts of complicating
factors like friction and non-spherical Earths, etc.) the same amount
of work has been done. And the work done could be computed as the
difference of the gravitational potential at the two points. This
intellectually represents a huge amount of freedom to do the
computation of the physics involved. |
 |
How can you tell if a vector field is a gradient vector field?
Well, we discussed this a bit last time. We could integrate each of
the components with respect to the appropriate variable. I know that
integrating, or, better, antidifferentiating, is
difficult. Differentiation is usually much easier. So if I want a
quick way to check if
<F1,F2,F3> is eligible to be a
gradient vector field, then I could compute first derivatives, and
consider (I know that second "cross partials" should be equal) the
results.
Example of the checking procedure
Suppose you want to consider the vector field
xy2i+(x2y+z)j+5z2k. Is
it a gradient vector field? I will check some derivatives.
Then ∂/∂y(xy2)=2xy should be the same as
∂/∂x(x2y+z)=2xy. (should because
∂2/∂x∂y=∂2/∂y∂x.)
That's true, but there's more to check.
Also ∂/∂z(xy2)=0 should be the same as
∂/∂x(5z2)=0. (should because
∂2/∂x∂z=∂2/∂z∂x.)
That's true, but there's more to check.
And finally, ∂/∂z(x2y+z)=1 should be the same
as ∂/∂y(5z2)=0. (should because
∂2/∂y∂z=∂2/∂z∂y.)
That is not true, so this vector field is
not a gradient vector field, and therefore it can't be conservative.
What can we say if the components of the vector field "pass" these
tests? (By the way, these equations are called compatibility
conditions because they show that the components of the vector
field get along (!) with each other.) Can we then conclude that there
is a potential? Well, there's some complications, and this will be
covered later in the course.
|
QotD
Suppose
F=xy2i+(x2y+z)j+Ayk
for some constant, A. Find the only value of A so that F is a
gradient vector field, and find a potential for the resulting
F.
You can do this by guessing, as I mentioned. Or be a bit more
systematically by antidifferentiating and comparing the results:
- ∂g/∂x=xy2 ⇒ g must be
(1/2)x2y2+C1(y,z).
- ∂g/∂y=x2y+z ⇒ g must be
(1/2)x2y2+zy+C2(x,z).
- ∂g/∂z=Ay ⇒ g must be
Azy+C3(x,y).
Here C1(y,z) and C2(x,z) and C3(x,y)
are functions of their variables ("constants" relative to each
"partial integration") and we have three descriptions of g(x,y,z). But
these descriptions are only consistent if A=1 and then
g(x,y,z)=(1/2)x2y2+zy (maybe if you wish to be
silly you might add "+C" which would describe all potentials
but only one was requested.)
Wednesday, April 7, lecture #21
I began with might have seemed some irrelevant observations, but these
"observations" were an effort to get students to expect that certain
kinds of integrals would be useful in investigating vector fields.
Derivative 0 always means the function must be constant (1
variable)
In calc 1, the following implication is noted and used almost
everywhere: if f´ is always 0, then f is constant. This is used
most prominently when people find antiderivatives. So, for
example, when I know that (1/3)x3 is an antiderivative of
x2, I can then assert that all antiderivatives of
x2 are (1/3)x3+Constant, for any value of
"Constant". And that uses the previous fact about derivatives being 0.
Gradient 0 always means the function must be constant (2
variables)
In two variables, I wanted an analogous statement. Here what we have
as hypotheses is gradient of f (a function of both x and y) is 0. But
∇f=0 means (first component) ∂f/∂x=0 and (second
component) ∂f/∂y=0. So I would like to conclude that such an
f must be constant. This was my first observation. I had
included this assertion in the previous diary entry. There I had
verified that two potentials of the same vector field differ by a
constant and I needed as part of that to look at the
difference. Please look here.
|
How to get from the gradient back to a
potential?
Suppose we suspect that f(x,y)i+g(x,y)j is ∇φ?
How can we guess φ? Here is a method. We can "integrate"
or, rather, compute antiderivatives of each component. Let's try this
with an example. Suppose that we are told the vector field
<2xycos(x2y)+x7,x2cos(x2y)–y5>
is a gradient vector field. So it is
<∂φ/∂x,∂φ/∂y>. What can we do now?
∂φ/∂x=2xycos(x2y)+x7,
and therefore to recover φ we should
compute
∫(∂φ/∂x)dx=∫2xycos(x2y)+x7dx.
We can do this but we need only remember that y is a constant in this
computation since we are integrating with respect to x. We can do the
cosine part of this with a simple substitution, and the result will be
sin(x2y)+(1/8)x8+Some stuff. O.k.: the trick now
is to think about what Some stuff could
represent. Indeed, it is the stuff that when we do ∂/∂x to
it, we get 0. Certainly constants like 12π+sqrt(117) qualify, but
also (we are in two variable calculus!) any function of y
disappears. Look: ∂/∂x of sin(e5y2))
is 0. So, in fact, Some stuff is Any function of y.
We also know that
∂φ/∂y=x2cos(x2y)–y5. We
can use this to recover information about φ directly by computing
another integral:
∫(∂φ/∂y)dy=∫x2cos(x2y)–y5dy.
This we can do also. Again, remember that anything involving x is a
constant for this integration. The first piece is a simple
substitution and the second is easy. In any case, the result is
sin(x2y)–(1/6)y6+Some other stuff. This is the result of
a dy integral, so Some other stuff is any
function of x (hey, it could be x/arctan(log(x)) or just about
anything!) involving y.
Combining the descriptions of φ
This process gives us two descriptions of φ and we need to compare
them to discover what we can do. So:
sin(x2y)+(1/8)x8+Any function of y
sin(x2y)–(1/6)y6+Some function of x
We need to think and compare definitions. Any part of φ involving
both x and y must appear in both descriptions, and that here is just
sin(x2y). Any y alone function must appear in the y
description and any x alone function must appear in the x
description. Anything else is truly just a constant -- it can't in any
way depend on either x or y. So combining the descriptions we get this
as our answer, a complete description of all potentials of the
given vector field:
φ(x,y)=sin(x2y)+(1/8)x8–(1/6)y6+Constant.
Try again ...
The vortex flow we looked at last time was –yi+xj. If
∂φ/∂x=–y then integrating with respect to x we get
φ(x,y)=–yx+Const involving y. If ∂φ/∂y=x,
then integrating with respect to y we get
xy+Const involving x.
Compare these descriptions!
Can we have –yx+(Const involving y)=xy+(Const involving x)?
Well, the xy and –yx cannot be buried in each other's constants,
because they involve both x and y. And –yx is not the same as xy. So,
darn it, there is no possible φ here. This vector field
cannot be a gradient vector field. This agrees with what we learned
last time, where a different method gave the same conclusion. People
usually like the method used last time which involved differentiation,
because in practice differentiation is much easier than
antidifferentiation.
How about 3 dimensions not just 2?
Similar statements are true for 3 dimensional vector fields. Look at
the textbook.
Segue
I've mostly heard the word "segue" used with music or movies or plays,
and it means "Smooth transition from one thought/idea to another."
These comments on integration are intended to help you realize why we
need the next technical tool of the course.
Line integrals
We need an additional technical tool to investigate vector fields:
line integrals. Line integrals will allow the computation of work for
force fields, and flux for fluid flow, and something for gradient
vector fields. Work and flux and other things are important physical
quantities and turn out to have nice mathematical properties. So here
we go.
 Mass of a wire
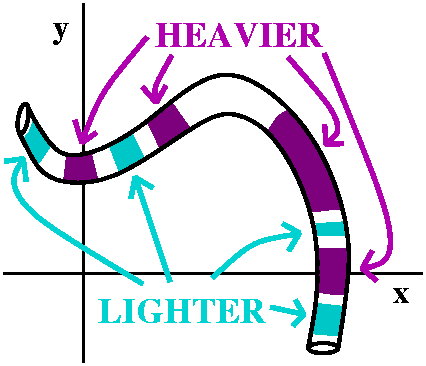
Mass of a wire
I'll introduce line integrals using the metaphor of the mass of a wire.
The integral calculus mantra is:
chop up, approximate, sum, limit.
Here I'll assume that there is a wire sitting in R2. Its
geometry is simple, with a constant cross-sectional area (assumed to
be 1 in the measurement system used). The density of the wire will
vary according to the position on the wire: at some points the density
will be high, and the wire heavy, and at other points, the density
will be low, and the wire rather light. The task is to create some
technical tool which will represent the total mass of the wire. By the
way, the accompanying picture looks like a particularly ugly
worm or snake. I am sorry.
Suppose I cut the wire up into lots of little chunks. How little?
Well, the length of each chunk will be ds, a tiny piece of arc length
(we discussed this in several lectures given late January, long, long
ago). If I assume that the density D(x,y) varies only a small amount
because the chunk of the wire is very small, then dm, the mass of this
piece, is nearly D(x,y) ds (remember I made the cross-sectional
area equal to 1). Further, I can add up these pieces of mass to get
the total mass. I can take the limit as the number of pieces gets
large and the length of the pieces gets small. The result is that the mass
of the wire should be given by
∫The wireD(x,y) ds.
This integral is called a line integral, where the word
line doesn't mean "straight line" but is used in the sense "A
thin continuous mark, as that made by a pen, pencil, or brush applied
to a surface." Now I need to show you what this means. So I will
compute a very artificial example.
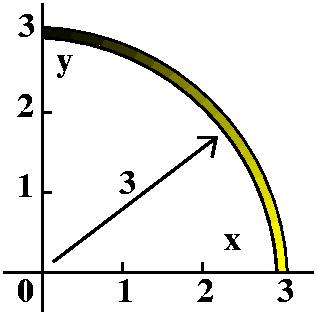 Silly example
Silly example
My example was the following: the wire follows the part of the circle
of radius 3 which is in the first quadrant. The density of the wire at
the point (x,y) is 7y+5. Find the mass of the wire. Well, I will take
the integral ∫The wireD(x,y) ds and parameterize
everything in sight. To me the natural parameterization of an arc of a
circle uses essentially the angle from the center. The text likes to
use t here, so I will parameterize this quarter circle with x=3cos(t)
and y=3sin(t). The interval of this parameterization is [0,Pi/2]. Now
ds is sqrt([dx/dt]2+[dy/dt]2) dt. The
square root stuff is the magnitude of the velocity vector, the
speed. And ds=SPEED·dt is a translation of
distance=rate·time of course. In this case, dx/dt=–3sin(t) and
dy/dt=3cos(t) so that
sqrt([dx/dt]2+[dy/dt]2) just happens (!!!) to
simplify to 3. And ds=3 dt. What about the density? Since
D(x,y)=–7y+5, we know that the density is 7(3sin(t))+5. And the
integral should go from 0 to Pi/2. Therefore
The mass=∫The wireD(x,y) ds=∫t=0t=Pi/2{21sin(t)+5}3 dt=–63cos(t)+15t]t=0t=Pi/2=63+(15/2)Pi.
This is a totally insignificant, physically unrealistic (to me)
computation. The only thing I had fun with is drawing the picture,
which with its varying colors is supposed to suggest the increasing
density of the wire as y increases. There is one very important
fact which should be mentioned now:
Independence of parameterization
In this line integral and in all line integrals, the result will be
the same no matter which parameterization is used. Verification of
this uses the one variable chain rule and is not too interesting right
now. So let me go on.
Random example
I then featured a really random example. I asked students for some
random (positive) integers which I then used to construct an example
very much like the one presented in what follows. The previous example
was arranged so that ds was nice. I now tried to compute something
like the mass of a wire where the wire was sitting on the curve
y=x4 from, say, (0,0) to (2, 16), and the density is
D(x,y)=x4y7. I not being totally idiotic
here. Any computational strategy in calculus should be able to handle
low-degree polynomials fairly efficiently, even by hand. So here's
what we did.
A simple parameterization of a graph of a function is just to use the
independent variable as the parameter. So I used x=t and
y=t4 and then the density x4y7 became
t4(t4)7=t28. This isn't
too bad, but I am saving the worst for last, and in this computation
the worst is ds. So dx/dt=1 and dy/dt=4t3,
and therefore ds/dt=sqrt(1+16t6). The line integral for
this "mass" translates in t-land as follows:
∫The wireD(x,y) ds=∫t=0t=2t28sqrt(1+16t6) dt.
This integral cannot be computed exactly in terms of standard
"familiar" functions. I found to my amazement that Maple does
have a storehouse of weird functions which it can use to "evaluate"
this integral. But then I have no feeling for the functions it used
and certainly not for the values of the functions.
ds is the obstacle
What is horrible about most line integrals is ds. Almost no ds except
for those included in textbook problems lead to familiar
antiderivatives. At the same time, important quantities such as work
and flux are defined as mathematical objects in terms of line
integrals, and the general expectation is that these quantities
can be computed exactly in terms of familiar functions (or
should be computable in terms of familiar functions).
To me this is an excellent example of the psychological phenomenon
known as cognitive
dissonance:
Cognitive dissonance arises from conflicting
cognitions. Cognitive dissonance is the perception of incompatibility
between two cognitions, which for the purpose of cognitive dissonance
theory can be defined as any element of knowledge, attitude, emotion,
belief or value, as well as a goal, plan, or an interest. In brief,
the theory of cognitive dissonance holds that contradicting cognitions
serve as a driving force that compels the mind to acquire or invent
new thoughts or beliefs, or to modify existing beliefs, so as to
minimize the amount of dissonance (conflict) between cognitions.
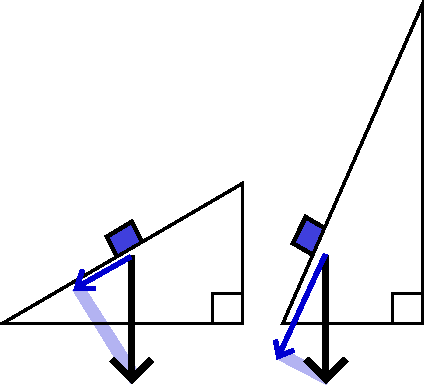 Work
Work
Let's consider the physical concept called work. This is
"force" times "distance", loosely, but we're going to need to be a bit
more specific. For example, consider a mass being pushed up a
frictionless triangle. If the triangle is steeper, then more force is
needed. In the picture, the force of gravity is directed down. The
blue arrows on each inclined plane (triangle) show the force component
needed to move the box up that triangle.
So instead of dieting, avoid steep triangles and your weight
will decrease ... no no no
... this is just more bad information from the lecturer!
Anyway, what really matters is the component of the force in the
direction of motion (we could take the dot product of the force and
the displacement also).
Work with a varying vector field along a curve
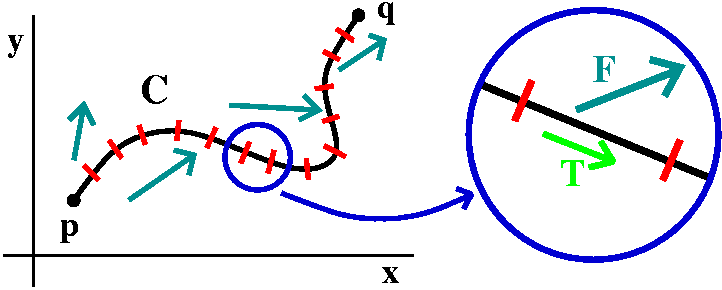 Again, chop up, approximate, sum,
limit.
Again, chop up, approximate, sum,
limit.
I would like to describe how to compute the work done against a
varying force field F as we travel from p to q (in
R2 but the same ideas will work in R3, also)
along a curve, C. We chop up C into small pieces (the red lines are
the chopping places). One of them is displayed under a "magnifying
glass" (sort of) in the picture. The piece is so small that it is
almost a straight line, and its length is ds. The piece is also so
small that the vector field, F, is almost constant near the
piece. Remember that a unit tangent vector, pointing in the direction
of the piece, is called T (go back and think of January!). Then
the part of the force field along the curve is F·T and
the piece of the work will be approximately F·Tds. All
of the work will be the integral along C of this quantity. Therefore
the work is ∫CF·Tds.
A computation
Let us "test" this definition with a random computation: well,
sort of "random". C will be the curve y=x4 and p will be
the point (0,0) and q will be the point (2,16). I will have the force
field be
x2y3i+xy5j. Now let
us compute. We need to change everything
into t-land, where I will choose a most routine parameter: x=t so that
y=t4.
ds
As before, the speed becomes
sqrt([dx/dt]2+[dy/dt]2)=sqrt([1]2+[4t3]2)=sqrt(1+16t6)
which is horrible enough. Thus ds=sqrt(1+16t6) dt.
F
At the point (x,y), F is
x2y3i+xy5j so that at
(t,t4) on the curve, F is
t2(t4)3i+t(t4)5j=t14i+t21j.
T
Now comes almost the miracle. In the movie Shakespeare in
Love, one
character states, "The natural condition is one of insurmountable
obstacles on the road to imminent disaster." He then says almost
immediately, "Strangely enough , it all turns out well." When asked
"How", the character replies, "I don't know. It's a mystery." So, if
not a miracle, let me show you the little mystery here.
The unit
tangent vector, T, is a vector in the direction of the
curve. The position vector of the curve is <t,t4> so
that the velocity vector is <1,4t3>. But we need a
unit vector to get the projection of F in the direction
of the curve. Divide by the magnitude of
<1,4t3>. Therefore,
T=<1,4t3>/sqrt(1+16t6).
Assembling the work integral
∫CF·T ds=∫t=0t=2(t14i+t21j)·
(<1,4t3>/sqrt(1+16t6))sqrt(1+16t6) dt. This is
∫t=0t=2t14+4t24 dt.
which with totally routine polynomial calculations can be evaluated:
it is 215/15+(4/25)225.
What happens?
The speed comes in to squeeze down the velocity vector to get the unit
tangent vector. The speed comes in as the factor which multiplies dt
to get ds. The two appearances of the speed cancel. They will always cancel!.
Using the notation to help
Here is how people use notation to guide their way through the
computation. No one computes the speed (the square root stuff) when
computing work because it will cancel. So:
Problem statement
Compute the work if
F(x,y)=x2y3i+xy5j
and the curve is y=x4 going from (0,0) to (2,16).
A solution
So I initially write ∫CF·T ds but then I immediately change
to ∫Cx2y3dx+xy5dy. I
evaluate this line integral again by changing everything to t-land. So
x=t and y=t4 and dx=1 dt and dy=4t3 dt, Also,
x2y3=t2(t4)3=t14
and
xy5=t(t4)5=t21. Therefore
x2y3dx+xy5dy=t14 dt+t214t3 dt.
Therefore ∫Cx2y3dx+xy5dy=∫t=0 [START]t=2 [END]
t14+4t24 dt. And the result will be the
same. Almost everyone uses this notation, and never bothers with
computing T and ds and then canceling, etc. Of course, the
ideas are important: the physical quantity we are computing has
certain properties which make this computation extremely interesting.
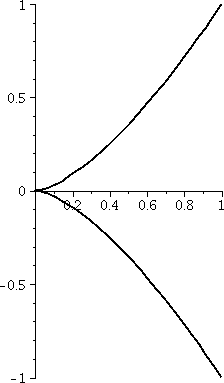
QotD
I decided to try to computed the work done if
F=<x2/y,xy4> and parametric
equations determining the curve C were x=t2 and
y=t3 for –1≤t≤1. The curve (known as a
cusp) is shown to the right. So this is is
∫CF·T ds but immediately I think
that I should compute
∫C(x2/y)dx+xy4dy. At the
suggestion of Mr. Gray this was made
the QotD. So here we go:
x=t2 so dx=2t dt;
y=t3 so dy=3t2dt.
x2/y becomes t;
xy4 becomes t14.
(x2/y)dx+xy4dy becomes
2t2+3t16dt.
∫C(x2/y)dx+xy4dy
becomes
∫–11(2t2+3t16) dt.
The value of the integral is 2({2/3}+{3/17}) or 86/51 if you must "simplify".
Monday, April 4, lecture #20
Where are we? Where are we going?
About 70% of the course has gone by. Much of what we've done will be
very useful for many of the students, but, perhaps, some of what we've
done will be neeeded less often (I am trying to be "diplomatic"). The
last portion of the course, about what is frequently called Vector
Calculus, can help students understand and model many complicated
phenomena they will likely encounter.
For example, consider a big "chunk" of "stuff". Look at the heat in
the chunk. Sometimes some of the heat might originate inside the
object, and sometimes there might be cooling. And there are also
boundary effects. If there's something really hot near part of the
boundary, heat will flow in around that part, and, similarly, there
might be cool things (?) near some other part of the boundary, and
heat will flow out that part of the boundary. This is all very
complicated. Somehow, there should be some way of balancing the heat
sources and sinks inside the region, and the boundary flow of heat,
and expressing this in a neat way. The tools we develop in this last
portion of the course will allow us to create a model of this
situation.
The Fundamental Theorem of Calculus is this:
If F´=f, then
∫x=ax=bf(x) dx=F(b)–F(a)
It is a wonderful result. Think about it. It states that some
sort of stuff inside the interval [a,b] (we could think about height
times width, f(x)dx, or some accumulation of "stuff": f(x) inside
[a,b] and added up over the whole interval, [a,b]) is equal to an edge
quantity. There isn't much "edge" to an interval. Here the edge
quantity is F(b)–F(a). You can, with some effort, see things as
some sort of balance between interior accumulation and stuff in and
out the edges. The remainder of the course is an effort to generalize
this to dimensions 2 (Green's Theorem) and 3 (Divergence Theorem) and
even dimension (sort of) 2.5: Stokes' Theorem and Gauss's
Theorem. These results provide a language for considering edge effects
compared to inside effects for things like heat flow and fluid flow
and ... lots of other phenomena. So please listen and look
carefully. We still need to learn a few more vocabulary notions.
Vector fields
I'm going to begin with two dimensional vector fields, since the
pictures are easier to draw. Those of you who have seen Euler's method
in calculus may remember bunches of arrows in the plane. So in the
most elementary sense, a vector field is such a "bunch of arrows". In
fact, it is an arrow, a vector, sitting at every point, (x,y).
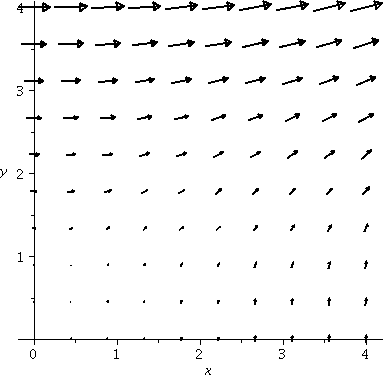 To the right is a "picture" of part of a vector field. The picture was
produced by Maple using a command I
don't know very well (there are thousands of commands, and I'm sure I
know less than a tenth of one percent of them). This command is in the
plots package. The picture was produced by
To the right is a "picture" of part of a vector field. The picture was
produced by Maple using a command I
don't know very well (there are thousands of commands, and I'm sure I
know less than a tenth of one percent of them). This command is in the
plots package. The picture was produced by
fieldplot([y^2,x], x=0..4,y=0..4, arrows=slim,
grid=[10,10], fieldstrength=maximal(.9), thickness=2);
This vector field is the vector x2i+y)j
at the point (x,y). The Maple command
sketches a few of the arrows ([10,10] gives 100 of them). Sometimes
such a picture of a vector field can be very helpful. Note that the
length of the arrows is automatically scaled by Maple so that the arrows don't overlap (it is
possible to override this default -- see the help page for the
command). In class when I attempted to sketch the vector field I got a
mess -- the arrows were too long and so I changed to
(x2/10)i+(y/10))j.
Models?
Vector fields are mathematical models of some basic physical
phenomena. Two that are immediate are force fields and fluid flows.
The force field (gravity, electromagnetism, etc.) might be the
simplest. The "arrow" at every point denotes the presence of a "force"
which can act on the proper kind of object (gravitation: an object
with mass, magnetism, an object with magnetic "stuff", etc.). In
Newton's law of gravitation, we could think of a powerful mass, M,
(the sun?) at the center of the universe, and other very small masses,
m's, scattered around. Ignore interactions between the m's. Each m
will be attracted to the M with a force of magnitude
GmM/(dist)2 where "dist" is the distance from m to M. The
direction of the attraction is from m to M. To get a vector field,
just sketch an arrow in the direction of the force, with a length
proportional to the magnitude of the force. Then to complete the
creation (?) of the force field, just remove all the little m's and
leave the arrows. This is quite an idea, really a big leap of
imagination. I have never seen any of these arrows, but imagining them
is sometimes quite helpful. A quote (New
York Times, March 19, 1940) from Albert
Einstein describing radio may be appropriate here:
You see, wire telegraph is a kind of a very, very long cat. You pull
his tail in New York and his head is meowing in Los Angeles. Do you
understand this? And radio operates exactly the same way: you send
signals here, they receive them there. The only difference is that
there is no cat.
More detail about the inverse square law
Suppose we stand at (x,y) with a mass m, and the origin has a mass,
M. Then the gravitational attraction is a force of magnitude
GmM/(x2+y2). What's on the bottom is the square
of the distance from (x,y) to (0,0). I'll forget the m now (erasing
the mass m and leaving the arrow). So we need a force of magnitude
GM/(x2+y2). The direction should be from (x,y)
to (0,0): the direction of –xi–yj. But that vector has
length sqrt(x2+y2). So to get a vector of the
correct magnitude and direction we need to divide by
sqrt(x2+y2) (that creates a unit vector pointing
in the correct direction) and then multiply by
GM/(x2+y2). So an inverse square law pointing at
the origin (dropping the constant multipliers) is
–[x/(x2+y2)3/2]i–[y/(x2+y2)3/2]j.
Is this complicated enough? It can be difficult to see the inverse
square law under all this algebra. To the right is a picture of this
inverse square vector field in the first quadrant. The magnitude of
the vector field decreases rapidly away from the origin.
| 
|
Fluid flow: vortex flow
The velocity field of a fluid flow may be less familiar. Here
we could think of water flowing in between two parallel planes, close
together. At a point we could insert a drop of ink, and look a very
short time later. The ink might be stretched into a short
segment. This would be the velocity vector of the fluid at that
point. It could change from one point to another, both in length and
in direction. The length of the segment will (hopefully!) depend on
the speed of the fluid, and the direction of the line segment will be
the direction of the fluid flow. | |
I tried to discuss one of the standard examples of a fluid flow: a
vortex. This is a counterclockwise velocity field of a fluid spinning
with uniform angular velocity. Suppose the vector field was
Ai+Bj at the point (x,y). This "vortex" would need to be
perpendicular to the circle centered at (0,0) going through
(x,y). That means the vector field would be perpendicular to the
radius vector, xi+yj. We can check perpendicularity with
the dot product: Ax+By must be 0. But the magnitude of the vector,
sqrt(A2+B2), also should increase directly in
proportion to the distance of (x,y) to the origin, so the fluid flow
will have constant angular velocity. After some computation we saw
that this would have to be –Kyi+Kxj, with K positive to
keep this counterclockwise. | 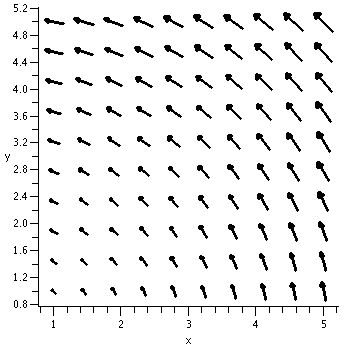 |
Other flows: 3i+0j (uniform flow to the right)
Please note that adjustments were made to the fieldstrength
option in this fieldplot command and others to avoid having
the arrows overlap each other and to display better some of the other
vector fields.
| 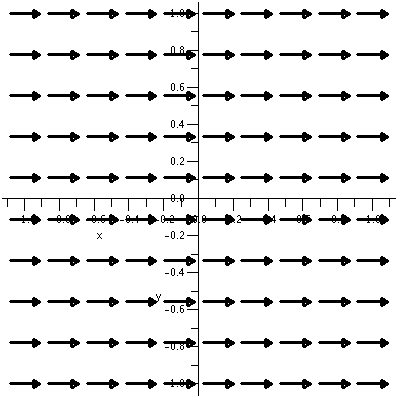
|
|
3xi+0j, a flow which doesn't move on the y-axis, but
flows away from the y-axis otherwise, and faster, the farther the
fluid was away from the axis.
|  |
|
x2i+y2j. This flow wasn't too easy
to describe in words. A Maple graph of it is
shown to the right. I don't think we drew enough "arrows" to show the
flow. We did decide that the flow followed y=x along that line, and
was also perpendicular to the line y=–x. But ... otherwise this seems
difficult to understand. The flow seems to always go up and to the
right. I'll come back to this later.
|  |
|
Associated to a fluid flow are streamlines, which would describe how a fluid
actually flows (the velocity vector field only would give what's called the
"instantaneous" flow). Such streamlines are investigated and can
sometimes be described exactly by solving differential equations.
|
| Not this kind of arrow! |
|---|
 |
| Is this a 251 student? An instructor?? Neither actually. This is not our
kind of vector field. |
|
Vector fields
- Geometrically, a vector field "is" a collection of arrows in the
plane.
- Algebraically, a vector field "is" a pair of functions,
f(x,y)i+g(x,y)j.
The simplest ways students discover vector fields in their studies
is:
Force fields A typical example is the inverse square
"law".
Fluid flow A vortex is one example. Explicitly, it is
–yi+xj. This sort of describes a swirling flow around
the origin.
Gradient vector fields We haven't discussed this so far, and
these are an important type of vector fields.
Gradient vector fields
This could be in either two or three variables. Let's suppose for
simplicity we have a function φ(x,y) of two variables (I'm
following your textbook's notation here). Then the gradient of φ
is
∇φ=[∂φ/∂x]i+[∂φ/∂y]j
and this is a vector field: it is a function multiplied by i
plus a function multiplied by j.
An example
I looked at φ(x,y)=x2+y2. Here I recalled
that the contour lines were
x2+y2=Constant. These are all circles centered
at the origin. If we draw a collection of contour lines for equally
spaced constants (for example, for 1 and 2 and 3 and 4 and ...) then
it turns out that the lines (level curves: they are curvy!) get
closer and closer together as the equally spaced constants
increase. This is because the function is increasing more rapidly as x
and y get larger in absolute value. The associated gradient vector
field is 2xi+2yj. At (x,y), these vectors are
perpendicular to the circles as theory declares and point away from
the origin in the direction of increase of φ. As (x,y) "moves"
farther from (0,0), the magnitude of the vectors increases.
To the right is a picture of this gradient vector field together with
some contour lines. Previously I had defined g:=x^2+y^2;. The
picture displays the output of these Maple
commands:
> contourplot(g,x=-2.5..2.5,y=-2.5..2.5, thickness=2,
contours=[1,2,3,4,5], grid=[40,40]);
>
fieldplot([2*x,2*y],x=-2.15..2.15,y=-2.15..2.15,arrows=slim,grid=[10,10],
fieldstrength=maximal(.9),color=blue,thickness=2);
| 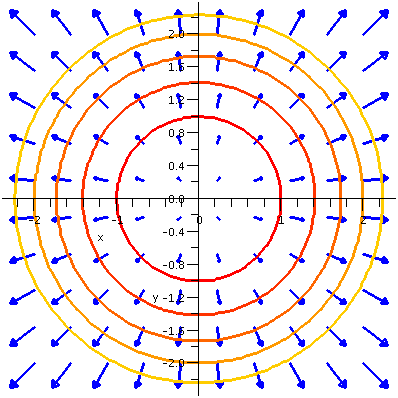 |
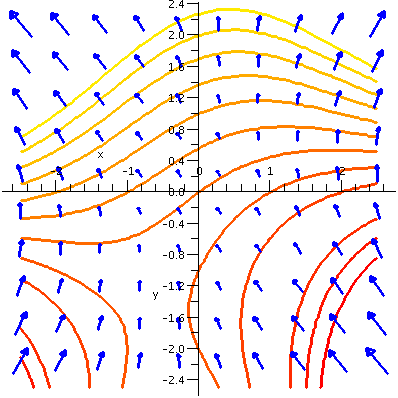 Another example
Another example
This example uses a function which is less symmetric and less
simple. I don't think I'd like to try to understand this "by hand"
unless you gave me a heck of a lot more time than I could take during
a class meeting.
The function is x2y–2x+y2+3y. The level curves
are shown for the values –12, –10, –8, –6, –4, –2, 0, 2, 4, 6, 8, and
10: the even integers from –12 to 12. Notice that the arrows seem to
be perpendicular to the level curves as they are supposed to be, and
that the arrows are longer when the spacing between the contour lines
(corresponding to equal differences in the constants) gets closer.
Comment
I looked at this picture and wondered what the
heck happened where the arrows got really small. What does
happen? Well, we can look for a critical point:
φx=2xy–2=0 and
φy=x2+3y+3=0. The first equation tells me
that y=1/x and then the second equation becomes x3+3x+3=0,
and I can't "solve" that. So I asked fsolve and was told there was one critical
point, at (approximately) x=–.596 and y=–1.678: this looks
correct. What kind of critical point? (Max/min/saddle) If you look at
the picture and the level curves you can probably guess. I actually
computed the Hessian, and it is a saddle. Ain't math fun?
|
In general ...
What was written above is generally true about a gradient vector field
and the contour lines or curves (contour surfaces in
R3). That is, the gradient vector field "arrows" are
perpendicular to the level curves. They "point" towards increasing
values of the function. Their magnitude (the length of the arrows) is
a measure of the density (?) of the contour lines: if the function is
rapidly changing (more dense contour lines) then the length of the
gradient will be longer.
By the way, if ∇φ=F,
then φ is called a potential of the vector field,
F. The word and concepts connected with it are important in
physics. I'll discuss more about this during the next class.
How many potentials?
If φ=x2+y2, then
∇φ=2xi+2yj. I asked if the vector field could
have other potentials? After some thought, we came up with
x2+y2+1 and x2+y2–17 as
other potentials, because the ∇ "process" would make the
constants go away.
Then I asked a harder question: could we list all possible
potentials of the vector field 2xi+2yj? Well, there
was a bit of discussion, and then I wrote
x2+y2+Constant, where "Constant" means any
possible constant. Why is this true? Well, if two functions have the
same gradient, then their difference will
have gradient equal to 0. Now the question is: why would a function,
let's call it g(x,y), with ∂g/∂x=0 always and
∂g/∂y=0 always have to be constant?
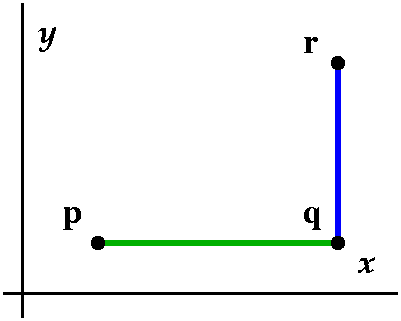 Theorem
Theorem
I didn't have time for this in class (it is in section 16.1,
though). But here is the information we know:
∂g/∂x=0 always
∂g/∂y=0 always
and I would like to convince you that g's values don't change.
|
The green path
Take the point p in the plane with coordinates
(x0,y0) and another point q, on the same
horizontal line. So q's coordinates are
(x1,y0). I would like to "compare" g's values at
p and q. So I would like to somehow "compute"
g(x1,y0)–g(x0,y0). Please
notice that nothing is happening in the second variable. But the
Fundamental Theorem of Calculus applies, and this is the same as
∫t=x0t=x1(∂g/∂x)(t,y0) dt. The
difference in the x variable is the same as the definite integral of
the partial derivative with respect to x from x0 to
x1. But we are assuming that this partial derivative is
always equal to 0. Therefore
g(x1,y0)–g(x0,y0)=0 (the
definite integral of 0 is 0) so that
g(x1,y0)=g(x0,y0).
|
The blue path
Take the point q in the plane with coordinates
(x1,y0) and another point r, on the same
vertical line. So r's coordinates are
(x1,y1). I would like to "compare" g's values at
q and r. So I would like to somehow "compute"
g(x1,y1)–g(x1,y0). Please
notice that nothing is happening in the first variable. But the
Fundamental Theorem of Calculus applies, and this is the same as
∫s=y0s=y1(∂g/∂y)(x1,s) ds. The
difference in the y variable is the same as the definite integral of
the partial derivative with respect to y from y0 to
y1. But we are assuming that this partial derivative is
always equal to 0. Therefore
g(x1,y1)–g(x1,y0)=0 (the
definite integral of 0 is 0) so that
g(x1,y1)=g(x1,y0).
|
This is very clever. As long as we can get from one
point to another by a succession of vertical and horizontal line
segments, the values of the potential won't change. In this course, we
will always have functions defined in such regions (regions which are
connected -- they have just one "piece"). So indeed we can conclude
that if ∇φ=0, then φ is constant. And further, if two
functions have the same gradient, they must differ by a constant. And
even further, if we can "guess" one potential, then we know all
potentials -- just add on an arbitrary constant. In physics terms, the
choice of the value of that constant is called "selecting a ground
state". Talk to the physics people about these words if you like.
|
Is the vortex flow a gradient vector field?
Look at –yi+xj. Is this vector field a gradient vector
field? If it is, can we find a potential for it? Some attempts were
made to guess a φ for this vector field. I then remarked that
maybe we should turn the question around, and consider: if there is
no potential for this vector field, can we If it is not,
explain why? This turns out to be a serious and interesting question,
because of things we will learn very soon. Also it has some
interesting physical consequences. Well, here is one way to decide the
answer.
Suppose φ(x,y) is a potential for –yi+xj. That
means ∂/∂y
φx= –y → φxy= –1
∂/∂x
φy= x → φyx= 1
But "mixed" partial derivatives are supposed to be equal (that is, if
some hypotheses are satisfied, but these are all very reasonable
functions and nothing weird happens). Since –1 is not equal to 1 we
know that the vortex flow is not a gradient vector field. I
don't think this is an obvious fact.
Return to x2i+y2j
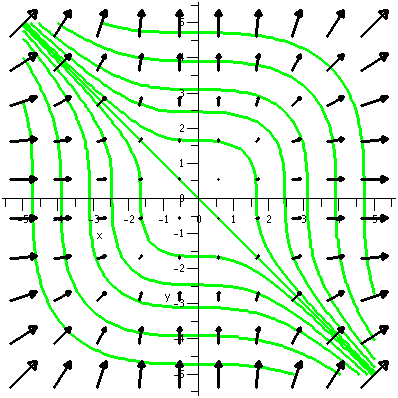 Is x2i+y2j a gradient vector
field? Let's see: if there is a potential φ then x2
should be ∂&phi/∂x which makes me think of
x3/3. And y2 should be ∂&phi/∂y which
makes me think of y3/3. So I decide to guess that
φ(x,y)=(1/3)x3+(1/3)y3 is a potential for
this vector field. By the way, so is
(1/3)x3+(1/3)y3–205.66783 but I will stick with
plain (1/3)x3+(1/3)y3. According to general
theory, the vector field will be perpendicular to the level curves of
φ. I will have Maple draw some of
these curves and display them along with the arrows of the vector
field that we saw before. The result is to the right.
Is x2i+y2j a gradient vector
field? Let's see: if there is a potential φ then x2
should be ∂&phi/∂x which makes me think of
x3/3. And y2 should be ∂&phi/∂y which
makes me think of y3/3. So I decide to guess that
φ(x,y)=(1/3)x3+(1/3)y3 is a potential for
this vector field. By the way, so is
(1/3)x3+(1/3)y3–205.66783 but I will stick with
plain (1/3)x3+(1/3)y3. According to general
theory, the vector field will be perpendicular to the level curves of
φ. I will have Maple draw some of
these curves and display them along with the arrows of the vector
field that we saw before. The result is to the right.
I hope but I certainly can't guarantee that the contour lines help you
understand the fluid flow. The streamlines of this flow are
perpendicular to the contour lines (these are orthogonal
collections of curves). But maybe you can see how the existence of the
potential function makes the picture more interesting. Potentials also
have other consequences, not just artistic. They make many
computations much easier, so knowing when a vector field has a
potential is useful.
Comment These level curves are not equally spaced. I
played with the contourplot command a
bit to get nice-looking curves. The values of the function that I used were
[-35,-20,-10,-5,-1.5,0,1.5,5,10,20,35].
|
Please look at the textbook, which also discusses and shows some
3-dimensional vector fields.
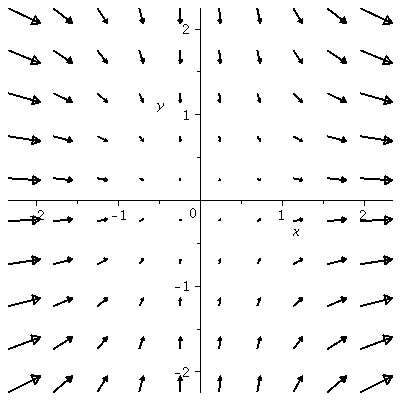 QotD
QotD
Sketch the vector field (x2/10)i–(y/10)j at
the points (–2,–1), (–2,0), (–2,1), (–1,–1), (–1,0), (–1,1), (0,–1),
(0,0), (0,1), (1,–1), (1,0), (1,1), (2,–1), (2,0), and (2,1) (3 by 5
grid of 15 dots).
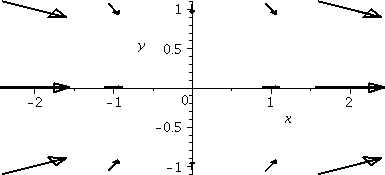 Maple's picture of this is shown to the
right. Notice the x2 in front of tne i. If x≠ 0,
this means the arrow at (x,y) must point from left to right. The
– in front of the j vector says that in the upper
halfplane, where y>0, the vector points down, and in the lower
halfplane, the vector points up.
Maple's picture of this is shown to the
right. Notice the x2 in front of tne i. If x≠ 0,
this means the arrow at (x,y) must point from left to right. The
– in front of the j vector says that in the upper
halfplane, where y>0, the vector points down, and in the lower
halfplane, the vector points up.
Another more extensive Maple picture is
shown to the left. Maybe you can see more about this "flow" in that picture.
Maintained by
greenfie@math.rutgers.edu and last modified 4/5/2010.
|
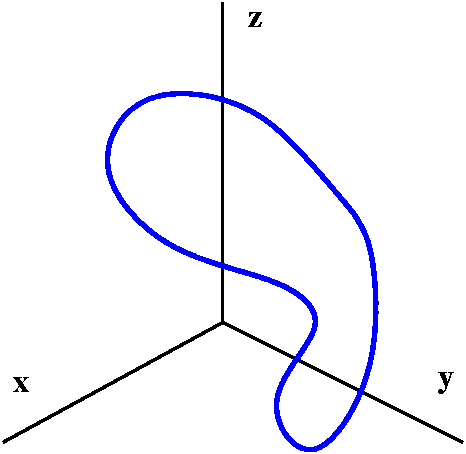
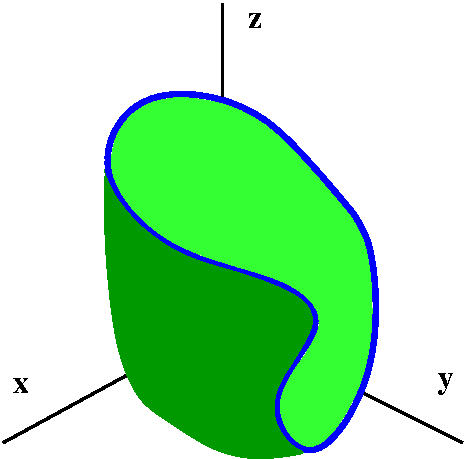 This should be a piece of a surface, all of whose boundary is the
curve mentioned above. As several students remarked, specifying the
boundary curve does not mean there's only one surface. In fact,
there are many really neat and clever computations which depend on
changing the surfaces involved. I'll show you one of these in a few
minutes.
This should be a piece of a surface, all of whose boundary is the
curve mentioned above. As several students remarked, specifying the
boundary curve does not mean there's only one surface. In fact,
there are many really neat and clever computations which depend on
changing the surfaces involved. I'll show you one of these in a few
minutes.
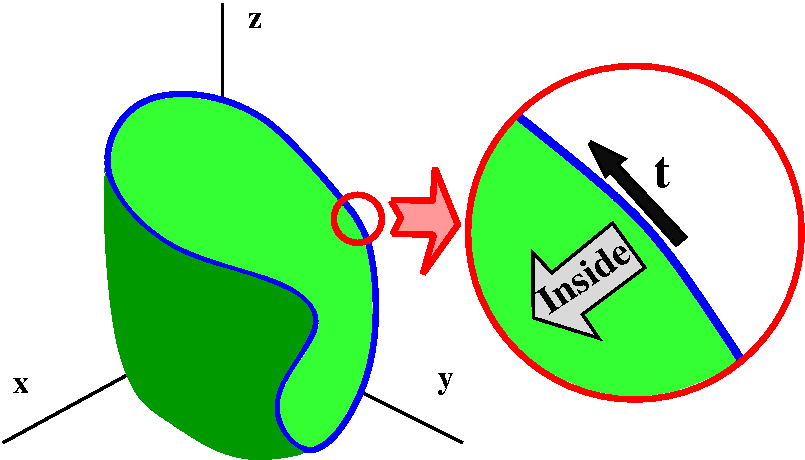 • How the surface and curve interact (by their orientations)
• How the surface and curve interact (by their orientations)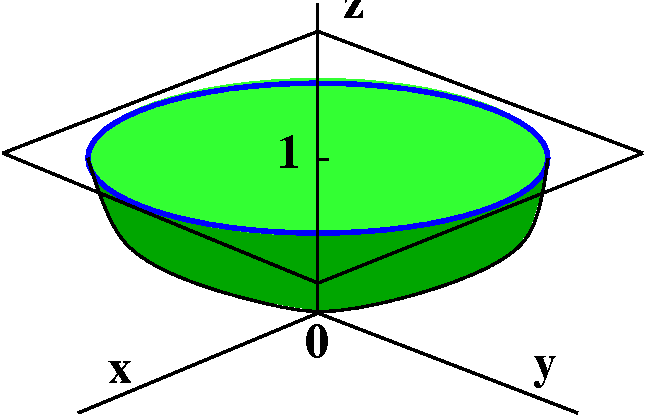 Here is a problem from a calculus textbook:
Here is a problem from a calculus textbook:
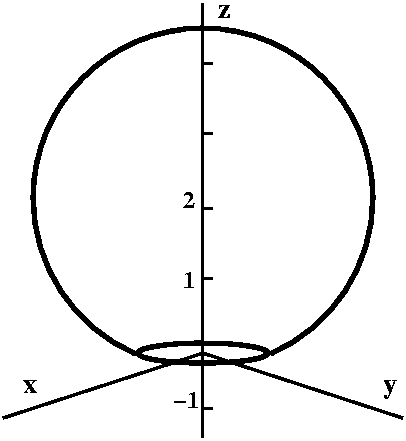 Another textbook problem
Another textbook problem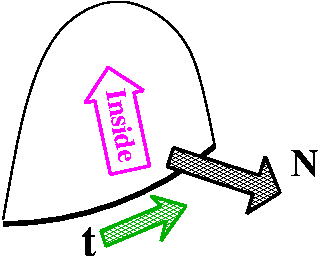 The boundary of the top portion occurs if z=0 in the
equation
x2+y2+(z–2)2=8. Then
x2+y2+(–2)2=8 and
x2+y2=4. This is a circle of radius 2 centered
at the origin in the xy-plane. We should establish the orientation of
this circle. If we look closely at a small piece of the surface near
the boundary curve, the outward unit normal points slightly down. We
must "walk" along the curve so that the surface is to the left. The
t direction is the standard counterclockwise direction on the
boundary circle. I hope the local picture to the right helps to
convince you of that. Again, the problem of deciding the resulting
orientation of one chunk (surface, boundary curve) from the other
(boundary curve, surface) seemed in class to be the most complicated
qualitative aspect of this problem.
The boundary of the top portion occurs if z=0 in the
equation
x2+y2+(z–2)2=8. Then
x2+y2+(–2)2=8 and
x2+y2=4. This is a circle of radius 2 centered
at the origin in the xy-plane. We should establish the orientation of
this circle. If we look closely at a small piece of the surface near
the boundary curve, the outward unit normal points slightly down. We
must "walk" along the curve so that the surface is to the left. The
t direction is the standard counterclockwise direction on the
boundary circle. I hope the local picture to the right helps to
convince you of that. Again, the problem of deciding the resulting
orientation of one chunk (surface, boundary curve) from the other
(boundary curve, surface) seemed in class to be the most complicated
qualitative aspect of this problem.
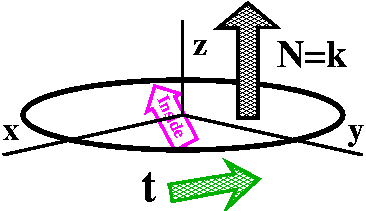 But notice:
this circle is also the correctly oriented boundary of the disc of
radius 2 centered at the origin in the xy-plane. So I can use Stokes'
Theorem a second time to change the line integral to a much
simpler surface integral:
But notice:
this circle is also the correctly oriented boundary of the disc of
radius 2 centered at the origin in the xy-plane. So I can use Stokes'
Theorem a second time to change the line integral to a much
simpler surface integral: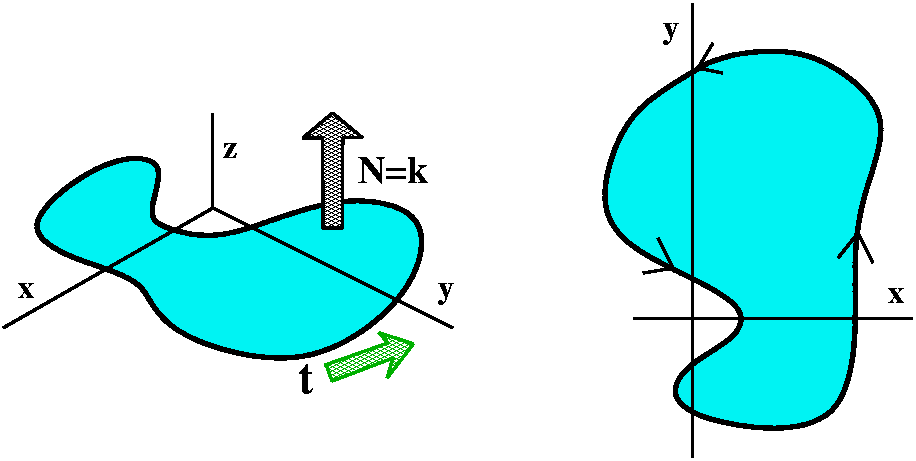
 Proving the Divergence Theorem for the unit cube
Proving the Divergence Theorem for the unit cube
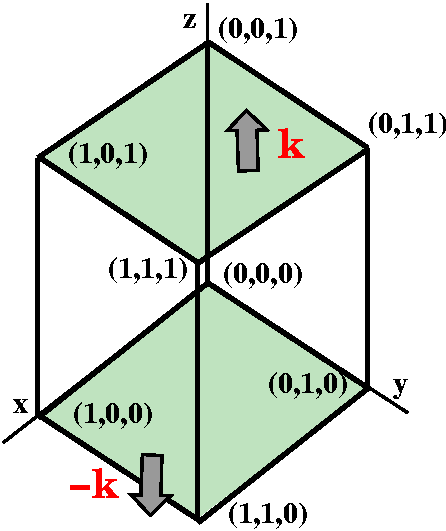
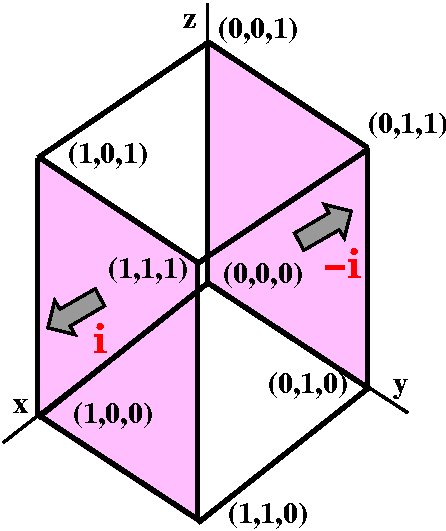
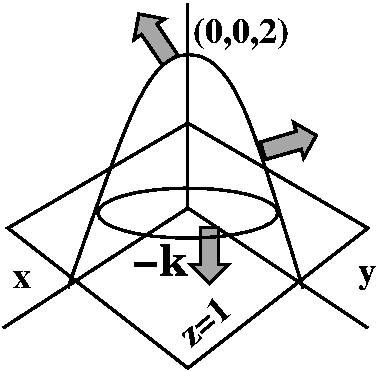

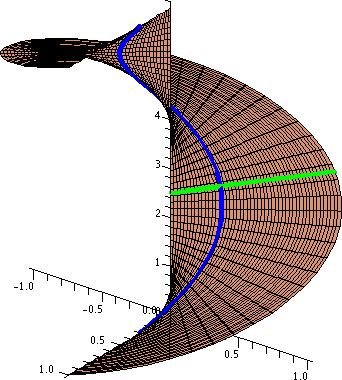 Textbook example
Textbook example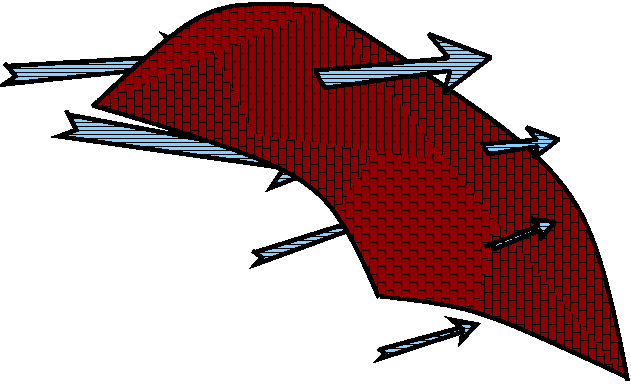 Suppose we have a vector field, F in R3. We could
imagine a surface in R3, and then try to see how the flow
of the vector field interacts with the surface. The picture to the
right is quite imaginary. I've never seen the arrows of a vector
field, and I want the surface, sort of like a net, not to give any
resistance to the imaginary arrows. It is, of course, an imaginary
surface.
Suppose we have a vector field, F in R3. We could
imagine a surface in R3, and then try to see how the flow
of the vector field interacts with the surface. The picture to the
right is quite imaginary. I've never seen the arrows of a vector
field, and I want the surface, sort of like a net, not to give any
resistance to the imaginary arrows. It is, of course, an imaginary
surface.
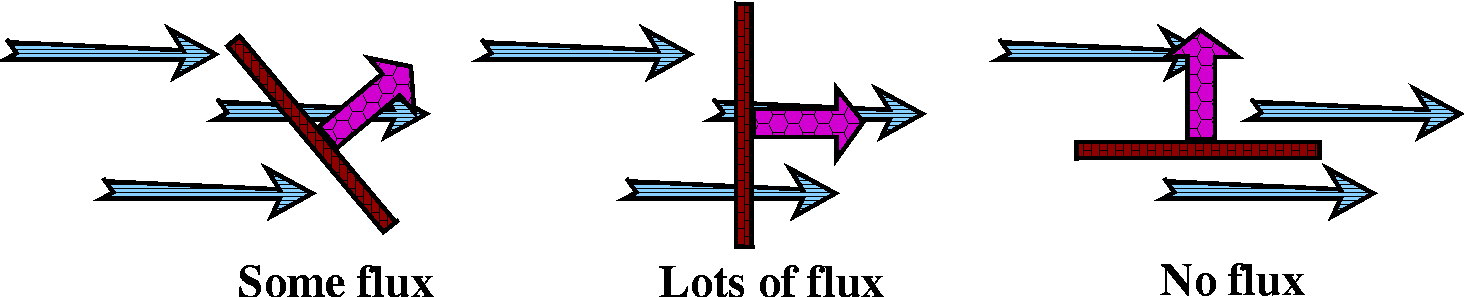 The flow through the surface is important. The same piece of surface
("dS") can have different flux, even if the vector field is constant
-- always the same direction and magnitude. What can then change is
the angle of the dS piece relative to the flow. If it is perpendicular
to the flow, there will be the most flux. If the dS is parallel to the
flow, there will be no flux. In between, there will be some "in
between" amount. In fact, if you think about this, the amount of flux
will depend on the cosine of the angle the surface makes with the
vector field. We can compute this with F·N where N is a unit vector normal or
perpendicular to the surface. Notice that the choice of N is
important. –N is also a unit normal, and using that choice will
change the sign of the flux.
The flow through the surface is important. The same piece of surface
("dS") can have different flux, even if the vector field is constant
-- always the same direction and magnitude. What can then change is
the angle of the dS piece relative to the flow. If it is perpendicular
to the flow, there will be the most flux. If the dS is parallel to the
flow, there will be no flux. In between, there will be some "in
between" amount. In fact, if you think about this, the amount of flux
will depend on the cosine of the angle the surface makes with the
vector field. We can compute this with F·N where N is a unit vector normal or
perpendicular to the surface. Notice that the choice of N is
important. –N is also a unit normal, and using that choice will
change the sign of the flux.
 The whole
surface
The whole
surface Suppose our vector field is F=<xy,z2,3> and
the surface we're interested in is the surface of the cube defined by
0≤x≤1, 0≤y≤1, and 0≤z≤1. It is not an accident that
this surface is an example of a closed surface which divides
all of space, R3, into two pieces, points inside and points
outside the surface. This is similar to a closed curve in
R2. Such surfaces are important in physical
applications. We will choose the normal to be the outward-pointing
unit normal, so flows out are positive. I would like to compute the
total flux of F through the surface of this cube. There are a
total of 6 faces. I'll do one face carefully, and then the others more
rapidly.
Suppose our vector field is F=<xy,z2,3> and
the surface we're interested in is the surface of the cube defined by
0≤x≤1, 0≤y≤1, and 0≤z≤1. It is not an accident that
this surface is an example of a closed surface which divides
all of space, R3, into two pieces, points inside and points
outside the surface. This is similar to a closed curve in
R2. Such surfaces are important in physical
applications. We will choose the normal to be the outward-pointing
unit normal, so flows out are positive. I would like to compute the
total flux of F through the surface of this cube. There are a
total of 6 faces. I'll do one face carefully, and then the others more
rapidly.
 This is a more qualitative problem. There's a picture given,
resembling what is to the right: a half of a circular cylinder whose
axis of symmetry is the z-axis, and the half-cylinder is the "forward"
half, where x≥0. An n, a unit normal, is given, and this
determines the selection of the unit normal at all other points (it
will be the normal pointing away from the z-axis). The problem
asks to determine whether the flux integral
∫∫half-cylinderF·dS representing the total flux is
positive, negative, or zero. The statement adds, "Explain your
reasoning." Several F's are given. I didn't have time to
discuss this in class. I believe (hope?) that the answers below are
correct, and they are done using simple reasoning about dot products
and symmetry.
This is a more qualitative problem. There's a picture given,
resembling what is to the right: a half of a circular cylinder whose
axis of symmetry is the z-axis, and the half-cylinder is the "forward"
half, where x≥0. An n, a unit normal, is given, and this
determines the selection of the unit normal at all other points (it
will be the normal pointing away from the z-axis). The problem
asks to determine whether the flux integral
∫∫half-cylinderF·dS representing the total flux is
positive, negative, or zero. The statement adds, "Explain your
reasoning." Several F's are given. I didn't have time to
discuss this in class. I believe (hope?) that the answers below are
correct, and they are done using simple reasoning about dot products
and symmetry.
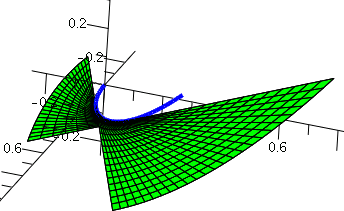 Once you have this idea, then check if there are values of s and t
satisfying the system of equations
Once you have this idea, then check if there are values of s and t
satisfying the system of equations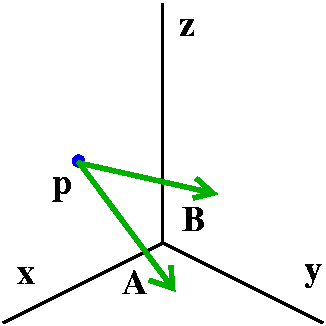
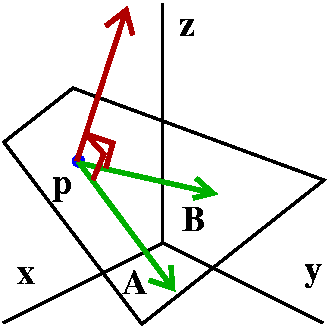 It is easy to check (I just did with some dot products) that the
resulting vector is perpendicular to both A and B and is
a normal vector to the plane we'd like to describe. A point with
coordinates (x,y,z) is on this plane if
It is easy to check (I just did with some dot products) that the
resulting vector is perpendicular to both A and B and is
a normal vector to the plane we'd like to describe. A point with
coordinates (x,y,z) is on this plane if
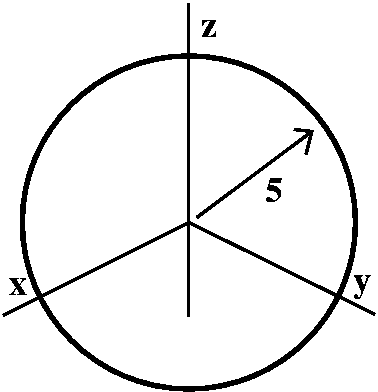
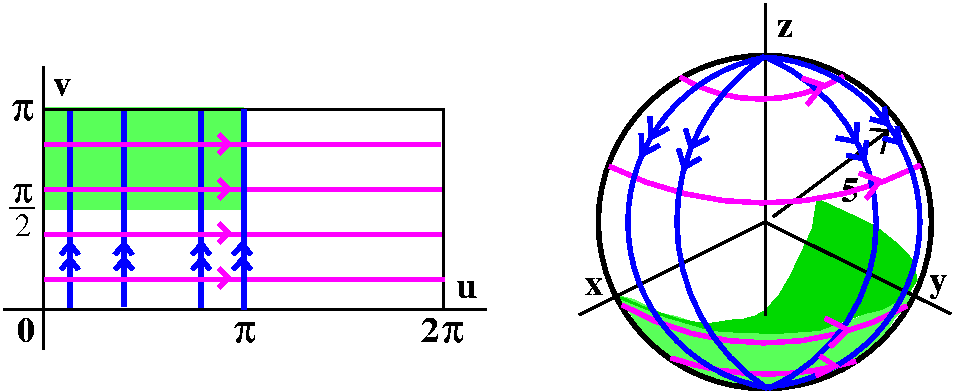
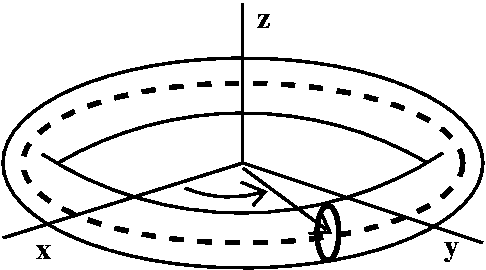


 The z coordinate of the point only involves v. The z coordinate is the
"opposite" side of a right triangle with acute angle v and hypotenuse
2. So z=2sin(v). The vector from the origin to the center of the
circle has length 4. The angle v adds on another 2cos(v) to that
length. But then we use this total length, 4=2cos(v), along with the
angle u (secretly, θ) to get the x and y coordinates. So
x=(4+2cos(v))cos(u) and y=(4+2cos(v))sin(u).
The z coordinate of the point only involves v. The z coordinate is the
"opposite" side of a right triangle with acute angle v and hypotenuse
2. So z=2sin(v). The vector from the origin to the center of the
circle has length 4. The angle v adds on another 2cos(v) to that
length. But then we use this total length, 4=2cos(v), along with the
angle u (secretly, θ) to get the x and y coordinates. So
x=(4+2cos(v))cos(u) and y=(4+2cos(v))sin(u).



 Jacobians?
Jacobians? Rectangular Green's Theorem
Rectangular Green's Theorem Computation on a semicircle
Computation on a semicircle

 One additional remark, please: simple closed curves don't have to be
so "simple" in the non-technical meaning of the word. I sketched
something like what is shown to the right. It may not even be clear
whether the point indicated in magenta
(purple?) is inside or outside the curve (but count the number
of crossings from the point to the outside and find the parity
[odd/even]). So things can really get complicated if you want to do
curves more complicated than circles or rectangles.
One additional remark, please: simple closed curves don't have to be
so "simple" in the non-technical meaning of the word. I sketched
something like what is shown to the right. It may not even be clear
whether the point indicated in magenta
(purple?) is inside or outside the curve (but count the number
of crossings from the point to the outside and find the parity
[odd/even]). So things can really get complicated if you want to do
curves more complicated than circles or rectangles.
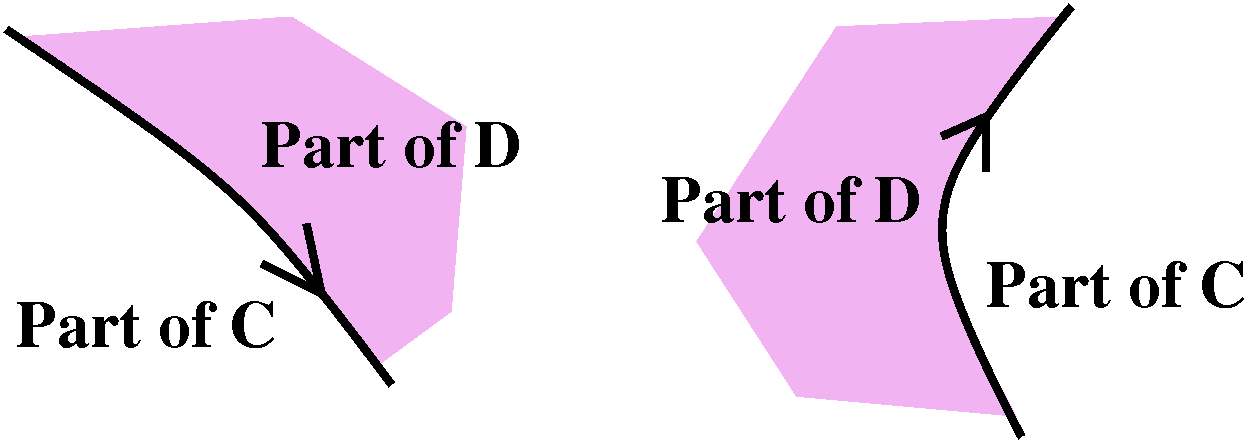 Look back at the rectangle picture. You should see, I hope, that the
boundary is a simple closed curve, which is positively oriented with
respect to the interior. And look again at the semidisc (can't be a
word!). The inside of the semidisc is to the left of the boundary as
the parameter increases.
Look back at the rectangle picture. You should see, I hope, that the
boundary is a simple closed curve, which is positively oriented with
respect to the interior. And look again at the semidisc (can't be a
word!). The inside of the semidisc is to the left of the boundary as
the parameter increases.
 Now let me compute the line integral ∫CP(x,y)dx+Q(x,y)dy, where C is, say, the circle of
radius 3 centered at (0,0). The first parameterization you should
consider is this: x=3cos(t) and y=3sin(t) so that dx=–3sin(t) dt
and dy=3cos(t) dt. Then x2+y2=32
because sin2+cos2=1. Thus
Now let me compute the line integral ∫CP(x,y)dx+Q(x,y)dy, where C is, say, the circle of
radius 3 centered at (0,0). The first parameterization you should
consider is this: x=3cos(t) and y=3sin(t) so that dx=–3sin(t) dt
and dy=3cos(t) dt. Then x2+y2=32
because sin2+cos2=1. Thus The example considered is, however, very important in practice. Let me
show why. Let's consider another path, W, which is a quadrilateral. W
is a simple closed curve made of four straight line segments. It
starts at (8,0), goes to (2,6), then to (7,–1), then to (0,–5), and
finally back to (8,0). I would like to compute ∫W–y/(x2+y2)dx+x/(x2+y2)dy. Here
I am not so sure I could "easily" compute the integrals which would
come out of parameterizing the four line segments, and changing the
x,y language to t language. At least the task would be lengthy. So let
me show you another way. Again, I can't just apply Green's Theorem to
W and the region inside W, since W encloses the same bad point. But I
can do something very clever using Green's Theorem.
The example considered is, however, very important in practice. Let me
show why. Let's consider another path, W, which is a quadrilateral. W
is a simple closed curve made of four straight line segments. It
starts at (8,0), goes to (2,6), then to (7,–1), then to (0,–5), and
finally back to (8,0). I would like to compute ∫W–y/(x2+y2)dx+x/(x2+y2)dy. Here
I am not so sure I could "easily" compute the integrals which would
come out of parameterizing the four line segments, and changing the
x,y language to t language. At least the task would be lengthy. So let
me show you another way. Again, I can't just apply Green's Theorem to
W and the region inside W, since W encloses the same bad point. But I
can do something very clever using Green's Theorem.


 I think the computations I've just done are difficult to
understand. Here is another physical model. Line integrals can also be
thought of as measuring flux, the net flow through the
curve. We will investigate this situation in R3 soon. But
consider the following physical setup: two parallel planes of plastic,
and a hose inserted through one of the planes, pumping water in at a
steady rate (the blue things in the picture are not minnows, they are
water drops!). If we surround this source with some sort of
circular detection "fence" then we can look at how the water goes
through the fence, and from that deduce the rate at which water is
being pumped in. But we could also install another detection fence. If
we do the same computations for that fence, the source rate should be
the same, because the hose is pumping water in steadily: its rate is
not varying. The mathematical computation with the crosscuts above is
a version of this physical situation. When
Py–Qx=0, away from the hose (at the origin) the
source rate is 0. Any comprehensive measurement of flow surrounding
the origin will get the same answer.
I think the computations I've just done are difficult to
understand. Here is another physical model. Line integrals can also be
thought of as measuring flux, the net flow through the
curve. We will investigate this situation in R3 soon. But
consider the following physical setup: two parallel planes of plastic,
and a hose inserted through one of the planes, pumping water in at a
steady rate (the blue things in the picture are not minnows, they are
water drops!). If we surround this source with some sort of
circular detection "fence" then we can look at how the water goes
through the fence, and from that deduce the rate at which water is
being pumped in. But we could also install another detection fence. If
we do the same computations for that fence, the source rate should be
the same, because the hose is pumping water in steadily: its rate is
not varying. The mathematical computation with the crosscuts above is
a version of this physical situation. When
Py–Qx=0, away from the hose (at the origin) the
source rate is 0. Any comprehensive measurement of flow surrounding
the origin will get the same answer.
 I returned exams to students who were in class today. The problem
whose answers were most interesting and frustrating to read was
probably the second one, about Lagrange multipliers. The non-zero
solutions to the system of equations give only one value of the
objective function, so if you believe that value is both max and min,
the function must be constant, which is certainly incorrect. There are
other solutions where some of the variables are 0, and they must be
considered.
I returned exams to students who were in class today. The problem
whose answers were most interesting and frustrating to read was
probably the second one, about Lagrange multipliers. The non-zero
solutions to the system of equations give only one value of the
objective function, so if you believe that value is both max and min,
the function must be constant, which is certainly incorrect. There are
other solutions where some of the variables are 0, and they must be
considered.
 One work computation
One work computation What if the integrals are the same?
What if the integrals are the same? We could pick a point at random, say (–2,6,3). Such a "random" point
was picked by a student in the class. This is called the ground
state physically. Then we could consider the function g(x,y,z),
the total work, which results from taking any path from (–2,6,3) to
(x,y,z). Since all paths result in the same work, this does define a
function. What can we say about g(x,y,z)? Well, select an order from
x and y and z. An order of the variables was picked by various
students in the class, I think the order was y to x to z. Then I will
show you that something neat happens. If we want to move from (–2,6,3)
to (x,y,z), then we could move in pieces, each by a line segment, and
only changing one variable at a time. We've done this repeatedly in
251. Changing lots of variables at once is difficult, so try to change
one at a time -- maybe things will be easier.
We could pick a point at random, say (–2,6,3). Such a "random" point
was picked by a student in the class. This is called the ground
state physically. Then we could consider the function g(x,y,z),
the total work, which results from taking any path from (–2,6,3) to
(x,y,z). Since all paths result in the same work, this does define a
function. What can we say about g(x,y,z)? Well, select an order from
x and y and z. An order of the variables was picked by various
students in the class, I think the order was y to x to z. Then I will
show you that something neat happens. If we want to move from (–2,6,3)
to (x,y,z), then we could move in pieces, each by a line segment, and
only changing one variable at a time. We've done this repeatedly in
251. Changing lots of variables at once is difficult, so try to change
one at a time -- maybe things will be easier.
 So let me now assume that
F=<F1,F2,F3> and that I
happen to know a function g so that
∂g/∂x=F1(x,y,z),
∂g/∂y=F2(x,y,z), and
∂g/∂z=F3(x,y,z). I would like to compute the line
integral of
F1(x,y,z) dx+F2(x,y,z) dy+F3(x,y,z) dz
along a curve going from p where t=Start to q where t=End. So we have a parameterization,
(x(t),y(t),z(t)) of the
curve.
So let me now assume that
F=<F1,F2,F3> and that I
happen to know a function g so that
∂g/∂x=F1(x,y,z),
∂g/∂y=F2(x,y,z), and
∂g/∂z=F3(x,y,z). I would like to compute the line
integral of
F1(x,y,z) dx+F2(x,y,z) dy+F3(x,y,z) dz
along a curve going from p where t=Start to q where t=End. So we have a parameterization,
(x(t),y(t),z(t)) of the
curve.
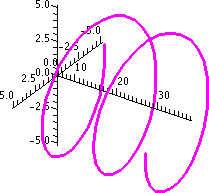 Example
Example Continue with this vector field and compute another example
Continue with this vector field and compute another example
 Mass of a wire
Mass of a wire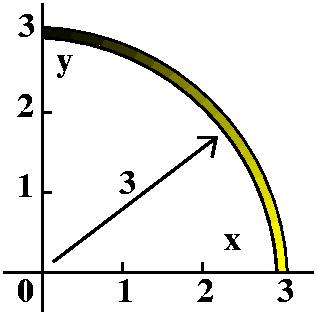 Silly example
Silly example Work
Work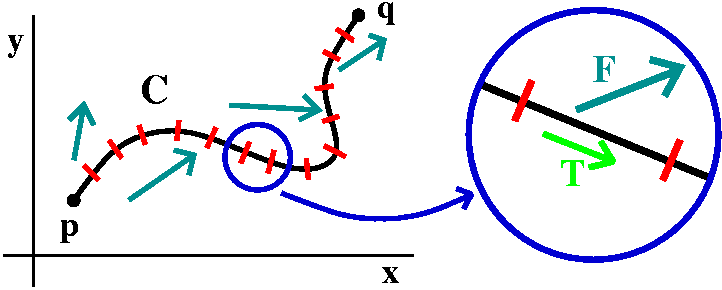 Again, chop up, approximate, sum,
limit.
Again, chop up, approximate, sum,
limit.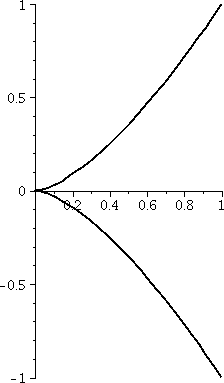
 To the right is a "picture" of part of a vector field. The picture was
produced by Maple using a command I
don't know very well (there are thousands of commands, and I'm sure I
know less than a tenth of one percent of them). This command is in the
plots package. The picture was produced by
To the right is a "picture" of part of a vector field. The picture was
produced by Maple using a command I
don't know very well (there are thousands of commands, and I'm sure I
know less than a tenth of one percent of them). This command is in the
plots package. The picture was produced by





 Another example
Another example Theorem
Theorem Is x2i+y2j a gradient vector
field? Let's see: if there is a potential φ then x2
should be ∂&phi/∂x which makes me think of
x3/3. And y2 should be ∂&phi/∂y which
makes me think of y3/3. So I decide to guess that
φ(x,y)=(1/3)x3+(1/3)y3 is a potential for
this vector field. By the way, so is
(1/3)x3+(1/3)y3–205.66783 but I will stick with
plain (1/3)x3+(1/3)y3. According to general
theory, the vector field will be perpendicular to the level curves of
φ. I will have Maple draw some of
these curves and display them along with the arrows of the vector
field that we saw before. The result is to the right.
Is x2i+y2j a gradient vector
field? Let's see: if there is a potential φ then x2
should be ∂&phi/∂x which makes me think of
x3/3. And y2 should be ∂&phi/∂y which
makes me think of y3/3. So I decide to guess that
φ(x,y)=(1/3)x3+(1/3)y3 is a potential for
this vector field. By the way, so is
(1/3)x3+(1/3)y3–205.66783 but I will stick with
plain (1/3)x3+(1/3)y3. According to general
theory, the vector field will be perpendicular to the level curves of
φ. I will have Maple draw some of
these curves and display them along with the arrows of the vector
field that we saw before. The result is to the right.
 QotD
QotD Maple's picture of this is shown to the
right. Notice the x2 in front of tne i. If x≠ 0,
this means the arrow at (x,y) must point from left to right. The
– in front of the j vector says that in the upper
halfplane, where y>0, the vector points down, and in the lower
halfplane, the vector points up.
Maple's picture of this is shown to the
right. Notice the x2 in front of tne i. If x≠ 0,
this means the arrow at (x,y) must point from left to right. The
– in front of the j vector says that in the upper
halfplane, where y>0, the vector points down, and in the lower
halfplane, the vector points up.