Math 152 diary, spring 2009: second section
Later material
Previous material
In reverse order: the most recent material is first.
| Monday,
April 13 | (Lecture #21) |
|---|
About the exam, etc.
We'll have an exam next Monday, April 20. Here is some review material. Here is an outline of (possibly!)
useful approaches to sequence/series problems. On Thursday, April 16,
students will work on the course coordinator's review problems. I will
not be available this Thursday and Friday (out of town for a
professional trip) but I will have a review session for the second
exam on Sunday, April 19, from 5 to 7 PM. The location for this is SEC
117.
Why the Root Test?
The Root Test is another method for exploiting similarity with
geometric series to diagnose absolute convergence (or divergence) of a
series. We consider a series ∑an. Suppose we think
that an "resembles" crn. Well, if we take the
nth root of crn, we get
(crn)1/n=c1/n(rn)1/n=c1/nrn·(1/n)=c1/nr. Now if
n→∞, we have already seen that a
sequence like {c1/n} has limit 1. So
(crn)1/n→r
as n→∞. So we can hope that the asymptotic behavior of
(an)1/n as n→∞ can help analyze the
convergence of ∑an.
Statement of the Root Test
The Root Test
Consider the series
∑n=0∞an, and the limit
limn→∞|an|1/n. Suppose
that this limit exists, and call its value, L. (L is what's used in
our textbook.)
| If L<1, the series converges absolutely and therefore
must converge. |
If L>1, the series diverges. |
If L=1, the Root Test supplies no
information |
Ludicrous example
Let's consider the series ∑n=1∞((5n+7)/(6n+8))n which
I invented specifically to use the Root Test. I don't know any
application where I've ever seen anything like this series which seems
fairly silly to me. Well, anyway, the terms are all positive, so I can
"forget" the absolute value signs. We take the nth root and
remember that repeated exponentiations multiply:
[((5n+7)/(6n+8))n]1/n=((5n+7)/(6n+8))n·(1/n)=((5n+7)/(6n+8))1=((5n+7)/(6n+8)).
Now we need to discover the limit (if it exists!) of ((5n+7)/(6n+8)). But
(L'Hôpital) this limit is 5/6. Since L=5/6<1, the series
converges absolutely and must converge.
I don't know what the sum is. Oh well.
Less silly (maybe) example
This may look almost as ludicrous, but it turns out to be more
significant. Again, though, this example is chosen to work well with
the Root Test.
For which x's does the series
∑n=1∞nnxn converge?
The powers of n signal to me that probably I should try the Root
Test. Here an is nnxn. We can't just
discard the absolute value here, but we can push it through to the x
because everything is multiplied. So:
|nnxn|1/n=(nn|x|n)1/n=nn·(1/n)|x|n·(1/n)=n|x|.
 As I mentioned in class, as n→∞ jumping to the
"conclusion" may be unwise. There are actually two cases. If x=0, the
limit is 0, If x≠0, the limit does not exist (it is "∞"). So we
can conclude that the series
∑n=1∞nnxn
converges exactly when x=0.
As I mentioned in class, as n→∞ jumping to the
"conclusion" may be unwise. There are actually two cases. If x=0, the
limit is 0, If x≠0, the limit does not exist (it is "∞"). So we
can conclude that the series
∑n=1∞nnxn
converges exactly when x=0.
Even less silly example
Let's try this: for which x's does
∑n=1∞xn/nn
converge? I hope you will see the resemblance and contrast with the
previous computation:
|xn/nn|1/n=(|x|n/nn)1/n=|x|n·(1/n)nn·(1/n)=|x|/n.
 In this example, there aren't any special cases. For any x,
limn→∞|x|/n=0=L. Since L<1 always, the series
∑n=1∞xn/nn
converges absolutely for all x's and therefore converges for all x's.
In this example, there aren't any special cases. For any x,
limn→∞|x|/n=0=L. Since L<1 always, the series
∑n=1∞xn/nn
converges absolutely for all x's and therefore converges for all x's.
Comment: Root vs. Ratio
As I mentioned in class, I have an emotional preference for the Ratio
Test that I can't explain. But I will admit that analyzing the two
previous examples with the Ratio Test would be very
difficult. However, the Ratio Test works exceptionally well when
series have factorials (you'll see why there are lots of series with
factorials in the next lecture). So series with similar results to the
two previous examples which I'd examine with the Ratio Test would be
∑n=0∞n!xn and
∑n=0∞xn/n!.
The next few examples were tedious to do in class, and I thank
students for the patience they mostly displayed, since the reasons for
doing them were not at all clear. I also made some dumb
mistakes some of the time.
Example 76
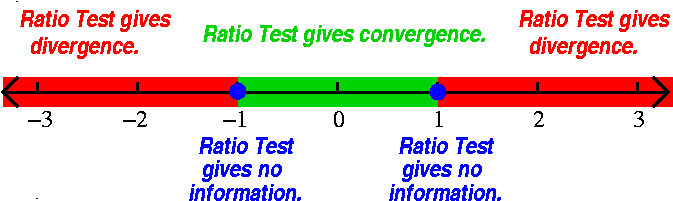 For which x's does
∑n=1∞xn/n converge? We used
the Ratio Test, and |an+1/an| simplified fairly
easily to |x|[(n+1)/n]. Now L'H or simple algebraic manipulation shows
that ρ=|x|. So we get guaranteed absolute convergence and
therefore convergence when |x|<1 and divergence when |x|>1. For
|x|=1, we don't get any information. I'll write the answer using
interval notation now: if x is in (–1,1), the series
converges. If x is in (1,∞), the series diverges. If x is in
(–∞,–1), the series diverges. There's no information
for x=1 or x=–1.
For which x's does
∑n=1∞xn/n converge? We used
the Ratio Test, and |an+1/an| simplified fairly
easily to |x|[(n+1)/n]. Now L'H or simple algebraic manipulation shows
that ρ=|x|. So we get guaranteed absolute convergence and
therefore convergence when |x|<1 and divergence when |x|>1. For
|x|=1, we don't get any information. I'll write the answer using
interval notation now: if x is in (–1,1), the series
converges. If x is in (1,∞), the series diverges. If x is in
(–∞,–1), the series diverges. There's no information
for x=1 or x=–1.
 If you insist on knowing what happens at x=+/–1, let's
"insert" these values of x into the series and investigate.
If you insist on knowing what happens at x=+/–1, let's
"insert" these values of x into the series and investigate.
If x=+1, the series becomes
∑n=1∞1n/n=∑n=1∞1/n,
the harmonic series. So the series diverges.
If x=–1, the series becomes
∑n=1∞(–1)n/n. This is
(almost) the alternating harmonic series (it is off by a sign). So the
series converges.
These results are reflected in the "improved" picture to the right.
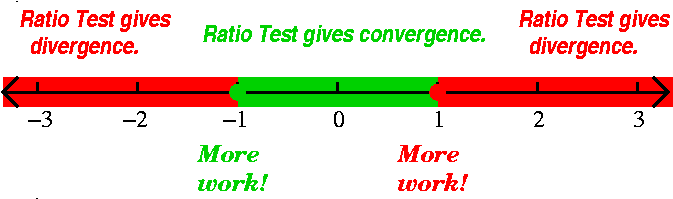
Example 77
 For which x's does
∑n=1∞xn/n2
converge? Again, the Ratio Test, and |an+1/an|
simplified fairly easily to |x|[n/(n+1)]. And again manipulation shows
that ρ=|x|. So we have absolute convergence and therefore
convergence when |x|<1 and divergence when |x|>1. For |x|=1, we
don't get any information. As intervals: if x is in (–1,1), the
series converges. If x is in (1,∞), the series diverges. If x is
in (–∞,–1), the series diverges. There's no
information for x=1 or x=–1. (Looks a lot the same, huh?)
For which x's does
∑n=1∞xn/n2
converge? Again, the Ratio Test, and |an+1/an|
simplified fairly easily to |x|[n/(n+1)]. And again manipulation shows
that ρ=|x|. So we have absolute convergence and therefore
convergence when |x|<1 and divergence when |x|>1. For |x|=1, we
don't get any information. As intervals: if x is in (–1,1), the
series converges. If x is in (1,∞), the series diverges. If x is
in (–∞,–1), the series diverges. There's no
information for x=1 or x=–1. (Looks a lot the same, huh?)
 To see what happens at x=+/–1, put these values of x into the
series and investigate the result directly (I don't know any other
ways to do this).
To see what happens at x=+/–1, put these values of x into the
series and investigate the result directly (I don't know any other
ways to do this).
If x=+1, the series becomes
∑n=1∞1n/n2=∑n=1∞1/n2. This is a p-series with p=2>1, so it converges.
If x=–1, the series becomes
∑n=1∞(–1)n/n2. But this series converges absolutely (it gives us the p-series just considered when the signs are stripped off) and therefore it must converve.
And again, look at the "improved" picture to the right.

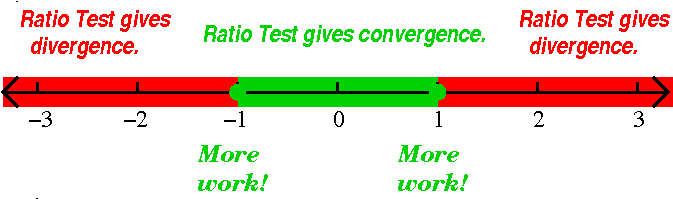
Example 78
For which x's does
∑n=1∞n xn converge?
The same limiting ratio is reported, and we get the same
convergence/divergence/no information result, with the same initial
picture.
 When x=1, the series is
∑n=1∞n=1+2+3+4+... and this certainly
diverges because the terms don't approach 0. The same reason shows
that the series diverges when x=–1. So the result, as shown, is
again slightly changed.
When x=1, the series is
∑n=1∞n=1+2+3+4+... and this certainly
diverges because the terms don't approach 0. The same reason shows
that the series diverges when x=–1. So the result, as shown, is
again slightly changed.
The reason for my going through all of these examples is that there
basically aren't any others. Well, what I mean is that, qualitatively,
there are no further types of behavior possible for this sort of
series. So let me tell you the accepted vocabulary for what we are
studying, and then describe the result.
What is a power series?
A power series centered at x0 (a fixed number) is an
infinite series of the form
∑n=0∞cn(x–x0)n
where the x is a variable and the cn are some collection of
coefficients. It is sort of like an infinite degree
polynomial. Usually I (and most people) like to take x0 to
be 0 because this just makes thinking easier.
Convergence and divergence of power series
It turns out that the collection of examples we looked is a complete
qualitative catalog of what can happen to the convergence and
divergence of a power series. This isn't obvious, but it also isn't
totally hard (it just involves comparing series to geometric series
and needs no theoretical equipment beyond what we've already
done). Here is the result:
A power series centered at x0 always has an interval of
convergence with the center of that interval equal to
x0. Inside the interval of convergence, the power series
converges absolutely and therefore converges. Outside the interval,
the power series diverges. The power series may or may not converge on
the two boundary points of the interval. The interval may have any
length between 0 and ∞. Half the length of the interval is
called the radius of convergence.
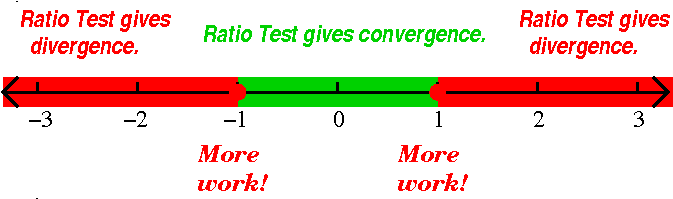
Going back to the examples
| The series | converges
for x in | and has
radius of con-
vergence equal to | Pictures: convergence in red and divergence
in green |
|---|
| ∑n=1∞nnxn | [0] | 0 |  |
| ∑n=1∞xn/nn | (–∞,+∞) | ∞ |  |
| ∑n=1∞xn/n | [–1,1) | 1 |  |
| ∑n=1∞xn/n2 | [–1,1] | 1 |  |
| ∑n=1∞n xn | (–1,1) | 1 |  |
These examples show that the interval of convergence of a power
series may or may not include one or both of the endpoints of the
interval. The reason for the number of examples was to show you,
explicitly, that it is possible for the series to converge on neither
or one or both of the boundary points. I wanted to show a "complete"
collection of examples.
It turns out that behavior on the edge of the interval is probably
only interesting (sigh) as an exam question in calc 2 (where it
is frequently asked!) because of some results you'll be told
about in a few lines. I mentioned that I could give a supporting
argument for this result using nothing but geometric series and
comparison (techniques on the level of this course) but we just don't
have enough time!
A suspiciously simple question ... (the "IQ" test in class)
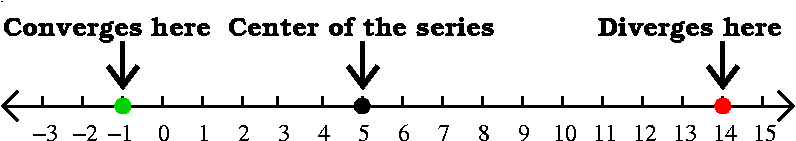 Suppose that you have a power series
∑n=0∞an (x–5)n
centered at x0=5. You are told that the series converges
when x=–1 and diverges when x=14. What can you say about the
radius of convergence? For which x's must this series converge
and for which x's must this series diverge? You are given no
other information.
Suppose that you have a power series
∑n=0∞an (x–5)n
centered at x0=5. You are told that the series converges
when x=–1 and diverges when x=14. What can you say about the
radius of convergence? For which x's must this series converge
and for which x's must this series diverge? You are given no
other information.
Answer The general theory, quoted above, states that a power
series converges in an interval, and the center of the series, here
x0=5, must be in the center of the interval. If the series
converges at x=–1, then, since the distance from –1 to 5
is 6, the series must (by the general theory) converge at every
number x whose distance to 5 is less than 6. I think to myself that
"convergence spreads inward". What about divergence? Actually,
"divergence spreads outward." The distance from 5 to 14, where we're
told that the series diverges, is 9. Therefore any x whose distance to
5 is greater than 9 (left or right!) must be a place where the series
diverges (because if it converged then the series would converge at
14, also, by the contagious (?) nature of convergence, and this isn't
true).

What we can conclude from this information is the following:
The series must converge at least in the interval [–1,11).
The series must diverge at least in the interval (–∞,–4) and
in the interval [14,∞).
We can't conclude anything about the
convergence of the series in the intervals [–4,–1) and [11,14).
The radius of convergence of the series is a number R with
6≤R≤9. We don't know more than that.
I hope you note that if I had told you this information:
The series, centered at 5,
diverged at –1 and converged at 14.
Then I would be lying ("I misspoke."). There is no such
series. Convergence at 14 with center at 5 would immediately imply
that the series converged at –1.
Calculus with power series
So I've said again and again in class that I'm never going to add up
infinitely many numbers, and that the notion of infinite series is a
short cut for the limit of the sequence of partial sums. All of this
is true, but the real reason that people use infinite series with
great energy and enthusiasm includes the following results about power
series:
Hypothesis Suppose the power series
∑n=0∞an (x–x0)n
has some positive radius of convergence, R, and suppose that f(x) is
the sum of this series inside its radius of convergence.
Differentiation The series
∑n=0∞n an (x–x0)n–1
has radius of convergence R, and for the x's where that series
converges, the function f(x) can be differentiated,
and f´(x) is equal to the sum of that series.
Integration The series
∑n=0∞[an/(n+1)] (x–x0)n+1
has radius of convergence R, and for the x's where that series
converges, the sum of that series is equal to an indefinite integral
of f(x), that is
∫f(x)dx.
These results are not obvious at all, and they take some effort to
verify, even in more advanced math courses. The results declare that
for calculus purposes, a power series inside its radius of convergence
can be treated just like a polynomial of infinite degree. You just
differentiate and integrate the terms and the sums are the derivative
and antiderivative of the original sum function.
Please note that other kinds of series many of you will likely see in
applications later (such as Fourier series or wavelet series) do not
behave as simply with calculus.
I wanted to show a use of this result. What follows is actually a
standard useful application, although both the question and the
solution technique may look silly to you now.
What is the value of ∑n=1∞n2/5n?
To compute
∑n=1∞n2/5n,
look carefully at the individual terms. We're adding up
n2/5n=(n2)(1/5n). In the
context of sequences and series, the (1/5n) part might make
me think of ∑n=1∞xn, a
geometric series, with x=1/3. Generally, this is a geometric series
with the first term, c, equal to x, and the ratio between successive
terms, r, also equal to x. Well, if
f(x)=∑n=1∞xn, then the
series converges for |x|<1 and with f(x)=x/(1–x).
How can we get an n in the front of the series terms? Well,
changing xn to n·something may push you (I hope!) to
differentiate. So f´(x) is
∑n=1∞nxn–1. I also get
the sum by differentiating x/(1–x). The Quotient Rule gives
[1(1–x)–(–1)x]/(1–x)2=1/(1–x)2. So this must be
∑n=1∞nxn–1 when |x|<1.
Step 1 Differentiate.
But I need two n's (n2) in front and now the power is
wrong. Let me fix up the power by multiplying by x, both the series
and its sum:
x·∑n=1∞nxn–1=∑n=1∞nxn
has sum x·(1/(1–x)2)=x/(1–x)2.
Step 2 Multiply by x.
Now I magically want another n to appear in front of the terms of
∑n=1∞nxn. This is just
like the first step: we differentiate. The derivative of the series is
∑n=1∞n2xn–1.
What about the sum of this series for |x|<1? We need to
differentiate x/(1–x)2. (This is certainly the most
irritating part of the whole exercise.) Again, the Quotient Rule:
The derivative of x/(1–x)2 is
[1(1–x)2–x{2(1–x)1(–1)}]/(1–x)4
(parentheses are your friends!).
This is valid for |x|<1.
Step 3 Differentiate.
We need to fix up the power in the sum. It is n–1 and I want n. So
let's multiply by x in both the series and the sum:
x·∑n=1∞n2xn–1=∑n=1∞n2xn
and
x·[1(1–x)2–x{2(1–x)1(–1)}]/(1–x)4
is the sum, for |x|<1.
Step 4 Multiply by x.
Now, clumsy as it looks, we have what's called a "closed form" (means
just: a formula involving functions we know) for
∑n=1∞n2xn and
we plug in x=1/5 into the formula. The answer is
{1/5}·[1(1–{1/5})2–{1/5}{2(1–{1/5})1(–1)}]/(1–{1/5})4.
That's the sum of the series.
Step 5 Plug in x=1/5.
This actually gives 15/32, just as I said last time. Of course, I
could have asked a friend.
> sum(n^2/5^n,n=1..infinity);
15
--
32
QotD
Verify that 15/32 actually is the result of plugging in x=1/5
into the formula. This was the QotD for sections 1 through 3. Iwas a
bit slower in the later lecture, and there I only asked (!) what the
sum of nxn was, and how to use it to find
∑n=1∞n/5n.
I actually would have liked to give the following as the QotD but
there wasn't time:
Discuss the convergence of
&sumn=1∞(–1)nxn/sqrt(n)
as thoroughly as possible. So: for which x's does this series
converge? For which x's does it converge absolutely? For which x's
does it converge conditionally? You can try this, and then look here for a solution.
| Wednesday,
April 8 | (Lecture #20) |
|---|
Scheduling ...
The scheduled subject for today's lecture is Ratio and Root
Tests, and for the next lecture, the subject is Power
Series. Today I will definitely motivate and state the Ratio Test,
and probably won't get to the Root Test. I will, however, show an
application to a power series. On Monday, I will continue with a
statement of the Root test, and then formally
define and state the principal properties of power series, and
use both of the "tests" to analyze power series.
Two neat Tests for convergence
The last lecture discussed the relationship between absolute
convergence and conditional convergence. Today we will begin to study
the two standard "tests" which are used to diagnose absolute
convergence. Both of these tests rely on some relationship with
geometric series. Let me begin with an example.
∑n=0∞(50)n/n!
We met the sequence of individual terms
{(50)n/n!} earlier. We showed that this
specific sequence converges to 0. We did this by looking at what
happens after the 100th term. Then each later sequence term is
less than half the size of the term immediately before it. Eventually
the terms squeeze down and their limit is 0.
But what about the series? Just knowing that the sequence of
individual terms →0 is not enough information to guarantee that
the series, the sum of the terms, is convergent. (That's what the
harmonic series shows!) But look here:
∑n=0∞(50)n/n!=∑n=0100(50)n/n!+∑n=101∞(50)n/n!.
Let's ignore the first big lump -- I don't care how big it is. It
actually doesn't influence whether the series converges or not. The
convergence of the series depends on whether the infinite tail
converges. Look at what can we say here:
50101/(101!)+50102/(102!)+50103/(103!)+...<50101/(101!)+50101/(101!)[1/2]+50101/(101!)[1/2]2+...
We can compare this infinite tail to a certain geometric series which
is larger than it, and this geometric series must converge
because it is a series with ratio 1/2 and 1/2<1.
Why -- what's happening?
The Ratio Test is a way of using the sort of logic that we considered
above. It systematically checks if there is a valid comparison to a
convergent or to a divergent geometric series. Here is the idea.
If we are studying a series ∑an, then we may hope
that somehow an resembles crn, a term of a
geometric series. We further hope that an+1 will
resemble crn+1. But then if the "resemblance" is good
enough, we might hope that the quotient,
an+1/an, will be like
(crn+1)/(crn), and this would be r. This is only
a resemblance, so the textbook actually uses a different letter in its
statement of the Ratio Test. And we put on absolute value signs, since
whether or not a geometric series converges only depends on whether
|r|, the absolute value of the ratio, is less than
1. Etc. So here is a formal statement:
The Ratio Test
Consider the series
∑n=0∞an, and the limit
limn→∞|an+1/an|. Suppose
that this limit exists, and call its value, ρ. (That's supposed to
be the Greek letter rho.) Then:
| If ρ<1, the series converges absolutely and therefore
must converge. |
If ρ>1, the series diverges. |
If ρ=1, the Ratio Test supplies no
information |
Applied to this problem
Let's see what happens when we try to apply this "Test" to the series
∑n=0∞(50)n/n!. Since
an=(50)n/n!, the next term, an+1,
will be (50)n+1/(n+1)!. Try to avoid possibly invalid
shortcuts: just plug in n+1 everywhere that n appears. Then let's consider the absolute value of the ratio:
| 50n+1| 50n+1
| ----- | -----
| (n+1)!| (n+1)! (50n+1)n! 50(n!) 50(n!) 50
|-------| = ------- = ----------- = ------- = ------- = ----
| 50n | 50n (50n)(n+1)! (n+1)! (n+1)n! n+1
| ----- | -----
| n! | n!
Step A Step B Step C Step D Step E Step F
Let me try to describe sort of carefully the various steps. This is
the first example, and I chose it not because it is especially
difficult, but because the sequence of things to do is typical of many
applications of the Ratio Test.
Step A Write |an+1/an|. I really try to
avoid "premature simplification" here. That is, I try to just insert
n+1 for n correctly, and then write things.
Step B In this case, the absolute value signs are not needed
because everything involved is a positive number. This is not always
going to be true!
Step C We have a compound fraction in Step B. I find them
difficult to understand. Life is easier if we convert the compound
fraction into a simple fraction, with one indicated division. So if
you were in class you may have heard me mumbling, "The top of the
bottom times the bottom of the bottom" which is the top of the simple
fraction, and "The bottom of the top times the top of the bottom"
which is the bottom of the simple fraction. O.k.: if you want, use
numerator and denominator instead of top and bottom.
Step D Now I'll start the simplification. Since
50n+1=50n·50, we can cancel
50n from the top and bottom.
Step E Here is possibly the most novel part, algebraically, of
this mess. We need to confront the factorials. (n+1)! is the product
of all the positive integers from n+1 down to 1. Therefore it is the
same as n+1 multiplied by the product of all the positive integers
from n down to 1. Algebraically, this statement is the equation
(n+1)!=(n+1)n!. I want to rewrite (n+1)! so that we can realize the
cancellation of the n!'s.
Step F And here is the result which can be used to compute ρ.
The Ratio Test for
∑n=0∞(50)n/n! leads
us to consider
limn→∞|an+1/an|=limn→∞50/(n+1)=0. So
for this series, ρ=0. Since 0<1, the series converges
absolutely and (using what we did last time) it converges.
I can identify the sum (and you will be able to also after a few more
classes). It is e50. Partial sums of series of this type
are exactly what your calculators use to compute values of the
exponential function.
Another example
Let's consider
∑n=1∞n2/5n. Again,
this is not a casual example. This sort of series occurs in the study
of the statistical properties of certain types of component failures
(it is involved with computing the standard deviation). Here
an is n2/5n and
an+1=(n+1)2/5n+1. So:
| (n+1)2| (n+1)2
| ----- | -----
| 5n+1 | 5n+1 (n+1)25n (n+1)2
|-------| = ------- = --------- = ------
| n2 | n2 n25n+1 n25
| ----- | -----
| 5n | 5n
Well, again I just forget the absolute value signs because the terms
are all positive. I rearrange from a compound fraction to a simple
fraction. I cancel powers of 5. The result I need to consider is
[(n+1)/n]2·(1/5). The core of this is what happens
to (n+1)/n as n→∞. We can use L'Hôpital's Rule since
this is an ∞/∞ case, and get 1/1, so the limit is 1. Or
we can just rewrite, as some students suggested: (n+1)/n=1+(1/n), and
this also →1 as n→∞. In any case, for the series
∑n=1∞n2/5n, we
can compute
limn→∞|an+1/an|=
limn→∞[(n+1)/n]2·(1/5)=1/5=ρ. Since
1/5 is less than 1, the Ratio Test implies that the series converges
absolutely and therefore converges.
The sum can actually be computed and it is 15/32 (really!). I will
show you how to compute this in a few more classes.
|
In all of these examples the terms are
quotients, and essentially we are trying to compare the rates of
growth of the top and the bottom. Exponentials (with a base>1) grow
faster than any polynomial. For example, we could consider the
infinite series
∑n=1∞n20/(1.01)n.
The 20th term in this series is about
2.6·1019. That's B-I-G. Does
this series converge? Well, the Ratio Test applies. If similar algebra
is done, then |an+1/an| becomes
[(n+1)/n]15/1.01 and, when n→∞, the limit is
ρ=1/1.01 which is less than 1, so the series converges
absolutely and therefore converges! I don't think this is obvious:
{con|di}vergence all depends on the
infinite tail -- you can't think about the "first few"
terms. Here is a little more numerical information. If
an=n20/(1.01)n, then
a1,000=4.7·1040 (approximately and this
is even bigger) and a10,000=6.1·1016 and
a100,000=7.3·10–358. The
last term is quite small, and the exponential growth has definitely
surpassed the polynomial growth.
|
And another
We consider
∑n=0∞72n/(n!)2. In
this series we contrast the exponential growth on top with factorial
growth on the bottom. Factorials increase faster (they are
"superexponential"). In this case, some care is needed with the
algebra using the Ratio Test. If
an=72n/(n!)2 then
an+1=72(n+1)/((n+1)!)2. Parentheses
are your friends so use many of them in computations and you likely
will make fewer errors!
| 72(n+1) | 72(n+1)
| -------- | --------
| ((n+1)!)2 | ((n+1)!)2 72(n+1)(n!)2
|-----------| = ---------- = ------------
| 72n | 72n 72n((n+1)!)2
| ------- | -------
| (n!)2 | (n!)2
But 72(n+1)=72n+2=72n72
and so part of that cancels with 72n. Analysis of the factorials can be more confusing, but here it is:
((n+1)!)2=((n+1)n!)2=(n+1)2(n!)2
So part of that is canceled by the (n!)2. Therefore we need
to compute
limn→∞|an+1/an|=limn→∞72/(n+1)2=0=ρ. Since
ρ<1, the series we are considering converges absolutely and
therefore converges.
Again, this is not a "random" series. The sum of
∑n=0∞72n/(n!)2 is
close to a value of a Bessel function, J0(14). The series
for J0(14) is actually
∑n=0∞(–1)n72n/(n!)2. It
has an alternating sign, also. One simple place such functions occur
is in the description of vibrations of circular drums (really!).
The series with alternating signs must also converge, since we just
verified that the series without signs converges since absolute
convergence implies convergence.
Textbook example
The textbook analyzes (Example 4, page 591, section 10.5) what the
Ratio Test tells about the series
∑n=1∞1/n and the series
∑n=1∞1/n2. Please see the
textbook (I did this in detail in class). In both cases the resulting
value of ρ is 1. Notice that one series (the harmonic series, a
p-series with p=1) diverges and the other series (a p-series with
p=2>1) converges. So truly if ρ=1 you can conclude
nothing about the convergence or divergence of the original
series.
It is certainly possible to have series where the limit of
|an+1/an| doesn't even exist, so there isn't
even any ρ to consider. I don't want to give such an example right
now, but you should know that things can be very strange.
For which x's does ...
Here's the question. For which x's does the series
∑n=1∞xn/(3n+n)
converge?
The Ratio Test does work here, but we need to be careful. First, the
bottom is more complicated. And second, certainly the signs of the
terms will vary because x can be negative.
Important facts about absolute value
|A·B|=|A|·|B| but |A|+|B| and |A+B| are not the same if the signs of
A and B differ.
Look: |(–3)7|=|–21|=21 and |–3|·|7|=3·7=21 but
|(–3)+7|=|4|=4 and |–3|+|7|=3+7=10. 10 and 4 are not the same.
If an=xn/(3n+n), then
|an|=|x|n/(n+3n) because the bottom
is always positive (so the signs agree) and the top is an absolute
value of a product of x's, so it becomes a product of absolute values
of x's. And |an+1| is similarly
|x|n+1/(n+1+3n+1). Now we need to analyze the
quotient. I am getting exhausted with all of this typing. I'll skip
the compound fraction and just write the simple fraction which
results:
|x|n+1(n+3n) (n+3n)
-------------- = |x|·---------
|x|n(n+1+3n+1) (n+1+3n+1)
We need to analyze the behavior of the somewhat complicated quotient
(n+3n)/(n+1+3n+1) as n→∞. When we're
done, we need to multiply by |x| in order to get ρ.
Informal analysis Well, as n increases, the polynomial growth
doesn't matter at all. It is negligible compared to the exponential
growth. So really we've got (approximately) just
3n/3n+1, and this is 1/3.
Formal analysis Look at (n+3n)/(n+1+3n+1)
and divide the top and bottom by 3n. The result is
([n/3n]+1)/([n/3n]+[1/3n]+[3n+1/3n])
which is
([n/3n]+1)/([n/3n]+[1/3n]+3). What
about [n/3n] as n→∞? We will use
L'Hôpital's Rule since this is again ∞/∞.
Remember that AB=eB ln(A), so that the
quotient [n/3n]=[n/en ln(3)]. The derivative of
the top (with respect to n) is 1, and the derivative of the bottom
with respect to n is en ln(3)ln(3) (what's in the exponent is just
a constant multiplying n, so the Chain Rule works easily. Therefore by
L'H, limn→∞[n/3n]=
limn→∞[1/en ln(3)ln(3)]=
limn→∞[1/3nln(3)]=0. So (wow!)
limn→∞(n+3n)/(n+1+3n+1)=limn→∞([n/3n]+1)/([n/3n]+[1/3n]+3)=1/3.
 What about the Ratio Test limit? We need to multiply by |x| since we
discarded it to get the fraction we just studied. So in this
complicated case, ρ=|x|(1/3). We get convergence (actually
absolute convergence) when ρ<1, which means that |x|<3. The
x's which satisfy this are an interval from –3 to 3 (not including the
endpoints). We get divergence when |x|>3. So for those x's
satisfying either –∞<x<–3 or 3<x<∞ there is
divergence. The Ratio Test doesn't work if x=3 or if x=–3. It turns
out that this situation is typical, and we will look at more examples
and more detail next time.
What about the Ratio Test limit? We need to multiply by |x| since we
discarded it to get the fraction we just studied. So in this
complicated case, ρ=|x|(1/3). We get convergence (actually
absolute convergence) when ρ<1, which means that |x|<3. The
x's which satisfy this are an interval from –3 to 3 (not including the
endpoints). We get divergence when |x|>3. So for those x's
satisfying either –∞<x<–3 or 3<x<∞ there is
divergence. The Ratio Test doesn't work if x=3 or if x=–3. It turns
out that this situation is typical, and we will look at more examples
and more detail next time.
The Root Test is another result which relies on how a series
resembles a geometric series. We'll discuss this next time.
What happens at the "edges"?
We saw that the Ratio Test doesn't give any information when x=3 or
x=–3. So if we really needed to know what happens, we will need more
work. Look at
∑n=1∞xn/(3n+n)
when x=3. This is
∑n=1∞3n/(3n+n). The
nth term is 3n/(3n+n) and if we
divide the top and bottom by 3n we see that the
nth term is 1/(1+[n/3n]). But we saw that as
n→∞, n/3n→0 so that
an→1. Any series which converges must have its
nth term go to 0. Since this one doesn't, the series must
diverges when x=3. Similarly, if you insert the value –3 for x in the
series, you'll see that the terms do not→0, so the series must
also diverge when x=3.
|
QotD
Use the Ratio Test to verify that
∑n=1∞[22n/{n!(n+1)!}]
converges.
This is also a series which comes up in analyzing the
vibrations of a circular membrane (a drum!). Really. Its approximate
value is 3.87973.
| Monday,
April 6 | (Lecture #19) |
|---|
And now, where and what?
So we discussed series with positive (actually all we needed was
non-negative) terms. The textbook has clean and coherent
statements of the results: the dichotomy, the Comparison Test,
the Limit Comparison Test, and the Integral Test.
The technical meanings of
these terms have been discussed: infinite series; sequence of partial
sums; infinite tails; convergence of an infinite series.
I will repeat the fundamental dichotomy, one of this week's
notable vocabulary words. (And dichotomy means, briefly, "a
division into two, esp. a sharply defined one." As I mentioned in
class, this will be very valuable to you when you repeat your whole
life and must take SAT's again.).
- For a series with positive terms, bounded partial
sums means the same thing as convergence.
- For a series with positive terms, unbounded
partial sums means the same thing as divergence.
Series with terms of varying signs
So now we will complicate things a bit, and look at series whose signs
vary. Let me start really easily but things will get more intricate
rapidly.
( Varying
stop
signs) (These are varying
signs, hah hah hah.)
1–1+1–1+1–...
This is just about the simplest example I could show. We got a formula
for the nth term. We need the sign to alternate, and that
will be given by (–1)something here. The sign will
alternate if the "something here" is either n or n+1. The first
term will be +1 and the second term will be –1 if we use n+1. So an
explicit formula is an=(–1)n+1. Next I asked
about convergences of the series
∑n=1∞(–1)n+1. For this
we must consider the sequence of partial sums.
S1=1; S2=1–1=0;
S3=1–1+1=1; S4=0, etc.
It isn't too difficult to see that Seven integer=0 and
Sodd integer=1. The partial sums flip back and
forth. This is exactly the kind of behavior we did not get when
we considered series with all positive terms. There the partial sums
just traveled "up", to the right. Well, this particular infinite
series does not converge, since the partial sums do not
approach a unique limit.
∑n=1∞(–1)n+1 diverges
even though the sequence of partial sums is bounded.
2–(1{1/2})+(1{1/3})–(1{1/4})-(1{1/5})+...
This is a more complicated series. I suggested that we try to "guess"
a formula by first getting a formula for the sign, and then a formula
for the absolute value (the direction and magnitude, thinking about
numbers as sort of one-dimensional vectors). In this case, the sign is
surely given by (–1)n+1, just as before. The magnitude
or absolute value is
1+{1/n}. The formula {n+1}/n was also suggested, another a good
answer. So putting these together,
an=(–1)n(1+{1/n}). And now we looked at the
{con|di}vergence of ∑n=1∞(–1)n+1(1+{1/n}).
The partial sums are more complicated and more interesting.
S1=2;
S2=2–(1{1/2})–{1/2}=.5;
S3=2–(1{1/2})+{1{1/3})=11/6=1.8333;
S4=2–(1{1/2})+(1{1/3})–(1{1/4})={7/12}=.58333
This is where I stopped in class, but, golly, I have a friend who
could compute S17 either exactly ({4218925/2450448}) or
approximately (1.72169). This is nearly silly. Richard
Hamming, one of the twentieth century's greatest applied
mathematicians, remarked that The
purpose of computing is insight, not numbers.
Let's try to get some insight. Look at the first four partial sums on
the number line.
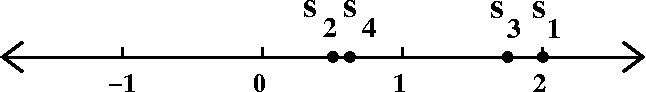
From S1 to S2, we move left since the
second term in the series is negative. From S2 to
S3 we move right, because the third term in the series is
positive. But notice that we don't get to S1. because the
jump right has magnitude 1{1/3} and this is less than 1{1/2}, the
magnitude of the previous jump left.
I hope you are willing to believe that what's described persists in general.
The even partial sums are increasing.
The odd partial sums are decreasing.
All of the even partial sums are less than all of the odd partial sums.
Does this series converge? Students had varied opinions about this,
but the question was definitively settled by the observations of
several clever students. The distance between any odd partial sum and
any even partial sum will be at least 1, since the magnitude of the
nth term is 1{1/n}, which is certainly >1. The
successive partial sums can't get close to each other! But the
collection of partial sums does not approach a unique limit.
∑n=1∞(–1)n+1(1+{1/n})
diverges.
1–1/2+1/3–1/4+1/5–...
Here an has sign (–1)n+1 again, and the absolute
value or magnitude is 1/n. Does ∑n=1∞(–1)n+1(1/n) converge?
The partial sums are more complicated and more interesting.
s1=1;
s2=1–(1/2)–1/2=.5;
s3=1–(1/2)+{1/3)=5/6=.8333;
s4=1–(1/2)+(1/3)–(1/4)=7/12=.58333
Here's a picture of these partial sums. Things are a bit more crowded
(that's good for convergence!) than in the previous picture.
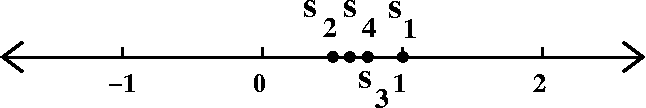
The previous three qualitative properties still hold. Since the signs
alternate, the partial sums wiggle left and right. Since the absolute
values decrease, the odd sums are less than the even sums, and all of
the even sums are less than all of the odd sums. But now the distance
between the odd and even sums→0 since the magnitude of the terms is
1/n, and this→0. So here is a rather subtle phenomenon:
∑n=1∞(–1)n+1(1/n) converges.
The theorem on alternating series (Alternating Series Test)
The following is a major result of section 10.4 of the text, where it
is called the Leibniz Test for Alternating Series.
Hypotheses Suppose that
The terms of a series alternate in sign (+ to – to + etc.).
The absolute value or magnitude of the terms decreases.
The limit of the absolute values of these terms is 0.
Conclusion The series converges.
This is a cute result and useful to analyze some special series. The
most famous example is the alternating harmonic series, ∑j=1∞(–1)n+1(1/n),
which we just saw. There are other examples in the textbook.
Notice that the alternating harmonic series converges but the original
harmonic series with the signs stripped off, ∑n=1∞(1/n), diverges. To me this
is somewhat subtle.
Some partial sums of the
alternating harmonic series |
|---|
S10=0.6456349206
S100=0.6456349206
S1,000=0.6881721793
S10,000=0.6926474305
S100,000=0.6930971829
S1,000,000=0.6931466807 |
Finally, to the right is some "experimental evidence" which might help
you believe that the alternating harmonic series converges.
The sum of the alternating
harmonic series is ln(2). But the convergence is actually incredibly
slow. The one millionth partial sum (which took almost 8 seconds for a
moderately fast PC to compute) only has 5 accurate decimal
digits. This is not the best and fastest way to compute things -- we
will see much faster methods.
|
But what if ...
The sign distribution
of terms in an infinite series could be more
complicated. I suggested that we consider something like
7cos(36n7–2n2)+2sin(55n+88)
∑n=1∞ ---------------------------
2n
Here the sign distribution of the top of the fraction defining
an is quite complicated. These are the first 20 signs:
–1, 1, 1, –1, –1, –1, 1, –1, 1, –1, 1, 1, –1, 1, 1, –1, –1, 1, 1, –1
There's no nice pattern that I can see. The reason for the strange and
truly unpredictable signs is because the positive integers and
multiples of Pi do not nicely relate to one another (Pi is
irrational). I believe that no one in the world can predict this sign
sequence.
Does this series converge?
Please notice that with a few modifications, the corresponding question
can be answered very easily. Look at:
7|cos(36n7–2n2)|+2|sin(55n+88)|
∑n=1∞ --------------------------------
2n
Absolute values signs have been put around the cosine and sine
functions. Now the series has all non-negative terms and we can use
our comparison ideas. How big is the top? Since the values of both
sine and cosince are in [–1,1], the top can't be any bigger than
9. The bottom is 2n. Therefore each term of this series is
at most 9/2n. But this larger series is a geometric series
with ratio 1/2<1 and so it must converge.
Proof via manipulative
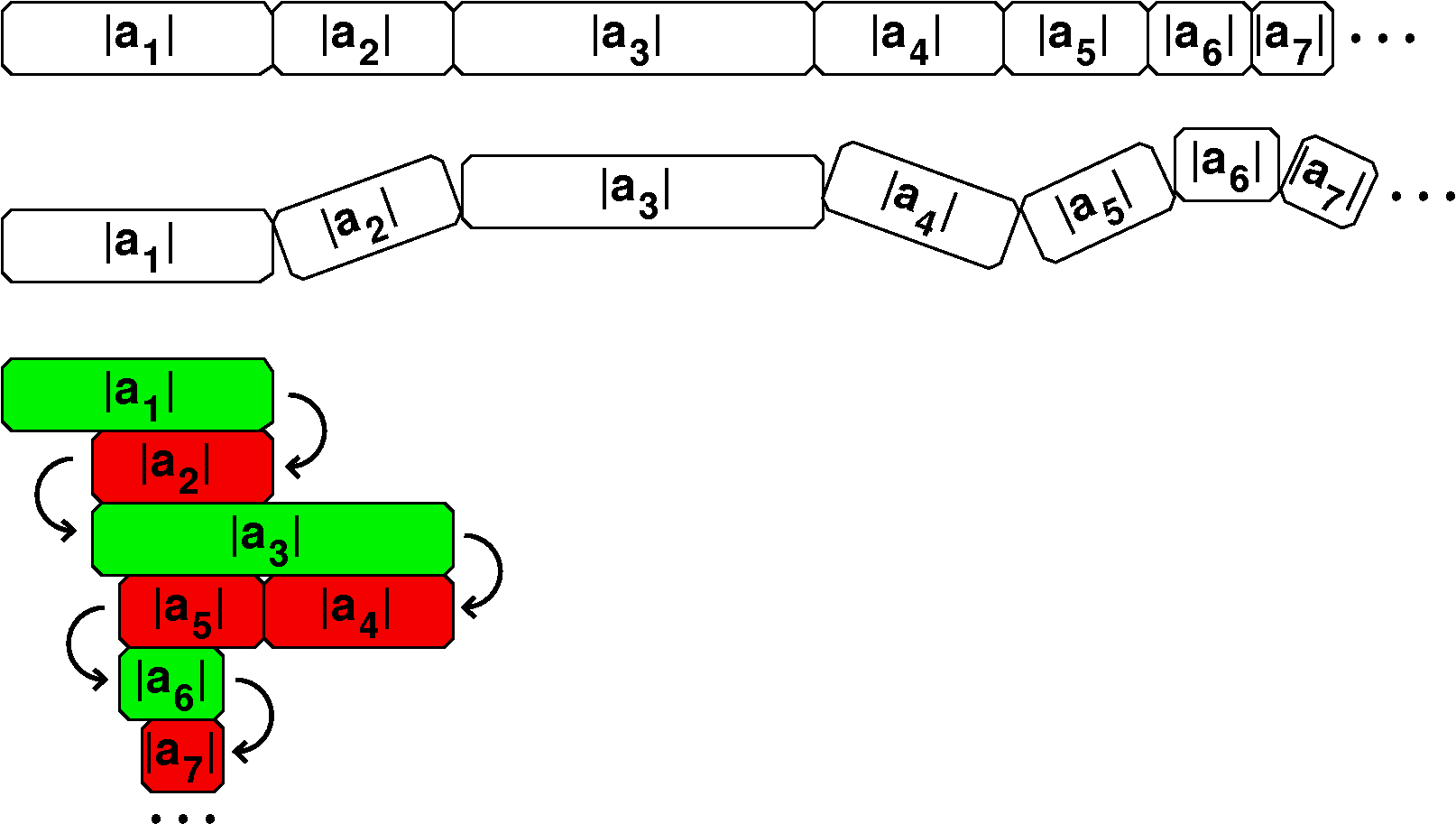 One definition of manipulative (as a noun) is: "In teaching or
learning arithmetic: a physical object which may be manipulated to
help demonstrate a concept or practise an operation."
There was a spectacular demonstration in
class! It was inspired by thinking about old-fashioned folding
carpenter's rulers. If we have an infinite series ∑n=1∞an, we could
consider the associated series ∑n=1∞|an|,
where we have stripped off the signs of the terms, and are just
adding up the magnitudes. This is sort of like an unfolded carpenter's
rule, stretched out as long as possible. It may happen that the series
of absolute values, a series of positive terms, may converge. So when
"the ruler" is stretched out as long as possible, it has finite
length. Well, if we then fold up the ruler, so some segments point
left (negative) and some point right (positive) then the resulting
length will also be finite.
One definition of manipulative (as a noun) is: "In teaching or
learning arithmetic: a physical object which may be manipulated to
help demonstrate a concept or practise an operation."
There was a spectacular demonstration in
class! It was inspired by thinking about old-fashioned folding
carpenter's rulers. If we have an infinite series ∑n=1∞an, we could
consider the associated series ∑n=1∞|an|,
where we have stripped off the signs of the terms, and are just
adding up the magnitudes. This is sort of like an unfolded carpenter's
rule, stretched out as long as possible. It may happen that the series
of absolute values, a series of positive terms, may converge. So when
"the ruler" is stretched out as long as possible, it has finite
length. Well, if we then fold up the ruler, so some segments point
left (negative) and some point right (positive) then the resulting
length will also be finite.
The picture here is an attempt to support this statement and to
duplicate the physical effect of what I displayed in class. The top
has the segments stretched out as far as possible. The next picture
shows some of the segments rotating, aimed backwards (negatively). The
last segment shows in red segments which are negative and in green the
other segments, oriented postively. I hope this makes sense, and
justifies the following:
The "folded" series compared to the "unfolded"
series
If ∑n=1∞|an|
converges, then ∑n=1∞an must converge
also (and, actually, |∑n=1∞an|≤∑n=1∞|an|).
I really screwed up the last part of the
statement of this result in the second lecture. Please read what is
written here -- it is correct. I thank Ms. Zhou for calling this to my attention and
certainly apologize for not writing the result correctly.
Proof via algebra
There is a verification of these statements in the textbook, using
algebra, on p.584, Theorem 1, in section 10.4, if you would like to
read it. Sigh.
And conversely?
Notice that the converse of
the assertion about absolute values and series may not be
correct. That is, a series may converge, and the series of absolute
values of its terms may not. The simplest example, already verified,
used the alternating harmonic series, covergent, and the harmonic
series, divergent.
Vocabulary
A series ∑n=1∞an which has ∑n=1∞|an|
converging is called absolutely convergent. Then the correct
implication above is:
If a series is absolutely convergent, then it is a
convergent series.
A series for which ∑n=1∞an converges and
∑n=1∞|an|
diverges is called conditionally convergent. The alternating
harmonic series is conditionally convergent.
Another example
Consider ∑n=1∞{sin(5n+8)}37/n5. I
don't know very much about {sin(5n+8)}37 except that, for
any n, this is a number inside the interval [–1,1]. Therefore ∑n=1∞|{sin(5n+8)}37/n5| has terms which are all smaller than ∑n=1∞1/n5 (a p-series
with p=5>1, so it must converge). The comparison test asserts that
∑n=1∞|(sin(5n+8)37/n5| converges, and therefore ∑n=1∞{sin(5n+8)}37/n5
itself must be a convergent series.
How to use these ideas quantitatively
What is I actually wanted to find
∑n=1∞{sin(5n+8)}37/n5,
say to an accuracy of +/-.00001? Well, I could split this series up
into SN+TN, a partial sum plus an infinite tail,
and try to select N so that |TN|<.00001. Once I do that, well
then I just (have a computer) compute the corresponding
SN. So how can I get N with |TN|<.00001? Here is
a way.
I know that
TN=∑n=N+1∞{sin(5n+8)}37/n5.
This is an infinite series. I bet (using the result of a preceding paragraph that |TN|=|∑n=N+1∞{sin(5n+8)}37/n5|≤∑n=N+1∞1/n5
again since the biggest that sine can be absolute value is 1, and
137=1. We looked at an
integral comparison technique for this series in the last lecture.
There we learned that this infinite series was less than
∫x=N&infin[1/x5]dx and we can
evaluate the improper integral. It is (see the link for computations!)
exactly 1/[4N4]. If we want this to be less than
.00001=1/105 I guess we could take N to be 13 (I cheated -- I
used a computer). Then the value of the sum, to 5 decimal place
accuracy, is
S13=∑n=113{sin(5n+8)}37/n5
which is .00317. Maybe this specific example isn't too impressive, but
the whole thing really does work in a large number of cases!
|
Given a series, take absolute values
The result just stated is a very powerful and easily used method. If
you "give" me a series with random signs, the first thing I will do is
strip off or discard the signs and try to decide if the series of
positive (non-negative, really) terms converges.
QotD
The question was something like this:
The series ∑n=1∞((6n sin(5n–7)+8)/n17
converges. Explain why!
| Wednesday,
April 1 | (Lecture #18) |
|---|
Where are we? What have we done?
The technical meanings of these terms have been discussed: infinite
series; sequence of partial sums; infinite tails; convergence of an
infinite series.
We spent much of the last lecture discussing the specific example of
the harmonic series, which is
∑n=1∞1/n. This series diverges even though
the sequence of terms, {1/n}, has limit 0.
We also discussed geometric series, in your text written as
c+cr+cr2+cr3+...=∑n=0∞crn–1. This
series converges if |r|<1, and its sum is c/(1–r) then. When
|r|≥1 and c is not 0, the series will diverge.
I made an important comment: I can only
cover what I hope is an overview of several useful examples in each
lecture. I do not believe that the lectures alone give a complete view
of the subject, and certainly the lectures alone are not enough for
exam preparation. Please read the textbook and practice
textbook problems.
The goal in today's lecture
I will show you some very useful (and usable!) techniques to decide if
a series converges, and to approximate (as closely as you want) the
sum of the series. So there will be lots of numbers today.
Series with positive terms
Today we will consider series whose terms are positive or, at worst,
non-negative (≥0). (In the next lecture we'll discuss what happens
if we allow different signs, but for now, only +'s.) What can we say
in general about series with positive (or even just non-negative)
terms? Well, the sequence of partial sums is
increasing, since we're just adding more and more non-negative
terms. What can happen? One thing is that the sequence of partial
sums can tend to ∞ (hey, this is what happens to the infinite
series ∑n=1∞1: the sequence of partial
sums is unbounded and the series diverges). Another
thing that can happen to a positive series is that the sequence of
partial sums can tend to a limit (a non-negative finite limit). This
happens, for example, with positive geometric series with ratio less
than 1. Then the sequence of partial sums is increasing and
also bounded and the series converges. This is a
consequence of the fact that "Bounded monotone sequences converge".
This theoretical alternative is everything.
- For a series with positive terms, bounded partial
sums means the same thing as convergence.
- For a series with positive terms, unbounded
partial sums means the same thing as divergence.
Today's vocabulary word
The principal meaning of the word dichotomy is (according to my online dictionary)
"a division into two, especially a sharply defined one." So what's
above is a dichotomy for series with positive terms.
A first use of comparison
I considered the series
∑n=1∞1/(2n+n). This is a rather
artificial example, and, as far as I know, does not occur in any
interesting "real" application. But we can play with it a bit. So the
first question I'd like to ask is: does this series converge?
One reason I'm starting with a series whose terms are
1/(2n+n) is that these terms are related to the terms of
the harmonic series, which we investigated, and to the geometric
series with ratio 1/2, which we also studied. What do we know?
Well, 1/(2n+n)<1/n always. So the partial sums for
∑n=1∞1/(2n+n) are all less than
the partial sums for ∑n=1∞1/n. The second
series is the harmonic series, and that series diverges and its
partial sums are not bounded: they →∞ as n→∞. So
what information do we get? The partial sums that we want to know
about are less than something which goes to ∞. We get no
information. From this alone, we cannot conclude that the smaller
partial sums are either bounded or unbounded. We need something else.
We also know that 1/(2n+n)<1/2n always. Now
we are comparing the series
∑n=1∞1/(2n+n) with
∑n=1∞1/2n. But this second,
larger series does converge: it is a geometric series with c=1/2 and
r=1/2<1. Its partial sums are bounded (all of them are less than 1,
the sum of the series), and so the smaller partial sums of the series
with terms 1/(2n+n) are also bounded by 1, and therefore
must converge.
It converges!
The series ∑n=1∞1/(2n+n)
converges. We tried two comparisons and only one of these
supplied enough information for a useful conclusion. Frequently
several different approaches need to be tried to hope for useful
information about an infinite series. Your tolerance for frustration
should be high in order to increase your likely success.
The sum is (to 3 decimal places) ...
We know that ∑n=1∞1/(2n+n)
converges. Certainly, since all the terms are positive, I guess the
sum will be positive. Also, since we compared this series to
∑n=1∞1/2n, which has sum=1
(c=1/2 and r=1/2 and c/(1–r)=1), I also guess (no: I actually
know!) that the sum is less than 1. So I know that
0<∑n=1∞1/(2n+n)<1.
This is nice, but if this series occurs as the answer to some
complicated question, we might want to know its sum more
accurately. What if we wanted to know the sum to 3 decimal places
(+/–.001)? This is a modest amount of accuracy. Let me show you
a useful approach.
Well,
∑n=1∞1/(2n+n)=SN+TN
where SN=∑n=1N1/(2n+n)
and TN=∑n=N+1∞1/(2n+n). If we can find
some nice specific value of N so that TN is guaranteed to
be less than .001, then we will know that the corresponding finite
sum, SN, will be within .001 of the true value of the sum
of the whole infinite series. So what can we do? I will
overestimate TN:
TN=∑n=N+1∞1/(2n+n)<∑n=N+1∞1/2n.
I choose the larger series to be one whose sum I can find easily. I
just want some sort of answer -- I don't necessarily need the best
answer, just some answer. Well,
∑n=N+1∞1/2n is a geometric
series. Be a bit careful in deducing c and r here, please. The first
term, c, is 1/2N+1. I get this by looking at the "lower
bound" in the ∑. The ratio between successive terms, r, is 1/2. So
the sum of this overestimate is
c/(1–r)=[1/2N+1]/(1–1/2)=[1/2N+1]/(1/2)=[2/2N+1]/(2/2)=1/2N.
Do the algebra slowly and try not to make errors. This is how I would
do this problem if I only had to make such estimates once in a
while. If I needed to do this four or five times a day, well, heck,
there are more systematic approaches. Well, what do we know? The
infinite tail, TN, which we want to estimate, is positive
and less than 1/2N. If we want TN<.001, then
we can force it to be less by choosing N so that
1/2N<.001. Let's see: when N=10, I think we saw that
1/210=1/(1,024)<.001=1/(1,000).
Therefore
S10=∑n=1101/(2n+n) will
be within .001 of the "true value" of the sum of the whole series. It
is easy for a computer or calculator to find this partial sum. It is
.696.
Comparison Test
The Comparison Test applies to series with positive (or non-negative)
terms. We have the following situation:
Suppose we know that 0<an≤bn for all n's.
If ∑n=1∞bn converges, then ∑n=1∞an converges.
If ∑n=1∞an diverges, then
∑n=1∞bn diverges.
No information is obtained if we know only either that the smaller
series converges or the larger series diverges.
So convergence is "inherited" downward and divergence is "inherited"
upward.
Another trick
There are two major tricks in the subject, and these two major tricks,
in practice, handle about 99% of the examples that come up. One trick
is comparison with geometric series, as we have just done. Here is a
version of the other trick.
What can we say about the series
1+1/25+1/35+1/45+...=∑n=1∞1/n5?
This is a different kind of series. This is not a geometric
series. The ratio connecting the first and the second terms is
1/32. The ratio between the second and third terms is 32/243. Since
these numbers are not equal, this is not a geometric series. We need a
different trick.
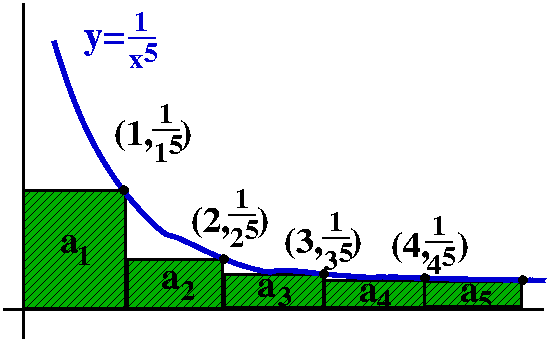 Comparison to a definite integral
Comparison to a definite integral
Here is the trick. If an=1/n5, think of this
quantity as an area of a rectangle whose width is 1 and whose height
is 1/n5. Put this rectangle on the xy-plane so that its
upper righthand corner is at the point (n,1/n5). The
rectangles will all fit together as shown in the graph to the
right. The corners are all on the curve y=1/x5. Everything
is arranged so things work. Now look: the improper integral
∫x=1∞[1/x5]dx is larger than
a2+a3+a4+... . I left out
a1 because I don't want to integrate all the way to 0,
since there is a different improperness there -- I just want to deal
with the improperness at ∞. But look:
∫x=1∞[1/x5]dx=limA→∞∫x=1x=A[1/x5]dx=limA→–1/4x4|x=1x=A=limA→∞(–1/4A4)–(–1/4)=1/4. (Whew!)
Integrals are frequently easier to compute than sums. As far as I
know, no one in the world knows either the true value of the sum of
this infinite series or a good representation of its partial sums (and
this series does occur in applications!). So what do we know? Don't
forget, please, the initial term, a1=1. We know that
∑n=1∞1/n5<1+∫x=1∞[1/x5]dx=5/4.
It converges!
The partial sums are all bounded above by 5/4. Since
∑n=1∞1/n5 is a series of
positive terms, bounded above is enough to imply that the series
converges. The series converges and its sum is some positive number
less than 5/4.
The sum is (to 3 decimal places) ...
Suppose I want the sum of this series to 3 decimal places. Then, just
as before, I will write
∑n=1∞1/n5=SN+TN,
where SN=∑n=1N1/n5 and
TN=∑n=N+1∞1/n5. I
will try to overestimate the infinite tail, TN, by
something convenient, and then force it to be less than .001.
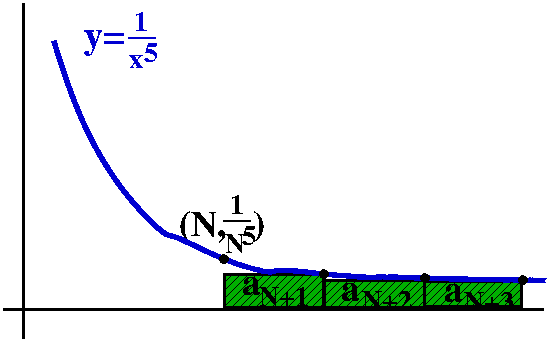 Here is how to overestimate this TN. Look at the picture to
the right. The curve y=1/x5 is again there, and I am
interested in what happens for x's bigger than N. I put the boxes
representing TN (remember, this starts with
1/(N+1)5) under this portion of the curve. So (very very
tricky!) I can make this estimate:
Here is how to overestimate this TN. Look at the picture to
the right. The curve y=1/x5 is again there, and I am
interested in what happens for x's bigger than N. I put the boxes
representing TN (remember, this starts with
1/(N+1)5) under this portion of the curve. So (very very
tricky!) I can make this estimate:
TN<∫x=N∞[1/x5]dx=limA→∞∫x=Nx=A[1/x5]dx=ETC.=1/[4N4].
I skipped some steps in the evaluation of the improper integral
because it is about the same as the previous computation. Now I want
to select N so that 1/[4N4]<.001. We decided if N=4,
then 1/[4(44)]=1/(1,024)<1/1,000. So the fourth infinite
tail will be less than one one-thousandth. And if we want the sum of
the series to 3 decimal places, we just need to compute
S4=∑n=141/n5 which is
easy for a machine (or is even tolerable by hand, really). The value
is 1.036 so that the sum of the series with error +/–.001 is
1.036.
By the way, every time I use this technique, I draw the pictures I've
shown here and wrote in class. I don't do this often enough to have it
"mechanized", so I need to remind myself how it works.
p-series in general
The other collection of examples you need to know are the p-series.
Suppose p is a positive number. Then the p-series is
∑n=1∞1/np=1+1/2p+1/3p+1/4p+.... This
series converges if p>1 and diverges if p<1. The reason that
this is true is the Integral Test which I will write later, but PLEASE read the textbook about this --
there's not enough lecture time to discuss everything. Please note
that the p-series is not a geometric series!
We just discussed the p-series for p=5. It converged. Last time we
considered p=1, which is the harmonic series, and saw that it
diverged. Let me investigate yet another example of a divergent
p-series.
A divergent series
Take p=1/2. The p-series is
1+1/sqrt(2)+1/sqrt(3)+1/sqrt(4)+1/sqrt(5)+... and, according to what
was written above, this series diverges. It diverges even
though the terms get very small, because they don't get small enough
fast enough. But if it diverges, there should be some partial sum
which is bigger than 100. I would like to find a specific partial sum
bigger than 100. Numerical questions like this actually arise in real
applications, and an integral technique can be used to answer them
without much difficulty.
 A partial sum bigger than 100
A partial sum bigger than 100
The idea is the same and the idea is different. I'm sorry for writing
such a silly sentence, but this sort of is the truth. Look at
this picture. I have sketched y=1/sqrt(x). Since what I want is to
underestimate SN I have placed the boxes over the
curve. Then the upper left-hand corners of the boxes are on the
curve. And to get all of the area representing SN over the
curve, I will need to integrate from 1 to N+1. I don't think this is
obvious or easy, but please look at the picture.
The estimate the picture implies is
∫x=1x=N+1[1/sqrt(x)]dx<SN. Now I
can "easily" compute this integral (well, more easily than I can
compute the partial sum!). Here:
∫x=1x=N+1[1/sqrt(x)]dx=2sqrt(x)|x=1x=N+1=2sqrt(N+1)–2sqrt(1)=2sqrt(N+1)–2.
This is an underestimate of SN. If I want to force
SN to be at least 100, then this will be done if I know
that 2sqrt(N+1)–2≥100 or sqrt(N+1)–1≥50 or sqrt(N+1)≥51 or
(sigh!) N+1≥512=2601. So N should be at least
2600. Some computed partial sums are listed below.
| N |
10 | 100 | 1,000 | 2,000 | 2,500 | 2,600 |
|---|
| SN | 5.02 | 18.59 | 61.80 | 87.99 | 98.55 | 100.53 |
I was amused when I computed these numbers slightly before class
because I didn't expect things to be so close. Usually the estimates
gotten with these methods are fairly rough. What matters is that the
method works -- it is effective, and usually easy to do.
The Integral Test
The textbook discusses the Integral Test in section 10.3.
PLEASE read the textbook! Here
is a version.
Suppose f(x) is a positive decreasing function, defined for
x≥1. Then the series ∑n=1∞f(n)
converges exactly when the improper integral
∫1∞f(x) dx converges.
|
QotD
Does ∑n=1∞1/(n2n) converge? (This is
problem #19 in section 10.3 of the textbook.)
Solution Since 0≤1/(n2n)≤1/2n for
all positive integer n, and since
∑n=1∞1/2n converges
(geometric series with absolute value of ratio equal to 1/2, less than
1) the series ∑n=1∞1/(n2n)
must converge by the comparison test.
Here is a bit of a "dialog" from Maple. The first response shows that the
program recognizes and can find the sums of (at least simple)
geometric series. The second response, which just echoes the question,
shows that the program can't automatically find a sum for the first
series we investigated in this lecture.> sum(1/2^n,n=1..infinity);
1
> sum(1/(2^n+n),n=1..infinity);
infinity
-----
\ 1
) ------
/ n
----- 2 + n
n =
1 |
| Monday,
March 30 | (Lecture #17) |
|---|
A recursive sequence
Many sequences that occur in applications are not defined by explicit
formulas (Newton's method, for example). Here is a simple example of a
sequence which is defined recursively -- that is, members of
the sequence are defined in terms of previous elements of the
sequence. (Again, my example is not random. I didn't have time to explain where it came from in class, but I will try to here.)
a1=1 and an+1=sqrt(an+5) for n>1.
So a2=sqrt(1+5)=sqrt(6). And
a3=sqrt(sqrt(6)+5). Etc. Here I don't know if this sort of
numerical computation helps much, but look at the first seven terms:
1, 2.449489743, 2.729375339, 2.780175415, 2.789296581, 2.790931132,
2.791223949. This is quite suggestive.
What can we see ...
A first observation Certainly I believe that the elements of
this sequence are all positive. We are adding 5 and taking square root
(remember that sqrt means non-negative square root here!). Also, I am
fairly sure that the terms in this sequence are all less than 100
(here 100 is really just a random bound). How do I know this? Well,
the first few are less than 100 (the numbers above). And if
an<100, then an+5<100+5=105, so that
sqrt(an+5)<sqrt(105). But the left-hand number is
an+1 and that is less than sqrt(105), which is less than
100. So I have proved that all of the an's are
between 0 and 100. That's not enough to conclude convergence, as we
saw with earlier simpler examples. Sequences can wiggle. But
this sequence does not wiggle.
A second observation Look a bit more closely at the terms I
computed above. They seem to increase. Is that an accident? Well, if I
know that an<an+1 then I can add 5 to both
sides and get an+5<an+1+5. Also square
rooting is increasing (remember the graph!) so that
sqrt(an+5)<sqrt(an+1+5). But this inequality
is exactly an+1<an+2. So increasingness is
inherited by later terms of the sequence. Since I know the sequence in
increasing for the beginning terms of the sequence because of the
computations above, I know that the sequence will always be
increasing.
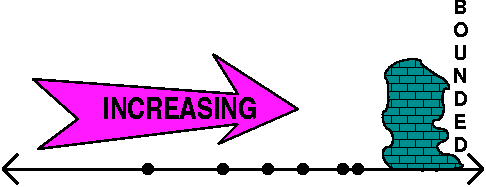 What happens?
What happens?
In this specific case we have an increasing sequence which is
bounded. But increasing bounded sequences converge because they
can't wiggle, and they can't (since they are bounded) jump out to
"infinity". The sequence {an} defined above is an
increasing bounded sequence, and it must converge. The sequence must
"pile up" somewhere less than the bound. (A similar result is also
true for decreasing bounded sequences -- please see the textbook. This
fact is not supposed to be obvious!)
Its limit
Once I know that the sequence converges, I can use the equation
an+1=sqrt(an+5) to find the limit quite nicely.
So if I know that limn→∞an=L then certainly (since {an+1}
is just about the same sequence, the numbers are all shoved along one
place) I know that limn→∞an+1 is L also. So look:
If an+1=sqrt(an+5) take
limn→∞. The result is L=sqrt(L+5). Square both
sides, so L2=L+5. Then L2–L–5=0. And (quadratic
formula) L=[1+/–sqrt((–1)2–4(1)(–5))]/2, and this is
1/2+/–sqrt(21)/2. Which root? As several students pointed out, the
terms are positive, so take +, and the limit is 1/2+sqrt(21)/2. This
is approximately 2.791287848 (close to the terms we computed above).
Where the recursive sequence came from
To the right is a computer-drawn graph (therefore we suppose it is
quite accurate!) of y=x and y=sqrt(x+5) on the interval [–5,3].
Please notice that the graphs intersect at one point in the first
quadrant. That point has coordinates (L,L) and is a point where
sqrt(L+5)=L.
| 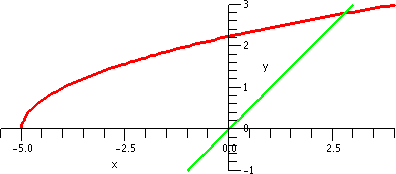 |
Now look at the picture below!
Start at 1 on the x-axis
and go up until we hit the curve. That will be at the point
(1,sqrt(1+5)) which is (1,sqrt(6)). Then move right until we hit the
line. That will be at (sqrt(6),sqrt(6)). Then up and hit the curve at
(sqrt(6),sqrt(sqrt(6)+5)), ETC. We move
back and forth, sort of bouncing between the curves. If you look at
the picture you will see that the points "accumulate" where the curves
intersect, and (L,L) is that point. This "silly" picture is actually a
simple version of a numerical method used to find roots.
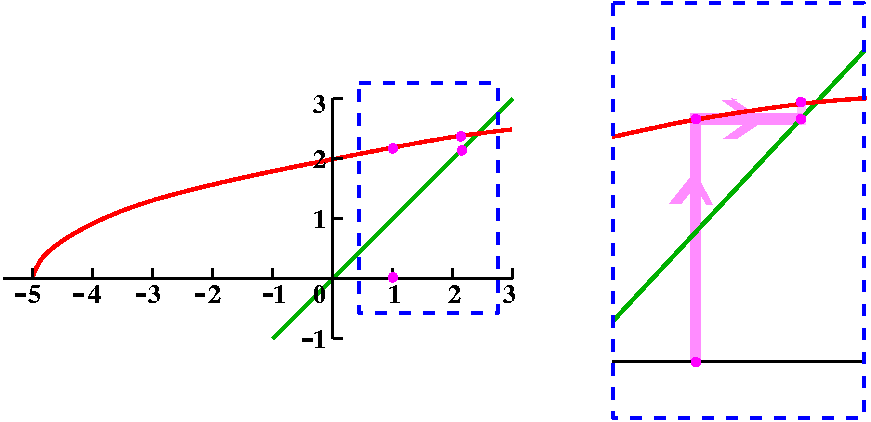
Don't trust numbers always!
O.k., I will throw some numbers at you. If you consider the sequence
{1+[1/n]} then 10-digit decimal approximations of the first 7 terms
are:
2., 1.500000000, 1.333333333, 1.250000000, 1.200000000, 1.166666667,
1.142857143
This doesn't look bad. And I bet that this sequence converges, and its
limit is 1: limn→∞(1+[1/n])=1. Fine.
I have a simple formula for another sequence. Here are the 10-digit
decimal approximations of the first 7 terms:
2.000000000, 1.500000000, 1.333333333, 1.250000001, 1.200000003,
1.166666675, 1.142857160
This looks just about the same as the first sequence, just a little
bit of fuzz in the bottom few digits. Well, the 1,000th
term in this sequence, a1,000, is approximately
2·10435. Here is the formula:
an=(1/n)+e[.000000000001]n5). This
sequence grows really really quickly after a while (it is positive const multiplied by
n5 inside the exponential function). So a few terms may not
give very much information at all about asymptotics.
|
What are series?
Most of these phrases are quotes from the text. I'm also making a
definite effort to use the notation in the text. So here we go:
An infinite series "is an
expression of the form
∑n=1∞an=a1+a2+a3+..."
Discussion This is a very strange concept, and you should
realize just how strange it is. I don't know any person or computer or
thing which could actually add up infinitely many numbers. I do
know people and machines which could add, approximately or in certain
cases, exactly, lots and lots (but finitely many!) numbers. So
whatever you believe, the infinite series expression above is just
some sort of symbolic "stuff" that needs to be correctly
interpreted. It doesn't and can't literally mean, o.k., this is what
you get when you add up all these numbers. That is just silly. Also, I
should mention that in, say, Math 151, and even in this course, I have
generally avoided using sigmas, that is,
∑'s, as an abbreviation for summation. I was trying to be
gentle. Starting now I won't be so careful, because we'll be doing
lots of things with summations, and the correct use of summation
notation will just save a great deal of writing. Please ask questions
if the notation becomes horribly intricate.
There are actually two different sequences which people naturally
associate with each infinite series,
∑n=1∞an. The situation can be
confusing. One sequence is just the sequence of
individual terms in the infinite series. This is
{an}. This sequence by itself is rarely of huge interest in
this context. The sequence which is of interest is
the sequence of partial sums. So I need to define partial
sums. Well, here are some of them:
S1=a1
S2=a1+a2
S3=a1+a2+a3
S4=a1+a2+a3+a4
S4=a1+a2+a3+a4+a5
ETC.
I don't think that "ETC." is very
clear, so I'd better tell you precisely what SN is:
SN=∑n=1Nan
(the sum of the first N terms of the infinite series).
This is the Nth partial sum. I hope you can see why this is
called a partial sum. It is the sum of what some people call an
initial segment of the infinite series. The
sequence of partial sums is then the sequence
{SN}. (The little n's are concealed inside the
SN's as a summation index.)
The sequence of partial sums may or may not
converge. If the sequence of partial sums converges,
then we say that the infinite series
converges and the limit of the sequence of partial sums is
called the sum of the infinite
series.
Metaphor?
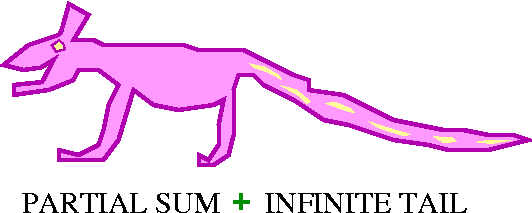 An infinite series ∑n=1∞an can
be thought of as ∑n=1Nan+∑n=N+1∞an. So
there is the Nth partial sum plus the "other" terms of the
series, an infinite tail. These other terms I may sometimes call
TN. I like to think of this maybe as some sort of
animal. The partial sum is the body, and the infinite tail is
... well, the tail. The question of whether the series converges or
not maybe is analogous to whether the whole weight of the animal is
finite (this is a good analogy only for series whose terms are all
positive -- we will deal later with series whose terms change
sign). The weight will be finite exactly when the infinite
tails→0 as n→∞. In fact, the first "few" terms of a
series have
nothing to do with convergence! You can change them, and the
convergence of the series won't change at all. (If the series
converges, the sum will change, but whether or not the series
converges won't be changed.)
An infinite series ∑n=1∞an can
be thought of as ∑n=1Nan+∑n=N+1∞an. So
there is the Nth partial sum plus the "other" terms of the
series, an infinite tail. These other terms I may sometimes call
TN. I like to think of this maybe as some sort of
animal. The partial sum is the body, and the infinite tail is
... well, the tail. The question of whether the series converges or
not maybe is analogous to whether the whole weight of the animal is
finite (this is a good analogy only for series whose terms are all
positive -- we will deal later with series whose terms change
sign). The weight will be finite exactly when the infinite
tails→0 as n→∞. In fact, the first "few" terms of a
series have
nothing to do with convergence! You can change them, and the
convergence of the series won't change at all. (If the series
converges, the sum will change, but whether or not the series
converges won't be changed.)
|
Maybe the simplest example
If all of the an's are 1, then the infinite series is
1+1+1+1+1+... and the partial sums are, well: S1=1 and
S2=1+1=2 and S3=1+1+1=3 and ... well, I hope you
are convinced that SN=N. The sequence {N} does not
converge, so the infinite series 1+1+1+1+1+... diverges.
A simple and very deceptive example
As I mentioned in class, in this lecture my instructional strategy is
the reverse of what I did last time. I will present as my first
example something which is notorious and defies intuition. It is a
very famous infinite series.
The harmonic series is the infinite
series ∑n=1∞1/n. Sometimes we might write
this series as 1+1/2+1/3+1/4+... and the "..." is supposed to
indicate, hey, you know the pattern, you understand the formula,
etc. There are examples of infinite series where I certainly don't
instantly "see" what ... means for those series. The harmonic series
occurs in many physical applications, and also arises in analyzing
lots of computer algorithms.
The sequence of the individual terms, {1/n}, isn't very
complicated. It was one of our first sequence examples.
The important question here is to understand the partial sums. Well,
S1=1 and S2=1+1/2=3/2 and
S3=1+1/2+1/3=11/6. This isn't helping. There is
no known explicit formula for the partial sums of this series.
I found decimal approximations for a bunch of partial sums. Look at
the table to the right, please.
| N | SN |
|---|
| 1 | 1.00000 |
| 2 | 1.50000 |
| 3 | 1.83333 |
| 10 | 2.92897 |
| 100 | 5.18738 |
| 1,000 | 7.48547 |
| 10,000 | 9.78761 |
| 100,000 | 12.09015 |
| 1,000,000 | 14.37273 |
I emphasize that I know no simple shortcut for actually
computing these darn numbers. The decimal approximations above were
the result of lots of divisions and additions (an unreliable timing of
the S1,000,000 computation is about 5 seconds). Just so you
know what the heck these numbers mean, what would
S1,000,001 be compared to the last table entry? Well,
S1,000,001=∑n=11,000,0011/n=(∑n=11,000,0001/n)+(1/1,000,001)=S1,000,000+(1/1,000,001). Whew!
Here are the actual (now 10-digit because the result wouldn't be
observable in 5 digits!) approximations:
S1,000,000=14.39272672 and
S1,000,001=14.39272772. They are different!
So what happens?
What can we conclude about the convergence of this series? The serious
answer is nothing. We have weighed the body, Ssome
numbers, but we have no idea what the size of Tthese
numbers is: the "infinite tail" might be very thin (hey, less
than 1/1,000,000) but it is very very long. Several ideas may occur.
|
Primitive idea #1
It diverges because we're adding up infinitely many numbers, and
therefore things get to be too darn large.
|
Primitive idea #2
It converges because, although we're adding lots of numbers, the
steps between the sums get smaller and smaller, so the sum
can't get very large.
|
A simple argument
The numbers above are, ultimately, not very persuasive. But let me
show you an elementary argument which will allow us to make a good
decision. Please realize that this is a very clever argument!
We first realized that the partial sums of the harmonic series were
all positive and they were increasing:
SN<SN+1. I will just look at some special
partial sums.
I wrote these lines on the board:
S1=1=2/2
S2=1+1/2=3/2
S4=1+1/2+1/3+1/4>1+1/2+(1/4+1/4)=1+1/2+2(1/4)=4/2
S8=1+1/2+1/3+1/4+1/5+1/6+1/7+1/8>1+1/2+(1/4+1/4)+(1/8+1/8+1/8+1/8)=1+1/2+2(1/4)+4(1/8)=5/2
Of course, in class (here is a reason to attend the lectures!) this
was done sort of interactively. At this point I stopped and asked
people what was the next line I should write. There was some
conversation and this was produced as a result:
S16=1+1/2+1/3+1/4+1/5+1/6+1/7+1/8
+1/9+1/10+1/11+1/12+1/13+1/14+1/15+1/16
>1+1/2+(1/4+1/4)+(1/8+1/8+1/8+1/8)+(1/16+1/16+1/16+1/16+1/16+1/16+1/16+1/16)
>=1+1/2+2(1/4)+4(1/8)+8(1/16)=6/2
We can group the partial sums when N is a power of 2. Here is the
general result: S2k>=(k+2)/2. For example, I
asked if we could give one specific partial sum which would be larger
than 100. Uhhhh ... if we took k=200, then (k+2)/2=101, larger than
100. So S2200 is bigger than 100.
How long would it take to add up this sort of partial
sum? Well, 2200 is a large number. It is about
1.6·1060. And, let's see, I would hope I could do
about 1011 additions and divisions in a second (that is an
overestimate). And there are about 1/3 of 108 seconds in a
year. So there would be maybe 1/3 of 1019 additions and
divisions in a year. The age of the universe is sometimes estimated to
be about 20 billion years, or 2·1010 years. So
... in one "universe age" we could compute maybe
2/3·1029 terms (this is a cruddy computational
model, by the way). So all we would need is about ... uhhh
... 1031 universe ages. This sort of exercise is useful if
it convinces you that computing some big partial sum is
silly.
Therefore ...
Does the harmonic series converge? If it did converge, then eventually
the partial sums would have to get close to a limit. But the estimate
we have just seen shows that the partial sums get bigger and bigger
and bigger. So the harmonic series diverges.
The discussion above is very special. We'll get a number of general
tricks within a few lectures which can be used to show divergence
rapidly. I just want to give you a reason for the divergence
result. For the harmonic series, the infinite tail is very thin, but
it is really really very long! Intuition?
Another kind of series
Let me turn to a series that behaves the way we'd like. A geometric
series is one where successive terms are related by a constant
ratio. In algebraic language, the text writes such a series as
c+cr+cr2+cr3+...=∑n=1∞crn–1.
Actually, I just noticed that the text writes this as ∑n=0∞crn, so the exponent
looks more normal but the index of summation begins with n=0. But I'll
continue with the way I actually did it in class.
An (exceptional!) explicit formula of a partial sum
The partial sum of this series is
SN=∑n=1Ncrn–1. Unlike
almost any other series, it is possible to find an explicit formula
for this SN. Here is the idea, which I think is usually
shown in some high school (and maybe even some middle school!) math or
physics courses:
SN=c+cr+cr2+cr3+...+crN
Multiply by r:
rSN=cr+cr2+cr3+cr4+...+crN+1
Subtract the second equation from the first:
SN–rSN=c+(all the inside terms
cancel!)–crN+1
Factor the left-hand side:
(1–r)SN=c–crN+1.
Now solve for SN: if r is not equal to 1,
SN=[(c–crN+1)/(1–r)].
Convergent geometric series
Now if |r|<1, powers of r, that is, the sequence {rn},
must approach 0. So in the formula for SN, when |r|<1, I
know that rN+1→0 and SN→c/(1–r). When
|r|>1, the series diverges (the powers of r grow).
If |r|<1, then the geometric series with first term c and ratio
between successive terms r,
∑n=1∞crn–1, converges, and its
sum is c/(1–r).
Example #1
Here is something which I hoped that many people saw before
college. The infinite repeating decimal 0.731731731...
represents a rational number (a quotient of integers). What rational
number does it represent?
Here the most interesting problem is recognizing the implied geometric
series. Decimal notation is very clever and conceals some true
subtleties. So 0.731 itself means 731·(.001) which is
731/1000. What about 0.000731? This is 731·(.000001) which is
731·(.001)·(.001). That is,
10–3·10–3=10–6. Therefore
0.000731 is 731/(1000)2. And similarly
0.000000731 is 731/(1000)3. So we see (maybe not so
"clearly"!) that:
0.731731731...=[731/1000]+[731/(1000)2]+731/(1000)3]+....
We therefore recognize that the repeating decimal indicates an
infinite series whose first term, c=731/1000, and whose constant ratio
between successive terms is r=1/1000 (this is certainly less than 1).
The sum is then
c/(1–r)=[731/1000]/(1–[1/1000])=[731/1000]/[999/1000]=731/1000.
Digression: how maybe this is done in earlier "grades"
A teacher might say the following:
Consider Q=0.731731731... and try to
figure out another way of looking at Q. Well,
1,000Q=(1,000)·(0.731731731...)=731.731731731...
so then:
1,000Q=731.731731731... and subtract
Q=0.731731731...
The result is 999Q=731, so that Q=731/999. Ain't that nice! My
"excuse" for pointing out the geometric series approach is that I want
to show you a use of geometric series, and also to maybe expose a bit
of the structure of the decimal system, which is actually a very
clever and intricate idea.
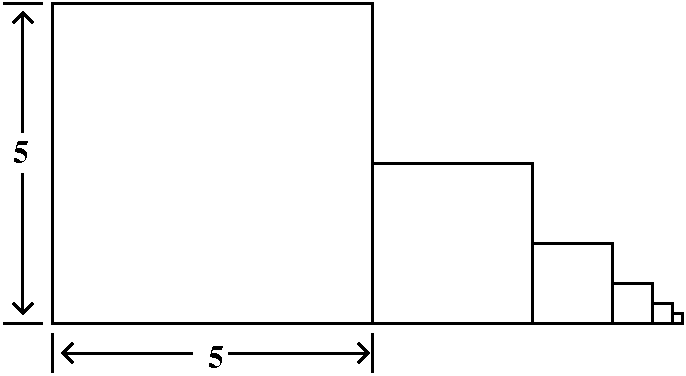 Example #2
Example #2
A square of side length 5 has another square whose side length is half
of that, placed outside but so that corners and an edge
coincide. Another square whose side length is half of that, placed
outside of both squares but so that corners and an edge coincide. And
...
My language is perhaps not too precise. A sort of picture of this
object (just the first 6 squares) is
shown to the right. The object is an example of a fractal. General
information about fractals is here and a source
which is very accessible is here.
The question What is the total area of all of the squares?
| The first square has area
5·5=52. |
The second square has area
(5/2)·(5/2)=52/4. |
The third square has area (5/2/2)·(5/2/2)=(5/22)·(5/22)=52/42 |
|---|
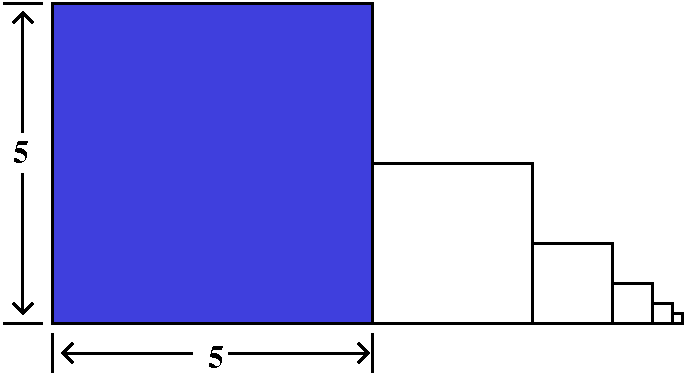 |
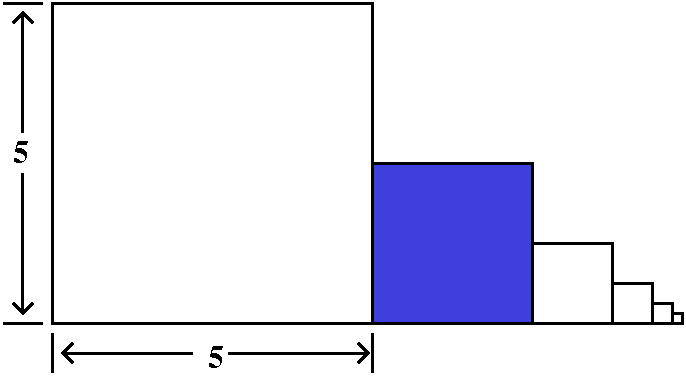 |
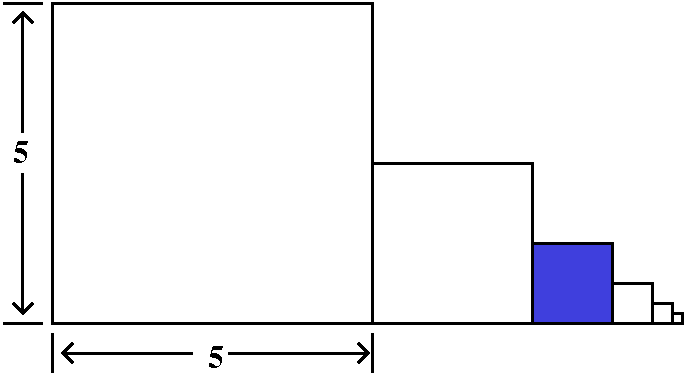 |
The pattern may convince you that the total area is the sum of
52+52/4+52/42+...
This is a geometric series whose first term is c=52, and the
constant ratio between successive terms is r=1/4. The sum is then
c/(1–r)=52/(1–[1/4])=100/3. This is the total area.
Questions about some other geometric quantities involving these
squares can be asked. For example,
The question What is the total perimeter of all of the squares?
| The first square has perimeter
4·5=20. |
The second square has perimeter
4·(5/2)=20/2. |
The third square has perimeter 4·(5/2/2)=4·(5/22)=20/22 |
|---|
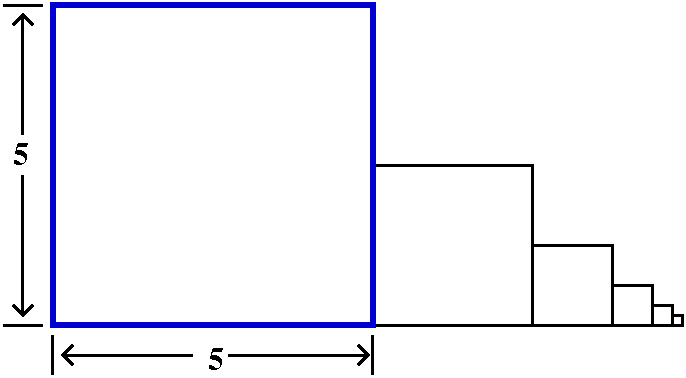 |
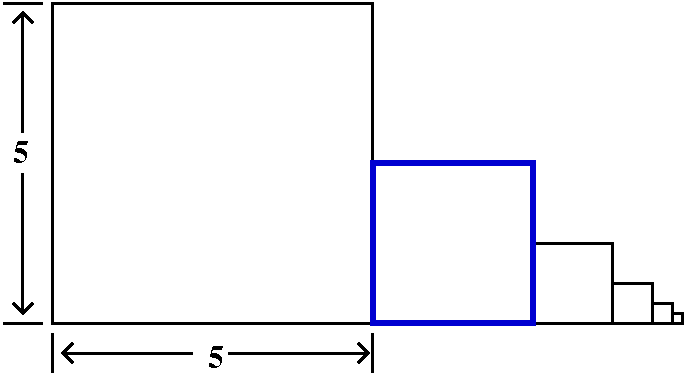 |
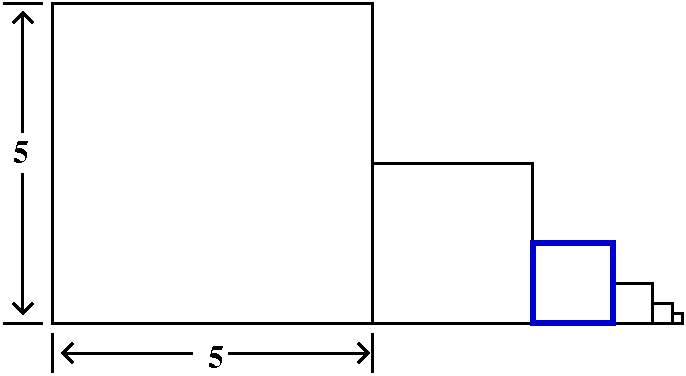 |
The pattern may convince you that the total perimeter is the sum of
20+20/2+20/22+...
This is a geometric series whose first term is a=20, and the
constant ratio between successive terms is r=1/2. The sum is then
a/(1–r)=20/(1–[1/2])=40. This is the total perimeter.
|
Example #3
Bruno and Igor have a loaf of bread. Bruno eats half the loaf and
passes what remains to Igor. Igor eats half of what he is given and
passes what remains to Bruno. Bruno eats half of what he is given and
passes what remains to Igor. Igor eats half of what he is given and
passes what remains to Bruno...
The question How much bread (the total amount) does Bruno eat?
As I mentioned in class, I know people who can somehow "solve" these
problems by inspection, that is, they read or listen to the problem,
and ZAP!!! the answer is
clear. (The same is true for the geometric problems mentioned
just previously.) I am not one of these "zap" people -- some of the students
seem to be! I would probably solve the problem by computing the amount
of bread Bruno and Igor eat, for at least a few rounds. I would try to
discover the pattern, and then I'd use this discovered pattern.
| Round # | Bruno eats | Igor eats |
|---|
| 1 | 1/2 | 1/4 |
| 2 | 1/8 | 1/16 |
| 3 | 1/32 | 1/64 |
I filled out this table dynamically in class, with explanations being
given as I did it. For example, I remarked that after Bruno ate half
the loaf, Igor would receive the other half loaf. Igor would eat half
of that, which is 1/4 loaf, and pass 1/4 loaf to Bruno. Bruno would
eat half of a 1/4, which is 1/8 loaf, and pass the remaining 1/8 loaf
to Igor, etc. It seems apparent ("clear") that Bruno eats
1/2+1/8+1/32+..., a quantity which we recognize as a geometric
series. The first term, c, is 1/2, and the constant ratio between
successive terms is 1/4. Therefore Bruno must eat
c/(1–r)=(1/2)/(1–[1/4])=2/3 of the loaf. Poor Igor will
eat 1–2/3=1/3 of the loaf. (Or you could compute what Igor eats
directly as the sum of another geometric series.)
It is easy to change this problem. You could imagine the named people
eating different quantities, or you could imagine there being more
people, etc. Sums like this do arise in real applications, and I hope
that you will be able to recognize them and cope with them.
QotD
Is the harmonic series 1+1/2+1/3+1/4+... a geometric series?
If your answer is YES, then you must supply me with the correct
values of the parameters c and r which will give the harmonic
series.
If your answer is NO, then you should give some specific fact
about the harmonic series which explains why it is not a
geometric series.
Answer
The answer is NO. If the harmonic series were
c+cr+cr2+... then (using just the initial segment
1+1/2+1/3) we see that r=cr/c=(1/2)/1=1/2 and
r=(cr2/cr)=(1/3)/(1/2)=2/3. Since 1/2 is not 2/3, the
harmonic series is not a geometric series.
Comment on student answers
Many student answers did not give sufficient information. Just
remarking that "The ratio is not constant" is not enough for me to
conclude that students understand what is and what is not a geometric
series. That bare sentence doesn't show what feature or fact about the
harmonic series is used. So more is needed. Specific evidence must be
given to show that the harmonic series is not a geometric series.
Students who answered "NO" and supported their assertion with the fact
that the harmonic series diverges ignore the fact that some geometric
series diverge also. For example,
∑n=1∞10n=10+100+1,000+10,000+...
is a geometric series, and it certainly does not converge.
| Wednesday,
March 25 | (Lecture #16) |
|---|
The previous (not given) QotD
The problem I would have given as the QotD is available, along with a
solution, if you want to check whether you can solve a separable
differential equation. Look here.
Exam warning
The second exam for these sections will be given on Monday, April
20 at the usual class time and place. This is certainly
about a week later than I'd like, but we missed a day due to snow,
there are conflicting exams, and some days have religious
obstructions. I hope that this date will work for all of us. Further
information about the exam will be available soon.
The workshop due tomorrow
To a certain extent, workshops are anti-exams. There is little real
time pressure. You can reflect, do over, understand, etc. the solution
as much as you want. So if you feel that exam performance doesn't
necessarily show the level of your understanding and knowledge, your
workshops can help. In this case, I bet that there will be a
problem on the second exam closely resembling the workshop problem due
tomorrow. So there would be several different "payoffs" for handing in
a good writeup!
What are sequences and what are they used for?
A sequence is a sort of ordered list of numbers (precise definition
below).
Much computation is done sequentially. For example better and
better approximations to roots of equations are gotten by Newton's
method. This scheme creates numbers which (ideally!) get closer and
closer to the root desired, even though there may be no exact
algebraic formula for this root. Definite integrals (except in
classrooms!) can only rarely be computed exactly. Instead, there are
usually collections of approximations which are computed, and this
collection of approximations is used to give a "value" for the
definite integral. In this part of the course (really this is the last
major part of the course!) we will study sequences and accompanying
ideas.
Formal definition of a sequence
A sequence is a real-valued function whose domain is the positive
integers. I will begin with what I hope are some rather simple
examples but the later examples will be complicated enough for everyone.
Example and notation
Well, one example of a sequence is a sequence whose nth
term or value or element (all these words are used!) is 1/n. So this
is the function f(x)=1/x when x is a positive integer. The usual
notation for this sequence is {1/n}. Yeah, a different notation is
used -- usually the sequence "function" doesn't get shown. The formula
is enclosed by the braces { and }. The letters that are used inside
the braces are usually n and m and p and q. If needed, we might refer
to the formula with a subscript. So, for example, we might write
an=1/n. Therefore, a5=1/5 and
a17=1/17. Also an+1=1/(n+1) and
a5m=1/(5m). Notice especially the last two equations which
might look strange. The stuff "down" in the subscript is the argument
to the function which defines the sequence. Please try not to get
confused. For example, if an=1/n, then a4=1/4,
but a4+1=a5=1/5 and a4+1=(1/4)+1=5/4.
People also frequently "define" functions by listing their first few
members. So this sequence might look like 1, 1/2, 1/3, 1/4, 1/5,
... and the "..." is supposed to indicate that the reader should now
recognize the pattern. To me this is another use of the strange
mathematical word "clearly". Clearly sometimes people will recognize
the pattern, but also clearly many times there will be difficulty.
 Maybe sometimes we might think of a picture of the sequence, but this
really has limited use as you will see. To the right is a picture of
the first 6 elements of this sequence, sitting on the number line.
Maybe sometimes we might think of a picture of the sequence, but this
really has limited use as you will see. To the right is a picture of
the first 6 elements of this sequence, sitting on the number line.
Preliminary remarks about convergence
Clearly (!) as n gets large, 1/n gets closer and closer to 0. This
behavior is abbreviated, not too surprisingly, by limit notation. So
here we would write limn→∞1/n=0. What could this
mean in more precise language? Well, one implication that occurs is
that as n increasing, 1/n gets close to 0. So maybe
limn→∞an=L means that, as n gets large,
an should get close to L. L is called the limit of the
sequence.
Another example
This example will look initially quite silly, but thinking about it is
useful. So the sequence is {(–1)n}. As a list, the elements
of the sequence are (–1)1=–1, (–1)2=1,
(–1)3=–1, (–1)4=1, etc. This sequence has only
two distinct values, and these values depend on the parity
(even/oddness) of its argument, n. When n is odd, the sequence value
is –1, and when n is even, the value is 1.
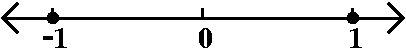 A rudimentary picture of the sequence is shown
to the right. Notice that there is something missing from this
sequence -- the dynamic aspect as the sequence wiggles and hops left
and right. Every element of the sequence is in the picture and the picture isn't very helpful to me at all. Does this sequence converge? Historically an answer to this
question wasn't obvious. People finally decided that the answer should
be no. The only numbers that are authentic candidates for the limit of
this sequence are 1 and –1. If we were going to use sequences as ways
of getting better and better approximations to a root of an equation,
then saying that the root is maybe 1 or maybe –1 is probably not the
best answer. People usually want one specific answer. So the
definition of limit, even if we want only to consider it informally,
needs to be stated slightly differently.
A rudimentary picture of the sequence is shown
to the right. Notice that there is something missing from this
sequence -- the dynamic aspect as the sequence wiggles and hops left
and right. Every element of the sequence is in the picture and the picture isn't very helpful to me at all. Does this sequence converge? Historically an answer to this
question wasn't obvious. People finally decided that the answer should
be no. The only numbers that are authentic candidates for the limit of
this sequence are 1 and –1. If we were going to use sequences as ways
of getting better and better approximations to a root of an equation,
then saying that the root is maybe 1 or maybe –1 is probably not the
best answer. People usually want one specific answer. So the
definition of limit, even if we want only to consider it informally,
needs to be stated slightly differently.
Better definition of convergence
We'll say that limn→∞an=L is true if
for n large enough, an gets close and stays close to
L.
Certainly {–1)n for certain values of n is close to 1 (heck,
it is equal to 1, and I don't know how much closer it could be). But
also we can always find even larger values of n (large enough odd n)
so that (–1)n is not at all close to 1. So the
sequence {(–1)n} does not converge and does not have any
limit. Another word is used: the sequence {(–1)n}
diverges. The problem is that, although the sequence is sort of tame
in that it never gets too large positive or too large negative, it
wiggles and never sort of stabilizes.
There is a formal definition of limit in section 10.1 of the
text. Later in your professional career, as you do more computations,
you may likely need to work with that definition. The word "close" for
example, is used to mean |an–L|, and usually people want to
be able to control the size of |an–L| by selecting some
number N so that when n>=N, then the size of |an–L| is
"small" (and this is some number to be specified in practice). Now
this is too detailed for Math 152 and a first visit to the
definition. So back to the examples.
More examples
{(1/2)n}. As
a list, we can look at 1/2, 1/4, 1/8, 1/16, .... and I bet that this
sequence converges, and its limit is 0:
limn→∞(1/2)n=0.
{10n}. This is 10, 100, 1000, 10000, etc. I think that
this sequence diverges. It gets too big. It is unbounded.
{(–1/2)n}. This sequence is more challenging. The
first few elements are –1/2, +1/4, –1/8, +1/16, etc. Here the signs
change, so the sequence wiggles, but the magnitude (the absolute
value) of the terms goes to 0. So in spite of the wiggling, I think
that this sequence converges and its limit is 0:
limn→∞(–1/2)n=0.
Algebra and sequences
Some straightforward limit facts still are true, such as:
If limn→∞an=L1 and
if limn→∞bn=L2, then
limn→∞an+bn=L1+L2
and
limn→∞an·bn=L1·L2.
Things like this are in the textbook, and I'd like to concentrate my
attention on more subtle behavior.
{51/n}
 Let's look at the sequence {51/n}. The first few terms, in
decimal form, are these: 5., 2.236067977, 1.709975947, 1.495348781,
1.379729661, 1.307660486, 1.258498951. A picture of the first 6 of
these is to the right. Maybe things here are not totally clear. In
fact, one of the reasons I want to discuss this example is that things
are not clear. We made some preliminary observations: certainly
any root of 5 would have to be positive, in fact any root would have
to be bigger than 1. And also any root would have to be less than
5. So what we know is that 1<51/n<5. The numbers in
the sequence are "trapped" inside the interval from 1 to 5. I asked
the class if just knowing this information was enough to guarantee
that the sequence converged. After some thought, one student came up
with the following example: {3+(–1)n}. Again depending on
parity, the values of this sequence are either 2 (n odd) or 4 (n
even). This sequence does not converge although its values are inside
the interval from 1 to 5.
Let's look at the sequence {51/n}. The first few terms, in
decimal form, are these: 5., 2.236067977, 1.709975947, 1.495348781,
1.379729661, 1.307660486, 1.258498951. A picture of the first 6 of
these is to the right. Maybe things here are not totally clear. In
fact, one of the reasons I want to discuss this example is that things
are not clear. We made some preliminary observations: certainly
any root of 5 would have to be positive, in fact any root would have
to be bigger than 1. And also any root would have to be less than
5. So what we know is that 1<51/n<5. The numbers in
the sequence are "trapped" inside the interval from 1 to 5. I asked
the class if just knowing this information was enough to guarantee
that the sequence converged. After some thought, one student came up
with the following example: {3+(–1)n}. Again depending on
parity, the values of this sequence are either 2 (n odd) or 4 (n
even). This sequence does not converge although its values are inside
the interval from 1 to 5.
Comments on boundedness and convergence of sequences
If a sequence convergences, then the numbers in the
sequence are bounded. (The reason is, essentially, that if there is
convergence, all but a few of the terms are close to the limit of the
sequence. Then the whole sequence is trapped near the limit and
finitely many other numbers, and that can be put inside a bounded
interval.)
The converse of the statement above is not true in general. I
mean: If a sequence is bounded, then it may not
converge. We've already seen several examples of this statement.
Here is a very
brief discussion of some of the words used with logical implications.
Back to {51/n}
Here is one way of analyzing the sequence. If
an=51/n, then
ln(an)=ln(51/n)=(1/n)ln(5). But (1/n)ln(5) is
just a constant multiple of the first sequence we looked at, and that
sequence had limit 0. So limn→∞(1/n)ln(5)=0. Here
is a general and quite useful fact:
If f(x) is a continuous function, and if {bn}
is a convergent sequence with
limn→∞bn=L, then the sequence
{f(bn)} converges, and
limn→∞f(bn)=f(L).
This is true because the bn's get close to L, and
continuous functions take close inputs to close outputs, so
an=f(bn) is close to f(L).
In the example {51/n} we know that {(1/n)ln(5)} converges
and its limit is 0. Since the exponential function is continuous,
{e(1/n)ln(5)} is a convergent sequence and its limit is
e0=1. That is, limn→∞51/n=1.
A more intricate example
Consider the sequence {n1/n}. This is a bit like the
preceding example. It has the form
BASEEXPONENT. Here the base is n, and is
growing. The exponent is 1/n, and is shrinking. Which one "wins"? That
is, is this sequence not bounded, and not converging? Is there some
other kind of behavior? Again, taking logs helps. So since
ln(n1/n)=(1/n)ln(n)=ln(n)/n, we need to analyze
limn→∞ln(n)/n. As n grows, the top and the bottom
separately grow and go to ∞. This
limit is eligible for L'Hôpital's Rule. (If you don't
check the eligibility, you are bound to make a serious mistake
sometime!) So:
limn→∞ln(n)/n=limn→∞(1/n)/1=0
Therefore just as before, the limit of the original sequence is
e0=1.
Here are the first 7 elements of the sequence: 1., 1.414213562,
1.442249570, 1.414213562, 1.379729661, 1.348006155, 1.320469248. These
don't signal to me immediately that the limit is 1. Computation can be
misleading! I mentioned in class that more complicated examples could
easily be written where the contest of base vs. exponent is not easy
to decide.
More examples
{(50}n}. This sequence diverges (it is certainly
unbounded).
{(1/50}n}. This sequence converges (its terms approach 0 rapidly).
Here is a rather sophisticated example: {(50)n/n!}. The top is
bigger and bigger powers of 50, while the bottom is n!. Both the top
and the bottom grow. Understanding the asymptotic behavior of this
sequence as n→∞ is asked to
decide which grows faster, the top or the bottom. I mentioned in class
that this bizarre looking sequence is not random, and really does
occur in applications. Here is some numerical evidence (the first 7
terms, rounded to 10 digit accuracy):
50, 1250, 20833.33333, 260416.6667, 2604166.667,
2.170138889·107, 1.550099206·108.
If you want more evidence, than the 20th is about
4·1015, and that's quite big to me. But, in fact,
this sequence converges. It is important not to be deceived by
what happens for small n's. We are interested in
the asymptotics as n grows really, really big.
Some students noticed something like the following argument. Take n
to be an integer larger than 100. (You will soon see why I selected
100: it is because it makes some computations and comparisons
easier). Then/ (50)n \ (50)(50)(50) ··· (50)
| ----- | = ----------------------
\ n! / 1·2·3·4·5···(n–1)n
Look at the product of the first 100 fractions above. This is some
enormous number (the top is (50)100 and the bottom
is 100! The valueof a100 is about 8·1011 actually. How
many terms are left over? The terms from 101 up to n, and that's n–100
(n minus 100) terms. Each of them has 50 on top, and a number bigger
than 100 on the bottom. So the leftover terms all are less than
1/2. That means:
{(50)n/n!}<
{(50)100/100!}(1/2)n–100.
The powers of 1/2 drive down the sequence values when n is
bigger than 100. I chose 100 because it would be nice to get some
definite number like 1/2, so you can see things decreasing. In fact,
when n=200, the value of the sequence element is about
7.89·10–36, quite small. I claim that the following
result is correct, but is definitely not "clear":
limn→∞{(50)n/n!}=0.
Squeezing a limit out ...
The formality behind the previous argument is a version of the Squeeze Theorem, which goes something like this.
If I have three sequences, {an} and {bn} and
{cn} and if I know for all n's that
an≤bn≤cn and if I know
that limn→∞an=L and
limn→∞cn=L, then the middle sequence
{bn} also converges, and its limit is L.
The preceding example had an=0 and
bn=(50)n/n! and
cn=[(50)100/100!](1/2)n–100. I don't
think the argument is obvious.
|
QotD
Well, I asked people to do problem 12 in section 10.1. This shouldn't
be difficult.
| Monday,
March 23 | (Lecture #15) |
|---|
The previous QotD
This was
Find the solution of y´=y2x3 which goes
through (2,1). Be sure to write the solution as y=some function of x.
Volunteers in both lectures did this problem on the board. In
the first lecture, these were Mr. Stebbins
and Mr. Weisser. In the second lecture,
they were Mr. Boemo and Mr. Fishbein.
Separate: y–2dy=x3dx
Integrate: ∫y–2dy=∫x3dx
The general solution is in implicit form as –y–1=[x4/4]+C
Initial condition leads to constant of integration:
–(1)–1=[24/4] so C=–5.
The transition from implicit description to explicit description
–y–1=[x4/4]–5
so y–1=–[x4/4]+5
and y=1/(–[x4/4]+5).
I mentioned the discouraging statistics about people who made
algebraic errors when going from implicit to explicit description of
the solution. I was unhappy. Anyone who believes that 1/(A+B) and
(1/A)+(1/B) are likely to be the same is invited to give me two
half-dollars ([1/2]+[1/2]) and I will give them in exchange a quarter
(1/[2+2]). You've got to think about what you write -- everyone
makes mistakes, but learn to check for them, and fix them. Please! At the end of this lecture is my
candidate for the QotD. It is a problem similar to the one just
discussed. You can try it and see if you get the correct answer.
Story #3
A hot object is brought into a room whose ambient temperature is
30oC. After 10 minutes, the temperature of the object is
measured and found to be 80oC. After another 10 minutes (20
minutes from start) the object's temperature is 40oC. What
was the initial temperature of the object? What is the temperature of
the object an hour after it was brought into the room?
Assume that the rate of temperature change is directly
proportional to the difference of the temperatures. (This is
Newton's Law of Cooling whose validity can be checked
experimentally.)
 Modeling this story to solve the problem
Modeling this story to solve the problem
Declaring that the quantity FROG is directly
proportional to the quantity TOAD is language meaning
that FROG=KTOAD for some positive constant K. So if
T represents the temperature of the hot object, then Newton's Law of
Cooling implies that RATE OF CHANGE OF T=K(difference
between T and 30). With the usual notation, realizing that "rate
of change" is a derivative, and using T in oC and t for
time measured in minutes since the object was brought into the room,
Newton's Law of Cooling becomes dT/dt=K(T–30) with some unknown
constant, K. What about the other information in the story? I've
collected the information in a possible graph of the temperature of
the object to the right. Our guess for the solution curve (the
description of the temperature as time changes) is in magenta. It should tend to 30 as t→∞.
Solving the model equation
dT/dt=K(T–30) is separable, so we get (I'm beginning to skip steps)
∫[1/(T–30)]dT=∫K dt so that ln(T–30)=Kt+C. We
have two constants, K and C, to be determined. But we know two
"chunks" of information about the temperature, (10,80) and
(20,40). Therefore (plugging in):
(10,80) gives us ln(50)=K(10)+C
and (20,40) gives us ln(10)=K(20)+C.
We have two linear equations in two unknowns. We can solve them. Use
your favorite method, or:
Double the first equation and subtract the second to get
2ln(50)–ln(10)=C. I will simplify using log properties, so
C=2ln(50)–ln(10)=ln({50}2)–ln(10)=ln(2500)–ln(10)=ln(250).
Let's put this value of C in the first equation. We have
ln(50)=K(10)+ln(250) so 10K=ln(50)–ln(250)=ln(50/250)=ln(1/5) and
K=(1/10)ln(1/5).
The solution and the solution curve
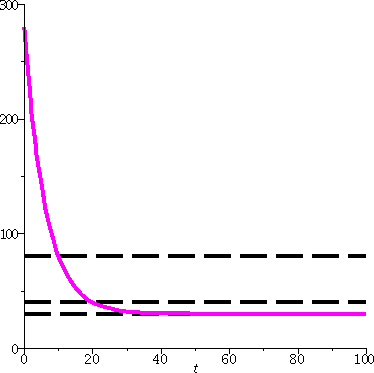 The implicit form of the equation is therefore
ln(T–30)=(1/10)ln(1/5)t+ln(250). Let's exponentiate, and use
exponentiation properties and log properties:
The implicit form of the equation is therefore
ln(T–30)=(1/10)ln(1/5)t+ln(250). Let's exponentiate, and use
exponentiation properties and log properties:
T–30=e(1/10)ln(1/5)t+ln(250)=e(1/10)ln(1/5)teln(250)=eln[(1/5)(1/10)t](250)=250(1/5)(1/10)t, and, finally,
T=250(1/5)(1/10)t+30. Whew! Please note that on an
exam I would not require so much "simplification" but when you go out
and work on such problems, people usually like the answers written in
such "simple" ways. Since T(t)=250(1/5)(1/10)t+30, the
initial temperature, T(0), was 250+30=280. The temperature after one
hour is T(60) (60 minutes=1 hour) and that is
250(1/5)6+30 which is 30.016 (no, I did not compute
this!). Also please note that as t→∞, since (1/5) is a positive number less than 1,
250(1/5)(1/10)t→0 so that T(t)→30 as we had guessed.
To the right is a graph of T(t)=250(1/5)(1/10)t+30 in magenta with dashed black lines at 80, 40, and
30. The 80 and 40 lines cross at 10 and 20, respectively, and the
curve overlays the 30 line as t grows. The curve seems to cross
the t=0 line at T=280.
Bacteria again ...
The differential equation dy/dx=Ky with K constant (so the solutions
can be written as y=CeKx) is widely used for modeling drug
levels in blood and radiocarbon dating (K negative) and for modeling
growth of bacteria, yeast, fungus, etc. when K is positive. x is
usually time. How valid is this? Well, if we had E. coli which would
"divide every twenty minutes" we should be 50 feet under E. coli even
if the darn things started only a few weeks ago. In fact, for such
growth there are limits to nourishment and other factors which retard
growth as the population increases. So people have considered many
differential equations which model growth. Let me discuss a very
simple case of a widely accepted model equation.
A better model: the logistic equation
Consider the
differential equation dy/dx=y(2–y). If y is close to 0 but positive,
then the right-hand side seems to be about "2-ish" multiplying y. So
this is very much like dy/dx=2y, exponential growth. If y is close to
2 but less than 2, then dy/dx is (really small number) multiplying y,
so y will grow very slowly. I will try to solve a specific initial
value problem for this equation, which is an example of the
Logistic Differential Equation. The numbers are selected to
make the algebra as easy as possible.
The initial value problem will consist of the differential equation
dy/dx=y(2–y) and the initial condition y(0)=1.
- Separate and integrate:
∫[1/{y(2–y)}]dy=∫dx.
- The left-hand side needs partial fractions:
[1/{y(2–y)}]=(z/y)+(w/{2–y}) so (tops only) 1=z(2–y)+wy. y=0 gives
z=1/2 and y=2 gives w=1/2. Now integrate.
- (1/2)ln(y)–(1/2)ln(2–y)=x+C where the minus sign before one of the
1/2's comes from the antiderivative of 1/(2–y). If x=0, y is supposed
to be 1. Then (1/2)ln(1)+(1/2)ln(1)=0+C so C=0 ("select the numbers
to make everything as easy as possible").
- The solution implicitly is therefore (1/2)ln(y)–(1/2)ln(2–y)=x but
people like explicit forms. So multiply by 2 and use the ln property
to get ln(y/{2–y})=2x. Exponentiate so y/{2–y}=e2x. We need
still to solve for y. Multiply by 2–y and
y=e2x(2–y)=2e2x–e2xy and
y+e2xy=2e2x and
y(1+e2x)=2e2x. Huh. So clearly ...
 An explicit form of the solution is
y=[2e2x]/[1+e2x]. This may be in a form that
"real people" can understand.
An explicit form of the solution is
y=[2e2x]/[1+e2x]. This may be in a form that
"real people" can understand.
A picture of this curve is shown to the right. The curve does pass
through (0,1). For t negative, the curve does sort of look
exponential. When t is large enough (t=0 in this case), the concavity
of the curve flips (it is always increasing!) and as t→∞, y→2. 2 is sometimes called the
carrying capacity of this "system". This function is sometimes
called (a version of) the logistic function.
But what happens if ...
What if we wanted to look at a different, even just slightly more
complicated model, say dy/dx=y(y–1)(y–2) etc. Then separating etc. is
possible. But trying to convert the implicit description of the
solution to an explicit description, one that can be analyzed more
easily, is essentially impossible unless we are very lucky.
A different kind of reasoning
There is a different way to study such equations, one where geometric
reasoning is used instead of lots of algebraic computations. When this
sort of reasoning applies, getting asymptotic information is usually
much easier than one would think possible. The tool I will discuss for
studying differential equations is called the direction field
in your textbook (in others it is called the slope field). I
will use this tool to get an approximate idea of the shape and
behavior of what are called solution curves or integral
curves of the differential equation. These are the graphs of
particular solutions of the differential equation.
Direction fields
Let's look at the differential equation
y´=x2–x–4y2. I can't "solve" this but let
me tell you just a small amount of information about the solution near
the point (3,1). A solution curve passing through the point (3,1) will
have its slope determined by the differential equation. I mean that
y´ when x=3 and y=1 will be the value of
x2–x–4y2 when x=3 and y=1. This is
32–3–4·12=9–3–4=2. So the tangent line to
the curve at (3,1) will have slope 2. Well, let's think about it. I'll
draw a thickened-up line segment of slope 2 at (3,1) and consider some
curves going through that point.
| Curve #1 I've drawn a little piece of
a curve, tangent to the chunk of line (it is formally called a line
element, I think). I think this curve, which is increasing, might
possibly be a solution to this differential equation near this point.
A possibility
|  |
| Curve #2 Here is another curve going
through (3,1). I believe that this could also be the solution
curve. O.k.: it is concave down, and I surely don't know what the
concavity of the solution curve is at (3,1) without more study. But in
my casual way, I have two possible candidates for the solution
curve. Certainly it is also increasing near (3,1) because the slope at
(3,1), which is 2, is positive.
A possibility
|  |
| Curve #3 Now this candidate is really
a different sort of curve. This curve does pass through (3,1) but it
is decreasing, and its slope is certainly not 2 at (3,1). This is a
losing candidate (!) and certainly can't be a little piece of
a solution curve.
Not possible!
|  |
I don't think that this "reasoning" is profound. I am merely asserting
that I can eliminate and (tentatively) accept certain candidate curves
as good candidates for solution curves. Now I will extend the
reasoning, by drawing lots of line segments at lots of points and see
what my brain's visual processing power can tell me about the
curves. In fact, (and this is somewhat amazing to me) with some
practice, most people can "see" the curves quite clearly. So here are
some examples. The direction fields were drawn by computer, but the
curves were (badly) drawn by me. At least what's here is clearer than
what happened in class!
| dy/dx=(1/20)x2 |
| This is the direction field |
This is the direction field with
some solution curves. |
|---|
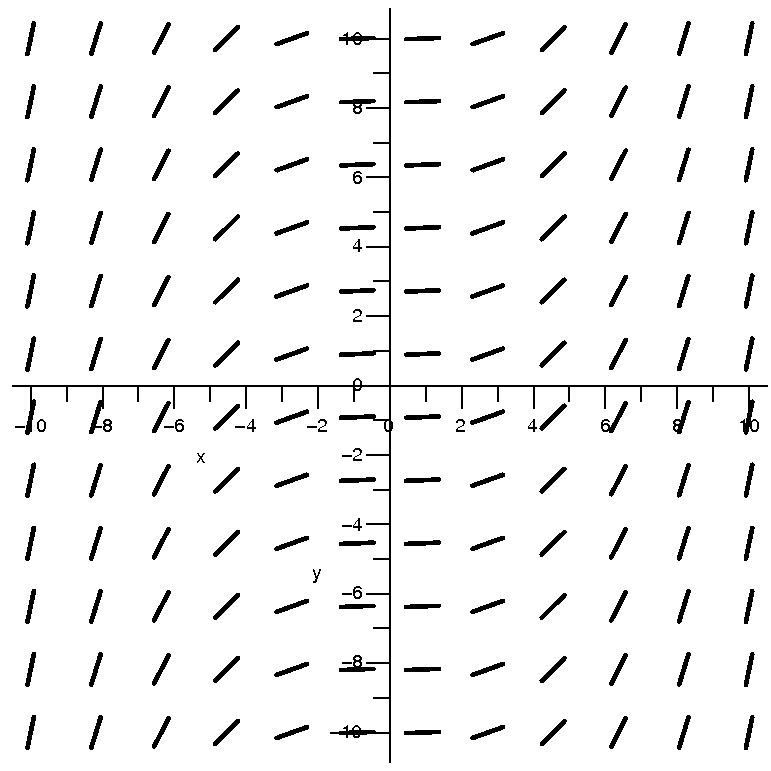
|
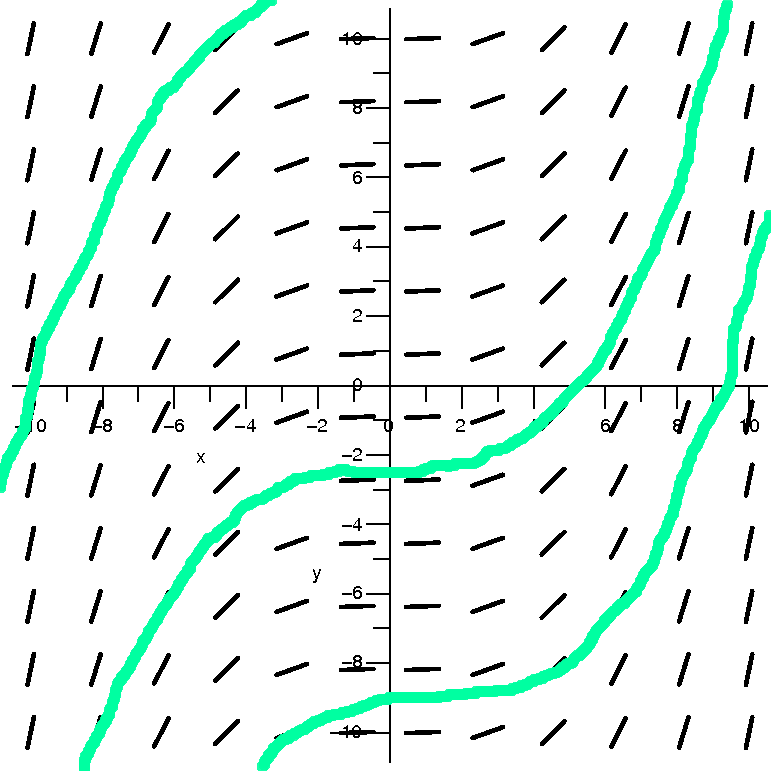
|
Discussion
I had Maple draw a bunch of direction
fields. I admit that the instructions took a bit of practice, but once
I understood them it wasn't too difficult to produce the pictures, and
I honestly tell you that there was a great deal less computation than
if I had requested any approximations to solution curves
numerically. There are 12·12=144 line elements in each
direction field picture. The rather strange numbers which appear in
the differential equations (for example, the (1/20) in this equation)
were chosen so that the tilts of the direction field elements would be
easier to see in these pictures.
This differential equation can be solved easily and its solutions are
(1/20)(1/3)x3+C. But I want to
look at the curves and not the formulas. Here to the left is
the direction field without any decoration. To the right is my attempt
to draw by "hand" curves which, whenever they touch a line element,
have the line elements as segments of tangent lines. I think you can
see that the solution curves are increasing, and that the concavity is
down on the left and up on the right. That's all I want from this
example.
|
| dy/dx=(1/10)xy
|
| This is the direction field |
This is the direction field with
some solution curves. |
|---|

|

|
Discussion
O.k., algebraically this differential equation is still something we
can handle fairly easily. This is a separable equation, and we can
solve it fairly easily. Let me take the 144 pieces of the direction
field and try to draw some curves which, when they touch any
part of the direction field, will have that tiny line segment looking
like it is tangent to the curve. To me these words more make things
harder to understand. Draw some curves!
The curves I "drew" are concave up when they are above the x-axis, and
they are concave down when they are below the x-axis. I feel that I
understand how initial conditions would "evolve" (?) forward and
backward. People frequent thing that x is a variable representing
time. So an initial condition located in the upper halfplane, above
the x-axis, evolves forward (the future) and gets very very
large. Also, in the past, it came from something very very
large. That's all I want here: just approximate
qualitative information about
solutions.
|
| dy/dx=(1/30)(y+2)(y–2)
|
| This is the direction field |
This is the direction field with
some solution curves. |
|---|
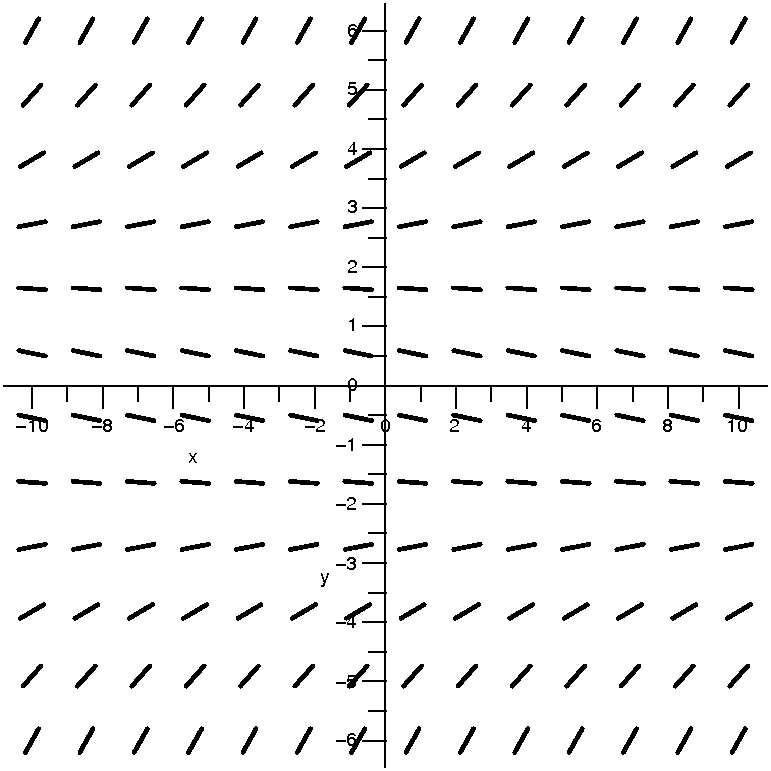
|
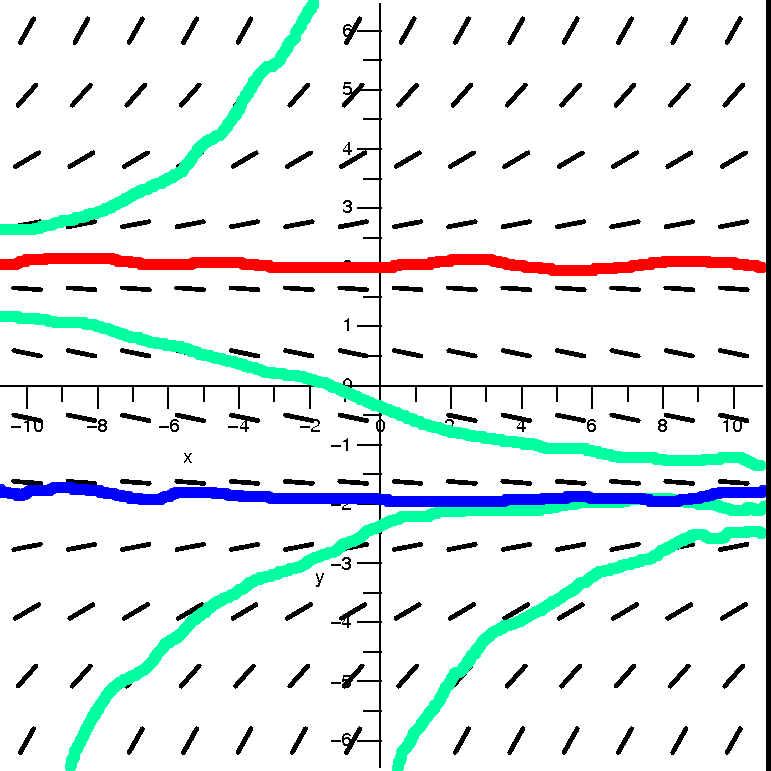
|
Discussion
I can still solve this algebraically, I think (I haven't tried). This
is a variant on the logistic equation which has a nicely worked out
solution above. Here the numbers are a bit more random, though. The
direction field tells me more in a short amount of time than working
algebraically would tell me in a long time.
Look at the picture of the direction field, and then look at the
solution curved indicated. There is a great deal going on in the
picture of the curves, and let me try to pick out some features.
First, there are some horizontal lines which are
solutions. How can I detect them? If y=Constant is a solution to some
complicated differential equation dy/dx=F(x,y), then
because the horizontal line always has dy/dx=0, it had better be true
the the complicated function F(x,y) is 0 when we plug
"Constant" in for y. This may seem complicated to you, but here look
at the right-hand side: (1/30)(y+2)(y–2). When is this equal to 0?
Without being silly, I think I can write that clearly this occurs for
y=–2 and y=+2. The horizontal lines defined by these questions are
then solutions to the differential equation dy/dx=(1/30)(y+2)(y–2)
because both sides are 0. These solutions don't change with "time" if
we think of x as time. Here is some vocabulary which is used when
discussing these solutions: they are called equilibrium
solutions or steady-state solutions.
Now I want to discuss other (non-equilibrium) solutions for this
differential equation. Consider first solutions near the equilibrium
solution y=–2. If we take initial
conditions (x0,y0) with y0 not
equal to –2 but near –2, soemthing sort of interesting
happens. The curves above y=–2 get moved down as we go futureward (x
increases). They get moved down towards –2, and as close to –2 as you
want (yes, a limit indeed). And if y0 is below or less than
–2, the curves below y=–2 move up towards –2. More precisely, if we
take an initial condition (x0,y0) with
y0 close to –2, the resulting solution y=f(x) has the
property that limx→∞f(x)=2. Nearby solution curves converge to the
equilibrium solution y=–2. This situation has its own name: y=–2 is
called a stable
equilibrium. There are many physical situations
(mechanical, chemical, etc.: many!) where learning about stable
equilibriums (equilibria?) is very important. In real life,
determining an exact measurement (y=–2) may be very difficult. It is
far better to know that, hey, starting something off near –2
will have the same long-term effect as starting it at –2. This is
useful and neat.
Let's look more closely at the other equilibrium solution,
y=2, and its neighboring solution
curves. Suppose we start near but above y=2. If you look at
the picture, you'll see that the direction field pushes (?) the curve
away from y=–2 (these curves go to ∞). Similarly, if we start near but below y=2, the curves get
pushed away from y=2. The lower curves go towards y=–2, which right
now is not interesting: I want to concentrate are things near y=2. So
if this differential equation described a physical situation, I would
now know that if my initial condition (x0,y0)
had y0 exactly at 2, then on the solution curve, I would
have y0 always equation to 2 as x0 increased
(the future). But if I didn't get y0 exactly equal
to 2, I have no ability to predict the future. Maybe y will tend to
∞ or maybe to –2. Here's the
vocabulary, which shouldn't be surprising: y=2 is called an unstable equilibrium.
|
Physical situation
 Stable equilibrium
Stable equilibrium
Think of a ball at the bottom of a bowl. It will just sit there,
position not changing. If you jiggle the bowl a bit, then the ball
will move, but eventually (if you stop jiggling) it will go towards
the bottom again. This "bottom" situation is a stable
equilibrium.
|
 Unstable equilibrium
Unstable equilibrium
Turn the bowl over and put the ball on top of the bowl. You may
conceive of a situation where you haved place the ball so carefully on
the top that is it totally balanced and still, motionless. Ideally the
situation would go on forever -- equilibrium. But now jiggle the ball
in any way, with a very small jiggle, in any direction. The ball will roll
off. This is unstable equilibrium.
|
|
| dy/dx=(1/30)y2(y–2)
|
| This is the direction field |
This is the direction field with
some solution curves. |
|---|
|
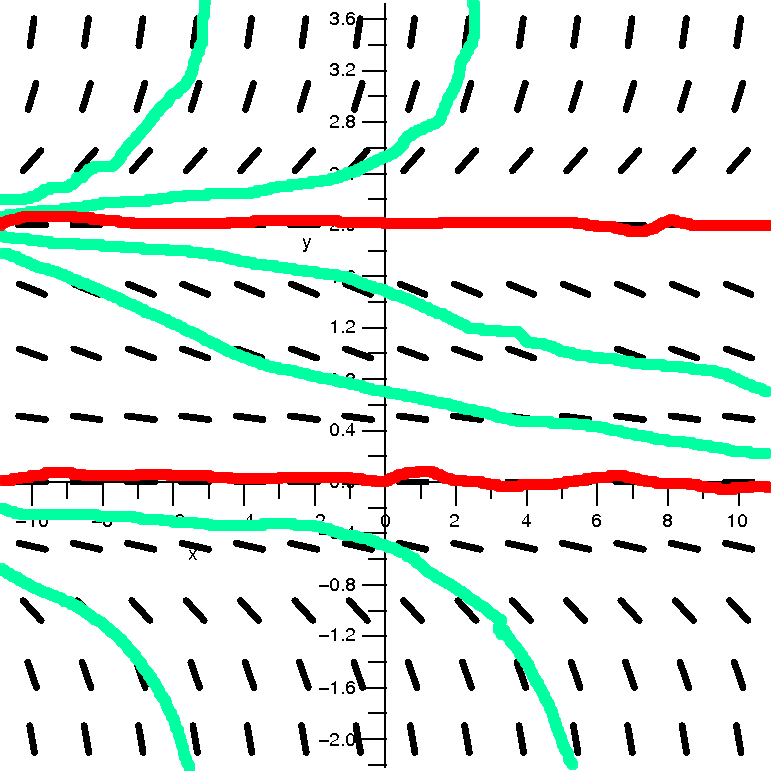
|
Discussion
O.k.: I definitely would not want to try to "solve" this
equation algebraically and get explicit solutions. But the direction
field approach combined with simple reasoning allows me to find
equilbrium solutions and even to detect which are stable and which are
unstable, and this can be very useful in practice.
I diagnose equilibrium solutions by considering
(1/30)y2(y–2)=0. The roots are 0 and 2. So y=0 and y=2 are
the only equilibirum solutions for this differential equation. Yes, I
admit it: this example is very carefully chosen so that the method
works, but the ideas are sufficiently nice so that the method will
work even for examples which aren't so "pretty".
What about stable and unstable? Again, look at the direction field,
and then examine the solution curves which are drawn. Both of the
equilibrium solutions are unstable. Nearby solution curves are not
"sucked into" the equilibrium solution. Yes, it is true that curves
above y=0 get pulled towards y=0, but to be an equilibrium solution,
both sides (up and down) must have solution curves which are attracted
to the equilibrium, and this does not occur here. Again, both of these
equilibrium solutions are unstable.
|
I really fouled up
time allocation in this lecture. Somehow I miscalculated. I didn't
get a chance to show this last picture and discuss it in either
class.
I also didn't
get a chance to give a QotD. So the last picture I wanted to show you
follows along with some discussion, and so does
the QotD, which you can do if you wish. A solution is also provided
via a link so you can compare your solution with mine.
|
| dy/dx=(1/20)(x+y2)
|
| This is the direction field |
This is the direction field with
some solution curves. |
|---|

|

|
Discussion
O.k., the last example for this method is really nearly random. The
right-hand side, (1/20)(x+y2), is a low-degree polynomial,
but I don't know how to solve the equation (see the remark below if
you are curious, though!). There are no equilibrium solutions because
there is no constant C which makes (1/20)(x+C2) equal to 0
for all values of x. So here's a complicated situation. But still,
consider the direction field, which is easy to have drawn, needing
very little computational effort. And consider the curves I drew. I
bet that the following occurs: if y=f(x) is a solution to this
differential equation, then there will be exactly one critical point
on the solution curve, and this critical point will be an absolute
minimum. To the right of the solution curve, the function will
increase. In fact, it will explode in finite time, that is,
there will be some Q so that
limx→Q–f(x)=∞, but I don't think the picture necessarily tells that. What
about to the left of the solution curve? I bet that somewhere the
concavity of the solution changes, and it becomes concave down, and
that the curve sort of tapers off to a sort of flat situation.
Everything predicted here is actually correct. It would be rather
difficult (but possible, I think, but I wouldn't want to do it!) to
confirm all this algebraically. I think the direction field idea is
worth using as a tool when analyzing differential equations,
especially when some quick asymptotic information is wanted.
|
The real thing
Much computation is needed to produce an "explicit" solution
to dy/dx=(1/20)(x+y2). To the right is a picture of the
solution curve which goes through (0,0). The function defining the
curve can't be written in terms of the standard functions you
know. The rather
simple-looking picture is the result of a bunch of Airy functions
combined in very strange ways. I am not inventing all this! The
situation is very complicated.
Here is the solution in detail, written by a silicon friend of mine: 2/3 2/3
50 x (2/3) 50 x (1/3) (1/6)
AiryAi(1, - -------) 150 + 5 AiryBi(1, - -------) 20 3
100 100
1/5 ---------------------------------------------------------------------
2/3 2/3
50 x (2/3) 50 x (1/6)
AiryAi(- -------) 3 + AiryBi(- -------) 3
100 100
I don't understand this complicated formula at all. But I
do understand the direction field and the solution curves.
|
|
QotD
Find the solution of y´=(ex/3)/y which satisfies
y(0)=2. Be sure to write the equation as y=some function of x. Here is a solution which you should look at
after you try the problem yourself.
| Wednesday,
March 11 | (Lecture #14) |
|---|
What's a differential equation?
A differential equation is an equation relating an unknown function
and one or more derivatives of the unknown function with some other
functions.
Examples
y´=x2 Done in 151; to be reviewed here.
y´=5y Done in 151; to be reviewed here.
y´=y2 We'll discuss this here.
y´=xy We'll discuss this here.
y´=x+y To be discussed in your differential equations course.
y´´=–y To be discussed in your differential equations course. This equation
governs simple harmonic motion (the movement of an ideal
vibrating spring).
y´=x2+y2 This can't be "solved" in terms of
standard functions.
Order of a differential equation
This is the highest numbered derivative which occurs in the
differential equation. In these two lectures we will look only at
first order equations. All of the examples above are first
order, except one (the simple harmonic motion equation) which is
second order. Please note that the differential equations course which
most of you will take will indeed study equations of higher order, and
that these do occur. Some standard vibrating beam equations studied in
mechanical engineering are fourth order, and many of the equations in
physics and chemistry are second order.
Story #1
Probably we have all been told that bacteria (usually) reproduce by,
say, binary fission. This is more or less correct, and more or less
the fact means that the rate of increase of bacteria at any time is
directly proportional to the number of bacteria at that time. So twice
as many bacteria "now" means that twice as many bacteria are being
born now. This is certainly dreadfully simplified, but this
approximation works in many circumstances. I wondered, when I first
heard this fact, why, if, say, E. coli doubles rather rapidly,
shouldn't the world be covered very soon by a layer of E. coli which
is 40 feet thick? In fact,
A single cell of the bacterium E. coli would, under ideal
circumstances, divide every twenty minutes.
(From Michael Crichton (1969) The Andromeda Strain, Dell, N.Y. p.247)
But of course anything growing so rapidly in the real world (mold in a
petri dish) enters a situation where the growth challenges the ability
of the environment to support the thing. Most environments have a
carrying capacity -- some sort of upper limit to the amount of the
thing which can live in the environment. Differential equations can
model this sort of situation fairly well, combined with the
"exponential growth". But exponential growth was studied last
semester, and the equation y´=5y sort of models unrestricted
exponential growth.
Story #2
We start with an 800 gallon tank of pure water. It is being filled
with a fluid at 50 gallons per minute, and these 50 gallons contain 5
lbs of salt. At the same time, 50 gallons per minute of the solution
in the tank is being drained. How much salt is in the tank at any
time? How much salt would you expect to be in the tank after a long
time?
Let's construct a differential equation which models the salt in the
tank. We'll call S(t) the number of pounds of salt in the tank at time
t. How much salt is being added? Well, 5 pounds per minute. How much
salt is being taken away? This is more subtle, and we had some
discussion of our assumptions during class. The simplest analysis,
which we will do here, is to assume that the tank contents are mixed
well: it is homogeneous. The situation with a large real tank might
not match this, of course. But, actually, real containers and tanks
sometimes have mixing devices installed to try to match this
assumption. Well, if there are S(t) pounds of salt in the tank at time
t, and if the tank holds 800 gallons, and if 50 gallons are taken out,
then the proportion of 50/800 of the salt is taken out:
[1/(16)]S(t). Now we put things together.
dS/dt, the rate of change of the salt, is +5–[1/(16)]S(t). The
differential equation is dS/dt=5–[1/(16)]S. We also shouldn't forget
that we start with no salt at all in the tank: S(0)=0.
Prediction? What should happen over the long term to the amount
of salt in the tank? It starts out at 0, and then increases ... to
what? Well, a guess is that the amount of salt in the tank
should increase to 80 pounds, which is the same as the salt
concentration (1 pound per 10 gallons) incoming. We will see how to
solve the differential equation and check this prediction.
The solution is discussed here.
Solution of a differential equation
A solution of a differential equation is a function which, when it and
all of its relevant derivatives are inserted into the differential
equation, makes the equation true for all values of the domain
variable. I know this may seem long-winded, but I hope the discussion
and examples which follow will shown why such elaboration is
necessary.
An example: y´=x2
Well, we know how to solve y´=x2: just integrate. We
did this repeatedly last semester (and even this semester). The
solutions are y=(1/3)x3+C, where C is any constant. There
are infinitely many solutions. A few of them are shown to the right.
The blue curve has C=1: y=(1/3)x3+1. It
is the solution curve which goes through (0,1).
The red curve has C=3: y=(1/3)x3+3. It is
the solution curve which goes through (0,3).
The green curve has C=–2:
y=(1/3)x3–2. It is the solution curve which goes through
(0,–2).
The solution curves are just vertical translates, up and down, of each
other. They are all the same shape, have the same domain, etc. This
situation is rather straightforward, as you will see.
General solution; particular solution
There is some special vocabulary used. The differential equation
y´=x2 has the general solution
f(x)=(1/3)x3+C. When C has a specific value, then the
function is called a particular solution. So
f(x)=(1/3)x3–2 is a particular solution, and it is the only
particular solution which passes through (0,–2). The specification
(0,–2) is called an initial condition. That comes from the
physical situation where x represents time, and we think that the
y-value corresponding to the given x-value represents a certain
starting place. Sometimes people write y(0)=–2 as the initial
condition. That can confuse me. The combination of an initial
condition and a differential equation is called an initial value
problem.
 An example: y´=y2
An example: y´=y2
Now let's change and consider y´=y2. I guess
that the general solution is f(x)=1/(C–x). (I'll show you how to
guess it also, very soon!) How could you check that my suggestion for
a solution actually is a solution? Well, if f(x)=1/(C–x) then,
since f(x)=(C–x)–1, we know that
f´(x)=(–1)(C–x)–2(–1). The first –1 comes from the
power, and the second –1 comes from the Chain Rule, so they
cancel. But (C–x)–2, the derivative of the function, is
actually the square of (C–x)–1, the original function. We
have now verified that f(x)=1/(C–x). does solve
y´=y2. Now let's look at some particular solutions.
The blue curve has C=1: y=1/(1–x). It is the
solution curve which goes through (0,1). It has domain (–∞,1), and is increasing and concave
up.
The red curve has C=1/3: y=1/({1/3}–x). It is the
solution curve which goes through (0,3). It has domain (–∞,1/3), and is increasing and concave
up.
The green curve has C=–1/2: y=1/(–{1/2}–x). It is
the solution curve which goes through (0,–2). It has domain (–1/2,∞), and is increasing and concave
down.
These solution curves are not just vertical translates of each
other. Their domains are different (yeah, this matters in real life)
and the solution curves have different shapes. The particular
solutions "blow up" at different numbers. And this is still a fairly
simple differential equation.
A big theorem and a joke
When I was young, so much younger than today, I was told the following
BIG THEOREM about differential equations.
THEOREM
Suppose we have some function of two variables,
F(x,y), and we are interested in the differential
equation y´=F(x,y), and a solution going through
the point (x0,y0). Then there always is a
solution, and there is exactly one solution.
The theorem's name is the Existence and Uniqueness Theorem for
solutions of differential equations. "Existence" because the theorem
declares that there is a solution, and "Uniqueness" because the
theorem declares there is exactly one solution. There are some mild
"technical" conditions the function F(x,y) should
satisfy, but almost everything you're likely to look at will be
covered theoretically by this theorem. You will see this result
later in your differential equations courses.
After I learned about this theorem, I thought that all this worry
about differential equations was totally silly -- the theorem tells
you
everything. This is false. In
practice, the theorem doesn't tell you how to compute or approximate
solutions efficiently. It doesn't tell you what the domains of the
solutions are (this is important in applications). It doesn't
tell you the asymptotic behavior of the solutions (how much salt there
is after a long time). These questions are very important, and they
are the questions which need to be answered in practice. All this
makes me think of my favorite math joke.
JOKE
Several people are in a hot-air balloon, trying to land over a
fog-shrouded countryside at the end of a long day. The balloon dips
down low and they see the ground faintly. Spotting a person, one of
them calls down: "Where are we?" Some minutes later the wind is
carrying them away and they hear faintly, "You're in a balloon!" One
person in the balloon gondola says thoughtfully to the other, "It's so
nice to get help from a mathematician." The other says, "How do you
know that was a mathematician?" The first replies, "There are three
reasons: it took a long time to get the answer, it was totally correct,
and, finally, it was absolutely useless."
While I love mathematics, and I think math is beautiful and helpful,
please remember the final sentence of this joke.
Separable equations
A separable first order differential equation is one which can
be written in the following way: dy/dx=F(y)G(x). The right-hand side
is a product of some function in y multiplied by some function in x.
I'll describe a procedure which leads, in many cases, to a solution.
- Separate: put all the y stuff on one side and put all the
x-stuff on the other side. The equation becomes dy/F(y)=G(x)dx.
- Integrate:∫dy/F(y)=∫G(x)dx. Of course, the practicality of
this (at least "by hand") depends on the specific functions F and G.
- Solve for y as a function of x. Again, this may or may not be
practical. Examples will help you to understand.
This method works because it is implicit differentiation in reverse. I
didn't discuss the reasoning because the examples right now are more
important.
Some examples
- Consider y´=y2 which is
dy/dx=y2. Here F(y)=y2 and G(x)=1. Well, the
first step gives dy/y2=dx. Now integrate both sides
(remember that 1/y2=y–2, please). We get
–1/y=x+C. This can be solved for y fairly easily, and so
y=1/(C–x). (Yes, if you are very alert you would have noticed that I
changed –C to C, and everyone does that, because I can stuff the minus
sign into the unknown constant C.) So at least I've shown you where
my guess above comes from.
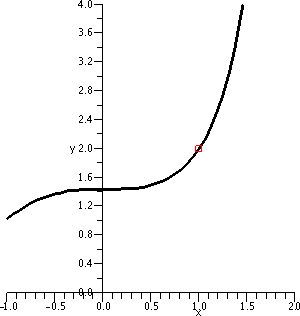 I've forgotten what I did, but I think it was something like:
let's find a solution of y´=x2y which goes through the
point (1,2). So if dy/dx=x2y then dy/y=x2dx and
then∫dy/y=∫x2dx so that
ln(y)=(1/3)x3+C. If we want this to "go through" (1,2) then
ln(2)=(1/3)13+C so that C=ln(2)–(1/3). And the particular
solution is ln(y)=(1/3)x3+ln(2)–(1/3). Most people,
especially in applications, prefer an explicit solution, so an attempt
to solve for y is made. I can do this here (the situation is simple)
but in general things may be too complicated. The equation
ln(y)=(1/3)x3+ln(2)–(1/3) can be exponentiated to give
y=e(1/3)x3+ln(2)–(1/3). Although for me on an
exam this would be fine, I would not want to mislead you. Again,
especially in applications, appropriate simplification is very
useful. Here this is what would be done:
I've forgotten what I did, but I think it was something like:
let's find a solution of y´=x2y which goes through the
point (1,2). So if dy/dx=x2y then dy/y=x2dx and
then∫dy/y=∫x2dx so that
ln(y)=(1/3)x3+C. If we want this to "go through" (1,2) then
ln(2)=(1/3)13+C so that C=ln(2)–(1/3). And the particular
solution is ln(y)=(1/3)x3+ln(2)–(1/3). Most people,
especially in applications, prefer an explicit solution, so an attempt
to solve for y is made. I can do this here (the situation is simple)
but in general things may be too complicated. The equation
ln(y)=(1/3)x3+ln(2)–(1/3) can be exponentiated to give
y=e(1/3)x3+ln(2)–(1/3). Although for me on an
exam this would be fine, I would not want to mislead you. Again,
especially in applications, appropriate simplification is very
useful. Here this is what would be done:
e(1/3)x3+ln(2)–(1/3)=e(1/3)x3eln(2)e–(1/3)=2e(1/3)[x3–1].
So the particular solution of y´=x2y satisfying the
initial condition y(1)=2 is
f(x)=2e(1/3)[x3–1]. Part of a graph of y=f(x) is
shown to the right. The function increases very quickly when x
is positive.
- Here is an important counterexample:
y´=x2+y2 is a differential equation which
is not separable. This is not totally obvious. Please let me
try to convince you.
If x2+y2=F(y)G(x) is true, I will "explore" the
possibilities using values of x and y. For example, if x=0 and y=0, we
see that 0=F(0)G(0). Therefore either F(0)=0 or G(0)=0 (or both, of
course). What if G(0)=0? Then try x=0 and y=1. The equation becomes
02+12=F(1)G(0), and this is 1=F(1)G(0). If
G(0)=0, this is impossible! If the alternative holds, that is, F(0)=0, just insert x=1 and y=0 to get a contradiction.
To the right is a picture of the solution curve to
y´=x2+y2 which goes through (1,2). The
function defining the curve can't be written in terms of the standard
functions you know. Quite a bit of computation is needed to produce
the rather simple-looking picture (the darn picture needs a dozen Bessel
functions combined in very strange ways).
Back to the salt tank ...
The differential equation dS/dt=5–[1/(16)]S is separable. There was
some difficulty in convincing students of this. Look:
5–[1/(16)]S=(5–[1/(16)]S)(1), and 5–[1/(16)]S is a function of S
alone, and 1 is a function of t alone.
Let's separate and solve. So dS/{5–[1/(16)]S}=dt, and the right-hand
side integrates to t+C. The left-hand side is maybe a bit more
intricate. You could substitute: w=5–[1/(16)]S so dw=–[1/(16)]dS and
dS=–16dw. The result is –16ln(w)=–16ln(5–[1/(16)]S). I generally
guess, get it wrong, and need to guess again. So after integrating we have
–16ln(5–[1/(16)]S)=t+C.
The initial condition here, a result of the tank originally being filled with pure water, is S(0)=0. So we can get C:
–16ln(5–[1/(16)]S)=t+C become –16ln(5–[1/(16)]0)=0+C and C is
–16ln(5).
The solution is –16ln(5–[1/(16)]S)=t–16ln(5). Most people prefer a
more explicit formulation, so we solve for S as a function of t.
Divide by –16: ln(5–[1/(16)]S)=–[1/(16)]t+ln(5).
Exponentiate: 5–[1/(16)]S=e–[1/(16)]t+ln(5).
Some algebra on the right:
e–[1/(16)]t+ln(5)=e–[1/(16)]teln(5)=5e–[1/(16)]t.
Now get S: 5–[1/(16)]S=5e–[1/(16)]t becomes
–[1/(16)]S=–5+5e–[1/(16)]t which turns into
S=80–80e–[1/(16)]t.
What does the solution look like?
If we believe S(t)=80–80e–[1/(16)]t, let's check the
initial condition:
S(0)=80–80e–[1/(16)]0=80–80·1=0. Good!
How about the long-range asymptotic behavior? That is, what happens
when t gets very large (t→∞)?
If t→∞, then
–[1/(16)]t→–∞,
so e–[1/(16)]t→0. The combination
80–80e–[1/(16)]t must therefore →80, which is what we
expected. Let's see what the S(t) curve looks like. But here, unlike
in class, I will try to explain the final picture.
| Here is 80e[1/(16)t for t between –50 and 0. This is
part of an exponential growth curve, and it starts small and increase
up to 80, the value at 0. It is concave up. |
Now I've flipped the curve across the vertical axis. This is
80e–[1/(16)t for t between 0 and 50. The curve is still
concave up, but it is decreasing: since the constant is negative, this is exponential decay. |
I flipped the previous curve across the horizontal axis. This is a
graph of –80e–[1/(16)t for t between 0 and 50. It is
concave down and increasing, from 80 to near 0. We'll get the real picture of S(t) by translating this up 80.
|
 |
 |
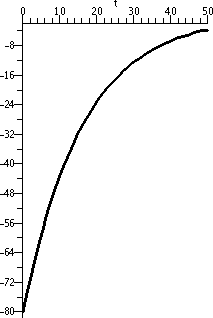 |
To the right is a graph of S(t)=80–80e–[1/(16)t for t
between 0 and 100. The dashed red horizontal line is at height 80, the
asymptotic level of the salt in the tank. You can see that the salt
starts at 0, the initial condition, and then increases and sort of
curves underneath the line at height 80. The curve is concave
down. The difference between 80 and S(t) becomes rather small as t
grows.
QotD
Find the solution of y´=y2x3 which goes
through (2,1). Be sure to write the solution as y=some function of x.
| Monday,
March 9 | (Lecture #13) |
|---|
 MVT simplified: just Rolle's Theorem
MVT simplified: just Rolle's Theorem
I wrote this on the board before the class began. It is a result I'll
use several times in the initial discussion. Here:
Suppose we have a differentiable function which is 0 at two distinct points. Then the derivative of
the function will be 0 at least once between
these two values.
Important and useful
Much of the remainder of the semester will be devoted to material
which is extremely useful to everyone involved with engineering and
science. Today is likely to be your first exposure to the ideas which
are generally used to compute values of functions. It is almost
certain that these ideas are at the center of how the calculators and
computers you use compute (and graph) most functions. You should know
something about these ideas.
When I taught this last year I jumped right into an example, and
didn't show people any of the structure. The examples, even the
easiest, can be intricate. I don't feel I was too successful here last
year, so I want to try a different approach today. Some of what I say
will not be in the textbook. I will begin with a totally
unmotivated question. The question will look somewhat weird.
What's K?
Suppose f(x) is a differentiable function, a and b are numbers with
a≠b, and we consider the equation:
f(b)=f(a)+f´(a)(b–a)+[f´´(a)/2](b–a)2+K(b–a)3.
Then there is some number K which makes this equation
correct. Why? Because since a≠b, (b–a)3 isn't 0, and I
could solve for K in this whole messy equation. So I want to
investigate what K is, and get another way of writing K. To do this I
will use the Mean Value Theorem repeatedly in the form quoted above.
Consider the function
G(x)=f(x)–(f(a)+f´(a)(x–a)+[f´´(a)/2](x–a)2+K(x–a)3).
What do I know about G(x)? Well, I know that G(a)=f(a)–(f(a)+f´(a)(a–a)+[f´´(a)/2](a–a)2+K(a–a)3) so that G(a)=0. I also know that G(b)=f(b)–(f(b)+f´(a)(b–a)+[f´´(a)/2](b–a)2+K(b–a)3). This is also 0 because K was chosen so that this
is true. So G(a)=0 and G(b)=0. Therefore (MVT/RT above) there is
some number in between a and b, I'll call it c1, so that
G´(c1)=0.
Now let's compute the derivative of G(x). There are many letters
around. I am differentiating with respect to x. With this in mind, I
see:
G´(x)=f´(x)–(0+f´(a)1+[f´´(a)/2]2(x–a)+3K(x–a)2).
Now what? Well, G´(a)=f´(a)–(0+f´(a)1+[f´´(a)/2]2(a–a)+3K(a–a)2) is 0 because of the a–a's and because the
f´(a)'s cancel. We also know that G´(c1)=0. Now
MVT/RT applied to the function G´(x) tells us that its derivative
is 0 somewhere between a and c1. That is, there is
c2 between a and c1 so that
G´(c2)=0.
Now let's compute the derivative of G´(x), again being
careful.
G´´(x)=f´´(x)–(0+0+[f´´(a)/2]21+3·2K(x–a)).
Of course we consider G´´(a) which is
f´´(a)–(0+0+[f´´(a)/2]21+3·2K(a–a)) and this is 0. Also G´(c2)=0. So
MVT/RT again applies to tell us that there is c3 between a
and c2 with G´´´(c3)=0. Wow.
The derivative of G´´(x):
G´´´(x)=f´´´(x)–(0+0+0+(3·2·1)(K)1).
Now we know when x=c3 this is 0. So we know that
f´´´(c3)–(3·2·1)K is
actually equal to 0. We can
solve this for K, and get
K=[f´´´(c3)/(3·3·1)].
c3 is between a and c2 and
c2 is between a and c1 and
c1 is between a and b so that c3 is itself
between a and b.
What's going on?
Here is what we know: If
f(b)=f(a)+f´(a)(b–a)+[f´´(a)/2](b–a)2+K(b–a)3.
then there is a number c between a and b so that
K=[f´´´(c)/(3·2·1)] (three of the ´
in this). This turns out to be
the beginning of a marvelous and successful computational strategy.
So what's your problem with all this? You might claim to not
understand what the heck is going on, and, more particularly,
why any moderately sane person might want to go through these
algebraic contortions. Yes I totally agree with
you. But it turns out (sit here, look at the fireworks (?) that
follow) this is extremely useful. There have been centuries
(!!) of thought involved in preparing and using all this stuff -- it
is really clever.
Taylor polynomials
This is copied from page 502 of your text. The Taylor polynomial of degree n for the function f(x)
centered at a (wow, what a collection of words!) is
Tn(x)=f(a)+f´(a)(x–a)+[f´´(a)/2](x–a)2+[f(3)(a)/3!](x–a)3+...+[f(n)(a)/n!](x–a)n
There are a whole bunch of things to discuss. Let's see. First, if
you've never seen it before, the appearance of the excitement
mark, !. This is called a
factorial. The value of the factorial of a positive integer is the
product of the integer together with all of the integers less than it
down to 1: n!=n(n–1)(n–2)(n–3)···(3)(2)(1). Here is a very brief table of factorials:
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|
| n! | 1 | 2 | 6 | 24 | 120 | 720 | 5,040 | 40,320 | 362,880 | 3,628,800 |
|---|
The major thing you should notice right now is that the factorials
grow very big very quickly. That's computationally important. I also
should mention that most people define 0! to be 1. That's so
certain formulas are easier to write (really). (It turns out to be
possible to define factorials of other numbers. For example, in 251,
you can define and compute (1/2)! -- wait for
that.)
More notation is in such things as f(4)(a). This means the
fourth derivative of f evaluated at a. So f´´(a) can also be
written as f(2)(a), and even just f´(a) is
f(1)(a). Again, in order to make writing certain formulas
easier, most people think that f(0)(a), the zeroth
derivative of f evaluated at a (so no derivatives are done!), should
just be f(a).
If all of this notation is clear, then here's another, very compact
way to write the Taylor polynomial.
Tn(x)=∑j=0n[f(j)(a)/j!](x–a)j.
I hope you can see where the zero factorial and zeroth derivative make
this much easier to write.
Example 1
Let's get T8(x) for sin(x) and a=0. So we need derivatives, and here they are:
| Derivative # | Function | Value at a=0 |
|---|
| 0 | sin(x) | 0 |
| 1 | cos(x) | 1 |
| 2 | –sin(x) | 0 |
| 3 | –cos(x) | –1 |
| 4 | sin(x) | 0 |
| 5 | cos(x) | 1 |
| 6 | –sin(x) | 0 |
| 7 | –cos(x) | –1 |
| 8 | sin(x) | 0 |
The numbers in the last column, together with the factorials, are the
coefficients which build the Taylor polynomial. I emphasized with all
of these examples that noticing patterns is the way to go. In the case
of sine, the derivatives repeated every four. I am not cheating
by choosing something excessively simple. Almost every function I know
that arises in modeling physical and geometrical situations has
patterns in its derivatives, and part of the fun (?) is finding these
patterns. Well, now I can write T8(x):
T8(x)=[0/1](x–0)0+[1/1](x–0)1+[0/2](x–0)2+[–1/6](x–0)3+[0/24](x–0)4+[1/120](x–0)5+
+[0/720](x–0)6+[–1/5,040](x–0)7+[0/40,320](x–0)8
Only a nitwit or a very pedantic math instructor would write it that
way. Most people would drop the 0 terms, change (x–0) to x, make a few
other notational simplifications,and get
T8(x)=x–[1/6]x3+[1/120]x5+[1/5,040]x7
Then there are some questions.
What is T4(x)? It must be
x–[1/6]x3.
What is T7(x)? It
must be
=x–[1/6]x3+[1/120]x5+[1/5,040]x7,
in this case just the same as T8(x).
What is
T10(x)? I bet it is the same as T9(x), and this
would be
T10(x)=x–[1/6]x3+[1/120]x5+[1/5,040]x7–[1/362,880]x9.
Graph of sin(x)
on the interval [–8,8].
 How can we compute values of the sine function? Here's a graph, but
even producing this graph requires a computer to get many values of
sine and then use them to pick out and color certain pixels. We could
construct a bunch of triangles, measure angles and lengths
carefully, and then get some values of sine. This is, more or less,
how things were done in Egypt and Greece. Certainly it is an intricate
process and very difficult to implement. But hundreds of years later,
a more systematic and accurate method was developed, first in India,
and then in Western Europe. The history in India was long
ignored. Here's a
web reference, and a more detailed and readable account is in an
article entitled Was Calculus Invented In India? by David
Bressoud, in the College Math Journal: Volume 33, 2002. If you are at
a Rutgers terminal, this
link should get you directly to the article (you might as well
take advantage of the fact that you're at a big-time university
purchasing big-time web access to lots of stuff!).
How can we compute values of the sine function? Here's a graph, but
even producing this graph requires a computer to get many values of
sine and then use them to pick out and color certain pixels. We could
construct a bunch of triangles, measure angles and lengths
carefully, and then get some values of sine. This is, more or less,
how things were done in Egypt and Greece. Certainly it is an intricate
process and very difficult to implement. But hundreds of years later,
a more systematic and accurate method was developed, first in India,
and then in Western Europe. The history in India was long
ignored. Here's a
web reference, and a more detailed and readable account is in an
article entitled Was Calculus Invented In India? by David
Bressoud, in the College Math Journal: Volume 33, 2002. If you are at
a Rutgers terminal, this
link should get you directly to the article (you might as well
take advantage of the fact that you're at a big-time university
purchasing big-time web access to lots of stuff!).
Graphs of sin(x) and
T1(x)=x
on the interval [–8,8].
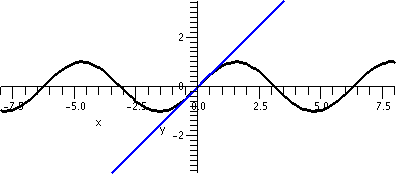 The start of this game is to look again at the tangent line
approximation which was discussed in calc 1. Let's try to
approximate sin(x) locally near 0. The tangent line goes through (0,0)
since sin(0)=0 (hey: one value of sine which is easy to know!) and it
has slope 1 since the derivative of sine is cosine and cos(0)=1. For
x's near 0, look at the picture, and realize that sin(x) will be
approximately equal to x.
The start of this game is to look again at the tangent line
approximation which was discussed in calc 1. Let's try to
approximate sin(x) locally near 0. The tangent line goes through (0,0)
since sin(0)=0 (hey: one value of sine which is easy to know!) and it
has slope 1 since the derivative of sine is cosine and cos(0)=1. For
x's near 0, look at the picture, and realize that sin(x) will be
approximately equal to x.
For example, sin(.05) is 0.04997916927,
so that's close. And sin(.0005) is 0.0004999999792: hey, lots
of agreement.
But what if we wanted sine's values for x's not
so close to 0, and what if we also wanted some measurement of
accuracy, some error analysis?
Graphs of sin(x) and
T3(x)=x–(1/6)x3
on the interval [–8,8].
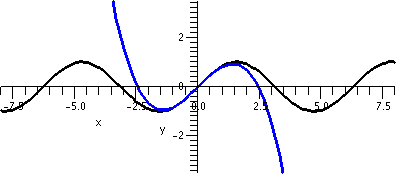 Now I displayed a mysterious (?) cubic (third degree) polynomial. It
turns out that this polynomial comes from a rather simple process, one
that can be described easily and efficiently to a computer or
calculator. In fact, it is a process which is simple enough so that
computations can be done by hand, as they were for several
centuries. The picture shows that the cubic polynomial stays closer to
sin(x) in a larger interval than the linear approximation, x, does. I
can't show you also a sort of microscopic picture, but I do assert
that cubic polynomial is a better approximation to sin(x) than just x alone. I'll give some numbers.
Now I displayed a mysterious (?) cubic (third degree) polynomial. It
turns out that this polynomial comes from a rather simple process, one
that can be described easily and efficiently to a computer or
calculator. In fact, it is a process which is simple enough so that
computations can be done by hand, as they were for several
centuries. The picture shows that the cubic polynomial stays closer to
sin(x) in a larger interval than the linear approximation, x, does. I
can't show you also a sort of microscopic picture, but I do assert
that cubic polynomial is a better approximation to sin(x) than just x alone. I'll give some numbers.
As I remarked, sin(.0005) is 0.0004999999792 to 10 digit accuracy. Of
course, the value of the polynomial "x" at .0005 is .0005. The value
of the polynomial x–(1/6)x3 at .0005 is, actually,
0.0004999999792 to 10 digit accuracy. In fact, more extensive
computation shows that they agree to 15 digits! I sincerely doubt that
anyone in this class will need 15 digits of accuracy in sine
computations.
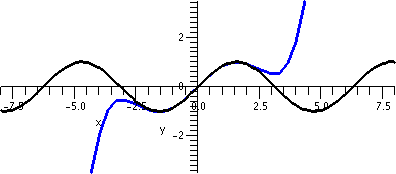
Graphs of sin(x) and
T5(x)=x–(1/6)x3+(1/120)x5
on the interval [–8,8].
Now the polynomial degree is 5, and the graph shows that this
polynomial again improves the accuracy of the approximation on a
larger interval.
Just a little more numerical evidence (all 10 digit accuracy):
sin(1)=0.8414709848; x at x=1 is 1., of course;
x–(1/6)x3 at x=1 is 0.8333333333, a bit closer;
and x–(1/6)x3+(1/120)x5 at x=1 is
0.8416666666, so the error is down to less than .001.
Graphs of sin(x) and
T9(x)=x–(1/6)x3+(1/120)x5–(1/5040)x7+(1/362880)x9
on the interval [–8,8].
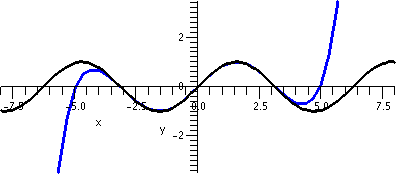 So I'm skipping a few polynomials and jumping up to the 9th
degree approximation. The numbers may look a bit strange (you will
get used to them!).
So I'm skipping a few polynomials and jumping up to the 9th
degree approximation. The numbers may look a bit strange (you will
get used to them!).
By now doing numerical computations is almost silly, but here is the
value of the 9th degree polynomial at x=1: it is
0.8414710096. This agrees with the true value of sin(1) to 6 places
(rounded). At x=.5, the approximation and true value agree to 10
decimal places.
Let me explain why T9(.5) and sin(.5) agree to so
many decimal places. Well, we need a generalization of the first
computation we did. Here is the result, a version of what's called
Taylor's Theorem:
If
Tn(x)=∑j=0n[f(j)(a)/j!](x–a)j,
then the difference between this and f(x) is
[f(n+1)(c)/(n+1)!](x–a)n+1 for some c between a
and x.
This is the error or remainder. In the case of sine and n=9, we need
to estimate
[f(n+1)(c)/(n+1)!](x–a)n+1 when a=0 and
x=.5. Well, the 10th derivative of sine is sine or –sine or
cosine or –cosine, and in any case the absolute value can't get bigger
than 1. So an overestimate of the absolute value of the error:
[f(n+1)(c)/(n+1)!](x–a)n+1
when a=0, x=1/2, and n=9 becomes [1/(10!)](1/2)10 and this is
[1/3,628,800](1/1,024) which is less than 10–10. That's
where the 10 place accuracy comes from.
Example 2
We get T8(x) for f(x)=ex and a=0.
| Derivative # | Function | Value at a=0 |
|---|
| ....blah.......blah.......blah.......blah.......blah..........blah... |
|---|
| any n you want! | ex | 1 |
| ....blah.......blah.......blah.......blah.......blah..........blah... |
|---|
T7(x)=1+x+[x2/2]+[x3/6]+[x4/24]+[x5/120]+[x6/720]+[x7/5,040]
It's supposed to be easy: this is a technique people actually use.
How good is T7(–.4) as an approximation to e–.4?
Here the remainder is
[f(n+1)(c)/(n+1)!](x–a)n+1
when a=0, x=–.4, and n=7 becomes
ec[1/(8!)](–.4)8. Now c is between –.4 and 0 and
since ex is increasing, the biggest value occurs at c=0,
where e0=1. (It is supposed to be easy, otherwise
people would not use it!) So the error is at most
[1/(8!)](–.4)8. This is less than .00000002.
The "true value" of e–.4 is 0.670320046035639
the value of T7(–.4) is 0.670320030476191. I had a machine
do these computations, of course. The reason I put quotes around "true
value" is that the machine used Taylor polynomials to do the
computation, of course.
QotDbr>
Suppose f(x)=x1/3 and a=8. Then f(8)=2. I asked people to
find T3(x)=f(8)+f´(8)(x–8)
+[f´´(8)/2](x–8)2
+[f´´´(8)/3!](x–8)3.
|
A silicon friend told
me that the answer may be
2+1/12*(x–8)–(1/288)*(x–8)^2+(5/20736)*(x–8)^3.
Remainder or error estimate in the textbook
There are many ways of estimating the error between the function f(x)
and the Taylor polynomial Tn(x). I think I've actually only
ever used one estimate, which is given in your book on page 506 and is
called the ERROR BOUND. The text also calls the error the
remainder. Here it is:
Suppose we want to consider f(x), maybe hard to compute, and the
nth degree Taylor polynomial centered at a,
Tn(x), which we hope is easier to compute. Then
|Tn(x)–f(x)|≤K[|x–a|n+1/(n+1)!]
where K
is some overestimate of |f(n+1)(x)| between x
and a.
|
The most important thing to notice here is the factorial
"downstairs". The growth of the factorial as n increases is what
frequently will make the error small. This actually happens in many,
many examples.
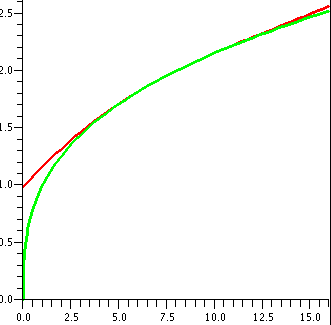 Let me show you a consequence of this estimate in connection with the
QotD. Here f(x)=x1/3 and
T3(x)=2+(1/12)(x–8)–(1/288)(x–8)2+(5/20736)(x–8)3.
To the right is a picture containing graphs of both y=x1/3
and y=T3(x) as x goes from 0
to 16.
Let me show you a consequence of this estimate in connection with the
QotD. Here f(x)=x1/3 and
T3(x)=2+(1/12)(x–8)–(1/288)(x–8)2+(5/20736)(x–8)3.
To the right is a picture containing graphs of both y=x1/3
and y=T3(x) as x goes from 0
to 16.
Look at the curves. Near x=8, the curves look very, very close. A bit
farther away, the curves separate. Indeed, the best way I can see
which curve is which is that x1/3 goes through (0,0) so
that must be the green curve.
I hope you can see that knowing the polynomial and using it instead
of x1/3 might be advantageous, maybe, maybe (you'll see
later but the idea is that polynomials are very easy to compute and
other functions might not be).
 To the right is another picture. Look at it very carefully
please. It is also a graph of both y=x1/3
and y=T3(x) as x goes from 6
to 10. Both curves are displayed. But I can only see one
curve. Maybe if I look really really really closely, maybe I can
see some dots of two colors but I am not sure. How close are these
curves?
To the right is another picture. Look at it very carefully
please. It is also a graph of both y=x1/3
and y=T3(x) as x goes from 6
to 10. Both curves are displayed. But I can only see one
curve. Maybe if I look really really really closely, maybe I can
see some dots of two colors but I am not sure. How close are these
curves?
Well, let's try to use the error estimate in the textbook. That error
estimate is quoted above. So an overestimate of the absolute value of
the difference between T3(x) and f(x) for x in [6,10] is
|Tn(x)–f(x)|≤K[|x–a|n+1/(n+1)!] where K
is some overestimate of |f(n+1)(x)| between x and a.
How can we use this? Well, here f(x)=x1/3 and n=3
and a=8 and the x's involved are between 6 and 10. So we need to
understand K[|x–a|n+1/(n+1)!]. This becomes
K[|x–8|4/4!]. Of course 4! is 24. What about
|x–8|? This is the distance from x to 8. If x is in [6,10], the
largest distance to 8 is 2, so |x–8| is always ≤2. Good: now
we know that the error is at most K[16/24] (because 24 is
16). What about K? To compute K we need f(4)(x). Well, here
are f(x) and a few of its derivatives:
f(x)=x1/3;
f´(x)=(1/3)x–2/3;
f´´(x)=f(2)(x)=–(2/9)x–5/3;
f(3)(x)=(10/27)x–8/3;
f(4)(x)=–(80/81)x–11/3.
I am interested in the absolute value (the size) of the
error, so I will forget the minus sign. Therefore I need to know how
large (80/81)x–11/3 can get on [6,10]. Because of the
negative sign in the exponent, this is a decreasing function of
x, and its largest value is at the left-hand endpoint. So the biggest
this can be is (80/81)6–11/3. O.k.: I give up -- I
will finally use a calculator. This number is about (rounding up!)
.0014, and I'll take that as my value for K.
 Therefore the error is at most (.0014)(16/24) and this is about
.00092. Now look carefully at the picture. Do you think you can
see a difference in height of less than .001? The difference
between two of the "hashmarks" on the vertical scale is .05, and the
graphs of the functions are separated by one-fiftieth (that's 1/50) of that
difference. I don't think that the pixels in the picture are small
enough to show this!
Therefore the error is at most (.0014)(16/24) and this is about
.00092. Now look carefully at the picture. Do you think you can
see a difference in height of less than .001? The difference
between two of the "hashmarks" on the vertical scale is .05, and the
graphs of the functions are separated by one-fiftieth (that's 1/50) of that
difference. I don't think that the pixels in the picture are small
enough to show this!
The picture to the right shown here is on a different interval, from 6
to 6.25 for x. The vertical scale is also different. Each vertical
hashmark here represents a height difference of .001, and now, in the
part of this interval which is farthest away from 8, near 6, I hope
you can indeed see two curves, separated by just a little bit. The error
estimate actually gives useful quantitative information.
|
| Wednesday,
March 4 | (Lecture #12) |
|---|
I wrote a version of L'Hôpital's Rule on the board, since I would need
it twice in the next few minutes. I copied it from the book (page 272).
L'H Suppose f(x) and g(x) are differentiable functions inside
an interval containing a and that f(a)=g(a)=0. Also assume g (x)
is not 0 for x near but not equal to a. Then f(x) f´(x)
lim ------ = lim ------
x→a g(x) x→a g´(x)
if the limit on the right-hand side exists. This result is also valid
if both of the limits of f(x) and g(x) as x→a are +∞ or
–∞.
It is very important that there is a quotient in the algebraic
form. Also, the symbolic quotients 0/0 or ∞/∞ are
sometimes called indeterminate forms.
 x·ln(x)
x·ln(x)
I asked people for the graph of y=x·ln(x) on the interval
[0,1]. Some people were willing to use their graphing calculators. A
graph much like what is shown to the left was produced.
The graph seems to be a slightly assymetrical bump below the x-axis,
hanging from (0,0) and (1,0). The "bottom" is at, about, –1/3 (near
x=1/3, actually). If you "ask" your computer or calculator for the
value of x·ln(x) at x=0, however, there will be some sort of
complaint rather than a number. The machines have been advised that 0
is not in the domain of ln. But the graph certainly seems to indicate
that (0,0) is there (wherever there is!). What's going on?
L'H
Really what the graph indicates is a suggested value for
limx→0+x·ln(x). The guess for this is
0. To verify this guess (in a math course!) we will use
L'Hôpital's Rule. As x→0+, we have a 0 multiplied by (–)
∞. L'Hôpital's Rule works on quotients, so we need to rearrange things algebraically. Here we go:
limx→0+x·ln(x)=rearranging=limx→0+[ln(x)/{1/x}]=using L'H=limx→0+[{1/x}/{–1/x2}]=rearranging back=limx→0+–x=0
so the limit is verified.
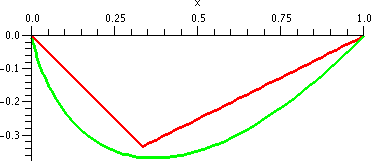 The integral
The integral
How much "area" is included in the bump above? More precisely, what is
the definite integral of x·ln(x) from 0 to 1. The bump is below
the x-axis so this integral should be negative. It sort of resembles a
triangle with base [0,1] and altitude about 1/3. So a guess is
that the area should be about –1/6. An actual
graph of the function and of this approximating
triangle is shown to the right. The function is concave down so
it bulges beneath the triangle. And, in fact, the "point" of the
triangle is above the graph. So there is more (absolute value!) area
in the bump than in the triangle.
Let's compute. The area is ∫01x·ln(x)dx. This is officially
an improper integral (it really is difficult to evaluate the integrand
at x=0!). So first I'll compute ∫Q1x·ln(x)dx for Q small positive,
and then let Q→0+. To use FTC we need an
antiderivative of x·ln(x). Integration by Parts again works. If
u=ln(x), then dv=x dx, and du=(1/x)dx and v=(1/2)x2. So:
∫x·ln(x)dx=(1/2)x2ln(x)–∫(1/2)x2(1/x)dx=(1/2)x2ln(x)–(1/4)x2+C
The definite integral is
(1/2)x2ln(x)–(1/4)x2|Q1=((1/2)Q2ln(Q)–(1/4)Q2)–((1/2)12ln(1)–(1/4)12).
L'H
I know that limQ→0+–(1/4)Q2=0 because
Q2 is continuous and I can just "plug in". What about
limQ→0+(1/2)Q2ln(Q)? Here we (officially!) need
L'Hôpital's Rule again. So:
limQ→0+(1/2)Q2ln(Q)=rearranging=limQ→0+(1/2)[ln(Q)/{1/Q2}=using L'H=limQ→0+(1/2)[1/Q}/{–2/Q3}=rearranging back=limQ→0+(–1/4)Q2=0.
If you now put everything together (and don't lose track of the minus signs!) you can see:
∫01x·ln(x)dx converges and its
value is –1/4. The –1/4 is certainly consistent with the estimate we
made earlier, backed up by the red and green graph.
A real application ...
This strange function with its somewhat strange graph is actually
related to a function used in applications. The function used in
applications is actually a bit more complicated (sigh). Here is how to
think about it.
|
A graph of y=x·ln(x) on [0,1]. The function is concave up and below the x-axis. The area is –1/4, as just computed.
|
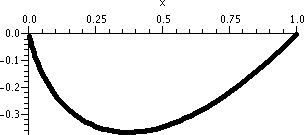
|
|
Flip the curve over the x-axis. So this is
a graph of y=–x·ln(x) on [0,1]. The function is concave down and above the x-axis. The area is +1/4, because now the region we're considering is above the x-axis.
|
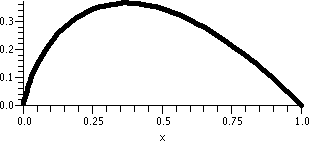
|
|
This is a more complicated flip. Replace x by 1–x. This is a flip which exchanges left and right because of the +/– change in the x multiplier. In fact, the left and right are exchanged, and the y-axis and x=1 are interchanged.
So this is a graph of y=–(1–x)·ln(1–x) on [0,1]. The function is concave up and above the x-axis. The area is 1/4.
|
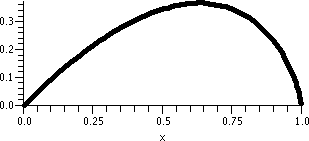
|
|
Now add up the two previous functions. Here is a graph of
y=–x·ln(x)–(1–x)·ln(1–x) on [0,1]. Yes, it
is weird. This function officially has two strange behaviors,
at both 0 and 1. The function is called the binary
symmetric entropy function and it is used to study the amount of
information flowing through a "channel" (you could think of a channel
as a wire, and the information as 0's and 1's -- bits). The entropy
function helps to analyze what happens in complicated situations where
there may be interference (noise). This function has one bump, and its total
area is 1/2.
|
|
Comment
You can't actually predict that the result of adding the two bumps
would be just one symmetric bump. In fact, that result may not occur.
|
Here is a graph of x[ln(x)]2 on [0,1]. Because of the
square, the function is positive, and the bump is more pronounced.
| And this is a graph of x[ln(x)]2+
(1–x)[ln(1–x)]2. So two distinct bumps
can show up. |
 |
 |
|
Two silly (?) formulas
The object of this lecture is to tell you about two formulas, one for
arc length and one for surface area (both discussed in section 8.1). I
called the formulas silly because of their limited usefulness, at
least limited in the sense that "hand computation" using FTC is not
very practical. Both arc length and surface area will be revisited in
calc 3, where much better perspectives can be given for both.
The philosophy behind the definite integral and its use
Maybe the formulas are not totally silly. Both of them are
illustrations of how definite integrals can be used to compute various
quantities. The procedure (which we have already used in various area
and volume situations, and also with work) represents an attempt to
compute "something" complicated:
- Break up the complicated quantity into little pieces.
- Approximate the little pieces by something simple.
- Add up the little pieces, and take a limit.
With some luck and skill and ... whatever, the errors which occur will
be small, and as the number of subdivisions or pieces or whatever
grow, the total error will get small.
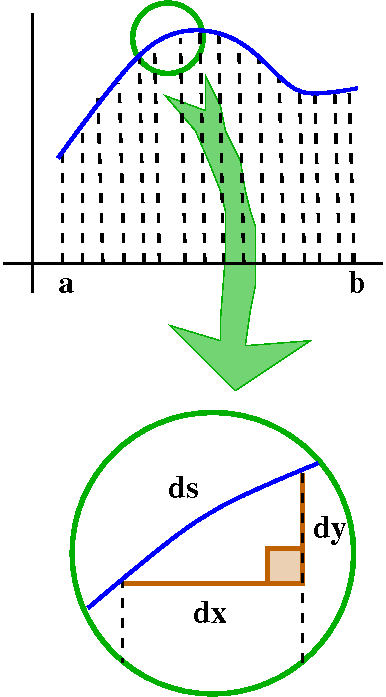 Arc length
Arc length
We're given a function, f(x), defined on the interval [a,b].
The quantity to be computed is the length of the graph, the curve
y=f(x). This is called arc length. Here is the idea.
Break up [a,b] into many little subintervals, whose length we will
call dx (or Δx). "Above" each little subinterval is a little
piece of the curve. The usual name for a little piece of curve is
ds. If you magnify the little piece, as shown, well, the result is
almost a right triangle. The curve length is still somewhat curvy,
but, well, maybe I can approximate it by a straight line segment. The
resulting picture is just about a right triangle. dy is the change in
y (the function) when the input variable, x, Pythagoras then
declares that (ds)2 should be the same (really,
approximately the same!) as
(dx)2+(dy)2. Therefore
ds=sqrt{(dx)2+(dy)2). Let's rewrite what's
inside the square root:
(dx)2+(dy)2=(dx)2(1+{dy/dx}2).
So sqrt(=(dx)2(1+{dy/dx}2))=dx·sqrt(1+{f´(x)}2).
Now we should add up these pieces and take limits. In this context,
this is all done by writing a definite integral. So the arc length
formula is ∫absqrt(1+[f´(x)]2)dx.
This is the official formula. Let's see how well it works with some
examples.
 Line segment
Line segment
Maybe the simplest curve is a straight line segment. Let me "find" the
length of the line segment joining (1,1) and (4,3). This should be the
same as the distance from (1,1) to (4,3), which is (square root of the
sum of the squares!) sqrt(13). Let's find this number using the
calculus formula above.
We need a formula for the line segment. The slope will be
(3–1)/(4–1) which 2/3. So f(x)=(2/3)x+something. What will the
"something" be? Since the line should pass through (1,1), when we put
x=1, the result should be 1. Therefore (2/3)(1)+something=1, so
something is 1/3. The formula is f(x)=(2/3)x+(1/3). The derivative is
f´(x)=(2/3). Now the arc length is ∫absqrt(1+[f´(x)]2)dx
which is
∫14sqrt(1+[2/3]2)dx. The
integrand is a constant, so the result is
sqrt(1+[2/3]2)x|14=sqrt(1+[2/3]2)4–sqrt(1+[2/3]2)1=sqrt(1+[2/3]2)3.
This is the same as sqrt(13).
 Circle
Circle
Maybe the next curve to look at is a circle, but we need the graph of
a function so let's try to find the arc length of a
semicircle. Let's look at the upper semicircle, radius 5, center at
(0,0). For this curve, f(x)=sqrt(52–x2). Now I
need sqrt(1+[f´(x)]2). So:
f´(x)=(1/2)(52–x2)–1/22x using
the Chain Rule. The 2's cancel, and we need to square the derivative,
so:
(f´(x))2=(52–x2)–1x2
but this is the same as x2
-----
52–x2 to which we must add 1:
x2 52–x2+x2 52
1 + ----- = --------- = ------
52–x2 52–x2 52–x2
Finally we supposed to take the square root of this result, so that
the integral we need to compute is ∫–55
5/sqrt(52–x2)dx.
This should look slightly familiar. The trig substitution x=5sin(θ) makes this integral into
∫5θ dθ=5arcsin(x/5)+C. I am skipping the
details because I've done many of these integrals already. Now
evaluate the definite integral:
5arcsin(x/5)|–55=5arcsin(1)–5arcsin(–1),
and (since I know arcsin(1)=Π/2 and arcsin(–1)=–Π/2) this works out
to 5Π, which is indeed half the circumference of a circle of radius
5.
|
Problems in the book
These two curves work out fairly well. But let's look at section 8.1,
and some of the problems there. The problems mostly have the form,
"Find the length of the graph of the function defined by the following
formula" and I think the instructions should be modified to read "the
following absurd formula." Here are some of the formulas from there:
(1/12)x3+x–1 (problem #3)
(x/4)4+(1/{2x2}) (problem #4)
x3/2 (problem #7)
(1/3)x3/2–x1/2 (problem #8)
(1/4)x2–(1/2)ln(x) (problem #9)
ln(cos(x)) (problem #10)
{ex+e–x}/2 (problem #18)
Why didn't the book ask something simpler, instead of functions
defined by such bizarre formulas? Let's see why. I will answer problem
1 of section 8.1, which asks for the arclength of y=x4
between x=2 and x=6. The problem actually asks only for the definite
integral and adds but do not evaluate.
We consider
∫absqrt(1+[f´(x)]2)dx. Here
a=2 and b=6, and since f(x)=x4,
f´(x)=4x3. The answer to problem 1 is therefore
∫26sqrt(1+16x6)dx.
What about evaluation? In the sense most often used in calculus
courses, this integral can't be evaluated. That is, there is no
antiderivative of sqrt(1+16x6) which can be written in terms
of standard functions. This isn't because we're ignorant, but because
it is impossible to do this. If you wanted to compute this
arclength, you would need to use one of the numerical techniques.
The secret to the problems in the textbook which were quoted above is
that all of the bizarre functions were selected so that
sqrt(1+[f´(x)]2) becomes something which it is
possible to integrate (in the sense of "find an antiderivative and use
FTC"). I did problem #18. Here it is.
Section 8.1, problem #18
Let's find the arc length of f(x)=(ex+e–x)/2
from x=–10 to x=10. Now
f´(x)=(ex–e–x)/2. Now let's
square.
(ex)2 –2 +(e–x)2
(f´(x))2= ------------------
4
All sorts of subtle things are going on here. Notice that
(–e‐x)2
is written (e‐x)2 because the two minuses
cancel. Also notice that –2 is really
–2exe–x. Now another subtle
observation: 1=4/4. Therefore (look closely!)
(ex)2 –2 +(e–x)2 4 + (ex)2 –2 +(e–x)2
1+(f´(x))2= 1+ ------------------ = ---------------------
4 4
Now the top of that fraction is (ex)2 +2
+(e–x)2. Realize that 2 is
2exe–. Notice (not an accident!)
that this top is actually a "perfect square". It is
(ex+e–x)2. So the mysterious
and almost always horrible sqrt(1+(f´(x))2) becomes,
in this case, exactly (ex+e–x)/2. Wow. The
arc length integral is
∫–1010[(ex+e–x)/2]dx
and this is (ex–e–x)/2|–1010, which is
[(e10–e–10)/2]–[(e–10–e10)/2]=e10–e–10.
These functions and these graphs
The functions quoted from the problems in section 8.1 are mostly
rather silly. This one, (ex+e–x)/2, is
not. Some pictures:
ex
Exponential growth |
e–x
Exponential decay |
(ex+e–x)/2
The average of the
two |
|---|
 |
 |
 |
The curve shown in the third box is called a catenary, and it is
the curve a uniform chain describes. The function
(ex+e–x)/2 is called the
hyperbolic cosine and is usually abbreviated cosh(x)
(pronounced cosh ecks). Its derivative is (naturally!) the
hyperbolic sine,
(ex–e–x)/2, and is abbreviated
sinh(x) (pronounced cinch ecks). Really.
"Truth"
The truth for arc length is that, more or less, the computability of
the arc length integral using FTC is impossible almost all of
the time! Therefore, from the elementary, student point of view, maybe
this is all a waste of time. But, really, it isn't. As soon as you
give me a definite integral and want to approximate the values, there
are all sorts of strategies. So what's important is that arc length
can be computed by a definite integral, and what's important for you
to try to understand is the philosophy of going from the vague idea of
arc length to the integral formula for the arc length. And that
philosophy will now be displayed again as we get an integral formula
for a certain type of surface area.
 Surface area
Surface area
Suppose we are again given a function y=f(x) defined on an interval
[a,b]. I would like to "compute" (the quotes are because we will get a
definite integral formula which will share the benefits and defects of
the previous result) the surface area which results when the
graph of y=f(x) is revolved around the x-axis.
We will get our formula using the same philosophical approach. We can
chop up [a,b] into many little pieces, each having length, say,
dx. Then (the picture!) the little piece of arc length laying over dx,
which we called ds, will be revolved around the x-axis. This gets us a
sort of ribbon. What is the area of that ribbon? We won't be able to
compute it exactly, but maybe we can approximate the area of the
ribbon nicely. Well, we can take the magic scissors (hey: I was able
to draw the darn scissors almost correctly this time!) and cut the
ribbon and then, sort of, almost, lay it out flat. The result will
sort of, almost, be a rectangle. What are the dimensions of this
rectangle? One side is the length of the piece of arc, ds. The other
side is the circumference of a circle whose radius is f(x), the height
of that part of the curve away from the x-axis. (The reason for the
repeated "sort of, almost" is that this is actually a distortion of
the true value - the ribbon really would not lie flat, and the ribbon
really would not be more than an approximate rectangle. I will try
later to address these sorts of slight (?) distortions.) So a piece of
the surface area is 2Π f(x) ds. We use a definite integral
to get the total surface area and add everything up. The result for
the area when the curve is revolved around the x-axis is ∫ab2Π f(x)sqrt(1+[f´(x)]2)dx.
Notice that sqrt(1+[f´(x)]2)dx (this uses what we had
for ds).
Sphere
Here is a result from a long time ago (thousands of years!): the
surface area of a sphere of radius R is 4Π R2. (This
is the area of four "great circles" of the sphere, circles made by
intersecting a plane with the center of the sphere.) I would like to
verify this result using the surface area formula. I'll use the same
semicircle as before: f(x)=sqrt(52–x2), with
a=–5 and b=5. Please note that revolving this semicircle around the
x-axis gets the area of the whole sphere of radius 5, so that the
answer should be 4Π(52).
We need to compute ∫ab2Π f(x)sqrt(1+[f´(x)]2)dx.
Notice that sqrt(1+[f´(x)]2)dx is what we called ds before, and we
did compute ds in a previous example. We
saw that ds was equal to 5/sqrt(52–x2)dx. But
f(x)=sqrt(52–x2) so, wow! (yeah, wow) there is
cancellation and the arclength becomes ∫–55(2Π)5dx which does indeed work out
to 100Π as it should.
More "truth"
There are very few simple powers of x (x2 and x3
and maybe x1) which give me integrands in the surface area
formula that I can find antiderivatives of. (That's a horrible
sentence!) If I want to compute surface areas for almost any "random"
function defined by a formula, I'll need to use numerical
approximations.
|
Returning the exam
The exam was returned. Also
available are an answer sheet and a discussion of the grades and
grading.
| Wednesday,
February 25 | (Lecture #11) |
|---|
Improper integrals: what are they?
 So far we have
discussed computing standard definite integrals. Although certainly a
definite integral like ∫abf(x)dx can represent many different
ideas, the most familiar instantiation is as an area (asssuming that
f(x)>0 for x in [a,b]) bounded by the x-axis, x=a, x=b, and the
graph of y=f(x). In most of the computations we've done, the function
f has been rather "nice" -- differentiable, mostly, and only a few
times has it had some discontinuities. In fact, there are many
applications where this simplicity is made more complicated because
the applications themselves demand a
"stronger" kind of integral.
So far we have
discussed computing standard definite integrals. Although certainly a
definite integral like ∫abf(x)dx can represent many different
ideas, the most familiar instantiation is as an area (asssuming that
f(x)>0 for x in [a,b]) bounded by the x-axis, x=a, x=b, and the
graph of y=f(x). In most of the computations we've done, the function
f has been rather "nice" -- differentiable, mostly, and only a few
times has it had some discontinuities. In fact, there are many
applications where this simplicity is made more complicated because
the applications themselves demand a
"stronger" kind of integral.
|
 For example, we might consider a situation where, say, b gets larger
and larger and
larger. Where, say, b→∞. I will give a real physical example of this at the next
lecture. This integral will have a domain which is an infinite
interval. It could be [a,∞) or
(–∞,b] or even (–∞,∞). Such integrals also occur very frequently in statistics
(and therefore they "infiltrate" almost all experimental sciences!).
For example, we might consider a situation where, say, b gets larger
and larger and
larger. Where, say, b→∞. I will give a real physical example of this at the next
lecture. This integral will have a domain which is an infinite
interval. It could be [a,∞) or
(–∞,b] or even (–∞,∞). Such integrals also occur very frequently in statistics
(and therefore they "infiltrate" almost all experimental sciences!).
A completely naive interpretation of the area would declare
that since the length of the base is infinite, the total area must
somehow be forced to be infinite. More subtly, the height in certain
cases will decrease fast enough so that the total integral can be
thought of as finite.
|
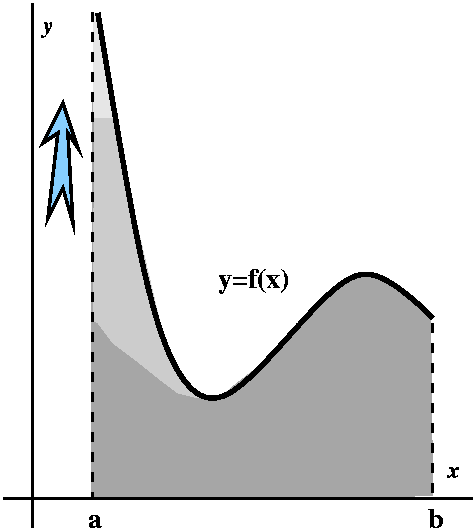 There may also be a sort of defect (?) in the range of f. For
simplicity, consider the situation where, although f is "nice" for
x>a, as x→a+, f(x) gets larger and
larger and larger: in fact, we might need
to try to "integrate" or compute the value of ∫abf(x)dx even if
f tends to ∞ as x→a.
There may also be a sort of defect (?) in the range of f. For
simplicity, consider the situation where, although f is "nice" for
x>a, as x→a+, f(x) gets larger and
larger and larger: in fact, we might need
to try to "integrate" or compute the value of ∫abf(x)dx even if
f tends to ∞ as x→a.
Again, a first look could convince you that such "areas" need to be
infinite, also, because the height is infinite. But, actually, the way
f grows as x→a+ is what matters. It is possible to
imagine that the growth of f is so controlled that the total
approximating areas don't tend to ∞. And maybe, in such
situations, we should be able to compute the integral.
I will first consider the "defect in the domain" case.
Toy example #1
Look at y=1/x2. The integral ∫1B(1/x2)dx (I'm using B as an
abbreviation for BIG) can be computed directly:
∫1B(1/x2)dx=–1/x|1B=1–(1/B) (be careful of the signs!)
Now if B→∞, certainly
1–(1/B)→1. Then we will declare that the improper integral
∫1∞(1/x2)dx converges and its value is 1.
Toy example #2
Look at y=1/x. Consider the analogous integral ∫1B(1/x)dx (again think of B as
a BIG number). We compute it:
∫1B(1/x)dx=ln(x)|1B=ln(B)–ln(1)=ln(B)–0
I wanted also to consider here the behavior as B→∞, but some students seemed to be
confused (this is confusing!). What does happen to ln(B) when B
gets large? If you only have a loose idea of the graph in your head,
well the log curve might not look like it is increasing too
fast. Well, it actually is not increasing very fast, but it is
increasing. Look: ln(10) is about 2.3, so ln(102)=2ln(10)
is about 4.6 (that's 2·2.3), and ln(103)=3ln(10) is
about 6.9 (that's 3·2.3), etc. Here etc. means I can get values
of ln as large as I want by taking ln's of large enough powers of 10
(hey, ln of 105,000 is bigger than ... 10,000: so
there!). So the values of ∫1B(1/x)dx do not approach a specific number as B→∞. Therefore we say:
the improper integral
∫1∞(1/x)dx diverges.
The distinction between converges (approaches a specific finite limit)
and diverges (does not approach a specific finite limit) is the one
that is important in applications and that motivates the distinct use
of the two words.
Geometric constrast
I love pictures. I like computation, but I can barely tolerate (!)
"algebra". But I introduced the actual definition of {con|di}vergent
improper integrals with some algebra, and didn't draw any
pictures. Why? Well, because pictures, while useful, don't help too
much. Here are qualitative pictures of the
two graphs.
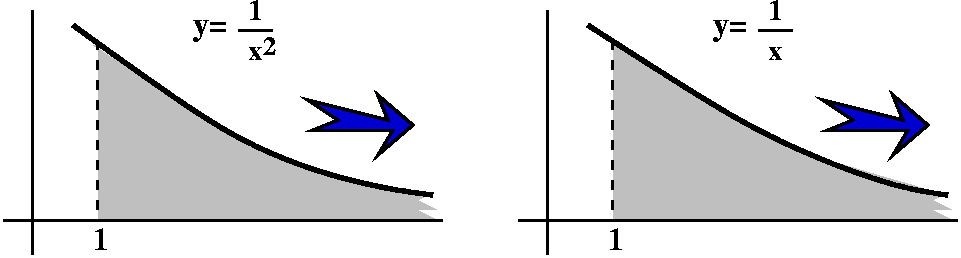
Well, they are actually different graphs, sorta. But I wanted
to emphasize, through sketching them not too carefully (and on
different axes, without scales!) these curves both "start at" (1,1),
and as they go right, are always positive, decreasing, concave up,
with 0 as limits. My eyes, at least, can't tell that one of them (on
the left?) has finite total area, and one of them (to the right!) has
infinite total area. The difference is quite surprising.
The exponential probability distribution
 Many real-life phenomena are described using something called the
exponential probability distribution. For example, the probable life-time of a lightbulb could be described with it. See here for more information.
Many real-life phenomena are described using something called the
exponential probability distribution. For example, the probable life-time of a lightbulb could be described with it. See here for more information.
I will just discuss lightbulbs now. Here is a first attempt to
be precise. If the probability that a light bulb will fail in t
minutes is proportional to e–Ct then the lifespan of the
bulb is said to have an exponential probability distribution. More
specifically, if t=0 is NOW, and t1<t2 are
later times, then then the probability of lightbulb failure between
the times t1 and t2 is proportional to ∫t1t2e–Ctdt.
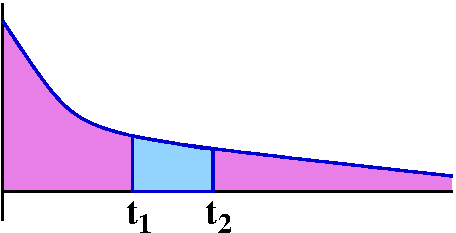
That is, that portion of the area to the right which is shaded
blue represents the chance of a lightbulb burning out during that
particular time interval.
What is the total probability from NOW to FOREVER?
Every (real!) lightbulb is going to fail some time. Probabilities of
an event range from 0 to 1, where an event which is certain
will have probability 1. Since any lightbulb will fail between t=0
(NOW) and t=∞ (FOREVER), we should consider the (improper)
integral ∫0∞e–Ctdt. Let me analyze this carefully.
Suppose A is a large positive number. Let's compute ∫0Ae–Ctdt=–(1/C)(e–Ct)]0A=–(1/C)e–CA+(1/C)e0=(1/C)–(1/C)e–CA.
The antiderivative has a –(1/C) factor because when e–Ct is
differentiated, the Chain Rule produces a multiplicative –C, and the
–(1/C) cancels this. Now what happens to (1/C)–(1/C)e–CA as
A gets large, A→∞? e–CA (with a negative sign,
with A and C positive) must go to 0 (this is exponential
decay). Therefore the improper integral ∫0∞e–Ctdt converges,
and its value is 1/C. But, wait: since every lightbulb fails,
shouldn't this be 1? Yes, surely. Let's fix this up. The key is
"proportional to". We should multiply the function e–Ct by
a constant so that the improper integral will turn out to be 1. The
computation we just did shows that the constant should be C. So the
probability distribution is actually Ce–Ct.
The {expectation|mean|average} of an exponential probability
distribution
Let me try to discuss something a little bit harder. First, some
background with (maybe) some easier ideas. We could imagine a
population of, say, bugs. Maybe there are three types of bugs in
my bug collection and I know the following information:
| My bug collection |
|---|
| Bug type | Observed lifespan | Proportion in
my collection |
|---|
| Orange spotted bug |
20 days |
30% |
| Blue striped bug |
50 days |
50% |
| Red plaid bug |
80 days |
20% |
What is the average lifespan of this bunch of bugs? Well, it isn't the
average of the 3 lifespans (the sum of 20, 50, and 80 divided by 3 --
a rather naive computation) since that doesn't take into account the
varying proportions of the bug types. If you think about it, the
average in this case is
20·(.3)+50·(.5)+80·(.25): a sort of weighted sum. It is a
sum of lifetimes multiplied by the proportion of the population. You
should convince yourself that this is the correct number.
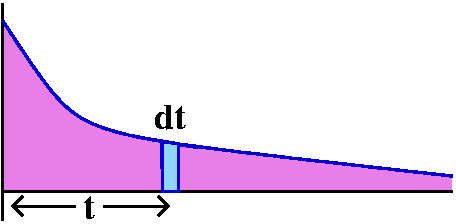
What about lightbulbs? What proportion of a lightbulb population will
"die" at time t? Well, that proportion is about
Ce–Ctdt. The appropriate weighted sum in this case
multiplied the proportion by t and adds it all up with an integral:
∫0∞tCe–Ctdt. If we
compute this integral, we maybe can get some idea of when an average
lightbulb dies. This quantity is called the mean or the expectation.
We can compute ∫tCe–Ctdt using integration by parts. If u=t then
dv=Ce–Ctdt and du=dt and v=–e–Ct. Therefore
uv–∫v du is
–te–Ct–∫–e–Ctdt=–te–Ct–(1/C)e–Ct.
The definite integral from t=0 to t=A is
–te–Ct–(1/C)e–Ct]0A=–Ae–CA–(1/C)e–CA–{–(1/C)e0}.
What happens at A→∞? Well, e–CA certainly goes to
0 (radioactive decay!). But the term Ae–CA has a sort of
conflict. Although the exponential decays, certainly A→∞?
Which factor "wins"? Exponential decay is faster than any degree of
polynomial growth, actually, so the limit is 0. You certainly can see
this with L'Hopital's rule:
limt→∞te–Ct=limt→∞t/[eCt]=limt→∞1/[Cexp(Ct)]=0.
So the integral from 0 to A, as A→∞, approaches a limit,
which is –{–(1/C)e0}=(1/C). This is the average
lifespan of a lightbulb. Incidentally, if we want to check that this
is a valid model, we can look at sample lifespans, and this can be
used to identify the value of the parameter C. The average lifespan
written on a package I just examined is 750 hours. Other technical
words which refer to average lifespan are mean and
expectation.
Other things ...
People who study statistics are interested in more details about life
and lightbulbs than are described here. For example, they may want to
know how dispersed the lifespans are around the mean. That is,
do all of the lightbulbs tend to die out right around 1/C, or is there
a considerable amount of variability? Various numbers measure this,
including variance and standard deviation. They all need computation
of ∫0∞t2Ce–Ctdt, a
different improper integral.
Another kind of improper integral
The integrals we've looked at are called improper because their
domains are infinite. But there is another collection of integrals
which are also labeled improper because something goes wrong in their
ranges: the function to be integrated becomes infinite. Here are some
simple examples.
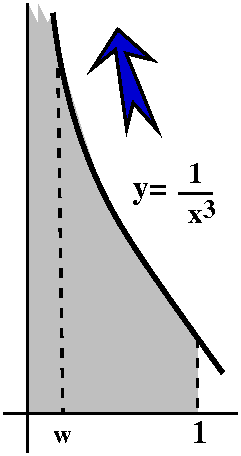
Toy example #1
Let's look at ∫01(1/x3)dx. Here
f(x)=1/x3 and surely as x→0+,
f(x)→+∞. Here is the official way to analyze this
improper integral. Suppose that w is a small positive number. Compute
∫w1(1/x3)dx. We can do this with
FTC by finding an antiderivative. The integral is
–1/(2x2)]w1=
–1/(2·12)–[–1/(2·12)]=(1/2w2)–(1/2).
Now as w→0+, certainly this→+∞. Therefore
the improper integral ∫01(1/x3)dx
diverges.
The picture accompanying this is, again, useless. It helps me to
organize the computation, but does not show enough quantitative
information to help decide convergence or divergence.
Toy example #2
Let's look at ∫01(1/sqrt(x))dx.
This became the QotD. In fact, this integral converges
and its value is 2.
|
Here is an extended example of how to use improper integrals in a
physical setting. I've used this example in our 152 instantiations,
but don't have time this semester.
Escape velocity
When I was very young, I read a science fiction novel by Robert
Heinlein which stated "... the escape velocity from the Earth is 7
miles per second ..." and now I would like to sort of verify this
using only well-known (?) facts and some big ideas of physics.
|
The radius of the earth
Well, a sketch of the (continental)
United States is shown to the right. There are 4 time zones. The
U.S. is about 3000+ (maybe 3200?) miles wide. Therefore one time zone
is about 1000 miles wide (I think the Pacific time zone actually slops
a bit into the ocean), and since there are 24 time zones around the
world, the circumference of the world is ... uhh ... about 25,000
miles. Or so. And therefore the radius of the earth is that divided by
2Pi, and therefore the radius of the earth is about 4,000 miles.
|  |
Newton and gravitation Two masses attract each other with a force
whose magnitude is proportional to the product of the masses and
inversely proportional to the square of the distance between
them. Therefore, if I have a mass, m, and if the Earth has mass M, the
magnitude of the force of gravity is GmM/r2. G is a
constant.
Work lifting up Suppose we want to lift a mass m from the surface
of the earth to a distance R, where R is very large. Then the work
done is force multiplied by distance. The force needed to act against
gravity certainly changes with distance. So I will compute the work
with calculus. If x is some distance between 4,000 and R, then the
force is GmM/x2. If the distance is a little bit, say, dx,
then the work dW needed is GmM/x2 dx. The total work,
W, is ∫x=4,000RGmM/x2 dx which
I can compute readily as –GmM/x]4,000R=GmM({1/4,000}–1/R). I
think I did the minus signs correctly. Notice that as R→∞,
this work →GmM/4,000: this is the most work you can do, to get
anywhere in the universe (assuming the universe is empty except for
the mass m and the earth, of course).
Kinetic energy How much kinetic energy would we need to supply
to the mass m so that it would equal the potential energy the mass
would have if it were lifted out to anywhere in the universe?
Well, kinetic energy is (1/2)mv2 and that potential energy
we already computed is GmM/4,000. So (1/2)mv2=GmM/4,000,
and thus v2=2GM/4,000. But what is GM?
But F=ma On the earth, a, the acceleration of gravity, is 32
ft/(sec)2. Yes, this is an archaic system of measurement,
but that's part of the fun. But also F=GmM/(4,000)2. So
GmM/(4,000)2=32m. Therefore
GM=(4,000)2·32.
And the answer is
...
v2=2GM/4,000=2[(4,000)2·32]/4,000=8,000·32=
(256,000)/(5,280)=(approximately)50. The 5,280 came from converting
feet to miles. Therefore v, the escape velocity, is about 7mps. I think
this computation is so silly that it is cool.
|
| Monday,
February 23 | (Lecture #10) |
|---|
This was our first exam.
Maintained by
greenfie@math.rutgers.edu and last modified 2/26/2009.
 As I mentioned in class, as n→∞ jumping to the
"conclusion" may be unwise. There are actually two cases. If x=0, the
limit is 0, If x≠0, the limit does not exist (it is "∞"). So we
can conclude that the series
∑n=1∞nnxn
converges exactly when x=0.
As I mentioned in class, as n→∞ jumping to the
"conclusion" may be unwise. There are actually two cases. If x=0, the
limit is 0, If x≠0, the limit does not exist (it is "∞"). So we
can conclude that the series
∑n=1∞nnxn
converges exactly when x=0.
 In this example, there aren't any special cases. For any x,
limn→∞|x|/n=0=L. Since L<1 always, the series
∑n=1∞xn/nn
converges absolutely for all x's and therefore converges for all x's.
In this example, there aren't any special cases. For any x,
limn→∞|x|/n=0=L. Since L<1 always, the series
∑n=1∞xn/nn
converges absolutely for all x's and therefore converges for all x's.
 For which x's does
∑n=1∞xn/n converge? We used
the Ratio Test, and |an+1/an| simplified fairly
easily to |x|[(n+1)/n]. Now L'H or simple algebraic manipulation shows
that ρ=|x|. So we get guaranteed absolute convergence and
therefore convergence when |x|<1 and divergence when |x|>1. For
|x|=1, we don't get any information. I'll write the answer using
interval notation now: if x is in (–1,1), the series
converges. If x is in (1,∞), the series diverges. If x is in
(–∞,–1), the series diverges. There's no information
for x=1 or x=–1.
For which x's does
∑n=1∞xn/n converge? We used
the Ratio Test, and |an+1/an| simplified fairly
easily to |x|[(n+1)/n]. Now L'H or simple algebraic manipulation shows
that ρ=|x|. So we get guaranteed absolute convergence and
therefore convergence when |x|<1 and divergence when |x|>1. For
|x|=1, we don't get any information. I'll write the answer using
interval notation now: if x is in (–1,1), the series
converges. If x is in (1,∞), the series diverges. If x is in
(–∞,–1), the series diverges. There's no information
for x=1 or x=–1.
 If you insist on knowing what happens at x=+/–1, let's
"insert" these values of x into the series and investigate.
If you insist on knowing what happens at x=+/–1, let's
"insert" these values of x into the series and investigate. To see what happens at x=+/–1, put these values of x into the
series and investigate the result directly (I don't know any other
ways to do this).
To see what happens at x=+/–1, put these values of x into the
series and investigate the result directly (I don't know any other
ways to do this). When x=1, the series is
∑n=1∞n=1+2+3+4+... and this certainly
diverges because the terms don't approach 0. The same reason shows
that the series diverges when x=–1. So the result, as shown, is
again slightly changed.
When x=1, the series is
∑n=1∞n=1+2+3+4+... and this certainly
diverges because the terms don't approach 0. The same reason shows
that the series diverges when x=–1. So the result, as shown, is
again slightly changed.
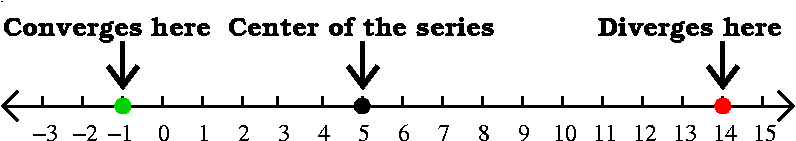 Suppose that you have a power series
∑n=0∞an (x–5)n
centered at x0=5. You are told that the series converges
when x=–1 and diverges when x=14. What can you say about the
radius of convergence? For which x's must this series converge
and for which x's must this series diverge? You are given no
other information.
Suppose that you have a power series
∑n=0∞an (x–5)n
centered at x0=5. You are told that the series converges
when x=–1 and diverges when x=14. What can you say about the
radius of convergence? For which x's must this series converge
and for which x's must this series diverge? You are given no
other information.

 What about the Ratio Test limit? We need to multiply by |x| since we
discarded it to get the fraction we just studied. So in this
complicated case, ρ=|x|(1/3). We get convergence (actually
absolute convergence) when ρ<1, which means that |x|<3. The
x's which satisfy this are an interval from –3 to 3 (not including the
endpoints). We get divergence when |x|>3. So for those x's
satisfying either –∞<x<–3 or 3<x<∞ there is
divergence. The Ratio Test doesn't work if x=3 or if x=–3. It turns
out that this situation is typical, and we will look at more examples
and more detail next time.
What about the Ratio Test limit? We need to multiply by |x| since we
discarded it to get the fraction we just studied. So in this
complicated case, ρ=|x|(1/3). We get convergence (actually
absolute convergence) when ρ<1, which means that |x|<3. The
x's which satisfy this are an interval from –3 to 3 (not including the
endpoints). We get divergence when |x|>3. So for those x's
satisfying either –∞<x<–3 or 3<x<∞ there is
divergence. The Ratio Test doesn't work if x=3 or if x=–3. It turns
out that this situation is typical, and we will look at more examples
and more detail next time.
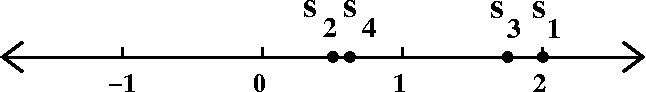
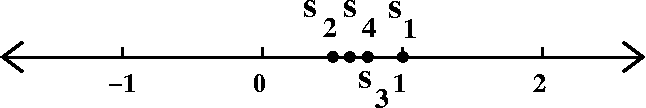
 One definition of manipulative (as a noun) is: "In teaching or
learning arithmetic: a physical object which may be manipulated to
help demonstrate a concept or practise an operation."
There was a spectacular demonstration in
class! It was inspired by thinking about old-fashioned folding
carpenter's rulers. If we have an infinite series ∑n=1∞an, we could
consider the associated series ∑n=1∞|an|,
where we have stripped off the signs of the terms, and are just
adding up the magnitudes. This is sort of like an unfolded carpenter's
rule, stretched out as long as possible. It may happen that the series
of absolute values, a series of positive terms, may converge. So when
"the ruler" is stretched out as long as possible, it has finite
length. Well, if we then fold up the ruler, so some segments point
left (negative) and some point right (positive) then the resulting
length will also be finite.
One definition of manipulative (as a noun) is: "In teaching or
learning arithmetic: a physical object which may be manipulated to
help demonstrate a concept or practise an operation."
There was a spectacular demonstration in
class! It was inspired by thinking about old-fashioned folding
carpenter's rulers. If we have an infinite series ∑n=1∞an, we could
consider the associated series ∑n=1∞|an|,
where we have stripped off the signs of the terms, and are just
adding up the magnitudes. This is sort of like an unfolded carpenter's
rule, stretched out as long as possible. It may happen that the series
of absolute values, a series of positive terms, may converge. So when
"the ruler" is stretched out as long as possible, it has finite
length. Well, if we then fold up the ruler, so some segments point
left (negative) and some point right (positive) then the resulting
length will also be finite.
 Comparison to a definite integral
Comparison to a definite integral Here is how to overestimate this TN. Look at the picture to
the right. The curve y=1/x5 is again there, and I am
interested in what happens for x's bigger than N. I put the boxes
representing TN (remember, this starts with
1/(N+1)5) under this portion of the curve. So (very very
tricky!) I can make this estimate:
Here is how to overestimate this TN. Look at the picture to
the right. The curve y=1/x5 is again there, and I am
interested in what happens for x's bigger than N. I put the boxes
representing TN (remember, this starts with
1/(N+1)5) under this portion of the curve. So (very very
tricky!) I can make this estimate: A partial sum bigger than 100
A partial sum bigger than 100 What happens?
What happens?

 An infinite series ∑n=1∞an can
be thought of as ∑n=1Nan+∑n=N+1∞an. So
there is the Nth partial sum plus the "other" terms of the
series, an infinite tail. These other terms I may sometimes call
TN. I like to think of this maybe as some sort of
animal. The partial sum is the body, and the infinite tail is
... well, the tail. The question of whether the series converges or
not maybe is analogous to whether the whole weight of the animal is
finite (this is a good analogy only for series whose terms are all
positive -- we will deal later with series whose terms change
sign). The weight will be finite exactly when the infinite
tails→0 as n→∞. In fact, the first "few" terms of a
series have
nothing to do with convergence! You can change them, and the
convergence of the series won't change at all. (If the series
converges, the sum will change, but whether or not the series
converges won't be changed.)
An infinite series ∑n=1∞an can
be thought of as ∑n=1Nan+∑n=N+1∞an. So
there is the Nth partial sum plus the "other" terms of the
series, an infinite tail. These other terms I may sometimes call
TN. I like to think of this maybe as some sort of
animal. The partial sum is the body, and the infinite tail is
... well, the tail. The question of whether the series converges or
not maybe is analogous to whether the whole weight of the animal is
finite (this is a good analogy only for series whose terms are all
positive -- we will deal later with series whose terms change
sign). The weight will be finite exactly when the infinite
tails→0 as n→∞. In fact, the first "few" terms of a
series have
nothing to do with convergence! You can change them, and the
convergence of the series won't change at all. (If the series
converges, the sum will change, but whether or not the series
converges won't be changed.)
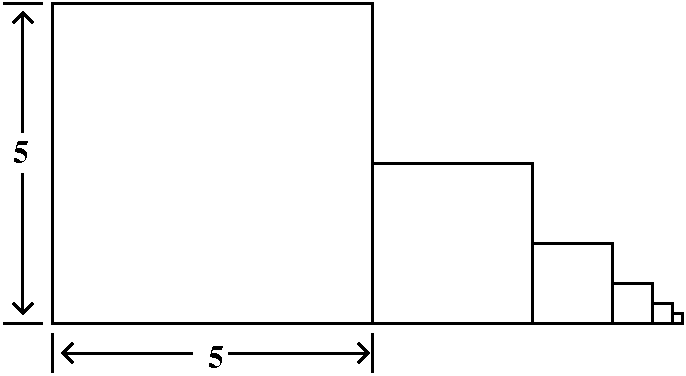 Example #2
Example #2
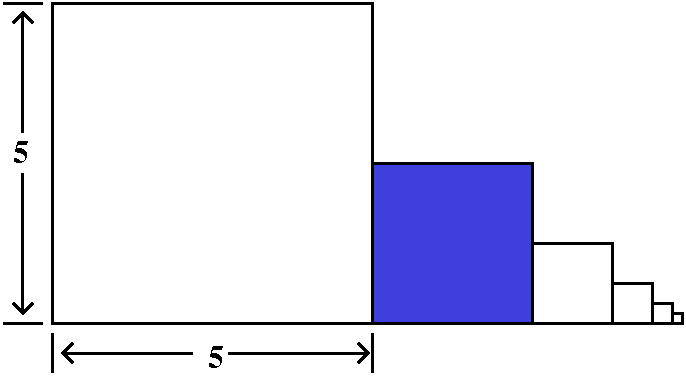
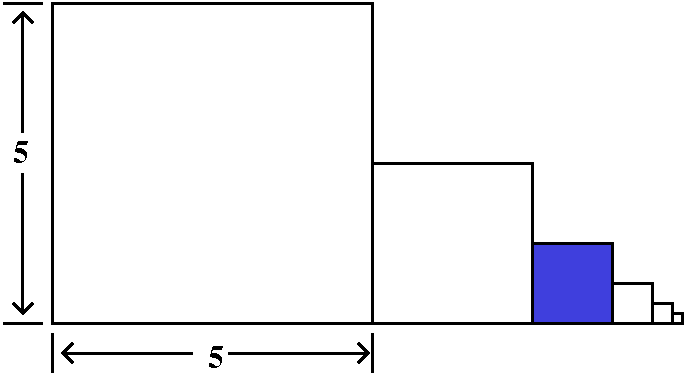



 Maybe sometimes we might think of a picture of the sequence, but this
really has limited use as you will see. To the right is a picture of
the first 6 elements of this sequence, sitting on the number line.
Maybe sometimes we might think of a picture of the sequence, but this
really has limited use as you will see. To the right is a picture of
the first 6 elements of this sequence, sitting on the number line.
 A rudimentary picture of the sequence is shown
to the right. Notice that there is something missing from this
sequence -- the dynamic aspect as the sequence wiggles and hops left
and right. Every element of the sequence is in the picture and the picture isn't very helpful to me at all. Does this sequence converge? Historically an answer to this
question wasn't obvious. People finally decided that the answer should
be no. The only numbers that are authentic candidates for the limit of
this sequence are 1 and –1. If we were going to use sequences as ways
of getting better and better approximations to a root of an equation,
then saying that the root is maybe 1 or maybe –1 is probably not the
best answer. People usually want one specific answer. So the
definition of limit, even if we want only to consider it informally,
needs to be stated slightly differently.
A rudimentary picture of the sequence is shown
to the right. Notice that there is something missing from this
sequence -- the dynamic aspect as the sequence wiggles and hops left
and right. Every element of the sequence is in the picture and the picture isn't very helpful to me at all. Does this sequence converge? Historically an answer to this
question wasn't obvious. People finally decided that the answer should
be no. The only numbers that are authentic candidates for the limit of
this sequence are 1 and –1. If we were going to use sequences as ways
of getting better and better approximations to a root of an equation,
then saying that the root is maybe 1 or maybe –1 is probably not the
best answer. People usually want one specific answer. So the
definition of limit, even if we want only to consider it informally,
needs to be stated slightly differently.
 Let's look at the sequence {51/n}. The first few terms, in
decimal form, are these: 5., 2.236067977, 1.709975947, 1.495348781,
1.379729661, 1.307660486, 1.258498951. A picture of the first 6 of
these is to the right. Maybe things here are not totally clear. In
fact, one of the reasons I want to discuss this example is that things
are not clear. We made some preliminary observations: certainly
any root of 5 would have to be positive, in fact any root would have
to be bigger than 1. And also any root would have to be less than
5. So what we know is that 1<51/n<5. The numbers in
the sequence are "trapped" inside the interval from 1 to 5. I asked
the class if just knowing this information was enough to guarantee
that the sequence converged. After some thought, one student came up
with the following example: {3+(–1)n}. Again depending on
parity, the values of this sequence are either 2 (n odd) or 4 (n
even). This sequence does not converge although its values are inside
the interval from 1 to 5.
Let's look at the sequence {51/n}. The first few terms, in
decimal form, are these: 5., 2.236067977, 1.709975947, 1.495348781,
1.379729661, 1.307660486, 1.258498951. A picture of the first 6 of
these is to the right. Maybe things here are not totally clear. In
fact, one of the reasons I want to discuss this example is that things
are not clear. We made some preliminary observations: certainly
any root of 5 would have to be positive, in fact any root would have
to be bigger than 1. And also any root would have to be less than
5. So what we know is that 1<51/n<5. The numbers in
the sequence are "trapped" inside the interval from 1 to 5. I asked
the class if just knowing this information was enough to guarantee
that the sequence converged. After some thought, one student came up
with the following example: {3+(–1)n}. Again depending on
parity, the values of this sequence are either 2 (n odd) or 4 (n
even). This sequence does not converge although its values are inside
the interval from 1 to 5.
 Modeling this story to solve the problem
Modeling this story to solve the problem The implicit form of the equation is therefore
ln(T–30)=(1/10)ln(1/5)t+ln(250). Let's exponentiate, and use
exponentiation properties and log properties:
The implicit form of the equation is therefore
ln(T–30)=(1/10)ln(1/5)t+ln(250). Let's exponentiate, and use
exponentiation properties and log properties: An explicit form of the solution is
y=[2e2x]/[1+e2x]. This may be in a form that
"real people" can understand.
An explicit form of the solution is
y=[2e2x]/[1+e2x]. This may be in a form that
"real people" can understand.








 Stable equilibrium
Stable equilibrium Unstable equilibrium
Unstable equilibrium





 An example: y´=y2
An example: y´=y2





 MVT simplified: just Rolle's Theorem
MVT simplified: just Rolle's Theorem How can we compute values of the sine function? Here's a graph, but
even producing this graph requires a computer to get many values of
sine and then use them to pick out and color certain pixels. We could
construct a bunch of triangles, measure angles and lengths
carefully, and then get some values of sine. This is, more or less,
how things were done in Egypt and Greece. Certainly it is an intricate
process and very difficult to implement. But hundreds of years later,
a more systematic and accurate method was developed, first in India,
and then in Western Europe. The history in India was long
ignored. Here's
How can we compute values of the sine function? Here's a graph, but
even producing this graph requires a computer to get many values of
sine and then use them to pick out and color certain pixels. We could
construct a bunch of triangles, measure angles and lengths
carefully, and then get some values of sine. This is, more or less,
how things were done in Egypt and Greece. Certainly it is an intricate
process and very difficult to implement. But hundreds of years later,
a more systematic and accurate method was developed, first in India,
and then in Western Europe. The history in India was long
ignored. Here's  The start of this game is to look again at the tangent line
approximation which was discussed in calc 1. Let's try to
approximate sin(x) locally near 0. The tangent line goes through (0,0)
since sin(0)=0 (hey: one value of sine which is easy to know!) and it
has slope 1 since the derivative of sine is cosine and cos(0)=1. For
x's near 0, look at the picture, and realize that sin(x) will be
approximately equal to x.
The start of this game is to look again at the tangent line
approximation which was discussed in calc 1. Let's try to
approximate sin(x) locally near 0. The tangent line goes through (0,0)
since sin(0)=0 (hey: one value of sine which is easy to know!) and it
has slope 1 since the derivative of sine is cosine and cos(0)=1. For
x's near 0, look at the picture, and realize that sin(x) will be
approximately equal to x. Now I displayed a mysterious (?) cubic (third degree) polynomial. It
turns out that this polynomial comes from a rather simple process, one
that can be described easily and efficiently to a computer or
calculator. In fact, it is a process which is simple enough so that
computations can be done by hand, as they were for several
centuries. The picture shows that the cubic polynomial stays closer to
sin(x) in a larger interval than the linear approximation, x, does. I
can't show you also a sort of microscopic picture, but I do assert
that cubic polynomial is a better approximation to sin(x) than just x alone. I'll give some numbers.
Now I displayed a mysterious (?) cubic (third degree) polynomial. It
turns out that this polynomial comes from a rather simple process, one
that can be described easily and efficiently to a computer or
calculator. In fact, it is a process which is simple enough so that
computations can be done by hand, as they were for several
centuries. The picture shows that the cubic polynomial stays closer to
sin(x) in a larger interval than the linear approximation, x, does. I
can't show you also a sort of microscopic picture, but I do assert
that cubic polynomial is a better approximation to sin(x) than just x alone. I'll give some numbers.
 So I'm skipping a few polynomials and jumping up to the 9th
degree approximation. The numbers may look a bit strange (you will
get used to them!).
So I'm skipping a few polynomials and jumping up to the 9th
degree approximation. The numbers may look a bit strange (you will
get used to them!). Let me show you a consequence of this estimate in connection with the
QotD. Here f(x)=x1/3 and
T3(x)=2+(1/12)(x–8)–(1/288)(x–8)2+(5/20736)(x–8)3.
To the right is a picture containing graphs of both y=x1/3
and y=T3(x) as x goes from 0
to 16.
Let me show you a consequence of this estimate in connection with the
QotD. Here f(x)=x1/3 and
T3(x)=2+(1/12)(x–8)–(1/288)(x–8)2+(5/20736)(x–8)3.
To the right is a picture containing graphs of both y=x1/3
and y=T3(x) as x goes from 0
to 16.
 To the right is another picture. Look at it very carefully
please. It is also a graph of both y=x1/3
and y=T3(x) as x goes from 6
to 10. Both curves are displayed. But I can only see one
curve. Maybe if I look really really really closely, maybe I can
see some dots of two colors but I am not sure. How close are these
curves?
To the right is another picture. Look at it very carefully
please. It is also a graph of both y=x1/3
and y=T3(x) as x goes from 6
to 10. Both curves are displayed. But I can only see one
curve. Maybe if I look really really really closely, maybe I can
see some dots of two colors but I am not sure. How close are these
curves?
 Therefore the error is at most (.0014)(16/24) and this is about
.00092. Now look carefully at the picture. Do you think you can
see a difference in height of less than .001? The difference
between two of the "hashmarks" on the vertical scale is .05, and the
graphs of the functions are separated by one-fiftieth (that's 1/50) of that
difference. I don't think that the pixels in the picture are small
enough to show this!
Therefore the error is at most (.0014)(16/24) and this is about
.00092. Now look carefully at the picture. Do you think you can
see a difference in height of less than .001? The difference
between two of the "hashmarks" on the vertical scale is .05, and the
graphs of the functions are separated by one-fiftieth (that's 1/50) of that
difference. I don't think that the pixels in the picture are small
enough to show this!
 x·ln(x)
x·ln(x) The integral
The integral





 Arc length
Arc length Line segment
Line segment



 Surface area
Surface area So far we have
discussed computing standard definite integrals. Although certainly a
definite integral like ∫abf(x)dx can represent many different
ideas, the most familiar instantiation is as an area (asssuming that
f(x)>0 for x in [a,b]) bounded by the x-axis, x=a, x=b, and the
graph of y=f(x). In most of the computations we've done, the function
f has been rather "nice" -- differentiable, mostly, and only a few
times has it had some discontinuities. In fact, there are many
applications where this simplicity is made more complicated because
the applications themselves demand a
"stronger" kind of integral.
So far we have
discussed computing standard definite integrals. Although certainly a
definite integral like ∫abf(x)dx can represent many different
ideas, the most familiar instantiation is as an area (asssuming that
f(x)>0 for x in [a,b]) bounded by the x-axis, x=a, x=b, and the
graph of y=f(x). In most of the computations we've done, the function
f has been rather "nice" -- differentiable, mostly, and only a few
times has it had some discontinuities. In fact, there are many
applications where this simplicity is made more complicated because
the applications themselves demand a
"stronger" kind of integral.
 For example, we might consider a situation where, say, b gets larger
and larger and
larger. Where, say, b→∞. I will give a real physical example of this at the next
lecture. This integral will have a domain which is an infinite
interval. It could be [a,∞) or
(–∞,b] or even (–∞,∞). Such integrals also occur very frequently in statistics
(and therefore they "infiltrate" almost all experimental sciences!).
For example, we might consider a situation where, say, b gets larger
and larger and
larger. Where, say, b→∞. I will give a real physical example of this at the next
lecture. This integral will have a domain which is an infinite
interval. It could be [a,∞) or
(–∞,b] or even (–∞,∞). Such integrals also occur very frequently in statistics
(and therefore they "infiltrate" almost all experimental sciences!). There may also be a sort of defect (?) in the range of f. For
simplicity, consider the situation where, although f is "nice" for
x>a, as x→a+, f(x) gets larger and
larger and larger: in fact, we might need
to try to "integrate" or compute the value of ∫abf(x)dx even if
f tends to ∞ as x→a.
There may also be a sort of defect (?) in the range of f. For
simplicity, consider the situation where, although f is "nice" for
x>a, as x→a+, f(x) gets larger and
larger and larger: in fact, we might need
to try to "integrate" or compute the value of ∫abf(x)dx even if
f tends to ∞ as x→a.

 Many real-life phenomena are described using something called the
exponential probability distribution. For example, the probable life-time of a lightbulb could be described with it. See
Many real-life phenomena are described using something called the
exponential probability distribution. For example, the probable life-time of a lightbulb could be described with it. See 


