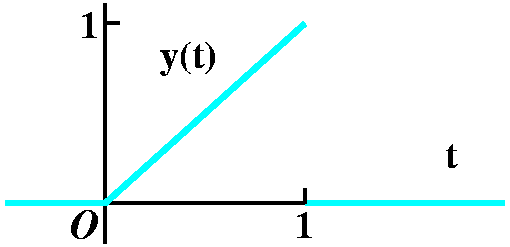y1(t)+y2(t)
Cy(t) (C is a constant)
|
Y1(s)+Y2(s)
CY(s)
| Linearity
This is used everywhere. First official mention
|
tn
n is a non-negative integer
| n!/sn+1
| Done for n=0;
done for n=1;
done for n=2;
statement for any n. Used very often
afterwards.
|
| eat
| 1/(s-a)
| Verification. Used often.
|
sin(kt)
cos(kt)
| k/(s2+k2)
s/(s2+k2)
| Verification for cosine using
complex exponents. The text proves this using integration by
parts. Both results are used often. You need to know and believe in Euler's formula.
|
sinh(kt)
cosh(kt)
| k/(s2-k2)
s/(s2-k2)
| Not verified in class, but a discussion here indicates
why sinh and cosh are useful.
|
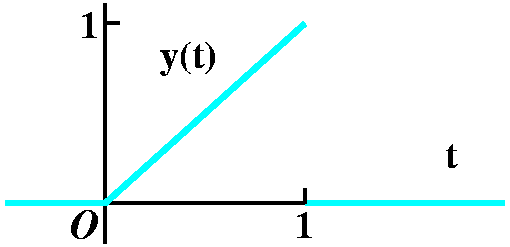
y(t)=t if t in [0,1] else y(t)=0.
| (-se-s-e-s+1)/s2
| Computed from the definition. Students should
also know how to do this with U and the translation theorems.
|
y(t) is a function
with exponential growth
| Y(s)-->0 as s-->infinity.
Y(s)-->the net area under
all of the y(t) function as s-->0+.
| Asymptotics
Discussed here. Please note
this does not apply to the Dirac delta function, which, in
spite of its name, is not a function.
|
| y´(t)
| sY(s)-y(0)
| Verified here. Used later frequently.
|
Solving
1y´(t)+2y(t)=3cos(t)
with y(0)=4
| -4+sY(s)+2Y(s)=3s/(s2+1)
| First use of Laplace transform method to solve
an initial value problem. The steps (transform, solve, inverse transform)
are used very often, so this should be considered a model. Here is a second order equation, and here is a link to a solution of
an integral equation from the course I gave a year ago, since the
choice I made this year didn't work out.
|
|
y(n)(t)
|
snY-sn-1y(0)-sn-2y´´(0)-...-y(n-1)(0)
| First mentioned here and first used
here to solve a second order ODE.
|
| eatf(t)
| F(s-a)
| First translation theorem. Examples.
Many other examples later, such as here
and here.
|
U(t)
U(t)=0 if t<0 &
=1 if t>=0.
| 1/s
| Defined here and its use in writing piecewise functions
algebraically follows immediately afterwards.
|
| f(t-a)U(t-a)
| e-asF(s)
| Second translation theorem. Examples.
|
| g(t)U(t-a)
| e-as multiplied by
the Laplace transform of g(t+a).
| Alternate form of the second translation theorem
Examples.
Many other examples later, such as here
and here.
|
| t·f(t)
| F´(s)
| Verification. Used here.
|
| (-1)ntn·f(t)
| (dn/dsn)F(s)
| Just the statement
|
f*g(t)= 0tf(tau)g(t-tau)dtau 0tf(tau)g(t-tau)dtau
| F(s)·G(s)
| Convolution defined. One and two direct computations of convolution.
and here's the statement of the Laplace
transform fact. And some simple uses. A more complicated use is
attempted here.
|
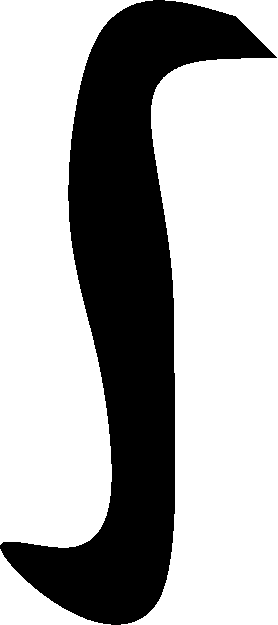 0tf(tau)dtau 0tf(tau)dtau
| F(s)/s
| Verified here
|
|
delta(t-t0)
|
e-t0s
| Verification here. Before and after this are
substantial discussions of the "theory", and then some examples using delta
in mathematical models.
|