The lecture
Here is a writeup of what I
discussed in class after the homework problems. In fact, there are
two proofs of Taylor's Theorem, and some further discussion.
No one has read this yet other than me, so there may be errors. Please
send comments, corrections, etc. Thanks.
I have revised (11/13/2005) the essay and corrected some typos and
added some interesting material (the last section) on the history of
this result.
Who was Taylor?
Here is a biography
of Taylor. Please also look at the last section of the essay on
Taylor's Theorem for more information about the non-Western history of
the result.
Graphical "evidence"
I think Taylor's Theorem is probably the most important result
both for theory and practice in the second half of the course
(integration by parts was the result in the first half). I not
only want to provide a detailed discussion but I want to give
supporting evidence. Since people may be convinced in different ways,
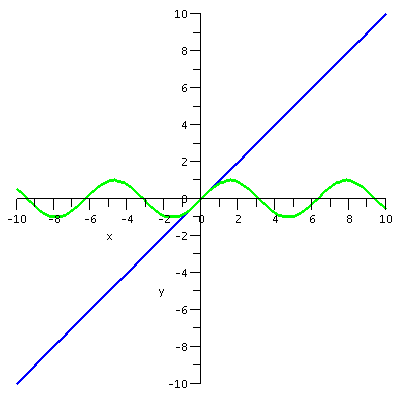
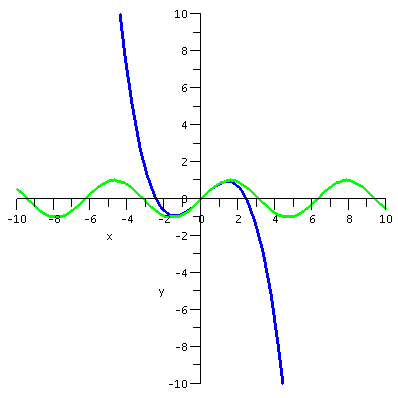
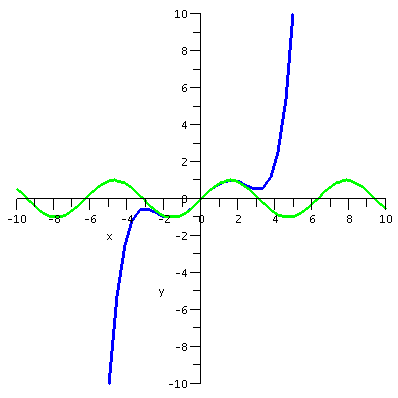
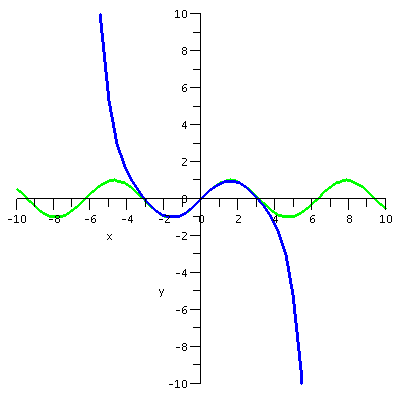
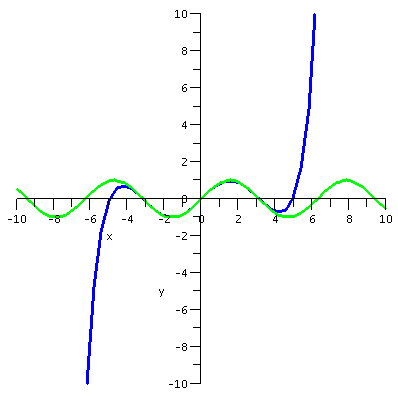
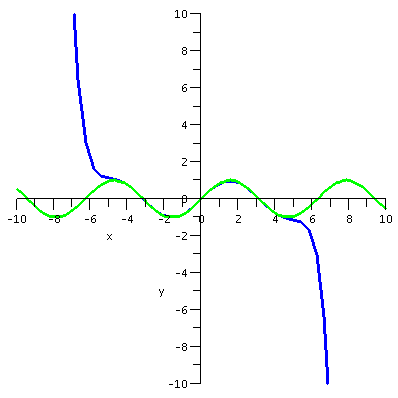
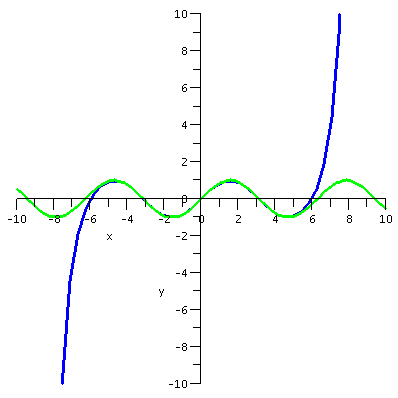
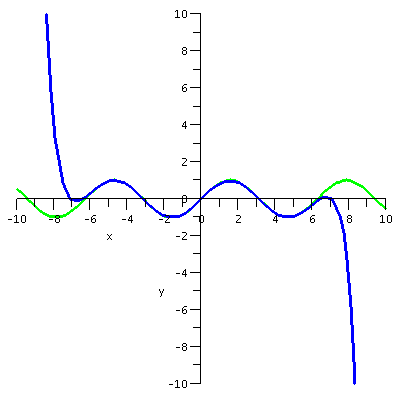
first I want to present some graphs. The graphs display sin(x) and
various Taylor polynomials. The Taylor polynomial of degree 15 is
T15(x)=x-(1/6)x3+(1/120)x5-(1/5,040)x7+(1/362,880)x9-(1/39,916,800)x11+(1/6,227,020,800)x13-(1/1,307,674,368,000)x15
Notice how big the denominators are: factorials certainly grow
fast. T7(x) is just the part of T15(x) up to
degree 7. These are the partial sums of the whole Taylor series for sin(x).
|
|
| sin(x) and T1(x) |
|---|
 | |
| sin(x) and
T3(x) |
 |
|
| sin(x) and T5(x) |
|---|
 | |
| sin(x) and
T7(x) |
 |
|
| sin(x) and T7(x) |
|---|
 | |
| sin(x) and
T9(x) |
 |
|
| sin(x) and T11(x) |
|---|
 | |
| sin(x) and
T13(x) |
 |
|
The polynomials can't approximate sin(x) closely on all
numbers, because sin(x) is always between -1 and 1, and any
non-constant polynomial will go to +infinity or -infinity as x gets
large positive or negative.
Numerical "evidence"
Below are some tables of values of sine and values of Taylor
polynomials at various x's. The Taylor polynomial values are colored
and in two fonts (for people may be weak on color discrimination). A
number like 0.8416666667 has digits 841 which
agree with the true value of sine, while the digits 6666667 disagree. Just the colors and the
fonts should show you what's going on numerically. For x's close to 0,
even low-degree Taylor polynomials are wonderful approximations, while
when x gets larged, higher degree Taylor polynomials are needed for
the same accuracy.
| x=.2 |
|---|
| sin(.2)= | 0.1986693308 |
|---|
| T1(.2)= | 0.2000000000 |
|---|
| T3(.2)= | 0.1986666667 |
|---|
| T5(.2)= | 0.1986693333 |
|---|
| T7(.2)= | 0.1986693308 |
|---|
| T9(.2)= | 0.1986693308 |
|---|
| T11(.2)= | 0.1986693308 |
|---|
| T13(.2)= | 0.1986693308 |
|---|
| T15(.2)= | 0.1986693308 |
|---|
|
| x=.5 |
|---|
| sin(.5)= | 0.4794255386 |
|---|
| T1(.5)= | 0.5000000000 |
|---|
| T3(.5)= | 0.4791666667 |
|---|
| T5(.5)= | 0.4794270833 |
|---|
| T7(.5)= | 0.4794255332 |
|---|
| T9(.5)= | 0.4794255386 |
|---|
| T11(.5)= | 0.4794255386 |
|---|
| T13(.5)= | 0.4794255386 |
|---|
| T15(.5)= | 0.4794255386 |
|---|
|
| x=1 |
|---|
| sin(1)= | 0.8414709848 |
|---|
| T1(1)= | 1.0000000000 |
|---|
| T3(1)= | 0.8333333333 |
|---|
| T5(1)= | 0.8416666667 |
|---|
| T7(1)= | 0.8414682540 |
|---|
| T9(1)= | 0.8414710097 |
|---|
| T11(1)= | 0.8414709846 |
|---|
| T13(1)= | 0.8414709848 |
|---|
| T15(1)= | 0.8414709848 |
|---|
|
| x=2 |
|---|
| sin(2)= | 0.9092974268 |
|---|
| T1(2)= | 2.0000000000 |
|---|
| T3(2)= | 0.6666666667 |
|---|
| T5(2)= | 0.9333333333 |
|---|
| T7(2)= | 0.9079365079 |
|---|
| T9(2)= | 0.9093474427 |
|---|
| T11(2)= | 0.9092961360 |
|---|
| T13(2)= | 0.9092974515 |
|---|
| T15(2)= | 0.9092974265 |
|---|
|
| x=4 |
|---|
| sin(4)= | -0.7568024953 |
|---|
| T1(4)= | 4.000000000 |
|---|
| T3(4)= | -6.666666667 |
|---|
| T5(4)= | 1.866666667 |
|---|
| T7(4)= | -1.384126984 |
|---|
| T9(4)= | -0.6617283951 |
|---|
| T11(4)= | -0.7668045535 |
|---|
| T13(4)= | -0.7560275116 |
|---|
| T15(4)= | -0.7568486195 |
|---|
|
| x=6 |
|---|
| sin(6)= | -0.2794154982 |
|---|
| T1(6)= | 6. |
|---|
| T3(6)= | -30. |
|---|
| T5(6)= | 34.80000000 |
|---|
| T7(6)= | -20.74285714 |
|---|
| T9(6)= | 7.028571429 |
|---|
| T11(6)= | -2.060259740 |
|---|
| T13(6)= | 0.03716283716 |
|---|
| T15(6)= | -0.3223953190 |
|---|
|







