Thin Filaments
Summary
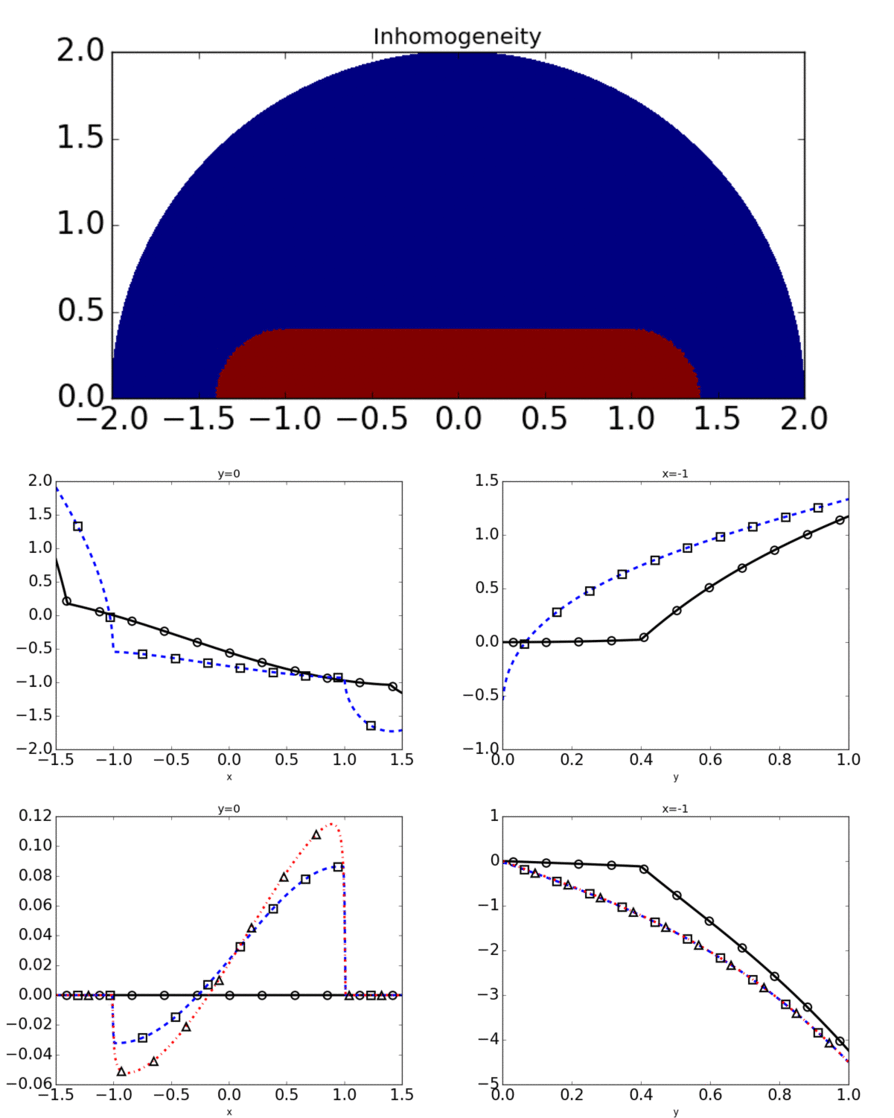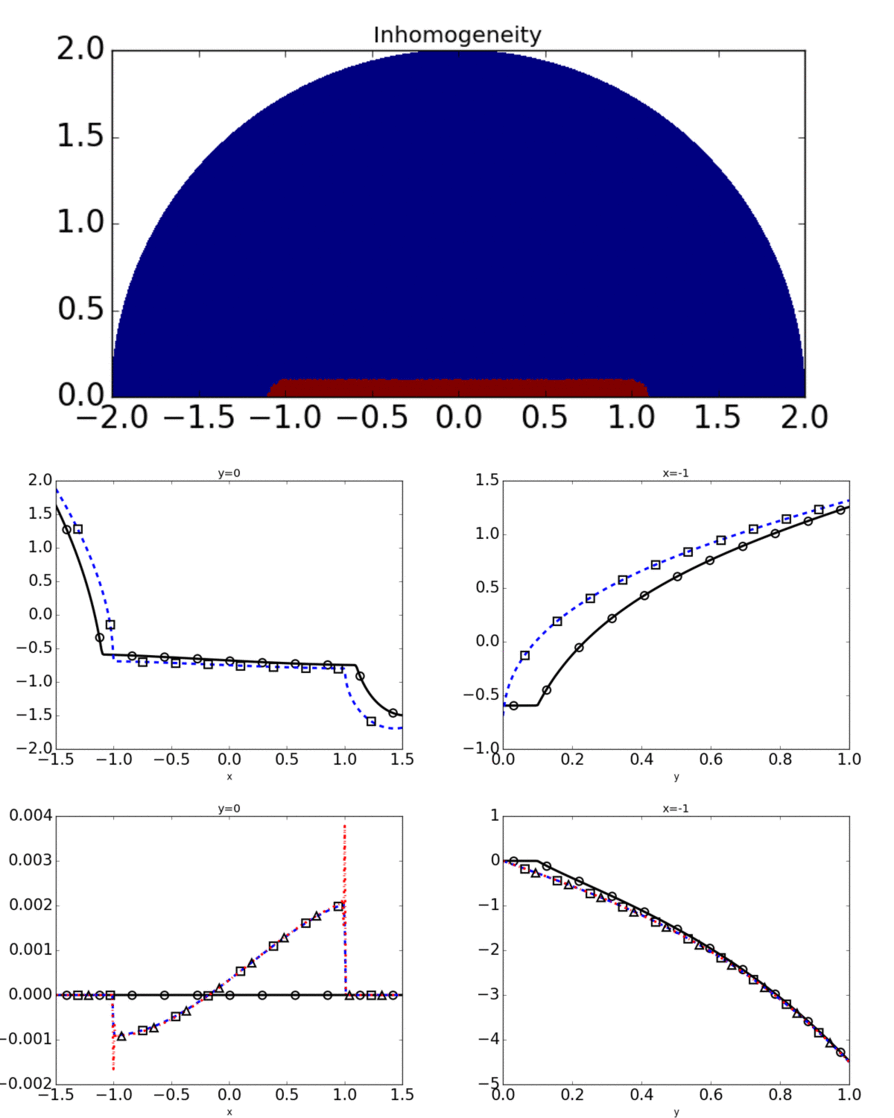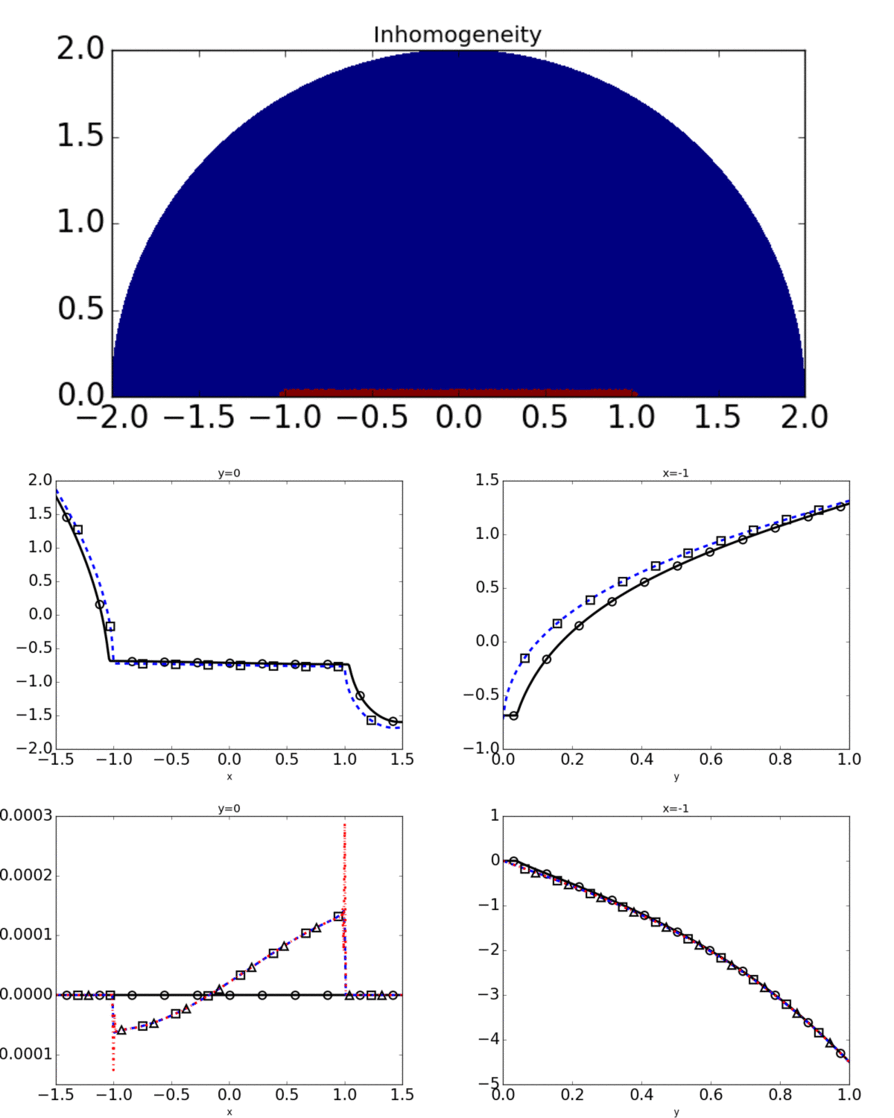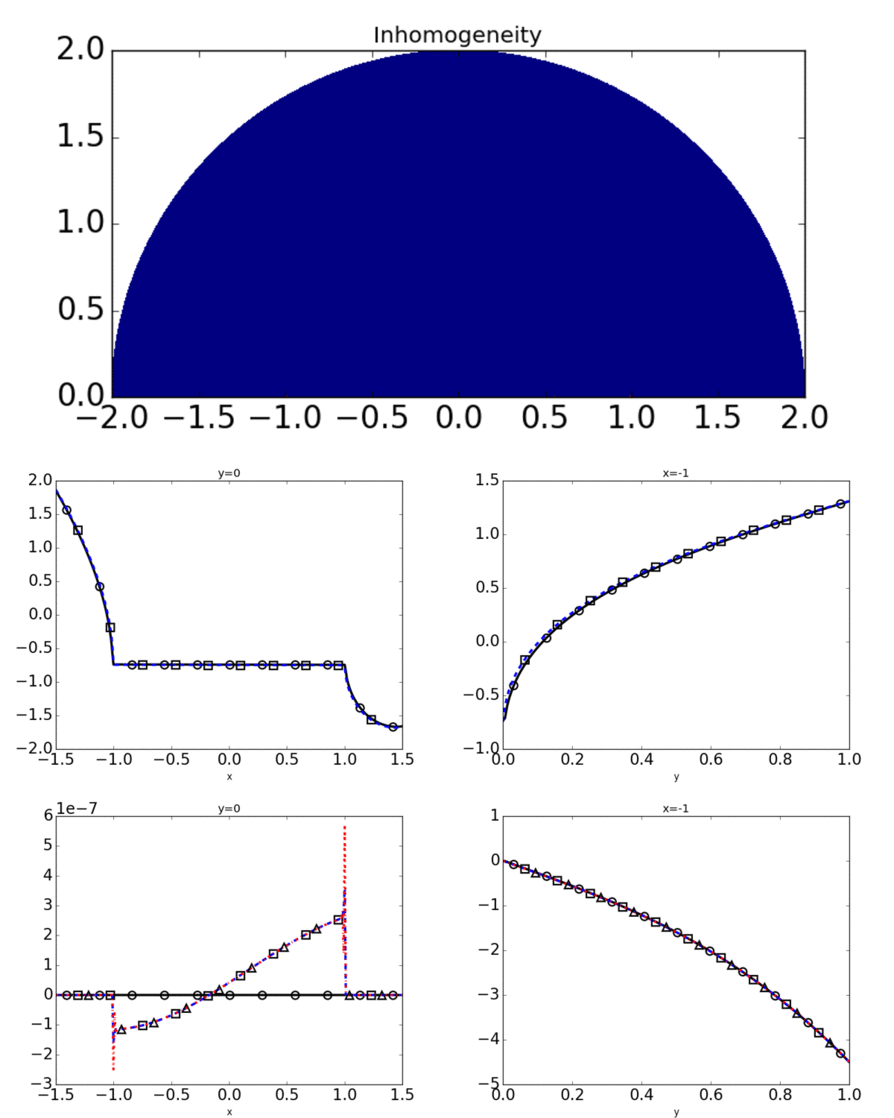
This project looks into the asymptotic accuracy of approximations to the conductivity problem in thin filaments. Previous results for closed mid-curves gives a possible
approximating problem on the domain minus the mid-cirve, and we prove that this same problem is a good approximation in the case of open mid-curves. This work requires a careful analysis of
the types of singularities that can arise from these problems and making sure that they still allow for an appropriate error estimate. I have also developed numerical simulations for these problems
to get a feel for how they behave.
Next Steps
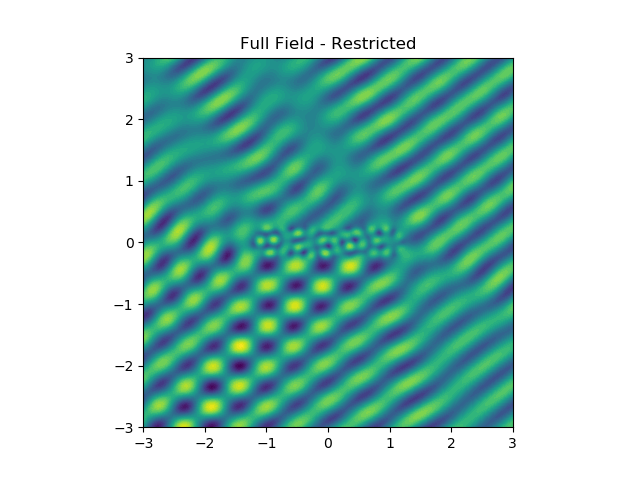
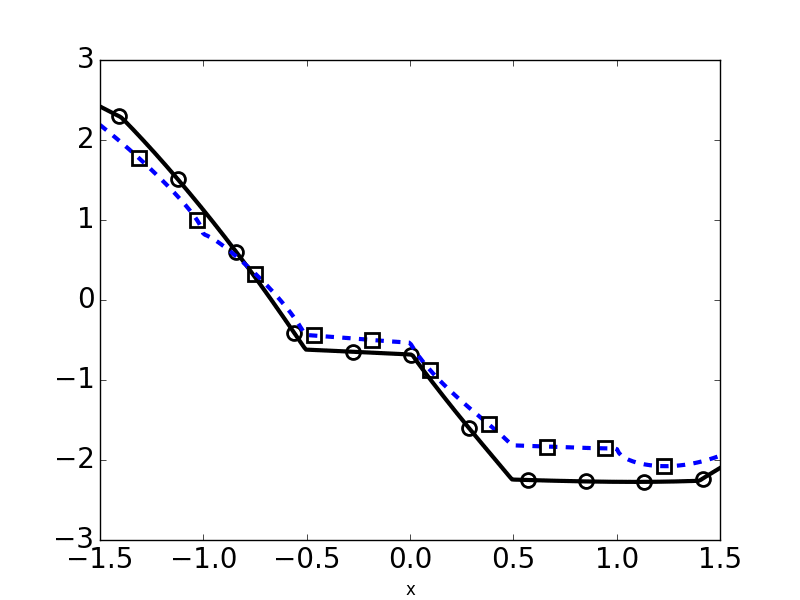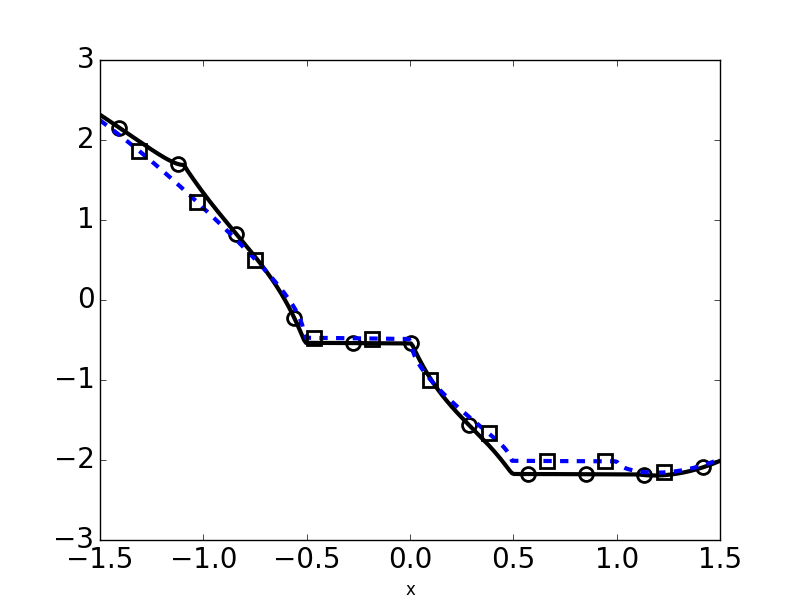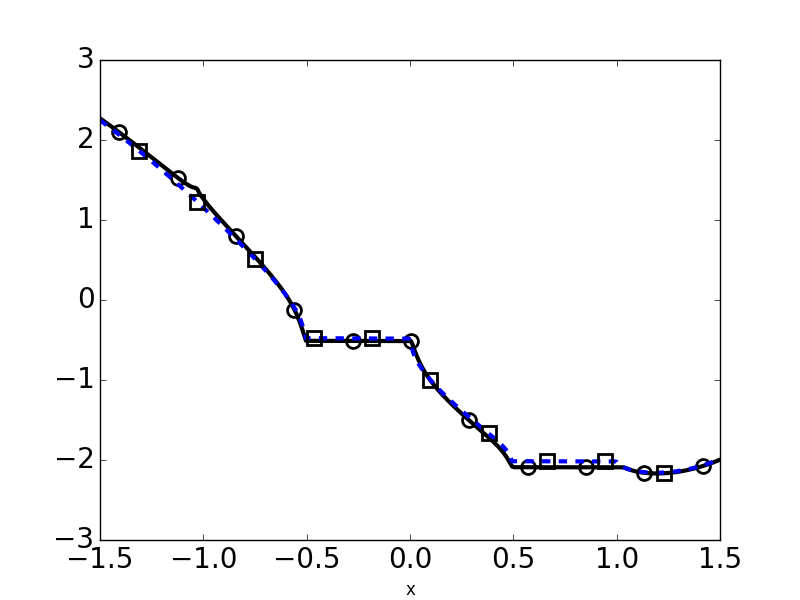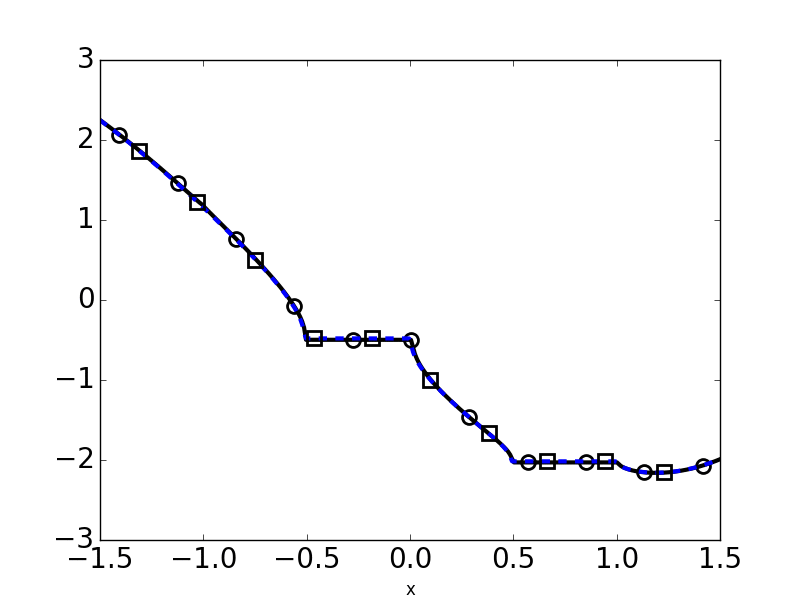
The next steps on this problem could go in a few different directions. Most physical problems in the area have either non-constant or anisotropic conductivities, and our current method
only deals with constant conductivities in the inhomogeneity. Most of the arguments should go through, but there are certain parts, namely the singluarity analysis, that require certain structure near the endpoints.
If this doesn't hold, there may be some issues with the proof. Also, it would be very interesting to see how this argument plays out for scattering theory and the Helmholtz equation.
References
- Part I
- Part II
 This project looks into the asymptotic accuracy of approximations to the conductivity problem in thin filaments. Previous results for closed mid-curves gives a possible
approximating problem on the domain minus the mid-cirve, and we prove that this same problem is a good approximation in the case of open mid-curves. This work requires a careful analysis of
the types of singularities that can arise from these problems and making sure that they still allow for an appropriate error estimate. I have also developed numerical simulations for these problems
to get a feel for how they behave.
This project looks into the asymptotic accuracy of approximations to the conductivity problem in thin filaments. Previous results for closed mid-curves gives a possible
approximating problem on the domain minus the mid-cirve, and we prove that this same problem is a good approximation in the case of open mid-curves. This work requires a careful analysis of
the types of singularities that can arise from these problems and making sure that they still allow for an appropriate error estimate. I have also developed numerical simulations for these problems
to get a feel for how they behave.

 The next steps on this problem could go in a few different directions. Most physical problems in the area have either non-constant or anisotropic conductivities, and our current method
only deals with constant conductivities in the inhomogeneity. Most of the arguments should go through, but there are certain parts, namely the singluarity analysis, that require certain structure near the endpoints.
If this doesn't hold, there may be some issues with the proof. Also, it would be very interesting to see how this argument plays out for scattering theory and the Helmholtz equation.
The next steps on this problem could go in a few different directions. Most physical problems in the area have either non-constant or anisotropic conductivities, and our current method
only deals with constant conductivities in the inhomogeneity. Most of the arguments should go through, but there are certain parts, namely the singluarity analysis, that require certain structure near the endpoints.
If this doesn't hold, there may be some issues with the proof. Also, it would be very interesting to see how this argument plays out for scattering theory and the Helmholtz equation.