Discussion of exam grading in Math 135, section F2, summer 2006
The semi exam
| Problem | #1 |
#2 |
#3 |
#4 |
#5 |
#6 |
Total |
|---|
| Max grade |
8 |
9 |
10 |
10 |
6 |
6 |
49 |
|---|
Min grade |
2 |
4 |
0 |
3 |
0 |
0 |
17 |
Mean grade |
5.76 |
6.76 |
5.12 |
8.88 |
2.88 |
2.53 |
31.94 |
Median grade |
6 |
7 |
3 |
10 |
0 |
2 |
30 |
17 students took this exam. Numerical grades will be retained for use
in computing the final letter grade in the course. This exam grade
will not be a major factor in determining the final course grade. The
chief purpose in giving this exam was to advise students as early as
reasonable about how they are doing in the course. Students take summer
courses for a variety of reasons, but many of the reasons have to do
with earning a suitable grade. The exam grade here will not
necessarily forecast the final course grade, but it should give both
students and instructor some guidance. Above all, I'd like
students to look at how they've done on this exam and see if a course
grade which will be acceptable for their purposes is likely. The
remainder of the course will be more difficult than what's
already happened. The course will almost inevitably seem to speed
up. Students should not and cannot anticipate that grades will
increase without putting in substantially more time and effort.
Letter
equivalent | A | B+ | B | C+ |
C | D | F |
|---|
| Range | [51,55] |
[46,50] |
[41,45] |
[36,40] |
[31,35] |
[26,30] |
[0,25] |
|---|
Discussion of the grading
Some general background
I tried to penalize arithmetic errors and "small" errors minimally,
unless the problem was materially simplified by the errors. Students
needed to read "my" problem and do that problem, though, and not one
they invented as a substitute. I also could read only what was written
on the exam paper, not what students may have intended. I wanted some
supporting evidence for most answers -- some idea of how students knew
the answer.
Problem 1 (8 points)
Computing f(2) earned 2 points. Computing f´(2) earned 2 points.
Putting these together properly in an equation for the tangent line
earned the remaining 4 points.
Problem 2 (9 points)
The answer in each part of the problem was worth 1 point. Supporting
reasoning would earn 2 more points for that part.
a) In this case, I was gentle, and awarded 3 points for "plugging in"
(sorry, substituting and evaluating) even without any further
comment.
b) Here some algebra needed to be shown to earn all 3 points.
c) I wanted some explanation. Certainly citation of
limh-->0sin(h)/h=1 is relevant, and earned 1 point. But
statements which were false or irrelevant did not earn credit.
Problem 3 (10 points)
1 point for correct evaluation of f(x+h); 2 points for using this in
[f(x+h)-f(x)]/h; 2 points for some preliminary algebraic treatment
(multiplication by srqt(A)+sqrt(B) top and bottom for suitable A and
B); 2 more points for further algebraic treatment; 2 points for final
algebraic treatment resulting in the h on the bottom disappearing; 1
point for the final answer.
Problem 4 (12 points)
a) The domain could earn 4 points. The correct answer is [-2,1) and
(1,2]. Each endpoint, correctly indicated (that is, "[-2" and "1)" and
"(1" and "2]") earned 1 point. Similarly, the range could earn 2
points. Omitting 0 from the range lost a point.
b) Each correct answer here earned 1 point. No partial credit was
given and no explanation was needed.
Problem 5 (10 points)
a) (6 points) Getting to the correct system of two linear equations in
two unknowns (A and B) was worth 4 points. Solving the equations was
worth 2 more points.
b) (4 points) Basically, 2 points for the parabolic part of the graph,
and 1 point for each line segment. Of course the graphs should be
correctly connected. No credit was earned if what was drawn was not
the graph of a function.
Problem 6 (6 points)
2 points for the restriction x&le 8 coming from sqrt(8-x); 2 points
for the restriction x> 4 coming from sqrt(x-4) on the bottom
(throwing out x=4 was worth 1 of these points); presenting the correct
answer was worth 2 points. The correct answer alone would earn 2
points. I wanted to read some supporting evidence for the asserted
answer.
The first exam
| Problem | #1 |
#2 |
#3 |
#4 |
#5 |
#6 |
#7 |
#8 |
Total |
|---|
| Max grade |
14 |
14 |
18 |
12 |
8 |
10 |
12 |
10 |
97 |
|---|
Min grade |
2 |
0 |
10 |
2 |
1 |
0 |
0 |
0 |
24 |
Mean grade |
10.58 |
8.95 |
14.16 |
8.37 |
3.95 |
7.47 |
5.74 |
6.00 |
65.21 |
Median grade |
13 |
12 |
14 |
10 |
4 |
7 |
3 |
7 |
68 |
19 students took this exam. Numerical grades will be retained for use
in computing the final letter grade in the course. Here are
approximate letter grade assignments for this exam:
Letter
equivalent | A | B+ | B | C+ |
C | D | F |
|---|
| Range | [88,100] |
[82,87] |
[73,81] |
[67,72] |
[60,66] |
[51,59] |
[0,50] |
|---|
Discussion of the grading
Some general background
Again, I tried to penalize arithmetic errors and "small" errors
minimally, unless the problem was materially simplified by the
errors. Students needed to read "my" problem and do that problem,
though, and not one they invented as a substitute. I also could read
only what was written on the exam paper, not what students may have
intended. I wanted some supporting evidence for most answers -- some
idea of how students knew the answer.
Problem 1 (14 points)
a) (10 points) 1 point for writing the definition of f´(x). 2
points for using this f(x) in the definition correctly. 2
points for combining the resulting fraction correctly. 2 points for
canceling terms in "the top of the top". 2 points for canceling h's. 1
point for the correct answer. Students who wrote the answer, without
any work or with just the quotient rule, earned no
points. Please answer the question which is asked.
b) (4 points) 1 point for finding the slope of the line. 1 point for finding
a point the line goes through. 2 points for writing the answer.
Problem 2 (14 points)
a) (8 points) 2 points for using data at x=-2 to deduce a condition on
A and B. 2 points for using data at x=1 to deduce a condition on A and
B. 2 points for work done towards "solving" for A and B. 1 point each
for the correct values of A and B.
b) (6 points) 2 points for a correct straight line to the left of
x=-2. 2 points for a parabolic arc opening up with a correct vertex in
the interval [-2,1]. 2 points for a correct straight line to the right
of x=1. A maximum of 3 points will be awarded if the graph drawn is
not continuous.
Problem 3 (20 points)
Each part is worth 5 points, and 1 point will be given for the correct
answer. The other points are for some supporting evidence in each case.
a) Factor, cancel, plug in.
b) Use sin(little)/little combined with a product.
c) Algebraic treatment such as factor, plug in, cancel.
d) Plug in. Know the value of cos(Pi) (1 point!).
Problem 4 (12 points)
The graph of y=f´(x) requested has some subtle features. Here is
how I will grade answers: 1 point for the overall continuity of the
function. I will also expect the answer to be "smooth" since I see
little evidence of pathological behavior in the graph of y=f(x).
The graph should intersect the horizontal axes three times: once
between c and d, once between d and 0, and once somewhere close to
e. Each intersection is worth 1 point.
The graph between the first two intersections should be a bump
downwards with a negative minimum (2 points). Between the second and
third intersection, there should be a positive maximum on a bump (2
points).
To the left of the first intersection there should be a positive
maximum (1 point), and then as x-->the left, the graph should be
positive and decrease to 0 (1 point).
To the right of the third intersection there should be a negative
minimum (1 point), and then as x-->the right, the graph should be
negative and increase to 0 (1 point). If the signs of f´(x) are
correct in these intervals and nothing horrible is drawn, then, even
if the graph may not have the features I';d like, I'll give 2 of the 4
points possible here.
Problem 5 (8 points)
a) (2 points) 1 point for some correct values of K and L, and 1 point
for support of this assertion.
b) (3 points) 1 point each for the {positive|negative} answers, and 1
point for support of the assertions.
c) (3 points) 1 point for a citation of the Intermediate Value
Theorem, 1 point for a correct use of the word "continuous" in
connection with this function and citation, and 1 point for an
appropriate interval in the (x) domain variable.
Problem 6 (10 points)
a) (3 points) Use the Quotient Rule and the Chain Rule. 1 point was
lost for each error.
b) (3 points) Use the Product Rule. 1 point was lost for each error.
c) (4 points) Each result was worth 2 points, and some supporting
computation needed to be shown. The first part used the Product Rule,
and the second part with the Chain Rule.
Problem 7 (12 points)
2 points for computing the derivation of f(x), and then 1 point for
writing f´(x)=0. Finding the roots of the resulting equation was
worth 3 points. Finding each of the answers, correctly, was worth 2
points each. If some correct answers are given without supporting
reasoning, each correct answer will earn 1 point. If answers are given
in the wrong order, 1 point will be lost.
Problem 8 (10 points)
a) (5 points) 2 points for a formula connecting H and D
(Pythagoras). 2 points for a solution
H=sqrt(82-D2) with only the + sign in front of
the square root. Since there is considerable algebraic symmetry
between D and H, I took off only 1 point for D as function of H. 1
point for the correct domain. I was willing to be "flexible" about the
end points of the domain.
b) (5 points) 2 points for a formula connecting 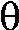 and H (the definition of sine). 1
points for H=8sin(
and H (the definition of sine). 1
points for H=8sin( ). 2 points
for the correct domain. I was willing to be "flexible" about the end
points of the domain.
). 2 points
for the correct domain. I was willing to be "flexible" about the end
points of the domain.
The take-home semi-exam
| Problem | #1 |
#2 |
#3 |
#4 |
#5 |
Total |
|---|
| Max grade |
9 |
9 |
9 |
6 |
4 |
35 |
|---|
Min grade |
1 |
0 |
0 |
1 |
0 |
2 |
Mean grade |
6.5 |
4.94 |
5.31 |
1.49 |
2.75 |
22.38 |
Median grade |
7 |
4 |
5 |
2.5 |
3 |
21.5 |
16 students took this exam. Numerical grades will be retained for use
in computing the final letter grade in the course. The chief purpose
in giving this exam was to allow students ample time to work on
graphing problems where some of the computational details would be
quite annoying.
Discussion of the grading
Each of the first 4 problems was worth 9 points. I scored 3 points
each for information relating to the function, the first derivative,
and the second derivative. I scored these points on more
"holistically" than is my custom. That is, I looked at all the
information I expected could be obtained from that level of reasoning
(including, when necessary, other levels, such as the case of range
informaion for the function). I gave 0, 1, 2, or 3 points out of 3
for what I read. I did not attempt to guess at what obscure notations
or diagrams meant. Effective communication is part of student
responsibility. I felt more justified than usual about this because
this was a take-home exam, and students had four days in which
to work on it. I did look for explicit answers to my questions. So on
the FUNC level, I wanted domain, range, limits, and
asymptotes. I looked for supporting reasoning, as well, in this case
and in all cases. For example, in problem 4, where the formula for the
function has a division, some reason shold be presented for the
declaration that the domain is "all x". On the FUNC´ level
I wanted a computation of the first derivative (hard to go on at all
if the derivative is not correct!) and then identification of critical
points and types (max/min/neither) and intervals of increase and
decrease, with reasoning when neeeded. For the FUNC´´
level, I wanted a correct computation of the second derivative and
then the conclusions which could be drawn by considering it. In
particular, I wanted intervals where the graph was concave up and
down, and the location of inflection points. Diagnosis of inflection
points does not coincide with roots of the second derivative.
Here is an example useful to note. The function f(x)=x10
has no changes in concavity and no inflection points -- the
graph is a very steep "parabola". But even though
f´´(x)=90x8 is 0 when x=0, this function has
no. So a place where f´´(x)=0 is not necessarily an
inflection point!
In problem 5, I gave 2 points to the part a) answers : identification
of f(2) and f´(2) (1 point each). I gave 1 point to the correct
answer in part b) (> or <?) and 1 point for supporting
reasoning. I read what students wrote, and thus the phrase "rate of
change" with no further explanation was not sufficient. I was
looking for a reference to concavity. The specific values (8 and 17
and 5) were unimportant here. The key fact is the positivity
of the second derivative.
Please realize that students were not asked or required to
sketch graphs of any functions in any problems. Initial device-drawn
graphs were supplied if students could
not use their own calculators to see them. The answers supplied should give enough
computational details to supply even the most greedy. I created some
graphs of the functions in these problems together with some tangent
line segements. They are below, with comments. These graphs are not
replacements for the answers
expected.
Problem 1
f(x)=(x-1)/e2x
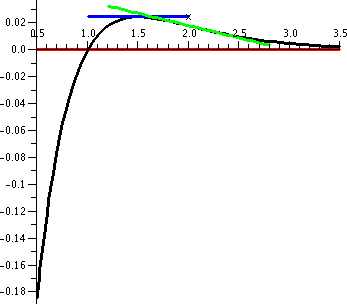
Each of these pictures has a carefully chosen "window", mostly
gotten by experimentation. Here x is in [.5,3.5] and y is in
[-3.2,3.04]. The graphics program always tries to show a sort of
filled square, so all of these pictures are somewhat distorted. For
example, here the y range is almost twice the x-range.
There's a short horizontal line segment in blue representing the tangent line at the
only critical point. The horizontal asymptote (the x-axis) is shown in
red. There is one inflection point and a
line segment representing the line tangent to the curve at that
inflection point is drawn in light
green. Please notice that the curve is below this line
segment to the left of the inflection point and it is above the line
segment to the right of the infliection point.
| 
|
Problem 2
f(x)=(x3+1)/x
Here the window is (x) [-2,2] by (y) [-6,4] so there is a 1:5
distortion of horizontal to vertical.
The blue (critical point) and red (the vertical asymptote) and light green (inflection point) signal
the same types of behavior as in the previous graph.
| 
|
Problem 3
f(x)=x+sin(x)
Here the window is square, [-10,10] in both x and y. The graph
is the curve which, in effect, wiggles around the main diagonal line,
y=x.
Look: the curve really does strictly increase as you move along
it from left to right. And it has infinitely many critical points (two
are shown), each of which is also an inflection point. These have
horizontal line segments drawn in blue. Additionally, there is an inflection
point on the curve between each pair of critical points. Three of
these are shown with their light
green tangential line segments. In this case, each critical
point is also an inflection point and the curve does appear on both
sides of both colors of line segments near the point of tangency.
| 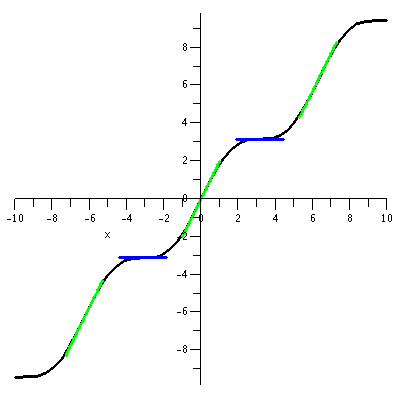 |
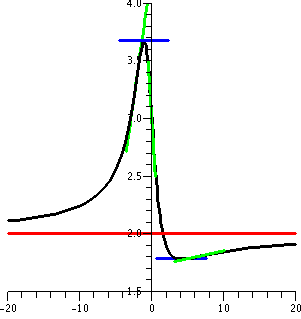
Problem 4
f(x)=(2x2+9)/(x2+x+3)
This was the graph whose window was most difficult to select. I
finally used [-20,20] in x and [2.5,4.0] in y, a distortion of 24:1. I
wanted to make the features visible. The result isn't perfect!
The horizontal asymptote is in red.
There are two critical points, and their horizontal tangent line
segments are in blue. The behavior
I find most difficult to see in this picture is near
each of the three inflection points. Again, there are light green tangential line segments at
each inflection point. If you look at them very closely, maybe
you can convince yourself that they actually cut through the graph of
y=f(x) in each case. In this window, with the "granularity" of the
image, the behavior may not be clear.
| 
|
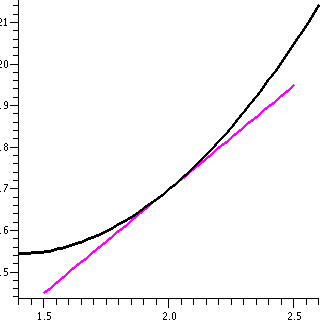
Problem 5
In this problem, only "point" information about f(x) was given, mostly indirectly though the equation of the line. The
window here is [1.4,2.6] by
[14.5,21.5], so there's a 1:7 distortion.
The line segment shown in magenta is
part of the given tangent line, y=5x+7. The curve is the simplest
example of a function with f(2)=17 and f´(2)=5 and
f´´(2)=8: it is f(x)=17+5(x-2)+4(x-2)2. Certainly
any function with the point data given would look locally like this,
with the only question being the scale of the locality (how close to
x=2 should the window be to look as shown). I hope this may help you
understand the answer to b).
| 
|
The second exam
| Problem | #1 |
#2 |
#3 |
#4 |
#5 |
#6 |
#7 |
Total |
|---|
| Max grade |
10 |
9 |
11 |
15 |
14 |
12 |
20 |
84 |
|---|
Min grade |
0 |
1 |
0 |
2 |
1 |
0 |
0 |
14 |
Mean grade |
4.44 |
3.22 |
3.48 |
8.67 |
10.67 |
4.34 |
6.04 |
45 |
Median grade |
4 |
3 |
6.5 |
10 |
11.5 |
6 |
5 |
42.5 |
18 students took this exam. Numerical grades will be retained for use
in computing the final letter grade in the course. Here are
approximate letter grade assignments for this exam:
Letter
equivalent | A | B+ | B | C+ |
C | D | F |
|---|
| Range | [80,100] |
[75,79] |
[65,74] |
[60,64] |
[50,59] |
[45,49] |
[0,44] |
|---|
Discussion of the grading
Some general background
Again, I tried to penalize arithmetic errors and "small" errors
minimally, unless the problem was materially simplified by the
errors. Students needed to read "my" problem and do that problem,
though, and not one they invented as a substitute. I also could read
only what was written on the exam paper, not what students may have
intended. I wanted some supporting evidence for most answers -- some
idea of how students knew the answer.
Problem 1 (10 points)
"Implied" arithmetic is o.k. in this problem, but unevaluated function
values in f(x), f´(x), and f´´(x) are not o.k.
1 point for F(2).
3 points for F´(2): 2 points for the correct use of the Chain Rule, and
1 point for the answer.
6 points for F´´(2): 2 points for the Product Rule, 2 points
for the Chain Rule, 1 point for differentiating the power correctly,
and 1 point for the answer.
Problem 2 (12 points)
a) (2 points) Some explicit attention to the top and ln earns 1 point,
and attention to the bottom earns the other point.
b) (5 points) 1 point for the answer, and 4 points for the
process. A use of L'H counts for 2 points, and the eligibility must be
specifically acknowledged.
c) (1 point) The correct equation.
d) (3 points) 1 point for the answer, and 2 points for the process.
e) (1 point) The correct equation.
Problem 3 (16 points)
a) (8 points) 2 points for computing f´(x). 1 point each for
detecting the critical numbers. 2 points each for describing the
nature of the critical point and why.
Again, please realize that points where the first derivative is 0 may
not be relative max/min points. Here is an example: f(x)=x3.
b) (8 points) 2 points for computing f´´(x). 1 point each
for detecting where the second derivative vanishes. 2 points each for
describing why each represents an inflection point.
Again, please realize that points where the second derivative is 0 may
not be inflection points. Here is an example: f(x)=x4.
Problem 4 (16 points)
Preparation (7 points) 2 points for constraint equation; 2
points for the objective function; 3 points for using these to
translate to a 1 variable calculus problem, including the
domain.
Analysis of the calculus problem (7 points)
2 points for finding the derivative of the function to be maximized.
5 points for the total analysis showing that a maximum has been
found. One roadmap: 2 points for checking endpoints, 2 points for
evaluating the function at the critical numbers, 1 point for putting
the information "together".
Stating the answer (2 points)
2 points for reporting the dimensions of the pasture with largest
area.
Problem 5 (14 points)
a) (1 point) Plug in the numbers and check.
b) (7 points) From left to right in the original equation: Chain Rule
(2 points); derivative of x3 (1 point); Product Rule (2
points). 2 points for getting a formula for dy/dx. The 2 points for
solving for dy/dx can be earned even if there is a mistake in
differentiation but only if dy/dx appears twice in the student's
previous computation and the successive algebraic manipulations are
correct. Also, the 2 points can only be earned for "uninstantiated"
dy/dx: that is, no substitutions for x or y have been made (the
problem does specifically request an answer "in terms of x and
y").
c) (4 points) 1 point for realizing that the line must go through
(-2,1), 1 point for the slope, and 2 points for a valid equation of
the line.
d) (2 points) The line should go through (-2,1) (1 point) and seem to
be tangent (not cross the curve at the point of tangency!). The
direction should be correct. (1 point)
Problem 6 (12 points)
2 points for giving a formula for A in terms of r and R. 2 points for
finding what A is when r=7 and R=10. 4 points for finding a formula
for A´ in terms of r, r´, R, and R´. 2 points for
computing A´ at the desired time. 2 points for reporting the
answers (decreasing and rate).
Problem 7 (20 points)
a) (12 points) 2 points for identifying the x where the maximum value
occurs, either graphically or in words. 4 points each for
explaining why f(at "that" x)>f(x) to the left and to the
right (in the interval [1,3]). 2 points for stating the conclusion in
some fashion.
b) (8 points) 2 points for writing the tangent line approximation in
this case, linking f(3.04) and f(3)+f´(3)(.04); 2 points for
giving the approximate linearized value; 2 points for detecting the
sign of f´´(3) in the graph of f´(x); 2 points for
using this information to correctly conclude the relationship between
the approximation and the true value of f(3.04). It is also possible
to give a convincing argument by just discussing f´(x) (it
increases as x increases from 3).
The final exam
| Problem | #1 |
#2 |
#3 |
#4 |
#5 |
#6 |
#7 |
#8 |
#9 |
#10 |
#11 |
#12 |
#13 |
#14 |
#15 |
Total |
|---|
| Max grade |
19 |
12 |
22 |
8 |
14 |
9 |
10 |
12 |
18 |
12 |
12 |
8 |
13 |
15 |
12 |
175 |
|---|
Min grade |
7 |
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
2 |
0 |
12 |
Mean grade |
14.41 |
10.12 |
18.53 |
3.76 |
4.29 |
6.24 |
5.06 |
9.35 |
10.47 |
5.59 |
6.53 |
6.82 |
4.42 |
2.47 |
7.29 |
125.73 |
Median grade |
15 |
12 |
21 |
3 |
3 |
6 |
9 |
11 |
12 |
4 |
6 |
7 |
11 |
6 |
8 |
123 |
17 students took this exam. Numerical grades will be retained for use
in computing the final letter grade in the course. Here are
approximate letter grade assignments for this exam, which are similar
to those used during the standard semesters:
Letter
equivalent | A | B+ | B | C+ |
C | D | F |
|---|
| Range | [175,200] |
[165,174] |
[150,164] |
[135,149] |
[110,134] |
[100,109] |
[0,99] |
|---|
Discussion of the grading
Some general background
The statement here would be the same as on previous exams. Most
students by now were answering "my" questions, and I noticed a general
improvement in giving reasons with words when that was
requested: thank you.
Problem 1 (20 points)
Each part was worth 5 points. The answer in each part earned 1 point,
and 4 points were awarded for some justification.
Problem 2 (12 points)
1 point for the definition, 2 points for using it with this function,
3 points for converting the compound fraction to a simple fraction, 2
points for "expanding" the square, 3 points for cancellations
(additive x2's and multiplicative h's) and 1 point for the
limit (the final asnwer).
Problem 3 (22 points)
a) (5 points) 2 points off for a misuse of the Chain Rule.
b) (7 points) 2 points off for a misuse of the Chain Rule.
2 points off for a misuse of the Product Rule.
c) (5 points) 2 points off for a misuse of the Quotient Rule.
d) (5 points) An answer alone is fine, but of course I welcomed any
mention of the Fundamental Theorem of Calculus.
Problem 4 (8 points)
a) (4 points) 2 points for the correct computation of f´(x). 2
points for a verification of the assertion, which should include use
of (-)(-)=+ and the evenness of 300.
b) (4 points) Direct citation of the Mean Value Theorem is
welcome, but I also accepted a use of this consequence: if
f´(x)>0, then f(x) is increasing. This "theory" (worth 2
points) had to be attached to the function in this problem, and this
"attachment" correctly done was worth the last 2 points.
Problem 5
Preparation (8 points) 2 points for constraint equation; 2
points for the objective function; 3 points for using these to
translate to a 1 variable calculus problem, including the
domain.
Analysis of the calculus problem (7 points) 2 points for
finding the derivative of the function to be maximized. 5 points for
the total analysis showing that a maximum has been found. One roadmap:
2 points for checking endpoints in some manner, 2 points for
evaluating the function at the critical number (just checking that it
is postive is sufficient!), 1 point for putting the information
"together".
Stating the answer (2 points)
2 points for reporting the dimensions of the box with largest volume.
Problem 6 (10 points)
Horizontal asymptotes: (6 points) Two equations should be the answer,
and each correct answer will earn 1. The verification that these
answers are correct will each earn 2 points: an appropriate limit must
be computed.
Vertical asymptote: (4 points) The answer (one equation) will earn 1
point. Detection that the bottom is 0 at a certain value of x earns 2
points, but this only establishes "eligibility" for a vertical
asymptote. Additionally, the student must verify (or even mention!)
that the top is not 0 at that value of x, and this will earn 1 point.
The problem statement carefully requests <1>equation of the
asymptotes. If equations are not given, 1 point will be deducted from
the score.
Problem 7 (10 points)
Comments and scoring
This was a "simple" problem but the questions were written so briefly
that they seemed (in retrospect!) almost designed so students
would not answer the questions appropriately. It is
certainly true that a function which is not defined at x=a
cannot be continuous or differentiable at x=a. Therefore a rather
trivial way to answer the question would be to give as example (for
both parts!) any function whose domain doesn't include some
number. I will give some credit (2 points of 5 in each part) to an
answer of that type. I believe such an answer essentially
"trivializes" the question and does not tell me if a student knows
much about continuity or differentiability.
On the other hand, there are contrasting techniques for attempting
"good faith" answers to the questions which were asked. An algebraic
definition of a function can be given. Then the student may try to
show that the function given does not have some necessary attribute of
the definition involved --
that some aspect of the definition is violated. A student could also
attempt to answer the question geometrically, by drawing the graph of
a function. Much of the course has involved considering and
contrasting numerical and algebraic and geometric properties of
functions so certainly here (regardless of the intentions of
the questioner!) a student can earn full credit with either
approach. In each part, 1 point will be given for an example, and 4
points for a discussion or computation validating the example. The
discussion or computation must include some reference to a key part of
the definition of continuity or the definition of derivative. This
must be given explicitly in words or symbolically using appropriate
algebra (such as certain limits not being equal).
If I give a question of this type again, I will certainly make the
statement more longer and more precise. Then I'd hope to read more
suitable answers.
Problem 8 (12 points)
a) (6 points) Differentiation is worth 5 points (differentiation of
the terms on the left side of the equation are worth 1 and 2 and 2
points). Solving for dy/dx correctly earns 1 point.
b) (4 points) 1 point for realizing that the line must go through
(3,1), 1 point for the slope, and 2 points for a valid equation of
the line.
c) (2 points) The line should go through (3,1) (1 point) and seem to
be tangent (not cross the curve at the point of tangency!). The
direction should be correct. (1 point)
Problem 9 (18 points)
a) (10 points) 3 points for the critical numbers, 3 points for
conclusions about the nature of the critical numbers, and 4 points for
supporting evidence, such as signs of f´(x).
b) (4 points) 1 point for m and 1 point for M.
1 point for continuity and 1 point for correct {in|de}creasing behavior.
c) (4 points) 1 point for the correct number of inflection points, and
1 point each for correctly marking them on the graph.
Problem 10 (12 points)
2 points for giving a formula for V in terms of r. 4 points for
finding a formula for V´ in terms of r and r´. 2 points for
computing r at the volume given. 4 points for combining it all into
the answer.
Students who don't have an expression connecting V´ and r and
r´ are not doing this problem and can earn only the 2
formula points and the 2 points for getting a specific value of r.
Problem 11 (12 points)
a) (8 points) 1 point for the derivtive. 2 points for the critical
numbers. 3 points for testing, which must include the endpoints or
else just 1 point. 2 points for reporting the correct answers which
are athe values of the function. Students who ignore the endpoints
will get 4 out of 8 for this part of the problem (1+2+1+0).
b) (4 points) 2 points for the correct answer or for an answer which
follows from the student's answer to a). 2 points for mentioning the
Intermediate Value Theorem.
Problem 12 (8 points)
Length of the subintervals (2 points), correct
sample points (2 points), computation and answer (4 points).
1 point deducted for not matching an interval with its correct sample
point. 2 points deducted if there are not 3 subintervals.
Problem 13 (13 points)
1 point will be deducted for the problem score if "+C" is missing from
any of the final answers.
a) (3 points) Powers of x and algebra.
b) (5 points) Substitution, antidifferentiation, solution.
c) (5 points) Substitution, antidifferentiation, solution. A bit of
algebra.
Problem 14 (15 points)
4 points for the graph, and 2 of those points were lost if the graph
was not labeled. 2 points for finding the first positive intersection
of the curves. 3 points for a setup: converting the area problem into
computation of one or two definite integrals. 6 points for the
subsequent computation, and 1 point of these was for the answer. The
two integrals were each worth 2 points (1 for antidifferentiation and
1 for substituting the limits of integratin) and their difference was
worth 1 point.
Problem 15 (12 points)
Each antidifferentiation was worth 4 points and each correct use of
the initial condition earned 2 points.
2 points were deducted (one time!) if the student incorrectly declared
that an antiderivative of e-t was e-t. More
elaborate and incorrect antiderivatives were penalized further. 2
points were deducted if the initial values were interchanged. 1 point
was deducted if somehow t's became x's (the function is x, and the
independent variable here is t).
Final grades
I computed the sum of students' grades in the three full and two
semi-exams. I used this number, along with numbers obtained from
previous number-to-letter conversions, to assign grades. According to
Rutgers regulations, I must retain possession of the final exams.
Students who would like to see their exams or discuss their course
grades should make appointments with me.
By the way, here's
a reference for the present value of an income stream.
Maintained by
greenfie@math.rutgers.edu and last modified 8/18/2006.




