Earlier material
| Tuesday,
December 11 | (Lecture #28) |
|---|
Notes by Jinwei Yang, edited, with
some comments, by the instructor.
We begin with some ideas used in the standard proof of the Riemann
Mapping Theorem (RMT). We won't have time to finish the proof. But
this is the now standard proof, given in many textbooks, so please
read the remainder of the proof there. In the proof, a proper simply
connected, connected open subset U of C is given. If there is a
biholomorphic mapping from U to D1(0), then (since we know
Aut(D1(0) very well now) we can require that the mapping
take a selected point p in U to 0 in D1(0), and we can also
ask that the derivative of this mapping at p be real. The Schwarz
Lemma also suggests that we make this derivative as large as possible,
so that the image will be all of the disc (this is just a
suggestion!). Many proofs of the RMT create a sequence of functions
{fn}, and the desired biholomorphic mapping is the limit of
the sequence. We should try to see when such sequences must
have a limit.
Problem Given a "collection" of functions F, when is it true
that every sequence in that collection has a subsequence which
converges uniformly?
A good collection of examples is
important. Our function space for examples was C[0,1], the continuous
functions on the unit interval. For simplicity, we will consider
real-valued continuous functions.
|
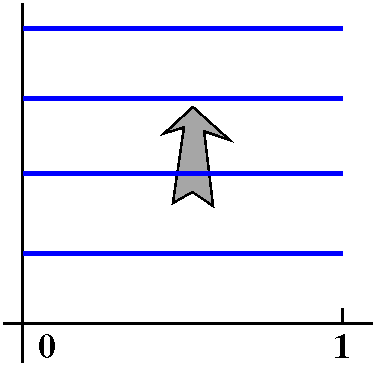
Example 1 The family of functions is the sequence
fn(x)=n. Certainly this sequence does not converge
uniformly. From this we learn that we'd better require that our family
of functions is bounded (sometimes called uniformly bounded):
that is, there is B>0 so that for all f's in F, we know that
|f(x)|<=B. This means, geometrically, that the graphs of f(x) are
between y=-B and y=B.
|
|
|
Example 2 The family of functions is the
sequence fn(x)=sin(nx). I claim that this sequence does
not converge uniformly, and, indeed, that it has no subsequence
which converges uniformly. Well, just look at x=0 and what happens
near 0. If there is a function g which is a limit of a subsequence of
the fn's, then I certainly know that g(0)=0 since all of
the fn's have value 0 at 0. Notice that for some very
large n, |fn(x)-g(x)|<1/2 for x's near 0. Well, since
g(0)=0, I bet that we can select an interval of x's near 0 ("some
[0,D] for D>0") so |g(x)|<1/2. Then for large enough n and for
those x's, |fn(x)|<=|fn(x)-g(x)|+|g(x)|<1/2+1/2=1. But, golly, fn has
period 2Pi/n. For large n's, this period certainly fits inside
[0,D]. And the values of sine on a period are [-1,1], so there is
no uniformly convergent subsequence of this sequence of
functions. The sequence of functions wiggles too much.
| 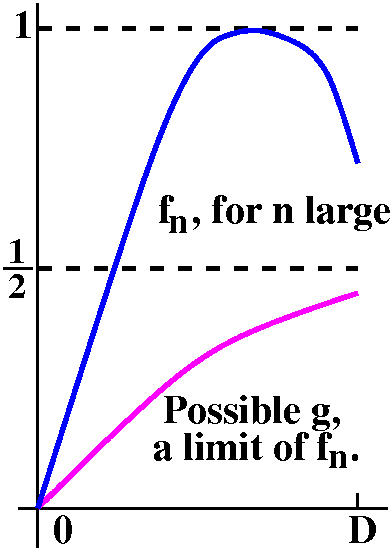
|
In general, if a sequence of functions converges uniformly to a limit
function, the limit function's wiggle must be close to the wiggle of
almost all of the sequence. Of course, it would be helpful if the word
or idea of wiggle were made more precise, and, in a real
variables courses, I am sure that you will all learn about the
oscillation of a function. For this course, we just need the following definition.
Definition F is equicontinuous at x0 if any e>0,
there exists d>0, such that for any f in F, if
|x-x0|<d, then
|f(x)-f(x0)|<e.
A true fact (what's a false fact?) is that a collection of continuous
functions defined on a compact metric space which is equicontinuous at
every point is actually uniformly equicontinuous (e doesn't
depend on x0). This follows from standard compactness
arguments.
Now we can state a famous theorem which says the necessary conditions
mentioned are actually sufficient. To me, this result is not
obvious. Its invention needed consideration of many more examples than
the few we have considered.
Theorem (Arzelà-Ascoli) If F is a
subset of C[0,1] which is bounded and (uniformly) equicontinuous, then
every sequence in F has a uniformly convergent subsequences.
You should try to prove this yourself, even if you've heard or read or
have sat through (!) a proof. Just look at a {xn}
which is dense in [0,1], and create a subsequence of any sequence in F
(diagonally selected!) converge everywhere uniformly.
How can we guarantee or "force" that a collection of functions is
equicontinuous at (even) one point? One simple condition follows:
Sufficient condition for equicontinuity
Suppose F is a subset of C[0,1], and suppose that all of the functons
in F are differentiable. IF there is a constant K
so that |f´(x)|<=K then F is equicontinuous. This follows from
the Mean Value Theorem. MVT says f(b)-f(a)=f´(c)(b-a). Now if
|b-a|<e/K, |f(b)-f(a)| will certainly be less than e. So d can be
e/K, the same for all of the f's in F.
This is not the only way to verify equicontinuity, of course. One can
ask for uniform Lipschitz conditions: there's q>0 and r>0
so that |f(b)-f(a)|<=r|b-a|q (think of sqrt(x) and
companions on [0,1]: certainly not Lipschitz (a q=1 condition won't be
satisfied near 0 but a q=1/2 will be) and certainly not
differentiable. There was some discussion
of this earlier in the diary (butterflies and boxes!).
Notice that we can put together intervals to get convergence on all of
R. For example, here is a result depending A-A for closed bounded
intervals:
UCC convergence on R
Suppose F is a collection of continuous functions on R and that we
know that the functions in F are uniformly bounded on any compact
interval in R, and also that F is uniformly equicontinuous on any
compact interval in R. Then every sequence in f has a uniformly
convergent subsequence.
Why is this true? Take any sequence of functions in F. We apply A-A on
[-1,1] and get a uniformly convergence subsequence. Then consider
this subsequence on [-2,2] and get a subsequence of that subsequence,
and then ... [-n,n] ... and choose the final subsequence to be a
diagonal subsequence of this sequence of subsequences. The result is a
sequence which converges uniformly on any compact subset of R (not
necessarily on R itself, though). So we use the sigma-compactness of
R. Any subset of C is also sigma-compact, so the same approach will
be successful there.
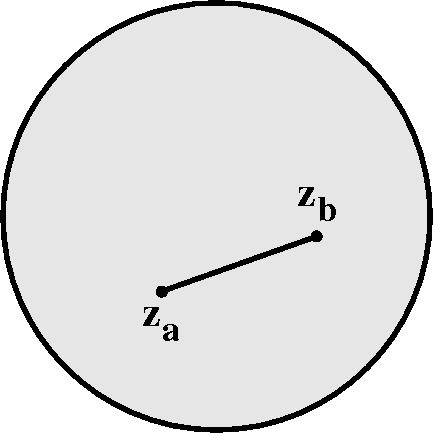 What happens when we consider holomorphic functions?
For example, suppose we have a function f holomorphic in a disc, with
|f´(z)|<=K. If za and zb are in the
disc, then
f(zb)-f(za)=
What happens when we consider holomorphic functions?
For example, suppose we have a function f holomorphic in a disc, with
|f´(z)|<=K. If za and zb are in the
disc, then
f(zb)-f(za)= pathf´(z) dz.
We can take the path to be, for example, a straight line
segment from za to zb. But ML then gives
|f(zb)-f(za|<=K|zb-za|,
a Lipschitz estimate, so a family of holomorphic functions whose
derivatives have uniformly bounded modulus would also be (uniformly)
equicontinuous. And since uniformly convergent sequences of
holomorphic functions have holomorphic limits, we see that the
limiting continuous function guaranteed by A-A is here also
holomorphic.
pathf´(z) dz.
We can take the path to be, for example, a straight line
segment from za to zb. But ML then gives
|f(zb)-f(za|<=K|zb-za|,
a Lipschitz estimate, so a family of holomorphic functions whose
derivatives have uniformly bounded modulus would also be (uniformly)
equicontinuous. And since uniformly convergent sequences of
holomorphic functions have holomorphic limits, we see that the
limiting continuous function guaranteed by A-A is here also
holomorphic.
Notice, please, we are using a sort of Mean Value inequality,
which is certainly valid under these circumstances. We aren't using an
equality form of MVT since that's not true.
It is amazing and wonderful and powerful that the requirements of
Arzelà-Ascoli can be combined in a simpler hypothesis for holomorphic
functions.
Theorem (called Montel's Theorem)
Suppose U is open, F is a collection of functions which are
holomorphic on U, and for any K compact in U,
supf in F||f||K is finite (so the
modulus of functions in F is bounded on any compact set).
Then every sequence in F has a subsequence which converges
uniformly on compact subsets.
The classical name for such F's is a normal family. These F's
are subsets of the holomorphic functions whose closure is compact
("precompact" sets of holomorphic functions).
Proof U is the increasing union of compact sets Kn.
We proved that
||f´||K<=(1/s)||f||Ks for
sufficiently small positive s. Here Ks is also compact in
U, and is the union of all the closed discs of radius s centered at
points in K. So combine this with the previous observation, and we see
that an F which is bounded on compact sets is also uniformly
equicontinuous on compact sets. So A-A applies. And sigma-compactness
also guarantees the existence of a (locally) uniformly convergent
sequence of holomorphic functions in F. The limit function will be
holomorphic.
(Not) finishing the proof of RMT: start with a well-chosen f on U. The
hypothesis of simply connected insures that holomorphic square roots
of non-zero holomorphic functions exist. The well-chosen f is
sqrt(z-b) for b not in U. We create the initial f
and then continue with a sequence of fn's. Montel's
Theorem is used to guarantee a limit, and Hurwitz's Theorem (limits of
1-1 holomorphic functions are either constant or 1-1) to show that the
limit is not constant. And the Schwarz Lemma essentially guarantees
that the whole disc D1(0) is filled up by the image of
U. Please read one of the classical proofs. The
text's version is in section 6.7.
For what follows we need one more classical result called the
Schwarz Reflection Principle.
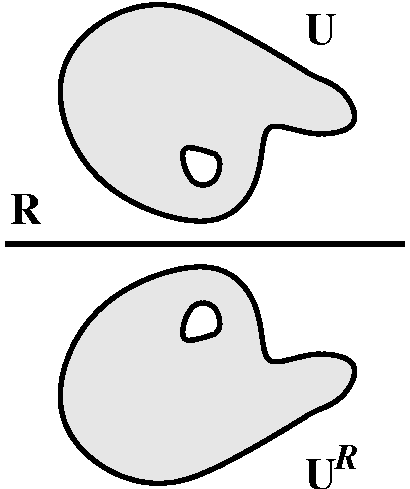 Schwarz Reflection (baby version) Suppose that U is open and
connected in C, and f(z)=f(x+iy)=u(x,y)+iv(x,y) is holomorphic in
U. If UR is the collection of "reflected" z's in U
(that is, all the zbar's for z in U), then the function
g(z)=[f(zbar)bar is holomorphic in
UR.
Schwarz Reflection (baby version) Suppose that U is open and
connected in C, and f(z)=f(x+iy)=u(x,y)+iv(x,y) is holomorphic in
U. If UR is the collection of "reflected" z's in U
(that is, all the zbar's for z in U), then the function
g(z)=[f(zbar)bar is holomorphic in
UR.
Why is this true? One way to think about this is to realize that f(z)
near z0 in U is the sum of a convergent power series. The
mapping z-->zbar is certainly continuous
(although it equally certainly is not holomorphic). But then the
series
 n=0
n=0 an(z-z0)n
becomes the series
an(z-z0)n
becomes the series
 n=0
n=0 {an}bar(z-{z0}bar)n
upon the stated reflection, and this is a convergent power
series in z, indeed.
{an}bar(z-{z0}bar)n
upon the stated reflection, and this is a convergent power
series in z, indeed.
Another way to verify holomorphicity is just to realize that
g(z)=u(x,-y)-iv(x,-y). The several variable Chain Rule from calculus
will show that g satisfies the Cauchy-Riemann equations.
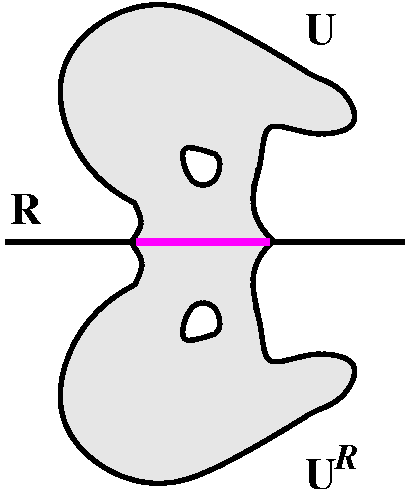 Schwarz Reflection (adolescent version) Suppose that U is open and
connected in H, the open upper halfplane (z's so that
Im z>0). Also suppose that the boundary of U contains an
interval I of the real line, R. Suppose that f is holomorphic in U and
has real continuous boundary values on I: that is,
limz-->xf(z)=Q(x) exists (x is in I and z is in U) and Q
is continuous in I. Then define V to be the union of U and
UR (as defined before) and I also. Let g(z) be f(z)
for z in U, [f(zbar)]bar for z in
UR, and Q(x) for x in I. Then g is holomorphic in
V.
Schwarz Reflection (adolescent version) Suppose that U is open and
connected in H, the open upper halfplane (z's so that
Im z>0). Also suppose that the boundary of U contains an
interval I of the real line, R. Suppose that f is holomorphic in U and
has real continuous boundary values on I: that is,
limz-->xf(z)=Q(x) exists (x is in I and z is in U) and Q
is continuous in I. Then define V to be the union of U and
UR (as defined before) and I also. Let g(z) be f(z)
for z in U, [f(zbar)]bar for z in
UR, and Q(x) for x in I. Then g is holomorphic in
V.
Proof Certainly the Baby Version of Schwarz Reflection shows
that g is holomorphic in U and in UR and we need to
check what happens near I. But g is continuous in all of V. If we can
show that the integral of g around a rectangle with sides parallel to
the coordinate axes is 0, we are done (Morera!). But it's enough to
consider a rectangle with one side on the x-axis. We can move it
up slightly, and the integral is 0 (Cauchy!). This integral is
continuous in the slight movement, so the desired rectangular
contour integral must be 0.
This sort of argument was part of an earlier homework problem and a
number of students recognized it. The hypotheses imply that the
original mapping of f sort of sits on one side of the image R inside
the image C. The reflection principle can be used in many contexts
because both the domain and the image R's can be changed into many
different curves by conformal mappings. This is used, for example, to
analyze the automorphism groups of complicated domains such as an
annulus, and can also be used to construct the elliptic modular
function, a very important classical holomorphic function with uses in
number theorem and hyperbolic geometry.
The adult version of the Schwarz Lemma weakens the hypothesis
in the adolescent version in one wonderful way. We ask that the
limz-->xf(z)=Q(x) still exist and be real, but no
additional conditions on Q are needed. Notice that one consequence
of the existence of the limit, using the adult version, is that the
resulting Q turns out to be real analytic: certainly this is
not obvious. It is not even obvious in the adolescent version, where
there is an almost magical transition from "Q is continuous" to "Q is
real analytic". This result is what's important in the very last
discussion of the course. The proof of the adult verions uses the
solution of the Dirichlet Problem and the consequence that continuous
functions which have the mean value property must be harmonic. This is
discussed in the textbook. See Theorem 7.5.2 in section 7.5.
The very last, very final, wonderful conclusion of the course is the Lewy example of a simple PDE with
no solutions.
Also available is a direct discussion of
the Mittag-Leffler and Weierstrass Theorems, results guaranteeing
the existence of holomorphic and meromorphic functions with strictly
prescribed behavior. This was proofread by Mr. Castro and Ms. Naqvi,
whose efforts I appreciated.
And, indeed, I appreciated the work of all the students in the course:
thank you. Here is information
about the final exam.
| Friday,
December 7 | (Lecture #27) |
|---|
Notes by Avital Oliver, edited, with
some comments, by the instructor.
A nice fact that we will use later
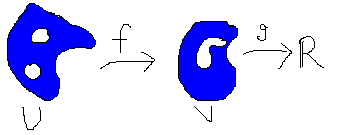
Assume the following: U and V are open sets in C, f:U-->V
holomorphic and h:V-->R harmonic. What do we know about hof? If V
is simply connected, then h has a harmonic conjugate, thus h is the
real part of a holomorphic function (h=Re(g)). In this case gof is
holomorphic, so hof=Re(gof) which is a harmonic function.
The image to the right was supplied by the
"scribe". Appropriate thanks are certainly due to him.
If V is not simply connected, it is still locally simply connected
(just choose small balls around each point), so this is all still true
locally. Since holomorphicity is a local property, the result is still
true:
Proposition The composition of a harmonic function with a
holomorphic function is harmonic.
Another proof of this fact is given on page 213 in the textbook (using
differential operators and the Chain Rule).
Why do we care about conformal (also known as biholomorphic)
mappings?
For many reasons (or else the instructor would not spend so much time
discussing it!). Here's an important example: The Dirichlet
Problem is an important problem, which arises from many fields in
Physics (electostatics, heat flow, etc.) and in probability, etc. The
general question is: given boundary data on some open set in C, is
there a harmonic function defined inside the open set which satisfies
the boundary data?
We will consider the simplest case: The function defined on the
boundary is continuous and the domain is simply connected. By the
Riemann Mapping Theorem (which we will not
be able to prove ... please see the textbook), this domain can
be conformally mapped to the unit disc. By our "nice fact that we will
use later" (later being now), solving the Dirichlet problem on our
open set is equivalent to solving the Dirichlet problem on the unit
disc.
Solving the Dirichlet problem on the unit disc
The instructor told us that there are many ways to solve this, some
including bugs (Brownian motion), electrons ("Kelvin's Method of
Images"), and other strange ideas. Also, there is the solution as
given in the textbook, which is something like "Here is the
solution. Just compute and see that it's right" (around page 214).
Instead, we will try to find the solution ourselves.
What we know about harmonic functions:
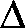 h=0, h is C2, and since such an h is locally the
real part of a holomorphic function, h must actually be real
analytic.
h=0, h is C2, and since such an h is locally the
real part of a holomorphic function, h must actually be real
analytic.- Maximum and minimum principles: a harmonic function which extends
continuously to the closure of a relatively compact set is either
constant or it achieves its strict maximum or minimum on the
boundary. (This actually follows from the next result!)
- Mean-Value property: If f is a holomorphic function, then by
the Cauchy Integral Formula, f(z)=
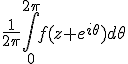 , therefore, since harmonic
functions are real parts of holomorphic functions, this is also true for
harmonic functions.
, therefore, since harmonic
functions are real parts of holomorphic functions, this is also true for
harmonic functions.
"Abstract nonsense" discussion
Suppose b is a continuous real-valued function on the boundary of the
unit disc, and we know that there is a harmonic function
hb defined on the disc with boundary values equal to
b. Also pick a point z inside the unit disc. The mapping Tz defined by
b-->hb(z) has the following properties (all verified
using what was just written):
Tz is linear: Tz(b1+b2)=Tz(b1)+Tz(b2) and
Tz(rb)=rTz(b) (r is a real
constant)
Tz is positive: if b>=0
everywhere, Tz(b)>=0.
Tz is bounded by 1:
-||b|| <=Tz(b)<=||b||
<=Tz(b)<=||b|| .
.
Under such conditions, the giant machinery of measure theory tells us
something important: there is always a positive measure of total mass
1 on the boundary, let's call it mz, so that
Tz(b)=
 D1(0)b dmz. But
this abstract fact doesn't describe the actual measure
specifically. This can be done, and that's what the computations which
follow show. The method used is fairly elementary, and is basically
separation of variables, looking at the radial and angular
parts of the problem.
D1(0)b dmz. But
this abstract fact doesn't describe the actual measure
specifically. This can be done, and that's what the computations which
follow show. The method used is fairly elementary, and is basically
separation of variables, looking at the radial and angular
parts of the problem.
O.k., it's time to start solving! We are trying to define a function L
from the set of continuous functions on  D1(0) to the set of
harmonic functions on D1(0). Let b be the boundary
function: b is a continuous function on
D1(0) to the set of
harmonic functions on D1(0). Let b be the boundary
function: b is a continuous function on  D1(0), so by Fourier
series (since b is also in L2),
D1(0), so by Fourier
series (since b is also in L2), 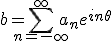 almost everywhere. The solution
to the Dirichlet problem is linear in b. L also maintains limits
because by the Max/Min Principles, if b1<=b2
then L(b1)<=L(b2). So we only need to solve
for one of the terms.
almost everywhere. The solution
to the Dirichlet problem is linear in b. L also maintains limits
because by the Max/Min Principles, if b1<=b2
then L(b1)<=L(b2). So we only need to solve
for one of the terms.
- If n>0 then
L(ein
 )=zn=rnein
)=zn=rnein .
.
- If n=0 then L(ein
 )=1.
)=1.
- If n<0 then L(ein
 )= zbarn
(NOT 1/zn which would be singular inside the disc: notice
that conjugate holomorphic functions are also harmonic!), which is
r-nein
)= zbarn
(NOT 1/zn which would be singular inside the disc: notice
that conjugate holomorphic functions are also harmonic!), which is
r-nein
In general, 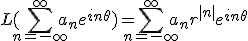
This gives us h if we know b's representation as a Fourier series
and things are computationally easier if we use the
complex form of the Fourier series, but we would also
like a closed form. Some manipulations (!!!) bring us to the
following:
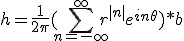 (* is convolution
on the circle).
This series can be represented more nicely.
(* is convolution
on the circle).
This series can be represented more nicely.
Here is the argument, I hope without many mistakes
in algebra:
Consider
 -
-
 r|n|ein
r|n|ein .
Split it up:
.
Split it up:
1+ 0
0 r|n|ein
r|n|ein +
+ -
- -1r|n|ein
-1r|n|ein .
.
The first sum is a geometric series (converging absolutely and
uniformly for r in an interval [0,A] with A is less than 1. It is
rei /(1-rei
/(1-rei ). The second sum is
similar, and the result is
re-i
). The second sum is
similar, and the result is
re-i /(1-re-i
/(1-re-i ). Add these two and
get:
). Add these two and
get:
rei (1-re-i
(1-re-i )+re-i
)+re-i (1-rei
(1-rei )
)
----------------------------------
(1-rei )(1-re-i
)(1-re-i )
)
which is, on the
bottom, 1-2rcos( )+r2, and on the top is
2cos(
)+r2, and on the top is
2cos( )-2r2. If we add the 1 which was also there (n=0)
we get the form of the Poisson kernel displayed in the following
result.
)-2r2. If we add the 1 which was also there (n=0)
we get the form of the Poisson kernel displayed in the following
result.
Solution to the Dirichlet Problem
If b is continuous on  D1(0) then the following h is continuous on the
closed unit disc, harmonic on its interior and agrees with b on its
boundary:
D1(0) then the following h is continuous on the
closed unit disc, harmonic on its interior and agrees with b on its
boundary: 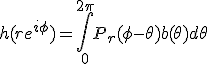 , where
, where 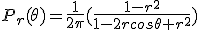 .
.
If you think this is hard to understand, try the textbook proof!
A proof of this is not difficult but I really think it belongs more in
a real variables course. The Poisson kernel which appears in
the solution quoted above is a standard example of what is called an
approximate identity. Here is most of an e-mail message I sent
to Mr. Pal about "approximate
identities".
An approximate identity is an attempt (!) to have an identity for the
convolution operation.
In basic analysis, convolution is defined usually for R or for
S1 (the circle: it is easiest to think of it as [0,2Pi],
or, even better, as R mod the subgroup generated by 2Pi).
Let me discuss only the situation on R. This may be easier. Also, for
the purposes of this message, let me use the notation I(F) for the
integral over all of R of a function F.
If f and g are functions on R, then the convolution of f*g of f and g
is defined by (f*g)(y)=I(f(y-x)g(x)). This is an integrated product
with a shift in one of the variables. This is defined if the integral
converges, of course. If the functions are continuous with compact
support or, more elaborately, are L1 (integrable functions)
then f*g is defined almost everywhere. Indeed, if you know the
appropriate version of the Fubini Theorem, convolution and the usual
function addition make L1(R) into an algebra. Convolution
is commutative and associative. The uses of convolution are many and
varied. For example, Oliver Heaviside used it to compute with
solutions of differential equations. Convolution is used in, say,
financial math to compute such quantities as the "present value" of an
income stream.
In the case of L1(R), convolution does NOT have an identity
(in the sense of multiplicative identity). Maybe the easiest way of
explaining this is to mention that the Fourier transform of
L1 functions are continuous functions which -->0 at
infinity, and that the Fourier transform of a convolution is just the
pointwise product of the Fourier transforms of each of the
"factors". Then a "convolution identity" would automatically
Fourier transform to the function 1, which does not -->0 at
infinity, so there is no identity for convolution.
In certain ways, convolution CAN have an identity. Oliver Heaviside
invented and used the delta function as an identity, and formalizing
this mathematically took decades. Another path is to replace the
algebraic considerations of an identity by using an "approximate"
identity. What is this?
It is usually either a sequence or perhaps a continuously
parameterized collection of eligible smooth functions (or in
L1) so that the limits behave like a convolution
identity. So, for example, you could ask if there is a sequence of
L1 functions, fn, so that fn*g
approaches g (in any sense you might like) as n-->infinity. It may
not be immediately apparent that such sequences exist.
Indeed they do. Here is one such sequence, fairly silly: take
fn to be the function which is n on the interval [0,1/n]
and which is 0 elsewhere. Then if g is in L1,
fn*g(x)-->g(x) for almost all x pointwise and also as a
sequence of functions in L1. And if g is continuous, then
fn*g(x)-->g(x) for all x in R (and some weak uniformity
claims can be made). But that sequence is really not so nice, because
a rectangular graph is not smooth. There are other sequences of
approximate identities. In the context of S1 and
convolution on S1, the Dirichlet kernel, Pr(t),
is an approximate identity. Here is the meaning:
Pr*g-->g as r-->1- (almost always if g is
L1 and more nicely if g is continuous). The proof of this
fact is NOT hard (and is part of the proof that we "solved" the
Dirichlet Problem: the recipe supplied gets back the boundary data as
you go towards the boundary).
I decided not to give a proof principally because the proof really is
a real variables fact, and is easiest to give when the correct limit
theorems about integrals are known. It is relatively easy to verify
that the Poisson kernel is an approximate identity. The Dirichlet
kernel, which also comes up in classical Fourier series, is also an
approximate identity, but this is somewhat more difficult to prove.
The qualities which make it easy to verify that Pr(t) is an
approximate identity are these:
i) Pr(t)>0 for all r and all t.
ii) Pr(t) eventually decreases to 0 as r increases towards
1 for t NOT equal to 0 (and here 0 and 2Pi are the same!).
iii) The total integral over [0,2Pi] is 1.
I think this is all that's required, and then the verification that
we've solved solved the Dirichlet problem works out easily.
An example Dirichlet problem on the unit disc
 In fact, we can also work with boundary data in L1 and not
only continuous. For this example our boundary data is: on the upper
half circle the value is 1, on the lower half circle the value is
0. If we stick this in our amazing formula for L(b), we get an
integral that isn't easy to understand. Instead of solving it for the
unit disc, we'll solve the corresponding Dirichlet problem for the
upper half plane (remember our nice fact from before!). By the
"standard" biholomorphic mapping to the upper half plane, we reduce
the problem to finding a harmonic function on the upper half plane
such that h(x)=1 for negative reals and h(x)=0 for positive reals. We
can guess what could work here: the imaginary part of the simplest branch
of log will work (dividing by Pi). This is of course a harmonic
function, which is equal to (1/Pi)arctan(y/x). Boom! Notice that we worked backwards. Although in general we
could "solve" the Dirichlet problem in a domain by transferring it to
the unit disc and solving it there, actually here we solved a disc
problem by working in a different domain, and recognizing an obvious
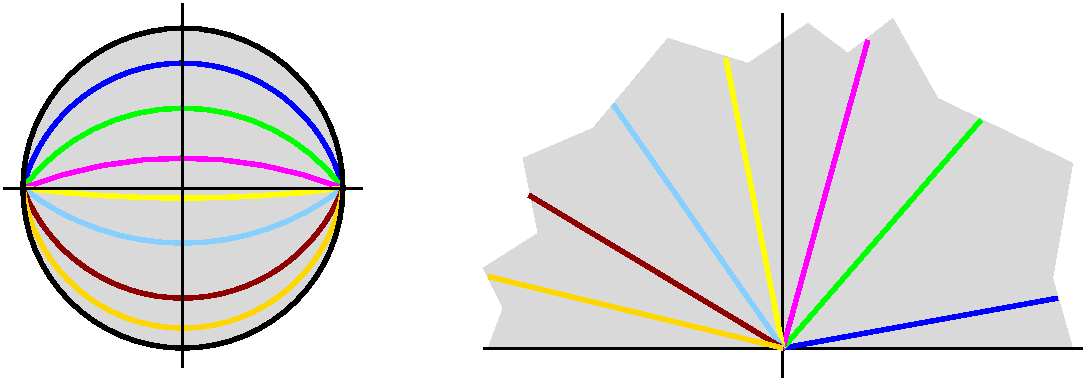
solution in the other domain! The colored lines and semicirles
in the accompanying picture are intended to be the corresponding level
lines of the solution function, and lines with the same colors
correspond to the same values of the functions.
In fact, we can also work with boundary data in L1 and not
only continuous. For this example our boundary data is: on the upper
half circle the value is 1, on the lower half circle the value is
0. If we stick this in our amazing formula for L(b), we get an
integral that isn't easy to understand. Instead of solving it for the
unit disc, we'll solve the corresponding Dirichlet problem for the
upper half plane (remember our nice fact from before!). By the
"standard" biholomorphic mapping to the upper half plane, we reduce
the problem to finding a harmonic function on the upper half plane
such that h(x)=1 for negative reals and h(x)=0 for positive reals. We
can guess what could work here: the imaginary part of the simplest branch
of log will work (dividing by Pi). This is of course a harmonic
function, which is equal to (1/Pi)arctan(y/x). Boom! Notice that we worked backwards. Although in general we
could "solve" the Dirichlet problem in a domain by transferring it to
the unit disc and solving it there, actually here we solved a disc
problem by working in a different domain, and recognizing an obvious
solution in the other domain! The colored lines and semicirles
in the accompanying picture are intended to be the corresponding level
lines of the solution function, and lines with the same colors
correspond to the same values of the functions.
But this is not all! After transfering back to the unit disc, if
we square root (???) we get the solution to the Dirichlet function
given a quarter of the circle having value 1. By iterating this
process, rotating and taking limits, we solve the Dirichlet problem
for all L1 functions. Again, approximate
in L1 by using a sum of step functions. This also
works!
 The next part of the "program" is to sketch a proof of the Riemann
Mapping Theorem: that any simply connected, connected open subset of
the plane which is not all of C is biholomorphic with the unit
disc. In fact, Riemann's original proof (or suggested proof!) of this
result relied first on solving the Dirichlet problem, and deducing the
RMT from that solution. One way he considered solving the Dirichlet
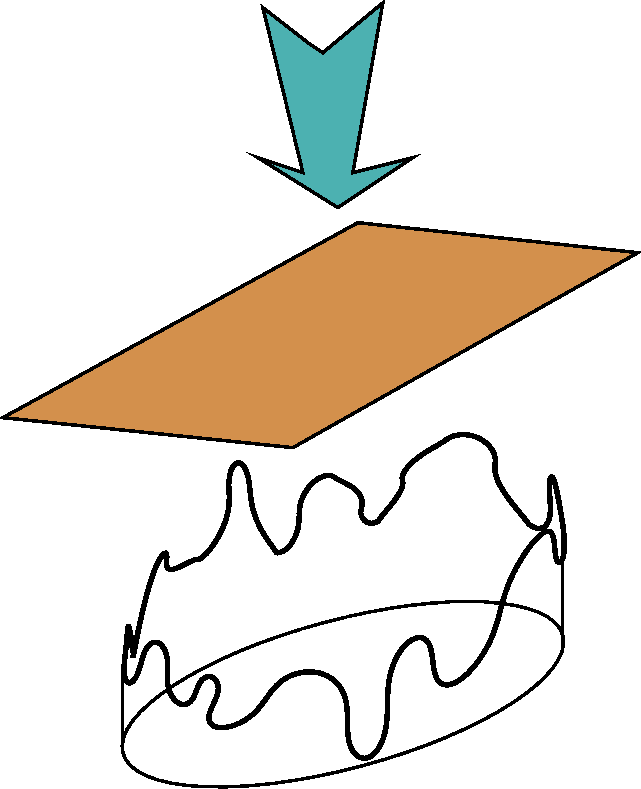
Problem was imagining a boundary height (the boundary data is a
real-valued function) and then lowering a flexible "membrane" over the
data. The membrance would naturally be tight, and would try to
minimize the energy, sort of hugging the boundary data. Then (this
isn't even neat enough to require a "clearly"!) the height of the
membrane over the interior is harmonic, and is the solution to the
Dirichlet Problem. This approach can actually be understood, and does
work, but, wow, it needs (from the point of view of current
mathematics) rather a lot of work. The energy is the integral over the
interior of the norm squared of the gradient of the membrane
height. And showing that there is actually a minimizer (something that
achieves the infimum of energy) is not easy. This leads to a whole
huge area of mathematics called the calculus of variations, and
variational methods of solving partial differential equations.
The next part of the "program" is to sketch a proof of the Riemann
Mapping Theorem: that any simply connected, connected open subset of
the plane which is not all of C is biholomorphic with the unit
disc. In fact, Riemann's original proof (or suggested proof!) of this
result relied first on solving the Dirichlet problem, and deducing the
RMT from that solution. One way he considered solving the Dirichlet
Problem was imagining a boundary height (the boundary data is a
real-valued function) and then lowering a flexible "membrane" over the
data. The membrance would naturally be tight, and would try to
minimize the energy, sort of hugging the boundary data. Then (this
isn't even neat enough to require a "clearly"!) the height of the
membrane over the interior is harmonic, and is the solution to the
Dirichlet Problem. This approach can actually be understood, and does
work, but, wow, it needs (from the point of view of current
mathematics) rather a lot of work. The energy is the integral over the
interior of the norm squared of the gradient of the membrane
height. And showing that there is actually a minimizer (something that
achieves the infimum of energy) is not easy. This leads to a whole
huge area of mathematics called the calculus of variations, and
variational methods of solving partial differential equations.

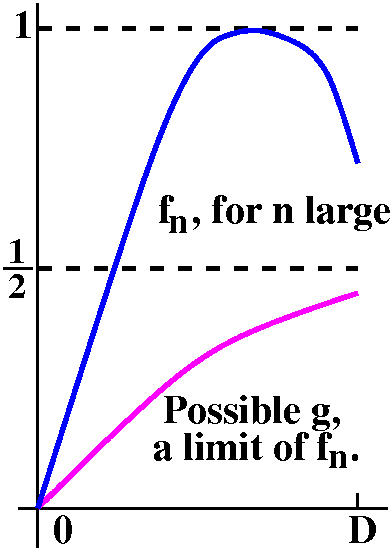
 What happens when we consider holomorphic functions?
For example, suppose we have a function f holomorphic in a disc, with
|f´(z)|<=K. If za and zb are in the
disc, then
f(zb)-f(za)=
What happens when we consider holomorphic functions?
For example, suppose we have a function f holomorphic in a disc, with
|f´(z)|<=K. If za and zb are in the
disc, then
f(zb)-f(za)= Schwarz Reflection (baby version) Suppose that U is open and
connected in C, and f(z)=f(x+iy)=u(x,y)+iv(x,y) is holomorphic in
U. If UR is the collection of "reflected" z's in U
(that is, all the zbar's for z in U), then the function
g(z)=[f(zbar)bar is holomorphic in
UR.
Schwarz Reflection (baby version) Suppose that U is open and
connected in C, and f(z)=f(x+iy)=u(x,y)+iv(x,y) is holomorphic in
U. If UR is the collection of "reflected" z's in U
(that is, all the zbar's for z in U), then the function
g(z)=[f(zbar)bar is holomorphic in
UR.
 Schwarz Reflection (adolescent version) Suppose that U is open and
connected in H, the open upper halfplane (z's so that
Im z>0). Also suppose that the boundary of U contains an
interval I of the real line, R. Suppose that f is holomorphic in U and
has real continuous boundary values on I: that is,
limz-->xf(z)=Q(x) exists (x is in I and z is in U) and Q
is continuous in I. Then define V to be the union of U and
UR (as defined before) and I also. Let g(z) be f(z)
for z in U, [f(zbar)]bar for z in
UR, and Q(x) for x in I. Then g is holomorphic in
V.
Schwarz Reflection (adolescent version) Suppose that U is open and
connected in H, the open upper halfplane (z's so that
Im z>0). Also suppose that the boundary of U contains an
interval I of the real line, R. Suppose that f is holomorphic in U and
has real continuous boundary values on I: that is,
limz-->xf(z)=Q(x) exists (x is in I and z is in U) and Q
is continuous in I. Then define V to be the union of U and
UR (as defined before) and I also. Let g(z) be f(z)
for z in U, [f(zbar)]bar for z in
UR, and Q(x) for x in I. Then g is holomorphic in
V.
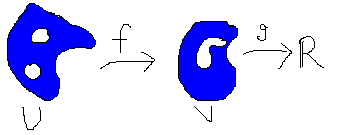
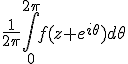 , therefore, since harmonic
functions are real parts of holomorphic functions, this is also true for
harmonic functions.
, therefore, since harmonic
functions are real parts of holomorphic functions, this is also true for
harmonic functions.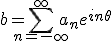 almost everywhere. The solution
to the Dirichlet problem is linear in b. L also maintains limits
because by the Max/Min Principles, if b1<=b2
then L(b1)<=L(b2). So we only need to solve
for one of the terms.
almost everywhere. The solution
to the Dirichlet problem is linear in b. L also maintains limits
because by the Max/Min Principles, if b1<=b2
then L(b1)<=L(b2). So we only need to solve
for one of the terms.
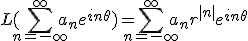
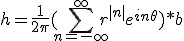 (* is convolution
on the circle).
This series can be represented more nicely.
(* is convolution
on the circle).
This series can be represented more nicely.
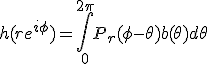 , where
, where 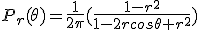 .
.
 In fact, we can also work with boundary data in L1 and not
only continuous. For this example our boundary data is: on the upper
half circle the value is 1, on the lower half circle the value is
0. If we stick this in our amazing formula for L(b), we get an
integral that isn't easy to understand. Instead of solving it for the
unit disc, we'll solve the corresponding Dirichlet problem for the
upper half plane (remember our nice fact from before!). By the
"standard" biholomorphic mapping to the upper half plane, we reduce
the problem to finding a harmonic function on the upper half plane
such that h(x)=1 for negative reals and h(x)=0 for positive reals. We
can guess what could work here: the imaginary part of the simplest branch
of log will work (dividing by Pi). This is of course a harmonic
function, which is equal to (1/Pi)arctan(y/x). Boom! Notice that we worked backwards. Although in general we
could "solve" the Dirichlet problem in a domain by transferring it to
the unit disc and solving it there, actually here we solved a disc
problem by working in a different domain, and recognizing an obvious
solution in the other domain! The colored lines and semicirles
in the accompanying picture are intended to be the corresponding level
lines of the solution function, and lines with the same colors
correspond to the same values of the functions.
In fact, we can also work with boundary data in L1 and not
only continuous. For this example our boundary data is: on the upper
half circle the value is 1, on the lower half circle the value is
0. If we stick this in our amazing formula for L(b), we get an
integral that isn't easy to understand. Instead of solving it for the
unit disc, we'll solve the corresponding Dirichlet problem for the
upper half plane (remember our nice fact from before!). By the
"standard" biholomorphic mapping to the upper half plane, we reduce
the problem to finding a harmonic function on the upper half plane
such that h(x)=1 for negative reals and h(x)=0 for positive reals. We
can guess what could work here: the imaginary part of the simplest branch
of log will work (dividing by Pi). This is of course a harmonic
function, which is equal to (1/Pi)arctan(y/x). Boom! Notice that we worked backwards. Although in general we
could "solve" the Dirichlet problem in a domain by transferring it to
the unit disc and solving it there, actually here we solved a disc
problem by working in a different domain, and recognizing an obvious
solution in the other domain! The colored lines and semicirles
in the accompanying picture are intended to be the corresponding level
lines of the solution function, and lines with the same colors
correspond to the same values of the functions.
 The next part of the "program" is to sketch a proof of the Riemann
Mapping Theorem: that any simply connected, connected open subset of
the plane which is not all of C is biholomorphic with the unit
disc. In fact, Riemann's original proof (or suggested proof!) of this
result relied first on solving the Dirichlet problem, and deducing the
RMT from that solution. One way he considered solving the Dirichlet
Problem was imagining a boundary height (the boundary data is a
real-valued function) and then lowering a flexible "membrane" over the
data. The membrance would naturally be tight, and would try to
minimize the energy, sort of hugging the boundary data. Then (this
isn't even neat enough to require a "clearly"!) the height of the
membrane over the interior is harmonic, and is the solution to the
Dirichlet Problem. This approach can actually be understood, and does
work, but, wow, it needs (from the point of view of current
mathematics) rather a lot of work. The energy is the integral over the
interior of the norm squared of the gradient of the membrane
height. And showing that there is actually a minimizer (something that
achieves the infimum of energy) is not easy. This leads to a whole
huge area of mathematics called the calculus of variations, and
variational methods of solving partial differential equations.
The next part of the "program" is to sketch a proof of the Riemann
Mapping Theorem: that any simply connected, connected open subset of
the plane which is not all of C is biholomorphic with the unit
disc. In fact, Riemann's original proof (or suggested proof!) of this
result relied first on solving the Dirichlet problem, and deducing the
RMT from that solution. One way he considered solving the Dirichlet
Problem was imagining a boundary height (the boundary data is a
real-valued function) and then lowering a flexible "membrane" over the
data. The membrance would naturally be tight, and would try to
minimize the energy, sort of hugging the boundary data. Then (this
isn't even neat enough to require a "clearly"!) the height of the
membrane over the interior is harmonic, and is the solution to the
Dirichlet Problem. This approach can actually be understood, and does
work, but, wow, it needs (from the point of view of current
mathematics) rather a lot of work. The energy is the integral over the
interior of the norm squared of the gradient of the membrane
height. And showing that there is actually a minimizer (something that
achieves the infimum of energy) is not easy. This leads to a whole
huge area of mathematics called the calculus of variations, and
variational methods of solving partial differential equations.