The final exam
| | Problem
#1 |
Problem
#2 |
Problem
#3 |
Problem
#4 |
Problem
#5 |
Problem
#6 |
Problem
#7 |
Problem
#8 |
Problem
#9 |
Problem
#10 |
Problem
#11 |
Total |
|---|
| Max grade |
18 |
18 |
12 |
18 |
12 |
16 |
16 |
14 |
19 |
18 |
12 |
171 |
|---|
Min grade |
5 |
4 |
0 |
4 |
2 |
1 |
3 |
0 |
1 |
0 |
0 |
53 |
Mean grade |
12.42 |
14 |
7 |
13.46 |
9.69 |
9.62 |
10.92 |
7.73 |
8.27 |
9.92 |
8.73 |
111.77 |
Median grade |
13 |
15.5 |
8.5 |
14 |
12 |
9 |
12.5 |
8.5 |
7.5 |
11 |
10 |
107 |
26 students took this exam. Numerical grades will be retained for use
in computing the final letter grade in the course. Here are
approximate letter grade assignments for this exam:
Letter
equivalent | A | B+ | B | C+ |
C | D | F |
|---|
| Range | [147.9,174] | [139.2,147.9) | [121.8,139.2) |
[113.1,121.8) | [104.4,113.1) | [95.7,104.4) | [0,95.7) |
|---|
Discussion of the grading
Generally arithmetic errors will be penalized only minimally. If,
however, your error makes the problem much simpler, more credit will
be deducted and your answer may not be eligible for all of the credit
of the problem.
Problem 1 (18 points)
a) (13 points) 3 points for the setup, which includes the correct
description of f(t) and the correct domain of integration. 4 points
for the integration by parts. 3 points for evaluation of one piece of
the integral with 1/s and 3 points for the evaluation with
1/s2. If I could not easily understand the computations, I
gave up. I think part of this problem is communication of the
limits of integration, the methods, etc. If the setup was f(t)=2t for
t<1 and 0 otherwise, a maximum of 10 out of 13 points could be
earned.
b) (5 points) 1 point for demonstrating the need for L'H once, and 1
point for correct top and bottom differentiation. Another 1+1 was
earned for the second L'H. The final point was earned for the correct
answer. I was rather strict here. Students had to show why L'H was
needed, and had to compute correctly. One consequence is that answers
from a) which were far from true led to ineligibility for the points
in this part. That should have been a signal to students that their
process and/or answer in a) was incorrect.
Problem 2 (18 points)
a) (12 points) 3 points for taking the correct Laplace transform of
the equation and solving for Y(s). 3 points for the partial fraction
decomposition. 3 points for the inverse Laplace transform of the
rational function. 3 points for the inverse Laplace transform of that
part involving the exponential function (one of the Shifting Theorems
is needed). Students who recognized the Laplace transforms of sinh and
cosh and used them correctly got full credit. I would have put these
on the table if anyone had asked (but then I would not have given this
precise problem!). Students who made errors which trivialized the
problem were penalized here, and might not have been eligible for full
credit in the parts below.
b) (3 points) 1 point for the first expression, and 2 points for the
second.
c) (3 points) 1 point for the first answer, 1 point for the second,
and 1 point for the third. Students needed to use their answer, and
compute correctly.
Problem 3 (12 points)
a) (6 points) The most common error was omitting the condition that v
not be 0. I gave credit only when I could understand the statement and
it was correct.
b) (6 points) An answer alone does not get full credit. A maximum of 2
points would be given to an answer supported by very little. I looked
for assurance that the student had checked that every coordinate of
the vector gave the same eigenvalue.
Problem 4 (12 points)
a) (10 points) The resulting polynomial should have degree 4, or the
student loses 2 points. Most students "expanded" along a row or
column, and I subtracted 2points if one of the resulting 3-by-3
determinants was incorrect. Other minor errors were handled
appropriately.
b) (2 points) For displaying the correct roots of the student's
characteristic polynomial. Almost all students got polynomials whose
roots could easily be found by hand (thank goodness!).
c) (4 points) To score points in this part of the problem, statements
needed to be supported by previous student work, and by valid reasons
for the conclusion. Therefore I did not give points to someone who
might have guessed the correct conclusion but was unable to give some
valid supporting evidence.
d) (2 points) The correct answer (1 point) and some correct reason (1
point).
Problem 5 (12 points)
a) (6 points) I gave 2 points for considering a linear combination
with "arbitrary" coefficients and then setting it equal to 0. The
resulting homogeneous system was easy to analyze and show that it had
only the trivial solution. I did not give credit if I could not
understand what students wrote.
b) (6 points) The part of this question certainly is the worst
constructed from the point of view of checking if a student knows the
subject matter of 421. That is because it is clear (at least, I
think, to me!) that a sum of polynomials whose degree is at most 2
cannot be x3. (It is clear, however, because all of us have
done so much computation in the "native" basis of the polynomials,
that is, the usual monomials.) Therefore any student who stated such a
belief in a way I could understand got full credit. Thus those
students did not have their 421 linear algebra knowledge
tested. Otherwise, I deduced points if students didn't describe the
problem clearly. In particular, I gave only 4 points if students
asserted that x3 was not a linear combination of two of the
three given functions, or if they asserted that x3 and two
of the given functions were linearly independent. Either of those is
not enough to conclude the desired result.
Problem 6 (16 points)
a) (8 points) I gave this problem so that people could show me they
knew what Fourier coefficients and Fourier terms were. There were
rather low scores on a similar problem on the second exam. Here I
wanted the terms, and not just the coefficients, as I
indicated. Any student who gave a linear combination of sin(x),
sin(2x), and sin(3x) with other than constant coefficients got
0 for this part. By now, students should know what Fourier
series look like. The 2/Pi normalization got 1 point. Each Fourier
coefficient got 1 point (3 points total). Each appropriate sine
function got 1 point (3 points total). 1 more point was given for
assembling the information and presenting it correctly.
b) (8 points) 4 points for the graph of g(x): 1 point each for
sticking to the continuous pieces "inside" the intervals of
continuity; 1 point for being continuous in the whole interval and
"leaping down" from the top to the bottom; 1 point for the Gibbs
wiggling in both places. 4 points for the graph of h(x): again, 1
point each for being identical to f(x) on the two intervals of
continuity; 1 point for having a value in the middle of the jump, and
1 point for noting in some way that there are holes on the bottom and
the top of the jump. I deduced points for extra information which was
contrary to the correct pictures.
Problem 7 (16 points)
a) (3 points) 1 point for the graph=1 away from the interval from 0 to
2, and 2 points for the parabolic bump up inside the interval.
b) (3 points) Just quoting the D'Alembert solution (with no g term!)
earns the points, with the implication being that the function f is
the one defined in the problem. Students who went on to state an
incorrect formula (that is, substituting the quadratic formula with no
indication of the valdity of the formula in terms of the values of the
variables) lost 1 point.
c) (4 points) 1 point each for the traveling wave to the left and the
right; 1 point for the correct height and location; 1 point for the
wave being 0 outside of intervals of the traveling waves.
d) (1 point) For identifying the correct time.
e) (4 points) 2 points for indicating that there are 2 maximums. 1
point each for the correct location of the maximums.
f) (1 point) For identifying the correct velocity.
Problem 8 (14 points)
a) (4 points) I looked for a solution which satisfied the initial
conditions (2 points) and which had the desired exponentials (2
points). The solution could just be written and not justified.
b) (8 points) I gave 2 points for some evidence of orthogonality
displayed. Otherwise, I looked for the double integral, I looked for
orthogonality, I looked for the appearance of the normalization
constants, and I looked for the t functions not being
integrated. Points were taken off appropriately for algebraic
errors. etc. In this part, an answer alone got little credit: I looked
for some supporting evidence.
c) (2 points) The answer, supported by some evidence derived from the
answer to b). I gave only 1 point to thos students who insisted that
the temperature oscillated, even if supported by b)'s answer. That's
just too unphysical.
Problem 9 (20 points)
a) (9 points) 2 points for separating variables correctly. 2 points
for handling the x function and coming up with sin(nx), where n is a
positive integer. 2 points for getting the differential equation for
Y(y) correct, and realizing that solutions are exponentials or
hyperbolic functions. 3 points for explicitly listing the solutions
(the case n=1 requires separate comment).
b) (11 points) 2 points for excluding the sinh term. 3 points for
writing the correct series. 2 points for explicitly writing how u(x,0)
is related to the initial condition. 2 points for writing u(x,0) as a
sum of a Fourier sine seres. 2 points for writing the formula for the
coefficients and 2 more points for writing the three initial terms.
Problem 10 (18 points)
I gave a total of 10 points for the separation of variables portion of
this problem. The t and x portions were graded in the same way: 2
points for getting the correct ordinary differential equation, 2
points for getting cos(n{x|t}) (not a general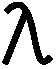 
) and 1 point for dropping sin(n{x|t}). 8
points for assemblling the general answer. Of this, 4 points for a sum
of the solutions with coefficients (ancos(nx)cos(nt),
summed from n=0 to infinity) and then 4 more points for connecting
with the initial conditions: first, for using u(x,0) in connection
with f(x), and then writing the coefficients an in terms of
cosine Fourier coefficients of f(x).
Comment This is about what's called the free boundary
condition for the wave equation. Some further information is here.
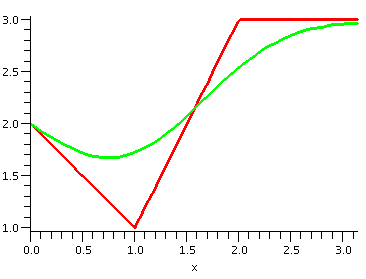
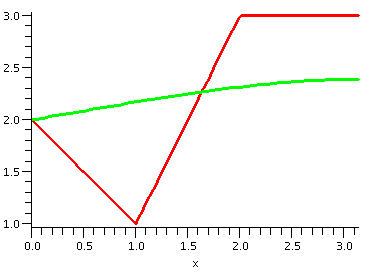
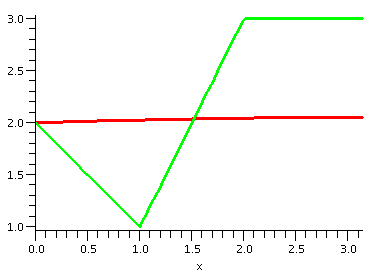
Problem 11 (12 points)
a) (6 points) The curve should be smooth and higher than the global
min, and lower than 3. It should have value 2 at x=0 and should have a
horizontal tangent at x=Pi. I gave 2 points for the smoothness, 2
points for the horizontal tangent, and 2 points for going through
(0,2). Sometimes the horizontal tangent at x=Pi was difficult to
score.
b) (6 points) A horizontal line earned at least 3 points. 2 points
were earned for a graph going through (0,2). The solution should be a
straight line (the only steady-state one dimensional heat equation
solutions), which accounted for the other points.
Here are some pictures of an approximate solution (with 100 Fourier
terms). The correct eigen{function|value}s are given as the third
example here. I used them to create
these graphs, after first subtracting the appropriate steady-state
solution.
 |
 |
 |
| Small positive time |
A bit later |
Much later |
|---|
Course grades
I weighed each of the first two exams equally and the final exam twice
as much as either of these. I also constructed another "exam score" using
the Entrance Exam (25%), the QotD (15%), and textbook homework
(60%). I then averaged these four "exams" (with the final weighted
twice) to get one number, which I used to give a final grade. This
final letter grade was given using standards close to the conversion
table used three times above (from numerical grades to letter grades).
Maintained by
greenfie@math.rutgers.edu and last modified 12/21/2005.