| Date | Topics discussed |
|---|
Thursday,
April 29 |
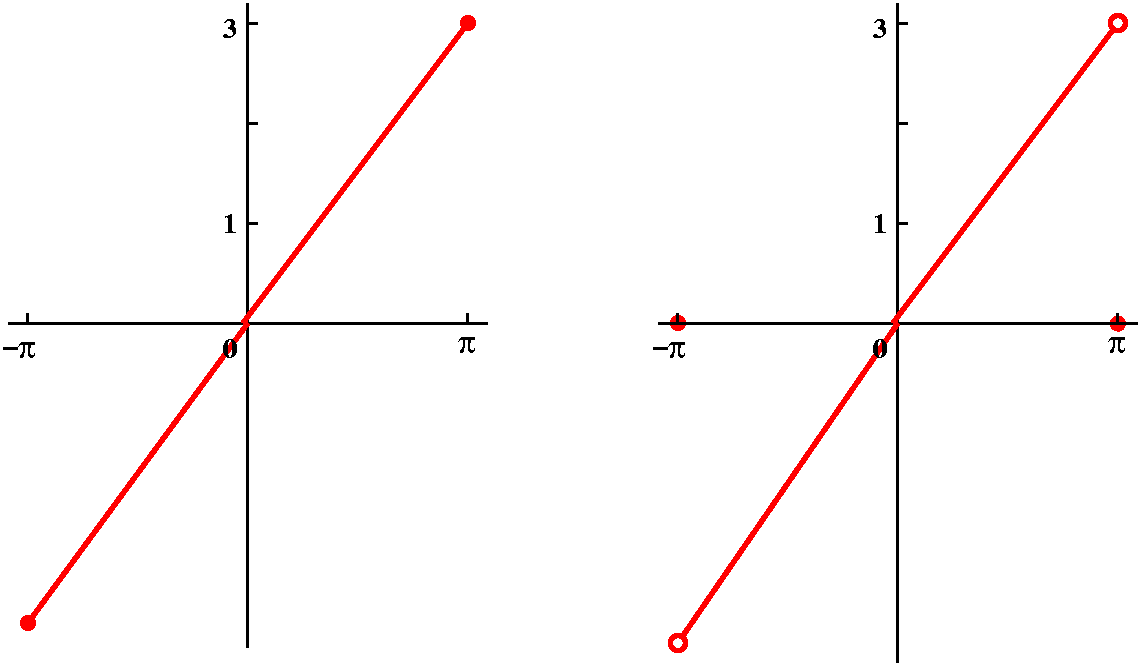
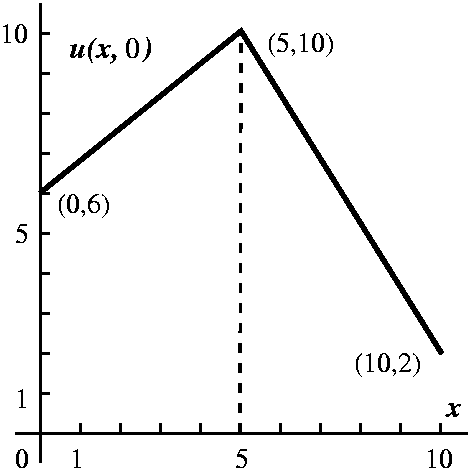 I will begin by asking part 1 of the QotD. The indicated heat
distribution is given initially, with boundary conditions u(0,t)=6 and
u(10,t)=2. Sketch the limit of u(x,t) as t-->infinity.
I will begin by asking part 1 of the QotD. The indicated heat
distribution is given initially, with boundary conditions u(0,t)=6 and
u(10,t)=2. Sketch the limit of u(x,t) as t-->infinity.
As we discussed this, I tried to indicate how heat would flow
"intuitively". But of course this intuition would be guided by our
past thought experiements and computations. Notice that the function
-(4/10)t+6 is a steady state heat flow: that is, it has the
desired boundary conditions and is only a function of t. Therefore the
difference between this function and the u(x,t) in the QotD is a steady
state heat flow for the 0 boundary conditions, which must be 0.
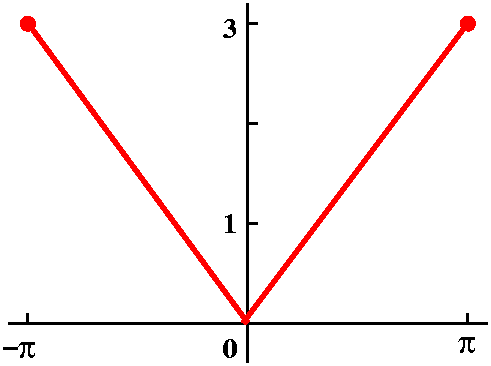
I also remarked that this initial temperature distribution could
not be the result of the time evolution of an earlier
temperature distribution. The principle reason for that is because
u(x,0) is not differentiable at x=1/2. Temperature distributions which
have evolved using the heat equation must be smooth.
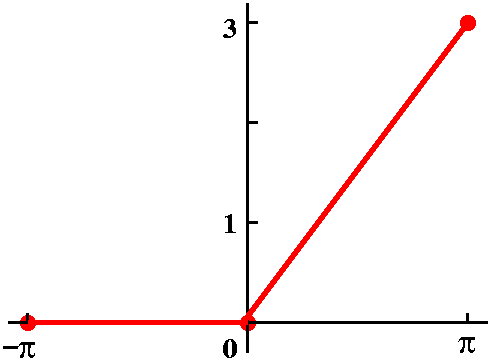
Then I discussed
temperature distributions in a rod with insulated ends (as well as
insulated sides). It took some convincing but the appropriate boundary
conditions are ux(0,t)=0 and ux(L,t)=0: u
doesn't change in the spatial directions across the ends of the bar. I
then asked the second part of the QotD: if the ends of the bar are
also insulated, what is the limiting heat distribution? Here we want
heat not to pile up (I tried to indicate that heat really dislikes
being at a local max or min): we want it to distribute itself as well
as possible ("entropy", disorganization, should be increasing at all
times). Therefore the limiting steady state heat distribution in this
case has temperature constant, equal to the average of the initial
temperature. In this case, the limiting (average) temperature is 7,
and the limiting temperature distribution is the constant 7.
I wanted to justify this limiting fact, and to analyze the general
boundary/initial value problem for the heat equation:
ut=
uxx;
ux(0,t)=0 and ux(L,t)=0; u(x,0)=f(x) given.
So for the fourth time (I think) we analyzed this problem with
separation of variables. Assume u(x,t)=X(x)T(t). Then, as before,
T'(t)X(x)=X''(x)T(t), so that T'(t)/T(t)=X''(x)/X(x). Again this must
be constant, as before. We call it, as before, - . .
Start with X(x): we know X''(x)/X(x)=- . Again, X''(x)+ . Again, X''(x)+ X(x)=0. The boundary conditions for
this equation are from
ux(0,t)=0 and ux(L,t)=0. Therefore X'(0)=0 and
X'(L)=0. If X(x)=0. The boundary conditions for
this equation are from
ux(0,t)=0 and ux(L,t)=0. Therefore X'(0)=0 and
X'(L)=0. If
 <0, solutions are linear
combinations of cosh(sqrt( <0, solutions are linear
combinations of cosh(sqrt( )x) and
sinh(sqrt( )x) and
sinh(sqrt( x). X'(0)=0 shows that there's
nothing coming from the cosh part, and X'(L)=0 shows that the sinh
part must vanish, also. Therefore x). X'(0)=0 shows that there's
nothing coming from the cosh part, and X'(L)=0 shows that the sinh
part must vanish, also. Therefore
 must be positive. must be positive.
Solutions are X(x)=C1sin(sqrt( )x)+C2cos(sqrt( )x)+C2cos(sqrt( )x). X'(0)=0 means that
C1=0 (the derivative of sine is cosine). And, finally,
X'(L)=0 means sin(sqrt( )x). X'(0)=0 means that
C1=0 (the derivative of sine is cosine). And, finally,
X'(L)=0 means sin(sqrt( )L)=0. Therefore sqrt( )L)=0. Therefore sqrt( )L is an integer (usually written,
n) times Pi, and )L is an integer (usually written,
n) times Pi, and  =[n2Pi2]/L. =[n2Pi2]/L.
What about T(t)? Since T'(t)/T(t)=-
 =-[n2Pi2]/L,
we know that T(t) must must scalar multiples of
e-([n2Pi2]/L)t. Notice that if
n>0, this -->0 very rapidly, and therefore the only term which
persists is the n=0 term. =-[n2Pi2]/L,
we know that T(t) must must scalar multiples of
e-([n2Pi2]/L)t. Notice that if
n>0, this -->0 very rapidly, and therefore the only term which
persists is the n=0 term.
You can check in the book (pp.921-2) to see that the general solution
for the time evolution of a heat equation in an insulated bar with
insulated ends is
u(x,t)=(c0/2+SUMn=1infinitycncos([nPi x]/L)e-([n2Pi2]/L)t
where
cn=(2/L) 0Lf(x)cos([nPi x]/L) dx for
n>=0. 0Lf(x)cos([nPi x]/L) dx for
n>=0.
c0/2 is the average value of f(x) over the interval [0,L],
which agrees with the intuition we may have developed giving this
constant function as the steady
state solution for this problem as t-->infinity.
Steady state heat flows in one dimension are solutions of
ut=kuxx which are functions of x alone. That is,
uxx=0. These functions are just Ax+B where A and B are
constants. So these steady state heat flows whose graphs are straight
lines have no bumps and no bending. These are the only functions with
those qualities. In two dimensions and more, things get more
complicated. There steady state heat flows must satisfy
uxx+uyy=0. Such functions are called harmonic
functions, there are infinitely many linearly independent harmonic
functions, and their behavior can be complicated.
The room was had numerous gnats in this last class, which
plagued bothstudents and instructor. The class ended slightly early.
Study for the final exam!
|
Tuesday,
April 27 |
Derivation of the Heat Equation
 I tried to "derive" the one-dimensional heat equation, also known as
the diffusion equation. You should realize that the heat equation is
also used to model a very wide variety of phenomena, such as drugs in
the bloodstream diffusing in the body or gossip (!) or spread of
disease in epidemics or ... The text discusses the temperature of a
thin homogeneous straight rod, whose long side is insulated (no heat
flow through that allowed) but heat can escape (or enter) through the
ends.
I tried to "derive" the one-dimensional heat equation, also known as
the diffusion equation. You should realize that the heat equation is
also used to model a very wide variety of phenomena, such as drugs in
the bloodstream diffusing in the body or gossip (!) or spread of
disease in epidemics or ... The text discusses the temperature of a
thin homogeneous straight rod, whose long side is insulated (no heat
flow through that allowed) but heat can escape (or enter) through the
ends.
I mostly followed the discussion in this
web page. Another derivation is given on this page. and
yet another is here.
If you are someone who learns more easily with pictures, as I do, you
may find the various animations of solutions of the initial value
problem for the heat equation on
this web page useful. Two questions which appear on a web page
linked to that reference are interesting to keep in mind:
- Describe in words the time evolution of a one-dimensional heat
flow for which the ends of the bar are both kept at zero degrees. How
does your answer depend on the initial temperature distribution?
- Describe in words the time evolution of a one-dimensional heat flow
for which the ends of the bar are kept at different temperatures. How
does your answer depend on the initial temperature distribution?
Separating ...
I separated variables for the initial value problem u(x,0)=f(x) with
boundary conditions u(0,t)=0 and u(Pi,t)=0. (The text does this with a
more general L instead of Pi.) I assumed a solution to
ut=uxx looked like u(x,t)=X(x)T(t), as in the
text. The development is very similar to what was done for the
wave equation on Tuesday, April 20. I got
X''(x)/X(x)=T'(t)/T(t). Therefore each side must be constant. Look at
the x side first. The boundary conditions imply that we need to solve
the ODE problem X''(x)=(constant)X(x) with X(0)=0 and
X(Pi)=0. Therefore to get a non-trivial solution, we must have
constant=-(nPi)2 for some positive integer n, and then
X(x)=sin(nx). Now here is where we differ from the wave equation: we
need to solve T'(t)=-n2T(t). Solutions of this are
multiplies of T(t)=e-n2t. Even for small n's
this exponential function rapidly decreases from 1 to nearly 0. A
general solution would be
u(x,t)=SUMn=1infinitycnsin(nx)e-n2t
where for the initial value problem u(x,0)=f(x) the cn's
would be the coefficients of the Fourier sine series of f(x).
What should be expected about heat flow if the ends are kept at
temperature 0? We discussed this, and then I gave out this which showed a good approximation to
a solution. The heat does flow out, and the heat profile gets
smoother. Notice this initial condition is one which I analyzed for
the wave equation, and the solutions there were very different. Also
notice that the original square profile can't be the result of a heat
diffusion (otherwise it would be smooth!) so we can't run the heat
equation backwards. The wave equation is time-reversible.
|
Comparing qualitative aspects of solutions of the wave and heat
equations |
|---|
| Wave equation | Heat equation |
|---|
- Conservation of energy: in what we studied, the sum of potential
and kinetic energy is constant (other models allow friction, etc.)
- Corners and shocks allowed to persist
- Finite propagation speed: model has a top speed (speed of sound or
light or ...)
- Time can be reversed: waves just reverse direction, etc.
|
- Diffusion: heat oozes away
- Model is smoothing: even if initial temperature distribution is
kinky, for later time, the temperature is smooth
- Propagation speed turns out to be infinite, but far-off effects
for small time are exponentially small.
- Time can't generally be reversed: you can't make heat flow
backwards.
|
I asked what would happen if instead of the boundary condition
u(0,t)=0 and u(Pi,t)=0 we substituted u(0,t)=0 and u(Pi,t)=5. First I
asked people to think about the physical situation. The general reply
is that the temperature distribution would eventually tend to a
steady state where one end (at 0) was 0 and the other end, at Pi, was
5. So what I did was write uss(x,t)=(5/Pi)x (this is a
guess, but based on the physical suggestion!). It turns out that this
uSS ("ss" for steady-state) does solve the
heat equation:
check that the t derivative is 0 and so is the second x derivative. If
we take a solution of the boundary value with u(0,t)=0 and u(Pi,t)=5
(call this solution unew) then
unew(x,t)-uss(x,t) does solve the heat equation
(since the heat equation is linear) and this solution satisfies
the old boundary conditions, u(0,t)=0 and u(Pi,t)=0.But we know
because of the )e-n2t factors that this solution
must -->0 as t-->infinity. So the difference between
unew(x,t) and uss(x,t) must -->0 as
t-->infinity. Therefore in fact the steady state is the limit for a
solution of this boundary value problem.
I should have asked a QotD. It could have been this: suppose
one end of a thin homogeneous bar is kept at temperature 7 and the
other is kept at temperature -2. Suppose some initial temperature
distribution
is given (something really complicated). Graph the resulting solution
of the heat equation for t=10,000.
Think about this: when should I have office
hours and possible review sessions for the final? I'll try to do some
problems from section 17.2 at the next (last) class.
|
Thursday,
April 22 |
 The spring, a one-dimensional system
The spring, a one-dimensional system
Everybody knows the vibrating spring, one of the simplest idealized
mechanical systems. Here the dynamics are shaped by Hooke's law, that
displacement from equilibrium results in a force of magnitude directly
proportional to the absolute value of the displacement and directed
opposite to the displacement. This together with Mr. Newton's F=mA gives
us D''(t)=-(k/m)D(t) where D(t) is the displacement from
equilibrium. The minus sign comes from the word "opposite". Solutions
are sines and cosines, yielding the model's solution as vibrating up
and down. (A typical vibrating string is the ammonia molecule,
NH3.)
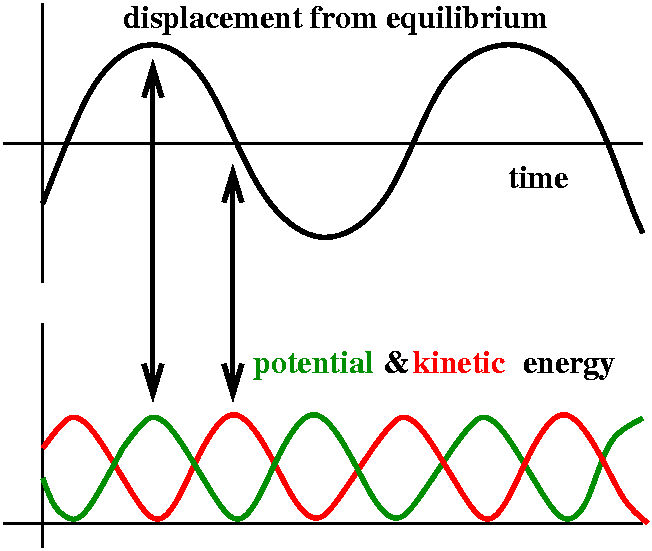 Looking at energy
Looking at energy
This model conserves energy, where energy is here the sum of kinetic
energy and potential energy. I won't worry about constants, since I
can almost never get them right. The kinetic
energy is (1/2)m(velocity)2. But velocity is
D'(t). What about the potential energy? This
is essentially the amount of work needed to move the spring from
equilibrium to another position. Well, moving the spring against the
varying resistant force of kD(t) means we need to integrate it with
respect to D. This gets me (1/2)kD(t)2. The total energy in
this model is therefore
(1/2)m(D'(t))2+(1/2)k(D(t))2. I can try to check
that energy is conserved by differentiating this total energy
with respect to time. The result (using the chain rule correctly) is
(1/2)m2(D'(t)D''(t))+(1/2)k2(D(t)D'(t)). This is
D'(t)(mD''(t)+kD(t)). But the differential equation of motion says
exactly that mD''(t)+kD(t) is always 0! So energy is conserved. Both
D(t) and D'(t) are sines/cosines, and the sum of their squares is
constant (sin2+cos2 is a well-known constant).
Taking a static picture at a fixed time can be rather deceptive. For
example, if the spring is wiggling (no friction: an ideal spring) it
always keeps wiggling. If we happened to snap a picture when the
spring is at the equilibrium point it is still moving. The kinetic
energy is largest at that position, and the potential energy is
smallest. When the spring is highest or lowest, the potential energy
is large, and the kinetic energy is 0 (the spring isn't moving, in the
sense of calculus: D'(t)=0).
I hope that energy considerations will help your understanding of the
vibrating string as well as the spring. In fact, we could almost
understand the vibrating string as a bunch of springs tied
together. This isn't totally correct, but if it helps ... In a very simple case (Warning! big file!) you can see the string in
equilibrium position momentarily, but it has relatively high velocity
(and therefore large kinetic energy) at that time.
The D'Alembert solution: the two waves
Here the vibrations of the string are written as a sum of left and
right moving waves. Again, y(x,t) is supposed to be the height of the
string at time t and position x. We write
y(x,t)=K(x-ct)+J(x+ct). Mr. Marchitello
helped me to understand that the K part is moving to the right and the
J part is moving to the left. Let me use the chain rule:
yt(x,t)=K'(x-ct)(-c)+J'(x+ct)c
ytt(x,t)=K''(x-ct)(-c)2+J''(x+ct)c2
yx(x,t)=K'(x-ct)+J'(x+ct)
yxx(x,t)=K''(x-ct)+J''(x+ct)
Now we see that ytt(x,t)=c2yxx(x,t),
so indeed this satisfies the wave equation.
Comparing initial conditions and the wavea
We worked hard to solve (via separation of variables and Fourier
series) the initial value problem for the wave equation. For this
initial value problem, we considered y(x,0)=f(x) and
yt(x,0)=g(x) as given. (Again Mr. Marchitello commented that I seemed to be
ignoring the boundary conditions, and I agreed that I was. These
details, which are not so trivial, are discussed in the text on
pp. 871-872.) So how can we go from the K and J description to the f
and g description, and back, and does this help? It turns out that it
will help a great deal with the understand of the physical
model. Since y(x,t)=K(x-ct)+J(x+ct) we know that
y(x,0)=K(x)+J(x)=f(x), and then since
yt(x,t)=K'(x-ct)(-c)+J'(x+ct)c we know that
yt(x,0)=K'(x)(-c)+J'(x)c=g(x). So this is how we could get
f and g from K and J.
A short intermission
The other example we discussed last time had f(x) equal to 4 on
[Pi/3,Pi/2] and 0 elsewhere on [0,Pi], while g(x) was 0 everywhere on
[0,Pi]. I produced a picture (Warning! big file!) of a Fourier approximation to
this string and its motion through time (for a short period of
time). What the heck is going on? Well, we know that K(x)+J(x)=f(x)
and (c=1) K'(x)-J'(x)=0, so that K'(x)=J'(x). Can you think of what
K(x) and J(x) could be? You are allowed to guess. I can guess,
especially when helped by that useful moving picture. K(x) and J(x)
are both equal to a bump half the size of f(x): they are both
equal to 2 on [Pi/3,Pi/2] and both 0 elsewhere. But one travels left
and one travels right. We just
happened at initial time to take a picture when the bumps
reinforced. When the bumps reach the end of the interval, the boundary
conditions (the string is pinned down) cause the bumps to be reflected
negatively. Several engineering students seemed to think that this was
correct physically. To me much of what is happening in this example is
unexpected.
Back to the general case
We'll try now to get K and J from f and g in general. Let's integrate
yt(x,0)=K'(x)(-c)+J'(x)c=g(x) from 0 to x. But first think:
should we really write  0xK'(x) dx? There are too many
x's. The x's inside the integral could easily get confused with the x
on the upper limit of integration. So, following a suggestion of Ms. Sirak, I'll use w for the
integration variable. Now we compute: 0xK'(x) dx? There are too many
x's. The x's inside the integral could easily get confused with the x
on the upper limit of integration. So, following a suggestion of Ms. Sirak, I'll use w for the
integration variable. Now we compute:
 0xK'(w) dw=K(w)|w=0w=x=K(x)-K(0), and 0xK'(w) dw=K(w)|w=0w=x=K(x)-K(0), and
 0xJ'(w) dw=J(x)-J(0). So if I do
the arithmetic correctly, the equation K'(x)(-c)+J'(x)c=g(x) leads to
[K(x)-K(0)](-c)+[J(x)-J(0)]c= 0xJ'(w) dw=J(x)-J(0). So if I do
the arithmetic correctly, the equation K'(x)(-c)+J'(x)c=g(x) leads to
[K(x)-K(0)](-c)+[J(x)-J(0)]c= 0xg(w) dw or (divide by c, and move
J(0) and K(0)): 0xg(w) dw or (divide by c, and move
J(0) and K(0)):
-K(x)+J(x)=(1/c) 0xg(w) dw+J(0)-K(0). 0xg(w) dw+J(0)-K(0).
This
together with K(x)+J(x)=f(x) allows me to solve for K(x) and J(x) in
terms of stuff involving f and g.
Here is what you get:
K(x)=-[1/(2c)] 0xg(w) ds+(1/2)f(x)-(1/2)J(0)+(1/2)K(0) 0xg(w) ds+(1/2)f(x)-(1/2)J(0)+(1/2)K(0)
and
J(x)=[1/(2c)] 0xg(w) ds+(1/2)f(x)-(1/2)K(0)+(1/2)J(0) 0xg(w) ds+(1/2)f(x)-(1/2)K(0)+(1/2)J(0)
I remarked in class and I will repeat now that this is one of the
derivations in the whole course that I think is very useful to know
about. It really does lead to very useful ideas in the "real
world". Let's see: the minus sign in front of the integral for K(x)
can be lost if we interchange the top and bottom limits:
K(x)=[1/(2c)] x0g(w) ds+(1/2)f(x)-(1/2)J(0)+(1/2)K(0) x0g(w) ds+(1/2)f(x)-(1/2)J(0)+(1/2)K(0)
and also I am really interested in y(x,t). But y(x,t) is
K(x-ct)+J(x+ct). So in the formulas for K and J, make the
substitutions x-->x-ct in K and x-->x+ct in J. Here is the result for
y(x,t):
[1/(2c)] x-ct0g(w) ds+(1/2)f(x-ct)-(1/2)J(0)+(1/2)K(0)+
[1/(2c)] x-ct0g(w) ds+(1/2)f(x-ct)-(1/2)J(0)+(1/2)K(0)+
[1/(2c)] 0x+ctg(w) ds+(1/2)f(x+ct)-(1/2)K(0)+(1/2)J(0) 0x+ctg(w) ds+(1/2)f(x+ct)-(1/2)K(0)+(1/2)J(0)
Now look closely, and see things collapse. Indeed (!) the K(0) and
J(0) just cancel. And the integrals? Well, the intervals are
adjoining, so the integrals can actually be combined into one. Here is
the resulting formula:
y(x,t)=[1/(2c)] x-ctx+ctg(w) ds+(1/2)f(x-ct)+(1/2)f(x+ct) x-ctx+ctg(w) ds+(1/2)f(x-ct)+(1/2)f(x+ct)
By the way, it is natural (to me) that g is integrated. g is a
velocity, and y(x,t) is a position. So g's information has to be
integrated to get the units to agree.
Using the formula to understand the physical situation
Look to the right. What's displayed is a different way to look at
solutions of the wave equation. The function y(x,t) is a function of
two variables, one which locates a position on the string, x, and one
which indicates time, t. Let's look down on (x,t) space.
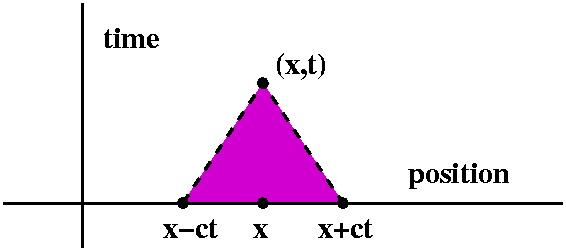 I would like to know
about y(x,t) and what part of the initial data influence
y(x,t). Certainly f's values at x+/-ct influence y(x,t) (look at the
formula above!) and g's values in the interval [x-ct,x+ct] influence
y(x,t). Mr. Tahir bravely came to the
board and completed a diagram which looks much like what is draw on
the left. The dotted lines have slopes +/-(1/c). (I got this wrong in
class!) So the influence of the initial conditions is as
shown.
I would like to know
about y(x,t) and what part of the initial data influence
y(x,t). Certainly f's values at x+/-ct influence y(x,t) (look at the
formula above!) and g's values in the interval [x-ct,x+ct] influence
y(x,t). Mr. Tahir bravely came to the
board and completed a diagram which looks much like what is draw on
the left. The dotted lines have slopes +/-(1/c). (I got this wrong in
class!) So the influence of the initial conditions is as
shown.
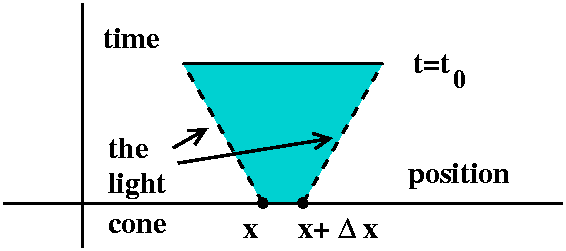 Here is yet another way to show what's going on. I could imagine a
short interval on the time=0 line, say from x to x+(delta)x (as usual,
(delta)x is supposed to be small). I could imagine changing f or g or
both on that interval, wiggling these initial conditions. Then what
parts of the string could be affected at a later time,
t=t0? Well, if you think about it and look at the formula,
the only parts could be in the upward part of the trapezoid
sketched. The wave equation models phenomena which have a finite
propagation speed (here the speed is c). Such phenomena include sound
and light. The slanted edges of the trapezoid sketched are usually
called the light cone and it represents the spreading the
maximum speed that the model allows. This name reflects the physical
theory that light travels at the maximum universal speed, and any
other "signal" travels more slowly. I remark that Mr. Woodrow courageously drew a picture
similar to this on the board.
Here is yet another way to show what's going on. I could imagine a
short interval on the time=0 line, say from x to x+(delta)x (as usual,
(delta)x is supposed to be small). I could imagine changing f or g or
both on that interval, wiggling these initial conditions. Then what
parts of the string could be affected at a later time,
t=t0? Well, if you think about it and look at the formula,
the only parts could be in the upward part of the trapezoid
sketched. The wave equation models phenomena which have a finite
propagation speed (here the speed is c). Such phenomena include sound
and light. The slanted edges of the trapezoid sketched are usually
called the light cone and it represents the spreading the
maximum speed that the model allows. This name reflects the physical
theory that light travels at the maximum universal speed, and any
other "signal" travels more slowly. I remark that Mr. Woodrow courageously drew a picture
similar to this on the board.
The QotD was ... well ... student evaluations were
requested. The local supply of explectives was exhausted. I remarked
that the welfare of my family members and pets (alligator, boa
constrictor, etc.) depended on these reviews. Ms.
Lu kindly agreed to take charge of the evaluations. I
wanted to bribe her to fill in the unused ones in a way beneficial to
me. This was not done.
16.2: #3 (try n=20 and t=0, t=.5,
t=1), #16 a and c, 16.4: #1, #22 (try t=0 and 1 and 2). Please read
the text. I remarked that I wanted to spend next week discussing the
heat equation, and that I would therefore not cover section 16.7: we
don't have enough time. Technically 16.7 covered the wave equation in
a rectangle. What's used are several variable Fourier series, but most
of the
qualitative aspects (about speed of influence, etc.) are much the same as
in one variable.
|
Tuesday,
April 20 |
Copying the book
The details of the material in section
16.2 are enormous. To me this material is probably the most
daunting (dictionary: discouraging, intimidating) of the whole
semester. What I wrote during the beginning of this lecture was
essentially copied from the
text. Although I have my own opinions about how the material should be
organized and presented, my belief is that right now is the wrong time
to display the results of these opinions. So here we go:
The setup
The text starts with a function y(x,t) which is
supposed to describe
the motion of a string at position x (x between 0 and L) and time t (t
non-negative). The string is fastened at the ends, and also has an
initial position and velocity. Physical intuition (?!) is supposed to
tell you that later positions of the string are determined by these
initial conditions and boundary conditions, if y(x,t) obeys the wave
equation, ytt=c2yxx.
Boundary conditions
Here y(0,t)=0 and y(L,t)=0 for all t: the
string is fastened down at the ends.
Initial conditions
y(x,0) is some function f(x) and
yt(x,0) is some function g(x). f(x) is supposed to be
initial position and g(x) is supposed to be initial velocity.
The importance of linearity
We will first solve the wave
equation with initial data any f(x) and the velocity equal to 0. Then
we will solve it with velocity g(x) and initial position equal to
0. The general solution will be the sum of these two
solutions. Also important in all this stuff (this is very
involved) is that the boundary conditions are homogeneous, so the sum
of solutions satisfying the boundary conditions still satisfies the
boundary conditions.
In what follows I first will ask that y(x,0)=f(x) and
yt(x,0)=0 for all x.
The boundary conditions lead to eigenvalues via separation of
variables
The word eigenvalue is also used with differential
equations. Please read on. We make the completely wild assumption that
the solution y(x,t) can be written as X(x)T(t). This assumption is
only being taught to you here because it is useful when considering
this equation and a whole bunch of other equations. So learn it!
Then (pp.862-863 of the text): XT''=c2TX''. This
becomes X''(x)/X(x)=c2T''(t)/T(t). This is sort of a
ridiculous equation. The left-hand side is a function of x,and the
right-hand side, a function of t. Only constants are such
functions. The constant is called - . The reason for the minus sign
is to make other computations easier. . The reason for the minus sign
is to make other computations easier.
Since X''(x)/X(x)=- , we get X''(x)+ , we get X''(x)+ X(x)=0. The boundary condition
y(0,t)=0 means that X(0)T(t)=0 for all t. Well, if the T(t) isn't
supposed to be 0 always, we must conclude X(0)=0. Similarly the
boundary y(L,t)=0 yields X(L)=0. So we are led to the problem: X(x)=0. The boundary condition
y(0,t)=0 means that X(0)T(t)=0 for all t. Well, if the T(t) isn't
supposed to be 0 always, we must conclude X(0)=0. Similarly the
boundary y(L,t)=0 yields X(L)=0. So we are led to the problem:
X''(x)+ X(x)=0 with X(0)=0 and X(L)=0. X(x)=0 with X(0)=0 and X(L)=0.
What can we say about the boundary value problem for this ordinary
differential equation? Well, I know a solution for it. The
solution X(x)=0 for all x is a solution. This resembles what
happens in linear homogeneous systems. There's always the trivial
solution. Are there other solutions? Consider the following.
Stupid example
Suppose we are looking for a solution to X''(x)+56X(x)=0 and
X(0)=0 and X(48)=0. Well, solutions to
X''(x)+56X(x)=0 are
C1sin(sqrt(56)x)+C2cos(sqrt(56)x). If X(0)=0,
then since cos(0)=1 and sin(0)=0, this means C2=0. So the
solution is now C1sin(sqrt(56)x). But if X(48)=0, we plug
in x=48: C1sin(48sqrt(56))=0. When is sin(x)=0? It is only
when x is an integer multiple of Pi. But I don't think that 48sqrt(56)
is an integer multiple of Pi. (Check me, darn it: compute
[48sqrt(56)]/Pi and see if this is an integer!) This means that if the
equation C1sin(48sqrt(56))=0 is true, then
C1=0. Therefore (blow horns and pound drums!!!!) the boundary
value problem X''(x)+56X(x)=0 and
X(0)=0 and X(48)=0 has only the trivial solution.
O.k., back to the general case: X''(x)+ X(x)=0 and X(0)=0
and X(L)=0. The solutions are
C1sin(sqrt( X(x)=0 and X(0)=0
and X(L)=0. The solutions are
C1sin(sqrt( )x)+C2cos(sqrt( )x)+C2cos(sqrt( )x). The X(0)=0
condition gives C2=0. What about inserting x=0 in the other
piece? C1sin(sqrt( )x). The X(0)=0
condition gives C2=0. What about inserting x=0 in the other
piece? C1sin(sqrt( )L)=0 has a solution with
C1 not equal to 0 exactly when sqrt( )L)=0 has a solution with
C1 not equal to 0 exactly when sqrt( )L=nPi for an integer
n. Then )L=nPi for an integer
n. Then  is [n2Pi2]/L2. Selecting is [n2Pi2]/L2. Selecting
 as one of these values (with n=1 and n=2 and n=3 and ...) allows
the possibility of non-trivial solutions. If as one of these values (with n=1 and n=2 and n=3 and ...) allows
the possibility of non-trivial solutions. If  is not only of
these values then the only solutions are the trivial solutions. These
special values of is not only of
these values then the only solutions are the trivial solutions. These
special values of  are called the eigenvalues of this
boundary value problem. are called the eigenvalues of this
boundary value problem.
Now let's consider the T(t) function. Well,
(1/c2)T''(t)/T(t)=- (where (where  is now identified as
above!). So
T''(t)+[n2Pi2c2]/[L2]T(t)=0.
We haven't used the initial condition yt(x,0)=0 for all
x. This leads to T'(0)X(x)=0 for all x. Again, either we have a really
silly (and trivial) solution X(x)=0 always or we require that
T'(0)=0. So if we know that
T''(t)+[n2Pi2c2]/[L2T(t)=0
then
T(t)=C1sin([nPi c/L]t)+C2cos([nPi c/L]t).
What's T'(t)? It has a sine and a cosine, and requiring that T'(0)=0
menas that the coefficient in front of cosine (in the
derivative!) must be 0. Then C1 must be 0. So T(t)
is C2cos([nPi c/L]t). is now identified as
above!). So
T''(t)+[n2Pi2c2]/[L2]T(t)=0.
We haven't used the initial condition yt(x,0)=0 for all
x. This leads to T'(0)X(x)=0 for all x. Again, either we have a really
silly (and trivial) solution X(x)=0 always or we require that
T'(0)=0. So if we know that
T''(t)+[n2Pi2c2]/[L2T(t)=0
then
T(t)=C1sin([nPi c/L]t)+C2cos([nPi c/L]t).
What's T'(t)? It has a sine and a cosine, and requiring that T'(0)=0
menas that the coefficient in front of cosine (in the
derivative!) must be 0. Then C1 must be 0. So T(t)
is C2cos([nPi c/L]t).
We then get the solution y(x,t)=X(x)T(t) is
(CONSTANT)sin([nPi/L]x)cos([nPi c/L]t). Here again n is a positive
integer. We have done lots of work to get to this place.
Linearity of the wave equation
When t=0 in the solution listed above we get
(CONSTANT)sin([nPi/L]x). So if you (we?) happen to be lucky, and your
c=1 and your L=Pi and your initial position is 36sin(5x) then you can
just "guess" a corresponding solution to the wave equation:
36sin(5x)cos(5t). Below to the left is the initial shape of this wave
form. Then to the right is an animation of what happens as t goes from
0 to 4.
Remember this is for an idealized vibrating string with no
friction, etc., so it just keeps going back and forth endlessly
(remember Hooke's law and its validity: the ideal spring compared to a
spring vibrating in thick honey, etc.) Energy is constant in this
system. When the string at max amplitutde, it is not moving: all the
energy is potential. When the string overlays to x-axis, its energy is
all kinetic. This is indeed just like an idealized vibrating spring.
But what happens if we want a more complicated initial wave? Well, we
take advantage of linearity. We can add up the simple waves, and we
get
y(x,t)=SUMn=1infinitycnsin([nPi/L]x)cos(nPi c/L]t)
(this is on p.864 of the text). When t=0, this becomes
y(x,0)=SUMn=1infinitycnsin([nPi/L]x)
since cosine of 0 is 1. Let me do an example.
Here I will suppose that c=1 and L=Pi. Then
y(x,0)=SUMn=1infinitycnsin(nx).
Let me ask that the initial shape of the string be like this: 0 if
x<Pi/3 or if x>Pi/2, and 4 for x in the interval [Pi/3,Pi/2].
This is a rectangular bump, and please ignore the fact that it is not
continuous. I would like to represent this function as a sum
of sines. We have the technology: we can extend the
function as an odd function and compute the Fourier coefficients.
Here is the result graphically. The picture on the left shows the
original rectangular bump, and compares it with the sum of the first
40 terms of the Fourier sine series (obtained by extending the
function in an odd way to [-Pi,Pi]). This static picture shows the
usual phenomena, including the Gibbs over- and undershoot. The next
picture shows the resulting vibration, if you can follow it, during
the interval from t=0 to t=4. Notice that fixing the boundary points
at 0 "reflects" the waves in a reversed fashion off the ends. This is
quite fascinating to me.
The initial value problem (velocity)
Here I suppose that y(x,0)=0 for all x, and yt(x,0)=g(x),
for x in [0,L]. Almost the same computations are used. Look at
p. 868. In this case, the boundary value problem for the t variable
makes the cosine term vanish, because y(x,0)=X(x)T(0)=0. So here
y(x,t)=SUMn=1infinitycnsin([nPi/L]x)sin(nPi c/L]t)
and you find the cn's from the derivative:
yt(x,0)=SUMn=1infinitycn[nPi/L]sin([nPi/L]x)=g(x)
where the coefficients are from the sine series of g(x). Wow. I
don't want to make more pictures because the storage space needed for the
animated gifs is enormous.
So what can you do ...
Not much is easy to do by hand. I would sincerely hope that anytime
you need to work with these things, you will have a program like
Maple or Matlab or Mathematica at hand.
Waves, moving right and left
I think it was Mr. Sosa who kindly let
me use the string from the hood of his jacket to show a rather
different representation of the wave shapes. I wiggled one end, and
Mr. Sosa wiggled the other. The result was something like what I show
below.

Here is an example of a solution to the wave equation which I checked in
class:
y(x,t)=(x-t)342+(x+t)221
To check this you must remember the Chain Rule carefully. The precise
numbers don't matter. It turns out that the dependency on x+t and x-t
are the only things that matter. As t grows, the x-t part represents a
wave moving to the right and the x+t part represents a wave moving to
the left. This is called the D'Alembert representation of the
solution, and I will try to understand it more on Thursday and connect
it with the work done earlier. Please look at section 16.4 of the
text.
The QotD was to look at two bumps, one moving right and one
moving left, and draw a picture some time later of what the profile
would look like. It was not a wonderful QotD.
Please read the text!
|
Thursday,
April 15 |
Homework: DONE
13.2 #9, was presented on the board
(thanks to Mr. Araujo),
13.3 #5, was presented on the board
(thanks to Ms. Mudrak),
and 13.5 #2, was presented on the board
(thanks to Mr. McNair).
These problems all had their technical difficulties (especially 13.3,
#5, when done "by hand") but are all straightforward applications of
formulas in the tex.
PDE's
In 244 you learned about ordinary differential equations and initial
value problems. The basic theory can be stated easily: a nice ODE with
the correct initial conditions (order n equation with n initial
conditions) has a solution. Of course, "solving" an ODE, in the sense
of getting a neat symbolic solution or even approximating the solution
well, required tricks and lots of thought. But the theory is there.
By contrast, partial differential equations are horrible. The
equations we will analyze in the short time remaining in this course
(the classical wave and heat equations) have been studied a great deal
for two hundred years, but even these PDE's have properties which are
difficult to understand, both theoretically and computationally. More
general PDE's have very little theory supporting their study. This is
a pity, because many "real" phenomena are best modeled by PDE's.
The Wave Equation
The wave equation is an attempt give a mathematical model of
vibrations of a string (space dimension=1) and a thin plate (space
dimension=2). Please read the assigned sections in the text in chapter
16. It will be very helpful if you read these sections in
advance, since the computational details are intricate!
In one dimension, the wave equation described the dynamics of a
string imagined drawn over the x-axis, whose height at
position x at time t is y(x,t), and gets a condition which is
satisfied by y(x,t):
ytt=c2yxx. Here the subscripts
tt and xx refer to partial derivatives with
respect to time (t) and position (x). To me, a really neat part of the
subject is discovering why this equation is true, based on
simple physical assumptions. Here and here
are two derivations of the wave equation I found on the web. Please
note that the wave equation describes small vibrations of an idealized
homogeneous string. If your string is lumpy (?) or if you want to pull
it a large amount, then such a simple description is not valid. The
wave equation will model fairly well the motion of a guitar string,
say.
One nice thing to notice is that
ytt=c2yxx is linear: if
y1 and y2 are solutions, then the sum
y1+y2 is a solution, and so is ky1
for any constant k. So the solutions of the wave equation form a
subspace. This is frequently called the principle of
superposition (yeah, there are over 86,000 web pages with this
phrase!). A random function is not likely to solve the wave
equation, which essentially asks that yxx and
ytt be constantly proportional: that's quite a stiff
requirement. Here are some candidates and how I might check them:
| y(x,t) | yt | ytt |
yx | yxx | Constantly
proportional? |
|---|
| x5+t3 |
3t2 | 6t |
5x4 | 20x3 |
No! |
| t3ex |
3t2ex | 6tex |
t3ex | t3ex |
No! |
| sin(xt) |
x cos(xt) | -x2sin(xt) |
t cos(xt) | -t2sin(xt) |
No! |
| cos(x2+5t) |
-5sin(x2+5t) | -25cos(x2+5t) |
-2x sin(x2+5t) | -2sin(x2+5t)-4x2cos(x2+5t) |
No! |
| sin(3x)cos(5t) |
-5sin(3x)sin(5t) | -25sin(3x)cos(5t) |
3cos(3x)sin(5t) | -9sin(3x)cos(5t) | Yes!
c2=9/25 |
| e4tcos(5x) |
4e4tcos(5x) | e4tcos(5x) |
-5e4tsin(5x) | -25e4tcos(5x) |
No! |
| | The constant of
proportionality, c2, must be positive! |
| log(6x+7y) |
7/(6x+7y) | -49/(6x+7y)2 |
6/(6x+7y) | -36/(6x+7y)2 |
Yes! c2=49/36 |
My reasons for compiling this table are to warm up by computing some
partial derivatives in case you have forgotten how, and, more
seriously, to show you how rarely the equation is satisfied.
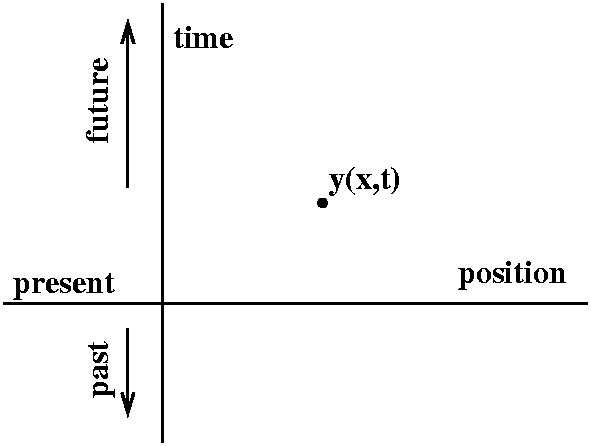
 Setting up a boundary value problem
Setting up a boundary value problem
The physical aspect of the wave equation is important in what we
should expect of solutions. It turns out that there are lots of
solutions, but which ones will make physical sense? Here maybe it does
help to think of a guitar string. Again, I'll follow the text closely
(please read the text!). Usually the guitar string is fastened at the
ends, so right now we will assume y(0,t)=0 and y(L,t)=0. But we need
to know more information: we need the position of the string at time
t=0, y(x,0) for x in [0,L], and, further, we need to know the velocity
of the string at time t=0, yt(x,0) for x in [0,L]. To the
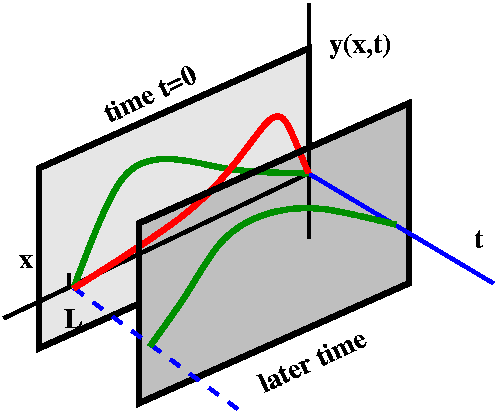
right is my effort to show you a picture of what is happening. There
is an x-axis on which the string is "vibrating". The other horizontal
axis is t, time. Time is progressing futurewards (?) as t
increases. The height from the (x,t) plane is y(x,t), the string's
height at time t and position x. Then y(x,t) actually describes a
surface, and each slice with a fixed time, t, is a frozen picture of
where the string is at time t. I specify that the string is fixed at
height 0
(blue line and dashed line) at x=0 and x=L. But I also specify the
initial position when t=0 (that's the green curve) and the initial
velocity when t=0 (that's the red curve). The red curve declares that
the string is moving up when t=0, and moving up faster when x is small
than when x is large. I also tried to show a picture of the string for
a little bit later time, and, indeed, wanted to make clear that the
part of the string for x small has moved up more than the part for x
large.
This is a complicated and maybe silly picture. You can look at it, but
maybe you should also try creating your own pictures. Your own
pictures will likely make more sense to you. The boundary conditions
y(0,t) and y(L,t) and the initial conditions y(x,0) and
yt(x,0) for x in [0,L] are generally what people expect
with the wave equation. Recognizing that these conditions are
appropriate comes from the physical situation.
Trying to solve the wave equation
There are several standard techniques for solving the wave
equation. Here is one of them, called separation of
variables. Look at
ytt=c2yxx and assume that
y(x,t)=X(x)T(t): that is, y(x,t) is a product a function of x
alone and a function of t alone. Then ytt is X(x)T''(t)
(you may need to think about this a bit!) and yxx is
X''(x)T(t). If this weird function satisfies the wave equation, then
X(x)T''(t)=c2X''(x)T(t) so that
T''(t)/T(t)=c2X''(x)/X(x). On the left side of this
equation we have a function of t alone, and on the right side of the
equation, we have a function of x alone. The only function that
is a function of both x alone and t alone is a constant. This constant
is usually called - (sorry about the minus sign, but everyone uses
it, and you will see why, very soon). Therefore, if
X(x)T(t) solves the wave equation, I know that T''(t)/T(t)=- (sorry about the minus sign, but everyone uses
it, and you will see why, very soon). Therefore, if
X(x)T(t) solves the wave equation, I know that T''(t)/T(t)=- so that
T''(t)+ so that
T''(t)+ T(t)=0 and I know a similar statement for X(x). So now I'll
use what I know about ODE's to find eligible T(t) and X(x). Please
look at the textbook. I will continue this next time. T(t)=0 and I know a similar statement for X(x). So now I'll
use what I know about ODE's to find eligible T(t) and X(x). Please
look at the textbook. I will continue this next time.
A proposal for the Final Exam
I suggested that instead of having a comprehensive final
covering all parts of the course that I do the following:
- Write an exam, whose length and difficulty will be
appropriate (similar to the past two exams) covering the Fourier
series part of the course. Everyone would take this, and I would grade
it, and count it as one of three similar exams in the course.
- Optionally offer a few problems on linear algebra and a few
problems on Laplace transforms for students who wish to improve their
grades in the exams.
After some discussion and e-mail with students, I would like to
specify the possible improvement so that no one can get more than
100. Here is one strategy, which is historically and physically
interesting: if a student got GLT on the Laplace transform
grade, and then got PLT on the optional few Laplace
transform problems then (GLT is in the interval
[0,100) and PLT, in the interval [0,{20 or 25 or 30}], I
would replace (for term grade purposes) GLT by
(GLT+PLT)/(1+GLT·PLT/104).
Some of you may recognize this as Lorentz addition of grades! So the
Lorentz sum of 55 and 15 is 64.67 (I'll use approximations
here). Using this formula, students could never score more than 100.
Comment and information
Here is a quote from a web
page entitled How Do You Add Velocities in Special
Relativity?:
|
w = (u + v)/(1 + uv/c2)
If u and v are both small compared to the speed of light c, then the
answer is approximately the same as the non-relativistic theory. In
the limit where u is equal to c (because C is a massless particle
moving to the left at the speed of light), the sum gives c. This
confirms that anything going at the speed of light does so in all
reference frames.
|
I think this penalizes students who got a fairly good grade already
too much, though. For example, the Lorentz sum of 75 and 15 is only
80.90. So maybe I should find something better.
There was no QotD! But I did ask people to:
Begin reading the sections of
chapter 16. Please hand in 13.5, #3 and #4, and 16.1, #4.
|
Tuesday,
April 13 |
I had prepared a sequence of handouts, which are reproduced here as
gifs. I basically wanted to discuss a sequence of examples to
illustrate
- The definition and computation of Fourier coefficients.
- The behavior of the partial sums of Fourier series.
- The (theoretical?) limiting behavior of the partial sums of
Fourier series: what is the sum of the whole Fourier series?
- The qualitative behavior of the Fourier series.
- The Parseval equality.
- Odd and even extensions of functions and the Fourier sine and
cosine series which result.
This is a lot to think about but we can only complete this by
beginning, so let's begin.
I remarked that Taylor series are good for "local" computations near a
fixed point, in some "tiny" interval around the point. Fourier series
are a wonderful thing to use on a whole interval.
I recalled some general facts: the definitions of Fourier coefficients
and Fourier series and how the partial sums
and the whole sum of the Fourier series behaves compared to f(x).
I also supplied a (very short) table of integrals we would need today:
| Function | Antiderivative |
|---|
| cos(Kx) | (1/K)sin(Kx)+C |
| sin(Kx) | -(1/K)cos(Kx)+C |
| x cos(Kx) | (1/K)x sin(Kx)+(1/K2)cos(Kx)+C |
| x sin(Kx) | -(1/K)x cos(Kx)+(1/K2)sin(Kx)+C |
A first example (an old QotD)
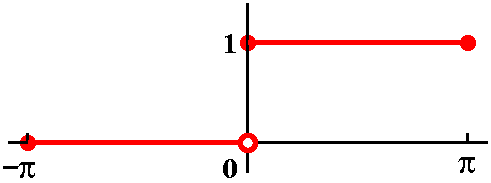 My first example analyzed the QotD from the previous regular class
meeting. So f(x) is 0 for x<0 and is 1 for x>=0. In everything I
am doing today, I will only care about the interval [-Pi,Pi]. If
you run across a situation where you "care" about the interval
[-5,11], say, probably you should first take x and change it into
y=(2Pi/16)x-(3Pi/8). Then as x runs from -5 to 11, y would go from -Pi
to Pi. Anyway, I used the following Maple commands to create
the pictures I will show and also the resulting computations.
My first example analyzed the QotD from the previous regular class
meeting. So f(x) is 0 for x<0 and is 1 for x>=0. In everything I
am doing today, I will only care about the interval [-Pi,Pi]. If
you run across a situation where you "care" about the interval
[-5,11], say, probably you should first take x and change it into
y=(2Pi/16)x-(3Pi/8). Then as x runs from -5 to 11, y would go from -Pi
to Pi. Anyway, I used the following Maple commands to create
the pictures I will show and also the resulting computations.
Maple commands
Here is how to write f(x), a piecewise defined function:
f:=x->piecewise(x>0,1,0);
This command creates a function q(n) which produces the cosine Fourier
coefficients:
q:=n->(1/Pi)*int(f(x)*cos(n*x),x=-Pi..Pi);
and here is r(n) which produces the sine Fourier coefficients:
r:=n->(1/Pi)*int(f(x)*sin(n*x),x=-Pi..Pi);
Here I have a function Q(k) which creates a pair of functions. The
first element of the pair is f(x), and the second element of the pair
is the partial sum of the Fourier series up to the terms sin(kx) and
cos(kx):
Q:=k->{f(x),(1/2)*q(0)+sum(q(n)*cos(n*x)+r(n)*sin(n*x),n=1..k)};
And then this command produces a graph of the previous pair.
QQ:=n->plot(Q(n),x=-Pi..Pi,scaling=constrained);
I try to write short and simple Maple commands rather than
write big programs. I can't understand big
programs easily. So all four of the pictures below were produced by
the one command line (one: only one!)
QQ(0);QQ(2);QQ(5);QQ(10);
| f(x) and the partial sums of the Fourier series for f(x) up to |
|---|
 |
 |
 |
 |
| n=0 | n=2 | n=5 | n=10 |
|---|
The hard part of this is figuring out what we can learn from such
pictures. I mention that these pictures and the others I'll show below
would be really irritating to obtain (at least for me!) without
technological help.
Observation 1
Please realize that the partial
sums (which are linear combinations of sin(mx) and cos(nx)) will
always have the same values at -Pi and Pi since sin(mx) and cos(nx) are
the same at -Pi and Pi. So these functions really "wrap around" on the
[-Pi,Pi] interval. Look at the pictures!
Observation 2
The first picture tells me that (1/2)a0, that horizontal
line, which here has height 1/2, is the mean square best constant
approximating our f(x). That is, if I sort of take values at random,
then the horizontal line will have the least error, on average, from
the function's value. I hope you can see this here, since the function
involved is quite simple.
 Observation 3
Observation 3
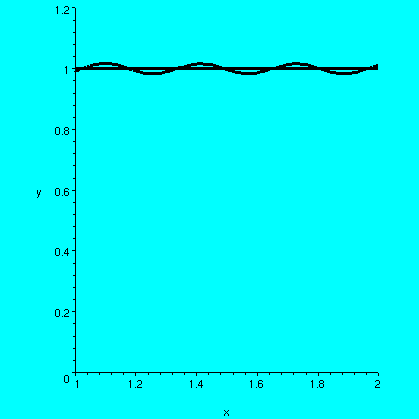
Go away from the jumps in the function. That is, imagine you restrict
your attention to x between -Pi and 0 or x between 0 and
Pi. What's happening there? Here's a picture of a piece of the graph
of f(x) and the partial sum, with n=20, in the interval for x between
1 and 2, away from the discontinuities.
You should notice that the error between the function and the partial
sum is very very small. In addition, the partial sum, in this
restricted interval, really does not wiggle very much. That is, its
derivative is quite close to 0. The derivative of f(x) is 0 oin this
interval, of course, since it is a horizontal line segment.
 Observation 4
Observation 4
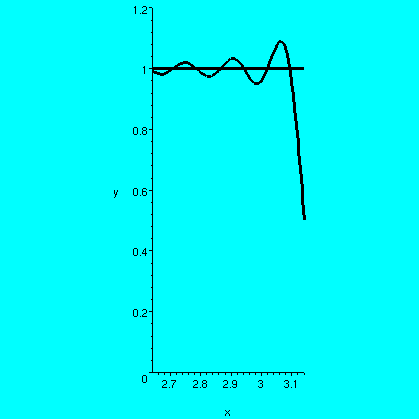
Here by contrast is a picture of what happens to the 40th
partial sum (I'm very glad I'm not doing these by hand!) and
f(x) on the interval [Pi-.5,Pi]. Of course (observation 0) the
partial sum hops "down" towards 1/2 at x=Pi. But it is sort of
interesting (as Mr. Dupersoy noticed!)
that there is sort of an overshoot. The overshoot is very very near
the jump. I will come back and discuss this a bit later. The overshoot
(which has an accompanying "undershoot" for this f(x) at -Pi) is
called Gibbs phenomenon, and is rather subtle.
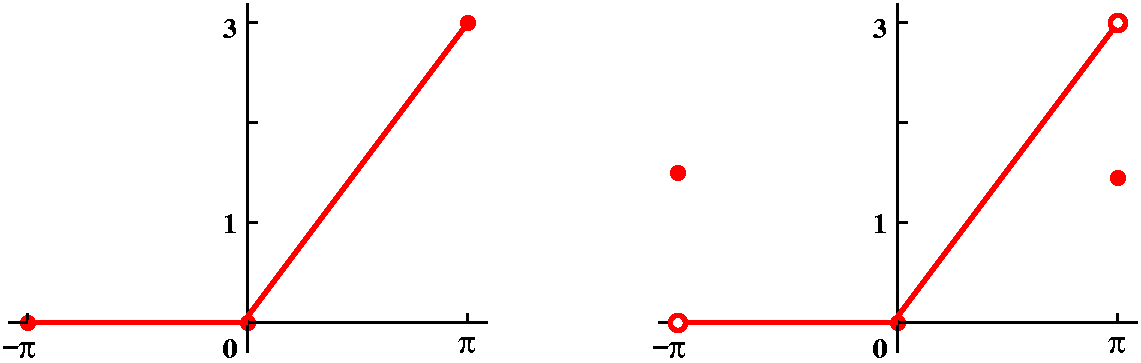
 The sum of the whole Fourier series
The sum of the whole Fourier series
Theory tells me what the sum of the whole Fourier series should
be. This function f(x) is "piecewise smooth". Theory then says that
the sum of the whole Fourier series is f(x) if x is a point where f(x)
is continuous. If the left- and right-hand limits of f(x) exist at a
point and if these limits are different, then the Fourier series
attempts to compromise (!) by converging to the average of the two
values: graphically, a point halfway in between the limiting values of
f(x). In our specific case, there are three (well, two, if you
consider -Pi and Pi to be the "same" which they are for sine and
cosine) points of discontinuity: -Pi, 0, and Pi. At each of those, the
whole Fourier series of f(x) converges to the values shown.
Maple code for Parseval
This command
s:=k->(1/2)*q(0)^2+sum(q(n)^2+r(n)^2,n=1..k);
adds up the Fourier coefficients (properly squared) and is a partial
sum of the infinite series appearing on one side of the Parseval
formula.
pars:=k->[s(k),evalf(s(k)),(1/Pi)*int(f(x)^2,x=-Pi..Pi),evalf((1/Pi)*int(f(x)^2,x=-Pi..Pi))];
asks Maple to produce four quantities: the first one is the
partial sum of the Parseval series symbolically evaluated (if
possible), the second
is a numerical approximation to that sum, the third is the integral
symbolically evaluated (if possible), and the fourth is a numerical
approximation to that integral. The command pars(10) gives
the response
469876
[1/2 + ---------, 0.9798023932, 1, 1.]
2
99225 Pi and pars(20) gives the
response
204698374253288
[1/2 + ------------------, 0.9898762955, 1, 1.]
2
42337793743245 Pi
Observation 5 (and something sneaky!)
Well, at least .989... is closer to 1 than .979..., so maybe the
partial sums of the Parseval series are equal to one. Well, to tell
you the truth, very few people in the real world use the Parseval
series to compute the integral of f(x)2 on the interval
[-Pi,Pi]. Instead, things like the following are done.
What's an? It is (1/Pi) -PiPif(x) cos(nx) dx, which is
(for our specific f(x)!)
(1/Pi) -PiPif(x) cos(nx) dx, which is
(for our specific f(x)!)
(1/Pi) 0Picos(nx) dx=(1/(nPi))sin(nx)|0Pi. But sine at integer
multiples of Pi is 0, so an is 0. Errrr .... except for
n=0, when that formula is not valid. We know that a0=1
(compute the integral of f(x)2, which is 0 on the left and
1 on the right!). 0Picos(nx) dx=(1/(nPi))sin(nx)|0Pi. But sine at integer
multiples of Pi is 0, so an is 0. Errrr .... except for
n=0, when that formula is not valid. We know that a0=1
(compute the integral of f(x)2, which is 0 on the left and
1 on the right!).
What's bn? It is (1/Pi) -PiPif(x) sin(nx) dx, which is
(for our specific f(x)!)
(1/Pi) -PiPif(x) sin(nx) dx, which is
(for our specific f(x)!)
(1/Pi) 0Pisin(nx) dx=-(1/(nPi))cos(nx)|0Pi. Now cos(n0) is
cos(0) which is 1. What about cos(nPi)? It is either +1 or -1,
depending on the parity (even/odd) of n. In fact, it is
(-1)n. Therefore we have a formula:
bn=(1/(nPi))((-1)n+1). 0Pisin(nx) dx=-(1/(nPi))cos(nx)|0Pi. Now cos(n0) is
cos(0) which is 1. What about cos(nPi)? It is either +1 or -1,
depending on the parity (even/odd) of n. In fact, it is
(-1)n. Therefore we have a formula:
bn=(1/(nPi))((-1)n+1).
(I screwed up this calculation in
class!)
What the heck does the Fourier series of f(x) look like? If you try
the first few terms (all of the cosine terms are 0 except for the
constant term!) you will get:
(1/2)+(2/Pi)sin(x)+(2/(3Pi))sin(3*x)+(2/(5Pi))sin(5*x)+(2/(7Pi))sin(7*x)+(2/(9Pi))sin(9*x)+...
Actually, what I did was just type the command
sum(r(n)*sin(n*x),n=1..10); into Maple, copy the
result and add on (1/2) in front. This allowed me to check all of my
computations.
Then the infinite series in Parseval becomes
(1/2)+(4/Pi2)SUMn=0infinity1/(2n+1)2
where I factored out the 4/Pi2 from each term
(uhhhh: 4/Pi2 is the square of 2/Pi). So we
actually have (now put in (1/Pi) -PiPif(x)2 dx, which in
our case is just 1): -PiPif(x)2 dx, which in
our case is just 1):
1=(1/2)+(4/Pi2)(the big SUM).
We can solve for the sum. And thus (non-obvious fact coming!)
The sum of 1/(all the odd squares) is Pi2/8.
Maple evidence for this silly assertion
I tried the following:
evalf(sum(1/(2*n+1)^2,n=0..100));
1.231225323
evalf(Pi^2/8);
1.233700550
which compares the sum of the first 100 terms with Pi2/8. And
then, heck, what's time to a computer?, I tried the first 1000 terms:
evalf(sum(1/(2*n+1)^2,n=0..1000));
1.233450800
But the convincing command is this:sum(1/(2*n+1)^2,n=0..infinity);
2
Pi
---
8
because Maple can recognize certain infinite series and
"remember" their values!
The second example
Here f(x) is the function 3x for x>0, and f(x)=0 for x<0. Here
are some pictures:
| f(x) and the partial sums of the Fourier series for f(x) up to |
|---|
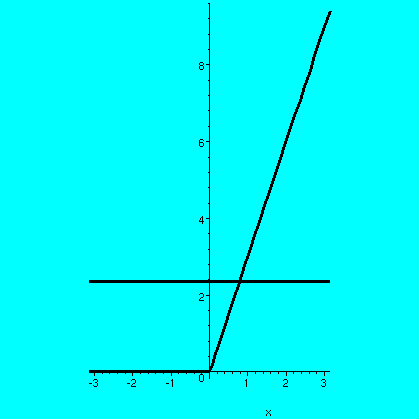 |
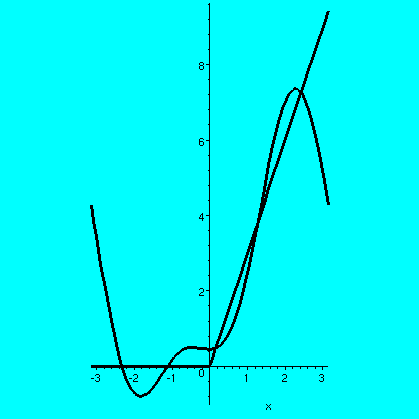 |
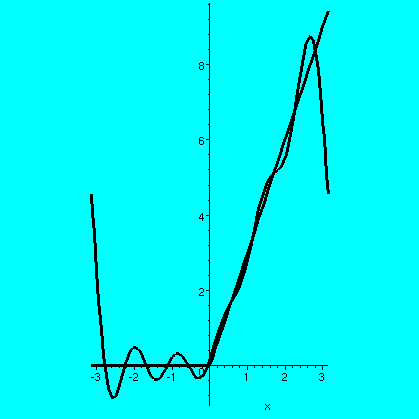 |
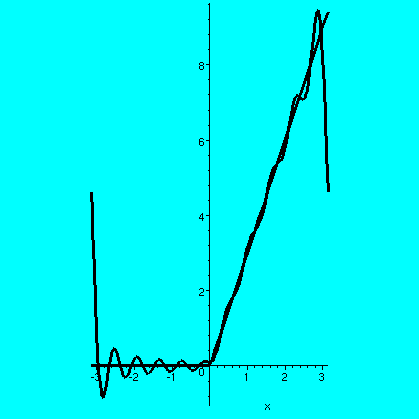 |
| n=0 | n=2 | n=5 | n=10 |
|---|
I hope you can see some of the same qualitative features in these pictures as in
the previous collection. So you should see in the first picture the
best constant that approximates this f(x). In the succeeding
pictures, you should see better and better approximations, away from
the points of discontinuity (Pi, -Pi, which the trig functions regard
as the "same"). Even the derivatives of the partial sums (for x not 0 or
+/-Pi) are approaching the derivatives of f(x). There's also a Gibbs
phenomenon, the bumps at +/-Pi. Here is:
 |
|
A graph of f(x) |
A graph of the sum of
the Fourier
series for f(x) |
|---|
Some Fourier coefficients for this f(x)
I tried to compute a11. This is
(1/Pi) -PiPif(x) cos(11x) dx=(1/Pi) -PiPif(x) cos(11x) dx=(1/Pi) 0Pi3x cos(11x) dx (because
f(x) is 0 for x<0). I can antidifferentiate this (especially with
the table above!). So it is
(3/(11))x sin(11x)+(3/(11)2)cos(11x)|0Pi. I know that
sin(11Pi) and sin(0) are 0. Also cos(0)=1 and cos(11Pi)=-1, so after
computing, -6/(121Pi). 0Pi3x cos(11x) dx (because
f(x) is 0 for x<0). I can antidifferentiate this (especially with
the table above!). So it is
(3/(11))x sin(11x)+(3/(11)2)cos(11x)|0Pi. I know that
sin(11Pi) and sin(0) are 0. Also cos(0)=1 and cos(11Pi)=-1, so after
computing, -6/(121Pi).
How about b10? This is
(1/Pi) -PiPif(x) sin(10x) dx=(1/Pi) -PiPif(x) sin(10x) dx=(1/Pi) 0Pi3x sin(10x) dx and this is
-(3/10)x cos(10x)+(3/(10)2)sin(10x))|0Pi, and, evaluating
carefully, this will be -3/(10). 0Pi3x sin(10x) dx and this is
-(3/10)x cos(10x)+(3/(10)2)sin(10x))|0Pi, and, evaluating
carefully, this will be -3/(10).
Hey: I just wanted to show you that some of each kind of Fourier
coefficient is not 0.
Cheap cosines?
We have seen that 3x, for x between 0 and Pi, is some crazy
infinite linear combination of sines and cosines. What if
evaluating cosines was very very cheap and easy, and
evaluating sines was really expensive. I will show you a clever way to
get 3x, for x between 0 and Pi, as a sum only of cosines.
The even extension
Fold over 3x on [0,Pi]. That is, define f(x) to be 3x for x>0 and
f(x) is -3x for x<0. Then the resulting new f(x) is even, so
that multiplying it by sin(mx), an odd function, and integrating the product
from -Pi to Pi must result in 0. The Fourier series of this new
function has only cosine terms.
| f(x) and the partial sums of the Fourier series for f(x) up to |
|---|
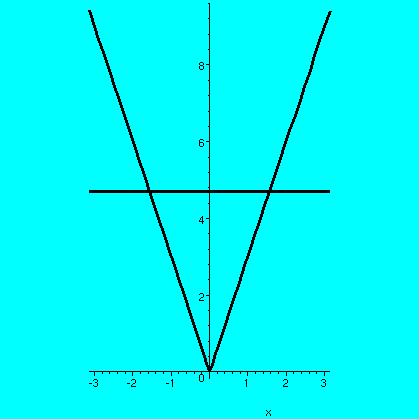 |
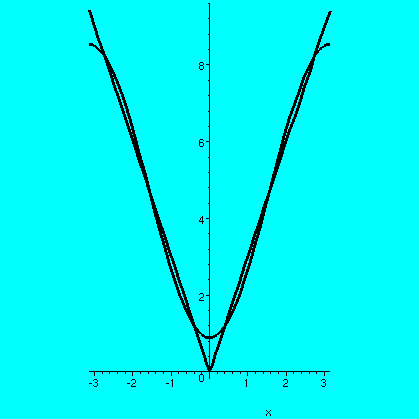 |
 |
 |
| n=0 | n=2 | n=5 | n=10 |
|---|
We're using only cosines, and the two graphs look really close for
n=10. The function and the sum of the whole Fourier series are
identical in this case (the function is continuous in [-Pi,Pi] and its
values at +/-Pi agree).
The odd extension
Change the game, so that now computing sines is cheap, and cosines are
impossibly expensive. So
we take 3x on [0,Pi] and extend it to an f(x) on [-Pi,Pi] with
f(-x)=f(x). This has a simple algebraic definition (no longer
piecewise): f(x)=3x for x in [-Pi,Pi]. Nows the integrals defining the
cosine coefficients are 0 (cosine is even, this f(x) odd, so the
product is odd). Here are the pictures which result:
| f(x) and the partial sums of the Fourier series for f(x) up to |
|---|
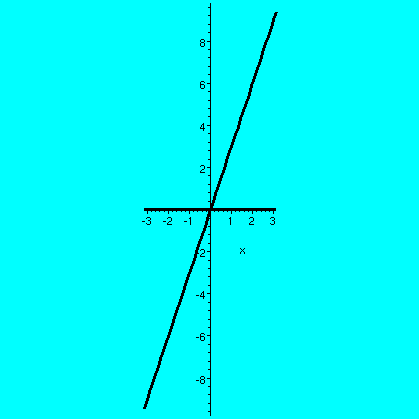 |
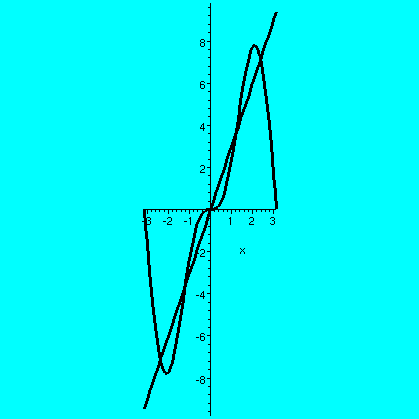 |
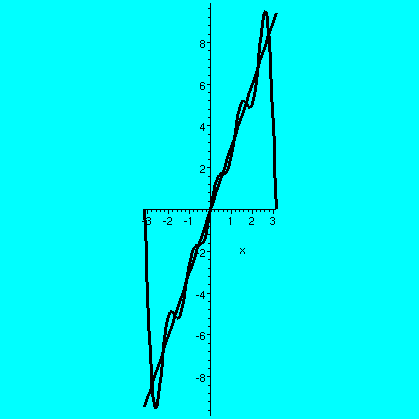 |
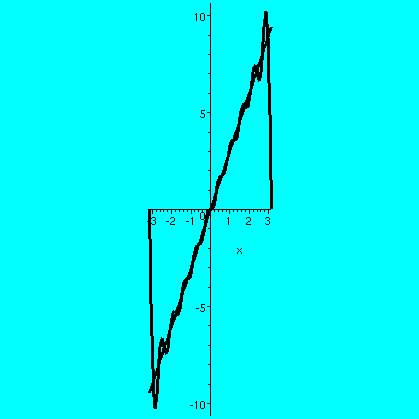 |
| n=0 | n=2 | n=5 | n=10 |
|---|
Again, I hope you see some neat qualitative aspects.
 |
|
A graph of f(x) |
A graph of the sum of
the Fourier
series for f(x) |
|---|
These graphs differ at the endpoints.
What are these darn things?
I asked Maple to compute the beginnings of each Fourier
series and I display the results. Please note (it is almost
unbelievable!) that each of these series has the same sum, 3x, for x
in the interval [0,Pi).
| Picture | Beginning of the Fourier series |
|---|
Original f(x)
|
3 Pi 5 cos(x) 3 2 cos(3x)
---- - -------- + 3 sin(x) - - sin(2x) - -------- + sin(3x)
4 Pi 2 3 Pi
|
Even extension from [0,Pi]
|
3Pi 12 cos(x) 4 cos(3x) 12 cos(5x)
--- - --------- - --------- - ----------
2 Pi 3 Pi 25 Pi
|
Odd extension from [0,Pi]
|
3 6
6 sin(x) - 3 sin(2x) + 2 sin(3x) - - sin(4 x) + - sin(5 x)
2 5
|
The Maple command I used here was
(1/2)*q(0)+sum(q(n)*cos(n*x)+r(n)*sin(n*x),n=1..5);
separately for each function.
The Gibbs phenomenon: (maybe) a simpler version
Here is a simple model situation to help you understand the Gibbs
phenomenon. I don't know any particular "real" application that needs
to pay attention to this overshoot idea, but lots of people (about
44,500 web pages mention it, according to Google!) are
curious about it.
In 1863,
J.
Willard Gibbs received the first U.S. doctorate in engineering. He
saw that at a jump discontinuity, there is always an overshoot of
about 9% in the Fourier series. The limit of the overshoot's behavior
vanishes! This is a bit difficult to understand at first. Here are
some pictures of a similar situation which may help you.
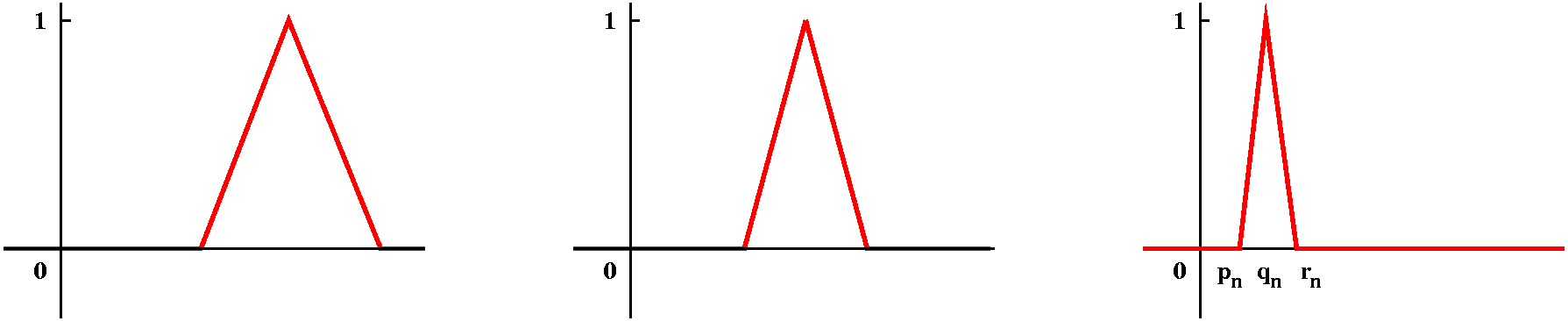
This is a picture of a moving bump. The bump is always
non-negative, and is always 1 unit high. It gets narrower and narrower
as n increases, and moves toward, but never actually reaches, 0. The
point pn is at 1/n, and qn is at 2/n, and
rn is at 3/n. The graph is made of four line
segments. Notice that if you "stand" at 0, you never feel the
bump. Of course, you also never will feel the bump if you are at any
negative x. But, and this is most subtle, if x is positive, then for n
large enough, the bump eventually passes you, goes toward 0, and your
value goes to 0 and stays at 0. So the limit
function of this sequence of moving bumps is 0 at every point, but
each bump has height 1! This is similar to the bumps found by
Gibbs. The partial sums display a sort of moving bump effect, but the
limit function (the sum of the whole series) doesn't show any
additional bump.
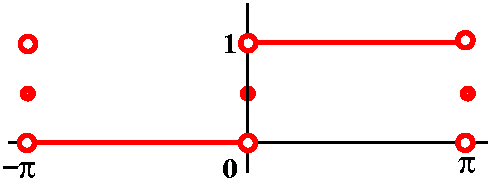
The QotD was: here is a function given graphically on the
interval [0,Pi]. The answer(s) will be a series of four graphs. First,
graph the odd extension of this function to [-Pi,Pi]. Then draw
the graph of the sum of the whole Fourier series of the odd extension
on the interval [-Pi,Pi]. For the third graph, draw the even
extension of this function to [-Pi,Pi]. Then draw the graph of the
sum of the whole Fourier series of the even extension on the interval
[-Pi,Pi].
|
Thursday,
April 8 |
We had fun with the linear algebra exam, and only about a quarter of
the students stayed past 10 PM.
|
Tuesday,
April 6 |
Real-life linear algebra [ADVT]
One step in the algorithm used by Google to develop PageRank
(a way of deciding which pages are more reputable or useful) is
finding the largest eigenvalue of a matrix which is about three billion
by three billion in size. This is a ludicrous but real application of
linear algebra. I have no idea how to effectively compute such
a thing.
End [ADVT]
I tried again to discuss closest approximation, but I am willing to
concede that this approach to Fourier series does not seem to
resonate with students. Perhaps it is my fault. I may not have
prepared the territory enough in linear algebra.
We will start with a function f(x) defined on the interval [-Pi,Pi].
In Fourier series, we try to write f(x) as a sum of sines and
cosines. That is, I want to write f(x) as a linear combination of
cos(nx) and sin(nx), where n and m are non-negative integers. As to
cos(nx), the term corresponding to n=0 is somewhat special: cos(0x) is
the constant 1. We can discard sin(0x) since sin(0x) is 0. There are
various constants that come up which occur so that orthogonal
functions are orthonormal. Here's a general approach which is useful
in many integrals.
Integrating certain exponentials
The interval of interest is [-Pi,Pi]. I would like to evaluate
 -PiPiein x dx,
where n is an integer. Please remember Euler's formula: -PiPiein x dx,
where n is an integer. Please remember Euler's formula:
ein x=cos(nx)+i sin(nx), so that
e-in x=cos(nx)-i sin(nx), since cosine is even
and sine is odd. Then adding, subtracting, dividing, etc., gives
us:
cos(nx)=(1/2)(ein x+e-in x) and
sin(nx)=(1/(2i))(ein x-e-in x).
Now  -PiPiein x dx=(1/(in))
ein x|Pi-Pi. This is
(1/(in))(einPi-e-inPi). Apparently this is
sin(nPi) with some multiplicative constant, if n is an integer, this
is 0. Hold it! There is exactly one integer for which
the given antiderivative is not valid: n=0. It is impossible and
forbidden to divide by 0. When n=0, -PiPiein x dx=(1/(in))
ein x|Pi-Pi. This is
(1/(in))(einPi-e-inPi). Apparently this is
sin(nPi) with some multiplicative constant, if n is an integer, this
is 0. Hold it! There is exactly one integer for which
the given antiderivative is not valid: n=0. It is impossible and
forbidden to divide by 0. When n=0,
 -PiPiein x dx= -PiPiein x dx= -PiPie0x dx= -PiPie0x dx= -PiPi1 dx=2Pi. -PiPi1 dx=2Pi.
 -PiPiein x dx= -PiPiein x dx= |
2Pi if n=0. |
|---|
0 if n is an
integer and not 0. |
|---|
Computing some trig integrals
Example #1 Let's compute  -PiPisin(5x)cos(7x) dx. Certainly
this integral can be done using integration by parts, twice. I will
compute it the complex because it is easier. -PiPisin(5x)cos(7x) dx. Certainly
this integral can be done using integration by parts, twice. I will
compute it the complex because it is easier.
We know sin(5x)=(1/{2i})(e5i x-e-5i x)
and cos(7x)=(1/2)(e7i x+e-7i x). Then
the product sin(5x)cos(7x) is
(1/{4i})(e12i x+e2i x+e-2i x-e-12i x.
What is the integral of this over the interval [-Pi,Pi}? Since the
function is a linear combination of functions eAi x
with A not equal to 0, and integration is linear, the integral is
0! Isn't this easier than several integration by parts?
Example #2 Let's compute  -PiPicos(8x)cos(8x) dx. Again,
cos(8x)=(1/2)(e7i x+e-7i x) so that
[cos(8x)]2 is (1/4)(e14i x+2e0 x
+e-14i x). Now the first and last terms integrate to 0
on [-Pi,Pi]. The middle term gives us (1/4)(2) on the interval
[-Pi,Pi], whose integral is Pi. -PiPicos(8x)cos(8x) dx. Again,
cos(8x)=(1/2)(e7i x+e-7i x) so that
[cos(8x)]2 is (1/4)(e14i x+2e0 x
+e-14i x). Now the first and last terms integrate to 0
on [-Pi,Pi]. The middle term gives us (1/4)(2) on the interval
[-Pi,Pi], whose integral is Pi.
Examples #1 and #2, revisited in the context of linear
algebra
This example, slightly generalized,
states that sin(mx) and cos(nx) are orthogonal on the interval
[-Pi,Pi], when the inner product is the integral of the product of the
two functions. Similarly, if m is not equal to n, the integral
of sin(nx) and sin(mx), and the integral of cos(nx) and cos(mx), are
also 0, so these pairs of functions are also orthogonal. The
collection of functions {sin(nx),cos(mx)} for n>0 and m>=0 is
not orthonormal, however, because the integrals of the squares
aren't 1. The integrals of [sin(nx)]2 and
[cos(mx)]2 over the interval [-Pi,Pi] (when n and m are at
least 1) are all Pi. The
integral of [cos(0x)]2 is 2Pi since cos(0x) is the constant
1. Notice that we don't need (we can't use!) [sin(0x)]2
because that is the 0 function, also known as the 0 vector in this
setup.
Consequences
Here are some formulas which need to be memorized, or at least thought
about a lot. The reason for the factors in front of the integrals
comes from the computations mentioned just previously. Here it all is:
| Suppose f(x) is a piecewise continuous function on the
interval [-Pi,Pi] |
| The Fourier coefficients of f(x) |
|---|
an=(1/[Pi]) -PiPif(x)cos(nx) dx for n>=0 -PiPif(x)cos(nx) dx for n>=0
bn=(1/[Pi]) -PiPif(x)sin(nx) dx for n>0 -PiPif(x)sin(nx) dx for n>0
|
|---|
| The Fourier series of f(x) |
|---|
|
This is (1/2)a0+SUMn=1infinityancos(nx)+SUMn=1infinitybnsin(nx).
|
|---|
The Fourier series tries very hard to converge to f(x).
- The partial sums of the Fourier series turn out to be the
best mean square approximations. Therefore, if you know some
Fourier coefficients, and you want to approximate f(x) at random for
x's in the interval [-Pi,Pi], the best that can be done is to compute
(1/2)a0+SUMn=1Nancos(nx)+SUMn=1Nbnsin(nx).
and your average error will be as small as possible.
- If f(x) is, say, at least piecewise "smooth", so it is
differentiable at all but a few points, then the whole Fourier series will try to converge to
f(x).
- Where f(x) jumps (has a discontinuity) it turns out that the
Fourier series will still converge, but it will converge to the
average of the left- and right-hand limits of f(x): so the sum
of the whole Fourier series at x0 converges to
(1/2)(limx-->x0-f(x)+limx-->x0+f(x))
|
|
Original graph of f(x)
Graph
of the sum of f(x)'s Fourier series |
|---|
 |
Please compare closely the sum of the Fourier series and the original
function. They are the same where f(x) is continuous, and the sum of
the Fourier series attempts to compromise (?) where f(x) is not
continuous.
I also mentioned
Parseval's Theorem:
(1/Pi) -PiPi(f(x))2 dx=(1/2)a02+SUMn=1infinity(an2+bn2). -PiPi(f(x))2 dx=(1/2)a02+SUMn=1infinity(an2+bn2).
This works because the Fourier series is actually sort of a linear
combination of an orthonormal basis, and therefore the length squared
of the sum ((1/Pi) -PiPi(f(x))2 dx) is the
same as the sum of the squares of the coefficients of the linear
combination (the other side of Parseval's equality). -PiPi(f(x))2 dx) is the
same as the sum of the squares of the coefficients of the linear
combination (the other side of Parseval's equality).
I only showed one example. I need to show many more examples and
show people how Fourier series are used.
One example
f(x)=x2-Pi2 on [-Pi,Pi]. Notice that this f(x)
is even: f(x)=f(-x). Therefore any integral of f(x) multiplied by the
odd function sin(nx) on [-Pi,Pi] is 0. We only need to deal with the
cosine terms.
I used Maple. Here I defined a function to compute the
Fourier coefficients:
q:=n->(1/Pi)*int((Pi^2-x^2)*cos(n*x),x=-Pi..Pi);
For example, the entry q(3) gets the response 4/9.
Here is the first (zeroth) term compared with the original
function. This is the constant which has the least mean square average
error from f(x) on the whole interval:
plot({Pi^2-x^2,(1/2)*q(0)}, x=-Pi..Pi,thickness=4,scaling=constrained);
|
|
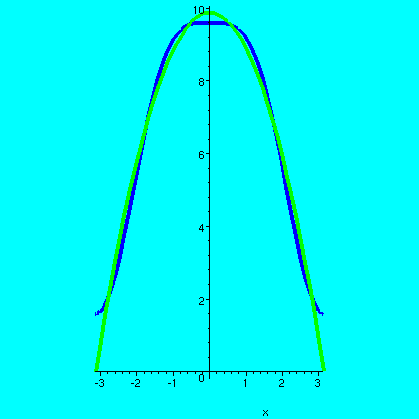
Here are the sum of the first three terms, compared with the original function (I
broke q(0) out from the others because it needs a different normalization):
plot({Pi^2-x^2,(1/2)*q(0)+sum(q(n)*cos(n*x),n=1..2)}, x=-Pi..Pi,thickness=4,scaling=constrained);
|
|
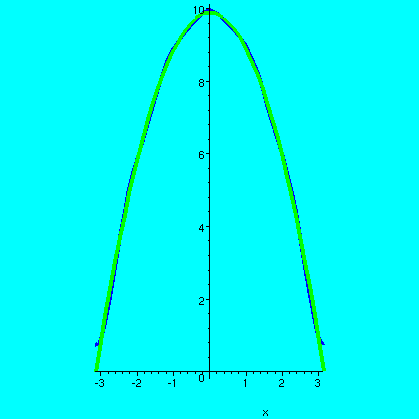
And the sum of the first 6 terms, which I find pretty darn close to
f(x) on all of [-Pi,Pi]:
plot({Pi^2-x^2,(1/2)*q(0)+sum(q(n)*cos(n*x),n=1..5)}, x=-Pi..Pi,thickness=4,scaling=constrained);
|
|
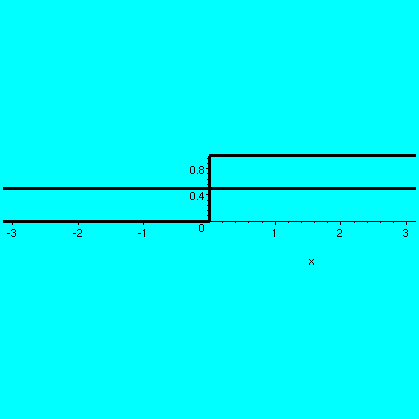
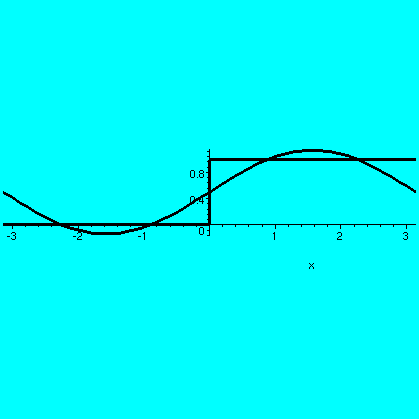
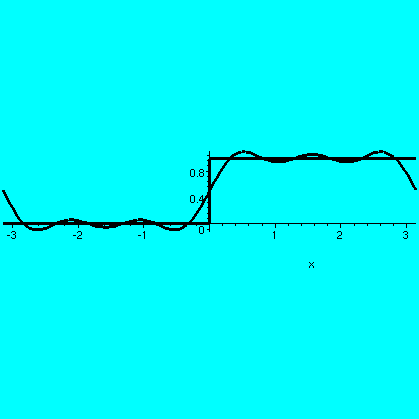
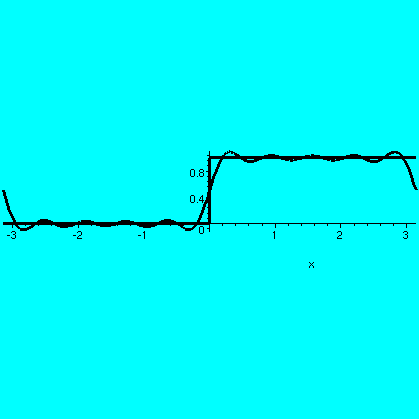
The QotD was to find the Fourier coefficients of the function
f(x) which is 0 for -Pi<x<0 and 1 for 0<x<Pi.
Please hand in 13.2 #9 and 13.3 #5
and 13.5 #2. Please read the applicable sections of chapter 13.
|
Thursday,
April 1 |
I tried to show some of the real linkage between linear algebra and
Fourier series. I began, though, with
the QotD: I asserted several times during the last lecture
that matrix multiplication was not necessarily
commutative. Find simple matrices A and B so that AB and BA are
defined (compute them!) and AB does not equal BA.
I put the QotD first because I didn't know how long I would last in
class, since I was miserable and suffering from the effects of an
upper respiratory infection. One
source declares
|
What are the risks to others?
Most upper respiratory infections are highly contagious. They are
transmitted through respiratory secretions. Sneezing and coughing can
spread these droplets. The germ can also be passed on when an
individual with an upper respiratory infection touches his or her nose
and then handles an object that another person later touches. The
second person can then pick up the germ from the object and transfer
it into his or her own respiratory tract by touching the face.
|
I tried diligently not to breath on anyone. Sympathy seemed meager.
Well, let's get to work. i began with an extended discussion of an
example of a matrix I had analyzed with Maple. What I did was
write a 5 by 5 symmetric matrix with small integer coefficients, and
find the characteristic polynomial. I kept making entries equal to 0
to simplify the characteristic polynomial. I finally ended up with
A=
( 0 -1 0 1 0)
(-1 0 0 0 0)
( 0 0 1 0 0)
( 1 0 0 0 0)
( 0 0 0 0 -1)
Since A=At, the general theory (almost all of which I
didn't verify!) says:
- All eigenvalues of A are real.
- Eigenvalues corresponding to distinct eigenvectors are orthogonal.
- Rn has a basis of eigenvectors of A.
The Maple command charpoly applied to A gives this
result:  5-3 5-3 3+2 3+2 . Then I can ask
Maple to factor this polynomial, resulting in . Then I can ask
Maple to factor this polynomial, resulting in
 ( ( -1)( -1)( +1)( +1)( 2-2). Maple can be told to factor
this further, using square roots, but this was enough for me. I then
used the command eigenvects to get associated
eigenvectors. Here is the result: 2-2). Maple can be told to factor
this further, using square roots, but this was enough for me. I then
used the command eigenvects to get associated
eigenvectors. Here is the result:
| Eigenvalue | An associated eigenvector |
|---|
| 0 | (0,1,0,1,0) |
| 1 | (0,0,1,0,0) |
| -1 | (0,0,0,0,1) |
| sqrt(2) | (sqrt(2),-1,0,1,0) |
| -sqrt(2) | (-sqrt(2),-1,0,1,0) |
You can check (as I did, first by myself before class, and then
quickly in class) that the list of associated eigenvectors are
orthogonal.
Now I would like to create a matrix which diagonalizes A. We can
normalize the eigenvectors and then create an orthogonal
matrix. This means get eigenvectors with length=1, and get a matrix C
so that C-1=Ct.
| Eigenvalue | Associated normalized
eigenvector |
|---|
| 0 | (0,1/sqrt(2),0,1/sqrt(2),0) |
| 1 | (0,0,1,0,0) |
| -1 | (0,0,0,0,1) |
| sqrt(2) | (sqrt(2)/2,-1/2,0,1/2,0) |
| -sqrt(2) | (-sqrt(2)/2,-1/2,0,1/2,0) |
We must write the normalized eigenvectors as column vectors to create
the matrix C:
( 0 0 0 sqrt(2)/2 -sqrt(2)/2)
(1/sqrt(2) 0 0 -1/2 -1/2 )
( 0 1 0 0 0 )
(1/sqrt(2) 0 0 1/2 1/2 )
( 0 0 1 0 0 )
then one can check that C-1=Ct and
C-1AC=D, where D is a diagonal matrix, with diagonal
entries in the same order as the corresponding eigenvectors of C:
(0 0 0 0 0 )
(0 1 0 0 0 )
(0 0 -1 0 0 )
(0 0 0 sqrt(2) 0 )
(0 0 0 0 -sqrt(2))
But this is all "review", things we've done before. I want to think
about a slightly different problem, a problem in a context for which
most people have little intuition (just means they haven't computed
enough examples!).
Closest point or best approximation
 Suppose we choose three of the eigenvectors of A, say
v1=(0,1/sqrt(2),0,1/sqrt(2),0) and
v2=(0,0,0,0,1) and
v3=(-sqrt(2)/2,-1/2,0,1/2,0). Let's call S the collection
of all linear combinations of v1 and v2 and
v3. That is, S is all vectors in R5 which can be
written as av1+bv2+cv3. Remember that
the vectors are normalized eigenvectors of a symmetric matrix, so each
of them has length 1 and they are mutually perpendicular. They are
linearly independent. Therefore S is a 3-dimensional subspace of
R5. Now suppose p=(2,3,4,-1,-7) is some "random" point of
R5. What is the closest point in S to p? That is, I would
like to find the best approximation, q, in S to p. Our
criterion for goodness is distance, and closer is better. Can we find
q in S so that the distance from q to p is smallest? We're considering
distance from a point in R5 to a 3-dimensional subspace.
Such problems may be difficult in general. Here, though, I would like
to convince you that the problem is very easy.
Suppose we choose three of the eigenvectors of A, say
v1=(0,1/sqrt(2),0,1/sqrt(2),0) and
v2=(0,0,0,0,1) and
v3=(-sqrt(2)/2,-1/2,0,1/2,0). Let's call S the collection
of all linear combinations of v1 and v2 and
v3. That is, S is all vectors in R5 which can be
written as av1+bv2+cv3. Remember that
the vectors are normalized eigenvectors of a symmetric matrix, so each
of them has length 1 and they are mutually perpendicular. They are
linearly independent. Therefore S is a 3-dimensional subspace of
R5. Now suppose p=(2,3,4,-1,-7) is some "random" point of
R5. What is the closest point in S to p? That is, I would
like to find the best approximation, q, in S to p. Our
criterion for goodness is distance, and closer is better. Can we find
q in S so that the distance from q to p is smallest? We're considering
distance from a point in R5 to a 3-dimensional subspace.
Such problems may be difficult in general. Here, though, I would like
to convince you that the problem is very easy.
Let's think about the distance from p to q. First, there's a square
root in the formula. Well, if we want to minimize something, and that
something is non-negative, we could also minimize its square. So we'll
be happy to find the minimum of the distance from p to q squared. The
distance is computed by taking the square root of a dot product, so we
need to minimize (q-p)·(q-p). Since
q=av1+bv2+cv3 we have to consider the
function
([av1+bv2+cv3]-p)·([av1+bv2+cv3]-p).
In this algebraic mess, v1 and v2 and v3
and p are fixed, and a and b and c are varying. So this is some
complicated function of three variables. I think I called it
F(a,b,c).
Dot product has some nice properties, like (av)·w=v·(aw)=a(v·w) if
v and w are vectors and a is a scalar, and v·w=w·v and
v·(wi+w2=(v·wi)+(v·w2).
So now I can take the formula for F(a,b,c) and use these
properties. Therefore F(a,b,c) is:
a2v1·v1+abv1·v2+acv1·v2+bav2·v1+b2v2·v2+bcv2·v3+cav3·v1+cbv3·v2+c2v3·v3
-av1·p-bv2·p-cv3·p-ap·v1-bp·v2-cp·v3
-p·p.
There are so many many terms. But ... but ... but: the vj's
are orthonormal. So dot products between them are either 0 or
1. The first row above simplifies a great deal. And dot product is
commutative, so the second row collapses a lot. The formula becomes:
F(a,b,c)=a2+b2+c2-2a v1·p-2b v2·p-2c v3·p-p·p.
That is quite a simplification. F(a,b,c) doesn't appear
quite as menacing any more. In fact, because of the algebraic
structure, I hope you can see that whenever any of the variables a or
b or c gets really large, the value of F(a,b,c) will
get large also, since the quadratic terms will eventually dominate any
linear term. We can find the minimum (candidates for the minimum,
maybe) by taking partial derivatives of F(a,b,c) and
setting them equal to 0. Here we go:
The partial derivative with respect to a is 2a-2v1·p, and
this is 0 only when a=v1·p.
The partial derivative with respect to b is 2b-2v2·p, and
this is 0 only when b=v2·p.
The partial derivative with respect to c is 2a-2v3·p, and
this is 0 only when c=v3·p.
We have solved the problem. The closest point, and the best
approximation in S, to p is
q=(v1·p)v1+(v2·p)v2+(v3·p)v3.
The dot products are very easy to compute. Notice, though, that this
problem was made easy exactly by the orthonormal nature of the
original collection of vectors v1 and v2 and
v3.
Do the same thing
 Now I would like to describe something similar but in a very different
setting. Again, this is likely to be unfamiliar territory, and please
realize that the similarities I'll show took more than a century to
recognize. Suppose f(x) is a function defined on an interval [a,b],
and we want to approximate this function by another function,
g(x). There could be several reasons for this. Maybe g(x) is easier
to compute. Maybe g(x) is easier to analyze theoretically. Maybe f(x)
might be "real-world" data, and it might be "noisy" and we might want
to clean up the noise. So there could be many reasons. I would like
the "closest" g(x) or the best approximation. Of course, I need to
specify how we will test our goodness of appproximation. I'd like one
number which could specify closeness. The integral
of f(x)-g(x) is not used very much, because (look at the picture) the
positive area (f above g) could easily cancel with the negative area
(f below g) and give a deceptively small result for
"closeness". What's another candidate? One is
Now I would like to describe something similar but in a very different
setting. Again, this is likely to be unfamiliar territory, and please
realize that the similarities I'll show took more than a century to
recognize. Suppose f(x) is a function defined on an interval [a,b],
and we want to approximate this function by another function,
g(x). There could be several reasons for this. Maybe g(x) is easier
to compute. Maybe g(x) is easier to analyze theoretically. Maybe f(x)
might be "real-world" data, and it might be "noisy" and we might want
to clean up the noise. So there could be many reasons. I would like
the "closest" g(x) or the best approximation. Of course, I need to
specify how we will test our goodness of appproximation. I'd like one
number which could specify closeness. The integral
of f(x)-g(x) is not used very much, because (look at the picture) the
positive area (f above g) could easily cancel with the negative area
(f below g) and give a deceptively small result for
"closeness". What's another candidate? One is
 ab|f(x)-g(x)| dx. Here there won't
be cancellation because of the absolute value. But absolute value has
a corner (o.k.: it is not differentiable) and people perhaps don't
like to use it for that reason. Instead, what is frequently
used is something like ab|f(x)-g(x)| dx. Here there won't
be cancellation because of the absolute value. But absolute value has
a corner (o.k.: it is not differentiable) and people perhaps don't
like to use it for that reason. Instead, what is frequently
used is something like
 ab(f(x)-g(x))2 dx.
Sometimes this is divided by b-a, and it maybe is called the mean
square error. This is a good definition of error, and leads to
some really neat computation. ab(f(x)-g(x))2 dx.
Sometimes this is divided by b-a, and it maybe is called the mean
square error. This is a good definition of error, and leads to
some really neat computation.
The textbook has formulas for more general intervals, but I think I
will use the interval [-Pi,Pi]. The analog of inner product is this:
take two functions f(x) and g(x) and compute
 -PiPif(x)g(x) dx. The most commonly
used analogs of orthonormal vectors are sines and cosines. -PiPif(x)g(x) dx. The most commonly
used analogs of orthonormal vectors are sines and cosines.
Sines and cosines and 0's and 1's
I tried to examine the values of various integrals. For example, what
is  -PiPisin(x)cos(2x) dx? I used only
ideas ab out even and odd functions. A function is even if
f(-x)=f(x). So cos(2x) is even. A function is odd if
f(-x)=-f(x). Here sin(x) is certainly odd. And [-Pi,Pi] is a balanced
interval, as much negative as positive. It is easy to forget the
following fact: the integral of an odd function over such an interval
([-Pi,Pi]) is 0. The product of an odd function and an even function
is odd, so the integral of sin(x)cos(2x) is 0: these functions are
orthogonal. I also tried to use pictures to convince people of this.
An example -PiPisin(x)cos(2x) dx? I used only
ideas ab out even and odd functions. A function is even if
f(-x)=f(x). So cos(2x) is even. A function is odd if
f(-x)=-f(x). Here sin(x) is certainly odd. And [-Pi,Pi] is a balanced
interval, as much negative as positive. It is easy to forget the
following fact: the integral of an odd function over such an interval
([-Pi,Pi]) is 0. The product of an odd function and an even function
is odd, so the integral of sin(x)cos(2x) is 0: these functions are
orthogonal. I also tried to use pictures to convince people of this.
An example
I gave an example which I will have to go over again on Tuesday. The
example was f(x)=Pi2-x2 on the interval
[-Pi,Pi].
Please hand in 8.2: 1,7 8.3:
1 at the next class meeting. Please study for the exam. You may also want to read
the beginning of chapter 13 on Fourier series.
|
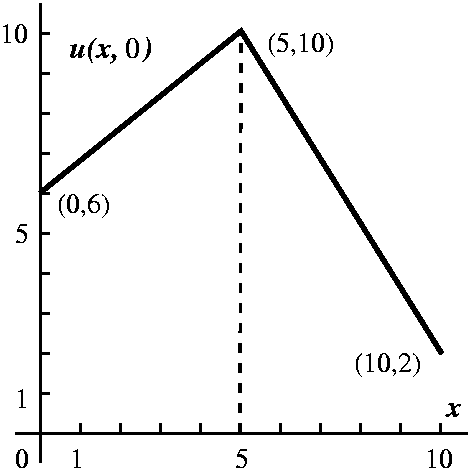 I will begin by asking part 1 of the QotD. The indicated heat
distribution is given initially, with boundary conditions u(0,t)=6 and
u(10,t)=2. Sketch the limit of u(x,t) as t-->infinity.
I will begin by asking part 1 of the QotD. The indicated heat
distribution is given initially, with boundary conditions u(0,t)=6 and
u(10,t)=2. Sketch the limit of u(x,t) as t-->infinity.
 I tried to "derive" the one-dimensional heat equation, also known as
the diffusion equation. You should realize that the heat equation is
also used to model a very wide variety of phenomena, such as drugs in
the bloodstream diffusing in the body or gossip (!) or spread of
disease in epidemics or ... The text discusses the temperature of a
thin homogeneous straight rod, whose long side is insulated (no heat
flow through that allowed) but heat can escape (or enter) through the
ends.
I tried to "derive" the one-dimensional heat equation, also known as
the diffusion equation. You should realize that the heat equation is
also used to model a very wide variety of phenomena, such as drugs in
the bloodstream diffusing in the body or gossip (!) or spread of
disease in epidemics or ... The text discusses the temperature of a
thin homogeneous straight rod, whose long side is insulated (no heat
flow through that allowed) but heat can escape (or enter) through the
ends.
 The spring, a one-dimensional system
The spring, a one-dimensional system Looking at energy
Looking at energy
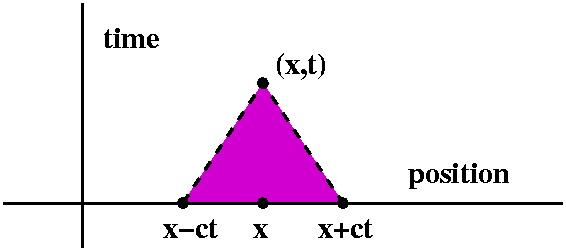 I would like to know
about y(x,t) and what part of the initial data influence
y(x,t). Certainly f's values at x+/-ct influence y(x,t) (look at the
formula above!) and g's values in the interval [x-ct,x+ct] influence
y(x,t). Mr. Tahir bravely came to the
board and completed a diagram which looks much like what is draw on
the left. The dotted lines have slopes +/-(1/c). (I got this wrong in
class!) So the influence of the initial conditions is as
shown.
I would like to know
about y(x,t) and what part of the initial data influence
y(x,t). Certainly f's values at x+/-ct influence y(x,t) (look at the
formula above!) and g's values in the interval [x-ct,x+ct] influence
y(x,t). Mr. Tahir bravely came to the
board and completed a diagram which looks much like what is draw on
the left. The dotted lines have slopes +/-(1/c). (I got this wrong in
class!) So the influence of the initial conditions is as
shown.
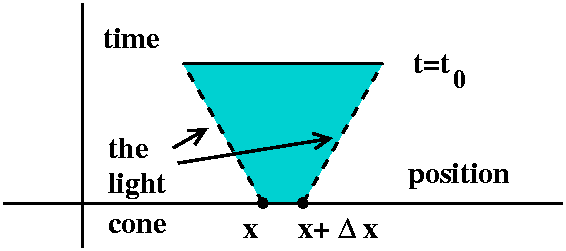 Here is yet another way to show what's going on. I could imagine a
short interval on the time=0 line, say from x to x+(delta)x (as usual,
(delta)x is supposed to be small). I could imagine changing f or g or
both on that interval, wiggling these initial conditions. Then what
parts of the string could be affected at a later time,
t=t0? Well, if you think about it and look at the formula,
the only parts could be in the upward part of the trapezoid
sketched. The wave equation models phenomena which have a finite
propagation speed (here the speed is c). Such phenomena include sound
and light. The slanted edges of the trapezoid sketched are usually
called the light cone and it represents the spreading the
maximum speed that the model allows. This name reflects the physical
theory that light travels at the maximum universal speed, and any
other "signal" travels more slowly. I remark that Mr. Woodrow courageously drew a picture
similar to this on the board.
Here is yet another way to show what's going on. I could imagine a
short interval on the time=0 line, say from x to x+(delta)x (as usual,
(delta)x is supposed to be small). I could imagine changing f or g or
both on that interval, wiggling these initial conditions. Then what
parts of the string could be affected at a later time,
t=t0? Well, if you think about it and look at the formula,
the only parts could be in the upward part of the trapezoid
sketched. The wave equation models phenomena which have a finite
propagation speed (here the speed is c). Such phenomena include sound
and light. The slanted edges of the trapezoid sketched are usually
called the light cone and it represents the spreading the
maximum speed that the model allows. This name reflects the physical
theory that light travels at the maximum universal speed, and any
other "signal" travels more slowly. I remark that Mr. Woodrow courageously drew a picture
similar to this on the board.

 Setting up a boundary value problem
Setting up a boundary value problem My first example analyzed the QotD from the previous regular class
meeting. So f(x) is 0 for x<0 and is 1 for x>=0. In everything I
am doing today, I will only care about the interval [-Pi,Pi]. If
you run across a situation where you "care" about the interval
[-5,11], say, probably you should first take x and change it into
y=(2Pi/16)x-(3Pi/8). Then as x runs from -5 to 11, y would go from -Pi
to Pi. Anyway, I used the following Maple commands to create
the pictures I will show and also the resulting computations.
My first example analyzed the QotD from the previous regular class
meeting. So f(x) is 0 for x<0 and is 1 for x>=0. In everything I
am doing today, I will only care about the interval [-Pi,Pi]. If
you run across a situation where you "care" about the interval
[-5,11], say, probably you should first take x and change it into
y=(2Pi/16)x-(3Pi/8). Then as x runs from -5 to 11, y would go from -Pi
to Pi. Anyway, I used the following Maple commands to create
the pictures I will show and also the resulting computations.




 Observation 3
Observation 3 Observation 4
Observation 4 The sum of the whole Fourier series
The sum of the whole Fourier series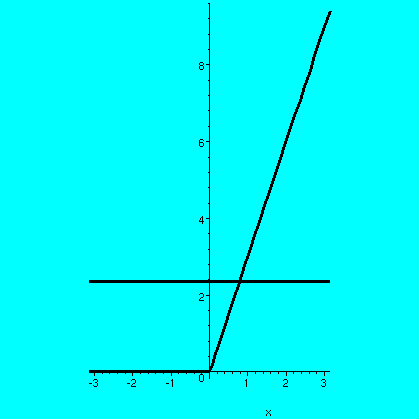
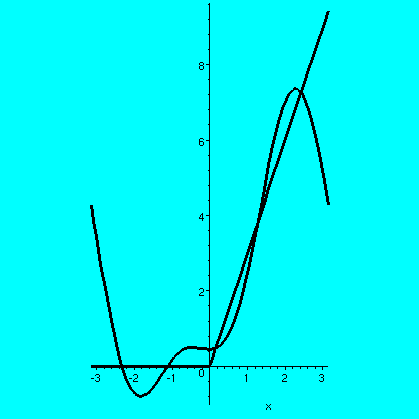
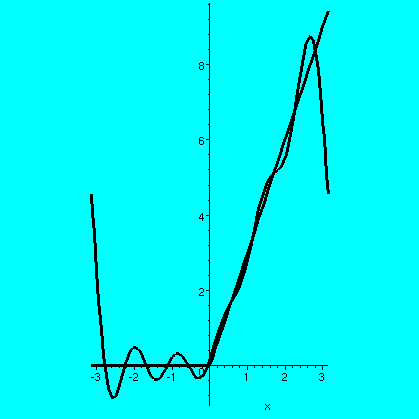


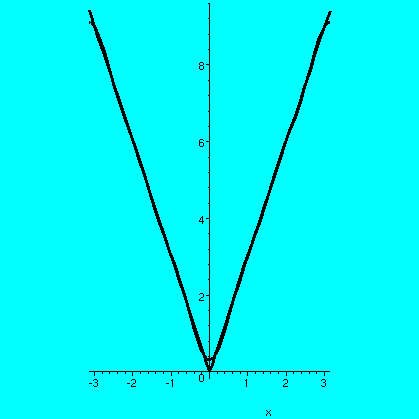
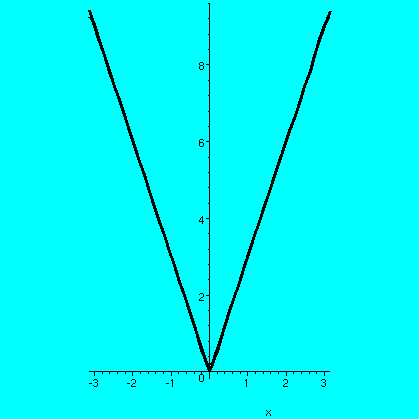
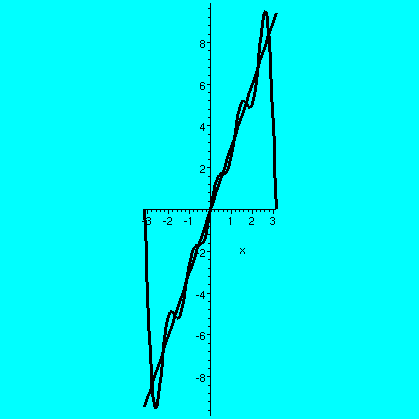
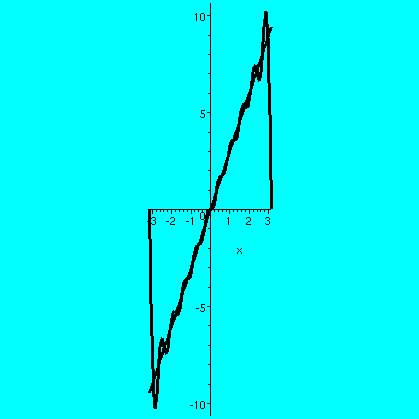





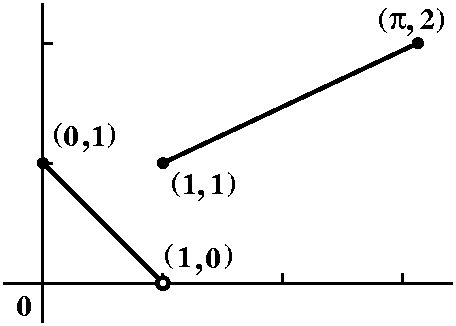
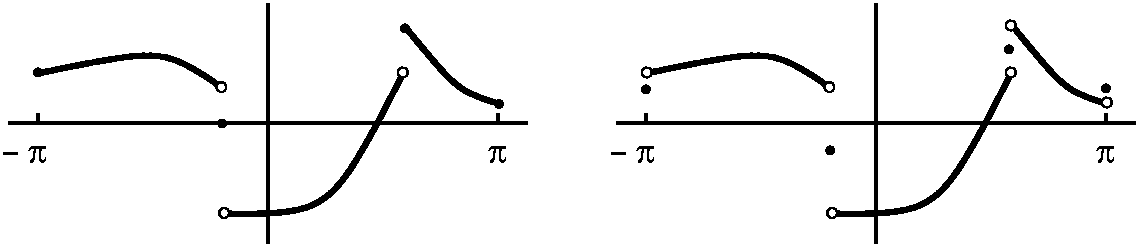



 Suppose we choose three of the eigenvectors of A, say
v1=(0,1/sqrt(2),0,1/sqrt(2),0) and
v2=(0,0,0,0,1) and
v3=(-sqrt(2)/2,-1/2,0,1/2,0). Let's call S the collection
of all linear combinations of v1 and v2 and
v3. That is, S is all vectors in R5 which can be
written as av1+bv2+cv3. Remember that
the vectors are normalized eigenvectors of a symmetric matrix, so each
of them has length 1 and they are mutually perpendicular. They are
linearly independent. Therefore S is a 3-dimensional subspace of
R5. Now suppose p=(2,3,4,-1,-7) is some "random" point of
R5. What is the closest point in S to p? That is, I would
like to find the best approximation, q, in S to p. Our
criterion for goodness is distance, and closer is better. Can we find
q in S so that the distance from q to p is smallest? We're considering
distance from a point in R5 to a 3-dimensional subspace.
Such problems may be difficult in general. Here, though, I would like
to convince you that the problem is very easy.
Suppose we choose three of the eigenvectors of A, say
v1=(0,1/sqrt(2),0,1/sqrt(2),0) and
v2=(0,0,0,0,1) and
v3=(-sqrt(2)/2,-1/2,0,1/2,0). Let's call S the collection
of all linear combinations of v1 and v2 and
v3. That is, S is all vectors in R5 which can be
written as av1+bv2+cv3. Remember that
the vectors are normalized eigenvectors of a symmetric matrix, so each
of them has length 1 and they are mutually perpendicular. They are
linearly independent. Therefore S is a 3-dimensional subspace of
R5. Now suppose p=(2,3,4,-1,-7) is some "random" point of
R5. What is the closest point in S to p? That is, I would
like to find the best approximation, q, in S to p. Our
criterion for goodness is distance, and closer is better. Can we find
q in S so that the distance from q to p is smallest? We're considering
distance from a point in R5 to a 3-dimensional subspace.
Such problems may be difficult in general. Here, though, I would like
to convince you that the problem is very easy.
 Now I would like to describe something similar but in a very different
setting. Again, this is likely to be unfamiliar territory, and please
realize that the similarities I'll show took more than a century to
recognize. Suppose f(x) is a function defined on an interval [a,b],
and we want to approximate this function by another function,
g(x). There could be several reasons for this. Maybe g(x) is easier
to compute. Maybe g(x) is easier to analyze theoretically. Maybe f(x)
might be "real-world" data, and it might be "noisy" and we might want
to clean up the noise. So there could be many reasons. I would like
the "closest" g(x) or the best approximation. Of course, I need to
specify how we will test our goodness of appproximation. I'd like one
number which could specify closeness. The integral
of f(x)-g(x) is not used very much, because (look at the picture) the
positive area (f above g) could easily cancel with the negative area
(f below g) and give a deceptively small result for
"closeness". What's another candidate? One is
Now I would like to describe something similar but in a very different
setting. Again, this is likely to be unfamiliar territory, and please
realize that the similarities I'll show took more than a century to
recognize. Suppose f(x) is a function defined on an interval [a,b],
and we want to approximate this function by another function,
g(x). There could be several reasons for this. Maybe g(x) is easier
to compute. Maybe g(x) is easier to analyze theoretically. Maybe f(x)
might be "real-world" data, and it might be "noisy" and we might want
to clean up the noise. So there could be many reasons. I would like
the "closest" g(x) or the best approximation. Of course, I need to
specify how we will test our goodness of appproximation. I'd like one
number which could specify closeness. The integral
of f(x)-g(x) is not used very much, because (look at the picture) the
positive area (f above g) could easily cancel with the negative area
(f below g) and give a deceptively small result for
"closeness". What's another candidate? One is