Math 291 diary, fall 2006
In reverse order: the most recent material is first.
More volunteers
These students have volunteered (well, they are in 291, darn it!) to answer questions next time about the
251 assigned homework problems in these sections:
| Textbook section | Names |
|---|
| 12.4 | Thomas Ehrlich
Evan Fitzgerald |
| 12.5 | Jacelyn Gerges
Andrew Harrison |
| 13.1, 13.2 | Pawan Harvu
David Hsiung |
| 13.3 | Gibson Kim
Kevin Kobilinski |
| 13.4 | Cosmo Kwok |
Monday, September 25
Brief repetition of PLANE curves
Motion in a straight line
The bug doesn't feel the sides.
Motion in a circle
The moving bug always feels a transverse force.
Differentiation and three kinds of multiplication for vector-valued
functions
Scalar multiplication
Dot product
Cross product
An ongoing example: the right circular helix
Space curves: the beginning
Tangent vector, unit tangent vector, speed
Trick #1: defining the principal normal
The definition of curvature
The binormal
The Frenet frame
How the binormal changes
The definition of torsion
Bending out of a plane
The derivative of the normal
The Frenet-Serret formulas
Check everything with the helix!
Wednesday, September 20
The dot product of a vector with a cross product
The volume of a parellelopiped
The vector triple product equals a determinant equals a volume
Curves in space and in the plane
A differentiable curve has differentiable coordinates
The derivative is velocity
Length is speed
Direction is tangent to the curve
Tangent vector and tangent line
Distance=rate·time as an approximation
Definition of distance traveled
And the length of a curve
And the intractibility of computation
How a plane curve bends
What's more; what's less
The bewildering effect of speed on "perceived" bending
Test cases
circles, line, parabola
The rate of change of angle
The rate of change of angle with respect to arc length
The formula defining curvature
Monday, September 18
Recursive definition of determinant
Too big! There must be other ways ...
More vector algebra
Is a point on a plane determined by three given points?
Description of a plane with a given point and a given normal vector
Description of a line through a given point in a given direction
Distance from a point to a plane
Other distances
Thursday, September 14
Word of the day
remiss
careless of duty; lax, negligent
Homework problems done, quite well, by terrific students!
Geometry, chirality, and prejudice
Flatland
Cross product
A multiplication table
A formula for the cross product
Deception? Lie? Well, only inferentially ....
Wednesday, September 13
Word of the day
ineluctable
Against which it is useless to struggle.
"Applications"
I stated the Cauchy-Schwarz inequality, the triangle inequality, and a
sort of reverse triangle inequality.
Me, dog, lamp post
More generally
Now with angles (a robot arm?)
Orthogonality
Resolving into parallel and perpendicular components
Volunteers
These students have volunteered (well, they are in 291, darn it!) to answer questions next time about the
251 assigned homework problems in these sections:
| Textbook section | Names |
|---|
| 12.1 | Valentyn Boginskey
Joshua Bryan |
| 12.2 | Albert Chen
Wei Chen |
| 12.3 | Alexander Crowell
Christophe Doe |
I thank them in advance.
Monday, September 11
Abstract math
Vector space
{Inner|scalr|dot} product
{Length|norm|magnitude}
A function
A quadratic function
The Cauchy-Schwarz inequality
The triangle inequality
Examples (at last!)
From quantum mechanics.
R3
Vectors are directed line segments. Vectors are forces.
Why?
Components of vectors
Dot product
Law of cosines
(messed up in class!)
Wednesday, September 6
The instructor tried to waste time. He made bravura (arrogant?)
capsule summaries of calc 1 and calc 2, and then tried to indicate how
things might be different in Rn for n>1.
Word of the day
bravura
Showy; ostentatious.
Calc 1
- The definition of derivative
- As a limit
- As another function
- Computing the darn thing (algebraic algorithms, the chain rule)
- The Mean Value Theorem
- Connection between {in|de}creasing and sign of the derivative
- Detecting extreme values
- Concavity
- Definition of the definite integral
- As a limit of Riemann sums (a very strange kind of limit!)
- Elementary properties: linearity in functions, positivity,
additivity over adjoining intervals
- The Fundamental Theorem of Calculus
- Computing definite integrals via antiderivatives
- Definite integral as accumulated change
- Simple numerical approximation schemes for the definite integral
- Initial value problems for simple ODE's.
Calc 2
Lots and lots of detailed schemes for
antidifferentiation. Wow!
More intricacies about sequences and
series. More wow!!
This stuff is all worthwhile, but everyone
would agree that the highlights of the course are:
- Integration by parts has wonderful,
perhaps amazing, consequences. Certainly it allows computation of
antiderivatives in unexpected ways. This is then applied to show that
an arbitrary "signal" has less and less high frequency vibrations in
it (Fourier series or integrals). Also integration by parts is
important in the study of what are called boundary value
problems, a different way of studying naturally occurring problems
in mathematical physics which use differential equations and specify
information at both an initial point and an endpoint.
- Taylor's Theorem which allows a sufficiently differentiable
function to be approximated by a polynomial, with an error that can be
described in several interesting ways, is also terrific. Polynomials can be
evaluated very quickly ("Horner's
method") and so any result which allows a polynomial to be used
instead of a more "nasty" function is very useful.
Several variable calculus
Several here means "more than one".
- Continuity and differentiability The actual definitions
have to be done more carefully than one might suspect. A century or so
of experience has enabled mathematicians to write the
definitions so that they look the same in Rn as in
r1. This tendency towards compact writing is
sometimes misleadingly terse. In this case, the definitions are made
in certain ways which don't really show that phenomena occur which
don't happen in one variable. Sigh. So part of the job is to take
apart the definitions and display the rather weird examples.
- Integration in one variable is defined (in a calc 1 course,
anyway!) by chopping up an interval into small subintervals. But in
even two variables, if a function is defined over a region in the
plane, the "chopping" can be done in many different ways, using pieces
that aren't necessarily congruent (equal subintervals) or even similar
(always two intervals are similar, but two little chunks of the plane
are not). How can such a definition be made? And looking at different
chopping strategies can be important in specific examples, to take
advantage of the symmetries in physics or geometry.
-
Relating the integral over a region to an integral on the
boundary
In the one-variable case, there seems to be only one
FTC. Things are quite a bit more complicated in several variables. In
Math 251, for example, maybe three (really, three) different analogues
of FTC are given towards the end of the semester. Things get
complicated. Certainly the theory is complicated But as well, the
phenomena which are being described are complicated. For example, I
cited the problem of trying to understand what happens to the interior
temperature of a thin metal plate which is subject to some boundary
heat distribution. In order to understand the isothermals in the
plate, and the heat flow in the plate, we need some method of
transferring information from the boundary to the inside of the
plate. And that is what the higher dimensional versions of FTC will
do. (Yeah, yeah, the plate also expands, but, y'know, for steel the
coefficient of thermal expansion is about
1.24·10-5cm per degree C, maybe not too large and
not the first thing to worry about.)
Distance in R1
We looked at distance in the real line. The distance between a and b
is defined by
dist(a,b)=|a-b|
This is a great definition. Notice that:
- dist(a,b) is always non-negative, and is equal to 0
exactly when a=b.
- dist(a,b)=dist(b,a): this is called
symmetry.
Then we had a discussion of how dist(a,b) and dist(b,c)
and dist(b,c) should be related. We considered some
examples. If we want an equality relating these
distances, then the result sort of depends on whether one number is
between the other two. But if we want a result that is
always true, then we need an inequality. Inequalities are good. Most data
in the real world is an approximation, accurate measurements are very
difficult ... inequalities better describe what really is.
- For any points a and b and c in R1,
dist(a,b)+dist(b,c)≥dist(a,c).
Those three "rules" for distance seem nice.
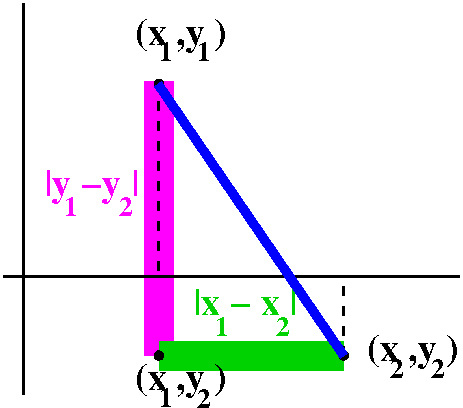 Distance in R2
Distance in R2
Well, I went through the usual diagram to try to motivate the
algebraic definition of distance in R2. Look, please, at
the diagram to the right. In the plane, points correspond to ordered
pairs of numbers. So a point p might correspond to an ordered pair,
(x1,y1), and q might correspond to (x2,y2). Then the point (x1,y2) is
the vertex of a right triangle whose hypotenuse is a line segment
connecting p and q. One leg of the right triangle is on a line where
all the first coordinates are x1, and the length of that leg is given
by the one dimensional formula, |y1-y2|. The other leg is on the line
where all the second coordinates are y2, and the length of that leg is
|x1-x2|. Then by Pythagoras, the hypotenuse has length
sqrt(|x1-x2|2+|y1-y2|2). And usually the
absolute values are discarded since we are squaring the
quantities. Therefore we officially define:
dist(p,q)=sqrt((x1-x2)2+(y1-y2)2) if p
has coordinates (x1,y1) and q has coordinates (x2,y2).
Are rules 1 and 2 and 3 above still valid? Well, 1 is true because,
first, the square root is always non-negative. And if the square root
defining dist is equal to zero, then since the terms inside it
are also non-negative, the only way the square root can be zero is if
both x1-x2=0 and y1-y2=0. The coordinates must be the same, so p and q
are the same points.
Rule 2, symmetry, is also true and equally simple to verify, since
squares of W and -W are the same. But rule 3 is a different sort of
thing.
Rule 3 for distance in R2
Well, if p
has coordinates (x1,y1) and q has coordinates (x2,y2) and r has
coordinates (x3,y3), then I want to know if
dist(p,q)+dist(q,r) is always ≥ dist(p,r).
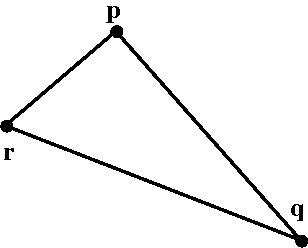
The geometric point of view
This is what I personally prefer, and this is what a student in the
class saw almost immediately. The length of one side of a triangle is
less than or equal to the sum of the lengths of the other two
sides. And that is exactly what Rule 3 states. So rule 3 is
clearly true!
The algebraic point of view
Maybe other people don't necessarily accept the picture, and don't
"see" the result. Let us try to verify algebraically that
sqrt((x1-x2)2+(y1-y2)2)+sqrt((x2-x3)2+(y2-y3)2)
if p≥sqrt((x1-x3)2+(y1-y3)2)>
I don't think this is totally, immediately "clear". In fact, this
inequality, if you want to worry, is a statement about six
variables. Six! I asked if there was any way to transform it into
another algebraic statement whose correctness we would accept
immediately. We began working. We squared, we rearranged ... it was a
mess. Then I suggested that maybe we should try to rewrite things a
bit:
Change x1-x2 to A
Change y1-y2 to B
Change x2-x3 to C
Change x2-x3 to A
Then x1-x3 will become A+C
and y1-y3 will become B+D.
The inequality we would like to verify now is:
sqrt(A2+B2)+sqrt(C2+D2)≥sqrt((A+C)2+(B+D)2).
At least we have only four variables now, rather than six. Now square:
A2+B2+2sqrt(A2+B2)sqrt(C2+D2)+C2+D2≥(A+C)2+(B+D)2
This step is reversible because we know that the inequality we began
with has only non-negative terms, and square roots and squaring will
preserve such inequalities. Now "expand":
(A+C)2+(B+D)2 becomes A2+2AC+C2+B2+2BD+D2.
We want to verify that:
A2+B2+2sqrt(A2+B2)sqrt(C2+D2)+C2+D2≥A2+2AC+C2+B2+2BD+D2
"Cancel" (subtract) everything that's equal on both sides. The result
is:
2sqrt(A2+B2)sqrt(C2+D2)≥2AC+2BD
Divide by 2:
sqrt(A2+B2)sqrt(C2+D2)≥AC+BD
And let's square again (amazing!):
(A2+B2)(C2+D2)≥(AC+BD)2
But (AC+BD)2=(AC)2+2(AC)(BD)+(BD)2
and
(A2+B2)(C2+D2)=A2C2+A2D2+B2C2+B2D2
Therefore the inequality we want is:
A2C2+A2D2+B2C2+B2D2≥(AC)2+2(AC)(BD)+(BD)2
Let's cancel stuff again. The result is:
A2D2+B2D2≥2(AC)(BD)
Well, uhhhh ... this is:
A2D2-2(AC)(BD)+B2D2≥0
and this is the same as:
(AC-BD)2≥0 and this is true
because squares are non-negative. Sigh.
What is going on?
Any student who followed this is either crazy or brilliant or
both. We have verified that the triangle inequality (rule 3 for
distance) is true for the distance formula in R2. These
inequalities are all quite famous, actually. I just took a rather "low
tech" way to verify them. The inequality
sqrt(A2+B2)sqrt(C2+D2)≥AC+BD
which we also verified in passing has its own name. It is called the
Cauchy-Schwarz inequality. It is important.
The approach I just used is what could have been done maybe two or
three hundred years ago. I will try to show you what the heck is going
on in a more modern fashion Monday.
Read the text!
Please read the first few sections of chapter 12, as on the Math 251
syllabus.
Maintained by
greenfie@math.rutgers.edu and last modified 9/7/2006.

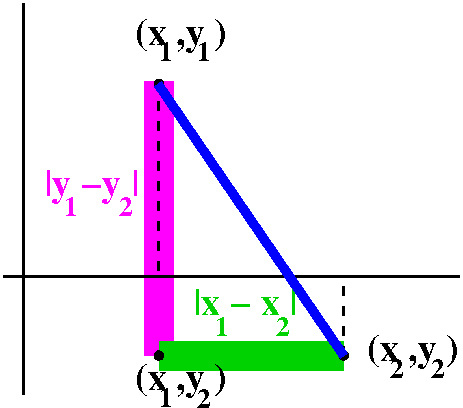 Distance in R2
Distance in R2