Can cheetahs swim?

Yes, they are capable, but they usually need a good motivation to do it. Carnivore biologist Luke Hunter reported seeing two male cheetahs swim across a river to get to a female cheetah on the other side.

In fact, straightforward research (including observation of many domestic cats) shows that not many felines like to swim. But the redoubtable Ms. Bloom Leeds provided further information about the Turkish Van, a kind of cat which likes to swim. To the right is a picture taken from the web page swimmingcats.com.

1. ₀⁵5(sin(x))e^cos(x)dx.
   We tried u=cos(x). My philosophy, which is frequently successful when used on problems from calculus books, is to substitute for the most troublesome thing (MTT).
2. [cos(8sqrt(x))]/[5sqrt(x)] dx
   Here we try, as MTT, u=8sqrt(x). This works.
3. 5x(5x-7)¹¹dx
   MTT is probably 5x-7. So try u=5x-7. I contrasted this with the "direct solution" -- expanding the 11^th power of 5x-7. This is much easier.

We did some further substitution problems.

John Henry
The Maple program can compute some antiderivatives. We can, also. But we can compute sqrt(1+sqrt(1+sqrt(x))) dx, and Maple can't, not even the latest version. The substitution u=sqrt(1+sqrt(1+sqrt(x))) will do it. Then ((u²-1)²-1)²=x, so a connection between du and dx can easily be deduced. Etc.

Reminders about various review sessions and about the final exam were said. And we parted, students and instructor, for the last time ...

Diary entry in progress! More to come.

The final exam for sections 21, 22, and 23 of Math 135 will be given Thursday, May 5, 4-7 PM, in Hickman 138 on the Douglass campus. Please try to be there on time, or even a bit early. Bring a graphing calculator, your student ID, and be familiar with the Official formula sheet for the final exam.

The lecturer will meet again on Sunday, May 1, from 6 PM to 8 PM in Hickman 216 and will have students go to the board and do problems from previous final exams which are related to the second half of the course. Helpful comments will be offered. Last Sunday most of these problems related to the first half of the course were discussed.

Mr. Jin, the recitation instructor, will hold a review session from 6 to 8 PM on Tuesday, May 3, in RAB 001, the usual classroom. He will discuss some of the Official review problems for the final exam

Some WeBWorK problems
I did problems 3 and 7 and 9 in one version of WeBWorK.

#3
I think this was something like:
(8x⁵+7)/x³ dx.
One way to see the answer is to play with the integrand. Break up the fraction:
(8x⁵+7)/x³=[8x⁵/x³]+[7/x³]. Then each term can be simplified: 8x²+7x^-3. And now the antiderivative is easy: 8(1/3)x³+7(-1/2)x^-2+C.

#7
My version of this problem goes like this:
Find the Riemann sum associated with f(x)=2x²+3, n=3 and the partition x₀=0, x₁=3, x₂=4, x₃=6, of [0,6] when x_k^* is the right end-point of [x_k-1,x_k]
Partitions and Riemann sums are complicated objects. Here the interval is [0,6], and I think graphically. Here's the interval with the partition marked:
0------3--4----6.
First chunk: 0------3. Length of subinterval is 3-0=3. Sample point is 3. Therefore we get f(3)(3).
Second chunk: 3--4. Length of subinterval is 4-3=1. Sample point is 4. Therefore we get f(4)(1).
Third chunk: 4----6. Length of subinterval is 6-1=2. Sample point is 6. Therefore we get f(6)(2).
The total will be f(3)(3)+f(4)(1)+f(6)(2). Since f(x)=2x²+3, this total is f(3)(3)+f(4)(1)+f(6)(2)=21(3)+35(1)+75(2).

#9
Here I have f(x)=-(1/2)x²-7. WeBWorK asks for a formula for the Riemann sum, which is called R_n, which will approximate the definite integral of f(x) on the interval [0,3] when the interval is divided up into n equal pieces and the sample points are taken at the right-hand sides of the subintervals. Further advice is given: "You will need the summation formulas on page 287 of your textbook." We are also asked for the limiting behavior of R_n as n-->infinity (this should be the value of the definite integral). We worked on this.

The details of this problem are obnoxious. Start with the interval from 0 to 3, divided into n equal parts. Since the interval has length 3, the n equal parts will each have length 3/n. The partition "looks like" this:
0--3/n--2(3/n)--3(3/n)--4(3/n)--......--n(3/n)
The starting point is 0 and the end is n(3/n) which is 3. What about the "chunks" of the Riemann sum?
First chunk: 0------3/n. Length of subinterval is 3/n. Sample point is 3/n. Therefore we get f(3/n)(3/n).
Second chunk: 3/n--2(3/n). Length of subinterval is 3/n. Sample point is 2(3/n). Therefore we get f(2(3/n))(3/n).
Third chunk: 2(3/n)--3(3/n). Length of subinterval is 3/n. Sample point is 3(3/n). Therefore we get f(3(3/n))(3/n).
Etc.

Well, what I mean by this is we should add up f(i(3/n))(3/n) as i goes from 1 to n. I am using i because that is the variable of summation in the WeBWorK problem. The darn thing would look like this:
SIGMA_i=1ⁿf(i(3/n))(3/n)= SIGMA_i=1ⁿ[-(1/2)(3i/n)²-7](3/n).
This is the same as -[(27/2)/n³]SIGMA_i=1ⁿi² -7SIGMA_i=1ⁿ(3/n).
The summation formulas on page 287 can now be consulted. Sigh. For example, SIGMA_i=1ⁿi² is equal to [n(n+1)(2n+1)/6]. All those folks in China and India knew this. And SIGMA_i=1ⁿ(3/n)=3. So the SIGMA stuff gives a formula for R_n.

R_n=-[27n(n+1)(2n+1)]/[12n³]-21. Then using L'H or some other method (can you tell I am not much interested?) I can guess lim_n-->infinityR_n. It is -(54/12)-21. (The 108 and 12 come from the coefficient of n³ top and bottom.)
Confession Since I am writing this without anyone "looking over my shoulder" and checking, I admit that I made several mistakes in getting the formula for R_n and had to redo it a few times. This work is definitely easier to do the process in class, where people frequently catch my errors!

Same computation with FTC
₀³-(1/2)x²-7 dx=-(1/6)x³-7x|₀³=-(1/6)3³-21 (the values at x=0 are 0).

It turns out that -(54/12)-21 and -(1/6)3³-21 are both -51/2. The methods give the same answer.
Which way would you like to use?

Restating part of FTC
FTC stands for Fundamental Theorem of Calculus.
If F´(x)=f(x), then _a^bf(x) dx=F(b)-F(a), abbreviated F(x)|_a^b.
F(x) is called an indefinite integral or antiderivative or primitive of f(x).

Example of FTC and a mild logical point
So over on the cute little side blackboard, I wrote:
     ₀¹x²dx=(1/3)x³|₀¹=(1/3)1³-(1/3)0³=(1/3)
     ₀¹v²dv=(1/3)v³|₀¹=(1/3)1³-(1/3)0³=(1/3)
     ₀¹q²dq=(1/3)q³|₀¹=(1/3)1³-(1/3)0³=(1/3)
The point I wanted to make here is that the x and the q and v are all really irrelevant outside of the computations. The variables don't change the answer. Logically these are dummy or bound variables. They tell you what to do to what. Even a program like Maple needs to be told things. For example, you can consider the following dialogue (?) between Maple and me.

 
>int(x^2);
Error, (in int) wrong number (or type) of arguments

>int(x^2,x);
                   1
                   -x3
                   3

 
>int(a^3*b^5,x);
                   a3b5x

>int(a^3*b^5,b);
                   1
                   -a3b6
                   6

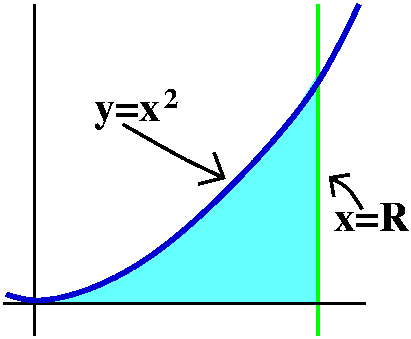
Silly FTC
Can we find a vertical line so that the region in the first quadrant bounded by the line, the x-axis, and the graph y=x² has area equal to 57?
Let's call the line x=R. This just means that a certain definite integral should be 57. So:
₀^Rx²dx=(1/3)x³|₀^R=(1/3)R³-(1/3)0³=(1/3)R³
and we can get this to be 57 by solving (1/3)R³=57, so that R=(3·57)^1/3.

Halving area vertically
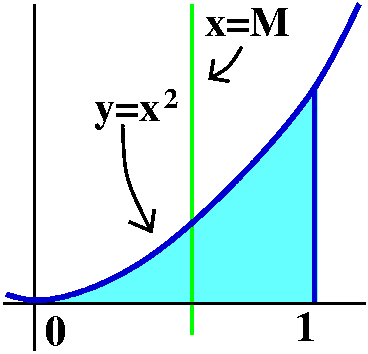Here is perhaps a slightly more interesting problem. Can we find the equation of a vertical line which will divide the region bounded by the x-axis, x=1, and y=x² into two equal parts?
Let me call the line x=M (for middle, I suppose). Since I know using the computations above that the area of the region bounded by the x-axis, x=1, and y=x² is 1/3, I need to find x=M so that the area to the left of the line is 1/6. That means I need ₀^Mx²dx=(1/3)x³|₀^M=(1/3)M³-(1/3)0³=(1/3)M³ to be 1/6. So (1/3)M³=1/6. Then M³=1/2, so finally M=(1/2)^1/3.
As I mentioned in class, I do not consider this problem of great significance, but what is impressive is that we can solve it so easily.

Halving area horizontally
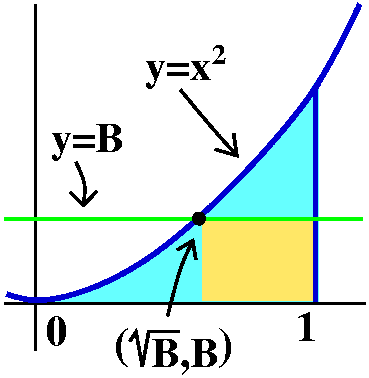This is more difficult. Can we find the equation of a horizontal line which will divide the region bounded by the x-axis, x=1, and y=x² into two equal parts?
I think I called the horizontal line y=B in class. We want to find B so that the area below y=B inside the region is 1/6, half of 1/3, as before. But the area below the line can be computed by dividing it into two pieces. The point where y=B interesects y=x² has B=x², so the point is (sqrt(B),B). The vertical line through that point combined with y=B cuts off a rectangle from the area below y=B. The rectangle has one side (the vertical side) with length equal to B. The horizontal side has length 1-sqrt(B). So the area of the rectangle is B(1-sqrt(B)). The other part of the region below y=B can be computed with an integral:
₀^sqrt(B)x²dx=(1/3)x³|₀^sqrt(B)=(1/3)(sqrt(B))³-(1/3)0³=(1/3)(sqrt(B))³.
The total area is therefore (1/3)(sqrt(B))³+B(1-sqrt(B)). The B wanted makes this equal to 1/6. Maybe we made a mistake. Maybe there is no such B. Well, if B=0, the formula's value is 0. If B=1, the formula's value is 1/3. I bet (Intermediate Value Theorem, since the formula looks continuous to me) that there is at least one B which makes the formula equal to 1/6.

So we can solve it!
I thought in class that I would have to use numerical or graphical methods to approximate a solution to the preceding equation. I was wrong. Look:
(1/3)B^3/2+B-B^3/2=1/6
-4B^3/2+3B-1=0
It turns out that this is -(2B^1/2-1)(2B-2B^1/2-1)=0 and the roots of this are B=1/4 from the first factor and B=(1/4)(1+sqrt(3))² from the second factor. This was not at all clear to me. Sigh. Maple, a computer program, factored this for me. The only root in our domain (between 0 and 1) is 1/4. So y=1/4 will split the region into two pieces of equal area.

Another form of the FTC
I remarked that we had verified a special case of the following result on Friday:
(d/dx)_a^xf(t) dt=f(x)
So if you want to differentiate a definite integral with a variable upper bound, you get back the function whose area (?) you are computing.
Example (d/dx)_a^xsqrt(e^t+cos(t)) dt=e^x+cos(x).
There are occasions when this result can be helpful. I don't think we'll see them in the short time remaining in the course.

Bird of the day

The Common Loon
Gavia Immer.

Exponential integrals
FTC tells me ₃⁴e^xdx=e^x|₃⁴=e⁴-e³.
Then FTC tells me ₃⁴5e^xdx=5e^x|₃⁴=5e⁴-5e³.
And I can try to use FTC on ₃⁴e^5xdx but first I need an antiderivative. What function has derivative equal to e^5x? If I try e^5x, the Chain Rule "spits out" an extra 5. I need to compensate for that, so I will guess (1/5)e^5x, and this is correct. You can check by differentiating that e^5x is the derivative of (1/5)e^5x. Now let's compute using FTC:
₃⁴e^5xdx =(1/5)e^5x|₃⁴=(1/5)e^5·4-(1/5)e^5·3.

More complicated: just "guess"
I think I asked for a really weird indefinite integral, but the weirdness was arranged carefully. Maybe it looked like:
(5x³+48)¹⁰⁰x²dx.
This is horrible, maybe, until you see some of the "structure" of the expression. There's a 100^th power. Maybe the antiderivative should have a 101^th power. But the Chain Rule implies ... well, there is an x² already there ... maybe we could somehow ...
If you continue dithering (dictionary: dither="hesitate; be indecisive") you won't get anywhere. But a good guess (not really a guess, an informed conjecture, let us say) leads to
(1/100)(1/5)(1/3)(5x³+48)¹⁰¹+C
Is this correct? I think so, but you can check it easily. Differentiation is easy but antidifferentiation is difficult. In this case, I hope when you check you will see first 100 then 5 then 3 get canceled by numbers excreted (?) by the Chain Rule.

The substitution method
The previous example should have convinced you that keeping track of various numbers can get to be difficult. The Substitution Method, a sort of Chain Rule in reverse, does help with all the numbers. It is basically a method of bookkeeping (an interesting word) applied to the constants which appear. Here is how people use it.

Start with
(5x³+48)¹⁰⁰x²dx.
If u=5x³+48 then du/dx=15x², and so (huh?) du=15x²dx, and (1/15)du=x²dx. Therefore:

From x-land to u-land
(5x³+48)¹⁰⁰x²dx is u¹⁰⁰(1/15) du.
The antiderivative of this is (1/15)(1/101)u¹⁰¹+C since I know how to find the antidervative of powers.

From u-land to x-land
Well since u=5x³+48, then (1/15)(1/101)u¹⁰¹+C becomes (1/15)(1/101)(5x³+48)¹⁰¹+C and you can check this is correct by differentiating. This is certainly the same answer we got by guessing. Most people prefer this method, since there are lots of mistakes which can be made by guessing.

HOMEWORK
Please study for the final exam. Do this by first working on the homework problems in the last sections we will cover. Please.

Some definite integrals I drew the graph shown to the right, and stated that this was a graph of y=f(x). I then asked for the following definite integrals: 13f(x) dx    24f(x) dx    35f(x) dx    46f(x) dx Since I "identified" pieces of the curve as rather simple shapes, probably the integrals can be computed.
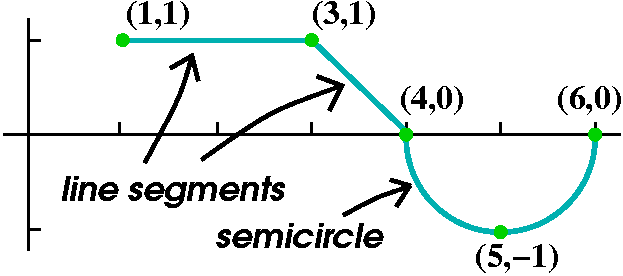
13f(x) dx Here the region is just a rectangle. The base is 2 units long, and the height is 1 unit, so that the area is 2. This is the value of the definite integral.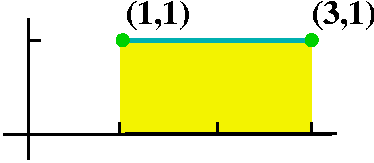
24f(x) dx Here the region is a square and a triangle joined on a side. The square is 1 by 1 unit and has area 1. The triangle, with base and height both 1, has area 1/2. Therefore the definite integral, in this case measuring the total area, has value 1.5.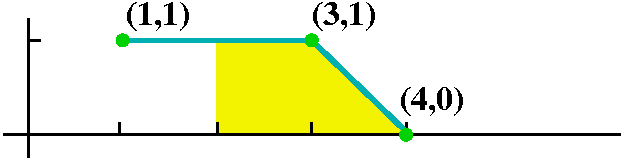
35f(x) dx The geometry is clear, but what the definite integral computes is sometimes not exactly what the geometry says. The Riemann sum definition of the definite integral makes area above the horizontal axis count positively and area below that axis, negatively. The picture below shows the signed area which a definite integral would compute. 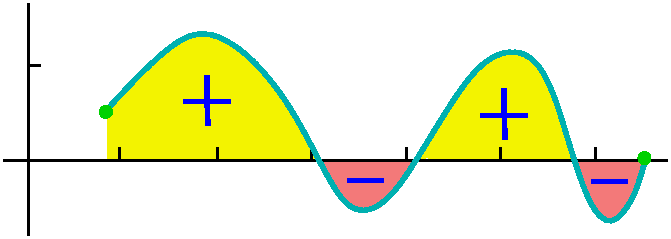The sign of the definite integral in applications can have meaning which is central to the computation: are those dollar amounts profit or loss? Is there a net amount of fluid being pumped around the body, or is there a backflow? In this case, the definite integral counts the triangle with positive area and the quarter circle with negative area. So the value of the definite integral is 1/2 -Pi(1)2/4. This is a negative number.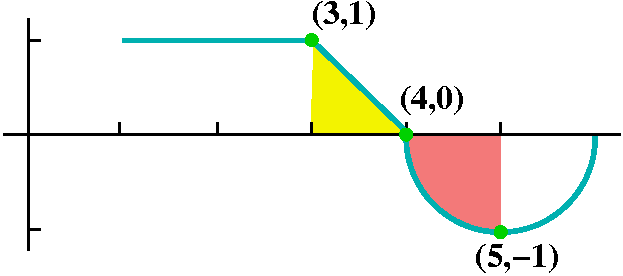
46f(x) dx Here all of the curve is below the axis, and we will "count" all of the area negatively. This is half a circle of radius 1. The value of the definite integral is -Pi(1)2/2.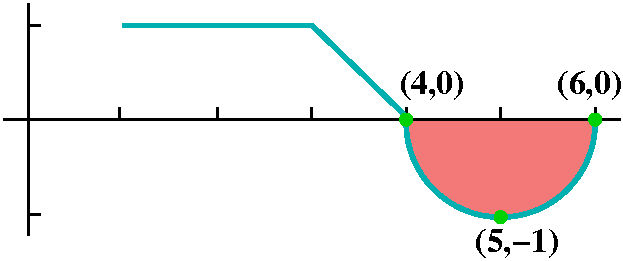

MORE TOP SECRET

During the class meetings, I've had two ambitions. One ambition has been to show that the reasoning involving calculus is valid, and the other is to convince students of the relevance and utility of the subject. From 6 PM to 8 PM on Sunday, April 24, and Sunday, May 1 in Hickman 216 on Douglass I won't continue these attempts. Then I'll only try to help people do as well as possible on a Math 135 final exam. That's it. The students will do the work. I will be the host and guide. Please come, but please come motivated to work on this "stuff".

Many of the methods of calculus have been discovered and rediscovered by different cultures over the last thousand or fifteen hundred years. Special successes have been achieved by efforts in China, India, Greece, and Egypt. I've seen copies of old manuscripts, with totally understandable diagrams, annotated in antique Chinese, Sanskrit, etc. It is wonderful to consider how such amazingly varied people have attempted (and, to a great extent) succeeded in approximation and computation of many strange quantities which we also have considered. I will describe a very simple example using methods which all of these participants would have understood.

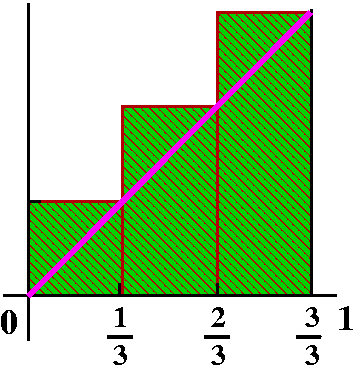How to find the area of a triangle
The triangle I'll look a region in the plane bounded by the x-axis, the line x=1, and the line y=x. I'm interested in the process, not just the answer. Here is an example of the process of approximation: chop up the interval [0,1] into three equal parts. Use the right-hand endpoints of each subinterval to determine the height of approximating rectangles. Then compute the sum of the areas of the resulting rectangles. In this example, the sum turns out to be

 1   1     2   1     3   1
---·--- + ---·--- + ---·---
 3   3     3   3     3   3

 1
--- · (1+2+3)
 32

What happens if we do the same process dividing the interval into n equal parts? I bet as n grows that the sum of the areas of the rectangles is closer to the area of the triangle. Also, I think I can guess that the algebraic form of the sum of the areas will be the following:

 1
--- · (1+2+3+...+n)
 n2

     1 +   2   +   3   + ... + (n-1) +  n
     n + (n-1) + (n-2) + ... +   2   +  1
The sums (columnwise):
    n+1   n+1     n+1  + ... +  n+1  + n+1 (n of these).

Since we started with two copies of 1+2+3+...+n, I think we need to divide the result by 2. Therefore 1+2+3+...+n is [(n+1)n]/2.
Therefore the sum of the areas of the rectangles is [(n+1)n]/[2n²]. What happens as n-->infinity? We can apply l'Hopital's rule twice, but folks like Archimedes (no, Irving was not his first name, darn it, the lecturer is just too silly) would probably have analyzed this a bit differently. Maybe they might have divided the top and bottom by n² and gotten [1+{1/n}]/2 which gets darn close to 1/2.

So that's the classical procedure, which was invented and used with a great deal of effort by several different cultures. Let me now try what they all would consider a much more difficult area to approximate. I think all those folks could do this problem, but they would regard it as a bit challenging.

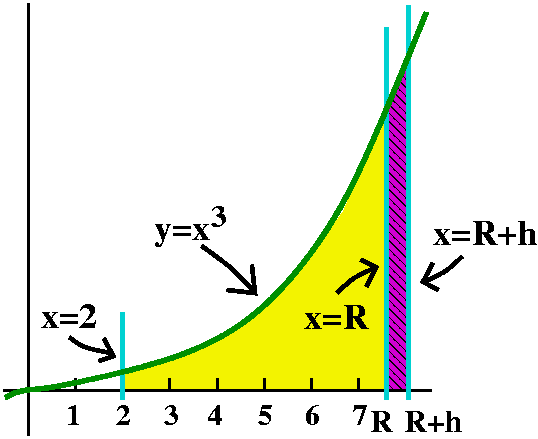
Another definite integral I would like to compute the area of the region which is bounded by y=x3, the x-axis, x=2, and x=7. The technology of the "old folks" could probably compute this area. The hard part would be finding a nice formula for 13+23+33+...+n3 but I think that they could do it. I want to solve this problem, that is, compute this area, by asking about a harder problem. (!)
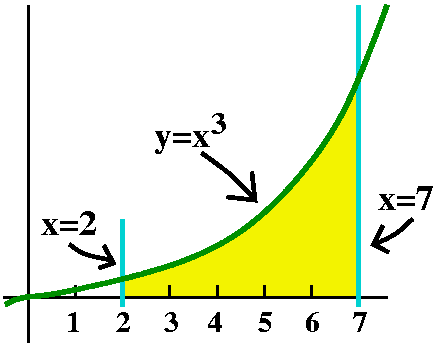
The harder problem Define a new function, A(R) (R is for right). This is an area function which will depend a varying right edge. So A(R) will be the area of the region whose boundary consists of a piece of y=x3, the x-axis, the line x=2, and the line x=R. The task is to understand A(R) well enough to compute A(7). The likely success of this approach is not clear at all, since we seem to have substituted a more difficult, and certainly a more general, problem for the one we started with.
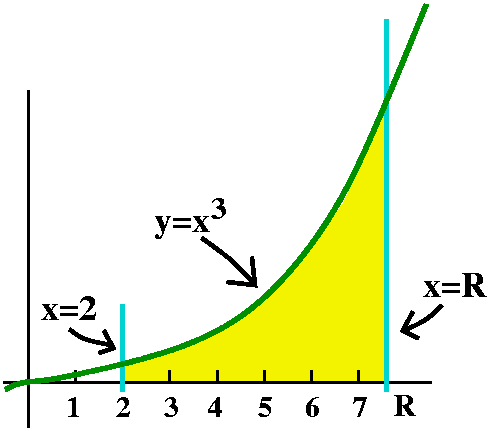
A silly value of A(R) Is there any specific value of A(R) we can "compute"? Well, the word "compute" may be too extravagant, but one value is almost obvious: A(2)=0. Look at the picture, and make the line x=R move inside your mind. Make it move left, until it coincides with x=2. I think the area gets smaller and smaller, until there is no area left. So A(2) should be 0.
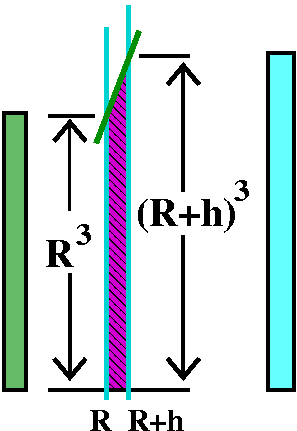
Differentiate A(R) Well those "old folks" didn't have the advantage of more than 90% of a semester of Rutgers calculus. Maybe one thing we can assert is that we should almost always try to differentiate a function. To find the derivative we will need to understand A(R+h)-A(R). I hope the picture helps. h is supposed to be very small. The regions whose areas define A(R+h) and A(R) have a large overlap. When we subtract A(R+h)-A(R) the overlaps cancel, and we just have a thin sliver of area. The width of the sliver is h (that's the difference between R+h and R) and the height varies. On the left the height is R3 (since y=x3) and on the right the height is (R+h)3.
Now think and let h-->0 The "sliver" whose area is A(R+h)-A(R) contains a rectangular box whose height is R3 and whose width is h. So the sliver contains at least an area of R3h. But the sliver also is itself contained inside a box whose height is (R+h)3 and whose width is h. This box has area (R+h)3h. So I know R3h<A(R+h)-A(R)<(R+h)3h. Divide this by h and get R3<[{A(R+h)-A(R)}/h]<(R+h)3. As h-->0, both R3 and (R+h)3 go to R3, and, in the middle, the quotient [{A(R+h)-A(R)}/h] is squeezed. Its limit must also be R3. Therefore A(R) is differentiable, and A´(R)=R3

Now we solve it
We know the following about A(R):
    A(2)=0;
    A´(R)=R³.
Since A´(R)=R³ we know from our study of differentiation that A(R) must be a function that can be written (1/4)R⁴+C for some constant, C. But let's use the "initial condition" A(2)=0. So plug in R=2 in the equation A(R)=(1/4)R⁴+C and get A(2)=(1/4)2⁴+C which is supposed to be 0. Then C should be -(1/4)2⁴. So now A(R) is: precisely:
A(R)=(1/4)R⁴-(1/4)2⁴.
Therefore, A(7), which is the quantity I wanted to get, must be (1/4)7⁴-(1/4)2⁴.

Make it easier!
We want to compute ₂⁷x³ dx. Maybe first let's guess some antiderivative of x³. My guess is (1/4)x⁴+338. Plug in x=7 in this function and get (1/4)7⁴+338. Also plug in x=2 and get (1/4)2⁴+338. Compute the difference, and this difference is [(1/4)7⁴+338]-[(1/4)2⁴+338]. This crazy number is the value of the definite integral.
Notice, please, that the 338 doesn't really do anything to the answer. You don't need to be lucky, because the constant just drops out. Just guess any antiderivative and plug in and subtract.

A part of the Fundamental Theorem of Calculus
Suppose you know that F´(x)=f(x). Then _a^bf(x) dx=F(b)-F(a).
There is even special notation for "F(b)-F(a)". Usually people will write F(x)]_a^b or F(x)|_a^b. The text uses the second version, without the little hooks at the end. The text used when I was taught calculus had the hooks, so surely I will slip sometimes and write them.

How big is the hump?
In fact, as students kindly (?) pointed out, I didn't state this too precisely. Well, o.k.: look at the curve y=sin(x). What is the area under the first bump of this sine curve? The accompanying picture is supposed to be very sloppy. I wanted to emphasize the need to have some size of the answer. I don't think the answer should be very large (456 is too darn large). I don't think the answer should be very small (1/456 is too darn small).

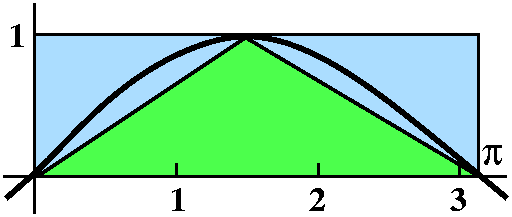Although I sincerely hope that in most situations in the future you will have computational help (machines!) you should have some idea of the size of your answer, so that when the machine reports something really far from the correct answer, you'll know enough to worry a bit. So I try to imagine the answer. Look at the (better!) picture to the right. The sine bump is inside a box whose height is 1 and whose width is Pi, so the area, when we compute it, should be less than Pi. Also the area under the bump contains a triangle (as shown) whose height is 1 which has a base of width Pi, so the area of the bump should be more than Pi/2. Now maybe I will compute the area.

So I need ₀^Pisin(x) dx. I know a function whose derivative is sin(x). Such a function is -cos(x) (keep track of minus signs!). So the area is -cos(x)|₀^Pi. This is -cos(Pi)-[-cos(0)]. This is -(-1)-(-1)=2 (keep track of minus signs!). You can check that 2 is between Pi and Pi/2 as we thought it should be.

How about the area under a bump of cosine?
Maybe this area should be ₀^Picos(x) dx. An antiderivative of cos(x) is sin(x), so this definite integral is sin(x)|₀^Pi=sin(Pi)-sin(0)=0.
Hey! Is there no area? Well, maybe there is area but the definite integral is 0. Remember, area above the horizontal axis counts + and area below the horizontal axis counts -.

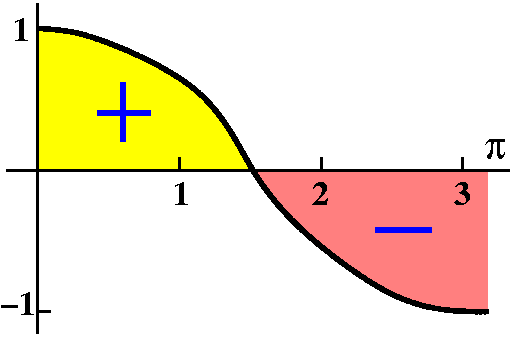
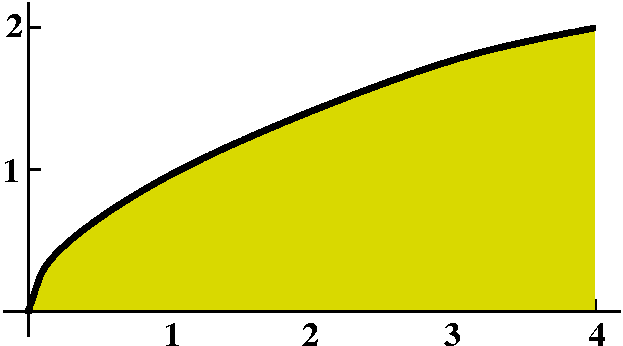
How about the area under square root?
What's the area under y=sqrt(x) between 0 and 4? This is ₀4sqrt(x) dx. Change sqrt(x) to x^1/2. Then an antiderivative is (2/3)x^3/2, so that
₀4sqrt(x) dx=(2/3)x^3/2|₀⁴ (2/3)4^3/2-(2/3)0^3/2. The number turns out to be 16/3. You can compare this again with the area of an enclosing rectangle (area 2·4=8) and a triangle inside (area (2·4)/2=4).

What about the old folks?
I certainly believe that appropriate representatives from the classical cultures of China, India, and Greece could do perform all of the computations we did today. (I'm not sure about Egypt.) But all of the computations would require extensive effort. Each computation would be, in the social context, a tour de force, "a masterly or brilliant feat". We have saved knowledge and built upon the efforts of many clever people: the computations are now routine, and can even be mechanized (e.g., Maple, etc.).

Michelin
This business, founded in France, was and still is a tire company. It opened a factory near New Brunswick in the early part of the twentieth century and "imported" Hungarian workers for the factory. This was one of the origins of the Hungarian presence in New Brunswick. Michelin also wanted to increase recreational car driving. So it began publishing tour guides and collections of restaurant reviews. Those attractions which were rated the best were called, "vaut-le-voyage", that is, worth a journey just for themselves. My claim is that the Fundamental Theorem of Calculus may make Math 135 vaut-le-voyage. You should decide.

Correction! Correction!! Correction!!!

I woke up the morning after this class, and worried. My scholarly conscience, which I too rarely consult, bothered me. I worried about whether what I told you above (Michelin, etc.) was correct. First I checked the web but couldn't find anything definitive. Then I looked at the recently published and wonderful Encyclopedia of New Jersey, trying to find connections between Michelin, New Brunswick, and Hungarians. Again, there was not enough information. So I sent e-mail asking for help to an acquaintance, Dr. Marc Mappen, who was one of the coeditors of the Encyclopedia and is executive director of the New Jersey Historical Commission. He very kindly got further and much better information from participants on the New Jersey history listserv. Here is most of one reply from Mr. Bruce B. Reynolds. I conflated ("blend or fuse together (esp. two variant texts into one)") some real history. The Michelin factory was in MILLTOWN from 1907 to 1930. The Raritan River Rail Road had a spur line which reached into the Michelin factory crossing the mill pond: it can easily be traced today. Johnson & Johnson attracted a large number of Hungarian immigrants to its factories in New Brunswick: as many as two-thirds of the employees in the "sewing department" of J & J were Hungarians, according to local histories which I have read.

TOP SECRET

So, anyway, I would prefer that students in this course be successful. A major measurement of success is performance on the final. I'd like to help students do well on the final. Here is what I will do: I will act as a host and guide to review for the final exam. Hickman 216 on Douglass has been reserved on two successive Sunday evenings, from 6 PM to 8 PM: Sunday, April 24, and Sunday, May 1. The reason for choosing such weird and unconventional (uncomfortable?) times is that maybe people might have more freedom to attend than if some standard hours were picked. In the first session, I will try to intelligently select problems which originate from the first half of the course, and in the first session, problems from the second half of the course. The rooms will be announced by Friday. Rules of the game This is totally voluntary, and aimed at motivated students. I will not lecture, but will supply problems. Lecturing has already been tried, and is not as successful as desired. Students who attend should expect to do at least one problem on the board and work at other problems as long as can. The aim is not to embarrass (I will help, if necessary) but to encourage students to participate actively. You don't need to stay -- you don't need to attend (but I would like you to). Motivation is the major ingredient, and I am willing to display my motivation first in arranging this.

Blood flow Suppose we now consider the following interesting physiological problem. A diagram of the human heart is shown. Blood flow through various "pipes" in the system is known to be an important indicator of health. How can we measure the blood flow through the aorta, the major artery emerging from the heart?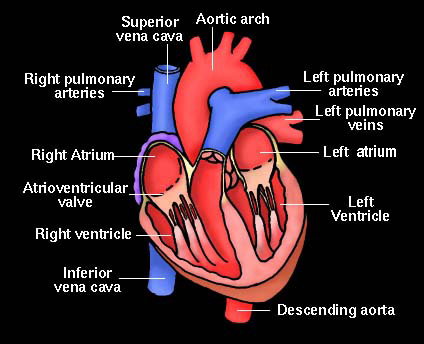

The Aztec solution One method might be to take a knife, preferably an obsidian knife, and rapidly cut through the chest wall, sever the aorta, and cause the blood that would flow through it to fill up a bucket. In about five minutes we'd probably have a good idea of how much blood flows through the aorta. There are several criticisms possible of this "protocol". One namby-pamby criticism (my online dictionary declares that "namby-pamby" means "insipidly pretty or sentimental") might be that, well, maybe the person involved might not be good for much afterwards. Another criticism could be that this would not show the actual pumping capacity of the aorta, because maybe within a minute or two some ... difficulties would occur. In some sense, this Aztec protocol is the ultimate in what might be called destructive testing.

Another solution: cardiac catheterization
The American Heart Association and the NIH (National Institutes of Health) both have lots of information about this. So:

• The AHA begins:
  This is a procedure done on the heart. In it, a doctor inserts a thin plastic tube (catheter) (KATH'eh-ter) into an artery or vein in the arm or leg. From there it can be advanced into the chambers of the heart or into the coronary arteries.
• Or from the NIH:
  Cardiac catheterization is used to study the various functions of the heart or to obtain diagnostic information about the heart or its vessels. A small incision is made in an artery or vein in the arm, neck, or groin. The catheter is threaded through the artery or vein into the heart. X-ray images called fluoroscopy are used to guide the insertion.

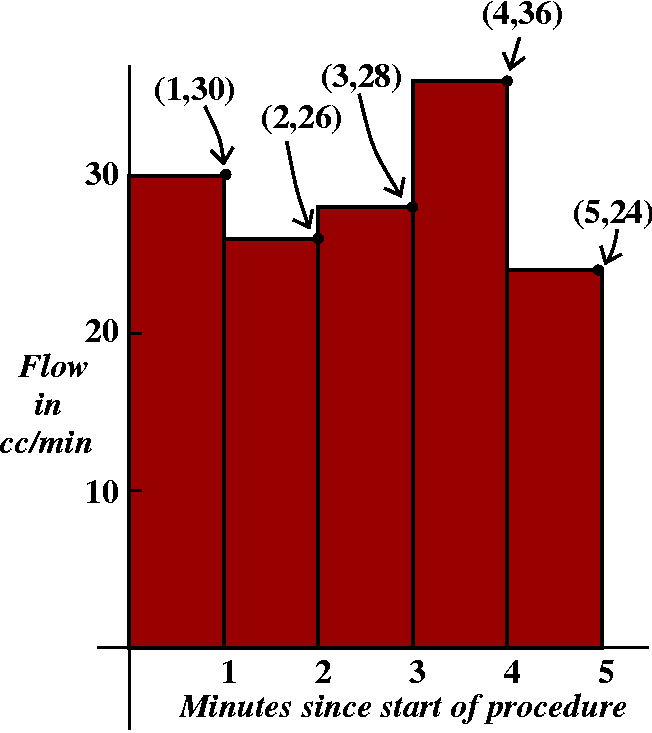
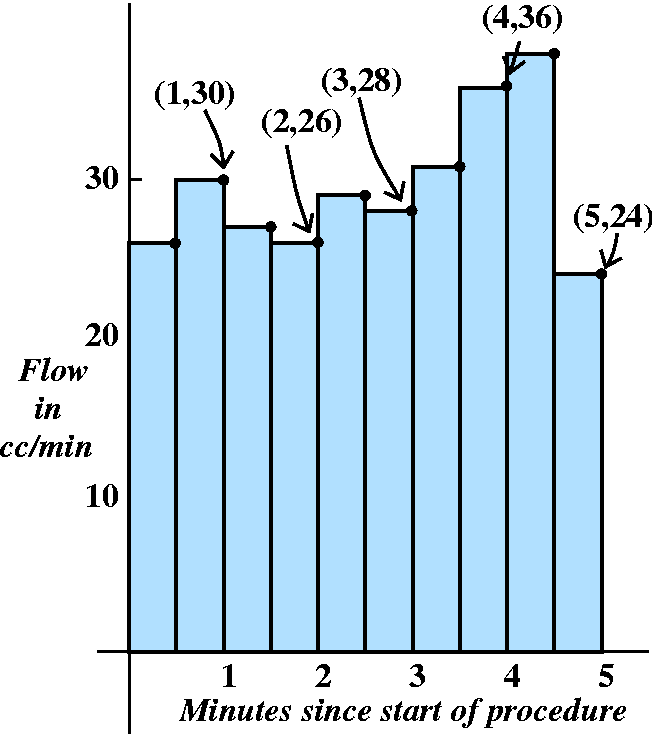
At the end of	Minute #1	Minute #2	Minute #3	Minute #4	Minute #5
blood flow  rate is	30 cc/min	26 cc/min	28 cc/min	36 cc/min	24 cc/min

As I mentioned in class, maybe the reason for the jump at the fourth minute is because a calc instructor walked into the room and murmured, "Chain Rule!" How can we use this information to get an approximation to the "real" blood flow? You might make the assumption that, hey, maybe the flow rate doesn't change too much in a minute, and maybe we can approximate the total blood flow by assuming the flow rate is constant during that minute. So then during the first minute, when the only measurement we have is 30 cc/min (cubic cows? no, cubic centimeters), we could conclude that during the first minute the total flow is (30 cc/min)·(1 min). The units cooperate -- that is, the minutes cancel, and we see that 30 cc's (maybe) flowed through the aorta in the first minute. During the second minute, we have the measuement (at the end of the second minute) of 26 cc/min. Therefore, same (perhaps and probably not totally correct) assumptions show that blood flow in the second minute is (26 cc/min)·(1 min). Etc.. The answer that we can get from the information supplied seems to be:
(30 cc/min)·(1 min)+(26 cc/min)·(1 min)+(28 cc/min)·(1 min)+(36 cc/min)·(1 min)+(24 cc/min)·(1 min).
I am not interested in these particular numbers, but I am very interested in the ideas they represent.

A better approximation
We might want a better approximation to the blood flow. I do not think it is realistic to assume that blood flow is steady, and jumps only at the minute marks. To improve our information, with just as much investmant in the (imagined!) equipment, we could (imagine!) examining and recording flow rates every 30 seconds during the 5 minutes. We might get some data like this:

At the end of	30 seconds	Minute #1	1 minute 30 seconds	Minute #2	2 minutes 30 seconds	Minute #3	3 minutes 30 seconds	Minute #4	4 minutes 30 seconds	Minute #5
blood flow  rate is	26 cc/min	30 cc/min	27 cc/min	26 cc/min	29 cc/min	28 cc/min	31 cc/min	36 cc/min	38 cc/min	24 cc/min

Again, there are lots of numbers. So what? How can we use these numbers? To begin, how could we use the measurement at 30 seconds? We could assume the flow rate of 29 cc/min is constant during that initial 30 seconds. Then the blood flow would be ... well, should I write 29·30? No: we shouldn't get confused about units. The time is in minutes, so 30 seconds is (1/2) minute. In fact, the new information allows us to write the following (probably better) approximation to the blood flow: (I am omitting the units here because I am a math geek.)
(26)·(1/2)+(30)·(1/2)+(27)·(1/2)+(26)·(1/2)+(29)·(1/2)+(28)·(1/2)+(31)·(1/2)+(36)·(1/2)+(38)·(1/2)+(24)·(1/2).

What is going on? The number of terms to add is increasing, but if you look very very carefully you will see that each term individually is getting smaller. In fact, these changes nearly balance: more terms/smaller terms. The totals are different, but not very different. The new total is "better", a refinement of the old sum. The approach here is computational and numerical, and for me obscures what's going on. A collection of pictures actually provides far more information for me here.

Approximating what, "exactly"? Well, we began by using only the information at five different times, at the end of each minute. If we were to plot points on a graph of blood flow, we would see the picture to the right. The first sum we wrote is exactly the total area under the five boxes shown, with "area" interpreted as the amount of blood.
When we put in the data points at 30 second intervals, we can see pictorically exactly what that second crazy sum represents: it is the total area in the boxes of width (1/2) minute, with "area" interpreted as the amount of blood.
Now what do the "Aztecs" get as their information? We could imagine a flow rate function which sort of threads its way through the data points supplied. The Aztecs, with the ridiculous bucket holding exactly the blood going through the aorta, would have an amount of blood which is exactly the area under the blood rate flow graph. You can see that we have these rectangular approximations to the area which we hope get better as the rectangles get thinner and the number of samples of the flow rate increases.

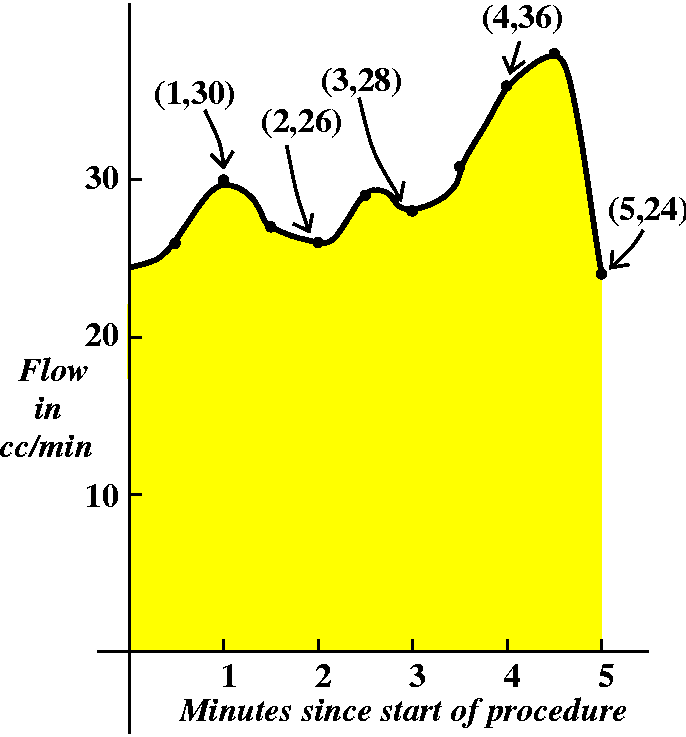
Future value of an income stream
I wanted to give an economic example of the same sort of sum, and I tried to discuss the future value of an income stream. I think I lost even the people with the most knowledge of the field here, and I am sorry. The idea is that you get a certain number of dollars paid back to you over a period of time. The total amount paid is always the same, but the paybacks are in chunks which get smaller as the number of payments increase. I then assumed that the paybacks are reinvested, and the value with interest as the end of the time is totaled. This is called the future value of an income stream. This may seem rather weird to you: I'm sorry. Here is a lecture from a math course at the University of Wisconsin which discusses the topic in more detail. I am sorry I covered it so hastily. The idea is difficult.

More vocabulary: calcspeak grows!
I will try to use the notation in your text (section 5.3).
We begin with a function f(x) defined (at least) on an interval a<=x<=b. Divide the interval up with a bunch of points. This is called a partition. The textbook writes this as
a=x₀<x₁<x₂<...<x_n-1<x_n=b.

Now in each "little" subinterval choose a sample point: so
x₁^* is in the interval with endpoints x₀ and x₁,
x₂^* is in the interval with endpoints x₁ and x₂,
... x_n^* is in the interval with endpoints x_n-1 and x_n.

Evaluate f(x) at each sample point: f(x₁^*), f(x₂^*), f(x₃^*), ..., f(x_n^*). Multiply each of these numbers by the width of the subinterval they came from:
f(x₁^*)·(x₁-x₀), f(x₂^*)·(x₂-x₁), f(x₃^*)·(x₃-x₂), ..., f(x_n^*)·(x_n-x_n-1).

Add up all these numbers. The result is called a Riemann sum corresponding to these choices of partition, sample points, function, latitude, irritation ... of course I am joking about the last two. But this "thing" is a very complicated object. I think some examples would be good.

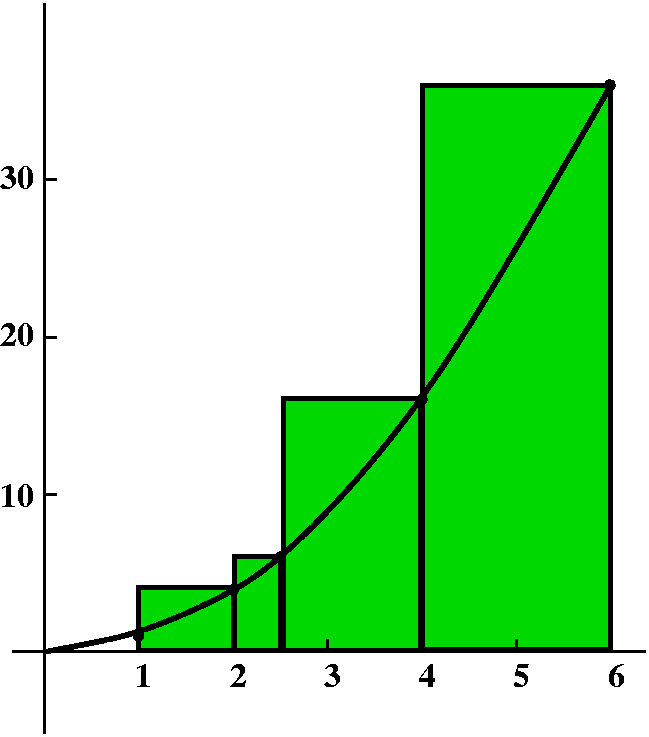Example 1
f(x)=x². The interval is 1<=x<=6. The partition is, let's say, x₀=1 and x₁=2 and x₂=2.5 and x₃=4.5 and x₄=6. Also I need to specify the sample points, and these will be the right-hand endpoints of each subinterval.
So for x₀=1 and x₁=2, we have x₁^*=2 and f(x₁^*)=2². So we get a contribution of 2²(2-1).
So for x₁=2 and x₂=2.5, we have x₂^*=2.5 and f(x₂^*)=(2.5)². So we get a contribution of (2.5)²(2.5-2).
So for x₂=2.5 and x₃=4.5, we have x₃^*=4.5 and f(x₃^*)=(4.5)². So we get a contribution of (4.5)²(4.5-2.5).
So for x₃=4.5 and x₄=5, we have x₄^*=5 and f(x₄^*)=5². So we get a contribution of 5²(5-4.5).
The Riemann sum is therefore:
2²(2-1)+(2.5)²(2.5-2)+(4.5)²(4.5-2.5)+5²(5-4.5).
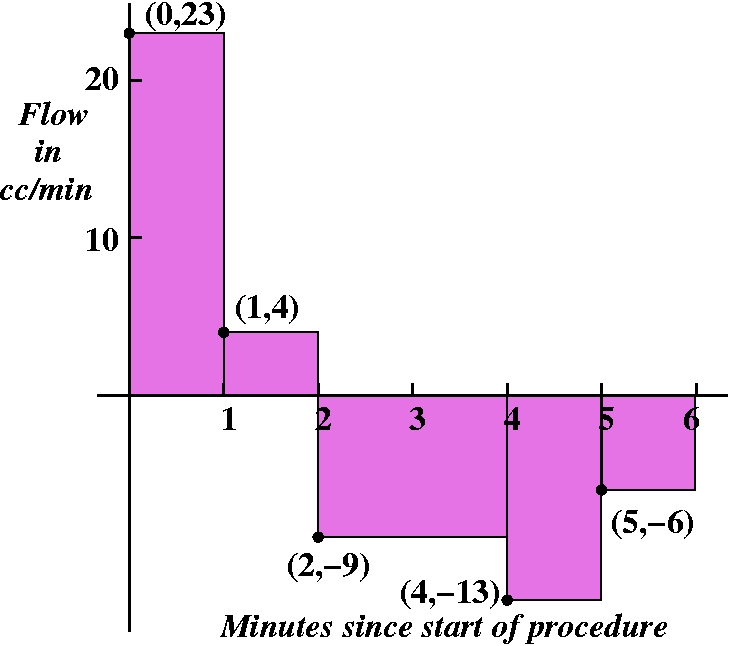Example 2
Here I gave some data on a graph. It is another blood measurement proceedure. At time 0 (minutes), we have 23 (cc's/min). I will omit the units from now on, since reality is receding from me at 77 furlongs per fortnight. Other observations during this proceedure, which lasts from time 0 to time 6, are (1,4), (2,-9), (4,-13), (5,-6). You may question the "reality", even remote, of negative readings. Well, unfortunately, that can be real. Valves in hearts and other places can leak, and there can be backflow. Here my sample points will be the left-hand endpoints of the intervals. And my Riemann sum will be:
23(1)+4(1)+(-9)2+(-13)1+(-6)1.
This total does happen to be negative, so I think the net effect of the "flow" is a backwards slosh of liquid.
In financial computations, positive could represent profit and negative could represent loss. Unfortunately in the real world, negative sums can occur. Sigh.

The definite integral As the number of points in the partition increases, as the length of the subintervals approaches 0, if the function involved is fairly nice (let's say piecewise continuous, which is continuous except maybe for a finite number of jumps) then the sums (properly, the Riemann sums), for any possible selection of sample points, approach a unique limit, which is called the definite integral of f(x) from a to b. I have so far omitted the rather wild traditional notation. Well, if you look in the text you will see that Riemann sums themselves are frequently abbreviated with capital Greek sigmas. I won't even write these in class. But the notation for the definite integral is one which I will need to use. Here it is:
_a^b f(x) dx
The long "S" is an abbreviation for Sum. So you can look at this notation and see that it is an abbreviation for summing up, as x goes from a to b, the "rectangles" of height f(x) and width dx. Here "dx" stands for some really really really small width.

HOMEWORK
Please read the first four sections of chapter 5 and hand in these problems on Thursday:
5.1: 43, 44;
5.2: 13a, 19;
5.3: 26, 27.

Maintained by greenfie@math.rutgers.edu and last modified 4/19/2005.