Math 135 diary, third part, spring 2005
Friday, April 15: this is lecture
24
Antiderivative
F(x) is an antiderivative of f(x) if F´(x)=f(x).
If you know one, you know them all ...
If F(x) is one antiderivative of f(x), then any other antiderivative
of f(x) is F(x)+C.
How to know one
How would you find antiderivatives?
- Guess them. This is essentially the "technology" of
Math 135. You should look at some familiar functions and be able to
guess the antiderivatives. What functions? Well, certainly things like
x43 or 7x-8 or ... and sin(x) and cos(x) and
ex. But it turns out that finding the antiderivatives of
functions defined by even rather simple formulas can be very
difficult.
- Ask an electronic pal. I just logged onto eden. I
typed the word maple on an eden command line. The
response was some stuff which looked like this:
er3% maple
|\^/| Maple 9.5 (SUN SPARC SOLARIS)
._|\| |/|_. Copyright (c) Maplesoft, a division of Waterloo Maple Inc. 2004
\ MAPLE / All rights reserved. Maple is a trademark of
<____ ____> Waterloo Maple Inc.
| Type ? for help.
>
The little > invited me to type something. So I did. The
program's answer follows. I did a differentiation, an
antidifferentiation, another differentiation and another
antidifferentiation. Take a look.
> diff(x^5,x);
4
5 x
> int(x^5,x);
6
x
----
6
> diff(sqrt(cos(1+x^6)),x);
6 5
3 sin(1 + x ) x
- ----------------
6 1/2
cos(1 + x )
> int(x^2*cos(5*x),x);
2
1/5 x sin(5 x) - 2/125 sin(5 x) + 2/25 x cos(5 x)
> quit
You should know that such programs exist. The programs won't think for
you, but they certainly will help with some computations!
- Call me at home and ask ... No, please don't do this. I am
a cranky guy, and also I make mistakes.
 Joni throws a ball
Joni throws a ball
Most people who have taken a high school physics course have seen
problems similar to what follows:
Joni stands on a hill 15 feet high and throws the ball straight up in
the air at 30 ft/sec. Remember that gravity pulls a ball down at 32
ft/sec2. What is the position of the ball t seconds after
it is thrown?
Solution
Well, suppose s(t) is the height (position) of the ball at time t,
with up being positive. And v(t) is the velocity of the ball at time
t. Finally, a(t) is the acceleration at time t. How do the statements
in the previous paragraph translate to calcspeak?
| English | calcspeak |
|---|
| Joni stands on a hill 15 feet high | s(0)=15 |
| throws the ball straight up in
the air at 30 ft/sec. | v(0)=30 |
| gravity pulls a ball down at 32
ft/sec2. | a(t)=-32
(the minus sign
means
down) |
Of course we need to remember that s´(t)=v(t) and
v´(t)=a(t). Since a(t)=-32, we guess an antiderivative:
v(t)=-32t+C. Since v(0)=30, we know v(t)=-32t+30. How about s(t)? We
guess s(t)=-16t2+30t+C. Since s(0)=15, this C is
15. Therefore s(t)=-16t2+30t+15.
Some standard questions
- At what time is the ball highest? What is its height at that
time?
The ball is highest when v(t)=0 (critical number!). Since
v(t)=-32t+30, -32t+30=0 implies that t=30/32. To get the height at
that time, plug into s(t). The height is s(30/32)=
-16(30/32)2+30(30/32)+15.
- At what time does the ball hit the ground? What is the velocity of
the ball when it hits the ground?
The ball hits the ground when s(t)=0. So we need
-16t2+30t+15=0 and (quadratic formula) t={-30+/-sqrt([30]2-4(-16)(15))}/(2[-16]). The roots turn out to be (approximately)
-.41 and 2.29. I think that Joni doesn't throw the ball backwards in
time, so the ball hits the ground at (about) t=2.29. Its velocity at
that time is v(2.29)=-32(2.29)+15=-58.28. The minus sign means the
ball is moving down.
Vocabulary
As I mentioned in class, specifications such as s(0)=15 and v(0)=30
are called initial conditions. In practice, initial conditions
are used to specify one out of a whole bunch of candidate
antiderivatives.
Become an expert witness
A car is speeding along at 60 miles per hour (which I remember from
high school is 88 ft/sec). Suppose the car hits a wall and comes to a
stop in a tenth of a second. If the deceleration is assumed to
be constant, what is the deceleration? If you can do such analysis,
maybe you could be an expert witness in car accident cases, and
make big bucks. Ooops, sorry: maybe you could help that the correct
side wins in the court case.

Here a(t)=K, a constant by assumption. I'll use the letter K for a
constant here instead of C, since we use that for the constant which
arises in antidifferentiation. So I know that a(t)=K, and then by
antidifferentiating, v(t)=Kt+C. But v(0)=88. I'm again using distance
measured in feet and time measured in seconds. Thus v(t)=Kt+88. Since
v(1/10)=0, we know K(1/10)+88=0, so that K=-880
ft/sec2. This is interesting and horrifying. Notice that
880/32 is 27.5: so this deceleration presses the "contents" of the car
(the passengers!) with a force twenty-seven and a half times that of
normal gravity. Imagine even briefy your weight multiplying by that
factor. The consequences are most unpleasant. A chapter in a book I
recently read, Stiff: The Curious Lives of Human Cadavers
by Mary Roach, has a chapter discussing this situation. Those of you
interested in becoming doctors might want to read this book.
An antiderivative
Here's a problem from a past final exam:
a) Suppose A is a constant. What is the derivative of
Aexcos(x)?
b) Suppose B is a constant. What is the derivative of
Bexsin(x)?
c) Find one antiderivative of exsin(x).
As I remarked, a) and b) were done successfully by most students. Here
are the solutions:
a) The derivative of Aexcos(x) is
Aexcos(x)-Aexsin(x).
b) The derivative of Aexsin(x) is
Aexsin(x)+Aexcos(x).
c) Correct answers to c) were supplied by only 20 to 25% of the
students. Let's see: the goal is to get
exsin(x). And we know
Aexcos(x) ---d/dx---> Aexcos(x)-Aexsin(x).
Bexsin(x) ---d/dx---> Bexcos(x)+Bexsin(x).
So if we added things, then we'd get (A+B) multiplying
excos(x) and we'd get (A-B) multiplying
exsin(x). But we want exsin(x): that is, I want
no excos(x) and I want exactly one
exsin(x). If you can find A and B so that -A+B=1 and A+B=0
then we'll be done. But, goodness, add the equations to get 2B=1 so
B=1/2, and then A=-1/2. I'll bet that an antiderivative
of exsin(x) is
-(1/2)excos(x)+(1/2)exsin(x).
How can you tell if I am correct? You can check by
differentiating. The result should be exsin(x).
An introduction to "How many get sick?"
It is extremely doubtful if any student in the class will need
to find the slope of a tangent line after they've passed the Math 135
final exam. The major idea of the course still needs to be told to
you, though. And it is this major idea which may "flavor" your
approach to a very wide variety of quantitative phenomena in the
future. I wanted to give a biological example to show what's going
on. I couldn't find simple enough data for a real example, so I needed
to invent something. So here it is, along with my apologies and
acknowledgement that the specifics are so simple as to be almost
silly. But there's a profound idea somewhere in what I'll try to
describe. Now let's get down to business.
How many get sick?
The scenario is that there's an epidemic, and we'd like to know how
many people get sick. One way we might try to get a total is by
calling the (only) local hospital at, say, 7 AM in the morning. You
could ask, "How many patients (sick with the disease) are waiting for
care in the emergency room?" Now I'll add some further simplifying
assumptions. I'll assume that patients in the emergency room are seen
and diagnosed and stuffed away within an hour. Suppose we get the
following information:
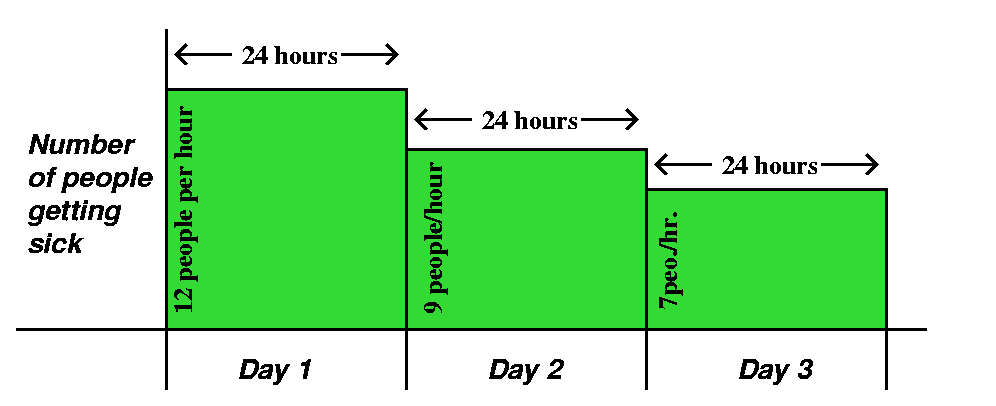
| Day 1 | Patient count at 7 AM | 12 |
|---|
| Day 2 | Patient count at 7 AM | 9 |
|---|
| Day 3 | Patient count at 7 AM | 7 |
|---|
So how many people are getting sick? I'd like to use the very simplest
kind of estimates. Well, on day 1, there are 12 people in the
emergency room. The hospital handles this crowd in an hour. But I
guess that the number of people getting sick is going to be constant
(this is simplicity!) until I am forced to change my assumption. So on
the first day, the hospital has 12·24 people getting
sick. There are 24 hours in a day! But on day 2, I've got to
change my analysis. I learn that 9 people are getting sick in an
hour. So on day 2, there are 9·24 more ill people, and the
information for day 3 tells me that there are 7·24 sick
folks.
There's a total of
12·24+9·24+7·24 people who
have gotten the disease.
This is really a very rough estimate. How could we get better
information? Many of the students in the room who were both alive and
awake replied that we could get better information by questioning the
hospital more often. I certainly agree. So let me assume that I not only
call at 7 AM but I also call at 7 PM. So I might get some numbers like
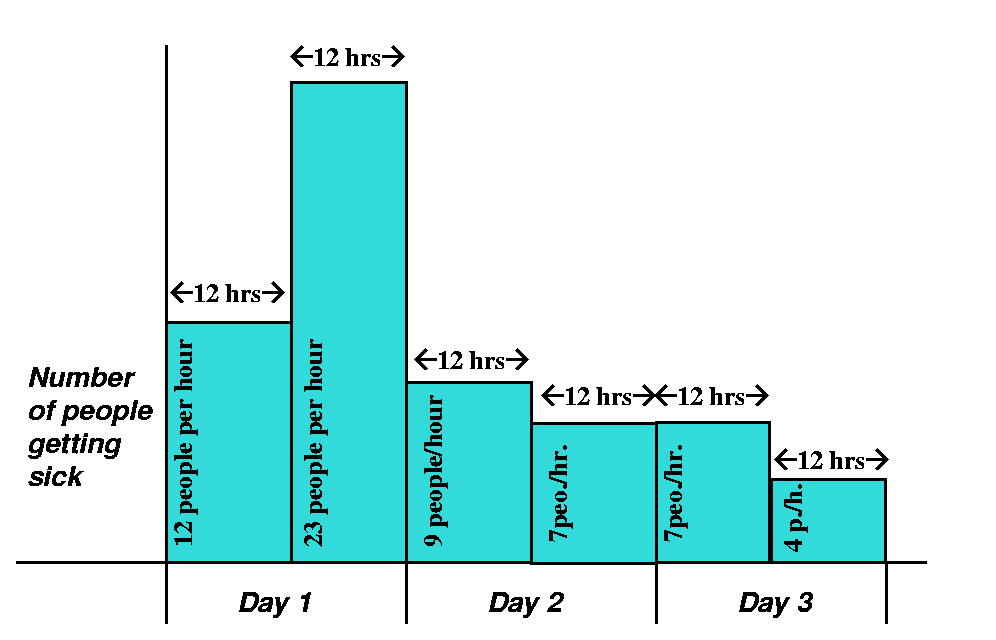
this:
| Day 1 | Patient count at 7 AM | 12 |
|---|
| Patient count at 7 PM | 23 |
| Day 2 | Patient count at 7 AM | 9 |
|---|
| Patient count at 7 PM | 7 |
| Day 3 | Patient count at 7 AM | 7 |
|---|
| Patient count at 7 PM | 4 |
Well, what estimate for the number of ill people can we now get? The
numbers should now be multiplied by only 12, because each reported
number is assumed to represent the patient "flow" in half a "day"
(half of 24 is 12, indeed).
The appropriate estimate is a total of 12·12+23·24+9·12+7·12+7·12+4·12
people who have gotten the disease.
This should be a better estimate, closer to the actual number of
people who have been infected and been treated by the hospital.
Well, I'm interested in the "structure" of the answers. The second,
(presumably) closer answer has more pieces, more things to add up. The
pieces, though, each have the reported patient numbers, but are
multiplied by a smaller number. Huh? Maybe you can see what is
happening if I "refined" this process and imagine "sampling" the
population in the emergency room more often. There would be more terms
in the sum. Each term would be multiplied by something smaller. Hey,
and maybe you might even see that somehow the number of terms getting
larger is balanced out by the multiplier getting smaller. Maybe we
could also hope that the approximations get better and better.
If you think in terms of pictures, something like the following might
help. This picture shows the results of just the 7 AM reports.
Now we move on to reports at both 7 AM and 7 PM.
Finally, there's this mysterious curve, in magenta. What might this
curve represent? It should represent the number of people getting
sick (although the number of people is an integer, well, one could
imagine that the population was very large, and maybe the curve
represents an integer number of people but the scale makes it look
smooth). And the total number of people who get sick during all three
days is ... the area under the curve.
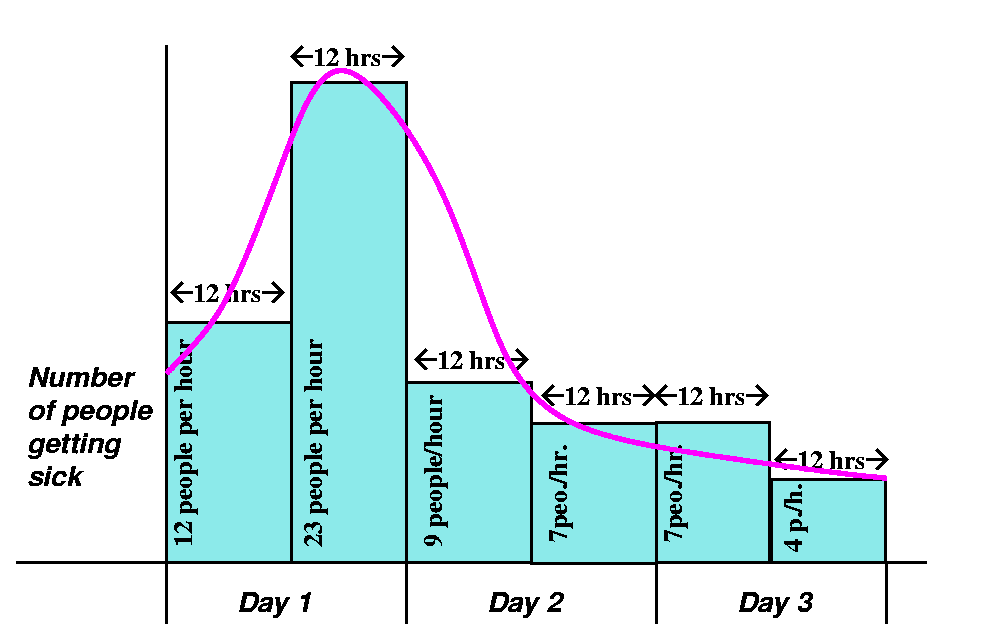
So this is the big idea?
The big idea is that the total number of people who get sick, which
you might somehow think of as a "chunk", a number just sitting
somewhere in our heads, is really related to the rate of people
getting sick. How? Well, the rate of people getting sick is the
derivative of the people who are ill. And you go backwards from the
rate of people getting sick to the total number of people who get
sick, by taking an antiderivative.
You can measure the total number of people getting sick by questioning the
whole population after the epidemic is over. Or: you can look at the
process, and see the rate of people getting sick, take its
antiderivative, and try to analyze things that way. This is two
different points of view, and the two different points of view give a
terrific intellectual leverage in understanding the
computation. Sometimes one way is more convenient, and sometimes the
other one is.
Please begin reading chapter 5. Please.
Tuesday, April 12: this is lecture
23
The fences of a farmer
A farmer wishes to enclose a rectangular area of 1200 square
feet with a fence. Additionally, the inside will be divided by two
fences which are both parallel to one of the sides of the
rectangle. Suppose the outside fence costs $2 per foot and the inside
fence costs a half dollar per foot. What dimensions will make the
fence cost least?
I tried to go through this problem very slowly, with some special
mention of what the inside of my head is doing during the stages.
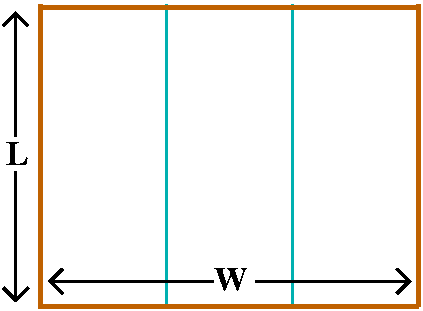 Step 1: translation
Step 1: translation
Translating the paragraph into algebra: I would first draw a picture
and label it. This is not always necessary, but my approach to these
problems frequently needs visual reinforcement. Then I go through the
problem sentence by sentence, or phrase by phrase, or even, if I am
very confused, word by word. I'll call the two sides of the rectangle
L and W. Here I see the constraint LW=1200. And actually the "reality"
of the problem imposes L>0 and W>0 also. What about the cost of
the fence? The length of the outer fence is 2L+2W (I imagine the units
are ), and the cost per foot is $2. Therefore the cost of the outer
part of the fence is 2(2L+2W). The inside fence seems to be 2W, with a
cost of $1/2 per foot. So its cost is 2W(1/2). The total cost is
2(2L+2W)+2W(1/2), and this is our objective function.
Exaggeration
I usually try to check my translation (from language to
algebra) at this stage. One way I do this is by looking at extreme or
exaggerated situations, and seeing if I get anything that makes
sense. In the two cases shown, I think that the area is constant, and
I can make L or W very very big, and then the other one is very very
small. The cost of the fences then will become large (if L or W is
really big, then 2(2L+2W)+2W(1/2) will be large -- remember that
both L and W are positive). So, internally, I think, aha, somehow the
collection of fence "scenarios" will yield costs, and the costs will
be large at the exaggerated cases, and somewhere there should be a
minimum cost. As I remarked in class, I might not write this down
explicitly if I were doing the problem myself, but I really assure you
that I think this way in every problem of this type. If I can't make
sense of the problem at this stage, maybe my translation was incorrect.
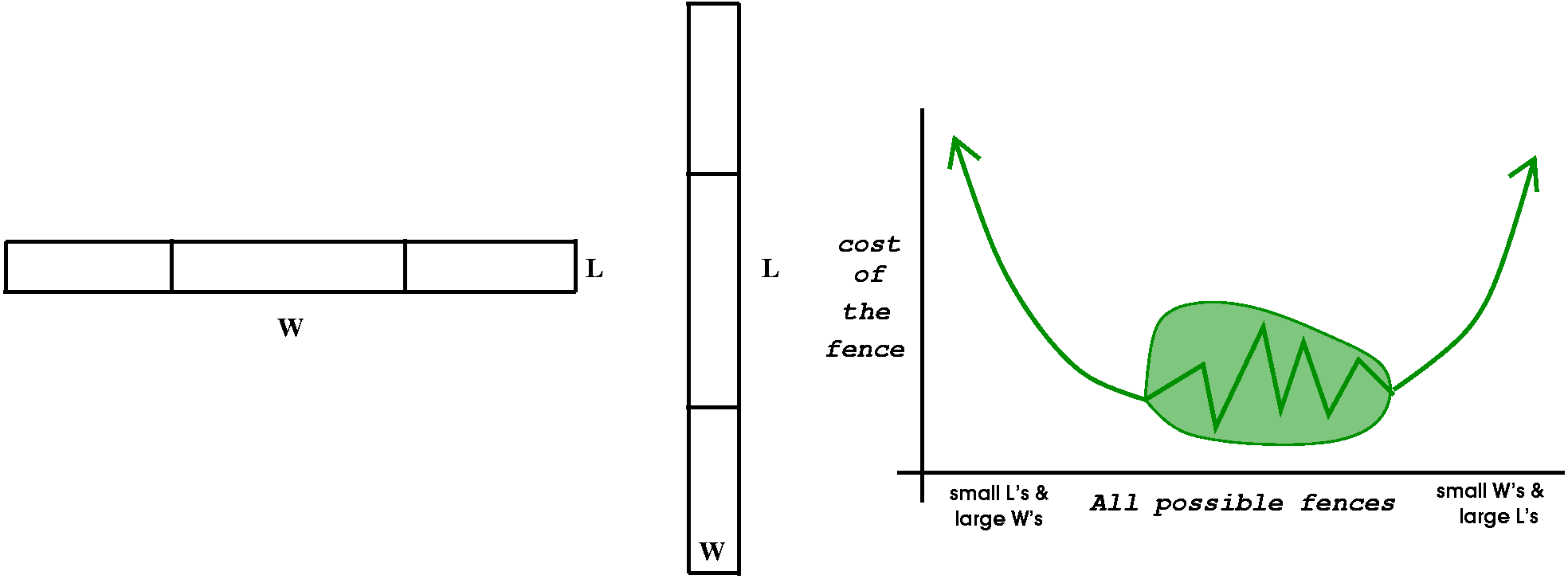
 Step 2: calculus
Step 2: calculus
Minimizing 2(2L+2W)+2W(1/2) while LW=1200 isn't a one variable
calculus problem. So I use the constraint to help me: L=1200/W. Then
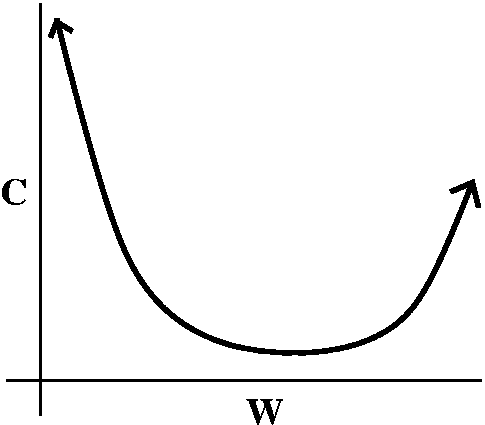
the cost is 2(2L+2W)+2W(1/2)=4L+4W+W=4L+5W=4(1200/W)+5W=[4800/W]+5W.
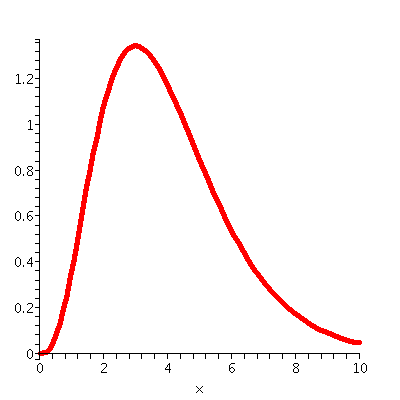
Now I need to minimze C=[4800/W]+5W. Here the domain is W>0. As
W-->infinity, the cost-->infinity also. As W-->0+, the term
4800/W-->infinity. I'll bet that there is a minimum somewhere
"inside" the domain. An approximate graph of C as a function of W is
shown to the right. This is a more precise picture than the
preliminary version shown above.
We computed dC/dW and got -[4800/W2]+5. The critical
numbers will occur when this is 0, so we must solve
-[4800/W2]+5=0. So 5=4800/W2 and
5W2=4800. Next, W2=960, and the solutions of
this
algebraic equation are +/-sqrt(960). The only solution inside our
domain is W=sqrt(960), and this must correspond to the minimum cost.
Step 3: going back to the problem
Why should this be a minimum, what are the dimensions of the resulting
rectangle, and what is the cost?
Mimimum? Well, if we have already checked that C-->infinity
as W-->0+ or W-->infinity, then I know this value of W
will correspond to a minimum.
One could check the first derivative: if 0<W<sqrt(96), then
dC/dW is negative and if sqrt(960)<W<infinity, dC/dW is
positive. Or we could look at the second derivative. Realize that for
this purpose all we need is the sign of the second derivative
-- we don't need the exact value. The derivative of
-[4800/W2]+5 is 2[4800]/W3. When W=sqrt(960),
this is clearly positive so (concave up!) we have found
a minimum.
Since LW=1200, at the mimimum cost L=1200/W=1200/sqrt(960). And what
is the mimimum cost? Since C=[4800/W]+5W, the cost must be
[4800/sqrt(960)]+5(sqrt(960).
Certainly this problem is silly, but I really did it to illustrate the
process, which is good even in many more complicated problems:
translate, check the translation, get a calculus problem, solve it, go
back to the original setting and look at the candidate solution.
One of my WeBWorK problems
Here's a problem about driving a truck in Mexico. The setting is
something like this:
The truck costs 51+.28v cents per mile to drive at v miles per
hour. (Well, yeah, one could imagine that driving a truck faster might
cause parts of the truck to wear out more. So maybe something
like this is true in real life.) Also, the cost of a driver is $12 per
hour. At what velocity v should one drive the truck on a trip of 2,000
miles in order to spend the least amount of money? Also, we're told
that the velocity, v, the "speed", should be at most 100 mph.
The cost is the sum of the cost of the truck plus the cost of the
driver. If the truck is driven 2,000 miles, then the truck costs
.51+.0028v dollars per mile (thanks, Ms. Dike, for the 00 in the cents) and
therefore the cost of the truck is 2000(.51+.0028v) dollars for the
trip.
What about the cost of the driver? If the truck moves steadily at v
miles per hour, then (dist=rate·time) the time needed to drive
the truck 2,000 miles is 2000/v hours. And the driver gets
$12/hour, so the resulting driver's cost is 12(2000/v).
The total cost is therefore the sum of the truck cost plus the driver
cost, which is 2000(.51+.0028v)+12(2000/v). This function is similar
to the one we analyzed in the fencing problem. Oh well: it was
silly for me to present both of these problems in class. Again as v
gets large, the cost gets large. And as v-->0+, the cost
also gets large.
What is the derivative of 2000(.51+.0028v)+12(2000/v)? It is
2000(.0028)-12(2000/v2). This is 5.6-(24000/v2)
and we need to know when 5.6-(24000/v2)=0. Again, we can
solve this just as before, so v=sqrt(24000/5.6) which is about 65
mph. And, just as before, we can justify our statement that this is a
minimum cost.
 Section 4.7 has a significant amount of applications in economics
(average and marginal cost, marginal profit, etc.). I strongly urge
interested students to read this material. I also urge all students to
do the next two WeBWorK assignments, which will practice your
translation skills on various optimization (max/min) problems.
Section 4.7 has a significant amount of applications in economics
(average and marginal cost, marginal profit, etc.). I strongly urge
interested students to read this material. I also urge all students to
do the next two WeBWorK assignments, which will practice your
translation skills on various optimization (max/min) problems.
To the right is a picture of several skuas which is "any large predatory sea
bird of the family Stercorariidae".
Moving ahead
We have only a few weeks left in the course. Most people who know and
use calculus would agree that the material still to follow is probably
the most important and most beautiful in the course. I think there is
barely enough instructional time, so I want to begin chapter 5
slightly early.
Antiderivatives
We'll begin with the principal definition of section 5.1.
F(x) is an antiderivative of f(x) if F´(x)=f(x). I gave several
examples of antiderivatives. They were something like what follows.
Uhhh, ________ is an antiderivative of 5x2-7x+3. What is
________ ?
There turn out to be many answers to this. By guessing and then
verifying, you can see that
(5/3)x3-(7/2)x2+3x+104.3 is an antiderivative of
5x2-7x+3. But you can also see that
(5/3)x3-(7/2)x2+3x-Pi/2 is an antiderivative of
5x2-7x+3. We did a few other examples, but what's going on?
The MVT steps in
Here is another consequence of the MVT:
If the derivative of a function is 0, then the function is
constant. Why is that? Well, one side of the MVT equation "compares"
f(b) and f(a). It declares that f(b)-f(a)=f´(c)(b-a). If the
derivative is always 0, then f(b)-f(a)=0 for any choices of b and a,
so that f's values stay the same.
If f(t) represents position at time t, then f´(t) is the
instantaneous change of position, or velocity. The math statement
inthe previous paragraph translates, "If velocity is always 0, then
positiion stays constant." Or, more plainly, "If you don't move, you
stay in one place." Ain't math profound?
All antiderivatives
Let's ask a more precise question. What are all antiderivatives
of 5x2-7x+3? Well, if I know one antiderivative, the
previous result states that I can get any other valid antiderivative
by adding/subtracting any constant from one known antiderivative,
which(at this stage) I can get by guessing and verifying. One
antiderivative of the function displayed is
(5/3)x3-(7/2)x2+3x+104.3, so that any
antiderivative is
(5/3)x3-(7/2)x2+3x+104.3+a constant. This
is more conventionally written as
(5/3)x3-(7/2)x2+3x+C. The constants are pushed
together, and the "+C" is a conventional abbreviation.
Exam return
The material in this course is important and I think it is
interesting. I tried to grade the exam carefully, and the letter grade
equivalents are given in the context of all students taking Math
135. Please evaluate carefully how much time you can spend and will
need for success in this course. You should not cheat or restrict your
future self: you may well value understanding of this material for
applications in both business and the biological sciences.
Although suitable use of "technology" (such as calculators and other
silicon pals) is very important, I very much believe that students
should be able to write explanations of their work, and that, in a
calculus course, students should be able to use calculus to explain
their conclusions. Such efforts are important and transferable to
other fields. They are therefore suitable examination requests in a
college calculus course.
-
... use calculus ... I believe this phrase appears four times on
the exam. Explanations supported by the subject of the course should
appear on the exam.
-
Why? The word "Why" appears four times on the exam. I looked
for responses to this word.
-
Supporting evidence There are several other places in the
grading rubric where I want some supporting evidence.
Errors? Please ...
In a class of this size, I almost certainly have made errors in
grading. These errors may range from the purely arithmetic ("2+7+3=
... 10 (?) ...") to more subtle ("You ignored my correct answer on the
back of the page."). I try to grade correctly. Please look at the answer sheet supplied and also look at
the description of partial credit
assignment. If you believe I have made errors in grading your exam,
please write a statement supporting your belief and give me the
statement together with your exam.
HOMEWORK
Please read sections 4.3 and 4.4 and hand in these problems on
Thursday:
4.6: 11, 17, 24
4.7: 5, 7, 43
Friday, April 8: this is lecture
22
The second exam.
Tuesday, April 5: this is lecture
21
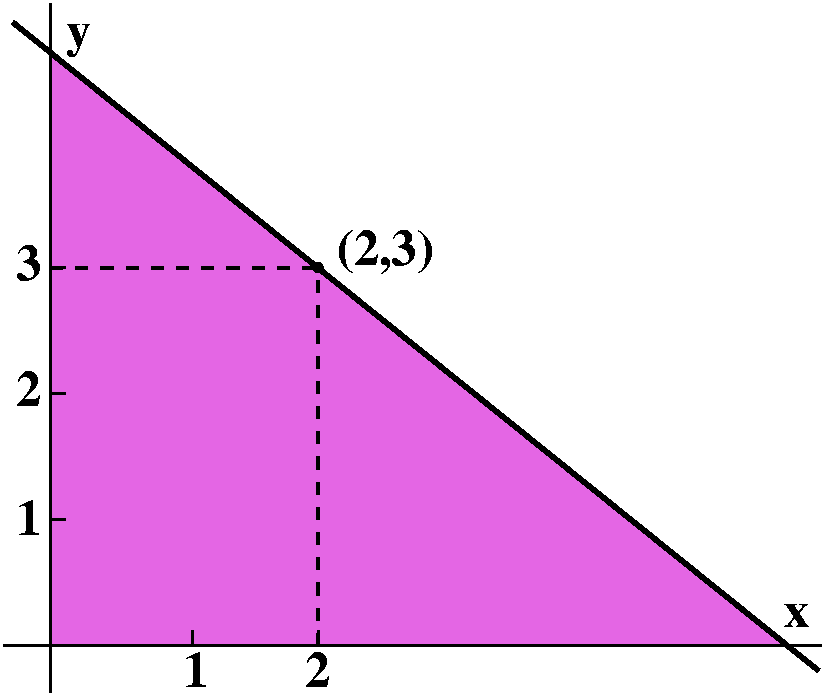 Third max/min problem
Third max/min problem
Suppose a line passes through the point (2,3) and cuts off a triangle
in the first quadrant. What is the area of the triangle which has the
smallest area?
The setup here was more complicated. I drew a picture, something like
what's shown here. and then ... got a triangle. I'll call the base,
x, and the height, y, so that the area is (1/2)xy. We need to minimize
this. But this is two variables. We need a constraint, one or more
restrictions on the variables, perhaps relating them, so that the
function we want to minimize will have only one variable, and the
techniques of Math 135 can be used.
I find the picture useful here. What restrictions on x and y seem to
"follow" (clearly?) from the picture. Certainly x>2 and y>3,
because otherwise a line passing through (2,3) will not cut both the x
and y axes in the first quadrant. There's a more precise restriction
on x and y, caused by the fact that (x,0), (2,3), and (0,y) must all
be on the same straight line. One way of getting an algebraic
condition is to follow a suggestion of a student: these points are on
the same straight line exactly when the slope of the line segment
connecting (x,0) and (2,3) equals the slope of the line segment
connecting (2,3) and (0,y). This means:
0-3 3-y
----- = -----
x-2 2-0
which (cross-multiplying) gives (-3)(2)=(3-y)(x-2). This means
3-y=-6/(x-2) so -y=[-6/(x-2)]-3 so y=[6/(x-2)]+3. I need to minimize
(1/2)xy, so now replacing y by [6/(x-2)]+3 the resulting function is
f(x)=(1/2)x{[6/(x-2)]+3}. The domain of this function is
3<x<infinity.
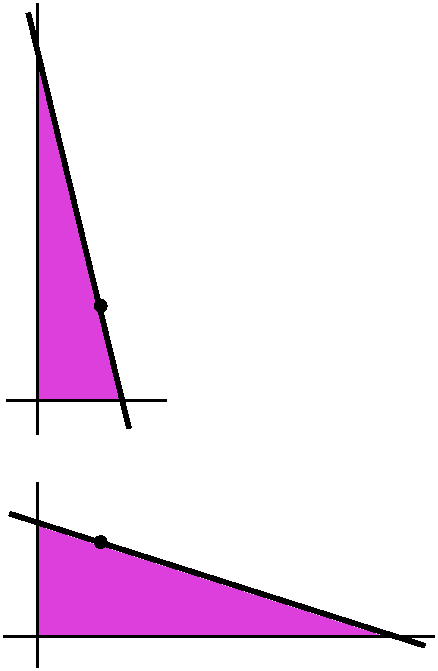
Does this function make sense? Well, if you look at the picture and
you let x-->2+ from the right, then you should see that
you'll get a triangle whose base, x, is very near 2, but whose height,
y, is quite large. Hey: the area-->infinity. On the algebraic side,
consider f(x)=(1/2)x{[6/(x-2)]+3}. If x is near 2 but slightly larger
than 2, the x-2 is a small positive number. But it is in the bottom of
a fraction whose top is 6. I bet that fraction is very large positive:
the function reflects the growth of the area as x-->2+.
On the other hand, if x-->infinity, the geometry as shown gives me a
very wide triangle, whose height gets near 3. But the area will also
be large. And the algebra agrees, since f(x)=(1/2)x{[6/(x-2)]+3}, as
x-->infinity becomes
(1/2)[large{[6/large-2]+3},
and this is (1/2)large{small+3} so it is
guaranteed to be large also.
If you think about it, we have just verified that if there
is only only critical point "inside" the interval, then that critical
point corresponds to a minimum which is an absolute minimum. So we
need to search for critical points, and hope (since this a problem in
a calculus class rather than a real problem) there will be only one,
and we will just about be done.
The vicissitudes of finding f´(x)
were many. By the way, "vicissitude" means, according to one
dictionary, " One of the sudden or unexpected changes or shifts often
encountered in one's life ..." The derivative is:
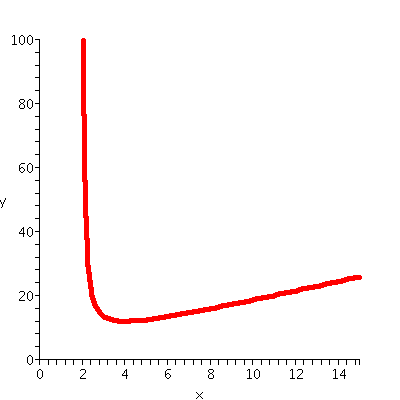 [3/(x-2)]+3/2-{3x/(x-2)2}
[3/(x-2)]+3/2-{3x/(x-2)2}
Never rely on student answers!
and this is
the same as (3/2)[x(x-4)]/(x-2)2. The only way this can be
0 is if the top is 0. But the top is x(x-4). The only root in the
domain of the f(x) in this problem is x=4. So I bet that f(4)=12
is the minimum area.
A graph of f(x)is displayed to the right. I hope you can "see" the
absolute minimum at the point (4,12).
If you look very carefully at the structure of the last two max/min
problems, you will see a weird correspondance between the objective
function and the constraint. They interchange in the two
problems. This weirdness has a name in mathematical economics: the
problems are called dual to one another. This pairing is used
to analyze more complicated problems.
 Fourth max/min problem
Fourth max/min problem
My darling ... is in trouble. She is a half-mile offshore, 4 miles
down from me along a straight beach. Suppose that I can run (hah, if
only I could!) at 10 mph, and swim at 4 mph. What is the best strategy
for me to get to her in the least amount of time?
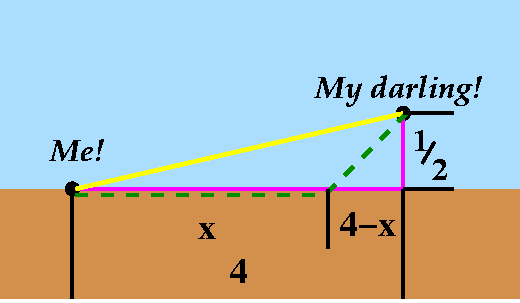
This is a more complicated problem, and we needed to discuss it quite
a while. There are a variety of strategies for "Me" to get to "My
darling". The strategies can be analyzed by assuming that they all
consist of running along the beach for a distance of x miles in a
straight line, followed by swimming along a straight line to the
darling. One extreme "pure" strategy is gotten by taking x=0. This is
shown in the yellow line straight from me to darling. I might want to
follow that strategy if I were a huge turtle. My running speed would
then be rather low, but my swimming speed would be relatively high. I
hope you can see that the "all swimming" strategy then would be a winner,
the least time path. On the other hand, if I were, uhhhh ....,
something which could run very fast but swim really slowly (a cheetah?
Animal science majors: can cheetahs swim?) the best strategy would
likely be to run as much as possible and swim as little as
possible. This would correspond to x=4, shown in red on the picture.
Analysis of a general mixed strategy, the dashed green path
If I run x miles, then (at 10 miles per hour, with
distance=rate·time) the running time would be x/10. How long a
distance will I need to swim? Well, the tilted part of the dashed
green path is the hypoteneuse of a right triangle. The remaining beach
distance is one leg of the right triangle, and is 4-x miles, while the
other leg is 1/2, the miles the darling is offshore. Then Pythagoras
gives the swimming distance as
sqrt{(x-4)2+(1/2)2}, so that (rate/time/distance
again) the swimming time is
sqrt{(x-4)2+(1/2)2}/4. Hey, this is some
function.
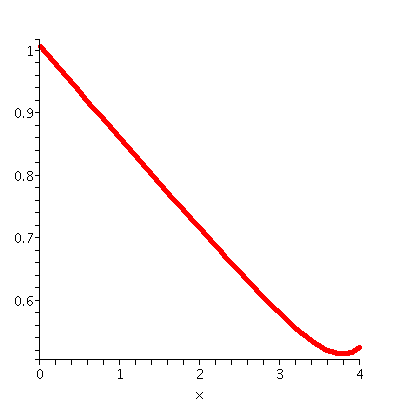 Darling time
Darling time
So we need to find the minimum of
f(x)=(x/10)+sqrt{(x-4)2+(1/2)2}/4 with domain
0<-x<=4. Well, we can graph the darn thing, and see that there
is actually an interior minimum (inside the intervalP, fairly close to 4. I gave up in class, but
(sigh!) you can actually differentiate this and then look for that
critical number, and then plug in. It turns out that the critical
number is 4-(21)-1/2 (this comes from solving a quadratic
equation) and this is approximately 3.781782110 miles and the minimum
time needed is (sigh!) about .5145643941 hours and this is definitely
not clear at all. Here is my secret: I admit that I did
this all with the help of a program called Maple. This
program is available on eden and many other Rutgers computer
systems. Maple can do many of the routine computations of
calculus and can be used as if it were a very smart graphing
calculator with algebraic manipulation capabilities. You should know
that such programs exist. You might need one of them some time.
Outline of things you should know
in
preparation for the exam on Friday
I will not be able to have a review session before this exam. I hope
that Mr. Lin will help you during your recitations. You should attend
the recitations with questions. Specific questions are better than
general inquiries such as, "Do you think this will be on the exam?"
When I run review sessions, the majority of the preparation I do is
writing an outline of the material on the exam. Such an outline is
below. Please let me know if you think I have omitted anything
important.
Students should be prepared for questions on major topics. They should
realize that there are usually several ways to ask about a topic.
This is perhaps most easily illustrated by the direct applications of
the MVT. How could I ask about this? I can give you a formula and ask
you to draw a picture. I could give you numerical properties of a
function, or I could ask about such properties. I could give you a
graph of a function and then ask you about the graph of the derivative
or properties of the derivative. Or I could give the graph of a
derivative and ask about the graph of the function or properties of
the derivative.
There will be a formula sheet. The formula sheet has information about
almost every topic below. I have observed that a need to consult
formula sheets frequently during an exam is usually correlated with
poor performance. Please: you should be familiar with the information
on the formula sheet.
- Differentiation methods
- Chain rule (on the formula sheet)
- Implicit differentiation
- Related rates
- Tangent line/differential
- Formula (on the formula sheet)
- Error {up|down} (from concavity of the function)
- MVT
- If f´(x)>0 then f(x) is increasing.
- If f´(x)<0 then f(x) is decreasing.
- Vocabulary
- {In|de}creasing
- Concave {up|down}
- Relative {max|min}
- Critical {number|point}
- Inflection point
- Absolute {max|min}
- Curve sketching
- Going from formula to picture
- Pictures give function properties
- The vocabulary (above) in pictures
- Asymptotes
- Horizontal: relies on limits as x-->+/- infinity;
possible use of l'Hop.
- Vertical: relies on limiting behavior near endpoints
or holes in the domain.
- Max/min: optimization
- Check critical numbers
- On an interval with endpoints: test endpoints also
- On open interval, what happens towards the edge
- The zeroth derivative test: does the function have
enough information to make conclusions about max/min?
- The first derivative test: use sign of f´(x).
- The second derivative test: use sign of f´´(x).
Apology Should I be writing l'Hopital as
l'Hôpital? If so, I apologize to those of French
ancestry whom I may have offended.
Friday, April 1: this is lecture
20
I discussed certain WeBWork problems which can be handled by
l'Hopital's Rule. The due time for this WeBWork assignment
has been changed to 9 PM, Tuesday, April 5.
L'Hopital's Rule
This is a computational method which can be applied to certain
recalcitrant limits. I don't believe that many
Math 135 students will need to use l'Hop after the course is over, but
it will appear on certain exams. l'Hop is on the formula sheet.
I began with an example, something like this:
What is limx-->0[sqrt(1+3x)-1]/sin(5x)?
Here if we try to plug in (the first thing I'd do if I had a limit
problem involving familiar functions), we get 0/0. This is called an
indeterminate form because you can't conclude anything from
just that much evidence.
Why indeterminate?
Look at these examples which all
have the plug in appearance of 0/0):
- limx-->05x/17x. This limit value is 5/17.
- limx-->088x/5x. This limit value is 88/5.
- limx-->0x2/x. This limit value is 0.
- limx-->0x/x2. This limit value does not exist.
I hope the examples persuade you that you can't predict anything from
just knowing that the situation is 0/0.
But what if we want limx-->0f(x)/g(x) where we know that
f(0)=0 and g(0)=0. The following is not a real proof, but is intended
to be an argument which might help you agree with l'Hop.
Since f(0)=0
and g(0), I know that f(x)/g(x)={f(x)-f(0)}/{g(x)-g(0)} but we can go
on a bit, and divide the top and the bottom both by x-0 to get a
complicated quotient which looks like this:
[{f(x)-f(0)}/{x-0}]/[{g(x)-g(0)}/{x-0}]
If you are clever now, you can see that the top alone would have limit
f´(0) as x-->0 and the bottom similarly would be g´(0). This
is not a real proof, because we used "the limit of the quotients is
the quotient of the limits" and that is really generally valid only
when we know all the limits exist, and l'Hop actually applies where
we don't know the original limit exists. Oh well. Here is a
statement for us to use:
L'Hop Rule
Suppose we want to compute limx-->af(x)/g(x) where f(x) and
g(x) are differentiable functions.
Eligibility criterion Suppose we know that f(0)=0
and g(0)=0.
If limx-->0f´(x)/g´(x)
exists, then limx-->0f(x)/g(x) exists and is equal to
limx-->0f´(x)/g´(x)
This is really what you wanted the quotient rule to be,
isn't it? Admit it!
The example
What is limx-->0[sqrt(1+3x)-1]/sin(5x)?
is exactly suited for l'Hop. We have already checked (with our plug in
attempt) that the eligibility criterion is satisfied (0/0). So we
compute the derivative of the top: (1/2)(1+3x)-1/2(3) and
the derivative of the bottom: cos(5x)5. Now plug in and the quotient
f´(0)/g´(0) is (1/2)3/5, or 3/10.
Note L'Hop can also be used with limmits with x-->infinity. And
it can also be used for indeterminate forms of the type
infinity/infinity.
Student question
"Hey, why didn't you teach us this nifty way of computing limits back
when we started doing limits?" My answer was that we needed to get the
technology of derivatives before we could even state and use
l'Hop.
I reminded people that the eligibility criterion must be checked,
or else you run into something like limx-->0(5+6x)/(7+2x)
which is certainly not the same value as
limx-->0(6)/(2) which could be gotten by applying L'Hop
without thought.
Some WeBWorK problems
These are from my own (personal!) set of problems.
8. (First part)
What is limx-->0[e-15x-1]/[sin(4x)]?
Plug in x=0, and get [1-1]/0, certainly 0/0. Now take the derivative
of the top divided by the derivative of the bottom. The result is
e-15x(-15)/cos(4x)4. Evaluating at x=0 (pugging in) gets us
-15/4.
(Second part)
Consider
limx-->infinity[-15sin(x)+4cos(x)]/x. Why can't we use
l'Hop? Then compute this limit with the Squeeze Technique.
The top function has no limit as x-->infinity, since it
wiggles. What do I know about the top? since the values of sine and
cosine are always between -1 and +1, I know that the top is
between -15-4=-19 and +15+4=19. Therefore we can sandwich or
squeeze when x>0:
-19/x<=[-15sin(x)+4cos(x)]/x<=19/x.
But +/-19/x-->0 as x-->infinity, so the original fraction must
also -->0 as x-->infinity.
9. (First part)
Compute
limx-->0[5x-2x]/x.
When x=0, the fraction becomes [1-1]/0, another 0/0. Remember the
derivative of ax is axln(a). Then the fraction
of derivatives becomes [5xln(5)-2xln(2)]/1. As
x-->0, this -->ln(5)-ln(2), which is the value of the original limit
by l'Hop.
The second part of problem 9 has a limit which reeds two uses of
l'Hop, and the third part suggests a dubious use of l'Hop.
10. (Just part 1)
Evaluate
limx-->0+-2x13ln(x).
Several clever ideas are needed here. First, if we plug in, we get
0·(-infinity), which isn't a l'Hop-type fraction. But we can
change this by algebra:
-2x13ln(x)=-2ln(x)/x-13
We changed a multiplication into a simple fraction, a very weird thing
to do. In this case, however, if we evaluate (plug in) now, we get
0/0. Let's try l'Hop: the derviative of the top is -2/x and the
derivative of the bottom is -13x-14. Now what? We've gotten
rid of ln(x) and are left with powers of x:
[-2/x]/[-13x-14]. But please realize that if we
write this as one power of x, the result is
(2/13)x13, and, as x-->0, this -->0. Whew.
So there are several tricks. One is to convert a multiplication into a
fraction. Then use l'Hop, and then convert back. If you don't believe
the result, I suggest that you ask your graphing calculator for a
picture of -2x13ln(x) for x positive and near 0. I hope the
result will give support to the fact that as x-->0+,
-2x13ln(x)-->0.
I then went on and did some max/min problems, as discussed in section
4.6, the last section of material which will be eligible for next
week's exam.
First max/min problem
Two non-negative numbers have sum 20. How should we choose the numbers
so that the product of the cube of one of them plus the square of the
other is a maximum? There didn't seem to be a useful picture to
draw. So we decided that x+y=20 with x>=0 and y>=0. We needed to
minimize x3·y2. This we reduced to a
calculus problem: find the minimum of
f(x)=x3(20-x)2 with 0<=x<=20.
f(0)=0 and f(20)=0. To be sure of finding the minimum, we need to look
at critical numbers.
f´(x)=3x2(20-x)2+x32(20-x)1(-1).
When is this equal to 0? The easiest way is to factor the mess, since
a product is zero exactly when at least one factor is zero. So:
f´(x)=x2(20-x)(3(20-x)+2x(-1)). This is zero when x=0 and x=20 (whose values we
previously checked) and for x=12 also. If we cube 12 and multiply by
the square of 8, we will get the max. value requested. (110,592).
In some economics applications, "x+y=20 with x>=0 and y>=0" would be
called the constraint and "x3·y2"
would be called the objective function.
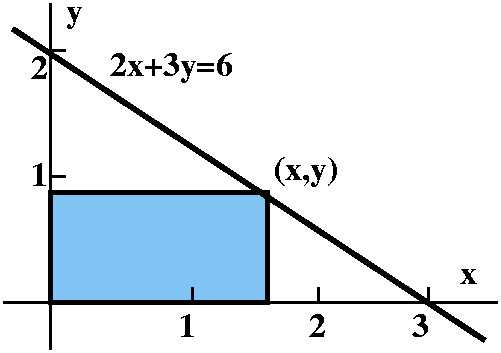 Second max/min problem
Second max/min problem
What is the rectangle of largest area which has two sides on the
positive x- and y-axes and one corner on the line 2x+3y=6?
First we drew some rectangles, just to get a feeling for the
problem. Then I asked how to make the geometry more algebraic: how can
we introduce variables and try to get a function and turn this into a
more routine calculus question. We decided that the corner of the
rectangle on the tilted line could be called (x,y) and then the area
of the rectangle would be xy, so we needed to maximize A=xy. A
constraint relating the two variables x and y was given by the line
2x+3y=6, so that y=2-(2/3)x, and thus A=x(2-(2/3)x). Which x's would
be allowed, I asked? Could we have x=10,000 or x=-10,000? We would be
guided in this by the original problem, and by the diagram which we
had sketched. It showed that candidate x's could vary from 0 to 3. Now
we had a "pure" calculus problem.
What is the maximum of f(x)=x(2-(2/3)x) when 0<=x<=3? Since f(0)=0 and
f(3)=0, we just need to find the critical numbers of f(x). I
multiplied out and got f(x)=2x-(2/3)x2, so that
f´(x)=2-(4/3)x. Since f´(x) exists everywhere in the domain,
the only critical numbers occur when f´(x)=0. The only critical
number of this function was x=6/4=3/2. Then we can find y, etc. So I
declared that we had found the rectangle whose area was maximum.
HOMEWORK
Review for the exam!
Tuesday, March 29: this is lecture
19
I very vaguely discussed the First and Second Derivative Tests, and
asked people to read the presentation and problem solutions which I
wrote in the last diary entry.
Which grows bigger faster?
A casual look at the graphs of
x3 and ex shows that when x gets large positive,
the values of these functions are also large positive numbers. The
question "Which
gets larger faster?" sounds funny but really represents key knowledge
in many applications, where two "processes" are occurring and we'd
like to know, in terms of our mathematical model, what happens for
large values of x. In typical applications, x represents time.
One way to analyze the situation, to see how the growth compares, is
to consider the quotient: x3/e3. This function
is easy enough to graph but I would like to use the methods of
calculus to be sure we understand what happens.
Step 1
This is artificial and a trick, but I hope that you'll see the need
for the trick and where the trick comes from after we're
done. So:
x3 x3 1
---- = -------- · ------
ex e(1/2)x e(1/2)x
What happens on the bottom is a use of
eA+B=eAeB with A=B=(1/2)x. Now I just
want to analyze the first factor, which I will call f(x). So
f(x)=x3/e(1/2)x.
Step 2
If x>0, then f(x) is positive since both x3 and
ex are positive. Now differentiate:
f´(x)=[3x2e(1/2)x-x3e(1/2)x(1/2)]/[e(1/2)x]2.
Here I used the quotient rule and then the chain rule applied to the
exponential part.
The bottom is positive. What about the top? We can factor it:
TOP=[3x2e(1/2)x-x3e(1/2)x(1/2)=x2e(1/2)x[3-(1/2)x].
I hope that what you have learned in the last few lectures is that the
sign of f´(x) is important. Because the bottom is always
positive, we need to know the sign of the top. Well, if x>0, the
first factor, x2 is certainly positive, and the second
factor, e(1/2)x is always positive. What about (3-(1/2)x)?
If x>6, 3-(1/2)x) is negative. Therefore f´(x) is
negative for x>6.
Step 3
Since f´(x) is
negative for x>6, f(x) is decreasing there, so f(x)<f(6)
when x>6. But f(x)<f(6) exactly means
x3/e(1/2)x<63/e(1/2)6.
I will give a name to the number 63/e(1/2)6
since I will get tired typing it. I will call this number TOAD.
So we know that if x>6, f(x)<TOAD.
Step 4
Now we reassemble the original fraction, and make some conclusions. We
started with the positive function x3/ex. We
split it up in step 1, and then in step 3 concluded something. The
specific application we can now make is: if x>6, then
x3 x3 1 1
---- = -------- · ------ < TOAD · ------
ex e(1/2)x e(1/2)x e(1/2)x
Hey: TOAD is a constant, and as x-->infiinity,
1/e(1/2)x=e-(1/2)x decays (exponentially) to 0.
 Now I can answer the original question. As x-->infinity,
x3/e3-->0. So ex grows bigger faster
than x3. The picture should show you that things work o.k.
Now I can answer the original question. As x-->infinity,
x3/e3-->0. So ex grows bigger faster
than x3. The picture should show you that things work o.k.
Huh? What happens when we deal with ... more numbers
I wanted to illustrate that the qualitative behavior is much that
same, so I asked, "Which of x12,304 and e.00027x
grows bigger faster?" Here the numbers are chosen so that the
functions aren't very easy to graph and aren't even very easy to
compute. When, say, x=2, well 212,304 is about
103703 and e(.00027)2 is about 1.00054.
The general shape of x12,304 for large positive x is "clear": it
goes up.
What about e.00027x? Maybe the weird number here confuses
you. Well, this is an expoential so that its values are always
positive. And the value when x=0 is 1. What could I tell you about
other values for positive x's? The derivative of e.00027x
is e.00027x(.00027). This is a positive number. So
e.00027x is increasing. Let's try a specific number. How big is
e.00027(555)? According to the MVT,
e.00027(555)- e.00027(0)
--------------------- = e.00027(c).00027
(555-0)
The stuff on the right-hand side is the derivative at c. The value of
the right-hand side is at least .00027 since the exponential is at
least 1. If you untwist this fraction, you can see that
e.00027(555) is at least 1+(.00027)(555). Hey, the bigger
the number is, the bigger this underestimate is.
Any exponential of the form ekx with k positive is
increasing, and eventually grows beyond any bound.
Now back to business:
Which of x12,304 and e.00027x grows bigger
faster? I need to analyze
x12,304/e.00027x as x-->infinity.
I will write everything in a fashion similar to the analysis above.
Step 1
This is artificial and a trick, but I hope that you'll see the need
for the trick and where the trick comes from after we're
done. So:
x12,304 x12,304 1
-------- = --------- · -------
e.00027x e.0002x e.0007x
What happens on the bottom is a use of
eA+B=eAeB with A=.0002x and
B=.00007x. Now I just
want to analyze the first factor, which I will call f(x). So
f(x)=x12,304/e.0002x.
Step 2
If x>0, then f(x) is positive since both x12,304 and
e.0002x are positive. Now differentiate:
f´(x)=[12,304x2e.0002x-x12,304e.0002x(.0002)]/[e.0002x]2.
Here I used the quotient rule and then the chain rule applied to the
exponential part. The bottom is positive. What about the top? We can
factor it:
TOP=[12,304x2e.0002x-x12,304e.0002x(.0002)=x12,303e.0002x[12,304-.0002x].
I hope that what you have learned in the last few lectures is that the
sign of f´(x) is important. Because the bottom is always
positive, we need to know the sign of the top. Well, if x>0, the
first factor, x12,303 is certainly positive, and the second
factor, e.0002x is always positive. What about
(12,304-.0002x)? This factor is 0 if x=12,304/.0002. The name I'll
give this number is FROG. If x>FROG, 12,304-.0002x) is
negative. Therefore f´(x) is negative for x>FROG.
Step 3
Since f´(x) is negative for x>FROG, f(x) is decreasing
there, so f(x)<f(FROG) when x>FROG. But f(x)<f(FROG) exactly
means
x12,304/e.0002x<FROG12,304/e(.0002)FROG.
I will give a name to the number FROG12,304/e(.0002)FROG
since I will get tired typing it. I will call this number TOAD.
So
we know that if x>FROG, f(x)<TOAD.
Step 4
Now we reassemble the original fraction, and make some conclusions. We
started with the positive function x12,304/ex. We
split it up in step 1, and then in step 3 concluded something. The
specific application we can now make is: if x>FROG, then
x12,304 x12,304 1 1
-------- = --------- · -------- < TOAD · -------
e.00027x e.0002x e.00007x e.00007x
Hey: TOAD is a constant, and as x-->infinity,
1/e.00007x=e-.00007x decays (expponentially) to 0.
Now I can answer the original question. As x-->infinity,
x12,304/e.00027x-->0. So e.00027x
grows bigger faster than x12,304. In fact,
(1010)12,304 is 10123,040 and
e.00027(1010) is larger than
101,172,595. So there!
Poly versus exp
|
Any sort of polynomial growth, no matter how big the degree is, is
eventually slower than any sort of exponential growth, no matter how
small the positive exponential constant is. |
Asymptotes
There is a companion geometric language to the algebraic stuff. We
verified that
limx-->infinityx12,304/e.00027x=0.
This means that the graph of the function gets closer to the x-axis,
the line y=0. This horizontal line is called a horizontal
asymptote of y=x12,304/e.00027x. There are
also vertical asymptotes.
Graphing [(x-3)(x-5)]/(x-1)
Here are some comments and a series of pictures which I hope will show
you how relatively straightforward manipulations can give a fairly
good picture of a graph.
I tried to consider the graph of y=[(x-3)(x-5)]/(x-1). I remarked that
I would like to see how much information I could get about the graph
without using a graphing calculator. Certainly I can get the
x-intercepts. The only places that y=0 on this graph are at 3 and 5,
so that (3,0) and (5,0) are on the graph. | 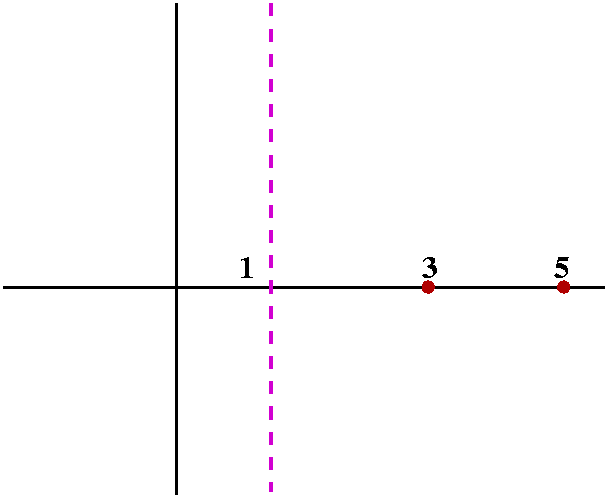 |
|
What about when x gets large
positive? Well, there are two powers of x on top, and only one power
of x on the bottom, so I bet that y gets large also. What is perhaps
more interesting is the x-1 on the bottom of the fraction.
|
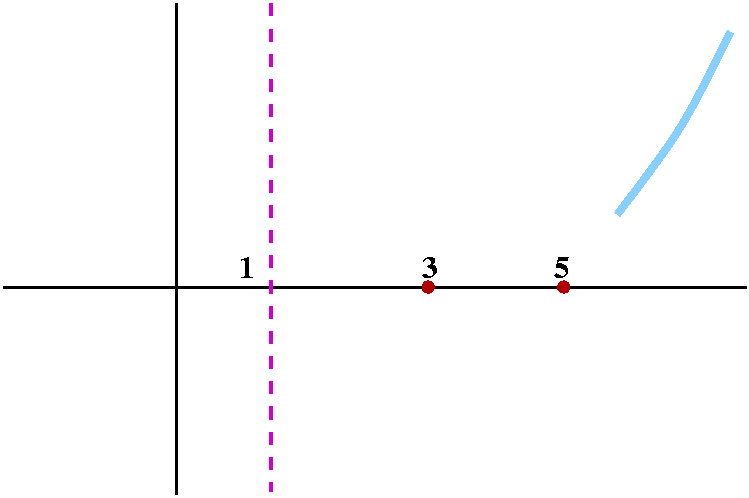 |
|
1 is not in the domain of [(x-3)(x-5)]/(x-1). What happens as
x-->1+, that is, x approaches 1 from the right? The top
gets close to (1-3)(1-5) which is 8. The bottom, x-1, is a small
positive number. So the quotient is 8/[small +]. This is a large
positive number. So as x-->1+, y-->+infinity.
| 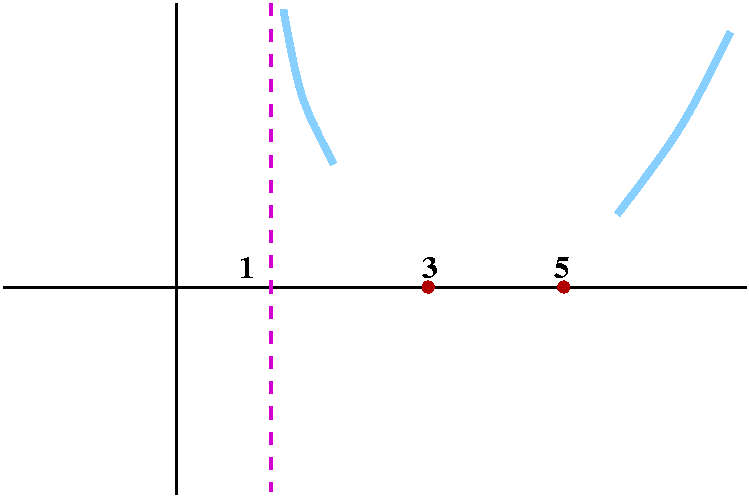 |
|
What happens as x-->1-, that is, x approaches 1 from the
left? The top gets close to (1-3)(1-5) which is 8 (just the same as
before). The bottom, x-1, is now a small negative number. So
the quotient is 8/[small -]. This is a large negative number. So
as x-->1-, y-->-infinity.
|
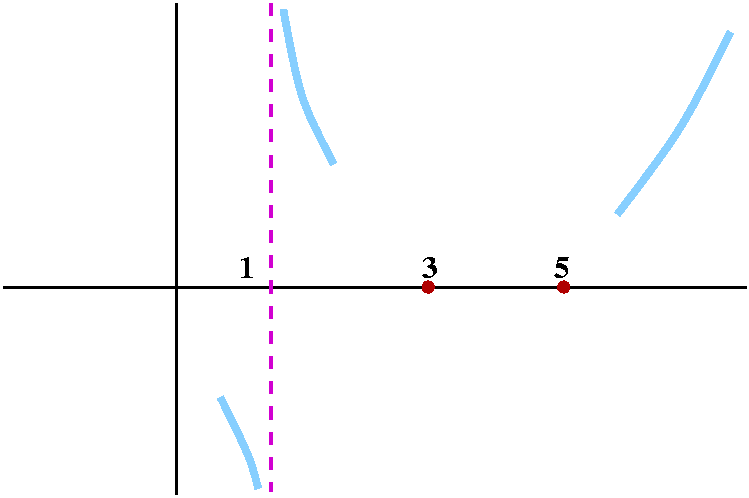 |
|
The vertical line x=1 is a vertical asymptote of
y=[(x-3)(x-5)]/(x-1). Now as x-->-infinity, the sign of y is
negative, and, again because there are two powers of x on the top and
only one on the bottom, y-->-infinity.
|
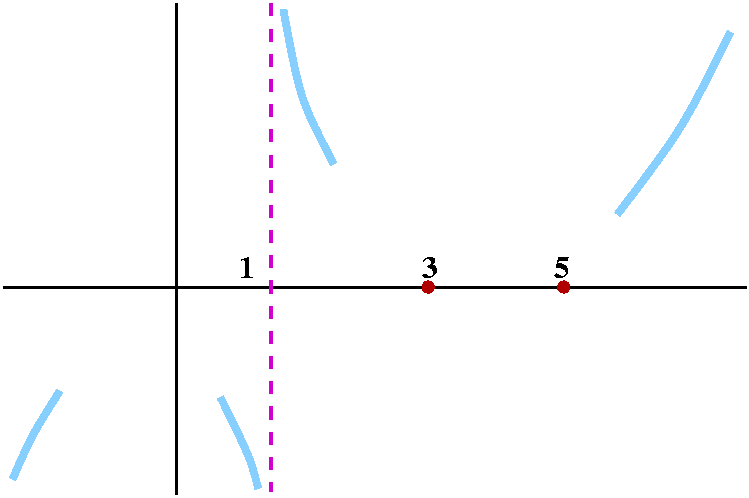 |
|
As I remarked in class, if we sort of interpolate the information we
already have in the simplest manner possible, we can guess at what the
graph looks like. In particular, the graph seems to have two critical
points. I wanted to check that.
|
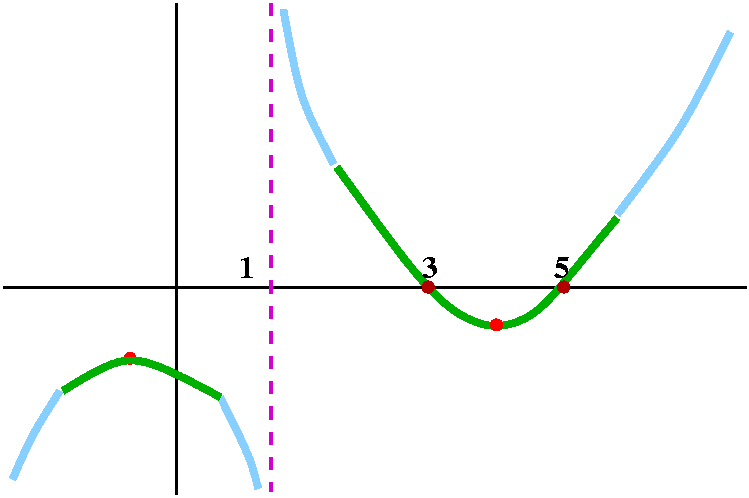 |
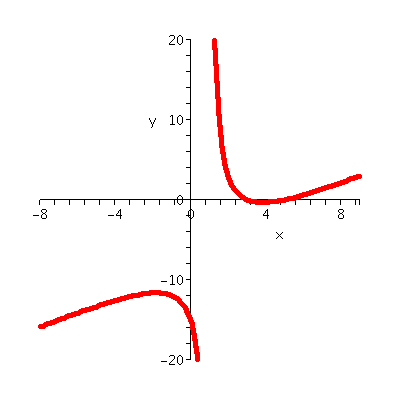 Well, y=[(x-3)(x-5)]/(x-1). I'll expand the top to differentiate it
more easily: y=[x2-8x+15]/[x-1]. Then
Well, y=[(x-3)(x-5)]/(x-1). I'll expand the top to differentiate it
more easily: y=[x2-8x+15]/[x-1]. Then
dy/dx=[(2x-8)(x-1)-(x2-8x+15)(1)]/(x-1)2=
[2x2-10x+8-x2+8x-15)]/(x-1)2
[x2-2x-7]/(x-1)2. Where is this fraction equal
to 0? Well, the roots of the quadratic top are at
[+2+/1sqrt{(-2)2-4(-7)}]/2. This is 1+/-sqrt{29}. The roots
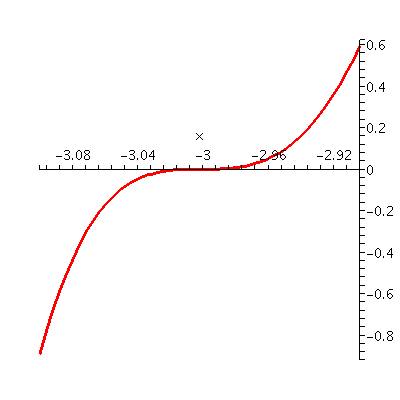
are at about 3.828 and -1.828, which you can see in the "real" graph I
had a computer draw.
Thursday:
4.3: 19, 28, 37, 40;
4.4: 9, 11, 15, 23.
Exam warning
The second exam will be on Friday, April 8. It will concentrate on the
material covered since the first exam, up to and including section
4.6. Please see the home page for review material, including the
formula sheet which will be distributed with the exam.
Friday, March 25: this is lecture
18
| Paradigm |
|---|
|
The Oxford English Dictionary says that paradigm, meaning
"A pattern, exemplar, example" was first used in (written) English
in 1483. I graphed y=x3-x and y=3x2-1 and y=6x.
I wanted to use the function f(x)=x3-x as a (relatively)
simple example of the material in section 4.3. There is a lot of
material in section 4.3.
This part of the text discusses the relationships between the graphs
of a function and its first and second derivatives. For example, (this
was my one moment of theory in the lecture), we know from the
MVT that there's a c between a and b so that
f´(c)=[f(b)-f(a)]/[b-a]. But look: if b>a and if f´(c) is
positive, then f(b)-f(a) must be positive so f(b)>f(a). Therefore:
If f´(x) is positive, then f(x) increases (the graph goes
up
as we travel from left to right).
Similarly:
If f´(x) is negative, then f(x) decreases (the graph goes
down
as we travel from left to right).
|
It's usually easier to see if a function is positive or negative,
rather than try to deduce directly if another function is increasing
and decreasing.
For example, here I look at f´(x)=3x2-1. I hope that
you believe the graph and, what's more, you see that the roots of this
quadratic are at {+/-}1/sqrt(3). Hey: to the left of -1/sqrt(3), the
function is increasing. I don't think the following is obvious:
f(-500)=(-500)3-(-500) is less than
f(-500)=(-400)3-(-400). And I don't need to compute those
numbers, either.
The second derivative shows how the slope of the tangent line changes
as we travel from left to right. If the second derivative is
positive in an interval, then the first derivative is
increasing in that interval, so as we "move" from left to
right, the slopes rotate "up" or counterclockwise. The graph of the
original function lies above the tangent lines in this case,
and the graph bends up: it is concave up. A similar phenomenon occurs
when the second derivative is negative. Summarizing:
If f´´(x) is positive, then f(x) lies above its tangent
lines:
the graph is concave up.
If f´´(x) is negative, then f(x) lies above its tangent
lines:
the graph is concave down.
|
Points where the graph switches concavity are called inflection
points. The situation is very analogous with first derivatives and
relative {max|min}s. So:
If a function is differentiable, its relative extrema (maxes
and mins) must occur at critical points where f´(x)=0.
If a function is differentiable, its inflection points (where
concavity changes) must occur where f´´(x)=0.
|
| 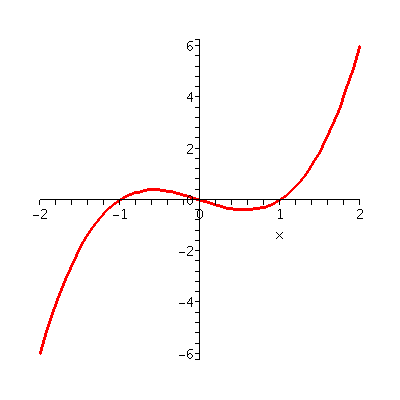
Graph of the function,
f(x)=x3-x
|
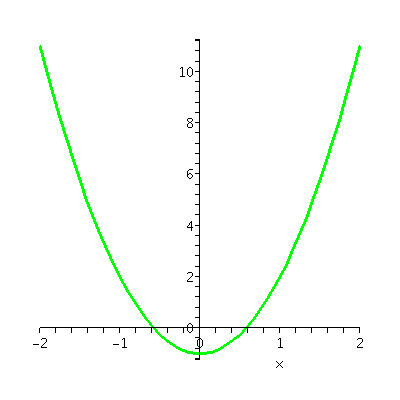
Graph of the first derivative,
f´(x)=3x2-1
|
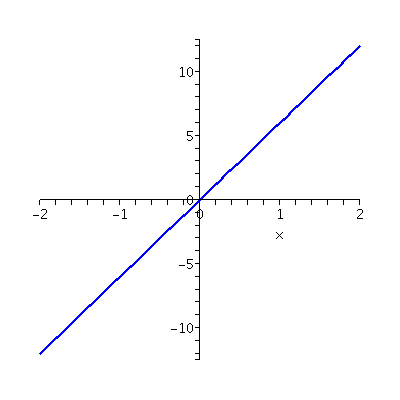
Graph of the second derivative,
f´´(x)=6x
|
The success of this approach is really how well it does in
practice. So let me do a sequence of problems, first one from
WeBWork and then a bunch of problems from section 4.3.
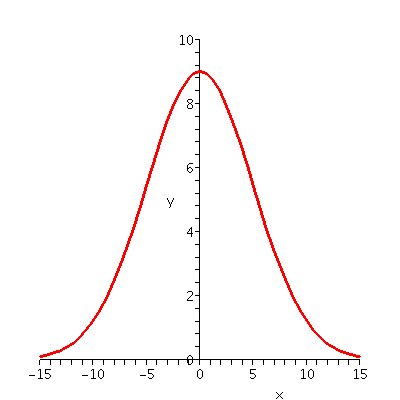 A WBWorK problem
A WBWorK problem
Suppose f(x)=9e-x2/50. Find the absolute maximum
of f(x) and find the x-coordinates of the inflection points of
f(x).
I said in class that generally the first thing I'd probably do is
use a graphing calculator to get some idea of what the function's
graph looks like. But you may not be
very familiar with how the calculator works, and
many keystrokes can be necessary to enter the function. A more
irritating problem is that the window for a suitable graph may
not be obvious. Unfortunately, the window problem is real and can't be
avoided, except for almost the simplest functions. And, of course, it
reflects difficulties in reality: what sizes are useful to deal with
particular phenomena (weights in milligrams might be good to handle
hummingbird food, but not so useful in discussing the diets of
elephants).
A graph is displayed to the right. The window is [-15,15] for x and
[0,10] for y. The absolute max
seems to occur when x=0. The value of this max is f(0)=9
since e0=1. Near the max, the curve is concave down. Out
towards the edges (where the curve is asymptotic to the x-axis) the
curve seems to be concave up. An initial guess would be that there are
at least two inflection points, one positive and one negative,
symmetric with respect to the origin.
Confirming the picture
Here we differentiate and do the algebra. If
f(x)=9e-x2/50 then
f´(x)=9e-x2/50(-2x/50) using the chain
rule. The second derivative needs both the product rule and the chain
rule:
f´#180;(x)=9e-x2/50(-2x/50)2+9e-x2/50(-2/50).
Now we try to find critical points, and therefore we search for x's
satisfying f´(x)=0 which is the same as
9e-x2/50(-2x/50)=0. Notice
The exponential function is always positive and never 0.
Therefore the only way 9e-x2/50(-2x/50) can be 0 is if
(2x/50)=0 or x=0. So 0 is the only critical point. Also please notice
that if x<0, 9e-x2/50(-2x/50)=0 is
positive (because of the minus sign in front of the 2x). Also
the first derivative is negative for x>0. This means that f(x)
increases to the left of 0 and decreases to the right of 0. So f(0)=9
must be the absolute max of f(x).
Let's look at f´´(x)=0 which is
9e-x2/50(-2x/50)2+9e-x2/50(-2/50)=0.
This is a more complicated expression. To see if "something"=0, if I
can factor the "something" then I will get A·B=0 which occurs
exactly when either A=0 or B=0. The factors here practically yell at
us, I think.
9e-x2/50(-2x/50)2+9e-x2/50(-2/50)=0
becomes
[9e-x2/50]·[(-2x/50)2+(-2/50)]=0.
Again, the exponential function (the "A") is never 0, so we need to
know when (-2x/50)2+(-2/50)=0. This is (square it
correctly!) [(4x2)/502]-2/50=0 or
[(4x2)/502]=2/50. Multiply by 502 and
divide by 4 to get x2=25 so that x=+/-5. Hey: here are the
x-coordinates of two inflection points which we saw.
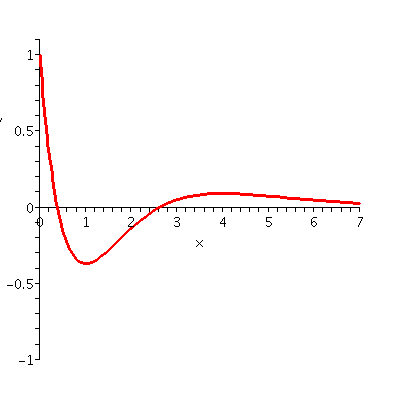
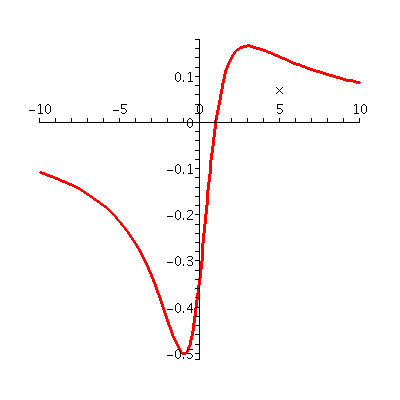 Textbook problem 4.3 #17
Textbook problem 4.3 #17
Well, I certainly wasted some class time with this problem. Let's
start: Here f(x)=(x-1)/(x2+3). The textbook requires
(please look at it) all of the information that can be gotten from the
first and second derivatives. So we need to find critical numbers,
intervals where the function is {in|de}creasing, critical points and
relative {max|min}'s, intervals of concavity ({up|down}), and
inflection points. To the right is a graph in the window where x is
between -10 and 10. I tried several candidates for the y interval to
get the good view shown of the curve. There seems to be two critical
points, one a max and one a min. Close inspection allows us toe guess
that there will be three inflection points. "Far" to the left the
curve looks concave down, then at the relative min it is concave up,
and then at the relative mx the concavity flips again down, and,
finally, away to the right the concavity is up. Please keep this in
mind as we do the algebra and the resulting computations.
The first derivative
The quotient rule gives
f´(x)=[1·(x2+3)-2x·(x-1)]/(x2+3)2.
At least this isn't as horrible as one might think. The bottom is a
square, and it is always positive. The sign of the fraction and
whether or not the fraction is 0 is totally ruled by the top. The top
is
1·(x2+3)-2x·(x-1)=x2+3-2x2+2x=-x2+2x+3.
Well, -x2+2x+3=-(x2-2x-3)=-(x-3)(x+1). Should I
say "clearly" here since I messed up my first factorization attempt in
class. Well, the roots are x=3 and x=-1. I bet these are
critical numbers (look at the picture!). What about the critical
points? These should be the points on the curve corresponding to the
critical numbers. The second coordinates will be gotten using
f(x)=(x-1)/(x2+3). So (-1,-1/2) and (3,1/6) are the
critical points. The function is increasing on the interval [-1,3]
and is decreasing on the two intervals (-infinity,-1] and [3,infinity).
The second derivative
We've got to differentiate
(-x2+2x+3)/(x2+3)2 so we will use the
quotient rule. Sigh. Therefore
f´´(x)=TOP/BOT where
TOP=(-2x+2)(x2+3)2-(-x2+2x+3)2(x2+3)(2x)
BOT=[(x2+3)2]2=(x2+3)4
Some thought will save some pain. Since TOP and BOT are part of a
fraction, we can factor and then delete any multiples which all
terms have. One thing that appears everywhere is
x2+3. There are four of these in BOT, and two in the first
part of TOP and one in the second part of TOP. Therefore I will drop
one power of x2+3, and get
f´´(x)=[
(-2x+2)(x2+3)-(-x2+2x+3)2(2x)]/(x2+3)3. The bottom of
this expression is always positive, so I can check for sign and for
where f´´(x)=0 just be considering the top. Wow, I
guess. Now the top of this expression for f´´(x) is
(-2x+2)(x2+3)-(-x2+2x+3)2(2x) which is
-2x3-6x+2x2+6+4x3-8x2-12x
and this is
2x3-6x2-18x+6
How to waste time pointlessly ...
Well, everyone has their favorites, but one of mine is to try to "solve"
an equation like 2x3-6x2-18x+6=0 or (dividing by
2)
x3-3x2-9x+3=0. I thought (darn it!) since this
was a textbook problem we could maybe get integer or simple fraction
solutions. Let me be polite to myself: this turns out not to be the
case. The only nice observation I made at this stage was to note that
since we've got a degree 3 polynomial, the roots will probably be the
three inflection points we guessed when we looked at the
graph. Well, after several students pushed and pushed, I yielded: the
roots seem to be (approximately!)
-2.06417 and .30561 and 4.75877. Yes, these are gotten from
silicon-based objects, not carbon-based objects, that is, from
calculators/computers, not my feeble brain. Sigh. These are the
x-coordinates of the three inflection points. From these, you can
state where the graph is concave up and concave down. I am
embarrassed.
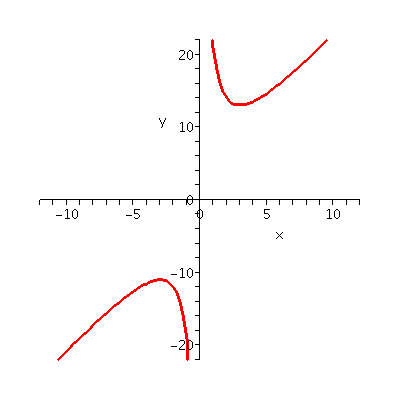 Textbook problem 4.3 #21
Textbook problem 4.3 #21
Here f(x)=1+2x+18/x. A quick graph is shown to the right, but even
with the relatively simple function, I admit that I played with the
window (finally showing you [-12,12] by [-21,21]) in order to get
something that I thought showed the curve nicely.
The first derivative
So f´(x)=0+2-18x-2. Hey I thought 18/x=18x-1
so the derivative of that piece is -18x-2. When is
2-18x-2=0? I would multiply by x2 and divide by 2
so that I get x2-9=0. I bet that the critical
numbers are +/-3 (look at the picture!). What about the critical
points? Well f(3)=1+2(3)+18/3=13 and f(-3)=-11, so that (3,13) is a
critical point (and a relative min) and (-3,-13) is a critical point
(and a relative max). The intervals of increase and decrease should be
apparent to you, I hope. f(x) is increasing on (-infinity,-3] and
[3,infinity) and f(x) is decreasing on [-3,0) and (0,3]. Please, there
is one "wrinkle" that happens here which has not previously
appeared. The domain of f(x) does not include 0, so therefore 0
should not be in any of the intervals we specify
({in|de}crease, concave {up|down}). In fact, you can look at the
picture and see that f(x) is not decreasing if you pack the
values [-3,0) and (0,3] together. Why? Well, f(-1)=-19 and f(1)=21 so
f(-1)<f(1). So there is some care and precision needed when the
domain has "holes".
The second derivative
Since f´(x)=0+2-18x-2,
f´´(x)=36x-3. Look at the graph, please! When x
is negative, the second derivative is negative (-3 is an odd integer
and odd powers of negative numbers are odd). Therefore f(x) is concave
down in (-infinity,0). Similary, f(x) is concave up in
(0,infinity). But here is the wrinkle again: f(x) has no points
of inflection, since 0 is not in f(x)'s domain. The official
definition of a point of inflection (p.207 of the text) begins, "A
point P(c,f(c) on the curve is called an inflection point ..."
and there is no point on the curve when c=0. So trick answer:
this curve has intervals where it is concave up and concave down, but
it has no point of inflection.
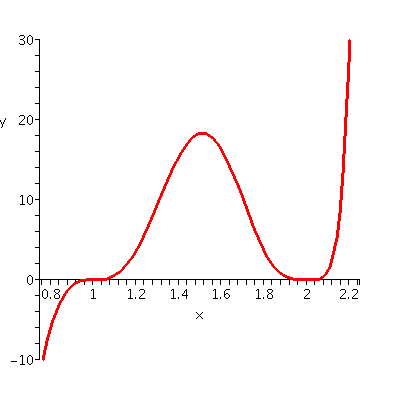
Textbook problem 4.3 #26
Here f(t)=(t3+3t2)3. O.k.: I said in
class that you should reach for the graphing calculator first. Here's
a case where good pictures are hard to get.
too big
Look at the
function. What are some values? Well, f(0)=0 (not too bad) but
f(1)=43=64 and
f(2)=(8+3·4)3=(20)3=8,000. So if you look
at this thing in a window like [-5,5] by [-5,5] you will miss
lots of stuff because the function is too big.
|
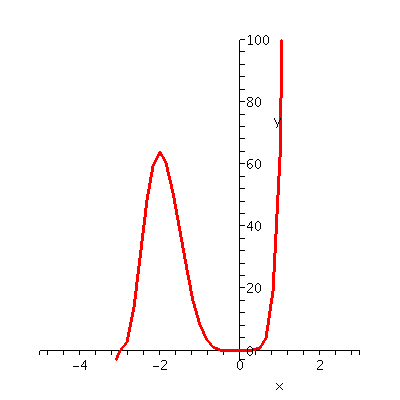
|
|
too small
Actually the situation is even worse for
the casual user of an electronic graphing device. Look at the first
picture, which I think is in the window [-4.5,2.5] by [-2,100]. Of
course we seem to be missing information on the left. Why? Well, for
example, f(-4) is the third power of
(-4)3+3(-4)2=-16 and this is -4096. O.k., so we
lose that. What is worse is the situation around x=-3. Golly, here the
function is too small. I don't
see anything too interesting in the big picture near -3. The second
picture, below the first, is in the ludicrous (at first consideration,
anyway) window [-3.1,-2.9] by [-.85,.62]. This window is really
focused at (-3,0). I only asked for this picture after I did
the work below. In some sense, I cheated. In fact, I got both windows
only after I did the algebraic work. In this case, the algebra guided
my use of the graphing device. Sometimes things can be very, very
strange.
|
|
The first derivative
Since f(t)=(t3+3t2)3,
f´(t)=3(t3+3t2)2(3t2+6t)
(the chain rule). This is already in a nicely factored form. It will
be equal to 0 when either t3+3t2=0 or when
3t2+6t=0. So
t3+3t2=t2(t+3) so there are critical
numbers at 0 and -3. And 3t2+6t=3t(t+2), so there is an
additional critical number at -2. What kinds of realtive {max|min} can
we expect? Hey, if we already know the pictures, then we know the
answers, but, as I wrote above, I got the pictures after I did
this. Since
f´(t)=3(t3+3t2)2(3t2+6t),
I can tell you that (after I think a bit!)
f´(t)=3(t3+3t2)2(3t2+6t)
is actually 3t3(t+2)(t+3)2. Here is where it
gets interesting (or difficult, depending on your attitude). There is
a sign change in f´(t) at -2 and 0 since the exponents of the
corresponding factors are both odd (1 and 3). But we've got
(t+3)2. When you look near the left and right sides of -3,
the square doesn't change sign. So -3 won't correspond to either a
relative max or a relative min. Sigh. Or look at the pretty pictures,
and hope that someone else will always be responsible for the pretty
pictures.
The second derivative
Since
f´(t)=3(t3+3t2)2(3t2+6t),
f´´(t)=6(t3+3t2)1(3t2+6t)2+3(t3+3t2)2(6t+6),
using both the product rule and the chain rule. Let me try to factor
this mess.
FROM HERE ON UNTIL THE QOTD I DID NOT DO THIS
STUFF IN CLASS. THE DETAILS ARE ... PAINFUL. BUT DUE TO POPULAR
DEMAND, I'M WRITING ALL THIS JUST FOR YOU!
I guess
6(t3+3t2)1(3t2+6t)2+3(t3+3t2)2(6t+6)=[6(t3+3t2)]·[(3t2+6t)2+3(t3+3t2)2(t+1)].
When it this mess equal to 0? One factor is
6(t3+3t2) and this is 0 when t=0 and t=-3.
The other factor is
(3t2+6t)2+3(t3+3t2)2(t+1). Ummmm
.... not clearly, this is 18 t4(2t+5)(2t+3)(t+3). I
refuse to write out the details. There are exactly three
inflection points. 0 is not an inflection point, because it is a
relative min, and the curve is concave up in an interval around 0. But
the numbers -5/2 and -3/2 and -3 are all inflection points. This
computation should not be shown to anyone under the age of 25.
Textbook problem 4.3 #38
The text states: "use the first-derivative test to classify each of the
given critical numbers as a relative minimum, a relative maximum, or
neither." The function in this problem is
f(x)=(x2-4)4(x2-1)3 and
the critical numbers given are x=1 and x=2.
The first derivative test for what happens at a
critical point
|
|---|
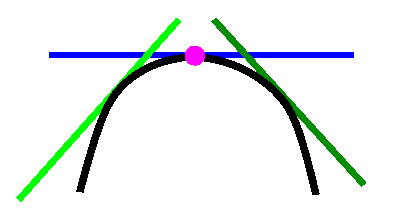
IF
immediately to the left,
the first derivative is positive
and
immediately to the right,
the first derivative is negative
THEN
there's a relative max. |
|
|
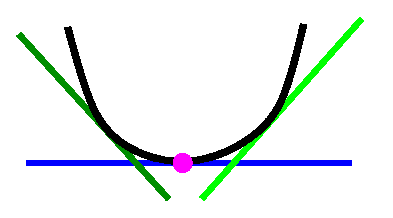
If
Immediately to the left,
the first derivative is negative
and
immediately to the right,
the first derivative is positive
THEN
there's a relative min. |
|
|
IF
the signs of the derivative are the same on
both sides
THEN
the critical point is an
inflection point. |
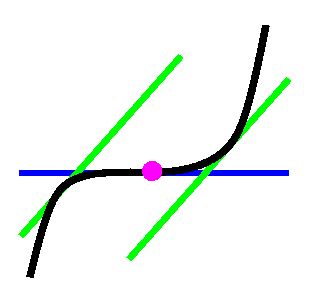 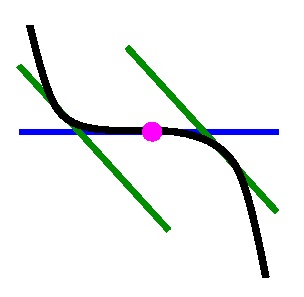
|
The picture gives it all away, but I will do the horrible algebra.
Since f(x)=(x2-4)4(x2-1)3
we get
f´(x)=4(x2-4)3(2x)(x2-1)3+(x2-4)43(x2-1)2(2x)
using the chain rule and the product rule. I'll factor this mess:
f´(x)=(x2-4)3(2x)(x2-1)2
[4(x2-1)+(x2-4)3]
What happens near x=1?
Near x=1, the factor (x2-4)3 looks to me like
(-3)3, negative.
Near x=1, the
factor 2x looks like 2, positive.
Near x=1,
the factor (x2-1)2 looks, well, the exponent is
even so I bet it is positive (except
exactly at x=1 where it is 0).
Near x=1, the factor
4(x2-1)+(x2-4)3 looks like ... uhhh ... 0 (from
the 4(x2-1) term) and -9 (from the (x2-4)3
term), so it looks negative.
The result (the
product of everything) is that the sign of the derivative looks
positive on both sides of x=1.
What happens near x=2?
Near x=2, the factor (x2-4)3 does change
sign because the power, 3, is odd. On the left, if x is a bit less
than 2, x2 is less than 4, so x2-4 is negative,
and the cube of this is negative. On the right, if x is a bit more
than 2, x2 is larger than 4, so x2-4 is positive
and the cube of this is positive.
Near x=2, the
factor 2x looks like 4, positive.
Near x=2,
the factor (x2-1)2 looks like
(22-1)3 which is positive.
Near x=2, the factor
4(x2-1)+(x2-4)3 looks like ... uhhh ... 12 (from
the 4(x2-1) term) and 0 (from the (x2-4)3
term), so it looks positive.
If you collect all this sign information, then the sign of the
derivative goes from negative to positive at x=2, so this must
be a relative minimum.
Hey: we can see this in the darn graph! This is a lot of work. Who cares?
Textbook problem 4.3 #42
Here the text states: "use the second-derivative test to classify each of the
given critical numbers as a relative minimum, a relative maximum, or
neither." The function in this problem is
f(x)=(x2-3x+1)e-x
and
the critical numbers given are x=1 and x=4.
The second derivative test for what happens at a
critical point
|
|---|
IF
the second derivative at
the
critical number is positive
THEN
there's a relative max. |

|
|
IF
the second derivative at
the
critical number is negative
THEN
there's a relative max. |

|
|
IF
the second derivative at
the
critical number is zero
THEN
no conclusion can be made. |
NO BENDING
INFORMATION IS
AVAILABLE. |
|
Again, the picture tells us what's going on, but I'll do the second
derivative test. Since f(x)=(x2-3x+1)e-x,
f´(x)=(2x-3)e-x+(x2-3x+1)e-x(-1)
(product rule and chain rule). Let me rearrange this slightly:
f´(x)=[(2x-3)+(x2-3x+1)(-1)]e-x=(-x2+5x-4)e-x.
Therefore
f´´(x)=(-2x+5)e-x+(-x2+5x-4)e-x(-1)=
[(-2x+5)+(-x2+5x-4)(1)]e-x=
(x2-7x+9)e-x.
What happens near x=1?
Since
f´´(1)=(12-7·1+9)e-1=3e-1
and values of ex are all positive, we see that
f´´(1)>0, so by the Second Derivative Test, f(x) has a
relative minimum at x=1.
What happens near x=4?
f´´(4)=(42-7·4+9)e-4=-3e-1
and values of ex are all positive, we see that
f´´(1)<0, so by the Second Derivative Test, f(x) has a
relative maximum at x=4.
Again, why does this matter, since we can see all this in the darn
graph! This is a lot of work. Who cares?
QotD
I drew a graph of a function on the board. I asked that students do
the following:
- Copy the graph carefully.
- Label each relative max with an M, each relative min with
an m, and each inflection point with an I.
- Draw another graph which is the graph of the derivative of the
function whose graph I drew.
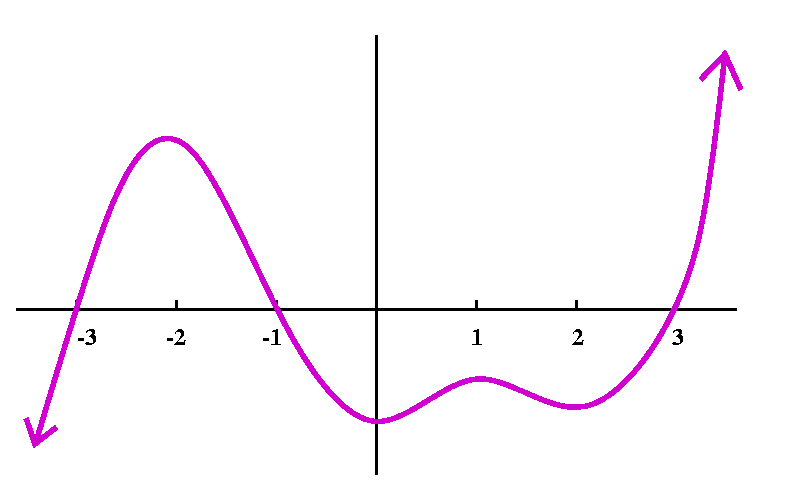
This exercise is an antidote to all the algebra. It is a qualitative
exercise, which means that reasonable people (even the instructor!)
can disagree about exact details. For example, I did not mean to have
inflection points out on the edges, but I am sure that some students
saw such points there.
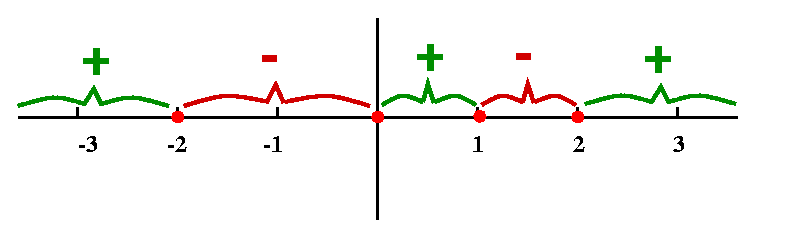
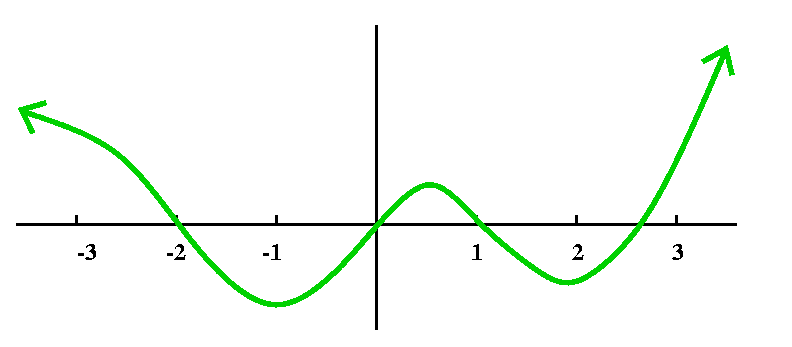
A solution to the QotD
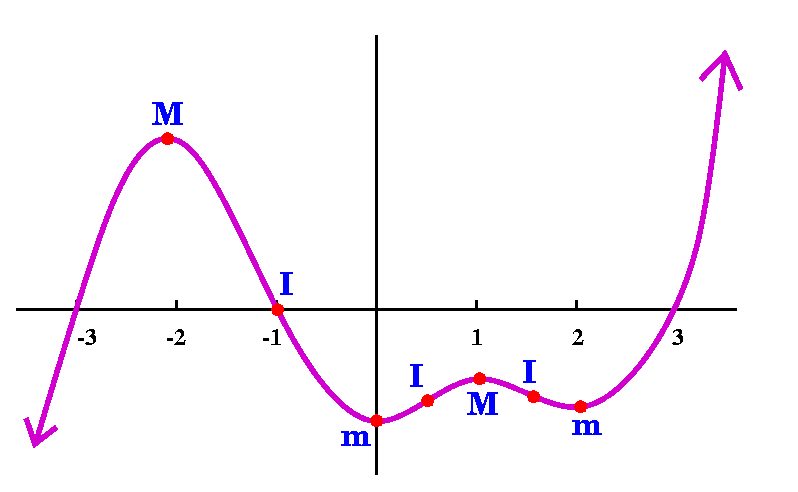
A simple sketch of the derivative follows mostly from noticing the
signs of the the slopes of the tangent lines.
Here is one possible answer:
Why should anyone care?
So there seem to be several ways to characterize maxes and mins. This
is good because sometimes what works in one situation doesn't work in
another. Also, because in some applications, the first and second
derivatives turn out to have important meaning in the subjects. For
example, I loathe the second derivative test because computing
second derivatives turns out to be very irritating for any moderately
complicated function. But in economics, the second derivative test is
very useful to describe certain max/min situations. Also, you should
realize that the examples we've been looking at usually can be graphed
easily (but not even all of them). In practice, the scale of certain
processes is not clear. Again, in biochemical reactions, some processes
occur much faster than others. Just graphing without any thinking
frequently may omit very useful information. The information could be
discerned by looked at the first and second derivatives.
joke?
Tuesday, March 22: this is lecture
17

Welcome to spring!
Review of the last lecture
Stuff to memorize:
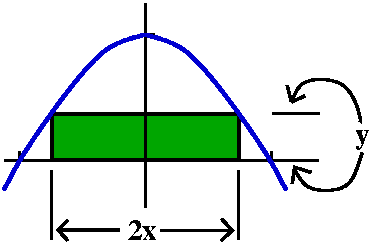 One example
One example
Here is an example of a problem which our "technology" can now handle
quite well. Consider the graph of y=1-x2. This is a
parabola opening downwards, with its vertex at (0,1) as shown in the
picture to the right. There is a region in the plane whose boundary is
an interval ([-1,1]) of the x-axis and the "top" arch of the
parabola. What is the rectangle inside that region whose area is
largest?
I do not believe this is a profound problem, but it is certainly a
problem whose exact solution is not obvious. There are many rectangles
inside that region of the plane. We can "swell up" a rectangle until
it touches the boundary, and then rotate the rectangle. Some thought
should convince you that the largest rectangle will sit as
shown, with one side along the x-axis, and two corners touching
the arch of the parabola. But there are many such rectangles:

How can we find the rectangle which has the most area? Well, let's
call the coordinates of the upper-righthand corner of the rectangle
(x,y). Then the area of the rectangle is 2xy (the "2" comes from the
total length of the horizontal edge). Since (x,y) is on the parabola,
y=1-x2, and the area must be
2x(1-x2)=2x-2x3. What x's are "eligible"? Surely
not x=500. If you look carefully, you can see that any x in the
interval [0,1] describes exactly one of the eligible rectangles. So
now we have a calculus problem.
The resulting calculus problem
What is the maximum of the function A(x)=2x-2x3 when the
domain of A(x) is [0,1]. Well, this absolute maximum will be attained
either at the endpoints or at a critical point. The endpoints are 0
and 1. What are the critical points? A´(x)=2-6x2. This
will be 0 when 6x2=2 or x2=1/3. Since x can't be
negative in the domain of A(x), the only solution is x=1/sqrt(3).
There are three candidates for values of x at which A(x) can have a
maximum value. The simplest way to find the absolute maximum and the
value of x at which it occurs is to evaluate A(x) at these numbers.
Now remember that A(x)=2x-2x3.
Left endpoint A(0)=0 (the rectangle of the five displayed which
is thin but about one unit high has very little area: look at the
rectangle on the right).
Right endpoint A(1)=0 (the rectangle of the five displayed
which is very short but about two units long has very little area:
look at the rectangle on the left).
Critical number A(1/sqrt(3))=2/sqrt(3)-2(1/sqrt(3))3. This
works out to 4/(3 sqrt(3)). This is the largest rectangle.
Again, this is not a profound problem, but the method is
straightforward and can be applied in many different ways. We will
come back to other such applications, but now I need to go on,
following the textbook:
Two dots on the graph ...
I drew coordinate axes with two big dots on the x-axis and urged
students to come up and draw a graph going through the two dots. I got
several graphs similar to what is displayed.

I observed that in each case there were points on the graph where the
tangent line was horitizontal. Below are the graphs with those points
and parts of the tangent lines displayed. Only, I was rude and after the students' graphs were
analyzed, I drew something like the first graph below, with a bad
point. People really like to draw s-m-o-o-t-h curves.

The logic of the situation is this: if the function is positive
between the two points, then it has a positive relative max inside the
interval. That must be a critical point (horizontal tangent or not
differentiable). If the function is negative, then ... the same
situation below the x-axis. (Hey, yeah, if the function is never
positive and never negative, then it has lots of horizontal tangents,
because the graph is itself a horizontal line.)
Several versions of Rolle's Theorem
My informal description was: if there are two dots
on the x-axis which are part of the graph of a function, then either
the function has a bad place in between or has a flat place somewhere
in between. Since "bad" and "flat" are not usually considered
precise and suitable words in Math 135 (and there are other implicit
assumptions such as continuity), I rephrased this statement. Also, the
way the result is applied usually assumes that the function is
differentiable everywhere, so the "bad" alternative vanishes.
Rolle's Theorem (official version)
Suppose f(x) is a
differentiable function, and f(a)=0 and f(b)=0. Then there is at least
one number c between a and b so that f´(c)=0.
|
Tilting Rolle's Theorem
People rarely use Rolle's Theorem directly. The hypotheses are rather
strict. Usually the result is tilted, as in the accompanying
picture. But the picture is not labeled conventionally, so the second
picture is what you see in calculus books most of the time. There are
some lines in the second picture which are parallel. The line
connecting the points (a,f(a)) and (b,f(b)) has slope
[f(b)-f(a)]/[b-a] (difference in second coordinates divided by the
difference in the first coordinates). The other lines have slope given
by the derivative of f(x). So you get the statement of the Mean Value
Theorem, which is below.
The Mean Value Theorem (MVT)
Suppose f(x) is differentiable. Then there is at least one number c
between a and b so that f´(c)=[f(b)-f(a)]/[b-a].
|
This is one of the major structural (?) results of calculus, and I
will call it MVT. I asserted in class, and really believe,
that the reasoning usind the MVT is often used by
everyone. Please keep this in mind as you read these
examples.
| 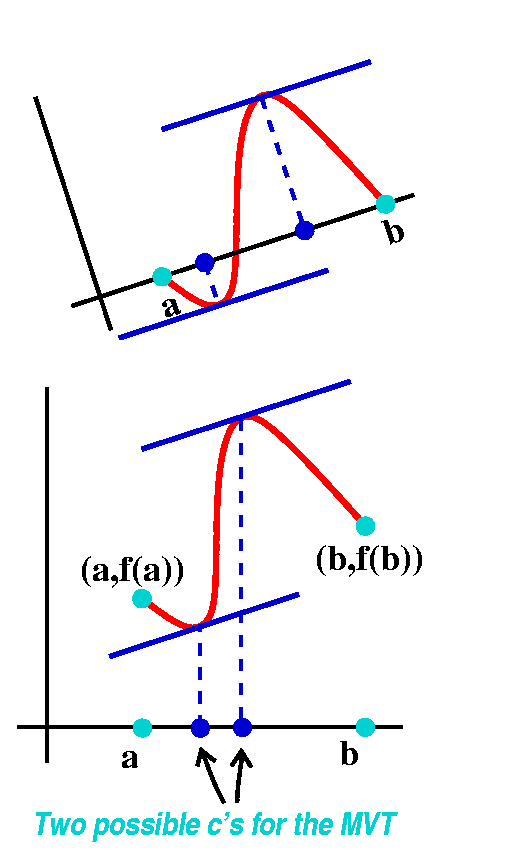
|
Return to Francine: distance gives information about "speed"
On February 1st we considered my friend Francine. Remember her,
please. She was driving on the Garden State Parkway. Here is the key
information about her travel:
 | Time | 7 AM | 10 AM |
Location
(in miles on
GSP) | 0 | 172 |
|---|
Let me make some assumptions about the Garden State, which are
actually not true, but will allow me to use some calculus.
So assume that:
First, access to the GSP is controlled by a ticket system (similar to
what the Turnpike uses) and these tickets are dispensed and read by
machines at each end of the trip.
Second, that the speed limit on the GSP is 55 miles per hour on its
whole length. What happens then?
Francine gets a speeding ticket
Here is the setup: suppose that s(t) describes the distance that
Francine travels along the GSP. I will meaaure time in hours, starting
the measurement at 7AM. I will measure s(t) in miles from the
beginning of the parkway in Cape May. What do I know from the table
above? I know that s(0)=0 and s(3)=172. I will also assume that
Francine's travel is differentiable, and now look at s´(t). This
is officially her velocity but I will call it "speed" here,
since that's what this quantity is usually called. The MVT declares
There is at least one number c between 0 and 3 so that
s´(c)=[s(3)-s(0)]/[3-0]=[172-0]/[3-0]=172/3. But this number is
57 (and a third) and is greater than 55, the official speed
limit. Therefore she must have been speeding at some time during the
trip.
Term paper (optional)
Explore whether this sort of thing is actually done in New Jersey or
elsewhere, wherever there are roads whose access is controlled in such
fashions. Explore that political and legal implications of using these
ideas in enforcing speed restrictions.
I am curious. Please tell me if you know any situations like this.
The reverse: "speed" gives information about distance
In Francine's case, information about the function was used to get
information about the derivative. The MVT can also be used the
other way, and I said that such ideas are used
very often in real life. So here is a sample situation.
Suppose you are driving down a road, and at time 0 you are 20 miles
from the start of the road: s(0)=20. Also suppose that you are driving
so that your speed is always between 30 and 40 miles per
hour. What can you say about your distance from the start of the road
3 hours later?
The reaction from the tired students (who had allo just spent a week
in a luxury hotel in Cozumel, I think) was not enthusiastic in
response. I did hope that people would start giving me answers. But
let's use the MVT: I know that
s´(c)=[s(3)-s(0)]/[3-0]=[s(3)-20]/3.
But we are told
30<=s´(c)<=40, so that
30<=[s(3)-20]/3<=40. Multiply by 3 and get
90<=s(3)-20<=120. Add 20 and get
110<=s(3)<=150.
Therefore three hours later the traveler will be
at least 110 miles from the start of the road, and will also be no
farther than 150 miles from the start of the road. So information
about the derivative gives you information about the function.
Increasing and decreasing
If the derivative is positive then the function increases
(drive forward and increase the distance from the start).
If the derivative is negative then the function decreases
(drive backward and decrease the distance from the start).
A specific function
This one is much uglier than what I wrote in class. Please: what I am
about to write is, of course, not a "random" function, but an
example I have invented to show you a sequence of ideas.
Suppose you want
to look at f(x)=445x301+678x501+19x+sin(3sin(2x)). (Is that ugly enough?)
Now I'd like to compare f(100) and f(50). Which number is
larger? Please realize that part of the consideration in writing this
function was to make the exponents so darn large that our simple
calculators can't compute f(100) and f(50). So some reasoning
is needed.
Step 1 Compute the derivative. By now, I hope you will agree
that this is basically easy. Yes, mistakes can be made in these
computations but we can probably usually get it correct.
f´(x)=445·301x300+
678·501x500
+19+cos(3sin(2x))3·cos(2x)2.
Step 2 Look at the derivative and try to figure out the sign
of the derivative. Look at the pieces:
-
445·301x300: the power is even, so this piece of the
function is always non-negative.
-
678·501x500: the power is even, so this piece of the
function is always non-negative.
-
19: this piece of the function is ... uh
... exactly nineteen.
-
cos(3sin(2x))3·cos(2x)2: o.k., what can we say about this
piece? I know how big cosine gets. It is always between -1 and +1. The
"stuff" inside the cosines doesn't matter in determining the possible
size of cosine (so, for example, cos(345,678), whatever it is, is
still between -1 and +1). But the 3 and the 2 outside the
parentheses involving cosine do affect how big this term
is. Therefore, I think that this term will be between -6 and +6.
So we have four pieces. If you consider now the sum of these, I bet
that the sum is at least 19-6=13.
Step 3 The derivative is positive. Therefore this function is
increasing: bigger values of the inputs to the function result in
bigger values of the outputs. So now I know that f(100) is larger than
f(50).
Yes, this function is ludicrous, but the ideas are what I want to show
you. Here they are:
|
Step 1: What is the behavior of a function defined by a complicated formula?
Step 2: Differentiate the function and get a mess. Now look for any
simple information you can about the sign of the derivative.
This search is frequently not difficult.
Step 3: Get conclusions about the {in|de}decreasing behavior
of the original function.
|
Another specific function
I think I looked at f(x)=sqrt(5x500+4). I computed (by
hand, a marvel of intelligence!) that f(0)=2 and f(1)=3. I asked what
could we conclude about f(x) for x between 0 and 1. I was told that
these values would be between 2 and 3.
QotD (Maybe an 8 point question on the next exam) Explain why
f(x) is between 2 and 3.
Hint Use the sign of the derivative of f(x).
Hint2 After a few minutes I think I wrote this on
the board:
(1/2)(5x500+4)-1/2(2500x499).
HOMEWORK
Please read sections 4.1 and 4.2 and hand in these problems on
Thursday:
4.1: 8, 10, 20, 25;
4.2: 5, 13, 16, 30.
Friday, March 11: this is lecture
16
This is the diary entry for the day
before vacation.
I did a WeBWorK problem involving error and relative error.
I try to be enthusiastic, and I was there. What did I want to
cover? Basically, I wanted to recite five definitions and an
inference, and give enough supporting examples so that students would
believe the inference. I did discuss adequately three of the fivce
definitions and the inference, but I ran out of time before I covered
the last two definitions very well. That's sort of annoying, and I
apologize, especially to the students who were present (about 60% of
the usual crowd).
Definition #1
A function f(x) has a relative maximum at c if
- The domain of f(x) includes an interval that c is
inside. (So endpoints of domains can't be relative maxes).
- In that interval, f(c)>=f(x) for all x's in the interval. (So
f(c) must be so smaller than all the f(x)'s in the interval.)
Definition #2
A function f(x) has a relative minimum at c if
- The domain of f(x) includes an interval that c is
inside. (So endpoints of domains can't be relative maxes).
- In that interval, f(c)<=f(x) for all x's in the interval. (So
f(c) must be no larger than all the f(x)'s in the interval.)
Then I sketched many many pictures on the board to illustrate these
concepts. The only amusing thing was that I used as examples graphs we
had already drawn in past lectures, and maybe that was sort of fun
(trees growing, tax revenue, etc.). Here are some examples of the
creatures I drew. In each case I labeled any relative minima with
rm and I labeled any relative maxima with RM. I have
also tried to include some useful comments on the results, that is,
the labels or the lack of labels, which sometimes is more
surprising.
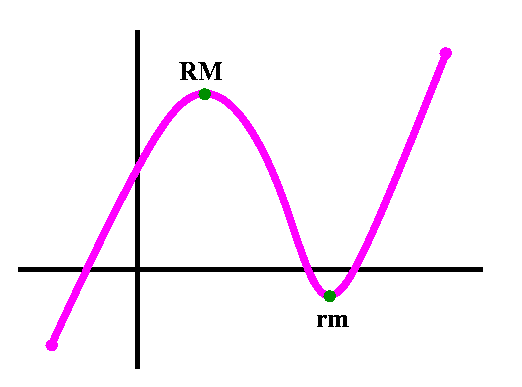
The top of the graph is a Relative Max and the
bottom is a Relative Min. The endpoints are not eligible
to be relative extrema because the function is not defined in an
interval containing either of them in its inside.
|
There is no Relative Max (again each endpoint is not
eligible since the function is not defined in an interval containing
that point). There's a Relative Min where indicated, because
nearby points (on both sides) have larger function values.
|
The bottom of the graph is a Relative Min. There are no points
representing a Relative Max.
|
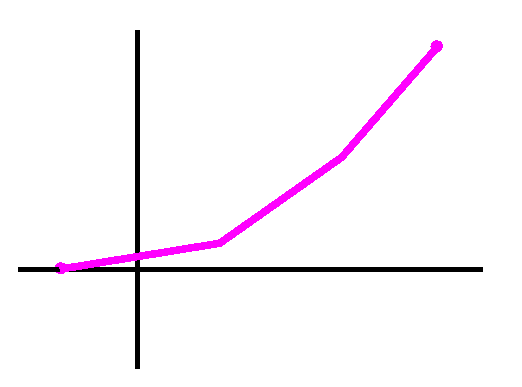
There are no Relative Max and no Relative
Min in this picture. The highest and lowest points are on the ends
which aren't eligible.
|
I actually went through about ten or a dozen such pictures. This was
not the best use of instructional time.
Definition #3
Suppose the function f(x) is defined at c. Then f(x) has a critical number at c if
- either f´(c)=0
- or f(x) is not differentiable at c.
Then (c,f(c)) is called a critical point of f(x).
The tangent line is horizontal at the top and the
bottom. At these points, f´(c)=0, so these points are
Critical Points.
|
The function is not continuous at a point so the derivative doesn't
exist there. But points where the derivative doesn't exist are still
Critical Points.
|
The function is not differentiable at the corner since the left- and
right-hand limits defining the derivative don't agree there. The
corner is a Critical Point.
|
There are two points where the derivative doesn't exist and these are
Critical Points.
|
Here's the inference
These examples and the others I displayed were supposed to help people
to believe that if f´(c) exists and wasn't 0, then nearby values
of f(x) were higher or lower, so that c was not a relative
extremum. The following statement (the "inference" I mentioned) would
be true:
|
Relative extrema occur only at critical points.
|
Here is an "if ... then" statement of the same inference:
|
If c is a relative max or min, then (c,f(c)) is a critical point.
|
Vocabulary
One definition of inference is "the forming of a conclusion
from premisses." Of course, a definition of premiss is "a
previous statement from which another is inferred." Does this help?
Some algebraic examples of critical points
| The functions | Sketch of the graphs
(A
machine helped me with these.) |
|---|
|
#1
What are the critical numbers of
f(x)=(1/3)x3+(1/2)x2-6x?
So f´(x)=x2+x-6=(x+3)(x-2), and this is 0 when x=-3 or
x=2.
The critical numbers are c=-3 and c=2.
|
|
|
#2 What are the critical numbers of
f(x)=x2e-3x?
Here
f´(x)=2xe-3x+x2(-3e-3x)=(2x-3x2)e-3x. Since
the exponential function is never 0, the derivative is 0 only when
2x-3x2=0, which is when x(2-3x)=0.
The critical numbers are
c=0 and c=2/3.
|
|
|
#3 What are the critical numbers of
f(x)=x1/3(x-2)?
Now f´(x)=(1/3)x-2/3(x-2)+x1/3(1). Stay alert! Algebra coming. I will rewrite this as
a product, because when I write it as a product,
the result will be equal to zero exactly when either of the factors is
0.
I get f´(x)=x-2/3[(1/3)(x-2)+x]. Now
when x=0, the first factor, x-2/3, doesn't make any sensed
because the negative exponent means that we would be dividing by 0. So
0 is a critical number of f(x), because the derivative is not defined
at 0. The second factor, (1/3)(x-2)+x, is equal to 0 when
(1/3)(x-2)+x=0, which happens when x-2+3x=0 or when 4x=2 or when
x=1/2. So 1/2 is also a critical number of this function.
The critical numbers are
c=0 and c=1/2.
|
|
In general, if I give you a "random" function, finding out where the
function is "highest" or "lowest" might be very difficult. But the
inference allows one to throw out points which can't be highest or
lowest. But here are two more definitions:
Definition #4
A function f(x) has an absolute maximum at c in an interval if
f(c)>=f(x) for all x in that interval.
Definition #5
A function f(x) has an absolute minimum at c in an interval if
f(c)<=f(x) for all x in that interval.
If you look at the examples and at the inference above then you
should believe that
|
Absolute maxes or mins can occur only at critical
numbers or endpoints.
|
QotD I asked people to answer problem #25 in section 4.1: find
the absolute maximum and the absolute minimum of
s(t)=t cos(t)-sin(t) on the interval [0,2Pi].
This was not a good QotD. I had not adequately explained the ideas and
had certainly not discussed the statement in
blue written above. I need to spend more time in class on this
and I plan to.
Maintained by
greenfie@math.rutgers.edu and last modified 3/22/2005.
 Joni throws a ball
Joni throws a ball



 Step 1: translation
Step 1: translation
 Step 2: calculus
Step 2: calculus Section 4.7 has a significant amount of applications in economics
(average and marginal cost, marginal profit, etc.). I strongly urge
interested students to read this material. I also urge all students to
do the next two WeBWorK assignments, which will practice your
translation skills on various optimization (max/min) problems.
Section 4.7 has a significant amount of applications in economics
(average and marginal cost, marginal profit, etc.). I strongly urge
interested students to read this material. I also urge all students to
do the next two WeBWorK assignments, which will practice your
translation skills on various optimization (max/min) problems.
 Third max/min problem
Third max/min problem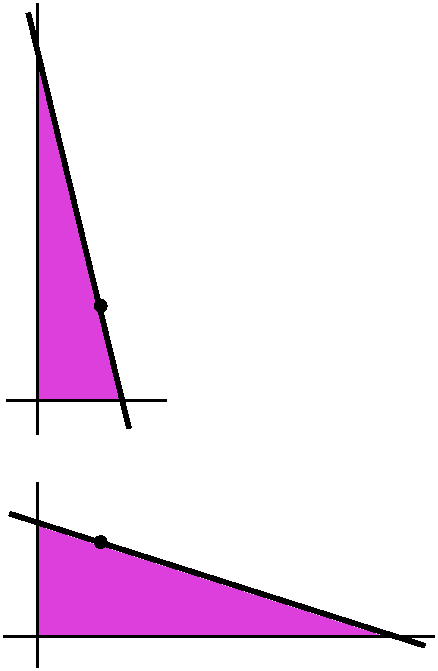

 [3/(x-2)]+3/2-{3x/(x-2)2}
[3/(x-2)]+3/2-{3x/(x-2)2}

 Darling time
Darling time Second max/min problem
Second max/min problem Now I can answer the original question. As x-->infinity,
x3/e3-->0. So ex grows bigger faster
than x3. The picture should show you that things work o.k.
Now I can answer the original question. As x-->infinity,
x3/e3-->0. So ex grows bigger faster
than x3. The picture should show you that things work o.k.






 Well, y=[(x-3)(x-5)]/(x-1). I'll expand the top to differentiate it
more easily: y=[x2-8x+15]/[x-1]. Then
Well, y=[(x-3)(x-5)]/(x-1). I'll expand the top to differentiate it
more easily: y=[x2-8x+15]/[x-1]. Then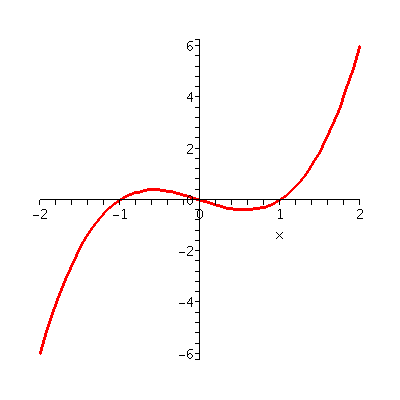

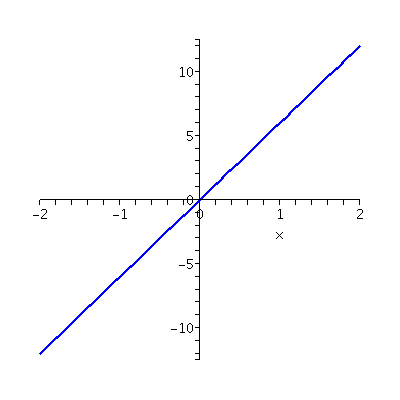
 A WBWorK problem
A WBWorK problem Textbook problem 4.3 #17
Textbook problem 4.3 #17 Textbook problem 4.3 #21
Textbook problem 4.3 #21














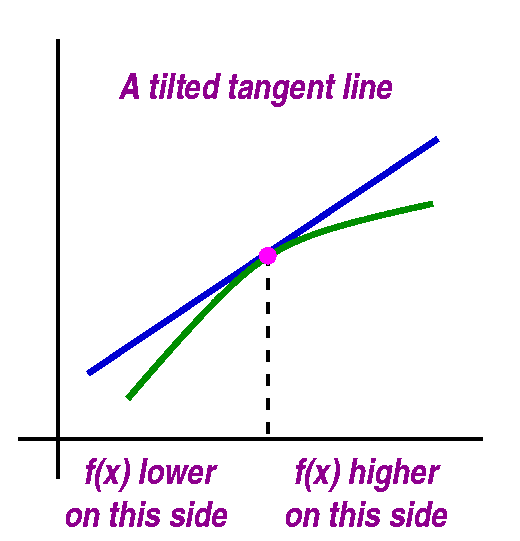
 One example
One example














