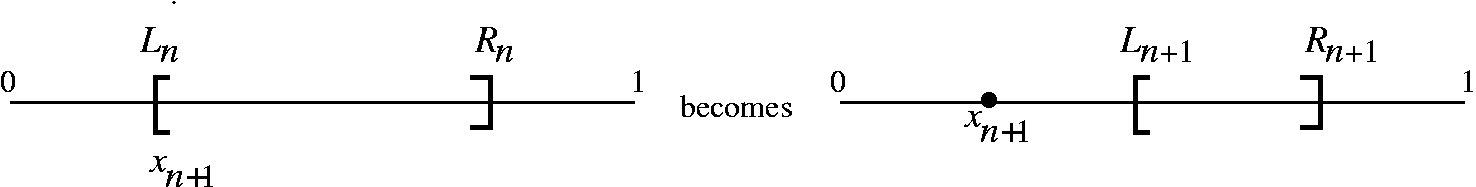• Fundamental facts
  • Limits are unique
  • The set of numbers in a convergent sequence is bounded*
  • Only tails matter
• Limits and arithmetic
  Theorems about sums and products and reciprocals and quotients
• Limits and order
  
  • If (x_n) converges to x then: x>0 implies x_n eventually>0.
    
  • If (x_n) converges to x then: x_n>=0 for all large enough n implies x>=0.
  • The Squeeze Theorem**
• Examples
  Polynomials, rational functions, and more coming today!***

If (x_n) converges to x, where x_n=(-1)ⁿ, then take epsilon=1. Then there is N in N so that if n>N, |x_n-x|<1. There are certainly even integers greater than n and certainly some odd integers greater than n. Let p be such an even integer and let q be such an odd integer. Then x_p=(-1)^p=1 and x_q=(-1)^q=-1. What else? By the triangle inequality, |x_p-x_q|= |x_p   -x_q|= |x_p-x+x-x_q|=< |x_p-x|+|x-x_q|<2. But |x_p-x_q|=|1-(-1)|=2, and 2<2 is false. So the assumption that (x_n) converges was wrong and the converse of the theorem is false.

Now let's try **the famous
Squeeze Theorem Suppose we have three sequences, (a_n), (b_n), (c_n), and we know the following:
i) (a_n) and (c_n) both converge to x.
ii) a_n<=b_n<=c_n for all n in N.
Then (b_n) converges, and its limit is x.
Proof: The proof is more or less "simple". We first write out the hypotheses i) using the definition of convergence of a sequence.
(a_n) converges to x means given epsilon>0, there is K(epsilon) in N so that if n>=N, then |a_n-x|<epsilon. This is the same as -epsilon<a_n-x<epsilon which is the same as x-epsilon<a_n<x+epsilon.
Similarly, (c_n) converges to x means given epsilon>0, there is J(epsilon) ( a possibly different number!) in N so that (unrolling, etc.) x-epsilon<c_n<x+epsilon.
Now we know a_n<=b_n<=c_n so we can concatenate some of these inequalities. b_n<=c_n<x+epsilon. Similarly, x-epsilon<a_n<b_n so that x-epsilon<b_n<x+epsilon which is the same as |b_n-x|<epsilon, if n is "large enough": how large? Well, certainly if n is at least max(K(epsilon),J(epsilon)) then all of the needed inequalities will be true. So we have verified the desired convergence.

Here is a somewhat poetic (?) view of the theorem. n increases as pictures of the real line descend. I am trying to illustrate how b_n is "forced" to converge to x.
A naive person might not recognize the importance of this result, but everyone who has gone through the various limit results of calculus is likely to remember the quotation of the Squeeze Theorem a few times. Here is a fairly simple (?!) example of how the theorem can be used. I recalled a "workshop problem" from Math 152, or, at least, one version of the problem. It went something like this: consider the sequence x_n=(5ⁿ+7ⁿ)^1/n. Does (x_n) converge, and, if it does, what is its limit? I expected the calculus students do do some numerical exploration, but let us be a bit more sophisticated. Notice that 7ⁿ<=5ⁿ+7ⁿ<=2·7ⁿ. Take n^th roots, and get 7<=(5ⁿ+7ⁿ)^1/n<2^1/n7. But what happens to "higher" and "higher" roots of 2? They "get close" to 1. So we seem to have the ideal hypotheses for using the Squeeze Theorem. I will now formalize everything. First, though, a detour to verify an important example (indeed, part of ***!).

Theorem Suppose c>=1. If (x_n) is the sequence defined by x_n=c^1/n, (x_n) converges and its limit is 1.
Proof: Here I give the proof that is in the text. I can follow it, but, somehow, I can't see what's really "happening". Oh well. Here we go.
Since c>=1, c^1/n>=1^1/n=1. That means c^1/n=1+d_n. But now take n^th powers: c=(1+d_n)ⁿ. Use Bernoulli's inequality (applicable since d_n>=0). Thus c>=1+nd_n. "Solve" for d_n: (c-1)/n>=d_n. Since (c-1)·(1/n)>=d_n>=0, we exactly have d_n "squeezed" between a multiple of (1/n), which approaches 0, and 0 itself. Therefore the Squeeze Theorem implies that (d_n) converges, and its limit is 0. And c^1/n1+d_n must also converge (sum of two convergent sequences) and its limit must be 1. We've proved the theorem.

I remarked that a proof similar to this but with more complicated details can be used to verify the following theorem:
Theorem If x_n=n^1/n, then (x_n) converges and its limit is 1.
The proof is in the text. I would hope that student who have gone through the calc curriculum would recognize that if x_n=n^1/n, then ln(x_n)=(1/n)(ln(n))=ln(n)/n, and if we want to learn what happens as n gets large, we will need l'Hopital's rule, and we differentiate the top and bottom to get (1/n)/1 which -->0 as n-->infinity. Of course, we are a month away from verifying l'Hopital's rule and using it officially.

Now we can do a more complicated version of the Math 152 workshop:
Example: Suppose a and b are positive numbers, and x_n=(aⁿ+bⁿ)^1/n. Then the sequence (x_n) converges and its limit is max(a,b).
Proof: Let c=max(a,b). Then cⁿ<=aⁿ+bⁿ (since certainly one of the expressions on the right is superfluous!). Also, both of aⁿ and bⁿ individually are <=cⁿ since c is the max of a and b. Therefore cⁿ<=aⁿ+bⁿ<=2cⁿ. We may take n^th roots and get c<=(aⁿ+bⁿ)^1/n<=2^1/nc. Now we have our sequence (x_n) "squeezed" between the sequence which is the constant c and the sequence which is c multiplied by 2^1/n. But we just saw that lim(2^1/n)=1 so (x_n) is squeezed between two sequences whose limit is c. Therefore (x_n) converges and its limit is c.

The Question of the day is does (7ⁿ+13ⁿ+46ⁿ)^1/n converge, and, if it does, what is its limit?

I'll go on to 3.3 next time. I encouraged people to send in answers to review questions, and I will post these answers. Due a week from today (Monday, March 10) are these textbook problems: 3.2: 4, 9, 11, 13a, 16.

We proved the reciprocal theorem.
Theorem (1/?) Suppose (x_n) converges to x and x is not 0. Then:
i) There is N in N so that for n>=N, x_n is not 0 (so x_n is "eventually" not equal to 0).
ii) if (y_n) is a sequence defined by y_n=1 for n<N and y_n=1/x_n for n>=N, then (y_n) converges, and its limit is 1/x.
Proof: Since (x_n) converges to x, for every epsilon>0 there is K(epsilon) in N so that for n>=K(epsilon), |x_n-x|<epsilon.
In class I discussed the case where x is positive. If we take epsilon=x/2 then epsilon is positive, and we know that |x_n-x|<x/2. This "unrolls" to -x/2<x_n-x<x/2 which further implies that x-x/2<x_n<x+x/2. So for n>=K(x/2), we know that 0<x/2<x_n<(3x)/2. In the language of the informal analysis written for yesterday's lecture, alpha is x/2 and beta is (3x)/2. Then I also know that 1/x_n is between 2/(3x) and 2/x.
Still motivated by yesterday's analysis, given epsilon>0, I ask for K(epsilon/(2/x²)). That is, if n>=K(epsilon/(2/x²)), an element of N, then |x_n-x|<epsilon/(2/x²). (This seems incredibly weird unless you have prepared yourself by looking at the informal discussion yesterday.)
Now suppose that n>max(K(x/2),K(epsilon/(2/x²))). We know then that x_n is not 0, and we even have a nice underestimate of 1/x_n. So consider |1/x_n-1/x|=|x_n-x|/(x_n·x)<|x_n-x|(2/|x|²) because of the first part of the specification in the max. The second part of this specification establishes that |x_n-x|(2/|x|²)<epsilon/(2/x²))(2/|x|²)=epsilon. So we have proved that |x_n-x|<epsilon, which is verifying convergence.
We leave to the struggling reader the case where x is negative.

A reward was given to all students present when this proof was completed.

Theorem(/) If (x_n) converges to x and if (y_n) converges to y, and if y is not 0, then for n large, z_n=x_n/y_n is defined, and (z_n) converges and its limit is x/y.
Proof: We can at least use a little bit of our technology. z_n is the product of x_n and 1/y_n. The (1/y_n) sequence behaves appropriately by the previous result. Then the product limit theorem applies to x_n·(1/y_n) to give the result of the theorem.

Whew! Now I remarked that we can do a few more examples, officially. These examples are still rather baby calculus, but we can prove them. So we could look at x_n=(5n²+7)/(3n²-2). Algebraically, this is the same as x_n=(5-7(1/n)²)/(3-2(1/n)²). We know that the sequence (1/n) converges and its limit is 0 (this uses the Archimedean Property). Then by all of our results involving limits and arithmetic (sums and products and quotients), we can deduce that (x_n) converges and its limit is 5/3. In fact, we can "handle" now limits of sequences of values of rational functions, just as yesterday we observed that we could analyze limits of sequences of values of polynomical functions.

Limits & order (maybe better: Limits and inequalities)

Theorem If (x_n) converges and its limit is x, then x>0 implies that there is M in N so x_n>0 for n>=M.
Proof: Various folks tried to force me to do this proof, but I knew it was a homework problem whose solution I had already written on the web.

I then tried to "perturb" this theorem a bit. I asked what happened if we changed the inequalities.

What about the converse? So we could look at some assertion similar to:
Candidate for a Theorem: If (x_n) converges and its limit is x, and if we know that x_n>0, then x???

In fact x does not "inherit" from x_n in this case. We can look at x_n=1/n. Then all the x_n's are positive, while x itself is not positive.

A simple repertoire of examples is very useful to check ideas! My online dictionary gives this as one definition of "repertiore":
a stock of regularly performed pieces, regularly used techniques, etc. ("went through his repertoire of excuses"{foreign word}).

Theorem If (x_n) converges and its limit is x, and if we know that x_n>=0, then x>=0
Proof: Since (x_n) converges to x, for every epsilon>0 there is K(epsilon) in N so that for n>=K(epsilon), |x_n-x|<epsilon.
Now we assumed the desired result was false (a proof by contradiction): suppose x<0. Then if we take epsilon=-x, epsilon is a positive real number, and we can find K(-x) in N so that if n>=K(-x), then |x_n-x|<-x. We unroll this inequality to get: -(-x)<x_n-x<-x or, adding x, 2x<x_n<0, so for these x_n's, x_n<0. These x_n's are negative. But this is a contradiction. So x>=0.

Again, I tried to examine what would happen if we changed the inequalities a bit.

Fascinating Question of the day: suppose (x_n) is a convergent sequence and its limit is x. If you know that 0<x_n<1 for all n in N, what can you conclude (with no additional information!) about x? I hope that most people will answer that x is in the closed interval [0,1]: 0<=x<=1. This answer uses the ideas of the last two theorems.

We are quite close to moderately sophisticated mathematics. Here is an almost realistic scenario. Suppose we want to solve some sort of equation, f(x)=0. We might have a root-finding technique (or even several of them) which creates a sequence of better and better approximations to a root. Well we might have the following setup: (x_n) converges to x and (y_n) converges to y. We happen to know that x_n<=y_n for all n in N. We also know that the approximations grow closer and closer together. Here is one specific type of "closer": we might know for for n in N, 0<=y_n-x_n<1/n. What can we conclude?

We decided, in fact, that in this case the limits would be equal. That is, x=y. Why would this occur? Well, we need all the information, but the key is the estimate with 1/n. We do know:
Proposition If (z_n) is a sequence with |z_n|<1/n, then (z_n) converges and its limit is 0.
The proof of this uses the Archimedean Property.

Now we look at z_n=y_n-x_n and apply the previous proposition, so the limit of z_n (which by our arithmetic results, must be y-x. Since z=0, we know y=x. What happens if we average our approximation schemes? That is, we create w_n=(1/2)(x_n+y_n). By our arithmetic limit theorems, this sequence (w_n), which is "trapped" between (x_n) and (y_n), will also converge and its limit will be the common limits x=y. This is a version of the Squeeze Theorem which we will do next time, and we'll do some interesting examples, too.

I handed out review problems for the first exam, which will be given in a week.

General properties

Theorem 1 If (x_n) converges to x and if (x_n) converges to y, then x=y.
We proved this last time. We now introduce the following notation:
If (x_n) converges to x, we will write lim(x_n)=x. We didn't use this notation previously, because if we had the preceding theorem would have looked like this: if lim(x_n)=x and lim(x_n)=y, then x=y. The result would have seemed an application of transitivity of equality, while the "(x_n) converges to x" is, in fact, a complicated logical phenomenon.

Theorem 2 If (x_n) converges to x, then there is M>0 so that the set S={x_n : n in N} is bounded by M: if s is in S, then |s|<=M.

The final fundamental result that we need is this:
Theorem 3 "Only tails matter." More precisely, suppose (x_n) is a sequence and (x_n) converges to x. If (y_n) is another sequence, and if there is N in N so that for n>=N, x_n=y_n, then (y_n) converges and its limit is x.
Proof: Since (x_n) converges, we know that given epsilon>0, there is K(epsilon) in N so that if n>=K(epsilon), then |x_n-x|<epsilon. Now if we let J(epsilon)=max(K(epsilon),N), and if n>=J(epsilon), then |x_n-x|<epsilon (since n>=K(epsilon)). But we also know that y_n=x_n (since n>=N), so that we may conclude |y_n-x|<epsilon.
Comment The use of "max" in order to get the "index" in the sequence high enough to satisfy varies different criteria is very common. We will see it again and again in the following proofs, some of which will be rather technical.

Limits and arithmetic (wasn't this Limts and algebra before?)

We see what happens with addition, multiplication, etc. Most of the results here are very familiar to any long-suffering calculus student, but the interest in this course is building the detailed proof structure. Addition is fairly easy.

Theorem (+) If (x_n) converges to x and (y_n) converges to y, then (x_n+y_n) converges to x+y.
Proof: In class I tried to describe an informal process leading to discovery (or, maybe rather, acknowledgment!) of the proof. I'll concentrate on just giving the steps of the proof here, and hope that this will be enough.
We know: given epsilon>0, there are integers K(epsilon) and J(epsilon) in N so that if n>=K(epsilon) then |x_n-x|<epsilon and if n>=J(epsilon) then |y_n-y|<epsilon. (This comes from the definition of convergence for both sequences). Then consider M(epsilon)=max(K(epsilon/2),J(epsilon/2)). If n>=M(epsilon), then:
|(x_n+y_n)-(x+y)|=|(x_n-x)-(y_n-y)|<=|x_n-x|+|y_n-y| by the triangle inequality. Since n>=M(epsilon)>=K(epsilon/2), |x_n-x|<epsilon/2. Since n>=M(epsilon)>=J(epsilon/2), |y_n-y|<epsilon/2. Therefore |(x_n+y_n)-(x+y)|<epsilon, which established the definitional assertion in "(x_n+y_n) converges to x+y".

That one isn't too bad. Slightly more difficult is multiplication.
Theorem (·) If (x_n) converges to x and (y_n) converges to y, then (x_n·y_n) converges to x·y.
Proof: We preliminarily examine the difference |x_n·y_n-xy|. It equals |x_n·y_n-x·y_n+x·y_n-xy|. This may be familiar to students who have seen it a number of times in various calculus courses -- I don't see much to say here, except that it is useful because, well, because it gives us something we can estimate easily. The triangle inequality then tells us this is less than or equal to |x_n·y_n-x·y_n|+|x·y_n-xy|. We would like to insure that for "suitable" n each of the terms |x_n·y_n-x·y_n| and |x·y_n-xy| are separately less than epsilon/2. We know that (x_n) and (y_n) converge to x and y, respectively. Thus we know: given epsilon>0, there are integers K(epsilon) and J(epsilon) in N so that if n>=K(epsilon) then |x_n-x|<epsilon and if n>=J(epsilon) then |y_n-y|<epsilon.
|x·y_n-xy|=|x|·|y_n-y|. If x=0, then this is certainly already less than epsilon/2. If x is not 0, we can make the product less than epsilon/2 by taking n to be at least J(epsilon/(2|x|)). This is because if n is that large, |x·y_n-xy|=|x|·|y_n-y|<|x|(epsilon/(2|x|))=epsilon/2.
How about |x_n·y_n-x·y_n|? This equals |x_n-x|·|y_n|. Since (y_n) converges, there is M>0 so that |y_n|<=M. Therefore, if n is at least K(epsilon/(2M)), then |x_n·y_n-x·y_n|<=|x_n-x|·|y_n|<=|x_n-x|·M<(epsilon/(2M))M=epsilon/2. Wow!
We must satisfy both restrictions on n. So now I will describe M(epsilon), which leads to a verification that (x_n·y_n) converges to x·y: M(epsilon)=max(J(epsilon/(2|x|)),K(epsilon/(2M))) for x not equal to 0, and otherwise M(epsilon)= K(epsilon/(2M)).
I comment that this is complicated.

Some examples The constant sequences converge (!). That is, suppose c is a real number, and the sequence (x_n) is defined by x_n=c for all n in N. Then (x_n) converges to c. (You can take K(epsilon) always to be 1 because |x_n-c|=|c-c| is always 0!)
Now we notice that polynomials are built out of repeated additions and multiplications, including multiplications by constants. I claim that we can prove the following result: suppose P(t) is some polynomial and suppose further than (x_n) is a sequence which converges to x. Then the sequence (y_n) defined by y_n=P(x_n) also converges, and its limit is P(x). So squares converge, cubes converge, etc. Of course, this is one step to proving what we hope is true: polynomials are continuous, but we are a few weeks away from defining continuity! (We are a giant tortoise, slowly trying to climb a mountain.)

Here's the last major algebraic result about limits (we'll use it to get an additional statement about quotients, of course!):
Theorem (1/?) This theorem should begin: if (x_n) converges to x then the sequence (y_n) defined by y_n=1/x_n ... to 1/x.
But we have a problem! Actually, there are several problems. First, the x involved could be 0. And then we should not expect any theorem about convergence to result (consider examples like x_n=1/n and x_n=-1/n and even x_n=(-1)ⁿ/n, where 1/x_n has different sorts of behavior). And even if x is not 0, we really can't expect every member of x_n to be non-zero (consider the sequence whose first 10⁷⁸ terms are 0, and all the rest of whose terms are 1). As our Question of the day I asked people to advise me on this. Eventually we got a new theorem, which certainly has some weird aspects, but has the advantage that it is true:
Theorem (1/?) Suppose (x_n) converges to x and x is not 0. Then:
i) There is N in N so that for n>=N, x_n is not 0 (so x_n is "eventually" not equal to 0).
ii) if (y_n) is a sequence defined by y_n=1 for n<N and y_n=1/x_n for n>=N, then (y_n) converges, and its limit is 1/x.
Proof:
Informal discussion: The thoughts behind this result are a bit intricate. Let's try to prove i): if x is not 0, then for big enough n, x_n and x are "close". How close would they have to be to guarantee that x_n is not 0? Here I think I need a geometric model, and the model is a line with 0 labeled and x labeled. x is at a distance of |x| from 0. The famous "neighborhood" V_epsilon(x) is an open interval whose endpoints are x-epsilon and x+epsilon. Now if epsilon is |x|, apparently 0 is not inside the neighborhood. We guarantee that by using the definition of convergence.
Let's see: since (x_n) converges to x, given epsilon>0, there is K(epsilon) in N so that if n>=K(epsilon), then |x_n-x|<epsilon. But x is not 0, so we can take epsilon=|x|, a positive number. Then for n>=K(|x|), we know |x_n-x|<|x|. We can "unravel" this to get the double inequality -|x|<x_n-x<|x| which becomes x-|x|<x_n<|x|+x. If x>0, then |x|=x, so the left-hand part becomes 0<x_n. If x<0, then |x|=-x, so the right-hand part becomes x_n<0. In either case, if n>=K(|x|), we see that x_n can't be 0, which is what we wanted to prove.
Informal discussion: this is fairly complicated. We need to make some estimate about how "small" |(1/x_n)-(1/x)| is for n large. What do we know? We know how to "control" |x_n-x|. So we look for some way to connect the two. Of course we can now (workshop #3, problem #1) add "fractions", so in fact |(1/x_n)-(1/x)|=|(x-x_n)/(x_n·x)|=|x_n-x|·1/|x_n|·1/|x|. How can we get this less than epsilon, if K(epsilon) "controls" |x_n-x|? If we only had |x_n-x|, we could use just K(epsilon). If we had |x_n-x|·1/|x|, we could use K(|x|epsilon), because then for n>= K(|x|epsilon) we would know |x_n-x|·1/|x|<|x|epsilon·1/|x|=epsilon. But we also have the darn 1/|x_n|. What does this do? The variable n fouls things up. We can't use a family of numbers inside the K specification -- it demands one number. How big or how small can x_n get? If we somehow knew that 0<alpha<=|x_n|<=beta (with no n's in the alpha and the beta) then we would know 1/(beta)<=1/|x_n|<=1/(alpha), and we could build in a specification via K(something·epsilon). Here is a very bright idea: essentially make more strict the "boundary" used to prove i). Try epsilon=|x|/2. Then those x_n's which satisfy |x_n-x|<|x|/2 will have to satisfy |x|/2<|x_n|<3|x|/2, so we can take alpha to be |x|/2 and beta to be 3|x|/2. And that is what I will try tomorrow!

Comment It is certainly true that this proof is very elaborate, and one may well question the applicability of the methods to almost anything that almost all students are likely to encounter in later life. Let's see: "learning things is good" could be one answer, and it is one which I agree with. Any student who learns about actual numerical or scientific computing will need to know some elements of what we're doing here. If x is an approximation to y in some computation, how good (or bad) will the approximation of 1/x be to 1/y? That sort of problem is implicit in the "guts" of many computational strategies. It can be analyzed using the tools we are beginning to assemble here. So ... that's a partial answer. I think more applicable for most students is that this is a part of the 311 experience. And we can debate later if that experience is "worhtwhile" or "meaningful". Meanwhile, there is more to do tomorrow!

Because the material of Workshop #4 is both important and complicated, I will meet with students in 6:30 PM on Thursday, February 27, in Hill 425, and I hope to write out complete solutions to all seven of these problems. As a spectator sport alone this should be fun (for you, maybe, and less so for me!). If someone takes good notes, I can scan them and put them on the web.

We will have an exam a week from Thursday (in class on March 3). I will give out a review sheet this Thursday instead of more workshop problems. The review sheet will contain full information about the exam (the format, sections to be covered, etc.). It will also have sample problems, mostly problems I will get from other instructors' past exams.

The reading for the week is sections 3.1 and 3.2 and 3.3.

I again wrote the definition of the limit of a sequence:
Definition A sequence (x_n) is said to converge to x if for all epsilon>0, there is K(epsilon) in N so that |x_n-x|<epsilon.

I tried an example: suppose x_n=(3n)/(4n+5). Should this sequence converge, and, if it does, what is its limit? Mr. Citterbart declared that it should converge, and that its limit should be 3/4. I agreed. But I wanted to provide a formal proof of this assertion. And we have very little "technology" to use: we only have the definition of limit. So I first did some informal preparation for the formal proof. I remarked that virtually everyone I know does this, although reading the text it might seem that the proofs should come forth beautifully formed from some divine source.

Informal preparation I want |(3n)/(4n+5)-3/4|<epsilon where epsilon is some unspecified positive number. Somehow I want n to be "controlled" by epsilon, so that if "the opponent" supplies an epsilon, then I can choose n so large that the difference above will be less than epsilon. The first thing we did was to work algebraically with the difference above:
|(3n)/(4n+5)-3/4|=|(4(3n)-3(4n+5))/(4(4n+5))|=|(-15)/(4(4n+5))|. We noticed that the absolute value sign could be removed if we deleted the - from before the 15. So we've got to get 15/(4(4n+5))<epsilon. What "condition" on n will guarantee this? Well, let's "cross multiply" (this is the informal preparation, and, anyway, everything involved is positive, so that the inequalities won't change their direction!). We get 15/epsilon<4(4n+5). More algebra gives me (15/(4epsilon))-5<4n and even more gives me: (1/4)((15/4epsilon)-5)<n. Wow! But why should there be any positive integers satisfying this inequality? Ah: the Archimedean property! And once integers are bigger than (1/4)((15/4epsilon)-5) we probably should be able to run the argument backwards (I hope!).

Formal proof We wish to show that ((3n)/(4n+5)) converges to 3/4. Suppose that epsilon>0 is given. By the Archimedean property, there is a positive integer, which we will call K(epsilon), so that K(epsilon)>(1/4)((15/4epsilon)-5). Now I must prove the following implication:
IF n>=K(epsilon), THEN |(3n)/(4n+5)-(3/4)|<epsilon.
Since n>=K(epsilon), we know n>(1/4)((15/4epsilon)-5). We may multiply by the positive integer 4 to obtain 4n>((15/4epsilon)-5). Now add 5 and get 4n+5>15/4epsilon. Since both epsilon and 4n+5 are positive, we may multiply by the positive number epsilon and the positive number 1/(4n+5) and not change the direction of the inequality. Thus we know that epsilon>15/4(4n+5). But 15/4(4n+5)=|(-15)/(4(4n+5))|=|(3n)/(4n+5)-(3/4)|. So we have proven that |(3n)/(4n+5)-(3/4)|<epsilon.

There are several comments to make about this formal proof. It seems really irritating, somehow redoing things we've already done. And it seems long and clumsy. In its defense I remark, as I did in class, that we right now have essentially no "technology" to do proofs about limits: all we have is the definition of limit, and that's the only way we can verify that a sequence has a limit.

I changed the problem a bit, from x_n=(3n)/(4n+5) to x_n=(3n)/(4n²+5). Now we decided that the sequence should converge, and its limit should be 0. I wanted to write a formal proof of this, also. I began as before with

Informal preparation Now epsilon>0 is specified, and I want to find n so that |(3n)/(4n²+5)-0|<epsilon. We can "clarify" the situation a bit algebraically. The absolute value is not needed, since what is inside is already positive. Again we "cross multiply", not changing the direction of the inequality since everything involved is positive: 1/epsilon<(4n²+5)/(3n). We're trying to uncover n so that we could once again use the Archimedean property to guarantee a K(epsilon). We notice that we have 3/epsilon<(4n²+5)/n=4n+(5/n). Now we need to think, since we don't seem to have a simple "recipe" where the Archimedean property can just apply. Mr. Kang suggested that we just ignore the 5/n! This is clever: notice that if 3/epsilon<4n then certainly 3/epsilon<4n+(5/n) since (5/n) is positive. And 3/epsilon<4n is a very easy inequality. We can satisfy it by requesting that 3/(4epsilon)<n, which can be "handled" by a direct reference to the Archimedean property. So here we get the following guess for K(epsilon): an integer greater than 3/(4epsilon).

Question of the day I asked the students to write the formal proof that 0 is a limit of the sequence (3/(4n²+5)). I hope that people were comfortable doing this. I will look at the answers later. The proof should include a step which is very very strange: the writer just casually adds on 5/n out of "thin air" -- I know that if I presented this proof to a class formally I would find that step extremely difficult to motivate!

I remarked that the balance of the week would be spent in developing "technology" to handle limits, so we won't have to verify every limit statement by direct checking of the definition. That would indeed be rather tedious. The agenda will be:

• General properties of limits ("simple" things, but in 311 everything must be proved!)
• Limits and algebra (such as limits of sums, quotients, etc.)
• Limits and order (when the terms of one sequence are less than another then etc.)
• Systematic Examples (so that we don't need to "reinvent the wheel" whenever we see a new limit).

Theorem Suppose (x_n) converges to x and suppose (x_n) converges to y. Then x=y.
Comment Well, golly, you might think this is "obvious", but everything in this course should be proved. And indeed this proof is especially tricky. It proves equality by verifying what seems to be a systematically sloppy estimation.
Proof: Consider |x-y|. We will prove that x=y by verifying that for all positive epsilon, |x-y|<epsilon. This, by previous results in lecture, in workshop problems, and in the text, will show that x-y=0 so x=y.
Now how do we get |x-y|<epsilon? Well, first observe that |x-y|=|x    -y|=|x-x_n+x_n-y|<=(by the triangle inequality)|x-x_n|+|x_n-y|. (Of course I tried to emphasize by putting in the space that to a certain extent the "insertion" -x_n+x_n seems random (I could have written -56+56, for example) but it isn't random. This specific algebraic "trick" allows me to consider |x-x_n| and |x_n-y|=|y=-x_n|. I do not think it is at all obvious when first seen!
Since (x_n) has limit x, for every v>0 there is J(v) in N so that if n>=J(v) then |x_n-x|<v (I am renaming the K(epsilon) of the definition here).
Also, since (x_n) has limit x, for every v>0 there is H(v) in N so that if n>=H(v) then |x_n-x|<v (I am renaming the K(epsilon) of the definition here).
Now consider H(epsilon/2) and J(epsilon/2). If n is a positive integer which is at least as large as both of these, then |x_n-x|<epsilon/2 and |x_n-y|<epsilon/2. We could take n=max(H(epsilon/2),J(epsilon/2)), for example (we must name some "specific" n or we will have a hole in the proof!). With that choice of n, |x-y|<=|x-x_n|+|x_n-y|<epsilon/2+epsilon/2=epsilon. So we are done: we have proved that |x-y| is less than any specified positive number, so that it must be 0.

Then I went on to ask how sup's and inf's interact with limits. More specifically, suppose (x_n) is a series which converges to x. Define the set S to be {x_n : n in N}. So S is the set of "values" of the sequence. Does sup(S) necessarily have to be the same as the limit, x? One example (x_n=1/n, where sup S =1 and x=0) showed that the answer is no. So I asked if inf(S) is the same as the limit, always. And another answer(x_n=1-1/n where x=1 and inf(S)=0) showed that equality can fail, too. Finally I asked if the limit always must be either the sup or the inf? And the example x_n=(-1)ⁿ/n which has the limit, x, equal to 0 and the inf equal to -1 and the sup equal to 1/2, showed that all three numbers could differ. But, in fact, more profoundly, I asked whether the set S has to be bounded in the first place (if it wasn't bounded, then actually the sup and the inf don't have to exist).

Theorem If (x_n) is a sequence which converges to x, and if S={x_n : n in N}, then S is bounded.
Proof: Well, since (x_n) converges to x, for every epsilon>0, there is K(epsilon) in N so that if n>=K(epsilon), then |x_n-x|<epsilon. Now, pick a number, say, uh, 56. Then if we look at N, the integer K(56) divides up N into finitely many numbers less than K(56) (which I don't know but which the definition guarantees me!) and all the integers, n in N, at least K(56). For the latter collection of numbers, I know |x_n-x|<56 (this is what the book would call V₅₆(x), a neighborhood of x). But |x_n-x|<56 is the same as -56<x_n-x<56 or x-56<x_n<x+56. So all those infinitely many elements of the sequence are bounded above by x+56. We can create the following number:
M=max(x₁,x₂,...x_K(56),x+56). M is the maximum of a finite collection of numbers, and we saw earlier in the course that every finite set had a maximum. I claim that M is actually an upper bound for S. That's because x_j is one of the "elements" that M maximizes for j<K(56), and for larger j, x_j must be inside V₅₆(x)=(x-56,x+56). And that's it for an upper bound.
A lower bound is m=min(x₁,x₂,...x_K(56),x-56) and is verified in a parallel fashion.

The last general principle I wanted to state was illustrated by the following example: suppose (x_n) is a convergent sequence and its limit is x. Now suppose we define another sequence (y_n) by the following rule: y_n=(x_n)^3+176,321 for n<=10⁷⁸ and y_n=x_n for n>10⁷⁸. Does (y_n) converge, and, if it does, what can you say about the limit of (y_n). The amazing fact is that (y_n) does converge and its limit is x! I don't think that a mortal human being could see this by "testing" values of x_n (huh? look at the first ... say the first ... well, if you "check" one term a second for about 3 three, you will only have looked at less than 100,000,000=10⁸ terms. But if K(epsilon) is the expression guaranteed to us by the convergence of (x_n), then any n greater than J(epsilon)=max(10⁷⁸,K(epsilon)) will certainly have |y_n-x|<epsilon. So you can change a sequence for "a while" and this won't change whether it converges or not, and it won't change the limiting value if it does converge.

We discussed this question. A suggestion that 1 was an upper bound of S was made. The assertion (M-N)/(M+N)<=1 would need to be verified. But this is not too hard, because if we begin with M<M, certainly a true statement, and then subtract a positive number (N) from the left-hand side, and add that positive number to the right-hand side, then M-N<=M+N. Since M+N>0, we can divide by M+N to get (M-N)/(M+N)<=1. Therefore 1 is an upper bound.

Then the suggestion was made that 1 is actually sup(S). It isn't totally clear to me how such things are guessed: look at lots of examples, try to see what happens when things get "big", etc. It is hard to explain human invention, and this is a modest example of such invention.

How can one verify that sup(S)=1? I suggested looking at the difference between 1 and a typical element of S. So consider 1-(M-N)/(M+N)=[(M+N)-(M-N)]/(M+N)=2N/(M+N). I would like this to be "small" to establish that 1 is the least upper bound. If N is very large, then my experience with calculus suggests that 2N/(M+N) would get close to 2. So maybe to make this small, I should take N small. Since N is in N, I will try N=1. Then 2N/(M+N)=2/(M+1). This is slightly simpler to analyze. How can I "make" this small? Can I choose M so that 2/(M+1) is less than epsilon, where epsilon is some positive number specified in some weird way? Well, 2/(M+1)<epsilon will be true exactly when (2/epsilon)-1<M is true. Can such an M be found? The existence of such an M in N is guaranteed by the Archimedean property of the integers. Well, but now what? Now we know that if epsilon>0, then there is an element s of S so that 1-s<epsilon. This means 1-epsilon<s. But, my goodness, we know that 1 is an upper bound of S, so here we know 1-epsilon<s<=1. We have exactly verified the criterion for 1 being a least upper bound of S. This was a theorem we proved a few lectures ago.

Similarly one can verify that this S is bounded below, and that inf(S)=-1. I remarked that it would be easy to get more examples of sets following this description. I could replace the "formula" x=(M-N)/(M+N) by something like

• x=(7M-3N)/(4M+5N). Then S would be bounded, and I think sup(S) would be 7/4 and inf(S) would be 3/5.
• x=(3M²-4N)/(2M²+N). Then S would be bounded, and I think sup(S) would be 3/2 and inf(S) would be -4.
• x=(3M²-2N)/(5M³+7N). Then I think S would be bounded, and sup(S) would be 3/5 and inf(S) would be -2/7.
• x=(5M-7N³)/(3M+2N²). Then I think this S is bounded above, with sup(S)=5/3. But S is not bounded below.

	We should follow the textbook. This should make life "easier" for students. So we must assume the following: Theorem If a>0 and if n is in N, then a has an nth root: there is a positive number b so that bn=a. The number b will be "called" a1/n, the positive nth root of a. If we assume this theorem, which can be proved in the same way that we showed there is a positive number whose square is 2, we will be able to do more examples at this stage of "technology". Later we will prove the Intermediate Value Theorem for continuous functions and apply the theorem to the functions xn (for n in N). A consequence will be the existence of such nth roots. We may further conclude that roots "act like" roots. That is, if 0<a<c and if n is in N, then a1/n<c1/n, and even that (a1/n)m= (am)1/n where m and n are positive integers, and this common value will be called am/n. These statements can be verified by fairly simple means (manipulation of inequalities and mathematical induction).

Now we come to the definition of limit of a sequence. As I wrote, this is "Almost surely the most important concept in Math 311". Although most sequences we think about are likely to be "simple", in fact sequences can be terrifically complicated. Usually the first example one thinks about is the sequence (1/n), or 1, 1/2, 1/3, 1/4, ... Note that with our definition, the limit of this sequence should be 0. Contrast that, please, with the fact that the sup of the elements of the sequence is 1.

Definition A sequence is a function whose domain is N and whose range is a subset of R.
So we could write a sequence like this: f:N-->R. In fact, this is rarely done. The traditional notation for sequences is for the "argument", the domain variable, to appear as a subscript. So a sequence would appear as (a_n). The parenthesis are the text's attempts to distinguish a sequence. Note that "n" is a dummy variable, which should (!?) be clear from context. So suppose a sequence is given by a simple formula, so its value on the n^th element of N is n². This sequence might be written (n²). But the same sequence is (s²) and the same sequence is (t²), etc. Also we will freqeuntly deal with recursively defined sequences. One example is a₁=3 and a_n+1=sqrt(4+a_n). Such recursively defined sequences may occur as harmlessly as in the Fibonacci numbers, or, more interestingly (?), with, say, Newton's method in the initial semester of calculus. It is possible to find a "nice" non-recursive formula for the Fibonacci numbers, but generally would be very difficult (and, in most people's opinion, fairly pointless!) to find an explicit formula for the n^th Newton's method approximation to the root of a function.

Definition A sequence (x_n) is said to converge to x if for all epsilon>0, there is K(epsilon) in N so that |x_n-x|<epsilon.
We tried to take apart the statement, look for the quantifiers and the logical connectives. Maybe we can rephrase it:
IF FOR ALL epsilon>0, THEN THERE EXISTS K in N, so that FOR ALL n>=K, |x_n-x|<epsilon.
The textbook writes K(epsilon) instead of the logically permissable K to be nice: to remind the reader that K could depend on the specification of epsilon.

I decided to do something weird, to try to write the negation of the statement above. So:
(x_n) does not converge to x is this:
There exists some epsilon>0 so that for all K in N there is n in N with n>=K so that |x_n-x|>=epsilon.

Notice that if we want to prove that a sequence does not converge to some x, we need to specify only one epsilon and not check every epsilon! I tried to show that the sequence (n²) does not converge to 17. Of course, I did screw up -- I insisted on checking every epsilon which was too much work. So, here it is better, improved: how can we show that (n²) does not converge to 17? Well, we can specify an epsilon, say, epsilon=1. Then we need to see if |n²-17|>=1. We can remove the absolute value signs if we knew that what was inside was positive. So, golly, if we insisted that n was at least, say, 5, then |n²-17|=n²-17. So we need to know when n²-17>=1. And we need to know that n is at least K, some unspecified integer. So the two requirements will be satisfied if n is some integer greater than or equal to max(5,K). If we wanted to know that |n²-17|>=epsilon, then we could request that n be some integer great than or equal to max(5,K,sqrt(epsilon+17)). Such an integer exists by the Archimedean Property.

I asked students to begin reading chapter 3 (at least 3.1 and 3.2), and to hand in textbook problems 2.4: 3, 4a and 3.1: 8, 10 in a week. Another set of workshop problems was also handed out. Also, I announced that an exam would probably be given in about two weeks.

We went over some of the workshop problems from workshop #4. I tried to emphasize that finding examples and understanding the statements were important. I repeated my comments written in the last diary entry about the general structure of many of the proofs at this point in the course (contradiction, inequalities, Archimedean property). In almost an hour of discussion, we were only able to cover some aspects of problems 2 and 3. So investigating these problems is very difficult, and very painstaking. Much patience is needed!

Somewhat more detail
Concerning problem #2, I first asked for an example, "Simple examples are better ..." I was told to consider A=(0,infinity), all positive numbers. Certain A is nonempty, and if a is in A then (2/3)a is in A since 2/3 is also positive. So here's an example.

Another example? We considered A=(0,1). Here A is nonempty, and A consists of positive numbers, and I asked why (III) was satisfied. We thought about this, and if a number is between 0 and 1, two-thirds of it would also be, since 2/3 is positive and 2/3 is less than 1.

After some inquiry, we were given (0,1) union {2} as another example. This certainly "works".

And another example: we considered S whose elements were 1/n where n was in N. If a=1/n, can we find b in S with b<(2/3)a? Ms. Chan suggested b=(1/3)(1/n)=1/(3n), certainly an element of S and certainly less than (2/3)a.

Now I made the game harder. I asked if there were an example of an S which satisfied (III) but which had the following qualifications:
Suppose (x,y) is a positive interval of positive length. That is, x>0 and y-x>0. Could we find an example of an S so that:
S intersect (x,y) (for every eligible x and y) was not empty. And
S "contains" no interval (x,y): that is, there is no (x,y) which is a subset of S.

The last requirements seem to mean that S has lots of holes. The suggestion was made that we consider an S which is the collection of positive rationals. And, actually, due to the density of both the rationals and the irrationals, the example "works".

For problem #3, the examples we considered seem far more "routine". For example, we looked at intervals "drifting" to the left: one example was A_n=(-n,-n+1). Then we proved that each A_n had to have an upper bound (this followed from the fact that A_n was a subset of B, which did have an upper bound). So each A_n had a least upper bound, sup(A_n). This was because we needed to verify that each u_n existed.

Then I tried to verify orally the equality suggested in the proof. I don't know how successful I was. What was the strategy I used? This: after we established that the two sup's mentioned in the problem exist, I also remarked that to prove A=B, we may prove both A<=B and A>=B. This strategy will certainly work for the equality requested in problem 3.

The question of the day
Consider the set S of real numbers x so that x=(M-N)/(M-N) where M and N are both in N (the natural numbers).
If S is bounded above, what is sup(S)?
If S is bounded below, what is inf(S)?

The results today contain further nearly paradoxical consequences of completeness. The discussion will also continue using various proof techniques which are common to the subject:

Manipulating inequalities. Proof by contradiction. Use of the Archimedean property whenever we "really" need big or small numbers.

Please try to see the structure of these proofs in spite of all of the details. All of the results below are discussed and proved in detail in the text (section 2.4).

Theorem The rationals are dense in the reals. More precisely, if x<y are real numbers, then there is q in Q with x<q<y.
Proof: First I suggested we look at 0<x<y. This seemed too hard. How can one "find" a rational number inside a random interval? Well, let us be even more special.

More special case: 0<x<y & y-x>1. Here the length of the interval is greater than 1. I'll bet that I should be able to find an integer inside the interval (x,y). Well, what integer? I defined the following set: W={w in R : w is in N and w>=y}. SO W is a subset of N. What do we know about W? First and most important and almost obvious: W is not the empty set. Why? (Everything must be proved in this course!) By the Archimedean property, there is n in N so that n>y. So W is not empty. Now how can we get "close" to the open interval (x,y)? Every nonempty subset of N has a least element (this is called "well-ordering" and many people in class may know about it through the "principle of the smallest counterexample"). Suppse that v is the smallest element of W. Then v>=y. What about v-1? I bet that this integer will "work" -- it will be inside (x,y). The proof that it is inside uses contradiction.

What if v-1 is not in (x,y)? Then either v-1>=y or v-1<=x.
First alternative: if v-1>=y, then v-1 is in W and is surely less than v. This contradicts the fact that v is supposed to be the smallest element of W.
Second alternative: if v-1<x, then v<=x+1. But since y-x>1, we know that y>x+1, so transitivity of > implies v<y (x+1 is between these) and this is impossible since v is in W.

So we have found an integer in (x,y) if y-x>1. Let's go back now to a less specific case: what if we only know that y-x>0? At the suggestion of a student, we will "stretch" the interval (x,y).

I claim there is m in N with (mx,my) having length greater than 1. Why is that? Well the length of (mx,my) is my-mx=m(y-x). Since (y-x)>0, the Archimedean property implies that there is m so that the product of m and y-x is at least 1. (Take m to be any integer greater than 1/(y-x).) Then the previous "analysis" applies to (mx,my). We can "find" an integer n which is inside (mx,my): mx<n<my. But if we divide this inequality by the positive integer m we get x<n/m<y, and n/m is in Q, so we are done with this case.

Sigh. So we have "handled" 0<x<y. What about 0=x<y? Well we can use the fact that 0<y/2<y and use the previous case: we can find a rational number between y/2 and y, so there must be one between y and 0. What about the case x<0<y? Well, we can use the previous case and find a rational number between 0 and y, and that will work here. Sigh. Now move "down": we have two further cases: x<y=0 and x<y<0. Both of these can be "transformed" into an earlier case by multiplying the inequalities by -1. Then positive rationals are found in the transformed cases, and changed back to the current cases by multiplying those rationals by -1: so if x<y<0, for example, then 0<-x<-y so that there is n/m with 0<-x<n/m<-y and therefore 0>x>-n/m>y.

So there is a rational number in every interval of positive length. Indeed, if you keep chopping up intervals, you can actually find an infinite number of rational numbers inside every interval of positive length!

Now the task is to analyze the irrationals. Well, here is a very irritating proof of a statement:
Theorem There are irrational numbers. That is, the set R\Q is not empty.
Proof: We have proved that R is not countable. But we know from early in the course that Q is countable. If R=Q then R would be countable, which is a contradiction. So the theorem is proved.
Many many people find the "proof" of this result extremely dissatisfying. Why? It is a pure existence proof. The proof claims there are lots and lots and lots (uncountably many!) irrational numbers, but doesn't produce one such. Please note that one common result which is one of the earliest proofs by contradiction in mathematics ("There is no rational number whose square is 2") does not produce or exhibit a real number whose square is 2. But if we can exhibit such a real number, then we will indeed have described a real number which is not rational. Whew! In fact, in probability terms, the event (a technical word) of picking a real number "at random" and coming up with a rational number has probability 0, and the event of coming up with an irrational number has probability 1. This is unsettling, and for those who know probability, it is an example of why probabilities model reality. The event of picking a number at random and coming up with 78/13 can occur. It just has probabilty 0.

Theorem There is a positive real number whose square is 2.
Proof: This proof is modeled on one in the book. We consider the set A={x in R : 0<=x & x²<=2}. This is a reasonable set to study in this problem. If you think about it, this set is sort of an interval, and the "top" boundary of this interval should be the desired sqrt(2). What's the "top" going to be? We will need to use the Completeness Axiom. There are two conditions about A which must be verified:
  1. A is not empty. This is surely true, since, say, 1 is in A.
  2. A is bounded above. We had some difficulty with this in class. How can we check that, say, 7 is an upper bound of A? We will proceed by contradiction. If 7 is not an upper bound, then there is w in A with w>7. But then w²>49. This contradicts one of the membership "requirements" of A, that w²<=2. So therefore 7 is indeed an upper bound of A.
Now that A is nonempty and bounded above, we can apply the completeness axiom to A.

So A has a least upper bound. Let's call a the sup(A). We know (1 is in A) that a is positive. We also know that a is less than 7. I am more interested in a². I bet that a² is equal to 2. But I need to more than bet in this course. I need to be sure and to verify. I will proceed by contradiction. If a² is not 2 then either a²<2 or a²>2. I will try to find contradictions in both of these cases.

The case a²<2
I think that I will try to increase a a small amount, and still get some real number whose square is less than 2. If I can do this, I will have a member of A which is bigger than a, and this will be a contradiction to a being the least upper bound of A.
Digression: how should I find this modification to a? I will call it b. b is a little bit larger than a. So in fact b will equal a+(1/n) where n is an integer I will try to determine.

b²=a²+2a/n+1/n² and we would like this to be less than 2. I am assuming here that a²<2. So 2-a² is positive. Therefore we want n so that 2a/n+1/n²<2-a². Let me "factor out" a 1/n, so that I want (1/n)(2a+1/n)<2-a². This is quite complicated in its dependence on n. Let me make my requirement a bit simpler: if I could get (1/n)(2a+1)<2-a² then since 1/n<1 I would know that (1/n)(2a+1/n)<(1/n)(2a+1)<2-a² and I would be done. So I need (1/n)(2a+1)<2-a². But ("solving for n") this means I want n so that (2a+1)/(2-a²)<n. I can find this n because of the Archimedean property. Whew! I am done with providing a contradiction to this alternative.

The case a²>2
Now we want to decrease a and get something (we'll call it b) whose square is still greater than 2. If w is in A, w²<2. If we find such an b, then b²>2. So w<b (part of a homework assignment: one positive number A is less than another positive number B if and only if A² is less than B²). If we find such an b we will get a smaller upper bound for A, and contradict the least upper bound nature of a. How do we "find" an b? We look for a positive integer n so that b=a-1/n has square greater than 2. Now b²=a²-2a/n+1/n². When is this greater than 2?

We know a²>2 and thus a²-2>0. So a²-2a/n+1/n²>2 means a²-2>2a/n-1/n². The n² on the right is confusing me. Let me "factor out" a 1/n: I want n so that a²-2>(1/n)(2a-1/n). The darn 1/n in the term (2a-1/n) is confusing me. Suppose I could find n so that a²-2>(1/n)2a. Then I know that a²-2>(1/n)2a>(1/n)(2a-1/n) so I would be done. (By the way, I think it is "wiggly" reasoning here that is close to the most difficult part of the proof for the newcomer. I don't totally know how to make this simpler: I am sorry.) To get a²-2>(1/n)2a is the same as getting an n in N so that n>2a/(a²-2) and such an n can be found because of the Archimedean property.

Therefore we have eliminated the two "undesirable" alternatives, and the Completenenss Axiom has guaranteed us a positive real number whose square is 2.

In calculus we could "create" a square root of 2 by considering the graph of y=x² on, say, the interval [1,2]. The graph goes from (1,1) to (2,4) and must cross y=2 somewhere, and that somewhere has x=sqrt(2). The "must" comes from the Intermediate Value Theorem. We will prove a version of the Intermediate Value Theorem in this course when we get the "technology". The reasoning in the theorem just proved is essentially a very stripped-down version of the reasoning in the Intermediate Value Theorem. The proof of the theorem is quite intricate! Please also note that the elaborate proof scheme does not provide a method for efficiently approximating sqrt(2). That's a very different thing, one which we may touch upon later.

Now we know one specific irrational number (but in fact, by the counting argument there are lots and lots and lots of them!). The enthusiastic and masochistic student could try the same argument to get a square root of 3 or a cube root of 4, etc. We now can "create" many irrational numbers: if P and Q are rational numbers, and Q is not 0, then I claim that P+Q*sqrt(2) is also irrational. Because if it were rational, say a rational number M, then sqrt(2)=(M-P)/Q would be rational which is false. Using this idea (multiples of sqrt(2) properly scaled) we could prove:

Theorem The irrationals are dense in the reals. More precisely, if x<y are real numbers, then there is an irrational number i withx<i<y.
Proof: Look in the text, please.

The question of the day
I told students that the function f(x) was piecewise defined by the following: f(x)=0 if x is rational and f(x)=1 is x is irrational. So f(13/78)=0 and f(sqrt(2)*5/7)=1. I asked students to sketch a graph of g as well as they could.
This is irritating. The "best" sketch approximating a graph of f would be, probably, two horizontal lines illustrating the density properties of the rationals and the irrationals. The graph would appear to violate the vertical line text, but there would be a hole in each line where there was a point in the other line. So there!!!

I may have made a serious error in exposition here. For the purposes of the course, the results I would like students to "internalize" from this lecture are the following:

• Any interval of positive length in the reals must contain rational numbers.
• Any interval of positive length in the reals must contain irrational numbers.

The first statement follows fairly directly from the Archimedean Property, and is discussed above. The second result got a very, very tortuous exposition. The online dictionary defines "tortuous" as
/tortuous/ adj.
1. full of twists and turns ("followed a tortuous route").
2. devious, circuitous, crooked ("has a tortuous mind").
I was "seduced" into following the text's exposition of the existence of a specific irrational number (sqrt(2)). The proof of that (essentially, as I explained, using an argument which we will do later in more general circumstances for the Intermediate Value Theorem) was very very intricate, and it is clear to me now (in retrospect!) that the gain was not worth the pain in this case.

Let me discuss a different way of getting the result desired. The "counting argument" already establishes that there are irrational numbers. That is, the rationals are countable, and the real numbers are not, so the irrationals must be uncountable. But must there be irrationals in, say, the closed interval [0,1]? Maybe some how (!?) that interval doesn't have any, and the irrationals are "somewhere else". Well, let's think a bit: if v is irrational, then v+1 is irrational, and, conversely, if v+1 is irrational, then v is irrational (for if v+1=q in Q, then v=q-1 is certainly rational). Therefore if [0,1] is "free" of irrationals, so is [1,2]. And so is [2,3], and ... The "..." indicate a proof via Mathematical Induction which could be run going "to the left" (to [-1,0] and [-2,-1] and ...) as well as "to the right". By the Archimedean Property, every number is in one of the intervals [m,m+1] for m in Z. So if there are no irrationals in [0,1], then there are no irrationals in all of R, which is a contradiction.

This idea should also appeal to a certain "naive" feeling about the "real line": the real line is or should be "homogeneous" -- any one piece of it should "look like" another piece. So [0,1] and [53,54] and [-109,-108] should "look" the same. And that's what the discussion in the previous paragraph says. We can go further. Look again at [0,1]. We now know it has irrationals in it. If we break up [0,1] into intervals, say, [0,1/3] and [1/3,2/3] and [2/3,1], then these look alike, also. If one of these intervals has irrationals in it, then translate by +/-1/3 or +/-2/3 to get irrationals in the others. And if one of those intervals does not have irrationals, then neither do the other two (again, the intervals look the same for the rational/irrational characterization, since we are translating by rationals). We could extend this argument, and divide intervals into n equal parts, etc. The natural conclusion would be: any interval of positive length which has rational endpoints must have irrationals inside it. Now take your interval (x,y) with length y-x>0, where you know nothing about the rationality or irrationality of x and y. But, golly, the earlier result says we know there are rationals in (x,y). Well, in fact, there is q₁ in (x,y) and then we can get q₂ in (q₁,y) with both q₁ and q₂ in Q. So we've put an interval with rational endpoints inside (x,y), and that interval must have irrationals in it.

Of course students must decide if they like this argument. One defect, certainly, is its "non-constructive" nature: no specific irrational is actually exhibited. It is a "soft" argument. But maybe it is easier to understand, and we now do get the density of the irrationals nicely and easily (at least, "nicely and easily" to me -- with much less "sweat" than the sqrt(2) proof above).

So, beginning backwards: I remarked that I would not at this time discuss decimal expansions. I hope to come back to them after we have done infinite series. Decimal expansions are a specific type of such, and they are really quite touchy to explain and understand. (Why then are we ever impatient if students in third and fourth [and tenth and eleventh] grades misunderstand them?)

Continuing backwards, I stated the
Nested Intervals Theorem Suppose I_n=[a_n,b_n], for n in N is a nested sequence of closed intervals: I_n+1 is a subset of I_n for all n in N. Then there is a number s in all of the intervals.
I remarked that I had essentially proved this result last time, "inside" the proof that R had uncountably many elements. But I will reproduce the proof, perhaps more systematically, here. It is also in the book.
Proof: Well, first maybe we should decide what a closed interval is. A closed interval is a set, I, where I={x in R : a<=x and x<=b} for a and b given. Sometime we will abbreviate the compound inequality in the definition: "a<=x and x<=b" by just writing "a<=x<=b". I also note that if we have a>b, the interval will be the empty set: so [5,3] is the empty set. Therefore when we discuss [a,b] we will implicitly assume that a<=b to avoid have to worry about this exceptional case. We also define b-a to be the length of I.

If I=[a,b] and J=[c,d], then I is a subset of J if and only if c<=a and b<=d. Note that almost everything from now on in the course will have inequalities in it, and this is one example. You should prove the equivalence of the statements in the initial sentence of this paragraph. Also, if I is a subset of J, then b-a<=d-c (multiply one of the inequalities by -1 which "reverses" it and then add it to the other).

Therefore the "nested sequence" I_n is really this: a collection of closed intervals [a_n,b_n] so that:

1. a_n<=b_n for all n in N (so I_n is not empty).
2. a_n<=a_n+1 and b_n+1<=b_n for all n in N (so I_n+1 is a subset of I_n).

I claim that b₁ is an upper bound of L. The proof will be a bit intricate.
Proof: Let P(n) be the statement b_n<=b₁. We will prove P(n) by Mathematical Induction.
Base Case The case n=1 is verified because b₁=b₁.
Inductive Step We assume P(n): b_n<=b₁. But now 2. in the definition of Nested Intervals applies, and we know b_n+1<=b_n. So by transitivity of <= we get b_n+1<=b₁ which is exactly P(n+1).
But now a_n<=b_n by 1. of the definition above, and again by transitivity, a_n<=b₁. So we are done.

(I) and (II) allow us to apply the Completeness Axiom, and we know that sup(L)=s exists. We also know that a_n<=s for all n in N. We can conclude that s is in I_n if we also know that s<=b_n. Why should this be true? (Here is where I did draw a picture of the geometric situation on "the real line" in class.) If we can establish that b_n is an upper bound of L for each n in N then we will know that s<=b_n. So all we need to prove is the statement: Q(k,n): a_k<b_n for all n and k in N.
Proof: Above we showed the statement b_n<=b₁ for all n in N. We may similarly prove (using math induction!) that a₁<=a_k. Now how can we "compare" these two? Well, suppose that t=max(k,n). Then a₁<=a_k<=a_t<=b_t<=b_n<=b₁. The inequality a_t<=b_t follows from requirement 2. of the nested intervals definition. So again transitivity of inequality implies the desired statement a_k<b_n.

Now we know that b_n is an upper bound of L, so s, the least upper bound must satisfy s<=b_n. This together with what we knew before implies that s is in I_n, for all n in N, and this is what we were supposed to prove.

Question What are "nested intervals" and who cares?
In fact, almost all root finding techniques I know in "the real world" use some sort of nested technique to insure the location of the roots. We somehow go from one interval where we know a root exist, I_n, to another, "smaller" interval, I_n+1. So in fact the framework of the result above is constantly around in numerical analysis. One further "tweak" to this idea is the following:

Proposition If inf({b_n-a_n}, n in N)=0, then s is unique: there is exactly one point which is inside all of the I_n's.
Proof: We will assume the contradiction and deduce something false. If there were two (unequal) points, s and t with s<t, consider t-s, a positive number. Since it is positive, and since inf({b_n-a_n}, n in N)=0, there must be m so that b_m-a_m<t-s. If t and s are both in [a_m,b_m], then [s,t] is inside that interval. But but but ... the lengths don't work right (see the comment on lengths of intervals inside intervals earlier): we must have t-s<=b_m-a_m. This is a contradiction.

Examples The remainder of the class was devoted to examples. The examples range fromt the stupendously silly to the somewhat subtle, and are good reviews of things we have already done.

1. If I_n=[0,1], then the Nested Intervals Theorem applies. There are many, many eligible s's: in fact, the collection of all the s's is exactly [0.1].

2. If I_n=[0,0], then the Nested Intervals Theorem applies. s=0 is the only number in all of the intervals.

3. If I_n=[0,1/n], then the Nested Intervals Theorem applies. Certainly s=0 is in all of these intervals. Can there be anything else? Since the intervals each contain 0 and positive numbers, the only possible candidate would be some v>0. But we already showed that if v is positive there is some n in N with 1/n<v. So there can't be any other v. s=0 is the only number in all of the intervals.

4. If I_n=[-1/n,1+1/n], then the Nested Interval Theorem applies, and both "sides" of the intervals are "moving". Here the collection of s's which are in all of the I_n's is all of [0,1]. (We need to know that if w>1, there is 1/n with 1+1/n<w, which follows from the same result we proved last time.)

5. Now I started fussing with various other hypotheses. What if we remove "bounded" from the hypotheses? A closed unbounded interval is one of two types: [A,infty)={x in R: x>=A} and (infty,B]={x in R: x<=B}. Then there are nested closed unbounded intervals having lots of numbers in common: take I_n=[0,infty) for all n in N. And there are nested closed unbounded intervals having no numbers in common: take I_n=[n,infty). Then a number s will be in all of these I_n's if s>=n for all n in N. But the existence of such an s would contradict the Archimedean Property that we have already proved!

6. What if we changed "closed" to "open" in the hypotheses, but kept all the other words: that is, we look at nested sequences of open bounded intervals. An interval is open if it is of the form (A,B)={x in R : a<x and x<b}. If we took I_n=(-1/n,1+1/n) for all n in N, then the set (0,1) is the collection of s's which are in all of the I_n's. If we took I_n=(-1/n,1/n), then s=0 is the only number which is in all of the I_n's (again, using Archimedean consequences). And, perhaps most subtle of all, if we took I_n=(0,1/n), then we have a nested sequence of open bounded intervals, and there is no number s which is in all of the I_n's!

Next time I will continue backwards and finish chapter 2. I will verify the density of the rationals, the existence of sqrt(2), and then the density of the irrationals.

• You cannot prove a logical implication of the form "If P then Q" by assuming Q and making deductions from that assumption. This procedure is invalid.
• Use of the word "equal" or the notation "=" to mean "logically equivalent" or "implies" (either!) is incorrect. It is bad grammar or syntax or ...
• In what a reader might presume is an induction proof, the assertion "n+1 is true" makes no sense. The adjectives true and false commonly apply to statements or assertions. They do not apply to integers.
• Poorly specified referents. Almost every student in the course has written statements similar to the quoted typical examples which follow.
  • "if we multiply the right hand [the word "side" is missing!] of the inequality" on a page with more than 10 preceding inequalities, none close to the statement given.
  • "assume that it holds for n" with no additional clarification of "it".
• Poor proofreading. This is close to a pun, but I mean both "proofreading" with its standard use: to find and correct errors, and reading a proof to make sure it is logically sound. A first casual writeup will almost surely not be adequate in this course. Arguments in 311 need to be precisely stated, and may be rather intricate. Misspelled words, sentence fragments, and circular arguments will detract from your work and may invalidate it.

Please proofread what you hand in. Ideally, you should read and reread and revise almost any formal communication. Neatness and clarity count, as you darn well know if you've tried to read any complicated document.

I began by rewriting a great deal of what I wrote last time. Then I asked students to write answers to
The Question of the Day (textbooks and notes closed)
1. Define inf(S).
2. State a criterion which would allow a lower bound of a set to be identified as the inf of a set. (Parallel to the theorem stated last time for sups.)

Proposition Suppose V={x in R : x=1/n for n in N }. Then V is bounded, and sup(V)=1 and inf(V)=0.
Proof: "Bounded" means bounded both above and below. In this case, if n is in N, then n>=1, so 1/n<=1 and n is positive. So in fact, every element of V is also in [0,1], a bounded set, so V is bounded.
1 is in V, and 1 is an upper bound of V. 1 is actually a maximum for V, therefore sup(V)=1. (Students are reminded that this was mentioned last time!)
The inf is more delicate, and we need to think about it. Since all the elements of N are positive, the elements of V (multiplicative inverses of positive numbers) are also positive (we proved this!). Therefore 0 is one lower bound for V. Why is 0 the greatest lower bound? We will prove this by contradiction. Suppose there is, in fact, a greater lower bound, which we called Daphne in class. What do we know about Daphne? Daphne <=1/n for all n in N, and Daphne>0 (she is the candidate for a greater lower bound than 0). What can we do with such numbers? Well, if 0<a<=b, then 1/b<=1/a. So in fact we know that 1/(1/n)<=1/Daphne. But 1/(1/n)=n, and 1/Daphne is "revealed" as a upper bound of N, and we already know that N is not bounded above. Therefore such a "Daphne" does not exist: we have a contradiction.

The online dictionary tells me this about daphne:
/daphne/ n.[Bot] any flowering shrub of the genus Daphne, e.g. the spurge laurel or mezereonDaphne.

Discussion I proceeded to investigate one "bad" consequence of completeness, the consequence which I labeled (a) during the last class: the disappearance of little, small, very small, infinitesimal numbers. "Everyone" has seen or endured or even said explanations of such symbols as dy/dx: this is a ratio of really really very very small numbers. And then sketched the curve y=f(x) and drawn an infinitesimal right triangle, with one side "dx", the other side "dy", and the ratio the "slope of the curve at the point". And then when questioned, one is told that dx is very small. How small? Well, it is smaller than 1/10 or 1/1,000 or ... very very small. It is not 0, because one can't divide by 0. It is very small, and dy is the consequential increase in y when x is "increased" by dx. Etc. 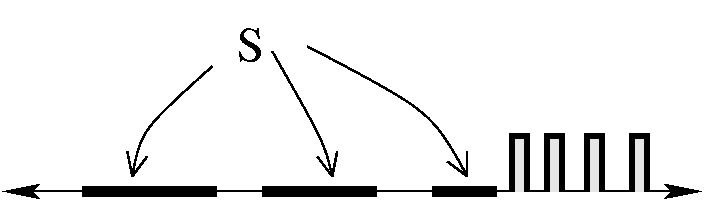This is all very embarrassing, because:
Corollary If w is positive, then there is n in N with 1/n<w.
This is true because if there were no such n, then w would be a positive lower bound of the set V we looked at above. And we saw that was impossible.
Now we know that there can't be dx's. But then (a rather disjunctive [?] attitude in the math trade?) how come many people who profess total belief in the completeness axiom still like to talk about very very very small numbers? In this class we will be "strict constructionists". We can't base any of our very strict results upon such "imaginings".

Then I turned to a analysis of the bad consequence (b) of completeness. This is more elaborate. I began with reminders (from the lecture of 1/23). I reminded people of the definition of a finite set (a set that had a bijection with {1,2,3,...,n} for some n in N). I reminded people of the definition of a countably infinite set (a set that had a bijection with N). And, finally, a set was countable if it was either finite or countably infinite. The startling result we are now about to prove needs these ideas.

Theorem R is not countable. (More positively stated, R is uncountable.)
Proof: The proof is fairly elaborate. I tried to follow more or less the proof in section 2.5 of the text. First I remarked that we will in fact prove that [0,1] is uncountable, and this will imply that R is uncountable, since R is bigger than [0,1] (if R were countable, then the bijection restricted to the subset [0,1] would in effect "count" the elements of [0,1]).
I know that [0,1] is infinite (hey, the set V analyzed just previously is in there!). I will assume that [0,1] is countable and try to deduce a contradiction. Well, if it were countably infinite, there would be a bijection with N. Thus we could label or list all of the real numbers in [0,1]: x₁, x₂, x₃, ... My job will now be to create another real number that isn't on this list.
Consider [0,1]. x₁ is somewhere in [0,1]. I claim it is possible to create another interval [L₁,R₁] so that:
BASE   0<=L₁<R₁<=1
  x₁ is not in [L₁,R₁].
Let me try to describe how to do this a bit more carefully than I did in class:
If x₁=0, then L₁=1/2 and R₁=1.
If x₁=1, then L₁=0 and R₁=1/2.
If x₁ is between 0 and 1, then take L₁=0 and R₁=(1/2)x₁.
I think this works, and BASE is true.
Now I will assume a big mess of stuff: I will assume that I have previously defined L₁,L₂,...L_n, and R₁, R₂, ...,R_n with the following properties:
  0<=L₁<L₂<=L₃<= ... <=L_n<R_n<=...<=R₃<=R₂<=R₁<=1
  x₁ is not in [L₁,R₁]; x₂ is not in [L₂,R₂]; ... x_n is not in [L_n,R_n].
We now do an INDUCTIVE STEP: we create L_n+1 and R_n+1 so that x_n+1 is not in [L_n+1,R_n+1], and L_n+1<R_n+1 (there is still lots of room between L_n+1 and R_n+1) and L_n<=L_n+1 and R_n+1<=R_n. Here is how to create x_n+1, more explicitly than in class: (the alert student will realize that I am merely copying the method above!)
If x_n+1=L_n, then L_n+1=(1/2)(L_n+R_n) and R_n+1=R_n. (Move halfway up)
If x_n+1=R_n, then L_n+1=L_n and R_n+1=(1/2).(Move halfway down.)
If x_n+1 is between L_n and R_n, then take L_n+1=L_n and R_n+1=(1/2)(L_n+x_n).
If x_n+1 is not in [L_n,R_n], then just take L_n+1=L_n and R_n+1=R_n. (Do nothing if you don't have to!)
Here is a picture of just the first alternative:

The reader can draw appropriate pictures of the others. We have used mathematical induction to define a sequence of closed intervals with really weird properties.
Now we will create a "new" real number with the help of the Completeness Axiom and these weird properties. We define Lt to be the set {L₁, L₂, L₃, ..., L_n, ...} (all the left-hand endpoints). We define Rt to be the set {R₁, R₂, R₃, ..., R_n, ...} (all the left-hand endpoints). I will concentrate temporarily on Lt. It is a non-empty subset of [0,1]. It is bounded above, by 1, for example. Therefore by the Completeness Axiom it has a least upper bound, sup(Lt) which I will call v. What do I know about v? v is in [0,1], since all of Lt is in [0,1]. Since all of the R_n's (right-hand sides) are greater than all of the L_n's (left-hand sides) each of the R_n's is one upper bound of Lt, and therefore v<=each R_n. So v is in the interval [L_n,R_n]. Therefore since we constructed this interval to exclude x_n, v can't be equal to x_n. But, but ... if v can't be x_n for any n, then ... we have "created" a new real number not in the "list" we started with! This is a contradiction. So we couldn't have started with a complete list of all real numbers.

Discussion Mathematical induction allows us to prove things about N. Indeed, mathematical induction allows us to prove things about sequences of statements. But one result of the theorem we just proved is that we cannot create a list of statements about individual real numbers, use mathematical induction to prove each statement, and then claim we have proved a statement about all real numbers. We can't make a sequential list of all real numbers. Therefore our proof techniques need to include somewhat different tools. Indeed, almost every proof we do later in this course will use inequalities. Inequalities are the chief tool of analysis.

What can "computer science" do? Let me take a somewhat simplistic view of what computers can do. They run with programs, and programs act on inputs. Each program is a finite sequence of instructions. Each input is a finite sequence of symbols. This vision of computation is "deterministic", by which I mean that the program + the input completely specify what will happen. This is a coarse (?) view of programs, but if you accept it a rather startling conclusion can be gotten. How many programs are there of length, say, 78? No matter what the computer language, anyone would agree that the total number of computer programs of a fixed length is finite. Here I don't even care how big this number is, just that it is finite (a list of all strings of symbols of a certain length). How many inputs of length 78 are there? Again, finite (another long list). Therefore, the number of outputs of computer programs which are length 78 acting on inputs of length 78 is finite. Note that 78 is not special here. The number of outputs of computer programs which are length N acting on inputs of length N is finite for any N in N. But that means (since the union of countably many countable sets is finite [see the diagonal process in lecture of 1/23]) the number of outputs of computer programs is at most countably infinite. Let me temporarily call those real numbers which can occur as outputs of computer programs as "the computable real numbers", then, oh my goodness, there are many many many more real numbers which are not computable! Some people find this quite distressing.

More or less, the discussion of (a) might convince someone that the Completeness Axiom proves there aren't enough real numbers, while the discussion of (b) could say that there are too many real numbers! This is complicated by a sort of disciplinary (math="the discipline" here) schizophrenia: essentially all professional mathematicians claim to believe in the Completeness Axiom, and many people think about "really small" numbers, and increasing numbers of people worry about the computability of "real numbers".

Although objections (a) and (b) above can be distracting at times, from now on we will officially "believe" in the Completeness Axiom. As for the students, it is, as I remarked in class, something you should believe (!) if only for the purposes of the course (just as a student who believed in creationism might need to learn enough about evolution to answer some test questions correctly).

We begin with a bunch of definitions>
Definition A nonempty subset S of F is bounded above if there is w in F so that for all x in S, x<=w. Such a w is called an upper bound of S.
Definition A nonempty subset S of F is bounded below if there is w in F so that for all x in S, x>=w. Such a w is called an lower bound of S.
Definition A nonempty subset S of F is bounded if it both bounded above and bounded below.

These definitions are actually designed to be tested -- the terms are defined by asserting that there are w's for which certain comparitive statements are true. So whenever we work with the definitions, we can always see what will happen to the "w".

(Counter)example(s): F itself is neither bounded above nor bounded below. For example, suppose an element w of F is an upper bound. Then x=1+w is greater than w (since 1 is in P) and this element x of F shows that w is not an upper bound of F. Similarly F has no lower bound.
P, the set of positive elements of F, or {x in F : x>0} is bounded below (by 0) and is not bounded above (the "1+" argument works here, also). The negative elements of F are bounded above but not below.
The set [0,1]={x in F : 0<=x and x<=1} is bounded above and below. 370 is an upper bound of [0,1] and -48 is a lower bound of [0,1]. Certainly these are not the most "pleasing" upper and lower bounds, but they do serve to illustrate the definition.
The most pleasing bounds are the ones which are defined below.

Definition Suppose S is a nonempty set of F which is bounded above. Then v is a least upper bound of S if

1. v is an upper bound of S: if x is in S, then x<=v.
2. If w is any upper bound of S, then v<=w. (v is smaller than any other upper bound of S.)

Definition Suppose S is a nonempty set of F which is bounded below. Then v is a greatest lower bound of S if

1. v is an lower bound of S: if x is in S, then x>=v.
2. If w is any lower bound of S, then v>=w. (v is larger than any other lower bound of S.)

We discussed some examples, which are here displayed in tabular form. The examples were accumulated during the class discussion. In addition to least upper bound and greatest lower bound, I also included maximum and minimum, as described previously in these lectures.

S	Least upper bound	Greatest lower bound	Maximum	Minimum
[0,1]	1	0	1	0
(0,1]	1	0	1	NONE
(0,1)	1	0	NONE	NONE
{1}	1	1	1	1
(0,1/3) union (2/3,1)	1	0	NONE	NONE

The next piece of business is restating the last axiom we need to do "calculus":
Completeness Axiom Suppose S is a non-empty subset of R. If S is bounded above, then S has a least upper bound.

This axiom carries considerable philosophical "baggage". The axiom will get rid of the "holes", at least if we identify cuts with holes. In the Dedekind approach, some cuts in Q seem to have nothing in between (such as the sqrt(2) cut). The axiom is now generally but not universally accepted. A reason for that is there are some implications of this axiom which people find distasteful.
(a) The axiom will force us to totally exclude from our strict "construction" of calculus little, small, very small, infinitesimal numbers. (We will totally throw out the elves from our mathematical world!)
(b) Also, it will turn out that computer programs and mathematical induction in some very serious sense can not deal with real numbers -- real numbers are more complicated (more human?) than either of these.
I will have to discuss each of these at length. First let us play a bit with the axiom and the definition. I also not that I have now, finally, changed the name of the field we are dealing with from F to R: R is a complete ordered field

How can we "identify" the least upper bound of a set? First, the text calls the least upper bound of S, sup(S), pronounced "soup of S". The greatest lower bound is inf(S). sup and inf are abbreviations of Latin words, supremum and infimum.

sup(S) is unique. By that I mean if both Bob and Charlie are sup's of S, then Bob=Charlie. That's because if Bob is a sup, then it is an upper bound. Since Charlie is a least upper bound, Charlie<=Bob. Similarly, since Charlie is a sup, it is an upper bound, and if Bob is also a least upper bound, then Bob<=Charlie. Thus (Trichotomy) Bob and Charlie must be equal. Similarly, an inf of a set, if it exists, must be unique.

To have a sup, a set must have an upper bound. If a set has a maximum, then the maximum is the sup of the set. But a set can have a sup without having a maximum. (Similar statements are true for inf's and minimums.)

How can one try to "find" a sup? Well, if S is a non-empty set and if S is bounded above, then the completeness axiom says that S has a sup, and the discussion above declares that the sup is unique. But what "properties" does sup(S) have (besides the definition)? Here is something to think about.

If w=sup(S), consider w-(1/2). Is w-(1/2) an upper bound of S? If it were an upper bound (subjunctive courtesy of Ms. Greenbaum), then it would be an upper bound less than w (since 1/2 is positive). But w is the least upper bound (the second part of the definition of least upper bound) so this is not possible. Therefore w-(1/2) is not an upper bound of S. What does it mean for something not to be an upper bound of S? That means there must be x in S with x greater than that number. That is, w-(1/2)<x. But notice that w, being an upper bound, must be greater than x. So we know that w-(1/2)<x<=w. Whew! It turns out that this weird intertwining characterizes sup's (and then, dually [?], inf's).

Theorem Suppose S is a non-empty subset of R which is bounded above. An upper bound w of s is sup(S) if and only if for every positive number e there is an element x of S so that w-e<e<=w.
Comment: Of course the text uses "epsilon" for e.
Proof: We need to prove two implications. One will begin: "If w is sup(S) then ..." and the other will begin "If w is an upper bound of S with the property that ...". So I'll do the first one:
I want to prove: If w=sup(S) and if e is any positive number, then there is an element x of S with w-e<x<=w.
w-e is less than w. w-e cannot be an upper bound of S because if it were, it would be less than w, and w is the least upper bound. Since w-e is not an upper bound, there is x in S with w-e<x. But w is sup(S) and therefore is an upper bound of S. So x<=w. So we know that there is an element x of S so that w-e<e<=w.
Now I want to prove that: If w is an upper bound of S and if, for every e>0, there is x in S with w-e<e<=w, then w=sup(S).
Suppose that w is not sup(S). Then S would have a smaller upper bound, call it v. Thus w>v. But now I want to "create" a contradiction. For this I will need a positive number, e. Well, w-v>0. so I will use e=w-v. Then the complicated hypothesis tells me that there is an x with w-e<e<=w. This means w-(w-v)<x, or v<x. This contradicts the fact that v is an upper bound of (all of) S. So we must have made a mistake: there is no upper bound of S which is less than w.

I more or less constantly use this theorem to find sup's of sets. Here's a picture (?) of how I think (!!):

I think of the upper bounds of a set S as a collection of walls "marching down" from far to the right, getting closer and closer to S. They begin to pile up, and where they "stop" is sup(S). The content of the theorem is that if I want to move the walls the least little bit to the left, something in S will end up on the wrong (right) side. Now of course the picture I have drawn is somewhat simple. The S seems to have 3 pieces, and in most of the more interesting applications of all this that we will consider, S will have infinitely many pieces. So things will be complicated.

The ideas I am outlining in this lecture took almost a century to shape. Although the reasoning is all displayed, it is often subtle, and may be difficult to understand. Here's one significant application.

THEOREM N (the natural numbers) has no upper bound.
Proof: (This is not supposed to be "clear": everything in this course will be proved from our axioms.) Well, if N had one upper bound, then, since N not the empty set, N would have a least upper bound, say the number w. We can "move" w a bit to the left and run into "trouble". How much should "a bit" be? The integers are separated by 1's. I will take e to be 1. Let me proceed more formally:
Since w is supposed to be the least upper bound of N and since 1>0, there is an element n of N with w-1<n<=w. But w-1<n implies w<n+1. Since N is "inductive", n+1 should be in N also. But that means w is less than some element of N. So w is not an upper bound, and it certainly can't be a least upper bound! So we are done.

I note that without the completeness axiom there are "models" of ordered fields where N can be "bounded above". The importance of the result is shown by the name used for it: the "Archimedean axiom". It isn't an axiom in our setup: we proved it! We will call it the "Archimedean Property". Some people like these models because the following corollary would not be true.

Corollary (The death of tiny numbers.) The set S={x in R : x=1/n where n is in N} (just the set of numbers {1,1/2,1/3,1/4,1/5,...}) has sup(S)=1 and inf(S)=0.

I will verify this next time. The following textbook problems will be due next Thursday: 2.3: 5 and 6 and 2.4: 2 and 8.

I also gave out the next workshop problems. I strongly urged people to work in a group and to proofread each other's work. This is good practice.

Covered with virus particles of the common cold, I persisted in trying to instruct. I proceeded further in the book. I discussed the content of section 2.2, absolute value. In this I totally followed the text, having little energy for anything else. The proofs I used are almost all in the text. The proof of the Triangle Inequality is quite "cute", and when I have taught the Triangle Inequality in more elementary courses, I have verified it using an argument of cases depending upon the "sign" of various terms.

The most important results I deduced we will use repeatedly in the course. Here they are:

• |AB|=|A| |B|.
• |A+B| is less than or equal to |A|+|B| (the Triangle Inequality)
• |A|-|B| is less than or equal to |A+B| (a sort of reverse triangle inequality)

I tried feebly to apply the results on absolute value in a fashion that will be typical in this course. Consider the function f(x)=x³-15x² on the domain [1,2] (that is the numbers x so that 1<=x<=2, what we will call a closed interval). After some stumbling around (thanks to several people for telling me that f has negative values on that interval!) I asked for the following: Find A and B so that 0<A<=|f(x)|<=B for all x in [1,2]. That is, I wanted positive upper and lower bounds for the absolute value of f's values on this interval. I wanted to use only the "technology" of the course as it so far existed.

An upper bound is clear with the triangle inequality: |x³-15x²|<|x³|+|-15x²|. Now look at |x³|=|x|₃. If 1<=x<2, then |x|₃<=2³. Also +|-15x²|=15|x|², so, again if 1<=x<2, then 15|x|²<=15·2². Therefore we can use B= 2³+15·2².

An underestimate is a bit trickier. We have |A|-|B|<=|A+B|. To analyze |x³-15x²| we could take A=x³ and B=-15x². Then we know that |x³|-|-15x²|<=|x³-15x²|. For an underestimate of this when x is in [1,2], for the |x³| part we want the smallest x. So the least this piece could be is 1 (or [sigh!] 1³). To get a valid underestimate using the other part, we need to find the largest the piece to be subtracted is: so how big is the largest value of |-15x²| when x is in [1,2]? This is 15·2²=60. So this elaborate effort results in an underestimate for |f(x)| of -59, which is not too satisfactory (logically, an absolute value is always non-negative, so telling us that such a number is bigger than -59 adds nothing).

The "split" should be different. Take A=-15x² and B=x³. Then an underestimate for |A| yields (for the smallest value of |A| when x is in [1,2]) 15. An overestimate for |B| yields 8 for the largest value of |B| when x is in [1,2]. And therefore we somehow have obtained an underestimate for |f(x)| when x is in [1,2]: |f(x)|>=15-8=7.

A "beginning" student in this subject might find this all highly unsatisfactory. You can get some information with a certain sequence of algebraic "manipulations" and not get any with another, very parallel collection of manipulations. How can one tell what to do?

I enlarged upon this by asking for positive over- and under- estimates of the same |f(x)| for x in the interval from [100,200]. Here the overestimate proceeds exactly as before with the triangle inequality, and we know that |f(x)|<=(200)³+15·(200)². HOw about the underestimate? Well, it is useful to try to decide which of |x|³ and 15·|x|^2 will be the "bigger" piece when x is in [100,200]. Here I think the first, higher degree, term will be bigger. So I will write: |x|³-15·|x|^2<=|f(x)|. When x is in [100,200], then |x|³>=(100)³. The subtracted term must be overestimated (yes, this can certainly get confusing after a while!). So I know 15·|x|^2<=15(200)². Now we finally get that if x is in [100,200] |f(x)|>=(100)³-15(200)². This is positive (a fact verified by several public-spirited students since the instructor's head was clearly filled with ... phlegm or some result of having a cold).

Note that the decomposition used for |f(x)| depended on the domain. Sigh. How can one tell what to do?

I also mentioned that we can "invert" or take the multiplicative inverse of all of these inequalities and obtain positive over- and underestimates of 1/|f(x)| on [1,2] and [100,200]. Frequently one can concatenate (online dictionary: v.tr. link together (a chain of events, things, etc.) estimates of this type to work with rational functions, which are quotients of polynomials.

I did a problem from the textbook: 2.2: 8(a). For which x is |x-1|>|x+1|. Several strategies were suggested for dealing with this inequality. We could use Trichotomy and an analysis of cases. That is, see where x-1>0 and etc.: lots of work. Or we could use the following idea: A>B>=0, if and only if A²>B²>=0. First, why should I believe it is true? It certainly isn't true without some assumption of non-negativity. For example, as supplied by Ms. Chan (?), if A=-1 and B=-5, then A>B, but A²=1<B²=25. But suppose they are both nonnegative. Then multiply A>B by A and also by B. We get A²>AB and AB>B². Transitivity of > then shows A²>B². On the other hand, if A=B, A²=B², a contradiction, and if A<B similarly implies A²<B², another contradiction.

So we investigate |x-1|>|x+1|, an inequality involving non-negative numbers, by equivalently considering its square: (|x-1|)²>|x+1|². We also know that (|A|)²=A², so this becomes x²-2x+1>x²+2x+1. We can "simplify" by subtracting the same things from both sides, and then shift -2x over to get 0>4x. Multiply by the positive number 1/4 and we see that the x's which satisfy this inequality are the negative numbers. We can also try to understand this problem from a "geometric" "number line" point of view: we are looking for x's whose distance to 1 (that's |x-1|) is greater than their distance to -1 (that's |x+1|=|x-(-1)|).

We'll move on next time.

Then we proved the following:
Theorem A finite nonempty set has a minimum and a maximum.
Proof: We rephrased this to be more obviously a statement depending on n in N:
P(n): If S has n elements, then S has a maximum, M, and a minimum, m.
I will try to prove this (only for maxima, M, leaving the minima for the reader to try!) using mathematical induction.
The base case P(1): If S has 1 element, then S has a maximum. Since S={a}, try M=a. Then M is in S (since a is in S) and if x is in S, x is less than or equal to M (we know that a is less than or equal to a).
The inductive step If P(n) is true, then P(n+1) is true.
Suppose S has n+1 elements. This means that there is a bijection of {1,2,3,...n+1} with S. The element corresponding to j in S will be called a_j. We write S as T union {a_n+1}. Now T has n elements (namely, in a list, a₁, a₂, a₃, ..., a_n ). We now use the inductive assumption on T. We know therefore that T has a maximum: there is a_j so that a_j is greater than or equal to a_k, for all k with k at least 1 and at most n. Now we want to write a "recipe" for M, the maximum of S. Here is the recipe:

1. If a_j<a_n+1, then M=a_n+1.
2. If a_j=a_n+1, then M=a_j.
3. If a_j>a_n+1, then M=a_j.

I commented that the logical outline of this proof (math induction!) is what's needed for most of the workshop problems. Problems 1 and 2 need more effort for the base case, while problem 3 needs more work for the inductive step.

Most students successfully answered the question I asked last time, to find a set which had a max and no min. One simple answer is the following: {x in F : x is less than or equal to 1}. The question made me think of one of the background ideas of the subject: Richard Dedekind and his "cuts". So I detoured and discussed this topic.

Consider F, a field satisfying the algebra axioms and the order axioms. The examples we know well are the rationals and the reals. There are actually many, many others, but here we'll try to distinguish between these two examples. In F, we will "cut" the number line, as if with a scissors, into two parts, a left part L and a right part R. So here are the requirements for such a cut:

1. Neither L nor R are empty (I forgot this in class until Mr. Benson called it to my attention! I thank him again and regret that I was careless!)
2. The union of L and R is all of F. (Every number is in one of the pieces!)
3. The intersection of L and R is empty. (No number is in both pieces!)
4. (Most important) If l is in L and r is in R, then l<r.

Examples of cuts:
If L={56} and R is everything else, this is not a cut. That's because 4 is not true.
If L= all numbers less than 1 and R is all numbers greater than or equal to 1, then this is a cut.
If L= all numbers less than or equal to 0 and R is all numbers greater than 0, then this is a cut.

In the second example, L has no minimum and has no maximum. R has a minimum of 1 and no maximum. In the third example, L has no minimum and has a maximum of 0. R has no minimum of 1 and no maximum.

It is almost "clear" (considering the positive and negative integers) that any L will never have a minimum, and any R will never have a maximum. I asked if it was possible to find an example of a cut in which L has a maximum and R has a minimum.

We discussed this a while. Let's consider such an example. Suppose the maximum of L is a and the minimum of R is b. Then a<b since a is in L and b is in R and these form a cut (requirement #4). What about the number c=(a+b)/2, suggested by Mr. LaCognata? Certainly c=(a/2)+(b/2). And since a<b and 1/2 is positive, we know a/2<b/2, so c<b/2+b/2=b. Because b is the supposed minimum of R, c can't be in R. But a similar argument shows that a<c so, since a is the maximum of L, c can't be in L. But now c, which is certainly a member of F, is in neither L nor R. This contradicts requirement #2 of being a cut. So we can't have a situation where the "left half" has a greatest element and the "right half" has a least element.

But what about the NO-NO situation, as I called it? That is, the situation where L has no maximum and R has no minimum. This can actually occur in the rationals. So here is an example of a cut of Q:
L={m/n with m,n integers, and n is not 0 : either m/n is negative or (m/n)²<2}
R={m/n with m,n integers, and n is not 0 : m/n is positive and (m/n)²>2}.
It is certainly true that this is a cut of Q. It maybe is not totally clear (!) that this is a NO-NO cut: we need really to show that if m/n is in L, then there is always a larger element in L, and a similar statement (with "smaller") for R. These statements are true but take some effort (I will probably prove them later in the course). So in Q there can be such "NO-NO" cuts. Each such cut corresponds to a metaphorical "hole" in an idealized geometric picture of the Q line. We don't want such holes in the real numbers.

In fact, L always has what are called upper bounds (each element of R is one!) and R always has what are called lower bounds (each element of L is one!) and we need to eliminate the NO-NO case, which means eliminating holes. This will be one consequence of assuming (!) that there will always be least upper bounds (and greatest lower bounds) if sets are non-empty and appropriately bounded.

Dedekind's original discussion of cuts is available: Essays on the Theory of Numbers, reprinted in English translation by Dover, with a cost of about 8 dollars. Much of the book is understandable to a high school student, as I explained in class. Surely some of the content and style is antique, but it is a neat source.

I began discussing absolute value. I defined it as in section 2.2 of the textbook. I asked if "absolute value" was a function with domain F. What does this mean? I want to consider in FxF the collection of pairs: {(x,|x|) : x in F}. Is this a function? Is its domain all of F?

A function from A to B with domain equal to A is a subset W of AxB with the following properties:
If a is in A, then there is b in B with (a,b) in W.
(The Vertical Line Test) If (a,b) and (a,c) are in W, then b=c.
Absolute value has domain all of F because if x is in F, |x| is defined: the three cases where absolute value is piecewise defined take care of all elements of F by Trichotomy. Absolute value fulfills the Vertical Line Test again by Trichotomy: only one of the alternative definitions of |x| holds for each x in F. We'll go on next time.

Method #1 Suppose x is the sum of x_j² as j goes from 1 to n. If x=0, then each of the x_j's is 0 (for j going from 1 to n).
Proof: This result is a sequence of statements, one for each n in N. In fact, call the statement above P(n). I will verify the sequence of statements with mathematical induction.
The Base Case (n=1) Suppose x=x₁². Then we know from the previous class that x is in P union {0}: x is either positive or 0. (Last time we saw that non-zero squares were positive.) We will look for a contradiction using the hypothesis of P(1), which is that x=0. But if x₁ is not 0, then x₁² is in P. This contradicts (Trichotomy) the assumption that x=0. Therefore x₁=0.
The Inductive Step We assume P(n), which is the statement:
If x is the sum of x_j² as j goes from 1 to n and if x=0, then each of the x_j's is 0 (for j going from 1 to n).
We want to prove P(n+1), which is the statement:
If x is the sum of x_j² as j goes from 1 to n+1 and if x=0, then each of the x_j's is 0 (for j going from 1 to n+1).
We concentrate on x_n+1 now. Suppose that x_n+1 is not 0. Then, just as before, x_n+1²>0. But we have assumed that the sum of the x_j² as j goes from 1 to n+1 is greater than or equal to 0. But if A is greater than or equal to 0 and B>0, then A+B>0. (Proof: If A=0, B>0, then A+B=B>0. If A>0 and B>0, then by additive closure of P, A+B>0. [Wow!]) So if x_n+1 is not 0, then x>0, a contradiction. Therefore x_n+1=0. But then x, the sum of x_j² as j goes from 1 to n+1 is equal to the sum of x_j² as j goes from 1 to n. And we know that this sum is 0. This is exactly the hypothesis of P(n), so the conclusion of P(n) applies, and the x_j's as j goes from 1 to n must all be 0.
Comments One reason for my doing this in detail is to outline an inductive proof, I hope correctly. Another reason is to mention that this result really is constantly used. If "x=0", people work to change x algebraically into a sum of squares, and then magically (?) can conclude that x=0 is logically the same as all of the x_j=0, for j going from 1 to n.

Method #2 If x is nonnegative, and if, for all w positive, z<w, then z=0.
Comment We will use this a great deal in the course. It may be difficult to verify directly that something is 0. It will be easier to (over)estimate the "something", and make this overestimate "small".
Proof: (Again using contradiction) If z is in P union {0}, then either z is in P or z=0. If z is in P, then there is one eligible "candidate" for w, z itself! So we know by the hypothesis that z<z. But this is false (Trichotomy). So we're done.
(Another) comment I think the text uses epsilon for w in its statement of this result. I think this is the first use of the fearsome epsilon in its conventional place as "a really really small number". Also the text in its proof uses z/2 for w.

Question Is there a smallest positive number? More precisely, is there t in P so that if s is in P, then t is less than or equal to s?
Answer: No. If there were, consider any candidate, t. Then take for s the number t/2. This is (1/2)·t. 1/2 is in P (this is discussed more next!) and t is in P, so since P is multiplicatively closed, (1/2)·t is in P. But (1/2)<1, and therefore (z/2)<z, a contradiction to t being smallest.

Let's discuss the status of N and order. Since 1 is in P, and P is additively closed, we know 1+1 (which is called 2) is in P, and 1+1+1 (which is called 3) is in P, etc. Indeed, we could prove that N is a subset of P using mathematical induction. That is, the "counting numbers" are all positive. We also know that 2<3, since 3-2=1 is in P. How about 1/2? We showed last time that if a is in P, then 1/a is in P. So 1/2 is positive. We know that 0<1<2<3<(etc.) but we can also learn that (1/2)-(1/3)>0. Why is this true (I reserve "adding fractions" for the next workshop!)? Certainly 6·((1/2)-(1/3))=3-2=1>0. But also 1/6>0. So since P is multiplicatively closed, (1/6)·6·((1/2)-(1/3))>0 and (wow again!) 1/2>1/3. In fact, more generally (proof by induction!) if n and m are in N, then n/m is in P.

Question Is there a largest number less than 1? More precisely we ask: is there z so that
1. z<1 and
2. If w<1, then w is less than or equal to z?
Answer: No, there is not. The proof will proceed by contradiction. Suppose there were such a number, z. We will follow a suggestion of Mr. Beckhorn to create a contradiction. Consider the following w: w=z+((1-z)/2). Since z<1, 1-z>0. We already know 1/2>0. So((1-z)/2) is in P. But, in fact, this w<1, Why?
START: 1-z is in P and 1/2<1.
So ((1-z)/2)<1-z.
Add z.
END: z+((1-z)/2)<1.
(Of course, most frequently such manipulation is invented by considering the END and then "untwisting" [using mathematical equivalences] to get to the START.)
Therefore z<w<1, and this contradicts requirement 2, above. (Notice that the negation of "If Alpha then Beta" is the statement "Alpha and NOT Beta", please, and this is what we've proved.)

Then I drew some illegal pictures (officially illegal in this course, that is). I attempted to show the part of the "real line" just (?) to the right of 0 and showed by picture that there was no point to the right of 0 which was closest. I attempted to show the part of the line just to the left of 1 and tried to illustrate that there was no point just to the left of 1 which was closest.

Definition Suppose S is a subset of F. Then M is a maximum of S if
1. M is in S.
2. If w is in S, then s is less than or equal to M.
Definition Suppose S is a subset of F. Then m is a minimum of S if
3. m is in S.
4. If w is in S, then s is greater than or equal to m.

Example(s) We begin with the simplest counterexample. The empty set has no maximum and no minimum. That's because the statements 1 and 3 are false for every element of F. The empty set will constantly need to be ruled out as an example in many logical statements.
What about N? N has no maximum. If n is a maximum element, then n+1, also in N, is larger. But N has a minimum, 1, since all other counting numbers are bigger than 1.
If S={0}, then 0 is both a maximum and a minimum for S.
If S=Z, then S has no maximum and no minimum.

Question of the day Give an example of a set which has a maximum and which does not have a minimum.

Next time I will prove that any finite nonempty set has a maximum and a minimum. But I will begin the class by asking students to write one of the following (I'll allow about 10 minutes):

1. Prove: If ab>0, then either a>0 and b>0 or a<0 and b<0.
2. Briefly discuss this implication:
   If a<b, then (1/b)<(1/a).
   Is this always true? Are there simple conditions which will guarantee that it is true? Are there examples showing that it is sometimes not true?
3. Prove Bernoulli's inequality: if x>-1 and n is in N, then (1+x)ⁿ is greater than or equal to 1+nx.

Observation 8(-1)·a=-a.
Comments Before proving this, students should realize that these results are not all "obvious". I know that everyone has seen such equations starting from age, what, about 13 or 14. Why should they be true? I remarked that cross-product, usually introduced in calc 3, has some nice properties (for example, linearity in each factor), but that, in spite of how it is written, it is not generally commutative or associative! So one does need to think a bit about these things.
Proof: a+(-1)·a=a·1+(-1)·a by (M3). But then (D) implies this equals (1+(-1))·a which by (M4) is 0·a which we saw last time had to be 0. Therefore (-1)·a is an additive inverse of a. But additive inverses are unique (Observation 4), and so -a must equal (-1)·a.

Corollary (-1)·(-1)=1.
Proof: (-1)·(-1) must equal -(-1) but this is just 1 by a previous "observation" (#5, I think).

Then I did some textbook problems. (Note that the "observation" above is 1b in section 2.1.) I think I did the following:

2.1 #2a) -(a+b)=(-a)+(-b)
Proof: Add (-a)+(-b) to a+b. Using (A1) and (A2) we go from
(a+b)+((-a)+(-b))=(b+a)+((-a)+(-b))=b+(a+((-a)+(-b))=b+((a+(-a))+(-b))
Then (A4) and (A3) show that this equals:
b+(0+(-b))=b+(-b)= [(A3) and (A4) again!]0.
Therefore (-a)+(-b) is an additive inverse of a=b. But additive inverses are unique (Observation 4), so -(a+b) must be equal to (-a)+(-b).

2.1 #2d)-(a/b)=(-a)/b if b is not equal to 0.
Proof: Add (-a)/b to a/b and see if you "get" 0.
(a/b)+((-a)/b)=a·(1/b)+(-a)·(1/b)= [using (D)](a+(-a))·(1/b)
and this is by (A4) just 0·(1/b) which is 0 by one of our observations. Thus (-a)/b is an additive inverse to (a/b), and "another" additive inverse is -(a/b). They must be the same, so -(a/b) equals (-a)/b.

2.1 4 If a·a=a, then either a=0 or a=1.
Proof: Here I'll give the proof Mr. Benson suggested rather than my clumsy one. Take the equation a·a=a. If a=0, we have one of the alternatives. If a is not equal to 0, then 1/a exists. Multiply the equation by 1/a and use (M2) and then (M3) and (M4) to get a=1. So we are done. This is much shorter than my clumsy proof given in class!

I again wrote the order axioms, and stated that we were now going to investigate their consequences. (O1) and (O2) are called "P is closed under addition and multiplication."

Observation 9 If a is in F and a is not 0, then a² is in P.
Comment This is an extremely important fact, and will allow us to "discard" a whole bunch of examples of fields from the course. Proof: If a is in F, then (O3), Trichotomy tells us that either a is in P or -a is in P. If a is in P, then a² (which is defined to be a·a) must (by (O2)) be in P. If -a is in P, then (-a)² must be in P. But (-a)·(-a)=(-1)(-1)a². And we saw already that (-1)² is 1. Therefore, (-a)²=a² must be in P. So in either case, a² is in P.

Corollary 1 is in P.
Proof: 1 is a square (either of 1 or of -1!).

Now I can assert the following: the complex numbers cannot be made into an ordered field/ That's because i² is -1, and on the one hand, squares are in P. But on the other hand, -1 is not in P: contradiction.

Also the integers mod 5 cannot be made into an ordered field. THis is because 1 must be in P. And therefore by (O1) 1+1+1+1+1 (five times) must be in P. But in mod 5 addition, this is 0. And this contradicts Trichotomy.

Question of the day Suppose a is in F. Can -a be in P?
Most people answered this correctly. An example is instructive: if a=-1, then -a=-(-1)=1 is in P. As I mentioned in class, this example is interesting psychologically, maybe. If one version of the question is: "Can MINUS something be positive?" then the response seems to be "No, never!" But if we ask the question in a more scholarly (pedantic?) way: "Can the additive inverse of an element of an ordered field be a member of the positive elements?" then there's so much effort involved in understanding the question that somehow the listenr is almost forced to think things through more carefully.

Notation/terminology Elements of P are called positive and if -a is in P, then a is called negative. We also write a>b if a-b is in P, etc. (All of this is in the text.)

Observation 74.3 If a is positive, then 1/a is positive.
Proof: a is not 0 by Trichotomy, so 1/a exists. 1/a can't be 0 (since then multiplying by a would give 0=1, which is not allowed!). If 1/a is in P, we are done. Otherwise -1/a is in P. But -1/a is (-1)(1/a) and multiplying that by a (using (O2)) we get (-1)a(1/a)=-1, which can't be in P. This is a contradiction. So we are done.

We can add inequalities: if a<b and c<d, then a+c<b+d.
Proof: The assumed facts are exactly b-a and d-c are in P. Then by (O1), (b-a)+(d-c) is in P. But by the exercise proved earlier, this is the same as (b+d)-(a+c), and since this is in P, a+c<b+d.

We showed with an example (a=0,b=1,c=-1,d=0) that a similar multiplication of inequalities may be false.

I returned the Entrance Exam and gave out the first workshop problems which must be done by groups of students.

The algebraic axioms (the axioms for a field; p.23)
Suppose F has two binary operations, + and x. Then
(A1) Commutativity of addition For all a,b in F, a+b=b+a.
(A2) Associativity of addition For all a,b,c in F, (a+b)+c=a+(b+c)
(A3) Existence of additive identity There is 0 in F so that for all a in F, 0+a=a.
(A4) Existence of additive inverses For all a in F, there exists an element AI(a) so that a+AI(a)=0.
(M1) Commutativity of multiplication For all a,b in F, axb=bxa.
(M2) Associativity of multiplication For all a,b,c in F, (axb)xc=ax(bxc)
(M3) Existence of multiplicative identity There is 1 in F so that for all a in F, 1xa=a.
(M4) Existence of multiplicative inverses For all a in F which are not 0, there exists an element MI(a) so that axMI(a)=1.
(D) Distributivity For all a,b,c in F, ax(b+c)=(axb)+(axc)

The order axioms (the additional axioms for an ordered field; p. 25)
F has a non-empty subset, P, so that: (O1) If a,b are in P, then a+b is in P.
(02) If a,b are in P, then axb is in P.
(03) Trichotomy If a is in F, exactly one of the following is true: either a=0 or a is in P or -a is in P.

The completeness axiom (the additional axiom for a complete ordered field; p. 37)
Every nonempty set of elements of F which has an upper bound must have a least upper bound.

All this will take quite a while to digest. Today we will primarily work on the first group of axioms, The algebraic axioms.

Binary operation on a set s is a function whose domain is SxS and whose range is S. Actually, the traditional notation in, say, (A2) would be expressed in function notation as follows. If we suppose that A(a,b) means the binary operation "a+b", then (A2) would be rewritten A(A(a,b),c))=A(a,A(b,c)). That certainly looks more official, but maybe I will stick with what is traditional. The goal of the course is to recreate "calculus" using only the three groups of axioms above.

Examples and counterexamples
Look at N and Z and Q. If we just go down the list, N does not satisfy (A3), so N is not a field. Z does not satisfy (M4) so Z is not a field. Q satisfies all of them. Q is a field. The real numbers R and the complex numbers C satisfy all of them, so these are fields also. In many applications, other examples are interesting. For example, we could look at the integers mod 5. As a set, this is the list {0,1,2,3,4}. Addition and multiplication are done mod 5. That is, take the usual sum and the usual product, and then divide by 5 and the remainder is the result reported. So 2+4"="1 and 4x3"="2. It is not immediately obvious, but these binary operations on this set define a field, of importance in signal processing and other applications.
Of the fields we've named, only Q and R are ordered fields (the standard ordering into positives and negatives will work). The other fields are not ordered. There are other examples of ordered fields which won't be discussed in this course.
The only complete ordered field turns out to be R. This is not at all obvious.

Obervation 1 The additive identity is unique. That is, if w is any element of F so that, for some a in F, w+a=a, then w=0.
Proof: w+a=a (assumption).
(w+a)+AI(a)=a+AI(a) (A4)
w+(a+AI(a))=a+AI(a) (A2)
w+0=0 (A4) w=0 (A3).

Then students proved:

Obervation 2 The multiplicative identity is unique. That is, if w is any element of F so that, for some a in F with a not equal to 0 , wxa=a, then w=1.
Comment The observation in red is needed in order to use (M4) in the formal proof. The situation regarding multiplication and addition is not totally "symmetric"!

Obervation 3 Multiplicative inverses are unique. That is, suppose a is not 0 and a is in F. If there is w so that wxa=1, then w=MI(a).
Proof: wxa=1 (assumption)
(wxa)xMI(a)=1xMI(a) (M4)
wx(axMI(a))=1xMI(a) (M2)
wx1=1xMI(a) (M4)
1xw=1xMI(a) (M1)
w=MI(a) (M3 twice)

The students proved:

Obervation 4 Additive inverses are unique That is, suppose a is in F. If there is w so that w+a=0, then w=AI(a).

I then defined some conventional words. "-a" (minus a) is the unique additive inverse of a. "b-a" ("b minus a", subtraction) is just b+(-a). And if a is not equal to 0. 1/a (1 over a) is the unique multiplicative inverse of a. And b/a (b divided by a) is exactly bx(1/a). And usually I'll abbreviate axb by a·b or even just ab.

Observation 5 If a is in F, then -(-a)=a.
Proof: -(-a) is AI(AI(a)), so it satisfies AI(AI(a))+AI(a)=0. But AI(a) itself is the additive inverse of a, so it satisfies the equation AI(a)+a=0. Now both a and AI(AI(a)) added to AI(a) give 0, so by uniqueness of additive inverse (applied to -a!) we see that -(-a) and a must be the same.

A similar result is true for multiplicative inverses:
Observation 6 1/(1/a)=a for a not equal to 0.

Here is a more subtle result which uses (D).

Observation 7 a·0=0 for all a in F.
Proof: a· +a·1=a·(0+1)=a·1=a. The first equation is true by (D), the second by (A3) and the third by (M3). Since a·1=a by (M3), we know that a·0 +a=a, so that by Observation 1, a·0=0.

I remarked that we could already get some reward for this abstraction.

One equation
Suppose a and A are given in F. Then consider the equation (*) ax=A where x is an "unknown" in F.
If a is NOT 0, then there is exactly one solution of (*). The solution is x=A/a.
If a is equal to 0, then:
   if A is equal to 0, then any element of F is a solution of (*).
   if A is not equal to 0, then there is no solution to (*).
So solving "one linear equation in one unknown" is completely done.

Two equations
Suppose a,b,c,d and A and B are given in F. Then consider the set of equations (**)
ax+by=A
cx+dy=B
where x and y are "unknowns" in F.
If ad-bc is not 0 in F, then ... well, I multiplied the first equation by d and the second equation by b and got
adx+bdy=Ad
cbx+dby=Bb
(here I have used (M1) and (M2) several times!). Then subtract the second equation from the first, and use (D) several times.
Then we get (ad-bc)x=Ad-Bb. Since (ad-bc) is not 0, we can get x=(Ad-Bb)/(ad-bc). A similar formula is true for y. And steps can be reversed to show that the pair x and y are the only solutions to (**). With more writing, a complete "theory" of how to solve 2 linear equations in 2 unknowns can be gotten, just as we "know" it must be true. Essentially all of "elementary" linear algebra can be done with any field, so one does not need to rethink how to solve such systems. or rethink things like basis and linear independence, etc. This is very neat, most economical application.

Next time, a bit more about algebra and then on to order.

In this lecture I will discuss matters which are not vital to the understanding of the central subject matter of the course, but which certainly form part of the context that was known to people originating this "central subject matter". the ideas almost all come from the work of Georg Cantor in the late 19^th century. Today we are interested in some rough measure of the size of a set. This is the material in section 1.3.

If f:A->B is a function, I reviewed what injective or one-one and surjective or onto and bijective mean. In a loose sense, if f were injective, then (maybe!) A is "smaller" than B. If f were surjective, then A might be called "larger" than B. Finally, the existence of a bijection between A and B should mean, roughly, that A and B are the same size: we have, with f, a way of pairing up the elements of A and B. Formally, we say that A and B are the same size (the technical phrase the same cardinality, is used) if there is some function f:A->B which is a bijection.

Pedagogical or psychological note When I wrote the official definitions of injective/surjective/bijective, the alert student may notice that after (and during) my writing of these definitions, I immediately asked for examples of functions that were not injective and surjective. For some reason, I and many other mathematicians find it easier to explore and understand a definition (and a theorem) by finding examples (well-chosen, one hopes!) that do not fulfill the defintion's requirements or the theorem's hypotheses, etc.

Then I ran through a string of definitions, all in the book. The empty set (I'll use 0 as the empty set symbol here) is said to have 0 (zero) elements. If n is a positive integer, N_n is defined to be the integers {1,2,...,n}, an initial segment of N. N_n is said to have n elements. A set S is called finite if it is the same size as either 0 or N_n for some n in N. Then it is a theorem (proved with mathematical induction, and a bit irritating to get right!) that if a set is finite, either the set is empty (so it has 0 elements) or it is bijective to N_n for a unique positive integer n. So the "size" of a finite set is uniquely determined. This isn't totally obvious (why can't N₁₂ and N₃₂₄ be bijective -- it is true that they can't but I don't think that a proof is totally obvious!).

A set is infinite if it is not finite (now there's a definition!). And another theorem: N is infinite. How would a "proof" of this go? The reason for the quotes is that I offered only an informal expression of a proof, not a detailed argument. If N were finite, then N is not empty, so it would have to be bijective with an initial segment, N_n. But if f:N_n->N were a bijection, look at the maximum of f(1) and f(2) and ... and f(n) and then add 1 ("take the successor"). This creates an element of N which is not f of anything (which is NOT in the range of f, more officially). So N is not finite.

Then I looked at the mapping D:N->N which "doubles": D(x)=2x. D is not surjective (hey, 1 is not twice any positive integer), and D is injective. Its image is Eb, the even integers. So apparently Eb and N have "the same number of elements" or are "the same size". So an infinite set can be the same size as a proper subset of itself. I mentioned the famous (?) Hilbert Hotel, which has a room for every positive integer. If all the rooms are filled, then a new guest can be accomodated by asking everyone to move up one room: x->x+1. In fact, 23 new guests can get rooms (just x->x+23). And, more amazingly, an infinite number of new guests can get rooms (x->2x leaves the odd integers empty). There is actually a theorem here which I stated but which is honestly difficult to prove precisely: A set is infinite if and only if there is a bijection between the set and a proper subset of itself. This was easy to see in the specific case of N, but if we are given a "random" infinite set (what does random mean?), proving the result is not clear.

I want big sets. N is infinite. Can we get a bigger set? I verified some bizarre facts.

Fact 1 N and Z have the same number of elements. That is, there is a bijection between N and Z. I didn't give a specific formula (although this can be done). Specific formulas don't yield too much understanding. Instead, I "grouped" the elements of Z in a sort of strange way. I defined A₀ to be {0}, and A₁ to be {-1,1}, and A₂ to be {-2,2}, etc. So A_n for n a positive integer was {-n,n}. Then the union of all of the A_n's is all of Z. "Clearly" I could "map" A₀ to 1, and then the elements of A₁ to 2 and 3, and the elements of A₂ to 4 and 5, etc. So everything in Z gets mapped to distinct things in N, and everything in N is the image of something in Z.

Fact 2 N and Q have the same number of elements. This is even more unbelievable, since the rationals look so darn much larger than the positive integers. Here I'll use the same outline as above. A₀ is the set {0}. But now I will be trickier, and define A_n for n a positive integer in rather an involved way (I will use recursion in the definition). So here goes: if n is a positive integer, A_n is the collection of rational numbers a/b so that: a/b is not in any of the A_j's for j<n and |a| and |b| are both at most n. This is an involved definition. I asked for A₁ and got {-1,1}. A₂ was {-2,-1/2,1/2,2}. What I wanted people to see was that every rational number is eventually in exactly one of these pieces. For example, 355/113 must be in one of the A_j's where j is at most 355 (it could be in A₃₅₅ itself, but it might already have been in one of the "earlier" ones). Then each piece A_j is finite (surely, since it can't be any larger than ... errr ... (2n+1)², the number of a's and b's with |a| and |b| at most n). Then "pair up" N and Q by first matching each element in A₀, then A₁, then A₂. etc. This uses up (?) all the elements of both N and Q.

By now you should be confused, as confused as many of Cantor's contemporaries were when they first saw all of this. "Clearly" Q and N are different, but we just saw that their sizes are the same. Weird, weird ...

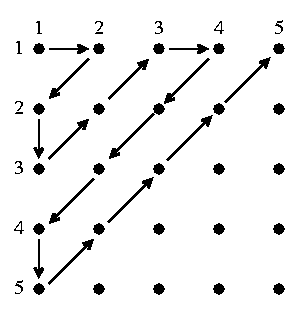
Fact 3 N and NxN have the same number of elements. For this I took a tour among the lattice points of a quarter of the plane (this is NxN). I started at the corner, and walked back and forth. This is weird and wonderful. Here is a picture of the beginning of the process, with just the first 5 rows and columns. Again, it is possible to write a formula for this "correspondance" (officially, this bijection) but to me the formula really conveys nothing immediately more useful.

In fact, N and NxNxN have the same number of elements. Etc. Is there no bigger set? I want a bigger set! The way to get one is to consider the power set "construction".

If S is a set, then the power set of S, called P(S) here, is the set of all subsets of S. For example, if S={a,b,c} then P(S) is {0,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}}. This is an 8 element set, and all of the darn braces ({ and }) are needed, because this is a set of sets! I then asked
The question of the day Is there a set S so that P(S) has 17 elements? I'll look at the answers later.
And now it's later: The answer is no. The majority of the respondants agree. Certainly the set has to be finite. But consider a finite set with n elements. How can we "construct" a subset? We must decide for each element whether it is or is not a member of the subset. The pattern of answers determines the subset. How many patterns of such answers are there? Yes|No and Yes|No and ... n times: there are 2 patterns and hence there are 2ⁿ subsets. But there is no positive integer n so that 17=2ⁿ, and this logic supports the negative answer to the question of the day.

Fact 4If S is any set, then there is NO surjection from S to P(S). This is Theorem 1.3.13 in the book, and I gave the proof in the book. It is an amazing proof, which is relevant to studies in physics, philospohy, computer science (most notably in the Halting Problem), and much of mathematics. The self-referential nature of the proof is discussed at length in the book Gödel Escher Bach by Hofstdter. The key idea: suppose F:S->P(S) is a surjection. Then consider the set T given by: x is in T if both x is in S and x is not in F(x). Then T is certainly a subset of S. If F is a surjection, what can we say about the element w of S which has F(w)=T? There must be such a w since we are supposing that F is a surjection. If w is in T, then w is in F(w), but this means w doesn't satisfy the description of an element of T, so w is not in T (contradiction). If w is not in T, then w is not in F(w), but then w satisfies the description of an element of T so w is in T (contradiction). Therefore no such w can exist, so there is no surjection. (Old idea: who shave the barber in a village where there is one barber and the barber shaves anyone who doesn't shave himself?)

Therefore P(N) is bigger than N. And P(P(N)) is bigger than that, etc. So there can somehow be arbitrarily (?) big sets.

Now that you are confused I will stop. What I'd like 311 students to get out of this is that the most naive measure of sizes of sets already leads to complications. I would like you to have some idea of answers to the following questions.

• When do two sets have the "same size"?
• What's a finite set?
• What's an infinite set, and what are some of the "peculair" properties of an infinite set?
• What is a countably infinite set, and what are some examples?
• Are there infinite sets which are "bigger" than countably infinite sets?

I asked for a session of free association about the course, and collected some written student reactions. I asked what students thought about the course, and what they expected from it. A somewhat vague tabulation of the results yielded what follows. I give brief descriptions what I thought each answer meant.

I was asked what my reasons might be for a student to take the course. I had anticipated this question and replied:

1. The course is required. (I reported myself as surprised that only 3 students wrote that, but I was assured that it was so well-known that it wa_n't worth including.)
2. Learning intricate math is a pleasure and informative (combination of the responses about learning and pleasure given above).
3. This is the "canon" in math (constructed by dead white European males, mostly in the 19th cent and a little in the 20th). This is what every person in math is expected to know, everywhere in the world now. Even if you don't like it, you should know enough about it to be knowledgeable about what you don't like. (Note: the online dictionary gives this as one meaning of "canon": "a collection or list of sacred books etc. accepted as genuine.").
4. Historically, errors were made -- as calculus/analysis began to be applied to more and more situations, there were serious problems with applications and extensions of "clear" results. Serious attention to details, as in this course, will lead to a decrease of errors.

Although we will prove almost everything in the course, I wanted to give some background and make sure we agreed on notation. So we started with N. This is the natural numbers, which in this course and with this text will be the set {1,2,3,4,...}. How can we characterize this set? It is inductive. Basically, it is the smallest set with the following property: 1 is in the set, and for each element of the set, there is a different element called the "successor". The set has the following property: If S is any subset of N, and if

1. 1 is in S
2. the successor of any element in the set is in the set.

This defining property is used in proofs by "mathematical induction". It is equivalent to the following "well-ordering property": every non-empty subset of N has a least element. (Trick here: the statement is false without "non-empty"!)

The using mathematical induction and the "successor" function, operations of addition and multiplication can be defined on N. Defining these corrrectly is a serious undertaking, and one which I neither want nor am prepared to undertake (students interested in such details can see the book Foundations of Analysis by Edmund Landau). Again, with some effort, it can be shown that these operations (really functions on NxN) are both commutative, associative, etc. and that 1 is a multiplicative identity.

The equation a+x=b can be solved only "sometimes" in N. So we "extend" the number system to Z, the Integers: as a set, Z could be thought of as two copies of N along with an extra element, 0. One copy of N could be thought of in red and one, in blue. The red elements could be thought of as being negative and the blue, as positive. Then additional work allows us to extend addition and multiplication to Z, with 1 as a multiplicative identity. All equations of the form a+x=b can be solved.

The next desire is to solve equations of the form a·x=b. This leads us to the "larger" (?) set Q, the Rational Numbers. In order to stretch our imaginations and to use some of the abstraction that students are supposed to have under control, I suggested that the rationals could be "constructed" in this way: take the product of ZxZ\{0}. So this is pairs of integers (a,b) with b NOT equal to 0. In this set introduce an equivalence relation: (a,b)~(c,d) if and only if ad=bc. We experimented with this a while (it comes from the fact that if ad=bc, then the equations ax=b and cx=d should have the "same" solution, represent the same rational number). A rational number is an equivalence class of ZxZ\{0} using ~, and the set of all rational numbers, Q, is the set of all such equivalence classes. Introducing addition and multiplication into Q with this definition is lengthy, and (in this course) I am not particularly interested in checking the details. Everything works (see Landau's book!). The integers fit into this Q by the mapping w->[(w,1)]. This is a one-to-one or injective mapping. By the way, just understanding that succession of symbols means that you have mastered quite a lot of abstraction. The rational number a/b correspnds to [(a,b)].

I mentioned one of the most famous results of mathematics: sqrt(2) is irrational. Or, more formally, there is no rational number a/b whose square is 2. This is Theorem 2.1.4 in the text (please look there if you've never seen it!). This led me to consider the following function, whose domain is the rationals, Q, and whose range is just {-1,1}. (I did mention that functions are "officially" supposed to be ordered pairs, etc., but that I would usually be a bit lazy and define functoins by how they "map" elements in their domains: there is an implied listing of the ordered pairs.) So F(x) is 1 if x²>2 and F(x) is -1 if x²<2

It took a while to understand this function (I should give credit to T. W. Körner from whose Cambridge University lectures I "borrowed" this example). I emphasized that this function is very computable for every number in its domain. We drew a graph of the function. The graph was drawn in the QxQ plane. We had trouble understanding the graph. Even worse was the fact that, if we allow the standard definition of derivative, then F' exists at every point (rational numbers can get small so limits as "h->0" can be considered!) and that F'(x)=0 for every x! Note that F, although defined "everywhere" with derivative existing and equal 0 "everywhere", is not constant! This should be somewhat distressing.

Another example, similar in spirit, is the function G(x)=x²-2, with domain and range both Q. We drew a graph, and this "parabola" did not intersect the horizontal axis! What's going on? All the natural geometric and calculus "facts" seem to be violated by these rather simple examples.

The major content of the course is the transition or enlargement of Q to R, the real numbers, and understanding this and its consequences will be the principal task before us.

I handed out the Entrance Exam. I urged students to begin reading chapter 1, and remarked that 1.1 and 1.2 should be familiar to them. I would try to discuss, more or less informally, the content of 1.3 next time, and would really begin the serious, proof-emphasizing part of the course next week.