Mathematical experiments
Almost every aspect of the practice of mathematics, both pure and
applied, has been improved and amplified in recent decades by the
widespread availability of "computer algebra systems", CAS. This
technology is much more than just algebra, of course. It is systematic
and powerful programs that permit algebraic manipulation
- What is the coefficient of
x6y4z2 in
(x+y+z)12?
13860
and numerical approximation
- What is an approximation to the only root of
3x+cos(2x2)=0?
-.3258460227
and graphing
- What do the points
(x,y,z) which satisfy the equation
z2+(x2+y2-1)(x2+y2-2)=0
look like?
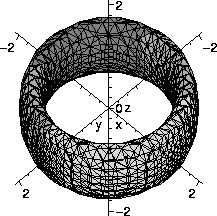
The freedom to work with "exact" symbolic computation, with numerical
approximation (with specified accuracy) and with visual display of data
(human beings learn much more from pictures than from lists of
numbers!) is very useful.
Almost all of my teaching and research is
now improved by access to powerful programs which allow me to
experiment. I can get examples which are useful for
instruction. I've also used these programs to try to understand
complicated phenomena which I could not easily explain (further
explanation is available!).
Computer help
Many students have graphing calculators. These are useful, but are
limited by speed and memory size. Simple
errors may occur. There are large computer programs with powerful
numerical, symbolic, and graphical capabilities. These still may have
the potential for errors, but much effort has gone into their
programming. The most widely distributed programs are
Maple, Mathematica, and
Derive. In this course Maple will be favored,
since almost every large computer system at Rutgers has Maple
installed. These programs are not infallible but they can be
very helpful. Other programs available with special capabilities. For
example, Matlab, a program originally directed at problems of
linear algebra, is installed on systems of the Engineering School.
Also, I usually use Maple because I have a copy at
home. Students should learn how to use such programs.
Maple in Math 291 on eden
Please become familiar with the capabilities of Maple. Most
students have accounts on the eden system. In order to
effectively use Maple with the xmaple interface
students need to get out of the menu system which they may have
with their default eden login. To do this they need to find
the command revert on their menu system, enable this command,
and then logoff and logon again. They will then get a unix
prompt and will be able to begin the sequence of exercises described
here. Students who want the menu system back will need to remove the
file .nolush and the menu system will return at their next
login.
Last semester Professor Costin wrote a nice sequence of "labs" to
teach students about the capabilities of Maple. You may want
to work though them: see the
paragraph labeled Maple. I hope to have a
sequence of exercises introducing Maple to students in a week
or so. Also I very much would like students to use Maple
(and/or their graphing calculators) when this is appropriate.
The Maple field trip
The class will meet in the instructional computer lab ARC 118 on Thursday,
September 12, from 4:30 to 5:50 PM. I hope that students
will work through the following sequence of exercises (copies will be
provided), here with links to pdf files.
The last question asked on the fourth handout is difficult. I've
written a complete solution
which is quite long, but verifying clear (!) geometric facts is
often tedious.
How to get those answers
The answers to the questions above were obtained with the following
Maple instructions. Please: this is not an effort to
impress you, but rather to show you how easy is is to get the answers.
- coeff(coeff(coeff((x+y+z)^12,x^6),y^4),z^2);
The command coeff(P,monomial) finds the coefficient of the
monomial in the expression P. Layering three repetitions of
coeff finds the desired coefficient.
- fsolve(3*x+cos(2*x^2)=0,x);
fsolve is a general "floating point" approximate equation
solver. Care must be used if there's more than one root. There are
also symbolic solvers, useful when there is a nice formula for the
solution.
- with(plots):
V:=((x^2+y^2)-1):
W:=((x^2+y^2)-2):
implicitplot3d(-V*W=z^2,x=-2..2,y=-2..2,z=-2..2,grid=[30,30,30],axes=normal);
The implicitplot3d command allows implicit equations to be
sketched. Since Maple has so many functions and libraries
available, many need to be specifically loaded before use. The command
with(plots) loads a variety of plotting commands. The
implicitplot3d command has a wide variety of options. The
grid option gives control over the spacing of sample
points. Of course increasing the number of sample points "costs"
computational time.
Programming in Maple
Maple is also a programming environment. Maple
programs are known as procedures. The language has many
statements supporting program flow such as if ...then and
while and do etc., and also has a variety of data
types. There's no time in this course to teach this material, but
students should know that programmng is possible.
I have several books on Maple programming. My current
favorite is Maple A comprehensive introduction by Roy
Nicolaides and Noel Walkington, Cambridge University Press ($55, 466
pages). There are also many web pages which discuss programming in
Maple. For example, here's an
online tutorial. Warning: such pages are only for the enthusiast!
|
