| Date | What happened (outline) |
|---|
Wednesday,
December 10 |
I discussed Monday's QotD. I mentioned that seeing x dx many
people would almost immediately try the substitution
u=x2. That doesn't exactly "work" but adjusting the
substitution to u=x2+a2 along with the
realization that the derivative of a2 is 0 since a is a
constant. I remarked that I knew perhaps three or four
ways to find an antiderivative for the integrand, which students
would learn in Math 152.
Then I computed the definite integral
 01x sqrt(x+1) dx. First I used
the substitution u=x+1, and did the computation in detail. Then I
used the substitution u=sqrt(x+1) so u2=x+1 and
2u du=dx etc. Both substitutions lead to the same answer, and it
seems almost amatter of personal taste (or style?) which should
be preferred. 01x sqrt(x+1) dx. First I used
the substitution u=x+1, and did the computation in detail. Then I
used the substitution u=sqrt(x+1) so u2=x+1 and
2u du=dx etc. Both substitutions lead to the same answer, and it
seems almost amatter of personal taste (or style?) which should
be preferred.
I repeated that the definite integral; representated alimit of Riemann
sums, and that using that representation, many quantities ofinterest
in applications can be recognized as definite integrals. Then the FTC
asserts that definite integrals can be computed by antiderivatives, if
we happen to know the relevant antiderivative. This distinction (the
definition of the definite integral and the FTC as a method of
computing them) is important.
I remarked that an antiderivative of xp is
(1/(p+1))xp+1+C. This formula is valid for all p except
p=-1: we don't want to divide by 0. But how should we then compute,
say, the area under the hyperbola y=1/x. I will restrict attention to
x>0 to avoid the problem at 0. For example, the area bounded by the
x-axis andx=5 and x=7 and y=1/x is represented by  571/x dx. This is the difference of 571/x dx. This is the difference of
 171/x dx and 171/x dx and  151/x dx. So we just need tocompute
integrals from 1 to "anything". For example, 151/x dx. So we just need tocompute
integrals from 1 to "anything". For example,  121/x dx could be approximated
easily (and badly!). An underestimate is gotten by taking a box with
height 1/2 and width 1 and an overestimate is gotten by taking a box
with height 1 and width 1. 121/x dx could be approximated
easily (and badly!). An underestimate is gotten by taking a box with
height 1/2 and width 1 and an overestimate is gotten by taking a box
with height 1 and width 1.
Motivated by experience with FTC, we
might decide to study the function F(w)= 1w1/x dx. For example, the last
sentences in the preceding paragraph establish that 1/2<F(2)<1:
not very good estimates, of course. What else do we know about
F(w)? Only (!!!) F'(w)=1/w and F(1)=0. Yes, I know I
seem to be idiotic here and in class about this, because, oh my
goodness, isn't this just ln or something like that ... but there is a
big point to make, so let me just continue to compute. 1w1/x dx. For example, the last
sentences in the preceding paragraph establish that 1/2<F(2)<1:
not very good estimates, of course. What else do we know about
F(w)? Only (!!!) F'(w)=1/w and F(1)=0. Yes, I know I
seem to be idiotic here and in class about this, because, oh my
goodness, isn't this just ln or something like that ... but there is a
big point to make, so let me just continue to compute.
Look at G(w)=F(3w). By the Chain Rule, G'(w)=F'(3w)·3, and this
means G'(w)=[1/(3w)]·3=1/w. So F(w) and G(w) have the same
derivative. Certainly if two functions have graphs which are
up/down translations of each other they have the same derivative. But
in fact the converse is also true, and this follows from the MVT: if
F'(w)=G'(w). then G(w)=F(w)+(some constant). Plug in w=1. Then
G(1) is F(3·1)=F(3), and the equation becomes
F(3)=F(1)+the conswtant. Since F(1)=0, this means the constant is
F(3). So what we verified is that F(3w)=F(w)+F(3). In fact, in all of
the previous discussion, we could change 3 to anything: to "v". We
would prove that F(vw)=F(v)+F(w). (Yeah, yeah, I know, looks like
... something that rhymes with "frog". For
example, Since F(4)=F(2·2)=F(2)+F(2), and 1/2<F(2)<1, we
know that (sin ce we can double the inequality!) 1<f(4)<2. Oh
my: F(w) is a continuous function with a positive derivative, so it is
always increasing. F(2)<1 and F(4)>1. Therefore (use the
Intermediate Value Theorem) there's is exactly one
number whose "F" value is 1, and that number must be between 2 and
4. In fact, it turns out the number is 2.7182818...: it is called e.
What's the point of all this? First, a pedagogical point: I wanted to
review some of the most important issues of the course. Second, it is
really true that hardly anyone cares about logs for the purpose of
computing these days (our little silicon friends do that just fine!)
but the use of logs in finding antiderivatives won't go away. (In fact,
many weird anduseful functions are defined by antiderivatives!)
logs won't go away
What is the antiderivative of x2/(x3+7)? Of
course, this is "cooked up" to use logs. But if we substitute
u=x3+7, then du=3x2dx and
(1/3)du=x2dx etc., so the answer will be
(1/3)ln(x3+7)+C. Maybe this example is too obvious. Look
now:
What's  tan(x) dx? Since tan(x)=sin(x)/cos(x), if u=cos(x), then
du=-sin(x)dx and the integral (switching over the - sign) becomes tan(x) dx? Since tan(x)=sin(x)/cos(x), if u=cos(x), then
du=-sin(x)dx and the integral (switching over the - sign) becomes  -(1/u)du=-ln(u)+C=-ln(cos(x))+C. (Some people will use
ln(1/A)=-ln(A) to change this answer to ln(sec(x))+C so look
carefully!) The point I'm making here is that if you want to
antidifferentiate tangent for any reason (maybe to compute areas, although I
doubt it, more likely to compute one of many other quantities) you
will need to use ln. It isn't immediately obvious that logs come into
computing areas under y=tan(x)! -(1/u)du=-ln(u)+C=-ln(cos(x))+C. (Some people will use
ln(1/A)=-ln(A) to change this answer to ln(sec(x))+C so look
carefully!) The point I'm making here is that if you want to
antidifferentiate tangent for any reason (maybe to compute areas, although I
doubt it, more likely to compute one of many other quantities) you
will need to use ln. It isn't immediately obvious that logs come into
computing areas under y=tan(x)!
The Question of the day had two parts: how used has that QotD
been and how useful has the web diary of the course been? I have not
looked at the answers yet, but I am very curious. I remarked that (on
average!) the QotD takes me about 3 hours a week outside of class) and
the diary takes me about 5 hours a week outside of class.
I hope that people will send me answers to the various sets of review
problems and that, if they like, they will attend the review session,
office hours, and send questions via e-mail.
Recognition of attendance was
distributed to appropriate individuals, along with a prize containing
a prize..
|
Monday,
December 8 |
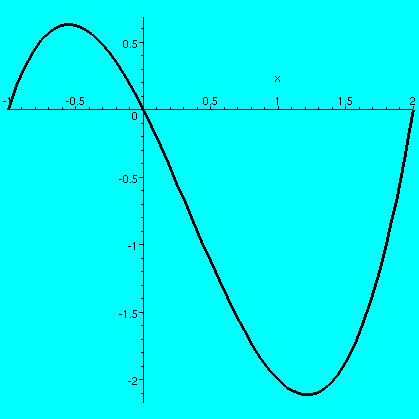
Area between two curves
Consider the curve defined by
y=x*(x+1)*(x+2)=x3-x2-2x. What is the "finite"
or bounded area between this curve and the x-axis? This question is
not terribly well written, but I am trying to ask what the total area
is of the region caught inside the two "bumps" shown. Is this total
geometric area exactly equal to the definite integral
 -12x3-x2-2x dx?
Well, between -1 and 0 the curve is on top of the x-axis. In fact, -12x3-x2-2x dx?
Well, between -1 and 0 the curve is on top of the x-axis. In fact,
 -10x3-x2-2x dx=(by
FTC)
(1/4)x4-(1/3)x3-x2|-10=0
(the value when
x=0)-[(1/4)(-1)4-(1/3)(-1)3-(-1)2](the
value when x=-1)=-[(1/4)+(1/3)-1]=5/(12), a positive number, as it
should be. -10x3-x2-2x dx=(by
FTC)
(1/4)x4-(1/3)x3-x2|-10=0
(the value when
x=0)-[(1/4)(-1)4-(1/3)(-1)3-(-1)2](the
value when x=-1)=-[(1/4)+(1/3)-1]=5/(12), a positive number, as it
should be.
I did a bunch of textbook problems.
What about  02x3-x2-2x dx?
Again, by FTC, this is
(1/4)x4-(1/3)x3-x2|02=
(1/4)24-(1/3)23-22(the value at
x=2)-0(the value at x=0). This turns out to be 4-8/3-4=-8/3, a
negative number.
The Question of
the day was problem #64: Compute 02x3-x2-2x dx?
Again, by FTC, this is
(1/4)x4-(1/3)x3-x2|02=
(1/4)24-(1/3)23-22(the value at
x=2)-0(the value at x=0). This turns out to be 4-8/3-4=-8/3, a
negative number.
The Question of
the day was problem #64: Compute  0ax sqrt(x2+a2) dx
when a>0. 0ax sqrt(x2+a2) dx
when a>0.
Here we need to "guess" an antiderivative of
>x sqrt(x2+a2). Try
u=x2+a2. Then du=2x dx, so (1/2)du=xdx, and
 x sqrt(x2+a2) dx=(1/2) x sqrt(x2+a2) dx=(1/2) sqrt(u) du=(1/2) sqrt(u) du=(1/2) u1/2 du=(1/2)(2/3)u3/2+C. We
convert back to x's. u1/2 du=(1/2)(2/3)u3/2+C. We
convert back to x's.
Caution because here's another common way to make a
mistake: substitute the wrong variable. The limits in the original
problem are x=0 and x=a and do not directly involve u.
The antiderivative becomes
(1/3)(x2+a2)3/2+C. The C's cancel out
in a definite integral computation. So we substitute in x=a:
(1/3)(2a2)3/2 and subtract off what we get from
x=0:(1/3)(a2)3/2. The result is therefore
(1/3)(2a2)3/2-(1/3)(a2)3/2.
This simplifies (if you must!) to
(1/3)(23/2-1)a3.
|
Wednesday,
December 3 |
I began by computing the definite integral of x7 from 0 to
4, and, of course, making my first error of the lecture. Oh
well. I will try a new method of writing integrals on the web. I will
use a little picture of an integral sign. Heh, heh. Here goes:
 04x7dx=(1/8)x8|x=0x=4=(1/8)48.
This computation is routine. The definite integral describes a certain
area, a roughly triangular-shaped one, bounded by the x-axis, and
y=x7, and x=4. The line x=0 hardly matters, since the
x-axis and the function graph intersect there. 04x7dx=(1/8)x8|x=0x=4=(1/8)48.
This computation is routine. The definite integral describes a certain
area, a roughly triangular-shaped one, bounded by the x-axis, and
y=x7, and x=4. The line x=0 hardly matters, since the
x-axis and the function graph intersect there.
I then tried another "simple" problem:  0Pi/2sin(x)dx. One suitable
antiderivative here is -cos(x). At Pi/2 cosine is 0, so the integral
is ... what? WHAT!! If you look at the graph of sine from 0 to
Pi/2 you will see that there is a big hunk of area: the result
certainly should not be 0. Why haven't we found
it? In fact, it is there, and we haven't found it because we did not
use the FTC correctly. It states that if F'=f, then the integral of f
from a to b is F(b)-F(a). When we're working with polynomials, and
when a=0, it may be easy to forget about F(a), because it will be 0
But, golly, here f(x)=sin(x) and F(x)=-cos(x), and a=0 and b=Pi/2 so
F(b)-F(a) is -cos(Pi/2)--cos(0) which is -0--1=1, so the area is
1. 0Pi/2sin(x)dx. One suitable
antiderivative here is -cos(x). At Pi/2 cosine is 0, so the integral
is ... what? WHAT!! If you look at the graph of sine from 0 to
Pi/2 you will see that there is a big hunk of area: the result
certainly should not be 0. Why haven't we found
it? In fact, it is there, and we haven't found it because we did not
use the FTC correctly. It states that if F'=f, then the integral of f
from a to b is F(b)-F(a). When we're working with polynomials, and
when a=0, it may be easy to forget about F(a), because it will be 0
But, golly, here f(x)=sin(x) and F(x)=-cos(x), and a=0 and b=Pi/2 so
F(b)-F(a) is -cos(Pi/2)--cos(0) which is -0--1=1, so the area is
1.
Be very careful to compute both F(b) and F(a) and
then subtract them. Also, be very careful about signs: repeated -
signs, two or three times repeated, arise quite often in these
computations.
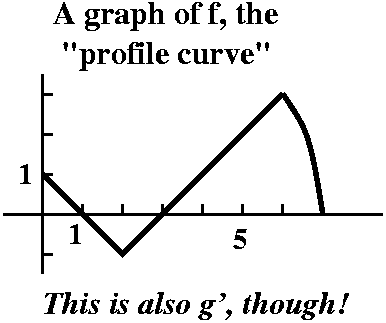
I discussed problem #2 of section 5.3 in detail. This problem gives
the graph of a curve f, and defines g by g(x)= 0xf(t)dt. Sometimes in problems like
this people call f the profile curve. THe text asked the
following questions: 0xf(t)dt. Sometimes in problems like
this people call f the profile curve. THe text asked the
following questions:
a) What are g(0), g(1), g(2), g(3), g(4), g(5), and g(6)?
Each of these can be evaluated independently, remembering that area
"over" the axis counts postively for the definite integral and area
"under" the axis counts negatively. So:
g(0)=0 (no area in a line!); g(1)=1/2; g(2)=0 (cancellation);
g(3)=-1/2;
g(4)=0 (more cancellation); g(5)=1.5; and g(6)? Well, g(6) adds on
2.5 (the stuff between 5 and 6) to g(5) (it "accumulates" the area,
some people say) so g(6)=g(5)+2.5=4.
b) Estimate g(7).
Few people appreciated my statement
-1010<g(7)<1010 so I more soberly
estimated 4+2<g(7)<4+3 because g(6) is 4.
c) Where does g have a max? Where does g have a min?
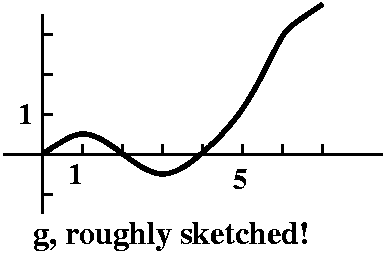 Here it becomes useful to observe that f is a graph of
g'. Thus, to the left of 1, g' is positive and to the right, it is
negative, so 1 is a local max. Similarly, 1 is a local min.
Here it becomes useful to observe that f is a graph of
g'. Thus, to the left of 1, g' is positive and to the right, it is
negative, so 1 is a local max. Similarly, 1 is a local min.
d) A rough graph of g: here I insist that we do this with some
knowledge of calc, so we see that g'', which is f', is negative for
x's between 0 and 2, so g is concave down in that interval, etc. I'd
like to show the graph of g curving appropriately.
Numbers are numbers are numbers
I then discussed numbers. I asked what people could tell me about
these numbers:
43
43
43
43
43
After some jeering (I felt bleak) we agreed that these
numbers were all the same number.
jeer
n : showing your contempt by derision [syn: {jeering}, {mockery},
{scoff}, {scoffing}]
v : laugh at with contempt and derision; "The crowd jeered at
the speaker"
bleak
adj 1: offering little or no hope; "the future looked bleak";
Then I asked what people could tell me about these numbers:
 35[x3]/[3+cos(x2)]dx 35[x3]/[3+cos(x2)]dx
 35[u3]/[3+cos(u2)]du 35[u3]/[3+cos(u2)]du
 35[t3]/[3+cos(t2)]dt 35[t3]/[3+cos(t2)]dt
 35[v3]/[3+cos(v2)]dv 35[v3]/[3+cos(v2)]dv
 35[s3]/[3+cos(s2)]ds 35[s3]/[3+cos(s2)]ds
These are all definite integrals, and they are all just
numbers. Of course they are all equal. Again, the letters inside the
integrand are dummy variables or bound variables. They are similar to
the local variables in subroutines of a computer program, and they
have no meaning outside of the integral itself. I guess that the
assembly of symbols
 3xxdx would make sense:
antidifferentiate, get (1/2)x2, evaluate at x and subtract
off the value at 3 to get (1/2)x2-9/2. But this is
considered bad grammar: people try not to use the same variables
inside the integral as in the limits -- it is difficult to understand. 3xxdx would make sense:
antidifferentiate, get (1/2)x2, evaluate at x and subtract
off the value at 3 to get (1/2)x2-9/2. But this is
considered bad grammar: people try not to use the same variables
inside the integral as in the limits -- it is difficult to understand.
I then tried to do some simple exercises with part of the FTC. It was
something like this: if f(x)= 2x
cos(t7)dt, then f'(x)=cos(x7).
And then if f(x)= 2x
cos(t7)dt, then f'(x)=cos(x7).
And then if f(x)= 2x
cos(s7)ds, then f'(x)=cos(x7). The "dummy
variable" strikes again! 2x
cos(s7)ds, then f'(x)=cos(x7). The "dummy
variable" strikes again!
 How about if f(x)=
How about if f(x)= x3
cos(s7)ds? Here we need to think a bit about definite
integrals. Here's a fact: x3
cos(s7)ds? Here we need to think a bit about definite
integrals. Here's a fact:
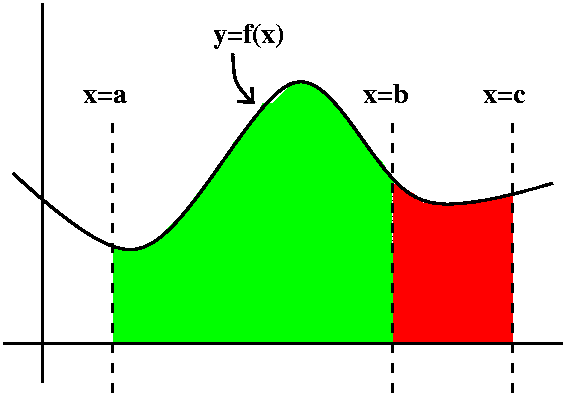
Adding areas fact
If a<b<c, and if f is continuous on the interval
from a to c, then
 abf+ abf+
 bcf= bcf=
 acf. acf.
So adjoining areas can be added up (something many of us learn as
infants, and it is a rather subtle fact!). But we also agree that
 aa=0: that
is, a region with 0 width should have 0 area. Suppose we make some
changes in the adding areas fact, and transform c into a. Then the
right-hand side becomes 0, and we see that aa=0: that
is, a region with 0 width should have 0 area. Suppose we make some
changes in the adding areas fact, and transform c into a. Then the
right-hand side becomes 0, and we see that
 abf+ abf+
 baf=0, which is the same as baf=0, which is the same as
 abf=- abf=- baf.
Therefore if we want to be able
to add areas and if we want to recognize that lines have area=0, we
must also acknowledge that interchanging limits causes a - sign to
prefix the integral. Therefore we can do this: baf.
Therefore if we want to be able
to add areas and if we want to recognize that lines have area=0, we
must also acknowledge that interchanging limits causes a - sign to
prefix the integral. Therefore we can do this:
if f(x)= x3
cos(s7)ds, then f(x)=- x3
cos(s7)ds, then f(x)=- 3xcos(s7)ds so that f'(x)
must be -cos(x7). Amazing! (Well, not really, but ...) 3xcos(s7)ds so that f'(x)
must be -cos(x7). Amazing! (Well, not really, but ...)
We can even do one further variation. Suppose F(x)= -2xsqrt(1+w6)dw. Then we know
that F'(x)=sqrt(1+x6) by FTC. What if I ask the following
ludicrous question: -2xsqrt(1+w6)dw. Then we know
that F'(x)=sqrt(1+x6) by FTC. What if I ask the following
ludicrous question:
Suppose G(x)= -2cos(x)sqrt(1+w6)dw. What is
G'(x)? -2cos(x)sqrt(1+w6)dw. What is
G'(x)?
How can we think about this? Since we know F'(x), and G(x)=F(cos(x)),
this is just (!?) an application of the Chain Rule (!):
G'(x)=F'(cos(x))·(the derivative of
cos)=sqrt(1+(cos(x))6)·(-sin(x)). Whew! This takes
some getting used to.
I tried to convince people that on the horizontal axis, if B is to the
right of A (A<B) then the distance from A to B is B-A. I then went
on to assert that on the vertical axis, if B is above A (A<B) then
the distance from A to B is B-A. It doesn't matter much what signs A
and B have: if A<B, the distance from A to B is B-A.
The distance from 2 to 7 is 7-2=5.
The distance from -2 to 8 is 8-(-2)=10.
The distance from -5 to -1 is (-1)-(-5)=4.
It really does work!
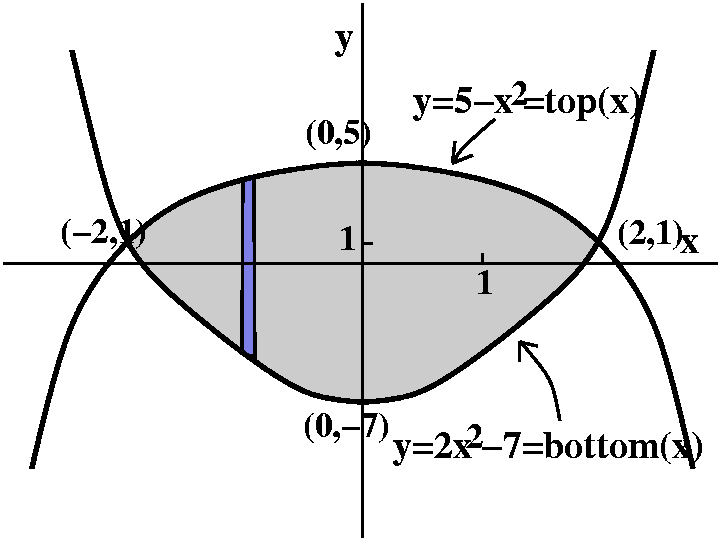
This was a sort of introduction to the following problem: sketch
y=5-x2 and y=2x2-7. Where do these curves
intersect? What is the area between them?
Since this is a problem in a calculus class, all of the
computational details will be easy! You should be warned,
however, that in "real life", the details are hardly ever
easy.
If (x,y) is on both curves, and if y=5-x2 and
y=2x2-7, we then know that 2x2-7=5-x2
so 12=3x, and x is +/-2. Then y is
5-(+/-2)2=1. Look to the right for a rather distorted
picture (the vertical and horizontal axes have rather different
scales!).
Now think about the area between these two curves. We can imagine lots
and lots of vertical lines dividing this area up into pieces which are
almost rectangles (there's a bit of error at the top and bottom). Look
at each almost rectangle: it is dx wide, and it is top(x)-bottom(x)
high. So the area is (top(x)-bottom(x))dx, and we add up these areas
from x=-2 to x=2. Therefore the total area which we would like is
 -22(top(x)-bottom(x))dx= -22(top(x)-bottom(x))dx= -22((5-x2)-(2x2-7)dx= -22((5-x2)-(2x2-7)dx= -2212-3x2dx=12x-x3|x=-2x=2=(24-8)-(-24-(-8))=32.
And that's the area. -2212-3x2dx=12x-x3|x=-2x=2=(24-8)-(-24-(-8))=32.
And that's the area.
We then had an interlude in which we discussed the final.
/interlude/
[Theatr]
a. a pause between the acts of a play.
Please look at the material I have
prepared to help the class study for the final.
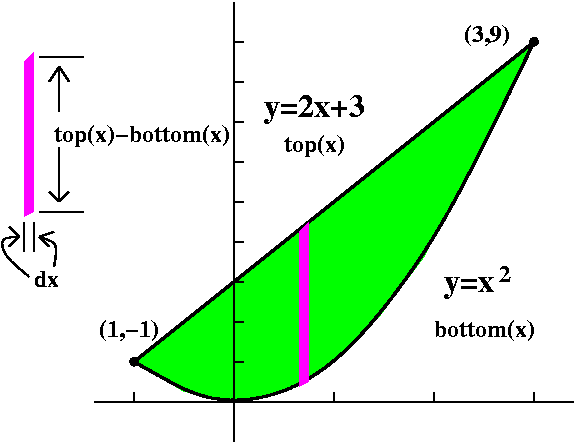
The Question of
the day was the following: I sketched y=x2 (a parabola) and
y=2x+3 (a line). I asked where they intersected and requested that people find
the area between these curves.
Since this is again a problem in a classroom, and not a very real
classroom (!), we solve x2=2x+3 and have
x2-2x-3=0 so (x-3)(x+1)=0. Roots are x=3 and x=-1. If x=3,
y=9 and if x=-1, y=1. The intersection points are at (3,9) and
(-1,1). The area is  LEFTRIGHTTOP-BOTTOMdx= LEFTRIGHTTOP-BOTTOMdx= -132x+3-x2dx which can be
computed by FTC and I think the answer turns out to be (32)/3. -132x+3-x2dx which can be
computed by FTC and I think the answer turns out to be (32)/3.
It is easy to make mistakes with signs in "simplifying".
|
Monday,
December 1 |
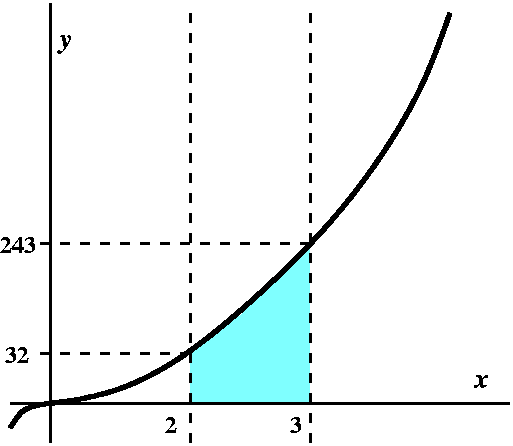 Today we disclose the climax of the course. I will begin with a
simple example. Our goal right now is to compute the area of the
region in the plane bounded by the x-axis, x=2, x=3, and the curve
y=x5. This is a definite integral:
S23x5dx/ Oh, I give up: this
is int(x^5,x=2..3). The last collection of symbols is easier to type,
and the traditional integral symbol isn't well indicated by S,
anyway. On the right is a picture of the region whose area I will try
to compute. Please note that although the picture I have drawn is
mostly qualitatively correct, I have certainly used very different
units on the vertical and horizontal axes (25=32 and
35=243). I will arbitrarily take the year 1600
as the dividing point in the two approaches to computing definite
integrals that I'll discuss
(the 1660's is probably more accurate historically). I'll begin with
the "old" style.
Today we disclose the climax of the course. I will begin with a
simple example. Our goal right now is to compute the area of the
region in the plane bounded by the x-axis, x=2, x=3, and the curve
y=x5. This is a definite integral:
S23x5dx/ Oh, I give up: this
is int(x^5,x=2..3). The last collection of symbols is easier to type,
and the traditional integral symbol isn't well indicated by S,
anyway. On the right is a picture of the region whose area I will try
to compute. Please note that although the picture I have drawn is
mostly qualitatively correct, I have certainly used very different
units on the vertical and horizontal axes (25=32 and
35=243). I will arbitrarily take the year 1600
as the dividing point in the two approaches to computing definite
integrals that I'll discuss
(the 1660's is probably more accurate historically). I'll begin with
the "old" style.
Getting the answer directly from the definition (before ~1600)
Here we will go through a four-step process: subdivide, approximate,
sum, and limit. This process is, in fact, quite important in many
applications. It is the reason that definite integrals represent many
different ideas.
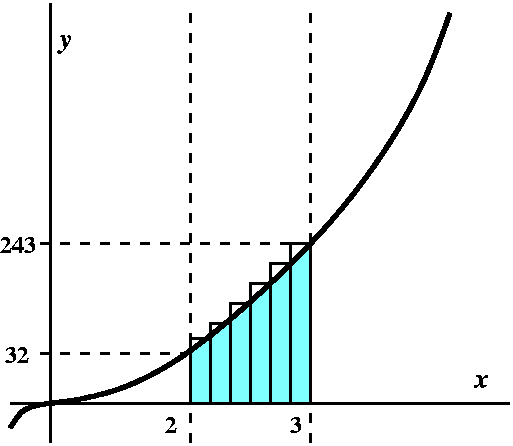 We divide the interval from 2 to 3 into n different equal parts. Here
you should think of n as some very large positive integer. (The
picture shows n=6, not terribly large -- imagine n=10,000!) Then each
piece of the interval will have width (3-2)/n=1/n. We will approximate
the area over the first subdivision, from 2 to 2+1/n, by a rectangle
whose height is the value of the function at the right-hand
endpoint. Similar things happen if we choose the left-hand endpoint or
the middle or ... any choice, in fact. So the right-hand height is
(2+1/n)5, and the area of the rectangle over the first
subinterval is
(2+1/n)5(1/n)
(area is
height·width). What about the second rectangle? It has the same
width but the right-hand endpoint's height is
(2+(2/n))5. So the second rectangle's area is
(2+(2/n))5(1/n). And the third rectangle's area is
(2+(3/n))5(1/n). Etc. What does this Etc. mean? We
are supposed to find the sum of all the rectangles and there are n of
them. So we have:
We divide the interval from 2 to 3 into n different equal parts. Here
you should think of n as some very large positive integer. (The
picture shows n=6, not terribly large -- imagine n=10,000!) Then each
piece of the interval will have width (3-2)/n=1/n. We will approximate
the area over the first subdivision, from 2 to 2+1/n, by a rectangle
whose height is the value of the function at the right-hand
endpoint. Similar things happen if we choose the left-hand endpoint or
the middle or ... any choice, in fact. So the right-hand height is
(2+1/n)5, and the area of the rectangle over the first
subinterval is
(2+1/n)5(1/n)
(area is
height·width). What about the second rectangle? It has the same
width but the right-hand endpoint's height is
(2+(2/n))5. So the second rectangle's area is
(2+(2/n))5(1/n). And the third rectangle's area is
(2+(3/n))5(1/n). Etc. What does this Etc. mean? We
are supposed to find the sum of all the rectangles and there are n of
them. So we have:
(2+1/n)5(1/n)+(2+(2/n))5+(2+(3/n))5+...+(2+(n/n))5
(There are n terms in this sum.)
Or this can be written with classical SIGMA notation.
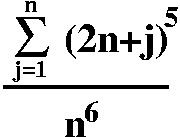
| Is this more frightening,
or is it just more compact? The sigma is an abbreviation for "sum",
and the whole thing is read as
"The sum, as j goes from 1 to n, of two n plus j
raised to the fith power, all divided by n to the sixth."
The fact that j is only supposed to be an integer is usually
understood and is not mentioned. |
By the way, the process we are discussing here would be familiar to
appropriate representatives of various classical civilizations,
including Greece, China, India, and north Africa. The are wonderful
medieval Chinese manuscripts which have diagrams that look exactly
like our definitions of the definite integral, with much commentary
written in Chinese surrounding the diagrams.
One
way to analyze the elaborate sum above begins by changing it
algebraically. For example, the first term,
(2+1/n)5(1/n), is actually
([2n+1]/n)5(1/n)=(2n+1)5/n6. The
second term, (2+(2/n))5(1/n), is
([2n+2]/n)5(1/n)=(2n+2)5/n6. In each
case we can rewrite the terms so that there is a factor of
1/n6, and we can factor out (undistribute?) and the big sum
becomes:
(1/n6)·[(2n+1)5+(2n+2)5+(2n+1)5++...(2n+n)5]
What can we do now? Well, in all of those civilizations mentioned
there was considerable research into finding "simpler" expressions for
sums of the type shown above. People made guesses, and then tried to
verify their guesses (prove them, in modern terms). Getting such
formulas is now well-understood, and in this case I will cheat a bit
and not follow historical precedent. I asked Maple to
tell me what the sum is. I typed the instruction
sum((2*n+j)^5,j=1..n); and got the result shown below:
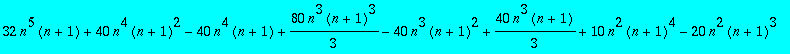
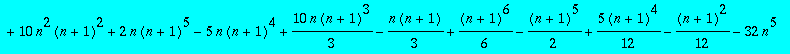
I assure you that this result is not immediately obvious to me!
I think if you gave me a while (a long while!), I could discover and
verify it by
hand. I don't think I would want to, though.
But now what's the next step? Divide by n6 and find the
limit as n-->infinity. This will be tedious until we recognize a
pattern. For example, let's look at the first term in that enormous
sum: 32n5(n+1). If we divide by n6 and simplify
we get 32[(n+1)/n] and this, as n-->infinity, becomes 32. Now
look please at the last term divided by n6:
-32n5/n6 which is -32/n and this -->0 as
n-->infinity. In fact, all of the terms in the enormous expression
above are polynomials, and the degree of each term is at most
6. (That's good, because otherwise the total area of the rectangular
approximation would be -->infinity as n increases.) Each term which
has degree less than 6 must -->0 as n-->infinity (hey, you could
use l'Hopital's rule or think about it!). The terms of degree
exactly equal to 6 each contribute a constant to the limit. Therefore
we can go through the whole list above and get the limiting value we
need. It will be:
32+40+0+(80/3)+0+0+10+0+0+2+0+0+0+(1/6)+0+0+0+0 (Yes, this is tedious!)
After some arithmetic (I did this in another order in class) we get
the result (665)/6.
I don't think this specific computation has much importance, but I
went through it to show how pre-1600 technology would work. I
don't think they had Maple so their task would have been even
more difficult: getting an appropriate summation formula would indeed
have been troublesome.
The new stuff! (after ~1600)
|
So now I will show you a very different point of view, a very
successful point of view, which is how almost everyone in the world
thinks about the original problem. This is the genius of the
subject. We want the definite integral of x5 from 2 to
3. It seems difficult to compute, so let's compute it by studying a
more difficult problem! The result of analyzing a very
carefully chosen more difficult problem is surprising, and will lead
to remarkably easy computations of many definite integrals. Using
"hindsight" this isn't too remarkable: the whole course (three
months!) has been aimed at this problem. But let's continue.
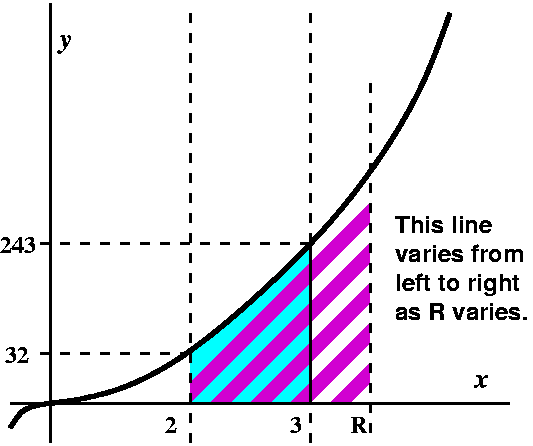
The carefully chosen more difficult problem is the following. Study
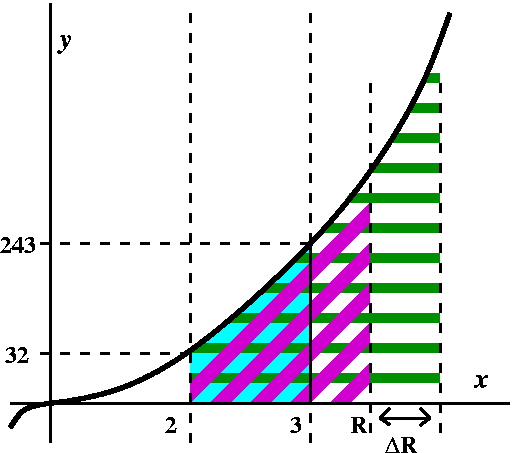
the area function of the variable R (suggested by a student):
A(R) is the area under y=x5 from x=2 to x=R. It is the area
of the diagonally
purple-striped region in the picture on the right. We would like
to compute A(3), but instead will study A(R). One value of A(R) is
obvious: A(2)=0 (the area from x=2 to x=2 has 0 width!). What else
should we do? The whole course comes down to: compute A'(R)!
|
 |
|
Remember that A'(R) is the limit as deltaR-->0 of the quotient
[A(R+deltaR)-A(R)]/deltaR. What can we say about this quotient? We
suppose in the accompanying picture that deltaR is a small positive
number. If deltaR were negative, a similar analysis would give an
identical answer for the limit. Positive deltaR is easier to draw.
In the picture to the right, A(R+deltaR) is the area of the region with
horizontal green stripes.
|
|
|
We
notice that the difference A(R+deltaR)-A(R) is a thin sliver of
area, with width deltaR: it is the area of the region with only
green stripes, no diagonal purple stripes. Now I'll take advantage of
the simple nature
of x5. It is an increasing function. Therefore
A(R+deltaR)-A(R) must be less than
(R+deltaR)5·deltaR and it must be greater than
R5·deltaR. This means that the difference quotient
[A(R+deltaR)-A(R)]/deltaR is bounded below by R5 and is
bounded above by (R+deltaR)5 (the deltaR's cancel
out!). But what happens as deltaR-->0? The lower bound, R5,
doesn't change at all. The upper bound, (R+deltaR)5, must
-->R5 as deltaR-->0. Therefore the difference quotient is
"sandwiched" (squeezed?) between two quantities which approach the
same limit. By the Squeeze Theorem, the limit of the difference
quotient exists, and the limit equals R5.
|
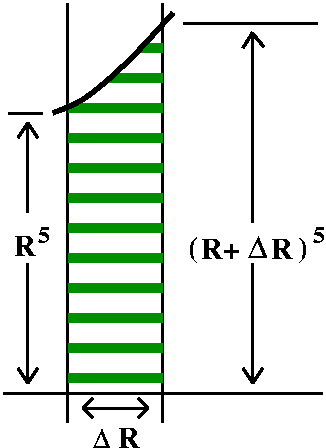
|
Let's summarize what we have learned about A(R):
A(2)=0 and A'(R)=R5.
But we know from studying the MVT and its results that if
A'(R)=R5 then A(R)=(1/6)R6+C, where C is some
constant. The "initial condition" A(2)=0 leads to
(1/6)26+C=0 so that C=-(1/6)26. Therefore we
have total knowledge of A(R). It must be
(1/6)R6-(1/6)26. And finally, A(3) is
(1/6)36-(1/6)26. Since 36 is
729 and 26 is 64, this answer is the same as (729-64)/6
which is (665)/6, agreeing with the answer we got using the old technology!
Is this a journey worth the trip?
We now have two ways to compute the definite integral, and the
insight this gives is thought to be valuable by many people. You will
have to determine if this journey (the intellectual effort to
understand the insight) is worth the trip (all of the words and
pictures and ... that you have worked through). I hope that you will
eventually answer "Yes" to this question. But now, back to work.
 Here I will use the notation in the textbook. Also I will refer to what
follows as FTC.
Here I will use the notation in the textbook. Also I will refer to what
follows as FTC.
The Fundamental Theorem of Calculus (FTC)
Suppose f(t) is a continuous function, and F(x) is the
definite integral of f from t=a to t=x.
Then F(x) is differentiable, and
its derivative is f(x).
Also, if F is any antiderivative of f, then
the definite integral of f from x=a to x=b is F(b)-F(a).
|
I then did a collection of problems from the text.
They were:
- 5.3 #21: What is the definite integral of 4x+3 from 2 to 8?
(Asked in the text using usual math symbols: the long S for integral
sign, etc.).
Solution According to FTC we just need to guess an
antiderivative. I guess F(x)=2x2+3x+83. You can
verify my guess by checking that F'(x)=4x+x, which it does. Now in
FTC, a=2 and b=8, so that the definite integral must be F(8)-F(2)=
[2·82+3·8+83]-[2·22+3·2+83].
Notice, please, that the silly 83 is added and subtracted: it
cancels out. In computing definite integrals we may omit the silly
constants.
You can't necessarily omit these silly
arbitrary constants in other types of computations, such as initial value
problems.
- 5.3 #28: What is the definite integral of cos(theta) as theta goes
from theta=Pi to theta=2Pi?
Solution According to the FTC, we just need to find an
antiderivative of cos(theta), and then ... well, sin(theta) is one
antiderivative. And then sin(2Pi)-sin(Pi) is 0. Does this mean there
is no area between cosine and the horizontal axis? That sounds
weird. If we look at the graph, we can "see" the area. But, golly, in
fact
(IMPORTANT!)
If we look at the
sums defining the definite integral, we can see that when f(x)<0,
the sums will be negative: the definite integral weights area
negatively when the curve is below the axis.
|
- 5.3 #37: what is the definite integral of 6/sqrt(1-t2)
as t goes from 1/2 to sqrt(3)/2?
Solution
We used what is standard notation. First,
though, guess an antiderivative: the suggestion was made that I look
at 6arcsin(x), which does work. Then I wrote 6arcsin(x)|x=1/2x=sqrt(3)/2. The
vertical bar is notation devised especially for the definite integral
computation, and means: substitute in the upper "limit" and evaluate,
and then substitute in the lower limit, evaluate, and subtract. After
some effort, we saw that this was 6·(Pi/3=Pi/6).
- 5.3 #8. Here g(x)=int(ln(t),t=1..x) and the text asks for g'(x).
Solution
so by FTC g'(x)=ln(x).
- 5.3 #10. Here g(u)=int(1/(x+x2),x=3..u) and the text
asks for g'(u).
Solution
so by FTC g'(u)=1/(u+u2).
In the last two problems it is important to see what is a "bound
variable" and what is varying. I will try to make this more clear than
what I did in class. Look:
int(x2,x=3..10)=int(q2,q=3..10)=int(w2,w=3..10)=int(z2,z=3..10)
So the interior variables in the definite integral have no meaning
outside the integration -- they are what is called "dummy variables"
or "bound variables". The functions in the last two textbook problems
depend on the limits of integration, not on what's inside the integrations!
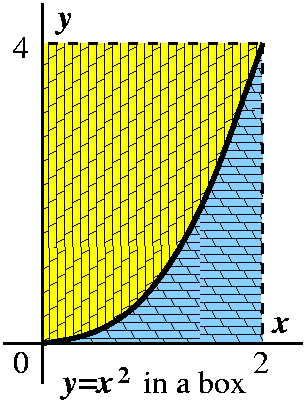 The Question of
the day was a bit involved. I first found the area under
y=x2 from x=0 to x=2 by quickly guessing an antiderivative
and taking its value at 2 and subtracting its value at 1: so start with
(1/3)x3 and get 8/3-0/3=8/3. Now look at the box this curve
is in. The box with corners at (0,0) and (2,4) has area 8. Therefore
the other part of the box has area 8-8/3=(16)/3. The QotD:
write that area as a definite integral with respect to y (and
rearrange the boundary equation so that it will read
"x=something"). Compute the integral, and make sure you get (16)/3.
The Question of
the day was a bit involved. I first found the area under
y=x2 from x=0 to x=2 by quickly guessing an antiderivative
and taking its value at 2 and subtracting its value at 1: so start with
(1/3)x3 and get 8/3-0/3=8/3. Now look at the box this curve
is in. The box with corners at (0,0) and (2,4) has area 8. Therefore
the other part of the box has area 8-8/3=(16)/3. The QotD:
write that area as a definite integral with respect to y (and
rearrange the boundary equation so that it will read
"x=something"). Compute the integral, and make sure you get (16)/3.
Answer
Since y=x2, we know x=y1/2. The integral we must
compute is int(y1/2,y=0..4). So we "guess" an
antiderivative: F(y)=(2/3)y3/2. We compute
F(4)-F(0). Certainly F(0) is 0, and F(4) is (2/3)43/2 and
41/2 is 2 and 23 is 8, so the answer is (16)/3
as desired.
|
Monday,
November 24 |
What will be done now is the definition of the definite integral. This
is a complicated object, and is the mathematical object which
corresponds to quantities which have properties similar to those we
discussed last time. I will concentrate on area in what follows
(because then I can draw simple pictures), but everything I'm doing is
applicable to many many many other things as well.
So again: the problem of area. In what follows I'll be looking at a
region bounded by y=f(x), x=a, x=b, and the x-axis. How can we
efficiently and accurately approximate the area of this region?
We will use rectangles as we did last time, only now I'll give you
the official names of everything. Here we go:
- First, we will make a partition of the interval
[a,b]. This means taking a finite collection of points in the
interval:
a=x0<x1<x2<...<xn=b.
We take n+1 points which chop up [a,b] into n
subintervals. x0 is always supposed to be a and
xn is always supposed to be b.
- Select sample points in each of the subintervals. Your
textbook refers to these points as x*j, and
this must be in the jth subinterval, which is the
subinterval [xj-1,xj].
- Finally, form the Riemann sum: this is the sum of
f(x*j) multiplied by
xj-xj-1 as j runs from 1 to n. So it is a sum of
n terms, and each term consists of a value of f multiplied by the
length of the subinterval. The textbook has a discussion of sigma
notation and you should look at it. I would like to concentrate on
the ideas right now.
Example 1
This is slightly different from what was discussed in class!
Consider the function f(x)=0 if x<2 and f(x)=3 if x>=2. So
f(1.3)=0 and f(2.3)=3. Note that this function is not
continuous. What's the area "under" y=f(x) from x=1 to x=5?
Well, if you consider the picture, you should guess that the area is 9.
Here is the question:
Can we find a partition of the interval [1,5] so that any
selection of sample points will yield Riemann sums within .001 (that's
one-one-thousandth) of 9? |
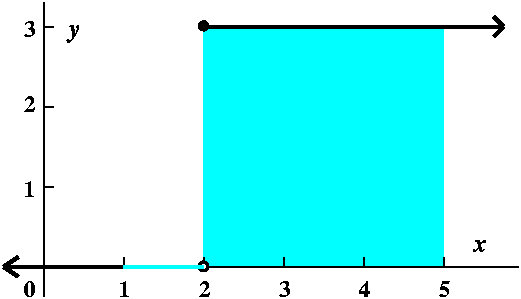 |
This is a bit difficult. If we take the partition to be
x0=1 and x1=1.9999 and x2=2 and
x3=5 then the sums will be either 9 or 9+3(.0001), and they
will differ by less than .001.
So the partition is sort of "localized" around the discontinuity, x=2.
|
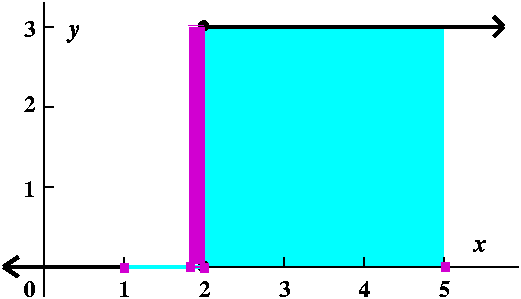 |
So for the non-continuous function f(x) we just analyzed, we can find
a partition all of whose Riemann sums are very close to 9. Let us try
something harder.
Example 2
Again, this is slightly different from what was discussed in class!
Suppose f(x)=sqrt(1+3x4). This is a function given by a
rather simple formula. I would like to consider the interval from x=0
to x=1. f(0)=1 and f(1)=2 (this is an invented example, after
all!). Since
f'(x)=(1/2)(1+3x4)-1/2(4x3 it is not
hard to see that f'(x)>0 on all of [0,1] (the - sign in the formula
for f'(x) is not a "real" - sign: as Mr. Colquit said, it is a "bottom"
sign). Therefore f(x) is increasing on [0,1], and the graph of the
function is rather simple, as shown.
Here is the question:
Can we find a partition of the interval [0,1] so that any
selection of sample points will yield Riemann sums within .001 (that's
one-one-thousandth) of the true area? |
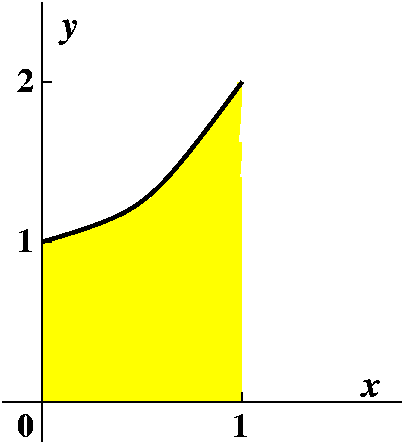 |
As I mentioned in class, I know that there is no way for any
one in the world to get an exact value for this area. Therefore I am
asking if there is a way to get an approximate value within .001 of
the "exact value". Here is one way to motivate the correct
answer. Suppose we chop up the interval [0,1] into four
equal parts, as shown.
Because the function is increasing any Riemann sums must be
between the sums obtained when using the left and right endpoints of
the subintervals. If we "move" the blocks between these "upper" and
"lower" Riemann sums to the right we can line them up: they won't hit
(except if you look at the boundaries). The region between the upper
and lower sums is 1/4 unit wide and 1 unit high, and so all the sums
with any sample points for the partition {0,1/4,2/4,3/4,1} and
for this function will be within 1/4 of the true answer.
We can do this in such a simple manner because the function is increasing.
|
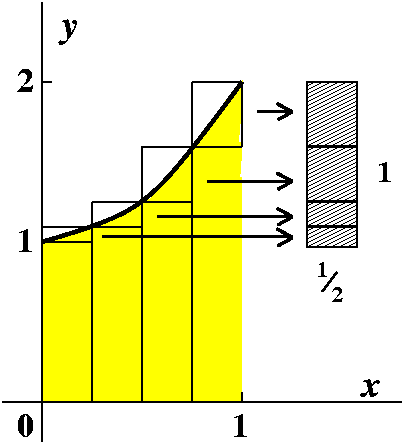 |
Now what if we wanted to get within .001 of the true area? A similar
picture for a partition with 1,000 equal subintervals of [0,1] would
be difficult to draw, but I hope you can imagine it. We could then
move over the boxes between the upper and lower Riemann sums, and they
would form a rectangle 1 unit high and 1/1,000 unit wide. So they
would be closer to the true area than
height·width=1/1,000=.001. Also, any choice of sample
points would lead to a Riemann sum between the upper and the lower
sum, so we indeed have a way of approximating areas within any
positive error we can specify.
Definition Suppose f is a function defined on the interval
[a,b], and the following occurs: as the partition gets "finer" (so the
length of all of the subintervals --> 0) and for any choice of
sample points, the Riemann sums --> one number, then that number is
called the definite integral of f on [a,b].
The great "freedom" (or, conversely, obligation) here is that any
choice of sample points is allowed. There are many Riemann sums
possible, and we would like them all to be close to one value, the
definite integral.
Of course, there is notation: an elongated S from the sum (just
replacing the capital sigma) and an a and a b and a "dx":
Sab f(x) dx. I think of this as
a sum of very, very thin rectangles of height f(x) and "width" dx,
added up from x=a to x=b.
It might be easier to use something like Maple notation:
int(f(x),x=a..b).
It is a true fact (much better than a false fact!), that every
continuous function has a definite integral. But there are functions
which are not continuous, such as the function of example 1 above,
which also have definite integrals.
I did two very examples that are "simple" if you recognize the
geometry supporting them:
S04 sqrt(16-x2) dx:
this is, geometrically, a quarter of a circle of radius 4, so its
value is 4Pi.
S-Pi/2Pi/2 sin x dx: here
the curve is over the x-axis and under the x-axis symmetrically. The
"rectangles" f(x) dx "balance" each other, so that the value of
this definite integral is 0.
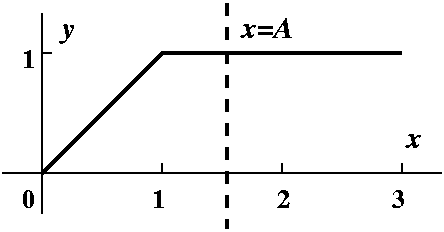 The Question of
the day was the following: what's shown is the graph of a
function, f(x), made up of two line segments. First compute the
definite integral of f from 0 to 3. Then find A so that the definite
integral from 0 to A is half of the total area.
The Question of
the day was the following: what's shown is the graph of a
function, f(x), made up of two line segments. First compute the
definite integral of f from 0 to 3. Then find A so that the definite
integral from 0 to A is half of the total area.
The area shown is either a trapezoid or a triangle and a rectangle. In
either case, the area, the definite integral from 0 to 3, is 2.5. Half
of that area is 1.25, and the area of the triangle is 1/2, so that we
need .75 from the area of the rectangle. Since the rectangle is 1 unit
high, we easily deduce that A must be .75 more than 1, so A=1.75.
Please read 5.1 and 5.2 of the textbook, and please hand in tomorrow
(Tuesday=Thursday!) at workshop these textbook problems:
5.1 #13 and 5.2 #34 |
Wednesday,
November 19 |
I remarked that we would be doing something significantly surprising
intellectually in the balance of the course. So far we have studied
various nice problems involving differentiation. Things like graphing
and optimization (min/max) and slopes of tangent lines and
... stuff. It turns out that the kind of things we've been studying
have great application to what looks like a collection of completely
different problems. It is and it will be amazing!
Please start reading chapter 5 of the text. I will cover today and
Monday the material in 5.1 and 5.2, in somewhat different ways than
the text does. I may even go a bit further.
I began with The problem of area
I drew a blob on the board, and asked how much area is inside the
blob. I told people that they could use any method they wanted to
answer the question. Some students whose minds were already
preconditioned by calculus gave rather strange answers, but no one
gave me a direct method until Mr.Colquit remarked essentially that we could
cut up the board and then weigh the blob and compare its weight to the
weight of a board of known area, such as a rectangular board. So here
is a direct method: cut it out!.
We will try to be a bit more indirect, more sneaky, and learn
properties of area which will let us approximate what we
want. What properties does "area" have?
- Area should assign a region in the plane a non-negative
number.
Comment This certainly seems reasonable. But there are things
in the plane
which have zero area: one point, or a line both should have
area equal to 0.
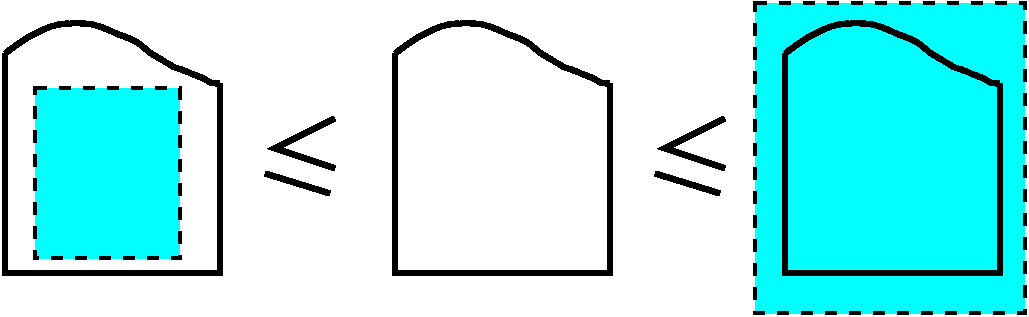
- If one region, R1, is inside another region,
R2, then the area of R1 is less than or equal to
the area of R2.
Comment The areas could actually be equal. For example,
R1 could be R2 with just 1 point taken out!
- Two regions which are congruent must have the same area.
Comment Again, this seems reasonable, but then the word
"congruent" needs to
be dealt with. The on-line dictionary I use says "congruent" means
"coinciding exactly when superimposed" and if clarity is wanted, then
the words there need to be explained further. In the plane, two shapes
or blobs are congruent if we can move them one onto the
other. Sometimes "flips" are allowed.
- If a region R is made up of two regions R1 and
R2 which don't overlap, then the area of R is equal to the
sum of the area of R1 and the area of R2.
Comment In fact, as was pointed out, we can weaken the
hypothesis a bit
here. The two regions R1 and R2 can overlap as
long as the overlapping takes place only on the boundary.
- The area of a rectangle is its length multiplied by its width.
Comment Without this assertion, assigning area to be 0 to
every region would
obey all the previous rules! Of course that's a silly example, but it
does show that some reference must be made to "normalize" area, to
give it units or something.
With RULES A THROUGH E we can begin
an organized campaign to compute or approximate areas. For example,
here is how we could compute the area of a typical blob. I will use
the RULES in the analysis that follows.
I would first slice the blob by line segments to get something which
had at most one curvy side.
I will be done if I describe to you how to compute the area of each of
the pieces. I will specialize to one of the pieces, and assert that
similar things can be done to all of the other pieces. So:
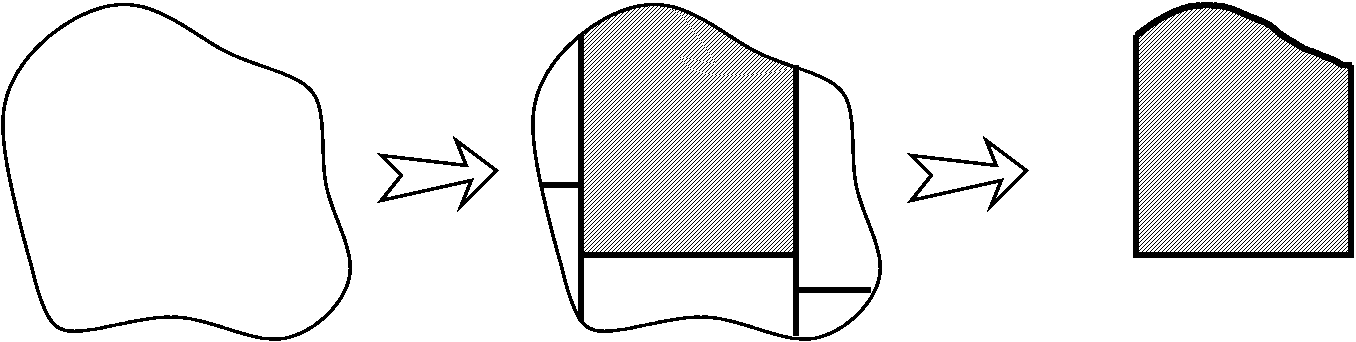
Now I can approximate inside this piece of the blob and outside the blob by
rectangles, and since I know the area of a rectangle, I can get some
estimate of the area of the piece of the blob.
Of course this estimate is not so good, but we could improve it with
some sort of scheme like this:

So we can get a collection of approximations which get closer and
closer and closer to the true value of the area, and maybe that's good
enough. (It is, in many cases.)
As I remarked, another instructor told me of a wonderful way of
bringing home the idea of area: look at your hand and ask, what is its
area? Giving a "good" answer to this may be difficult and involve
quite a lot of approximation.
Now let's look briefly at The problem of blood flow
I looked at blood flowing through the heart, and asked how much blood
would flow through the heart in a given amount of time, say a
minute. Knowledge of this could be rather important in study of
certain conditions or diseases or whatever. One rather destructive
method would be to cut it up: that is, just slice into the
heart and let the blood drip to fill a bucket for a minute. Well, this
method might not be too satisfactory for several reasons which you can
you think about yourself. But how do people answer such questions? You
insert a catheter into the appropriate blood vessel (Google lists
about 135,000 links in response to the search words "blood flow
catheter" so there are ample references). At the end of the catheter
there's a mechanism, which you can think of as a sort of paddlewheel,
and the blood flow sets it spinning, and the spinning makes an
electric current which is passed up the catheter and measured. How is
the actual blood flow computed? It turns out that the blood flow obeys
rules which are totally analogous to the area rules.
RULES A THROUGH E now state, sort of:
- The blood flow is a non-negative number.
Comment
Assume for simplicity
that the blood flow in a vessel goes only in one direction. In fact, in
certain vessels of the body
there are "mechanisms" preventing back flow!
- Blood flow over longer periods of time is at least equal to blood
flow over shorter periods of time which are "inside" the longer
periods.
- If the flow rate is identical over two periods of time (for
example, the same portion of two heartbeats) then the flow is also the
same.
- The blood flow during a sum of two intervals which may overlap
only at "the edges" is the sum of the flow during the intervals
considered separately.
- If the flow rate is constant, then the blood flow is the product
of the duration and the flow rate.
 With these observations, it is possible to make good approximations to
the blood flow using a discrete collection of flow rate measurements,
and this is what's done (without filling a bucket!).
With these observations, it is possible to make good approximations to
the blood flow using a discrete collection of flow rate measurements,
and this is what's done (without filling a bucket!).
By the way, I found a number of authentic pictures of the heart on the
web and decided I didn't need to illustrate this discussion with what
could be a grim and upsetting picture.
And now Aliens land in Piscataway and leave a bar
This is somewhat speculative. The type of bar I am referring is
not one selling alcoholic beverages (!) but a long and very
very heavy bar, a bar which is 100 meters long (metric aliens!) and
made of a number of distinct substances. Additional conditions are
that the bar is too heavy to move, that we can scrape and sample it,
and that we would like to determine its total weight, or, rather, its
total mass. Here maybe is a picture, with the different shapes/colors
representing substances of perhaps vastly differing densities.

Since the bar is geometrically very simple, we can just take a sample
scraping somewhere on it, find the density, and approximate the total
mass by multiplying the density recorded by the geometric shape's
volume. But this is a very rough approximation, since there are
different substances and the bar could be complicated. So what we
could do is periodically sample the bar, find the densities, and
multiply by chunks of the volume. It seems likely that we will get a
better estimate of the total mass if we take more samples.
The alert student will observe that in these imaginary measurements
and computations we are being guided by metallurgical (I checked the
spelling!) analogs of RULES A THROUGH
E. Look at these rules, and try to formulate which they
would be for density/mass computations.
Finally A last look at Francine
 In this case, Francine is traveling north on the Garden State
Parkway. She leaves mile 0 in Cape May at 9:00 AM. You have only the
following "equipment" (it is another "thought experiment"):
In this case, Francine is traveling north on the Garden State
Parkway. She leaves mile 0 in Cape May at 9:00 AM. You have only the
following "equipment" (it is another "thought experiment"):
You can look at the speedometer on her car and you can look at your
watch.
You are asked to tell where she is (what mile on the GSP) at 10:00
AM.
What procedure can you follow? Here is one: look at the speedometer
at, say, 9:30, record the miles per hour, and multiply by 1 (hour,
that is). This gives an estimate of her position. A more "proactive"
(means: "creating or controlling a situation by
taking the initiative") method would be to take several measurements
(say, record the speed every 5 minutes) and then multiply each speed
reading by 5/60, and add these up. This would likely give a better
estimate of the position she will be in.
Again, if you are alert, you will see in all this we are again using
the analogs of RULES A THROUGH
E. Here the quantity to be computed is distance, and we are
approximating distance by a sum of "rectangles" where we assume
constant speed and multiply by a time interval.
Big news
Any quantity which obeys the analogs of RULES A
THROUGH E can be computed (either approximated efficiently,
or in a large number of cases, computed exactly) using the
methods we will learn. There are many many such quantities, ranging
from such physical "objects" as force and work to quantities in
economics. And it is really amazing (to me, at least!) that
what we've done so far can be applied to this problem. It is a bit
difficult to "see" derivatives and slopes in all of these problems,
without being shown where to look.
So the idea will be to take a quantity, break it up into small, more
easily approximated parts, and then to add these approximations up,
and the resulting sum will give a good approximation (or, even,
sometimes, an equality!) to what we want to compute. This is a method
of disintegration and integration: taking apart and putting
back together. On Monday I will go into the technical details of the
method, and there will be much notation to struggle with. But if you
can "internalize" the ideas of what I'm describing here, you will see
that the result is worthwhile.
Exam 2 returned
I returned and discussed the results of the second exam. I
apologized for the excess length, but not for the level of the
problems. The difficulty of the problems was probably appropriate, but
the length was not: I think I had about one problem too many -- I
should have had 8 rather than 9. But I additionally remarked that the
performance of students on some of the exam was clearly below the
level expected. Students must learn how to study.
Bonus points!
I offer the following as a way to increase the grades, so everyone
(both "management" and students!)
will feel better. Go home, look at your exam, and at the answer sheet. Learn how to do the problems
you did not do well. At each workshop tomorrow, question the
recitation instructor, Ms. Calinescu, aggressively and make sure that
you understand how to do the problems and others. You must
also, however, prepare aggressively. She will
allow 40 minutes for questions, and then will give you an exam for 40
minutes. This exam will be worth 30 points, and I hope to boost
everyone's grade on the second exam by a large portion of those
points. You can show me you do know the material, and I will
happily acknowledge this.
No calculators or formula sheets or notes will be allowed on the
exam.
|
I forgot to ask a Question of
the day!
|


 Today we disclose the climax of the course. I will begin with a
simple example. Our goal right now is to compute the area of the
region in the plane bounded by the x-axis, x=2, x=3, and the curve
y=x5. This is a definite integral:
S23x5dx/ Oh, I give up: this
is int(x^5,x=2..3). The last collection of symbols is easier to type,
and the traditional integral symbol isn't well indicated by S,
anyway. On the right is a picture of the region whose area I will try
to compute. Please note that although the picture I have drawn is
mostly qualitatively correct, I have certainly used very different
units on the vertical and horizontal axes (25=32 and
35=243). I will arbitrarily take the year 1600
as the dividing point in the two approaches to computing definite
integrals that I'll discuss
(the 1660's is probably more accurate historically). I'll begin with
the "old" style.
Today we disclose the climax of the course. I will begin with a
simple example. Our goal right now is to compute the area of the
region in the plane bounded by the x-axis, x=2, x=3, and the curve
y=x5. This is a definite integral:
S23x5dx/ Oh, I give up: this
is int(x^5,x=2..3). The last collection of symbols is easier to type,
and the traditional integral symbol isn't well indicated by S,
anyway. On the right is a picture of the region whose area I will try
to compute. Please note that although the picture I have drawn is
mostly qualitatively correct, I have certainly used very different
units on the vertical and horizontal axes (25=32 and
35=243). I will arbitrarily take the year 1600
as the dividing point in the two approaches to computing definite
integrals that I'll discuss
(the 1660's is probably more accurate historically). I'll begin with
the "old" style.



 With these observations, it is possible to make good approximations to
the blood flow using a discrete collection of flow rate measurements,
and this is what's done (without filling a bucket!).
With these observations, it is possible to make good approximations to
the blood flow using a discrete collection of flow rate measurements,
and this is what's done (without filling a bucket!).

 In this case, Francine is traveling north on the Garden State
Parkway. She leaves mile 0 in Cape May at 9:00 AM. You have only the
following "equipment" (it is another "thought experiment"):
In this case, Francine is traveling north on the Garden State
Parkway. She leaves mile 0 in Cape May at 9:00 AM. You have only the
following "equipment" (it is another "thought experiment"):
 Here it becomes useful to observe that f is a graph of
g'. Thus, to the left of 1, g' is positive and to the right, it is
negative, so 1 is a local max. Similarly, 1 is a local min.
Here it becomes useful to observe that f is a graph of
g'. Thus, to the left of 1, g' is positive and to the right, it is
negative, so 1 is a local max. Similarly, 1 is a local min. How about if f(x)=
How about if f(x)=
 We divide the interval from 2 to 3 into n different equal parts. Here
you should think of n as some very large positive integer. (The
picture shows n=6, not terribly large -- imagine n=10,000!) Then each
piece of the interval will have width (3-2)/n=1/n. We will approximate
the area over the first subdivision, from 2 to 2+1/n, by a rectangle
whose height is the value of the function at the right-hand
endpoint. Similar things happen if we choose the left-hand endpoint or
the middle or ... any choice, in fact. So the right-hand height is
(2+1/n)5, and the area of the rectangle over the first
subinterval is
(2+1/n)5(1/n)
(area is
height·width). What about the second rectangle? It has the same
width but the right-hand endpoint's height is
(2+(2/n))5. So the second rectangle's area is
(2+(2/n))5(1/n). And the third rectangle's area is
(2+(3/n))5(1/n). Etc. What does this Etc. mean? We
are supposed to find the sum of all the rectangles and there are n of
them. So we have:
We divide the interval from 2 to 3 into n different equal parts. Here
you should think of n as some very large positive integer. (The
picture shows n=6, not terribly large -- imagine n=10,000!) Then each
piece of the interval will have width (3-2)/n=1/n. We will approximate
the area over the first subdivision, from 2 to 2+1/n, by a rectangle
whose height is the value of the function at the right-hand
endpoint. Similar things happen if we choose the left-hand endpoint or
the middle or ... any choice, in fact. So the right-hand height is
(2+1/n)5, and the area of the rectangle over the first
subinterval is
(2+1/n)5(1/n)
(area is
height·width). What about the second rectangle? It has the same
width but the right-hand endpoint's height is
(2+(2/n))5. So the second rectangle's area is
(2+(2/n))5(1/n). And the third rectangle's area is
(2+(3/n))5(1/n). Etc. What does this Etc. mean? We
are supposed to find the sum of all the rectangles and there are n of
them. So we have:
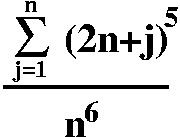
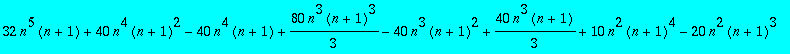
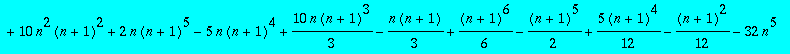



 Here I will use the notation in the textbook. Also I will refer to what
follows as FTC.
Here I will use the notation in the textbook. Also I will refer to what
follows as FTC. The Question of
the day was a bit involved. I first found the area under
y=x2 from x=0 to x=2 by quickly guessing an antiderivative
and taking its value at 2 and subtracting its value at 1: so start with
(1/3)x3 and get 8/3-0/3=8/3. Now look at the box this curve
is in. The box with corners at (0,0) and (2,4) has area 8. Therefore
the other part of the box has area 8-8/3=(16)/3. The QotD:
write that area as a definite integral with respect to y (and
rearrange the boundary equation so that it will read
"x=something"). Compute the integral, and make sure you get (16)/3.
The Question of
the day was a bit involved. I first found the area under
y=x2 from x=0 to x=2 by quickly guessing an antiderivative
and taking its value at 2 and subtracting its value at 1: so start with
(1/3)x3 and get 8/3-0/3=8/3. Now look at the box this curve
is in. The box with corners at (0,0) and (2,4) has area 8. Therefore
the other part of the box has area 8-8/3=(16)/3. The QotD:
write that area as a definite integral with respect to y (and
rearrange the boundary equation so that it will read
"x=something"). Compute the integral, and make sure you get (16)/3.




 The Question of
the day was the following: what's shown is the graph of a
function, f(x), made up of two line segments. First compute the
definite integral of f from 0 to 3. Then find A so that the definite
integral from 0 to A is half of the total area.
The Question of
the day was the following: what's shown is the graph of a
function, f(x), made up of two line segments. First compute the
definite integral of f from 0 to 3. Then find A so that the definite
integral from 0 to A is half of the total area.