Wednesday,
November 12 |
Please hand in solutions to problems 4.7 #26 and
4.10 #36. If you need hints, let me know.
We had a contest between two teams of students. Each team did an
optimization (finding a max or finding a min) problem. Real big prizes
were given out.
The (wonderful) Optimization Contest
Problem
What is the rectangle of largest area which can be drawn inside the
triangle with vertices (0,0), (3,0), and (0,2)?
Why do you know it
is largest?
The team which competed consisted of Ms. Sandoval, Ms. Smallwood,
Mr. Szabo, Mr. Morris, and Ms. Meleka. They all earned some
glory, I think.
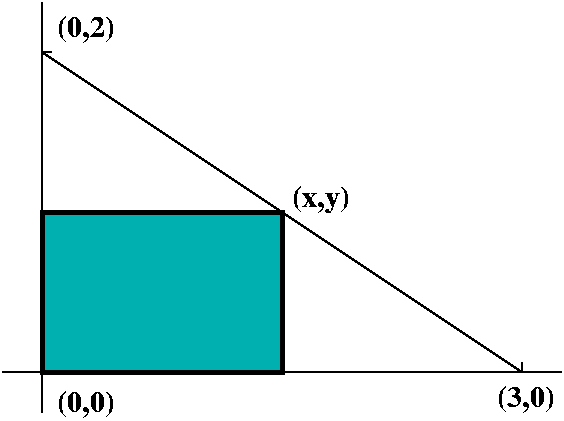 They sketched the picture shown. The rectangle has opposite corners
(x,y) and (0,0), with side lengths x and y. Its area is therefore
xy. What can we say about the relationship between x and y? The point
(x,y) is on the line connecting (0,2) and (3,0), and therefore if we
find an equation for this line, x and y must satisfy this equation,
and this will be a relationship between x and y. One equation
satisfied by both (0,2) and (3,0) is x/3+y/2=1. Therefore
y=2(1-x/3). The area becomes
A(x)=x·2(1-x/3)=2x-(2/3)x2. What x's will be
acceptable in this problem? If we look at the picture, x should be in
the interval [0,3]. So we need to maximize A(x)=2x-(2/3)x2
when x is in [0,3]. Some candidates can be found by looking for
critical numbers. A'(x)=2-(4/3)x, and the only x for which this is 0
is x=3/2. Then A(3/2)=3/2 seems to be the rectangle of largest
area.
They sketched the picture shown. The rectangle has opposite corners
(x,y) and (0,0), with side lengths x and y. Its area is therefore
xy. What can we say about the relationship between x and y? The point
(x,y) is on the line connecting (0,2) and (3,0), and therefore if we
find an equation for this line, x and y must satisfy this equation,
and this will be a relationship between x and y. One equation
satisfied by both (0,2) and (3,0) is x/3+y/2=1. Therefore
y=2(1-x/3). The area becomes
A(x)=x·2(1-x/3)=2x-(2/3)x2. What x's will be
acceptable in this problem? If we look at the picture, x should be in
the interval [0,3]. So we need to maximize A(x)=2x-(2/3)x2
when x is in [0,3]. Some candidates can be found by looking for
critical numbers. A'(x)=2-(4/3)x, and the only x for which this is 0
is x=3/2. Then A(3/2)=3/2 seems to be the rectangle of largest
area.
Why is it largest?
I will try to give several reasons. The students needed to give only
one reason!
- Look at A(x) and the domain, [0,3]. A(0)=0 and A(3)=0 by
direct computation, and A(x) must attain its max at either an endpoint
or a critical number. Since A(3/2) is positive, A(3/2) must be
the maximum value.
- Look at A'(x) to the left and to the right of x=3/2. Notice that
3/2 is the only critical number of A. To the left of 3/2,
A'(x)=2-(4/3)x is positive (A'(1)=2/3 for example) and to the right of
3/2, A'(x) is negative (A'(2)=-2/3). So A increases up to x=3/2 and
then decreases. Therefore A(x) must have a maximum at x=3/2.
- Let's compute: A''(x)=-4/3 so A(x) is concave down, and we have a
local max.
So there are several ways to complete this problem.
Problem
What is the triangle of smallest area which can be drawn with vertices
at (0,0) and on the positive x- and y- axes so that (3,2) touches the
edge of the triangle?
Why do you know it is smallest?
The team which competed consisted of Sunny, Anthony, Alex, Amit, and
Sonya ... perhaps they could not afford last names.
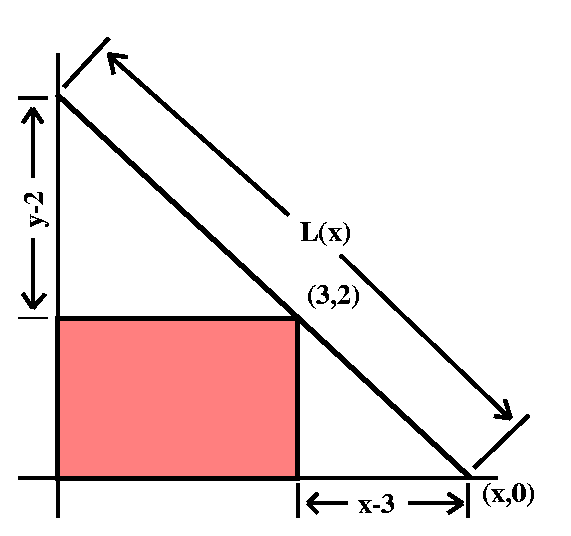
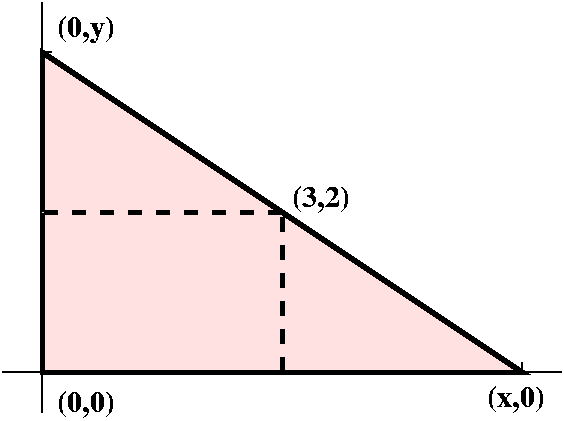 We begin with the picture shown. The triangle has height y and base
length x. Its area is therefore xy/2. Is there some relationship
between x and y? Look at the picture and see that (3,2) is on the same
line as (x,0) and (0,y). Well, the slope of the line between (3,2) and
(x,0) is -2/(x-3) and the slope of the line between (0,y) and (3,2) is
(y-2)/(-3). So these slopes must be equal, and we have (-2)/(x-3)=(y-2)/(-3).
Therefore y=[6/(x-3)]+2 and now A(x)=(1/2)x·([6/(x-3)]+2). What
is the domain of this function? Look at the picture: x must be greater
than 3.
We begin with the picture shown. The triangle has height y and base
length x. Its area is therefore xy/2. Is there some relationship
between x and y? Look at the picture and see that (3,2) is on the same
line as (x,0) and (0,y). Well, the slope of the line between (3,2) and
(x,0) is -2/(x-3) and the slope of the line between (0,y) and (3,2) is
(y-2)/(-3). So these slopes must be equal, and we have (-2)/(x-3)=(y-2)/(-3).
Therefore y=[6/(x-3)]+2 and now A(x)=(1/2)x·([6/(x-3)]+2). What
is the domain of this function? Look at the picture: x must be greater
than 3.
Let's find A'(x). Since
A(x)=(3x)/(x-3)+x=(3x+x2-3x)/(x-3)=x2/(x-3) we get
A'(x)=[2x(x-3)-x2]/[(x-3)2], and A'(x)=0 when
2x(x-3)-x2=0, which is x2-6=0 so x=0 and
x=6. Now we throw out x=0. It need not be considered since it
is not in the domain of this problem. x=6 is the only critical number
we need to look at, and for x=6, A(6)=12, and we have a 12 by 6
triangle, I think.
How do we know we have found a smallest triangle? Here we can again
find several reasons, each of which is enough to justify the
conclusion.
- Consider A(x) as x-->infinity. Since
A(x)=x2/(x-3), A(x) gets large (A(x)-->infinity).
Also, as x-->3+, A(x)-->infinity. Therefore somewhere in
between there is a smallest value of A(x), and the only critical point
is at x=6, so the critical point must be there.
- Now a reason related to A'(x). We know
A'(x)=[x·(x-6)]/[(x-3)2]. In the interval from 3 to
infinity, A'(x) has a negative sign for 3<x<6 and it has a
positive sign for 6<x. Therefore A(x) is decreasing to the left of
x=6 and is increasing afterwards. x=6 must represent a local (and
absolute!) minimum for A(x).
- Now consider A''(x). I probably wouldn't, but you can compute it
and then simplify the result: you will get
A''(x)=18/(x-3)3. Therefore if x>3, A''(x) is positive,
so A(x) is concave up in our domain, and its value at x=6 must
represent a minimum.
One of the teams got the first prize, and the other got the second
prize. The prizes were professionally wrapped, and were incredibly
precious: historically, most Kings of England would never have been
able to get (or taste) anything like these prizes!
Comments about the problems
First, in each problem there seemed to be three different ways to
check that the numbers found were the desired extreme values. I would
classify them as Zeroth Derivative Test (depends on the
function itself!), First Derivative Test and Second
Derivative Test. Of course, sometimes one "test" may be more or
less useful than others, depending on computational difficulties,
etc. You need to decide which of them is easiest to use.
Second the alert student will notice some similarities and some
differences between the two problems done. The economists call the
function to be extremized the objective function. Any
relationships between variables are called constraints. The
problems done above are sort of dual to each other. The
constraint/objective functions almost reverse each other in the
problems, as does the max/min nature. This is used in many real world
settings.
I then discussed some common difficulties which I saw in yesterday's
QotD. Please look at the comments there.
And on to antiderivatives, which we had already discussed in
connection with the MVT. Now I discussed this very briefly again. F(x)
is an antiderivative of f(x) if F'(x)=f(x). The MVT tells us that if
we know F(x) is an antiderivative of f(x) in some interval
a<x<b, then all antiderivatives of f(x) in that interval
are F(x)+C, where C is a constant.
Therefore all antiderivatives of, say, -7x3 are (first
guess, then verify, then write "+C") (-7/4)x4+C. In fact,
all derivative "tables" and derivative information is, by reversing
the order of looking at them, also antiderivative tables. I mentioned
a few specific functions (the antiderivative of xn is
(1/(n+1))xn+1+C for n not 0, and 1/x has
antiderivative ln(x)+C for x positive, and 1/(1+x2) has
antiderivative arctan(x)+C etc.). I actually did one problem.
A silly 6 foot tall calculus instructor throws a ball straight up into
the air with initial velocity of 15 ft/sec. When does the ball hit the
ground? (We assume the calc instructor has moved away from the ball's
path, I guess).
Well, if H(t)=the ball's height in feet at time t, measured in seconds
from when the ball started up, we know that H(0)=6 and H'(0)=15. These
equations are sometimes called the initial conditions of the
problem. We also know that gravity pulls the ball down. Well, then,
what do we know? H''(t) is the acceleration of gravity. In the
"English system" of measurement, gravity on Earth is about 32
ft/sec2. Of course here is something tricky: gravity is
directed down, so in fact we know H''(t)=-32. The minus sign is
rather important. If we omit it, the ball will steadily gain speed and
never come down. Since H''(t)=-32, H'(t)=-32t+C. But H'(0)=15,
so this C is 15. Since H'(t)=-32t+15, we know that
H(t)=-16t2+15t+C. Again, the other initial condition
implies this C is 6. So H(t)=-16t2+15t+6. When is H(t)=0?
We used the quadratic formula:
t=[-15+/-sqrt((15)2-4·(-16)(6))]/2(-16). Which root
should we use? If we try the + sign, we will get a negative time (the
bottom is negative .. tricky). Therefore the ball hits the ground when
t=[-15-sqrt((15)2-4·(-16)(6))]/2(-16). This is (if
you must!) [480+sqrt(609)]/32, or, approximately 1.239935168, sigh.
The Question of
the day was: suppose that y''(x)=x2+1/(x2)
and we know that y(1)=3 and y'(1)=-3. Find y(x).
The first antiderivative gives us
y'(x)=(1/3)x3-1/x+C. Notice: 1/(x2 is actually
x-2: you need to love exponents here! Now y'(1)=3 gives us
(1/3)-1+C=-3, so C=-(7/3) I think. Now we know
y'(x)=(1/3)x3-1/x-(7/3) so that (antidifferentiating
again!)
y(x)=(1/(12))x4-ln(x)-(7/3)x+C. But we can now use y(1)=3
and get: (1/(12))14-ln(1)-(7/3)1+C=3. ln(1)=0 at least. The
equation for C becomes:(1/12)-(7/3)+C=3. Thus (!!) C=63/12. And
y(x)=(1/(12))x4-ln(x)-(7/3)x+(63/12). (Yeah, yeah: that last
thing is 21/4. I guess.
Comment about the workshop problem
Notice that the circle and the parabola both go through (0,0) and both
have the x-axis as tangent lines there. Should they maybe bend the
same at x=0 to match up well? Can you find an equation y=stuff(x)
for the lower half of the circle, and then figure out how to
match it up really well?
Maple allows one to graph these things. If you type
with(plots):
F:=a->implicitplot({y=x^2,x^2+(y-a)^2=a^2},x=-1.5..1.5,y=-.1..2,color=black, thickness=2,scaling=constrained,grid=[75,75]);
Then the statement F(.3) causes the first picture below to
be shown (too small!), and F(.8) gives the second picture
(too large!).
|
Monday,
November 10 |
Our next exam will be in one week.
I urged students to look at
the draft of the formula sheet for the second exam, and give me
comments about it. I also asked that student look at the review problems for the second exam
and, if they wish, help to assemble an
answer collection for these problems.
Next I must report the presence of my evil twin, NEHPETS, who escaped from confinement
and taught the rest of the class. As I later determined during
discussion with several students, each class costs about $16.07 in
tuition money for each student, more than a good movie, and the
efforts of NEHPETS do not deserve
such payment. Refunds can be applied for.
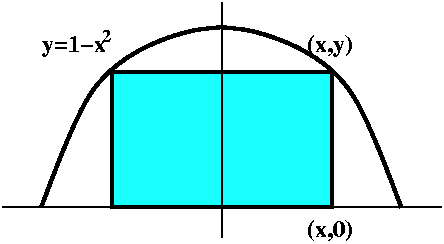 Problem #1
Problem #1
So the class discussed some optimization problems. We first talked
about how to find the rectangle of largest area enclosed between the
curve y=1-x2 and the x-axis. Here is a picture of such a
rectangle. It takes some geometrical thought to see that the largest
rectangle will be placed symmetric with the x-axis with one edge on
the x-axis. Once that is observed, we can take the formula for the
area of a rectangle, A=length·width, and observe that, as the
rectangle is presented, width (if that is the horizontal measurement)
is 2x and length is 1-x2. Therefore the area will depend
only on x, and A(x)=x(1-x2). Here we can describe all
rectangles by taking x in [0,1]. Therefore we have now changed the
problem into a "purely" mathematical one:
Find the maximum of A(x)=x-x3 for x in the unit interval,
[0,1].
We developed general theory to cover this. Either the max value is
achieved at one of the endpoints (x=0 or x=1) or at an interior
critical point. Well, A(0)=0 (plug in x=0 into the formula) and A(1)=0
(again, plug in x=1 into the formula). Since it seems unlikely that
all of the rectangles have 0 area, the max rectangle will occur at a
critical point in [0,1], with positive area. But
A'(x)=1-3x2, and since the derivative exists at all points,
the only critical points will be where A'(x)=0. The x's satisfying
this are just +\-1/sqrt(3). We can throw out -1/sqrt(3), because this
number is not in our domain for this problem. If x=1/sqrt(3),
A(1/sqrt(3))=1/sqrt(3)(1-(1/sqrt(3))2)=2/(3sqrt(3)), a
positive value, so this is the maximum area.
I then remarked that there were theoretical ways to insure we have a
local max (or a local miniumum). Here are some of them:
| How to tell if you have a local maximum or minimum |
|---|
The First Derivative Test
MAX VERSION
If a<x0<b, and x0 is the only critical
point of f in the interval, and if f'(x) is positive to the left of
x0 and negative to the right of x0, then
x0 is a local maximum of f.
Reason f is increasing to the left and decreasing to the right
of x0.
MIN VERSION
If a<x0<b, and x0 is the only critical
point of f in the interval, and if f'(x) is negative to the left of
x0 and positive to the right of x0, then
x0 is a local minimum of f.
Reason f is decreasing to the left and increasing to the right
of x0.
|
The Second Derivative Test
MAX VERSION Suppose that f'(x0)=0. If also f''(x0)<0,
then x0 is a local maximum of f.
Reason f is concave down at x0, so x0
must be the top of a little hill.
MIN VERSION Suppose that f'(x0)=0. If also f''(x0)>0,
then x0 is a local minimum of f.
Reason f is concave down at x0, so x0
must be the bottom of a little valley.
|
Why didn't we use any of these results here?
We don't need to use either of these in connection with this problem,
because we can directly compute and compare f's values. In fact, we
may rarely need these results. The Second Derivative Test may seem
initially appealing, but I can tell you from personal experience that
computing and then evaluating the second derivative of a complicated
function is rarely appealing. Also, the Second Derivative Test may
unfortunately not give you any information. For example, the function
x5 has a critical point at 0 but its second derivative is
0, so the second derivative test does not apply.
 Problem #2
Problem #2
We discussed the problem of finding the shortest (or longest!)
line segment touching the positive x and y axes and the point (3,2).
That was a disaster, truly one of the finest efforts of NEHPETS. This is a serious problem, and
it is not clear how well it was presented.
We discussed for a while how to proceed. The sketch is one I drew
after the most important decision was made, which is what should the
controlling variable be? (More technically, how should the situation
be parameterized?) In this case, there are certainly several
choices. One choice could be the angle made by the line segment with
the positive x-axis. Another choice, which we adapted, is to describe
the whole situation in terms of x, the first coordinate of the point
on the x-axis and the line segment. I called the total length,
L(x). It naturally is a sum of two "subsegments". The subsegment from
(x,0) to (3,2) has length sqrt((x-3)2+4). The subsegment
from (3,2) to (0,y) has length sqrt(9+(y-2)2) but we need
to describe this length in terms of y. There are some similar
triangles, so that (x-3)/2=3/(y-2), so that y=3/(x-3)+2, and the
length of the second subsegment in terms of x is
sqrt(9+9/(x-3)2). Therefore we have the interesting formula
L(x)= sqrt((x-3)2+4)+sqrt(9+9/(x-3)2). More
interesting is that the domain of L(x) needs some thought. The
picture eventually tells us that the domain is x>3. Now our purely
mathematical problem has become:
Find the minimum of L(x)=
sqrt((x-3)2+4)+sqrt(9+9/(x-3)2) on the domain
3<x<infinity.
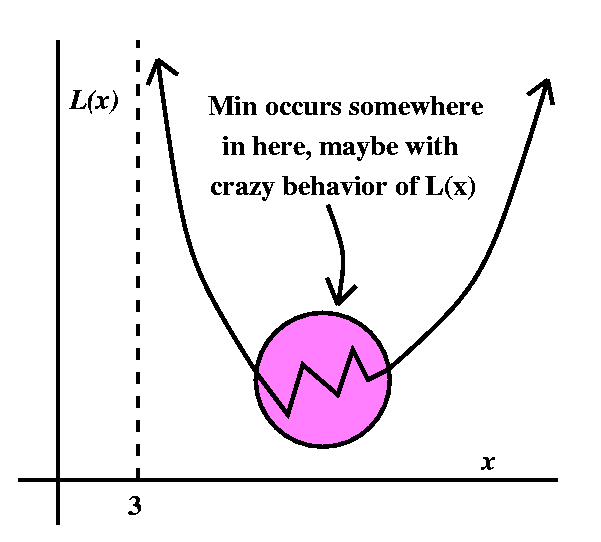 This is different from the first problem. That was more
straightforward: a function to be maximized on a closed interval. Here
we need to worry about various things. For example, if we changed the
word "minimum" in this problem to "maximum" then we would have an
optimization problem with no solution!!! We'll see that
L(x) has no upper bound at all. For example, if x-->infinity, then the
length of the first subsegment, sqrt((x-3)2+4), gets very
large. The
other subsegment can't cancel this growth, since both of them are
postive. Therefore L(x) has no maximum in this domain. What happens at
x-->3+, that is, x is getting close to the other edge of
the domain? Now length of the second subsegment,
sqrt(9+9/(x-3)2), gets large (because (x-3)2 is
in the bottom of the fraction). So I now see that L(x) has some sort
of behavior looking like what is shown here (a not-so-accurate
sketch). Of course, we could use Maple or some other
computational tool to make a better sketch, but:
This is different from the first problem. That was more
straightforward: a function to be maximized on a closed interval. Here
we need to worry about various things. For example, if we changed the
word "minimum" in this problem to "maximum" then we would have an
optimization problem with no solution!!! We'll see that
L(x) has no upper bound at all. For example, if x-->infinity, then the
length of the first subsegment, sqrt((x-3)2+4), gets very
large. The
other subsegment can't cancel this growth, since both of them are
postive. Therefore L(x) has no maximum in this domain. What happens at
x-->3+, that is, x is getting close to the other edge of
the domain? Now length of the second subsegment,
sqrt(9+9/(x-3)2), gets large (because (x-3)2 is
in the bottom of the fraction). So I now see that L(x) has some sort
of behavior looking like what is shown here (a not-so-accurate
sketch). Of course, we could use Maple or some other
computational tool to make a better sketch, but:
- There will be times in your life that computational resources
will not be available: for example, our final exam (!) or when you are
stranded on a desert island.
- More likely, there will be times in your life when the available
computational resources are not adequate or are expensive or ... many
things: and this has happened to me.
In any case, it is useful and important to be able to do as much as
possible by "pure thought".
What about L'(x)? We computed, and got something like this:
L'(x)=(x-3)/sqrt((x-3)2+4)-9(x-3)-3/sqrt(9+9/(x-3)2).
Some considerable thought shows that as x-->infinity, L'(x)-->1 and as
x-->3+, L'(x)-->-infinity. Therefore by the Intermidiate
Value Theorem, L'(x) must have at least one x0 for which
L(x0)=0. That x0 (I think there is only one!)
will give the shortest length. (Maple reports that there is
only one number in L's domain with L'(x)=0, and that number is
[approximately] 4.597222619.)
Here is a further embarrassing comment on technology (or at least my
use of such!): I used Maple as I described to find the
critical number. But I worked fast, or tried to!
Maple has a command called fsolve which tried to
find approximate roots of functions. So I typed fsolve(DL);
(I had already told the program to cal the derivative of L, DL). The
program returned a number near 1.4022 -- what! How could there be a minimum
length inside the box? Well, I don't think there can be, but
there sure can be an x in [0,1] where L'(x)=0. That's a different
question. I had not thought about this. In fact, the routine
fsolve allows initial guesses (think about Newton's method!)
and when I typed fsolve(DL,x=4) I got the approximate root
that I reported previously. Use technology carefully!
This problem is similar to numerous problems arising in physics, most
immediately in connection with optics ("Snell's Law"). Sometimes you
can't just "solve" in any simple way for the minimum or maximum, and
numerical methods must be used for an approximate solution.
General ideas (?)
I usually try to do the following:
- Draw a picture, as well as I can.
- Label the picture, paying special attention to label any
interesting variables.
- Write any equations connecting the variables.
- Try to decide what should be the "controlling" (parameterizing)
variable, and writing things in terms of that variable.
- Changing the situation to a "simple" optimization problem in one
variable.
- Look at what you've got: does it make sense?
- Solve the optimization problem (are you sure that you have
an extreme value, and the correct kind of extreme value?).
- Does your "solution" make sense in terms of your model?
I admit that I very rarely write all the details of this process, but
I honestly report that in almost all cases this is what I do. Maybe
the description helps you.
Problem #47
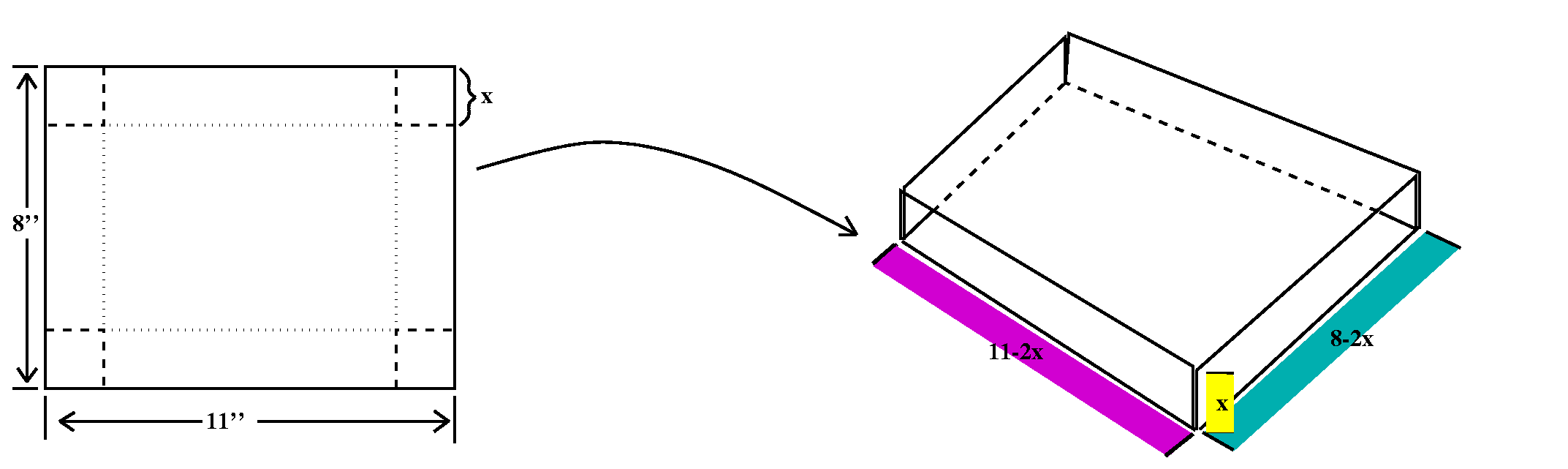
Then I took an 8 inch by 11 inch piece of paper, cut square corners
from it, folded up the edges, and asked what size corners should we
cut out to get the maximum volume. This is complex, and takes some
thought. I'll say that the corners are "x by x". Then the resulting
sides of the three dimensional "parallelepiped" (?) are 11-2x and 8-2x and
x. The volume is V(x)=(11-2x)(8-2x)x. What is the domain? The edges
should all be non-negative, so the domain is [0,4]. V(0)=0 and V(4)=0,
so that the max volume will be in between somewhere. The derivative
turns out to be 12x2-76x+88, and the roots are
(19+/-sqrt(97))/6. These are 4.80814 and 1.52519, approximately. The
root of interest is 1.52519: the other one is not in the domain. Since
at the endpoints the volume is 0, and this volume is positive, this
volume is the max volume.
Note From personal experience, I can assure you that this
problem is done correctly. I have actually cut out (paper dolls,
anyone?) squares from papers, folded, etc. There does seem to be a
unique largest one. I think the one identified here is that one.
The Question of
the day was suppose that two non-negative numbers add up to
10. What is the maximum that the product of the square of one number
multiplied by the other number could be?
Let's see: suppose x is in [0,10]. Define y by x+y=10. The problem
requestions the maximum value of x2y. But y=10-x, and
therefore we have a "math question":
Find the maximum of f(x)=x2(10-x) if x is in [0,10]. But
the max will occur at endpoints or critical points of f inside the
interval. f(0)=0 and f(10)=0 (that's is fairly clear!) so we
much search for critical points. Now
f'(x)=2x(10-x)-x2=20x-3x2=x(20-3x). This is 0
when x=0 (alreadly considered!) and when x=20/3. Indeed,
f(20/3)=[(20/3)]2[10-(20/3)] is a positive number, so that
this must be the max value.
Comments (please read these in anticipation of exam questions!)
1. I didn't use any decimal approximations, and I didn't simplify the
final answer. No one asked me to do any of these things, and I am lazy
(!~?). At least three students who did this problem in any optherwise
correct fashion made erros "simplifying" and approximating.
2. I didn't use the First or Second Derivative Tests to check that my
answer was a max (this could have been done -- both of them are
applicable here). But this problem asks me to maximize a continuous
function on a closed interval, [0,10], and I know if I just check the
function's values at the endpoints and the critical points, then I
will have "captured" the max value. If the problem involved finding
extreme values on, say, the collection of x's for which x>0, then I
would have to work more. For example, what is the minimum value of
f(x)=3x2+5/x when x>0? And why have you
found a minimum?
3. Some students answered the QotD with "x=20/3". As I wrote, this
answer is not responsive to what is asked: it gives the "x" but not
the "f(x)". Read and answer the question, please.
4. Some (at least three) students tried to answer this question by, in
effect, computing f(x) for each of the integers in [0,10] and giving
me the largest result. The question as asked did not restrict
consideration to integers, and therefore this approach is not
correct.
|
Wednesday,
November 5 |
Please do and hand in problems 4.3 #42 and 4.5 #48 on Thursday.
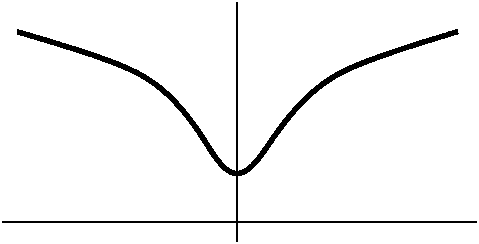 We sketched the graphs of a few more functions. We began with problem
#24 of section 4.5 which asked for a graph of y=ln(x4+27).
First I urged people to use a graphing calculator to get an
approximate idea of what the graph looks like. The result was
something like what's shown at the right. We can use derivatives to
confirm some of the aspects of the curve's shape.
We sketched the graphs of a few more functions. We began with problem
#24 of section 4.5 which asked for a graph of y=ln(x4+27).
First I urged people to use a graphing calculator to get an
approximate idea of what the graph looks like. The result was
something like what's shown at the right. We can use derivatives to
confirm some of the aspects of the curve's shape.
If f(x)=ln(x4+27), then
f'(x)=4x3/(x4+27). Since the bottom of this is
always positive, the sign of f'(x) is determined by the sign of the
top. f'(x) is positive when x is positive and negative when x is
negative. Therefore f(x) is increasing when x is positive and
decreasing when x is negative. 0 is the only critical point, and it is
a local (and, actually, an absolute) minimum. There aren't any
maxima.
If f'(x)=4x3/(x4+27), then
f''(x)=(12x2(x4+27)-4x3·4x3)/[x4+27]2.
Since the bottom is the square of something, it is always positive (it
can't be 0!). The sign of f''(x) is determined by the sign of the
top. We write
12x2(x4+27)-4x3·4x3=12x6+27x2-16x6=-4x6+12·27x2=-4x2(x4-81).
This is a textbook problem, so therefore the roots are easy: 0
and 3 and -3. The function is positive for x between -3 and 0 and
between 0 and 3, so that 0 is not a point of inflection. The
function must change concavity at a point of inflection. Since
the f''(x) is negative for x<-3 and is also negative for x>3,
the graph does change concavity at +/-3, and these are points of
inflection. We seem to have confirmed the appearance of the graph on
the calculator.
We then discussed the rates of growth of log, and found that this
function grows very slowly for large x. For example, the function we
just graphed: if x>0, the tangent line slopes up. But although
the function goes up and up and up (is never bounded!) it goes up
really slowly. When x=10100, we approximated the slope of
the tangent line, and it was really, really flat (about
4·10-100, a very very small positive number).
We also discussed the logical linage between the "pointwise"
information f'(x)=0 and the existence of a local max or min. I urged
students to think about certain graphs to convince themselves that
knowing some numbers are 0 is not enough information to
conclude that the point is a local extremum or an inflection point.
 |
| Here is y=x4. f'(0)=0 and f''(0)=0. Although
f''(0)=0, 0 is not an inflection point. You need to check the
concavity on both sides of 0 (and the function is concave up on both
sides of 0!).
| Here is y=x5. f'(0)=0 and f''(0)=0. Although
f'(0)=0, 0 is not a local extremum (max or min). You need to
check the behavior on both sides of 0 (and the function is increasing
on both sides of 0!).
| f(x)=x2/3. The behavior at the origin is
interesting. f'(0) does not exist, so that the function has a critical
number at 0. It turns out that 0 is a local min of f (and, actually,
an absolute min). But 0 is not an inflection point, although 0
is weird: the function is concave down on both sides of 0.
|
I think we looked at (e100x)/(1+e100x). On many
plotting devices, this looks very much like the function which is 0
for x<0 and 1 for x>0, which of course is not too continuous.
Such functions occur in considering physical problems whose time
scales are very different from "ours", for example, small-scale
chemical processes. The graph is increasing everywhere, and it has one
point of inflection. The can be seen by looking at the first and
second derivatives. The first derivative is
[100e100x(1+e100x)-(100e100x)(100e100x)]/[(1+e100x)2]
and the top simplifies just to100e100x which is always
positive. The bottom is always positive, so this function is always
increasing.
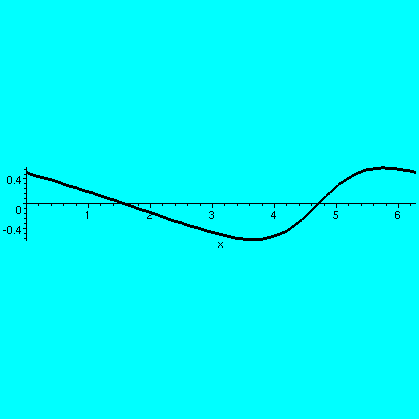 Then I tried to do problem #40 from section 4.5, to sketch a graph of
y=cos(x)/(2+sin(x)). I urged people to first graph the function in a
window of width 2Pi (the function has 2Pi periodicity). It looks like
what Maple gave me on the right. And we guessed that there
were two critical points, and (at least!) two inflection points. By
taking the first and second derivatives we verified these claims.
(More algebra and more simplification of the first and second
derivatives.) If f(x)= cos(x)/(2+sin(x)), then
f'(x)=[-sin(x)·(2+sin(x))-(cos(x)·cos(x))]/[(2+sin(x))2].
Again the bottom is always positive, and the top does simplify a bit:
-sin(x)·(2+sin(x))-(cos(x)·cos(x))=-2sin(x)-(sin(x))2-(cos(x))2=-2sin(x)-1.
(There are only a few trig identities that I keep in the top of my
brain, and (sin(x))2+(cos(x))2=1 is one of
them.) Now what can we say about the sign of -2sin(x)-1? I
class I actually sketched a graph of this function. To me this is the
simplest reasoning, because I tend to think in pictures. I learned
from the graph that -2sin(x)-1 is 0 at two places (where sin(x) is
-1/2) and is positive in a certain range and negative in a certain
range. After some thought, we found that the derivative is positive
between (7Pi)/6 and (11Pi)/6, and is 0 at both (7Pi)/6 and
(11Pi)/6. Elsewhere in the interval [0,2Pi] the derivative is
negative. Therefore our initial "feelings" about {in|de}crease and
local extrema are correct. Since
f'(x)=[-2sin(x)-1]/[(2+sin(x))2], we can compute the second
derivative:
f''(x)=[(-2cos(x)·(2+sin(x))2)-2(2+sin(x))(cos(x)))/[(2+sin(x))4].
This can be simplified by canceling just one power of 2+sin(x)
everywhere. Then
f''(x)=[(-2cos(x)·(2+sin(x)))-2(cos(x)))/[(2+sin(x))3].
The top is -2cos(x)(1+sin(x)), and the top is 0 at Pi/2 and 3Pi/2, and
further analysis here will confirm completely our initial "suspicions" about
inflection points and concavity. Please think about this:
Then I tried to do problem #40 from section 4.5, to sketch a graph of
y=cos(x)/(2+sin(x)). I urged people to first graph the function in a
window of width 2Pi (the function has 2Pi periodicity). It looks like
what Maple gave me on the right. And we guessed that there
were two critical points, and (at least!) two inflection points. By
taking the first and second derivatives we verified these claims.
(More algebra and more simplification of the first and second
derivatives.) If f(x)= cos(x)/(2+sin(x)), then
f'(x)=[-sin(x)·(2+sin(x))-(cos(x)·cos(x))]/[(2+sin(x))2].
Again the bottom is always positive, and the top does simplify a bit:
-sin(x)·(2+sin(x))-(cos(x)·cos(x))=-2sin(x)-(sin(x))2-(cos(x))2=-2sin(x)-1.
(There are only a few trig identities that I keep in the top of my
brain, and (sin(x))2+(cos(x))2=1 is one of
them.) Now what can we say about the sign of -2sin(x)-1? I
class I actually sketched a graph of this function. To me this is the
simplest reasoning, because I tend to think in pictures. I learned
from the graph that -2sin(x)-1 is 0 at two places (where sin(x) is
-1/2) and is positive in a certain range and negative in a certain
range. After some thought, we found that the derivative is positive
between (7Pi)/6 and (11Pi)/6, and is 0 at both (7Pi)/6 and
(11Pi)/6. Elsewhere in the interval [0,2Pi] the derivative is
negative. Therefore our initial "feelings" about {in|de}crease and
local extrema are correct. Since
f'(x)=[-2sin(x)-1]/[(2+sin(x))2], we can compute the second
derivative:
f''(x)=[(-2cos(x)·(2+sin(x))2)-2(2+sin(x))(cos(x)))/[(2+sin(x))4].
This can be simplified by canceling just one power of 2+sin(x)
everywhere. Then
f''(x)=[(-2cos(x)·(2+sin(x)))-2(cos(x)))/[(2+sin(x))3].
The top is -2cos(x)(1+sin(x)), and the top is 0 at Pi/2 and 3Pi/2, and
further analysis here will confirm completely our initial "suspicions" about
inflection points and concavity. Please think about this:
We can use a
graphing device to suggest what the detailed features of a graph are,
and we can use the logic of calculus to confirm these features. We
can constantly confirm and check for consistency.
This is very
useful.
The Question of
the day was the following:
Farmer Brown has a long straight stone wall. He also has 100 meters of
fence which he will use to make a rectangular pen, one side of which
will be the stone wall. What dimensions should he use to get the
maximum area?
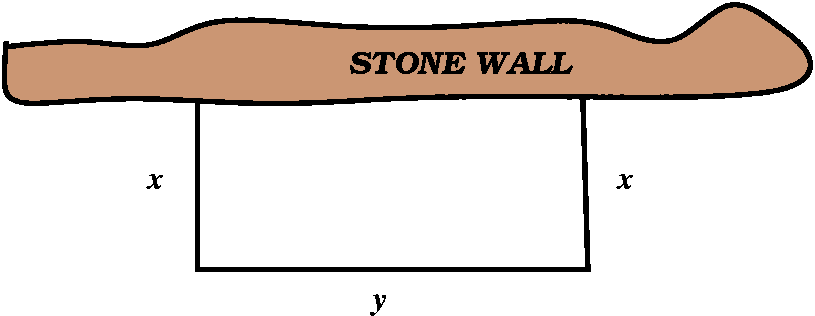
Here one dimension is x and the other is y. A relationship between
the variables x and y (a constraint) is given by the total
length: 2x+y=100. We need to maximize the area, A=xy. Then A=x(100-2x)
with 0<=x<=100. At the two ends, A is 0, so the max must occur
at an interior critical point, and since A is a differentiable
function of x, this happens when A'=0. But A'=(100-2x)-2x. This is 0
when x=25, so that y=100-2(25)=50, and then A=50·25=1250.
We will do more problems of this type next week.
|
Monday,
November 3 |
| ... summer's lease hath all too short a date |
|---|
|
For those who came to class: thank you. Today seemed like an extra
summer day, a wonderful gift, and Mr. Shakespeare (quoted here from
Sonnet #19) was correct.
We will have months of chill and gray skies. Now to
work. |
Today's theme is drawing pictures of functions, especially with the
help of the first and second derivatives. We know from the MVT that
|
If f'(x)>0 for all x in an interval, then f(x) is increasing in
that interval. |
|
If f'(x)<0 for all x in an interval, then f(x) is decreasing in
that interval. |
It is generally much harder to check directly if a function is
increasing than to check if its derivative is positive. That's because
a serious direct check of the increasing nature of a function
would mean checking every pair of numbers and function values on an
interval, or verifying the intended comparison in some other
way. Looking at the derivative and somehow observing its sign is
frequently much easier.
We also will get information from the second derivative.
|
If f''(x)>0 for all x in an interval, then f(x) is concave up in
that interval. |
|
If f''(x)<0 for all x in an interval, then f(x) is concave down in
that interval. |
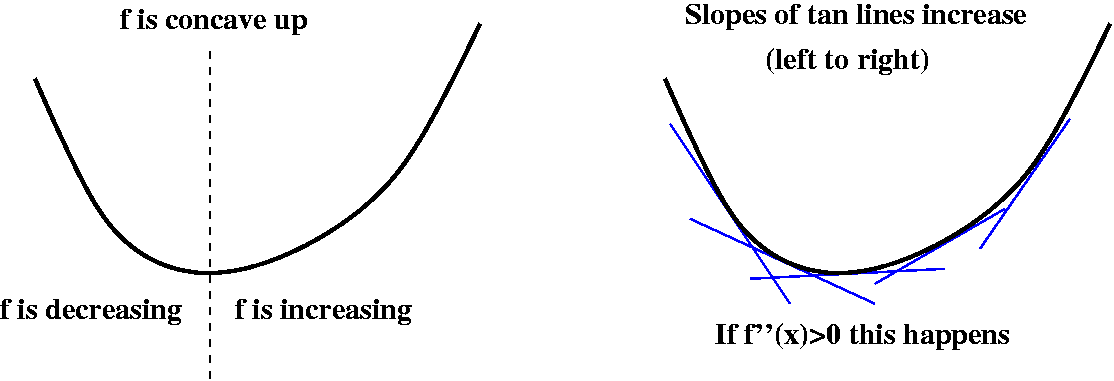
But I should give an illustration of what concavity is.
A curve is concave up when it "holds water" -- at least so I
was told years ago when I first learned calculus. The purpose of the
first picture is to convince you that a function could be concave up
and increasing, and could be concave up and decreasing.
The second picture illustrates a way of diagnosing where a curve is
concave up. If the slopes of the tangent lines (moving from left to
right) increase, then the curve will be concave up. But the slopes of
the tangent lines are given by the derivative of the function, and
that's f'(x). We can insure that f'(x) itself is increasing by
requiring that f''(x) be positive. And the second picture attempts to
illustrate this logical connection.
|
 |
|
These pictures illustrate the "complementary" case: concave
down. This, I was told years ago, "loses water" (I was never able to
understand that!). Again, there is no logical implication between
concave {up|down} and {in|de}creasing: one of any of them does not
imply any of the
others.
|
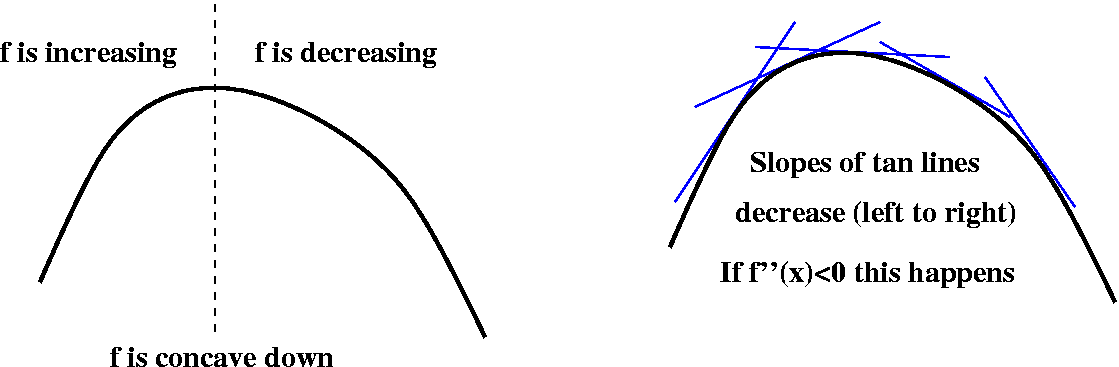 |
Remember that secant lines connect two points on the graph. Sometimes
the following is useful to know:
- For concave up graphs, the tangent lines are below the graph and the secant
line segments are above the graph.
- For concave down graphs, the tangent lines are above the graph and the secant
line segments are below the graph.
|
Concavity and
{in|de}creasing behavior are not logically related.
You must analyze them separately.
|
 |
 |
| A dromedary | A Bactrian camel |
|---|
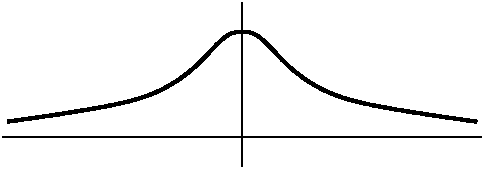
We first considered e-x2 and its graph.
That is, I asked students to have and
use a graphing calculator, and asked that this function be graphed. Mr. Morris remarked that it is a camel, but a
dromedary, not a Bactrian camel.
 Begin sincere sermon
Begin sincere sermon
This is supposed to be what the graph
of e-x2 looks like. Can we confirm and make more
precise some features of this graph by examining the derivatives?
Please note the precise nature of the preceding sentence. I will not
ignore the current date and technology (that is, the existence of
graphing calculators and such programs as Maple). But you
should know that features of the graphs can be confirmed and made more
precise using the intellectual tools of calculus, and that sometimes
(as a later example will show!) the results of "technology" can be
difficult to interpret.
End sincere sermon
If f(x)=e-x2 then
f'(x)=(e-x2)(-2x). The exponential function is
very nice. It is never 0 and always positive. Therefore the
only x for which f(x)=0 is when -2x=0. So x=0 is the only critical
number. Now reasoning using the Intermediate Value Theorem says that f
(which is certainly continuous!) can have only one sign for x<0 and
one sign for x>0 (or else f(x) would have to have to be 0
again). We can check signs at, say. x=1 and x=-1. f is increasing in
(-infinity,0) and f is decreasing in (0,infinity). Naturally 0
represents a local (and indeed, absolute!) maximum.
What information can we get from the second derivative? If we use the
product and the chain rule correctly, then
f''(x)=(e-x2)(4x2-2). Logic similar
to the preceding asserts that this is 0 exactly when the
non-exponential factor is 0. But 4x2-2=0 when
x=+/-sqrt(2). Again, we can check signs in between the 0's of f'', and
f will be concave up for x<-1/sqrt(2) and for x>1/sqrt(2). For x
between -1/sqrt(2) and +1/sqrt(2), the graph will be concave down. The
points where x=+/-1/sqrt(2) are where the concavity of f changes:
these are called inflection points. These particular inflection
points are related to the standard deviation, which represents
dispersal from an average when this function is used in statistics.
Some examples from the textbook
I then did three more textbook problems: 4.3: #26 and #30, and 4.5
#3. I'll try to write up solutions, but I am a bit busy. The first
two problems are quite "qualitative" and different from manipulating
formulas.
And another example from the textbook
The third, from section
4.5, is more routine (a cubic polynomial whose first derivative is a
quadratic which "accidentally" factors!). Here
y=2-15x+9x2-x3.
How I prepared the high-tech class example
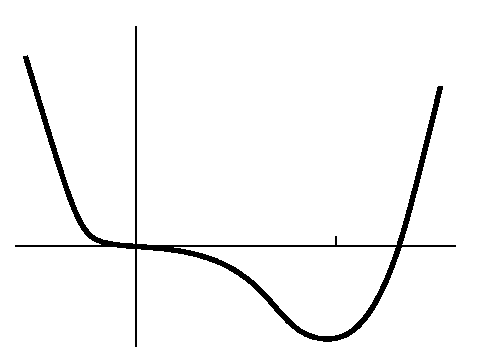 Then I discussed the following idea: graphing a polynomial. Of course
I had chose a rather non-random (!?) polynomial. I really started with
the polynomial x20(x-1)31, a polynomial of
degree 51, having only two roots, 0 and 1. I used Maple to
write an "expanded" form of this polynomial and called it H(x). Then I
had Maple antidifferentiate it (again, for a
polynomial, this is totally "mechanical") and got Q(x). I presented
this polynomial
to the class. I asked what its graph looked like. Notice that near,
say, 1, there will be things that are almost 0 computationally:
very difficult to keep track of using what is called "floating
point". In expanded form, Maple, even with 20 digit
precision which I requested, can't keep close enough track to
actually tell what the graph looks like. We got a mess from the
qualitative (and even quantitative!) point of view. The graph is
actually quite simple. If the derivative is
x20(x-1)31, there is no sign change passing 0
(this turns out to be a point of inflection of f) and there is a sign
change (in the derivative) passing x=1, so this is a local
extremum for f. In fact, checking signs, for x<1, f'(x)<0 (except for
x=0) and for x>0, f'(x)>0. Therefore f is decreasing to the left
of 1 (but has a horizontal tangent at x=0) and f is increasing to the
right of 1: f has a local minimum at x=1. It actually isn't even that complicated: to the right is a
glimpse of how the graph looks qualitatively. Follow this link to see the material I presented
in class. You can even find the other inflection point of the
polynomial Q(x) by taking the derivative of
x20(x-1)31 and finding the root between 0
and 1.
Then I discussed the following idea: graphing a polynomial. Of course
I had chose a rather non-random (!?) polynomial. I really started with
the polynomial x20(x-1)31, a polynomial of
degree 51, having only two roots, 0 and 1. I used Maple to
write an "expanded" form of this polynomial and called it H(x). Then I
had Maple antidifferentiate it (again, for a
polynomial, this is totally "mechanical") and got Q(x). I presented
this polynomial
to the class. I asked what its graph looked like. Notice that near,
say, 1, there will be things that are almost 0 computationally:
very difficult to keep track of using what is called "floating
point". In expanded form, Maple, even with 20 digit
precision which I requested, can't keep close enough track to
actually tell what the graph looks like. We got a mess from the
qualitative (and even quantitative!) point of view. The graph is
actually quite simple. If the derivative is
x20(x-1)31, there is no sign change passing 0
(this turns out to be a point of inflection of f) and there is a sign
change (in the derivative) passing x=1, so this is a local
extremum for f. In fact, checking signs, for x<1, f'(x)<0 (except for
x=0) and for x>0, f'(x)>0. Therefore f is decreasing to the left
of 1 (but has a horizontal tangent at x=0) and f is increasing to the
right of 1: f has a local minimum at x=1. It actually isn't even that complicated: to the right is a
glimpse of how the graph looks qualitatively. Follow this link to see the material I presented
in class. You can even find the other inflection point of the
polynomial Q(x) by taking the derivative of
x20(x-1)31 and finding the root between 0
and 1.
The purpose of this example was to warn you that even very
sophisticated technology can be difficult to apply succesfully.
Be careful!
The Question of
the day was: suppose f(x)=xex.
- Compute f'(x). Where is f increasing and decreasing? Does f
have any local extreme points? If it does, where are they?
Answer
f'(x)=f(x)=ex+f(x)=xex=(x+1)ex. Since
the exponential function is never 0, this is only 0 when x=-1, the
only critical number of f. Testing the sign of f' is easy, since the
exponential factor is always positive. To the left of -1, the function
is decreasing and to the right, the function is increasing. Since
f(-1)=-1/e, I know that (-1,-1/e) is a local minimum, and, indeed, in
this case an absolute minimum.
- Compute f''(x). Where is f concave up and concave down? Does f
have any inflection points? If it does, where are they?
Answer
Since f'(x)=(x+1)ex, we see that
f''(x)=ex+(x+1)ex=(x+2)ex. The only
time this is 0 is when x=-2. To the left of -2 (for x<-2) f'' is
negative (check the sign), so f is concave down. To the right of -2
(for x>-2) f'' is positive (check the sign), so f is concave up.
When x=-2, concavity changes. Since f(-2)=-2/e2, I know
that (-2,-2/e2) is the only inflection point of f.
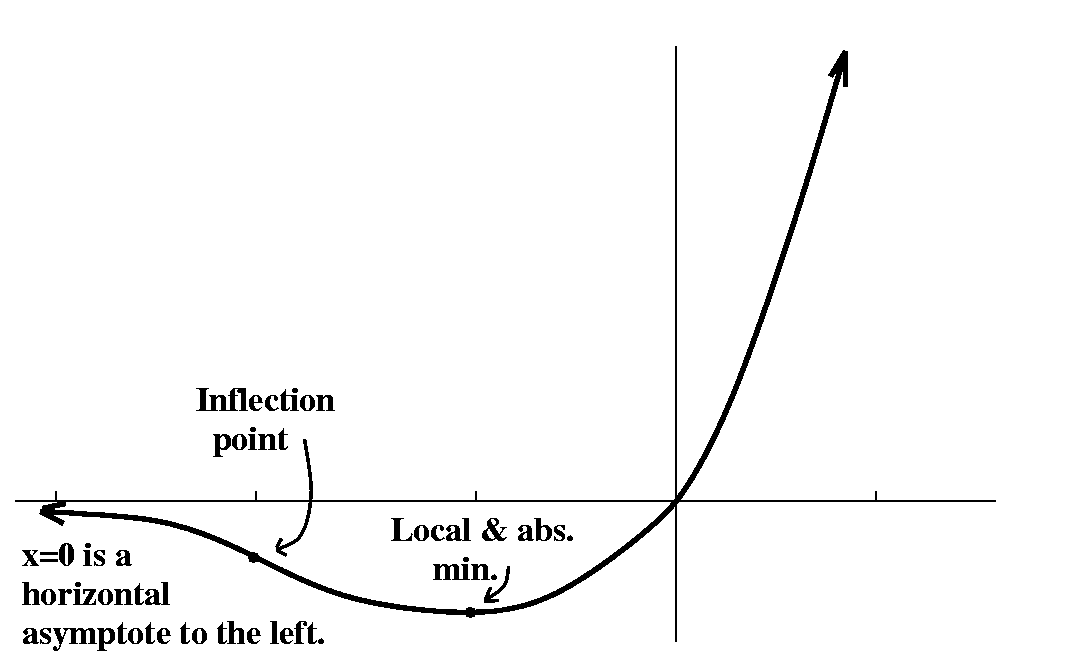
- Draw a graph of f. (I suggested using the graphing calculator, and
then confirming the picture with what you deduced with f' and f'').
Answer
The only part of the picture I haven't completely verified is the
claim that the x-axis is a left asymptote for the function. But
limx-->-infinityxex=limx-->-infinityx/e-x,
and this second form is infinity/infinity (look: x-->-infinity,
ao the exponential is growing also). But use L'H on this, to get
limx-->-infinity1/-e-x=0, verifying the
asymptotic claim.
Please do and hand in problems 4.3 #40 and 4.5 #48 on Thursday.
|
Wednesday,
October 29 |
Please hand in problems 4.1: #8 and 4.2 #18 on
Thursday.
Warning! Today we will do some
very tricky stuff: I repeat that this is the core of the
course. Please read the textbook and do the homework problems!
The root of an equation
I asked people if P(x)=1-6x+3x2+4x3 had a root
in the interval [0,1]. If we try to apply simple Intermediate Value
Theorem logic we will not get enough information, because P(0)=1 and
P(1)=2, so the signs of P's values at the endpoints agree, and we
can't right now conclude that P must have a root. Now we will use
analysis of a more interesting and powerfulkind.
P(x) is the derivative of
Q(x)=x-3x2+x3+x4. Why would anyone
think of looking at this Q, an "antiderivative"? Well, there is
certainly no immediate reason, but maybe the pieces of P like
4x3 and 3x2 might suggest it. Now analyze Q on
[0,1]. I compute easily that Q(0)=0, and that Q(1)=0 (this is a
very carefully arranged example!). What could Q look like? I
distinguished three cases.
- Q could possibly (I highly doubt it!) be 0 at every
point inside the interval [0,1]. In that case there are lots of points
where Q'(x)=0 inside [0,1]. (This case is included to make sure that
the logical analysis is complete.)
- Q could possibly have some positive values inside [0,1]. In that case,
Q will have a positive maximum in [0,1] and the maximum will be
an "interior" maximum, that is, somewhere in between 0 and 1. We
discussed this during the last lecture. At such
a point, since Q is differentiable, Q'(x) will be 0.
- Q could possibly have some negative values inside [0,1]. In that case,
Q will have a negative minimum in [0,1] and the miniimum will be
an "interior" minimum, that is, somewhere in between 0 and 1. We
discussed this during the last lecture. At such
a point, since Q is differentiable, Q'(x) will be 0.
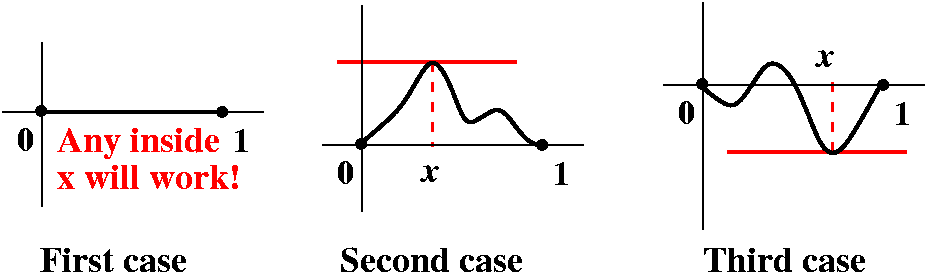
In all three cases, there is at least one x between 0 and 1 which has
Q'(x)=0. Since Q'(x) is the P(x) we started with, that means P(x) must
have at least one root inside [0,1], as I had claimed from the
beginning. You could graph P with some mysterious device, but now I am
sure using "pure thought" that P has such a root (actually it
has two roots inside that interval).
The root of some equations
If P(x)=a+bx+cx2+dx3 and if I know that
a and b and c and d are real numbers (not further specified!) which
satisfy the equation a+(b/2)+(c/3)+(d/4)=0, then P(x)=0 must
have at least one root somewhere inside the interval [0,1]. Why is
this? (And, of course, the numbers I used in the previous example were
selected to obey this constraint.) Well, look at
Q(x)=ax+(b/2)x2+(c/3)x3+(d/4)x4. This
non-randomly selected function has value 0 when x=0 (because all of
the terms have x's in them). When x=1, the condition
a+(b/2)+(c/3)+(d/4)=0 exactly shows that Q(1)=0. Well, then, the logic
displayed along with the pictures above guarantee that Q'(x), the
derivative, must be 0 somewhere inside the interval [0,1]. But since
Q'(x) is P(x), I have just shown the existence of the root I suggested
at the beginning of this paragraph. Notice that this is more subtle
reasoning than the Intermediate Value Theorem: I didn't look for a
sign disagreement of P(0) and P(1), but some other features of the
derivative of P(x).
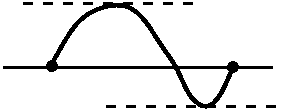 Rolle's Theorem
Rolle's Theorem
Suppose that f(x) is a differentiable function in the interval
[a,b]. Suppose also that f(a)=0 and f(b)=0. Then there must be at
least one x inside [a,b] (so a<x<b) with f'(x)=0.
The picture accompanying this statement is how many people remember
Rolle's Theorem. The points are at x=a and x=b and the curve is
supposed to be the
graph of y=f(x) and the dashed lines are two possible candidate lines
satisfying the conclusion of Rolle's Theorem: they are horizontal
tangents, so the slope, f'(x), is 0 there.
Rolle's Theorem tilted: the Mean Value Theorem
Suppose we rotate the Rolle's Theorem picture a bit. We would get
something like what is shown. So some version of a statement of this
situation could be this:
|
Take two points on the graph of a differentiable function, and join
these points by a line. There always will be at least one line tangent to the
graph in between these points which will be parallel to this line.
|
It turns out that this statement is true (a detailed discussion of how
to "rotate" to get a verification from Rolle's Theorem is in the text). This
statement is a version of the Mean Value Theorem which is one
of the two major results of calculus, and the MVT (as I will call it)
will contribute to everything we cover in the course from now on. For
example, it turns out the MVT can be used to estimate errors in such
processes as Newton's method, and, generally, estimation of errors in
most of the calculus algorithms I know, when they are really used with
numbers begins with the MVT.
A better statement of MVT
I will restate the MVT in a more algebraic fashion. For example, the
word "parallel" usually is implement by looking at the slopes of the
lines involved. If the two points on the graph of f are, say, (a,f(a))
and (b,f(b)), then the slope of the line connecting these points is
[f(b)-f(a)]/[b-a]. The slope of a line tangent to the graph when x=c
is f'(c). (My choice of letters is designed to agree with tradition
and with your text.) Here is an algebraic way to phrase the MVT:
|
| The Mean Value Theorem
Suppose f is a function differentiable on the interval
[a,b]. Then there is at least one point c inside this interval so that
f'(c)=[f(b)-f(a)]/[b-a]. |
Meeting Francine again
 We first met my pal Francine on September
17. Francine drives on the Garden State Parkway. Now suppose we
know the following. She leaves Cape May (Mile 0 on the GSP) at 7 Am in
the morning. At 9:30 AM the same day, she arrives at the other end of
the parkway (Mile 172, somewhere in or near Mahwah or Ho-Ho-Kus. There
is now enough evidence to convict her of speeding. Why is this? Let
s(t)=her position in miles along the GSP with Cape May as the origin,
and suppose that t is measured in hours starting at 7 AM. We then know
that s(0)=0 and s(2.5)=172. Take a=0 and b=2.5 in the MVT. Then we
know that there must be a c between 0 and 2.5 so that
s'(c)=(172-0)/(2.5-0)=68.8. The GSP has varying speed limits on
different portions of the road, but the current highest speed limit is
65. Since 68.8>65, Francine must have been speeding at some
time. Note that this conclusion is slightly unattractive from a
"practical" point of view, since it doesn't local or approximate c
very much ("Judge, at some time between 7 AM and 98:30 AM she
really, really, really was speeding ..."), but we have mathematically
verified a violation.
We first met my pal Francine on September
17. Francine drives on the Garden State Parkway. Now suppose we
know the following. She leaves Cape May (Mile 0 on the GSP) at 7 Am in
the morning. At 9:30 AM the same day, she arrives at the other end of
the parkway (Mile 172, somewhere in or near Mahwah or Ho-Ho-Kus. There
is now enough evidence to convict her of speeding. Why is this? Let
s(t)=her position in miles along the GSP with Cape May as the origin,
and suppose that t is measured in hours starting at 7 AM. We then know
that s(0)=0 and s(2.5)=172. Take a=0 and b=2.5 in the MVT. Then we
know that there must be a c between 0 and 2.5 so that
s'(c)=(172-0)/(2.5-0)=68.8. The GSP has varying speed limits on
different portions of the road, but the current highest speed limit is
65. Since 68.8>65, Francine must have been speeding at some
time. Note that this conclusion is slightly unattractive from a
"practical" point of view, since it doesn't local or approximate c
very much ("Judge, at some time between 7 AM and 98:30 AM she
really, really, really was speeding ..."), but we have mathematically
verified a violation.
Speed limits
I didn't make these remarks in class, but I should have. If Francine
were driving on a highway with a maximum and a minimum speed limit,
then the MVT actually gives information about future positions. In
this context the statements come close to being trivial, but let me
analyze them anyway. Suppose Francine is driving on a restricted
access highway, and at 2 in the afternoon, she is at, say, milepost
75. Also suppose the road has posted a minimum speed limit of 40 and a
maximum speed limit of 60. If Francine obeys the law, where could she
be at 5 in the afternoon? The MVT tells us that
[s(5 PM)-s(2 PM)]/[5-2]=s'(t). But s'(t) must be between 40
and 60. So [s(5 PM)-75]/3=something between 40 and 60. Then
clearly (well, maybe it is almost clear) that Francine's lowest
position at 5 PM is 195 (40·3+75) and Francine's highest
possible position is 255 (60·3+75). I guess this seems all
sensible, but it is proved, as far as I know, only by using the
MVT.
Guessing a function given its derivative: consequences of MVT
Suppose a function f(x) is defined in the interval 0<x<23, and
we know that f'(x)=4x6+(5/x4. What can you say
about f(x)? Well we thought about this, and after a while a student
guessed that f(x) could be
(4/7)x7-(5/3)(1/x3). I didn't want to know how
the student got this answer, but I did want to know how to check the
answer. Of course, it can be checked very easily by
differentiating. And it works. I then asked if there were another
answer. I was told (4/7)x7-(5/3)(1/x3)+1. How
about another? Well, look at
(4/7)x7-(5/3)(1/x3)+sqrt(38) or
(4/7)x7-(5/3)(1/x3)-.0003, etc. Are these all of
the answers? It turns out that all of the answers are
(4/7)x7-(5/3)(1/x3) plus some
constant. Historically this was not obvious. The simplest physical
situation this would refer to is that a velocity is given for a
particle moving on a line. The successive positions all differ by a
constant, and that constant is always determined by an initial
position. The background for believing that we always get one function
plus a constant in answer to these sorts of questions is the
following:
|
Fact 1, a consequece of the MVT
Suppose f is a function differentiable on an interval, and that
f'(x)=0 for all x in that interval. Then f(x) is constant in
the interval. |
This is true because if x1 and x2 are different
points in the interval,
f(x2)-f(x1)=f'(c)(x2-x1)
by MVT, and f'(c) has to be 0 so that
f(x1)=f(x2), so f always has the same values.
No if two functions have the same derivative, their difference
will have derivative 0: for example, if F(x)=x2 and
G(x)=x2 then (F-G)'(x)=0, so F-G is a constant. Therefore,
if we can somehow guess at one F(x) -- in this case, not too hard,
since I can (1/3)x3 -- then all F's and G's with
this derivative must be (1/3)x3+Constant. These are called
antiderivatives of x2.
If derivatives are positive in an interval, we also can learn
something. Suppose f'(x) is positive in an interval, and
x1<x2 are points in the interval. Then the
MVT says
f(x2)-f(x1)=f'(c)(x2-x1).
Since we are assuming f'(c)>0 and that
x2>x1, the right-hand side of the equation is
positive, so the left-hand side must be also. Therefore as we
move to the right on the number line, the f-values get bigger. Such a
function is called increasing.
|
Fact 2, a consequece of the MVT
Suppose f is a function differentiable on an interval, and that
f'(x)>0 for all x in that interval. Then f(x) is increasing in
the interval. |
There is a "dual" statement. If the derivative is negative, then the
function values go down as we travel from left to right.
|
Fact 3, a consequence of the MVT
Suppose f is a function differentiable on an interval, and that
f'(x)<0 for all x in that interval. Then f(x) is decreasing in
the interval. |
These two statements are useful because determining the signs of
functions can be substantially easier than telling that a function is
increasing. For example, if
f(x)=x15+6x3+17x+cos(5·sin(x)), then
f(200) is less than f(300). This is true because f'(x) is
15x14+18x2+17-sin(34·sin(x))·(5(cos(x))),
and the powers are even (so always non-negative, and sines and cosines
are between -1 and +1 and the 17 overpowers the
sin(34·sin(x))·(5(cos(x))) which must be between -5 and
+5: the derivative is always positive, so f(200)<f(300).
Sketching graphs and MVT
Here's the graph of a function:
|
The first challenge is: what does the graph of the derivative of this
function look like? Let's progress from left to right on the graph of
the function we were given. The function is decreasing until x=A. The slopes
of tangent lines in that region are negative, so the derivative
graph will be negative. At x=A, the tangent line has zero slope, and
after it, the tangent lines begin to have positive slope. They
continue to have
positive slope until x=B, and after that they have negative slope.
In this graph, the original function is in
green. The derivative of this function is in black.
| 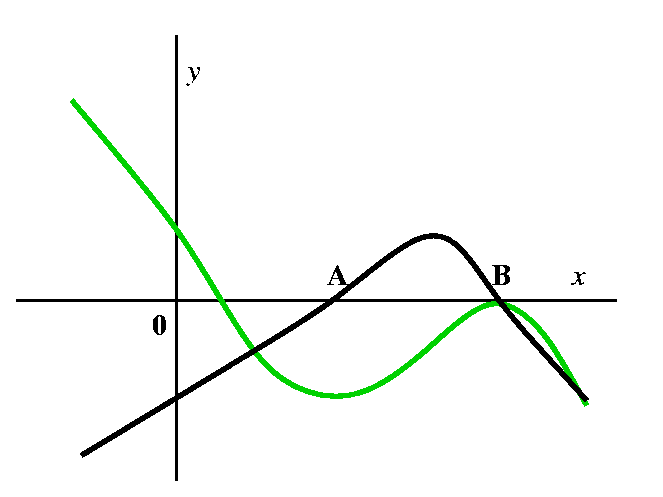 |
|
Now let's try to sketch a graph of a function whose derivative graph
is the graph we were given. This is harder. First, Fact 1 of the MVT
implies that there are many such graphs. As soon as you have one (such
as (1/3)x3 would be for x2) you would actually
have many (such as (1/3)x3+5 and
(1/3)x3-2). Physically we are given velocity varying over
time, and to get position we need to specify an original
position. Here I will ask that the graph of the antiderivative (which
is what we are asking) go through the blue dot. Then we use facts 2
and 3 which are consequences of MVT: in an interval where the
derivative is positive (such as the interval from the left until x=C)
the antiderivative function must increase. Since the original function
is 0 at x=C the function we are now sketching must have a horizontal
tangent line at x=C. Now progress to the right. The original function
is negative, so by Fact 2 from x=C to x=B the new function must
decrease. An interesting phenomenon occurs around x=B in the new
function. It must have a horizontal tangent because the original
function is 0 there, but to both sides the original function is
negative, so the new function must decrease on both sides of x=B. This
sort of "step" (it looks locally like -x3) is an inflection
point. In fact, there are two inflection points. The other one is at
x=A when the new function changes from concave down to concave up.
| 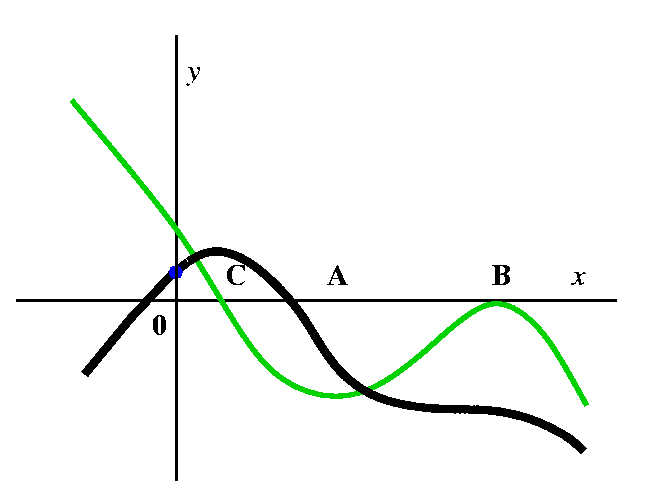 |
Here is all of the information combined. Things are rather
complicated. There are three graphs involved: a function and its first
and second derivatives. I have tried coloring parts of the background,
and describing features.
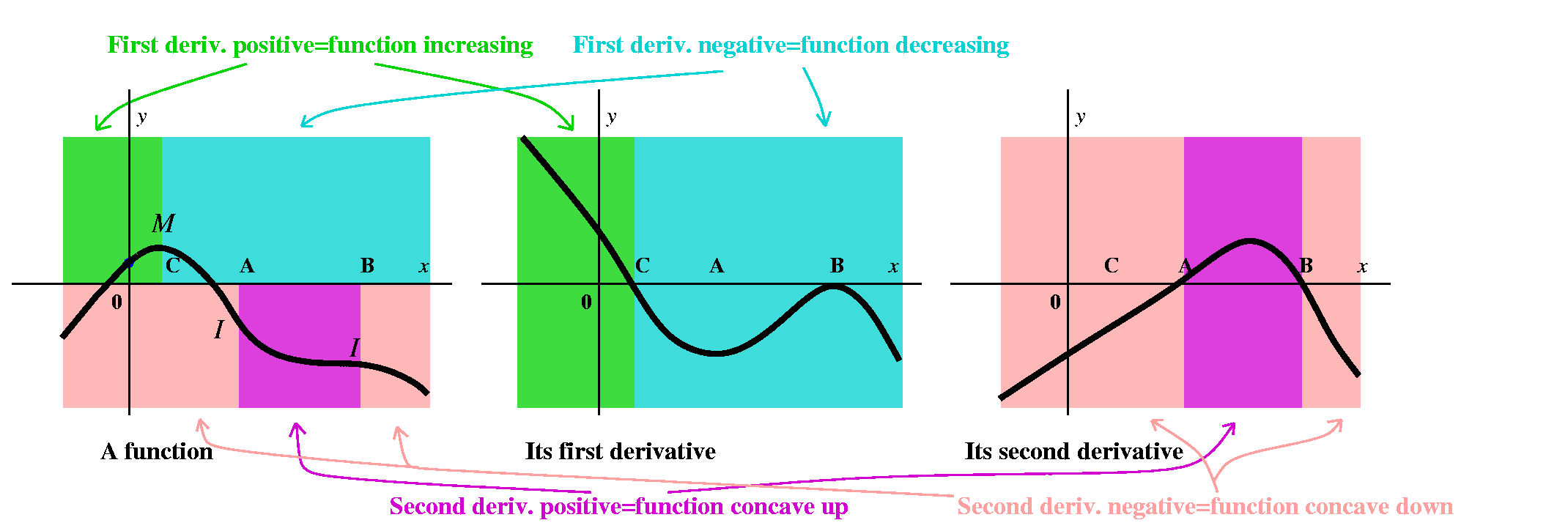
On the graph of the function, the letter M indicates a local
maximum. The I's indicate inflection points, where the graph
changes concavity. The function increases when its first derivative is
positive, and it decreases when that first derivative is negative. The
information about the second derivative's sign shows up in the
concavity of the original function. The original function is concave
up when its first derivative is increasing, so that the tangent lines
lie below the graph. When the first derivative is decreasing, the
tangent lines lie above the graph of the function, and that function
is then concave down.
What is likely to be confusing is that in this exercise we
began with a graph of the first derivative, then sketched the second
derivative, and then sketched a candidate for the original function. I
will go into further details on this next time. Please read the text!
The Question of
the day was: if you know that f(2)=3 and f'(x)=x2-2x,
what is f(5)? Well, we can guess one f(x):
(1/3)x3-x2. It is easy to check by
differentiation that this is a correct guess. Then by logic similar to
what we did earlier, any f with the specified derivative must
be (1/3)x3-x2+a constant. What constant
should it be? Since f(2) is supposed to be 3, we know that
(1/3)23-22+a constant=3, so that the
constant must be 3-(1/3)23+22. Then
f(x) is exactly
(1/3)x3-x2+3-(1/3)23+22 so
that f(5) is
(1/3)53-52+3-(1/3)23+22.
This is the way I would leave the answer, but if you insist on
"simplifying", it becomes
(125/3)-25+3-(8/3)+4=(117/3)-26=39-18=21. (Wow, to get an integer from
such a random problem!)
This is what is called an initial value problem. A simple
physical interpretation is that I give the velocity and an initial
position at time 2, and then ask for the position at a later time.
|
Monday,
October 27 |
The math computer systems were not working for most of the afternoon,
so I am late getting this diary entry written. I thank those students,
some looking nearly drowned, who came to class today. Neither the
weather nor an impending physics test stopped them. I also wish
everyone taking the test tonight good luck.
Please do as many of the homework problems in chapter 4 as you
can. This material is the heart of the course.
The major themes in this chapter are
| Max-min problems | Curve sketching using
derivative information
|
|---|
Mathematicians have made a living for almost three centuries using
what we're going to discuss!
I began by going over a few more L'Hopital's Rule examples.
- What is the
limx-->infinity[ln(x)]/[x1/300]?
Analysis and answer
Before using L'H we must check that some appropriate set of
hypotheses are satisfied. Here certainly ln(x) gets larger when x gets
large "enough" and so does x1/300. That is, the limit of
the top as x-->infinity is infinity, and the bottom has the same
limiting behavior. It isn't hard, by the way, to see that both the top
and the bottom get large. Try a big number (?), like
10100. Then ln(10100)=100ln(10) is approximately
230, and (10100)1/300=101/3 is about
2.15. Well they do get big, but they get big "slowly" and this limit
is essentially asking which of the two, the top or the bottom, gets
bigger slower.
In any case, this is an indeteriminate form of the type,
"infinity/infinity" and we can try to use L'H.
limx-->infinity[ln(x)]/[x1/300]=(using L'H)=limx-->infinity[1/x]/[(1/300)x(1/300)-1].
Let's get rid of the compound fraction in the last expression. We then
need to evaluate limx->300x-1+1-1/300. I think I
did the exponents correctly, and the result is the limit as x-->infinity
of a constant (300) multiplying a negative (-1/300) power of x. The
result is certainly 0.
Therefore we conclude that the limit is 0 and x1/300 gets
bigger faster than ln(x)! But what about the numbers? We just didn't
take numbers that are big enough to see what's happening.
Try (10100)100. A little bit of juggling with
exponents will show that
ln((10100)100)=10,000ln(10) which is about
23,000. And ((10100)100)1/300 is
(10100)1/3 which is about 1033. And
it is true that 1033 is much much bigger that
23,000. Logs
grow more slowly than any positive power of x. (See problem #67 in
section 4.4.)
- I looked again at
limx-->infinity[x300]/[ex].
Analysis and answer
We had done this last time, but I wanted to repeat it, to emphasize
the point. You can check that this is again eligible for L'H (again,
it is infinity/infinity) and then 300 uses of L'H get us the
limx-->infinity[300!]/{ex. The top is a HUGE
constant, but it is a constant, and the bottom gets ever larger. The
result is 0.
Exponential growth is faster than any polynomial
growth. (See problem #66 in section 4.4.)
The results comparing log and polynomial and exponential growth are
very important in many applications, and should essentially be
in your head when you think about growth and decay.
- I think this is problem #9 of section 4.4:
limt-->0(5t-3t)/t.
Analysis and answer
If I "plug in" t=0, the indeterminate form 0/0 appears, and this
makes the problem eligible for L'H. I need to know the derivative of
at. I can memorize it
(d/dt(at)=atln(a) or if clever, I can deduce it
(look: at=(eln(a))t since exponential
and logarithm are inverse functions, and then
(eln(a))t=e[ln(a)]t, and realize that
ln(a) is just a constant, so that
d/dt{e[ln(a)]t}=e[ln(a)]t·ln(a)=at·ln(a)
by the chain rule).) So we compute:
limt-->0(5t-3t)/t=(using L'H)=limt-->0(5tln(5)-3tln(3))/1,
and we can evaluate this limit by just plugging in: the answer is
ln(5)-ln(3).
- While the other three examples we fairly realisitic, here is a
problem I would only expect to see in a calculus class or a text or an
exam: what is limx-->0xsin x?
Analysis and answer
This is a weird problem. Look at it: x-->0 and sin x-->0
also. It isn't clear to me what happens to the result of
exponentiating one with the other. I would like to use L'H, and I need
to
somehow algebraically change this function into something that looks
like a candidate for L'H: that is, something like TOP/BOTTOM which, as
x-->0, will look like, say, 0/0 or infinity/infinity. There are really
several ways to do this problem. I'll show one strategy here.
If y=xsin x, then ln(y)=ln(xsin x), and then
ln(y)=(sin x)ln(x). Now as x-->0, certainly ln(x)-->-infinity ("look"
at the graph of ln(x) you should have installed in your head!) and
certainly sin x-->0. Can I somehow change (sin x)ln(x) into a
quotient? Well, here is a way: (sin x)ln(x)=[ln(x)]/[1/(sin
x)]. Those of you who object to this should be advised that I'm doing
it because it works which is about the best answer which can be
given at this stage (I'm showing it to you because someone showed it
to me and that person was shown it by ... all the way back maybe to
the Marquis de L'H himself, maybe). Anyway, the fraction
[ln(x)]/[1/(sin x)] as x-->0 does look like -infinity/infinity, so I
will use L'H, and get (with some care, now, doing the derivative of
the bottom!) limx-->[1/x]/[{-1/(sin
x)2}·cos x]=limx-->0[(sin
x)2]/[x·cos(x)]. This last fraction is again 0/0 as
x-->0. Do L'H again, and get limx-->0[2(sin x)(cos
x)]/[cos(x)-x·sin x]. All of these darn derivatives need care:
for
example, the derivative of the bottom uses the product rule. Now what
happens as x-->0? The top is again 0 (it is 2·0·0) but
the bottom is 1. So the result is finally, 0. But wait! Is it? Only
if you are very alert will you notice that we have
found limx-->0ln(y), and that it is ln(y) which has limit
0. We can undo ln with an exponential. So y itself has
limit exp(0)=1. Wow.
NOTE I don't want to distress you but Maple's response
to the command limit(x^(sin(x)),x=0); is the answer
1. Are human beings obsolete?
A preliminary version of what your text calls "Fernat's Theorem" is
something like this: At a local maximum, the tangent line to a graph is
flat. Well, let's see: I guess "flat" means the line is horizontal, so
the derivative is 0 (I should hastily add, if the derivative
exists: functions can have corners and other "interesting" (?)
features. The other part of this statement of Fermat's Theorem
involves the term, "local maximum". I want to spend a little time on
that, and try to insure that we have a shared understanding of this
term.
Suppose a function f is defined on an interval I, and p is a point
inside I. Then p is called a local maximum of f if
f(p)>=f(x) for all x in I: that is, f's value at p is at least as
big as f's values nearby. The definition of local minimum just
changes f(p)>=f(x) to f(p)<=f(x). Together, the local maxes and
mins of a function are called the local extreme values, or local
extrema of the function. All of the examples we present
to learn about local maxima can be changed to examples about local
minima if we multiply the functions by -1.
So let's look at some examples. Please note that all of the examples
were accompanied by pictures but for various reasons I can't provide
pictures here at this time.
- f(x)=-x2. Where does f have local maximums?
(In this
case and in all that follow, the assumed domain of the function will
be "all numbers for which the function makes sense", so for this f
the domain is "all real numbers".)
Answer and discussion
The graph is familiar, an upside down parabola with "top" at (0,0). As
one student remarked, the function squares numbers and then puts on a
- sign, so the largest value it can have is 0, and other values are
negative. The only 0 of this f is at 0, and all other x's have
negative values of f. So 0 is the only local maximum of f.
- f(x)=384. Where does f have local maximums?
Answer and discussion
This is a somewhat silly example, but again agreement on language is
very important in what follows. The graph of this f is a horizontal
line, and the interesting fact is that every number is a local
maximum (and is also a local minimum -- weird but correct!).
- f(x)=x. Where does f have local maximums?
Answer and discussion
This function, on its natural domain (all real numbers) has no
local maximums and no local minimums. Because if p were a local max,
then to the right of p there is an x with f(x)=x>p=f(p). So p is
not eligible.
- This f(x) is defined piecewise. So f(x)=x if -1<x<1,
and f(x)=0 for all other numbers. Where does f have local maximums?
Answer and discussion
A picture of this function's graph should be drawn. There's a tilted
open interval (no endpoints included) going from (-1,-1) to (1,1). The
rest of the graph are two closed (including endpoints) horizontal half
lines. All the points with x<=-1 are local maxes, and so are
the points with x>1 (but not 1 itself, because immediately to its
left are higher points on the graph).
Please notice that the tilted
interval does not have any local maxes. A student asked after
class why the number which is somehow "immediately before" 1 is not a
local max, since it would be the highest point on the tilted
line. Well, this is an interesting and subtle question. Suppose, say,
that "Fred" is the number which is immediately before 1. Then
thedistance from 1 to Fred is 1-Fred. What if we halve the distance?
We would get the number 1-Fred/2. And f's value at this number is
larger than Fred, so Fred can't be a local max. I think
we really showed that such a Fred can't exist: there can't be
a number immediately before another number! The real numbers
themselves are rather weird.
- f(x)=x3-x. Where does f have local maximums?
Answer and discussion
Again it is best to draw a graph of this f as we have several times
before (!). The local extrema will occur where the tangent line is
horizontal if we believe the "Fermat" result quoted above. So look
where f'(x)=3x2-1 is 0. This is when x=+/-1/sqrt(3). And a
local max occurs at -1/sqrt(3).
Commercial breakSponsored by the Newton-Leibniz Company, purveyors of fine ideas
This is really easy. If we
didn't have calculus it would be awkward and difficult. Easy is
better than hard. Good morning! We send you now back to your regular
lecture, with all our sympathy! |
We discussed a more precise form of Fermat's result.
Fermat's Theorem Suppose f is defined in an interval I, and p
is inside I. If f has a local extremum (a local max or local min)
at p, then either f'(p) does not exist or f'(p)=0.
I tried to show why, if f'(p) does exist, it would have to be 0. Here
I drew a picture (I always draw a picture whenever possible)
If f has a local maximum at p then consider the difference quotient,
[f(p+h)-f(p)]/h. If h is a small positive number, this quotient is
<=0. You can see this geometrically by looking at the picture, or
algebraically by realizing that f(p) is at least as large as f(p+h)
and the sign of the quotient can't be negativ e since h is
positive. If h is a small negative number, then the graph shows you
that the slope of the secant line is <=0, and so does examining the
algebra(because h is negative now). Therefore f'(p) is the limit of
things that are both <=0 (from the right) and >0 (from the
left). The only value f'(p) can have if these limits are to agree is
0. Whew: this argument is worth following since the result is used
very often.
Important examples, important definition, and a restatement
I mentioned that the function |x| has a local minimum at 0, but that
the derivative of this function doesnot exist at 0 (there's a
"corner" at 0). A function f has a critical point at p if either f'(p)
does not exist at p or if f'(p) exists and f'(p)=0. So |x| has
a critical point at x=0 and x3-x has critical points at
x=+/-1/sqrt(3). We restate Fermat's Theorem: local extrema occur only
at critical points. This is compact and most people like this
restatement.
Warning Look at just
f(x)=x3 alone. What are f's critical points? Since
f'(x)=3x2 for all x, we just need to look for where
3x2=0, which is only at x=0. But f(0)=0. (I realize it may be
difficult to keep the references clear to all of the functions and
derivatives floating around: I am sorry.) But to the left of 0 f has
negative values, so 0 can't be a local minimum. To the right of 0 f
has positive values, so 0 can't be a local maximum. So the critical
point 0 of this function is not a local extremuim. The converse of Fermat's Theorem is not valid: a
critical points may not be a local extremum!
I then asked how we could determine the maximum and minimum
values of a function f defined in an interval
a<=x<=b. Ms. Farley with
correctly with great precision:
Given: f defined on [a,b]. Wanted: f's max and
min values on this interval.
- If these values occur where a<x<b (called
interior extrema), look
for critical points and compute f's values at these points.
- Also look at end points and compute f's values there.
The max and min values must occur on the list of the numbers computed.
|
I drew some pictures which showed how the max and min values could
occur at any of the candidates mentioned by Ms. Farley's algorithm.
The Question of
the day was: find the maximum and minimum values of
f(x)=x3-2x2+7 on the interval -1<=x<=2.
How did expect people to solve this? I remarked that I did not
ask for a graph, and a graph is not necessary. f'(x)=3x2-4x, and the
roots of this are 0 and 4/3. These are the critical points of this
function and they are inside the interval [-1,2]. Therefore the
maximum and minimum values of f must be on the list f(-1),
f(0), f(4/3), and f(2). Since f(-1)=4, f(0)=7, f(4/3)=5+(22/27), and
f(2)=7, the min value is 4 (achieved at -1) and the max
value is 7 (achieved at both 0 and 2). A picture of a graph of
this function on the interval [-1,2] is shown to the right.
By the way, the answers 4 and 7 are not the same as the answers -1 and
0 and 2. If someone asked a farmer, how much will each of your watermelons
weigh at the end of the growing season, and the answer given was,
"August 28" I believe all of you would agree that the answer was not
too useful. Please understand the question and
try to respond to it.
I had a perfectly splendid QotD involving a pasture along the Raritan
River with a bull in it, but people shouted at it.
Please notice I have fallen behind the syllabus, and I will
discuss the Mean Value Theorem next time.
Please hand in problems 4.1: #8 and 4.2 #18 on
Thursday. |
Wednesday,
October 22 |
More happy volunteers computed some derivatives: Ms. Smallwood and Mr. Gehrmann and
Mr. Bruno, who had the assistance of
Mr. Rodriguez.
Discussion of exam results
As I wrote in the diary when I returned the first exam:
| |
|
Please realize that there will be another
exam (100 points) and a final (200 points) and more points from the
QotD, textbook problems, and workshop problems. I urge students to
study and work for improvement.
|
|
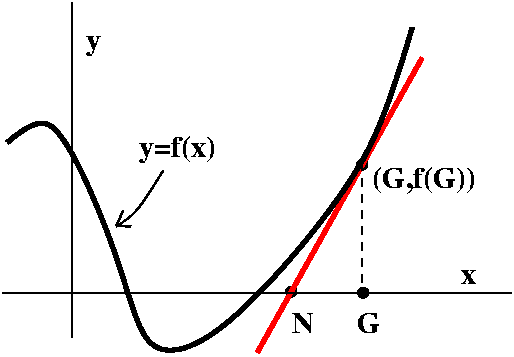 Some more about Newton's method
Some more about Newton's method
Here is what you should know at this stage:
- Newton's method is a way to (try to) improve a guess at a root
of f(x)=0 when f is a differentiable function.
- The formula for going from an old guess, G, to a new guess, N, is
N=G-[f(G)/f'(G)].
- The geometry of the Newton's method iteration is that the line tangent
to y=f(x) (a line of slope f'(G)) is drawn at the point (G,f(G)), and
the next guess, N, is obtained by sliding down this tangent
line until it hits the x-axis. That intersection is the new guess, N.
A caution
Newton's method can give some surprising
answers. It definitely should be used, since under good
circumstances it converges very rapidly, but you should be warned that
it can also misbehave.
An example
Here is one example of the use of Newton's
method with quite a simple function, selected to show some problems. I
hope the analysis will not be too hard to understand. If you try a
random polynomial you will probably get very messy results, much more
difficult to understand and analyze than this example. But the example
does show behavior that does happen in general.
The function is
f(x)=x/(1+x2). Let's look at the derivative:
f'(x)=[1·(1+x2)-2x(x)]/[(1+x2)2].
Here it is worthwhile to simplify, since I would like to work with
f'(x). The result is
f'(x)=(1-x2)/[(1+x2)2]. The Newton's
method iteration for going from an old guess, G, to a new guess, N, is
to take G to G-f(G)/f'(G). In this particular case, N=G-f(G)/f'(G) is
G-[x/(1+x2)]/[(1-x2)/[(1+x2)2]].
The second term is a compound fraction. The expression can be
simplified quite a lot with some algebraic work. In fact, for going
from an old guess, G, to a new guess, N, the formula is:
N=(2G3)/(G2-1).
Also notice that y=x/(1+x2/) has a root at exactly one value
of x, x=0. What I would like to do now is color the points of
the curve green if starting from that
point the sequence of Newton's method iterations converges to the only
root, 0. I would like to color the points red if the iterations do not converge to 0. I
would also like to discuss any weird behavior that occurs.
Here is a picture (qualitatively correct) of
x/(1+x2). |
|
Probably geometry may be more of a help to us than the algebra
alone. In fact, they should be used together, to reinforce each
other. The curve drawn is symmetric with respect to the origin. It has
pieces only in the first and third quadrants. So the colors I draw
should reflect that symmetry. The analysis I present here is more
complicated than what I said in class. That was overly simple (!) and
I made errors. I apologize! So
here we go: |
A green point, then some more green points
Certainly, starting with G=0 gets N=0, so that
the root itself is green. Are there other green points? Well, drawing
a few pictures near O should convince you that if you try
starting near 0, the Newton's method iteration rapidly approaches
0. The picture here tries to show that with a few iterations.
|
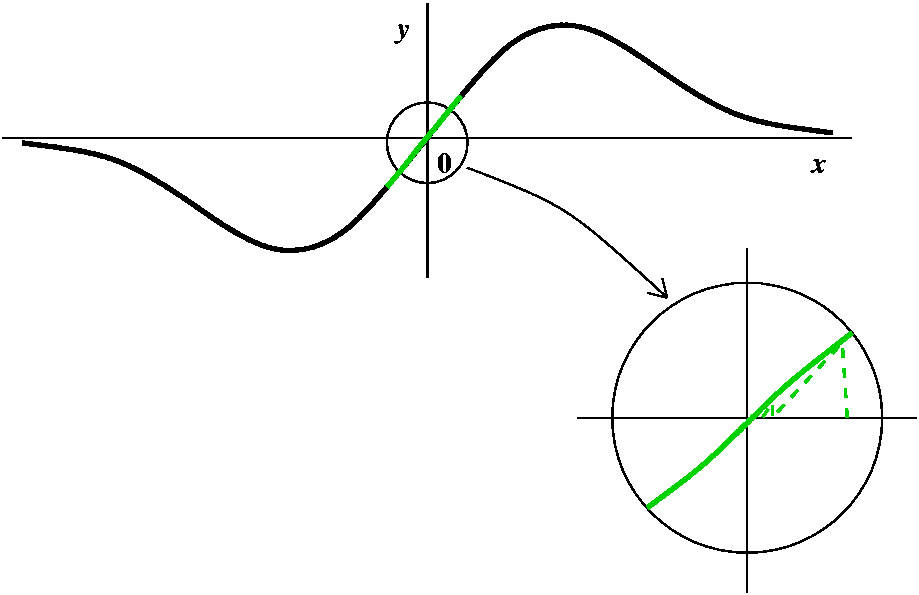
|
Some red, then some more red points
Suppose we try x=10 as G, our initial guess. Then the formula gives
N=(2G3)/(G2-1). How does N compare with G? G
seems fairly "large", and the top has twice G cubed, while the bottom
only has G squared. I bet that the new guess, N, is to the right of
G. In fact, the top of the bump (the maximum, we will officially call
it on Monday) is located at (1,1/2) (just see where f'(x)=0 -- remember
that f'(x) is (1-x2)/[(1+x2)2], so it
is 0 only when the top, 1-x2, is 0, and that is at
x=+/-1. So 10 is far to the right. And if G=10, N is even larger, more
to the right. For me, looking at the picture is much easier than
trying to understand the algebra. And if you look to the right of the
top bump, you can see that the tangent lines will all slant "down"
(have negative slope) and that therefore for guesses which are bigger
than x=1, the new guesses are being driven away from 0, the root. So
all of the points on the curve which are bigger than 1 must be red. Of
course, a symmetric conclusion is reach for points less than -1, where
the iteration drives guesses to the left.
|
|
Weird things or not so weird at all
The algebraic formula N=(2G3)/(G2-1) isn't so good when
G=+/-1. We are not supposed to divide by 0. What happens in the
picture? The tangent lines at those points are horizontal, and they
never intersect the x-axis. So maybe I should color those two points
some special color just to show that the red/green distinction doesn't
apply to them. I guess I will color them brown, a silly color for a
silly point.
|
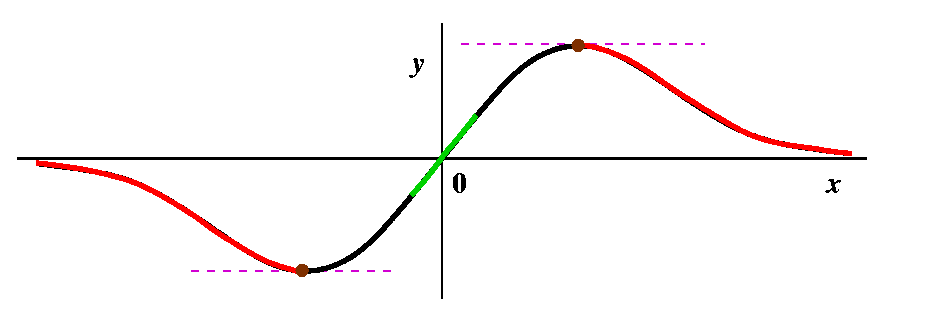
|
More red in towards 0
Suppose now we look at the curve a tiny bit to the left of where
x=1. Then the tangent line has very small positive slope, and will hit
the x-axis on the far left. Above that point, the curve is red, and
redness spreads contagiously backwards so the point we started
with is red. So some part of the left-hand side of the top bump is
red, and similarly, by (anti)symmetry, something on the right-hand
side of the bottom bump must be red.
|
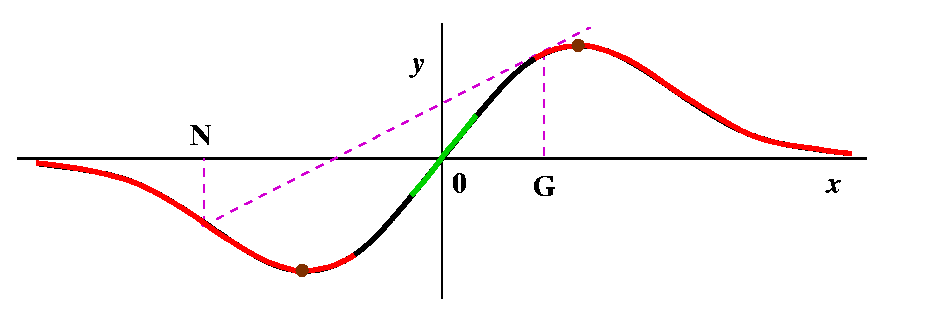
|
Brown: how can there be more brown?
Keep traveling left on the top bump, in the red stuff. The next new
guess will begin traveling right on a part of the curve where
x<0. Eventually, though, the line will intersect the x-axis at
x=-1. Do you believe me? well, let us solve
N=(2G3)/(G2-1) when N=-1. Then
2G3=1-G2 (by cross-multiplying) and so we need
to find numbers for which 2G3+G2-1=0. There is
exactly one such number (verify this on your own graphing calculator,
please) and its approximate value is .657298, so I think since this
number is shoved into -1 it should be brown also. And so should its
negative, since that gets pushed into +1.
|
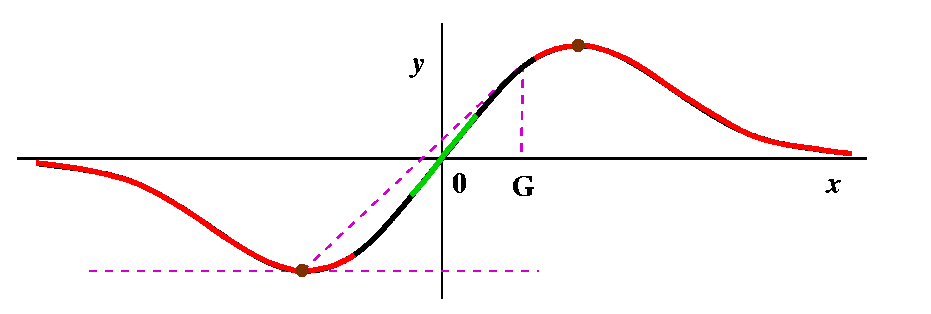
|
And more red
Push to the left from the previous point. Then the Newton's method
iteration takes us into the red region directly to the left of the
point on the curve where x=-1. And then, if you can imagine it,
further to the left we come to a point which gets pushed into the
second brown point on the left. So that point should be brown also,
and then there should be a part of the curve which is red and then ...
This is very complicated. There are actually on each side of the curve
infinitely many intervals of red, and each red interval has
brown points on its edge, so there are also infinitely many brown
points. The red intervals are getting shorter and shorter, though,
until:
|
Something new happens
If you look at the picture closely, you will see that there is a
positive number G so that when we compute N and then compute N again,
the two tangent lines are parallel! For this point Newton's method
does not go to +/-infinity and does not go to 0: it oscillates
repeatedly. We can even compute this number. By symmetry, at this
point, N should be -G, so the equation N=(2G3)/(G2-1)
becomes -G=(2G3)/(G2-1) and if we cross-multiply
we will eventually get 3G3=G. One root is G=0 which gives
us nothing new. The other roots are G=+/-sqrt(3). So I have shown these
two points in pink: pink for periodic. In general, Newton's method
does have points that sort of wander around, and don't converge to
anything, and don't "escape" to +/-infinity. Newton's method can be
very complicated. I have also indicated the behavior of
infinitely alternating red strips and brown points with !?
because I (and all other people!) can't draw this very well. This
behavior is an example of a fractal set.
|
|
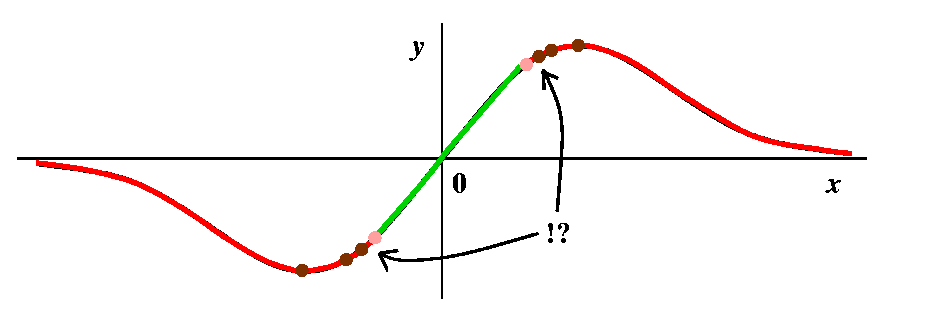
|
|
This picture tries to display a completely colored graph. The green points are attracted to the root, 0,
by Newton's method. The red points go
out to +/- infinity (alternate strips of red go to alternate
infinities [here by infinity I just mean eventual travel steadily out
to the left or the right]), and each red strip is bordered by brown points which eventually under
iteration don't go anywhere (!): they get sent to the wastebasket,
outside of the domain of Newton's method. The region labelled
!? is too hard to draw, with infinitely many alternations of
color. Finally, the two pink points
represent points which are alternated with each other
periodically by Newton's method.
This is already complicated. A "random" function would likely have
even more complicated behavior.
|
I think I began with consideration of a limit like this one:
limx-->0[e4x-1]/sin(3x). We had some limits like
this in problem 2 of workshop #5 but
here I would like to show you a more organized way to compute these
limits. Of course I begin my consideration of the limit, which is made
up of familiar functions, by just plugging in x=0 in the hope that the
functions, which are individually continuous, will be continuous near
and at 0. Since this is an invented example, we get 0/0: no hope. We
can do the following. Remember that
f(a+b)=f(a)+f'(a)b+Err·b. Well, make a into 0 and make b into
x. Then f(x)=f(0)+f'(0)x+Err·x where Err-->0 as x-->0.
Suppose we try this with f(x)=e4x-1, the "top" function
inside the limit above. Since f'(x)=4e4x, we can compute
f(0)=e0-1=1-1=0 and f'(0)=4. Then f(0)+f'(0)x+Err·x
becomes 0+4x+Err·x. What about the bottom? Here f(x)=sin(3x)
so f'(x)=cos(3x)3, and f(0)=sin(3·0)=0 and
f'(0)=cos(3·0)3=3. The bottom changes into
0+3x+Err·x. Everything is working out so neatly, of course,
because this is an arranged example, but the example was "arranged" so
that it illustrates a method which is useful often.
Then limx-->0[e4x-1]/sin(3x)
becomes limx-->0[0+4x+Err·x]/[0+3x+Err·x]
which (factoring out an x everywhere) is
limx-->0[4+Err]/[3+Err]. The error terms are different,
but qualitatively they have this common property: as x-->0, both
error terms-->0. Now we see "easily" that the limit is 4/3.
The preceding discussion is not a proof, but merely presents heuristic
evidence that the result below is true. ("heuristic" is defined in the
October 6 diary entry, and it is the appropriate word here.)
L'Hopital's Rule (version 1)
Suppose that f and g have continuous derivatives, and that
f(a)=g(a)=0. If limx-->af'(x)/g'(x) exists, then
limx-->af(x)/g(x) exists and is the same value.
Warnings
L'Hopital's rule (abbreviated now by L'H is very powerful and
also very easy to misuse. One quote I found on the Internet declared,
"Giving l'Hopital's Rule to a calculus student is like handing a
chainsaw to a three year old."
- L'H resembles the way we might like to differentiate quotients
in our dreams. Please try not to get confused:
- L'H is a method to
evaluate limits.
- The quotient rule is a method to compute
derivatives.
- You must check the hypotheses of L'H. A simple limit like
limx-->0[x^2-3x-4]/[x3+5x-6] is not equal
to limx-->0[2x-3]/[3x2+5], the limit of the
quotient of the derivatives. The first limit can be evaluated by
direct substitution, due to the continuity and nonvanishing of the
denominator: it is 4/6. The second limit can be evaluated similarly
and is -3/5. These are not equal. You must check the hypotheses
and in work submitted for this class you must show that you
have checked them.
I did a few more L'H examples, some fairly ludicrous. Please look at
the text for more examples. More serious examples arise frequently in
computer science: given various procedures for doing a task, which is
likely to be faster. An example of the kind of decisions that need to
be made is in problem 5 of workshop #3:
which sorting algorithm is faster.
To analyze this kind of limit, we usually look at
limx-->infinity. It turns out that L'H works for many
different "indeterminate forms": 0/0 is one, and infinity/infinity is
another. There are more (please see your text, and see there for more
formally stated versions of L'H). Here is one limit which may still
look ludicrous, but which I assure you is actually realistic.
What is limx-->infinity[x300]/ex?
In order to supply information which may inform or, more likely,
distract you (!) I evaluated the top and bottom at x=2.
2300, I said, was about 10100. I was again
incorrect, since it is only about 1090. This is 1
followed by 90 zeros. How about ex at x=2? In class I was told
"Less than 9", and, indeed, it is about 7.3. So the quotient is
approximately
1090/7.3, which looks pretty darn big to me. As
x-->infinity, but the top and the bottom -->infinity. I will use
L'H. Therefore I have to evaluate the limit
limx-->infinity[300x299]/ex (the
exponential function is really wonderful). Well, what happens as
x-->infinity? Again, this is the indeterminate form infinity/infinity.
I try again to use L'H and get
limx-->infinity[300·299x298]/ex.
Nothing works. Or does it? In fact, if we can imagine using L'H
another 298 times, we get
limx-->infinity[300!/ex. A few things about the
top: if you differentiate a polynomial long enough, it eventually is a
constant. And the 300th derivative of x300 is a
constant, and it is a constant with some structure: the product of the
positive integers from 300 down to 1. Such numbers arise very
frequently in calculus and in many many other applications. So
frequently that they have their own notation: !. The
exclamation point, in context, is read, factorial (it is not
read, "excitement mark"). 300! is quite large: about
10614. But it is a constant so that this limit is
0. The actual numbers are all a distraction from the true fact:
The exponential function
eventually
grows more rapidly than any polynomial!
|
|---|
The Question of
the day was: compute the limit as x-->infinity of
[(ln(x))2]/sqrt(x).
As x--> infinity, ln(x)-->infinity and sqrt(x)-->infinity, and so we have an indeterminate
form of the infinity/infinity type. Use L'Hopital's rule and try to
find the limit as x-->infinity of the quotient:
[2(ln(x))·(1/x)]/[1/(2·sqrt(x)]. I generally don't like
simplifying if it is only to present a final answer, but this is an
intermediate step in a complicated computation and it is a compound
fraction, which is ugly to me. So if you change this to a simple
fraction you will get [4(ln(x))·sqrt(x)]/x. This itself can be
made simpler by getting the powers of x together: there's an
x1/2 on top and an x1 on the bottom. So the
result is [4(ln(x))]/sqrt(x). As x-->infinity, this still is an
indeterminate form of the type infinity/infinity. I will use
L'Hopital's rule again to get
[4·(1/x)]/[1/(2·sqrt(x)]. This simplifies to 8/sqrt(x)
which I see directly -->0 as x-->infinity. You can't use L'Hopital on
this last limit since it deson't satisfy the hypotheses.
There are other ways to do this computation correctly, but I emphasize
the word "correctly". Unsubstantiated assertions that something -->0
or -->infinity are not useful.
This QotD was supposed to illustrate the following fact:
The logarithm function
eventually
grows more slowly than any power of x!
|
|---|
Please hand in tomorrow 3.11:13 (yes, I know
this is an odd problem but you need to show how you got
the linear approximation and then show some evidence that the
interval given is valid)
and
4.4:22.
A historical note
L'H is named after
Guillaume François Antoine, Marquis de
l'Hôpital (1661 - 1704), who published it in his book
Analyse des infiniment petits pour l'intelligence des lignes courbes
(1692), recognized as the first calculus textbook. It seems, though,
that the "rule"
and other results were due to Johann Bernoulli, who was paid well by
the Marquis. Bernoilli only complained about the lack of attribution
to him after the death of the
Marquis. See: math for money, isn't it easy?
|
I spent some
time giving blood after Wednesday's
class so I only finished these notes on Friday. Giving blood doesn't
really hurt and is not even very inconvenient, and one feels good after
doing it. I recommend it if you can do it.
|
|
Monday,
October 20 |
Three happy volunteers
(Ms. Brundage and
Mr. Guzman
and
Mr. Stivers)
differentiated three of the functions in the review problems for
chapter 3. I recommended that people who were not confident about
computing derivatives of functions defined by formulas show try a
bunch of these problems.
Now I considered again a remarkable equation.
|
[REMARKABLE] f(a+b)=f(a)+f'(a)b+Err·b |
This equation was first stated in our class on September 24 which now (to me, at least!)
seems like a l-o-n-g time ago. It resulted from unrolling the
formal definition of derivative. The most important qualitative aspect
of this equation is that Err-->0 as b-->0, so that the term
Err·b should go to 0 faster than first order.
A silly example
In this example, f(x)=x2. Let us look at f(a+b). In this
case we can compute f(a+b) exactly. It is
a2+2ab+b2. We can "match up" the terms here with
parts of the REMARKABLE equation above. So
f(a)=a2, and since f'(x)=2x, the term f'(a)b is exactly
2ab. The "Err·b" term is b2, and certainly when b is
small, this gets smaller faster than b. A numerical example is
something like (5.01)2 which we compute exactly as 25.1001,
and here a=5 and b=.01. This splits up as
25+.1+.0001=52+2(5)(.1)+(.01>2, and the result
of omitting the last term is a very small error.
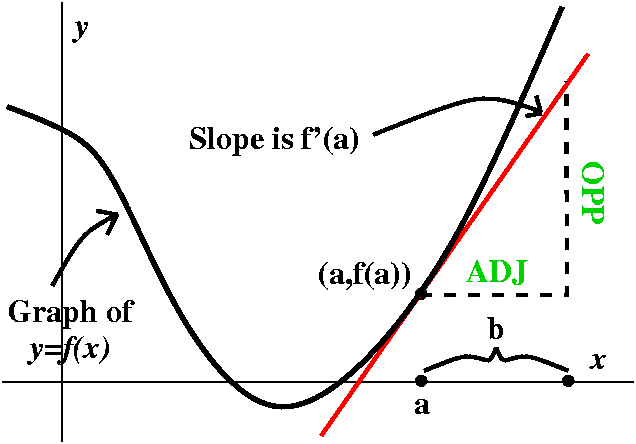
The official name
The use of f(a)+f'(a)b in place of f(a+b) is called the linear
approximation to f at a. There are several reasons it is called
the linear approximation. First, algebraic formulas (here thinking of
b as the variable) which only involve constant and first degree terms
are called linear. Second, consider the tangent line to y=f(x) at
x=a. The slope of that line is f'(a). It goes through (a,f(a)). If we
increase a by an amount b, the line's height is increased by f'(a)b
(because OPP/ADJ is f'(a) and ADJ is b in the right triangle
shown). So the linear approximation gives a formula which instead of
using the correct value of f(a+b) substitutes the value obtained by
"extrapolating" using the value on the tangent line.
Another example, perhaps less silly
What is the square root of a number close to 1? Since square root is a
continuous function, such a value of square root should be
approximately the square root of 1, which is 1. But how should we
"correct" the answer if we want sqrt(1+x) for x small? Here we have
f(x)=sqrt(x) and a=1 and b=x. So we need f'(1) which is easy, since
f'(x) is (1/2)x-1/2 and f'(1)=1/2. Therefore the linear
approximation to f(a+b), that is, to sqrt(1+x), is just 1+(1/2)x. Now
I tried to do some arithmetic. The following table is somewhat more
extensive than I computed in class with student help. Here my help was
Maple and the computations were done to 30 digits accuracy. (!)
| Values of x | "True" values of
sqrt(1+x) | Linear approximation
values | 3rd column - 2nd
column |
|---|
| 1 | 1 | 1 | 0 |
| 1.5 | 1.2247448713915890491 |
1.25 | -0.0252551286084109509 |
| 1.05 | 1.0246950765959598383 | 1.025 | -0.0003049234040401617 |
| 1.005 | 1.0024968827881710675 | 1.025 | -0.0000031172118289324 |
| 1.0005 | 1.0002499687578100594 | 1.00025 | -0.0000000312421899406 |
| 1.00005 | 1.0000249996875078123 | 1.000025 | -0.0000000003124921877 |
| 1.000005 | 1.0000024999968750078 | 1.0000025 | -0.0000000000031249922 |
| 1.0000005 | 1.0000002499999687500 | 1.0000005 | -0.0000000000000312499 |
Richard Hamming, a very famous applied mathematician of the
20th, declared that The purpose of computing is insight,
not numbers.
So what can we learn from
these numbers? Actually, we can observe some characteristics which
will always be true, although giving a good argument for them
will have to wait a week or two.
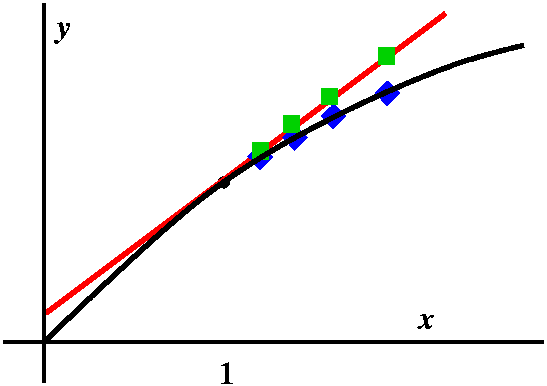
- Consider the number of zeros in the first column and in the
last column. In the first column, the transition from one number to
the next is gotten by "adding" one 0. So the a+b becomes a+(b/10). The
last column shows the discrepancy, the difference, between the linear
approximation and the true value. Look at the number of zeros. In each
step (and this is true data!) the number of zeros increases by
two, so while b changes to b/10, the difference gets divided by
100. In other words, the term "Err·b" is actually sort of a
constant multiplied by b2: it is a second-order term. This
is generally true.
- What about the sign in the last column. It is always
negative. Why is that? The curve lies under the
tangent, which means that the linear approximation will be an
overestimate of the true value.
I did one more numerical example with this function. So what about
f(101)? The "true value" of sqrt(101) is about 10.04987, and the
linear approximation based at a=1 is 51. The difference is
enormous: don't use the linear approximation when the "b" is
big. (In fact, if you needed to use a linear approximation for
sqrt(101), try a=10. Then this more appropriate linear approximation
gives 10.05
I was asked if I could give a quantitative estimate for the error, and
again I muttered that I will need to wait a week or two but I would
then be able to show one.
One more example
Finally, I asked what happened to the three-halves powers of numbers
near 9. Here f(x)=x3/2, so f'(x)=(3/2)x1/2. If
a=9 and b is a small number, we can hope that (9+b)3/2 is
close to f(9)+f'(9)b. Since f(9)=27 (hey, I chose 9 because the 3/2's
power of 9 is "simple") and f'(9)=(3/2)(3)=4.5, we now know that
(9+b)3/2 is approximately 27+(4.5)b. This may or may not be
interesting to you, but if you need to really think about many values of
x3/2 near 9, this approximation provides some insight. I
also can tell you that this approximation is an overestimate of
the true value, since x3/2 curves "up" and the tangent line
at (9,27) is under the curve. A picture that Maple drew of
this situation is to the right. We will soon learn how to tell if the
tangent line is underneath or over the curve without looking at the
graph.
 An implicit function example
An implicit function example
Look at the curve in the plane defined by the points whose coordinates
satisfy the equation xy4+x2y=6. One point on
this curve is (2,1): check me by substituting the numbers into the
equation. Now I think there is a point on the curve close to this one
with x-coordinate equation to 1.96, so it will be
(1.96,?). I would like to find an approximate value for
?. I think the curve is continuous, so an approximate value is
about 1, but I can do better. The x-coordinate is "perturbed" by a
delta&nbps;x which is -.04, and I would like to know the corresponding
linear perturbation in y. The linear approximation idea says that the
multiplier will be dy/dx. Let's compute this, using the ideas
Mr. Stivers used in his example. So we
d/dx the whole equation xy4+x2y=6 and obtain
1·y4+x·4y3y'+2x·y+x2·y'=0.
We can solve for y' and we will get:
y'=-(y4+2xy)/(4xy3+x2). At the point
(2,1) this gives us y'=-5/12, so that
delta y=y'·delta x becomes
delta y=-(5/12)(-.04). Therefore the new value of y is
approximately 1+(5/12)(.04).
Note that the "true" new value for y is about 1.0167, and our
approximation is 1.0166, an error less than 1/10,000.
Could you find the points where the tangent line to this curve is
horizontal? Where it is vertical?
Magic?
I asked how a calculator computes square roots. Most of the answers I
got were, "By pushing the button," but I repeated my question. Here
are my suggested answers.
- Since World War II smaller and smaller genetically modified people
have been raised. I think in '47 the two foot high person was the
standard of excellence in this direction,
and then in '53, the first 1/4 inch person ... and then in the 70's
really teensy people were created and put inside calculators and they
just used clever guessing to get square roots. They were also put on
super-amphetamines to work really fast.
- If your calculator can manipulate 10 decimal digit numbers, then
(since each number position can hold one of 10 choices of digits) the
calculator can only be asked to find the square root of
1010 numbers. These square roots were all computed in 1975
in a massive research project similar to sequencing the human genome. The
cost was about 47 billion dollars to compute all these square roots,
but the task was
finally done when Horace and Myrna Whiteapple of Frog's Throat,
Georgia, announced ten digits of the square root of 37: 6.0827625302.
- The calculator uses ancient Babylonian mysteries to compute each
square root very efficiently.
Well, no one believed answer #1 although it was very
dramatically presented. Sigh. And #2 was (correctly!)
criticized because there wasn't enough storage space (and actually it
would take rather a lot of time to compute those square roots). The
correct answer is actually #3.
Babylonian square roots
People were smart even
long ago. Here is a method which was used to approximate square
roots about four thousand years ago.
Finding the square root of A
- Take an initial guess, B.
- Replace your initial guess by [B+(A/B)]/2, the average of B and
A/B.
- Continue step 2 until you are satisfied with the accuracy of your
approximation.
|
This looks quite weird. Well, is it? First, if your "guess" is too
large (so B2>A) then B>sqrt(A) and
(B/A)>(1/sqrt(A)) so that (A/B)<sqrt(A). We are averaging
numbers that are on either side of sqrt(A). So maybe we will get
closer. The amazing result is that we get very much closer, very
fast. Here is an example, again computed by Maple:
I wanted to compute the square root of 2. As is well-known (but not by
me!) this is 1.4142135623730950488 to 20-digit accuracy. My first
guess, A, was 3. Here is a table of next guesses using the Babylonian
method, and the difference between the guess and the true value of
sqrt(2):
| Next guess | 1.8333333333333333333 | 0.41911977096023828453164460912 |
| Next guess | 1.4621212121212121212 | 0.04790764974811707241043248791 |
| Next guess | 1.4149984298948029517 | 0.00078486752170790299608172641 |
| Next guess | 1.4142137800471975839 | 0.00000021767410253511833468993 |
| Next guess | 1.4142135623731118008 | 0.00000000000001675206944769266 |
| Next guess | 1.4142135623730950488 | 0.000000000:27
consecutive 0's! |
Notice how rapidly the sequence of guesses converges to sqrt(2):
here the number of 0's in the difference between the true value and
the guesses seems to double at each step (this is true in
general, which is why this method is so nice to use).
I don't know how the Babylonians came up with this method, but I can
give you an explanation in the context of this course. Consider the
function f(x)=x2-2. Certainly f(x)=0 when x=+/-sqrt(2). So
how can we get a sequence of good guesses to the positive root of f?
Suppose we have a guess, and then try to improve it. Let's
suppose our guess is at x=G. Then the coordinates of the corresponding
point on y=x2-2 are just (G,G2-2). The line
tangent to y=2-2 at x=G has slope 2G (the derivative of
x2-2, which is 2x, at x=G). Therefore OPP/ADJ=2G, so that
the adjustment we make to our guess G is to subtract ADJ. But OPP is
G2-2, soafter some algebra we see that ADJ is
(G2-2)/(2G), and, if we call our new guess N,
N=(old guess)-(adjustment)=G-(G2-2)/(2G). Now some
more algebra:
G-(G2-2)/(2G)=[2G2-(G2-2)]/(2G)=[G2+2]/(2G)=[G+(2/G)]/2.
That is, the new guess is the average of G and 2/G, which is exactly
the Babylonian method described above with A=2.
As far as I know this is the method which is used for square roots in
most computational devices. It is rapid and easy to program, and the
error analysis (not presented here) is not hard.
Newton's Method
The Bablyonian square root technique can be generalized to other
functions. Try an initial guess, and then improve the guess. A diagram
similar to what is above can be drawn for y=f(x), and the improvement
method can be written as follows:
| Newton's Method N=G-(f(G)/f'(G))
|
|---|
This "scheme" of forming a new guess from the old is called Newton's
Method.
The Question of
the day was to explicitly write the "new guess from old" for
21/3, the cube root of 2, and compute the first new guess
with 3 as the original guess.
What's the answer? The simplest choice for f(x) seems to be
x3-2. Then f'(x)=3x2. So Newton's method
becomes:
N=G-[(G3-2)/(3G2)]. If G=3, then N turns out to
be 56/27, or about 2.074074074. The "true value" of the cube root of 2
is 1.259921050. Here are the first 6 iterations of Newton's method
with starting value 3 for this function (the correct digits are boldfaced):
2.074074074, 1.537690539, 1.307076219, 1.261601801, 1.259923288, 1.259921050
The sixth iteration turns out to be correct to 12 decimal places (so
the error is less than 10-12).
WARNING! Newton's method certainly can
produce weird or wrong results. I'll show some of them on
Wednesday. It must be used with some care.
History and Current Practice
The history (from the Wikipedia)
"Newton's method was discovered by Isaac Newton and published in
Method of Fluxions in 1736. Although the method was described
by Joseph Raphson in Analysis Aequationum in 1690, the relevant
sections of Method of Fluxions were written earlier, in 1671."
Current practice
There has been evolution and change in how square roots have been
computed. At times in the last few decades, specific hardware has been
designed to use Newton's method. The "latest" broadly marketed chip is
the Intel 64 bit "Itanium". Here
(load carefully: 131 page PDF file!)
is something only a true fanatic would want to read. It is the Intel
description of how reciprocals and square roots are calculated. The
title is Divide, Square Root, and Remainder Algorithms for the
IA-64 Architecture. Square root routines
in assembly language (software, not hardware!) are described on pages
40 through 70. The introduction says that "iterative methods such
as the Newton-Raphson ..." are used, but I found that I needed lots of
work to
recognize Newton's method in the assembly language routines.
The programs are very optimized, so,
for example, the repeated nature of the "old guess to new guess"
transition is not called as a subroutine, but is written out in
detail for a fixed number of repetitions. It is all quite
complicated. This is only the assembly language programming. There are
references to specific Intel documents proving that the
suggested programs give the correct results. There have been many
reports of errors in Intel computation, of which this is the
most prominent. Perhaps it is better to implement algorithms in
"software" because then in the event of errors, the programs can be
changed, rather than having to trade in chips because the circuits are
wrong.
|
|
Thursday,
October 16 |
Another workshop.
Please hand in a writeup of
the third question. |
Wednesday,
October 15 |
These problems are due tomorrow in workshop: 3.8 #50 and 3.10
#24.
I reviewed the derivatives of arcsin x: this is
1/sqrt(1-x2); and arctan x: this is
1/(1+x2); and ln x: this is 1/x.
If y=ax is an exponential function, we could take log
(really "ln") of both sides and get ln y= x ln a. Then
we could differentiate both sides, remembering the chain rule. We
would get (1/y)(dy/dx)=ln a (remember that a and therefore
ln a are both constants!). Therefore dy/dx=y·ln a so
that the derivative of ax is
ax·ln a.
If we were interested in the
derivative of 10x we would be looking at
10x(ln(10)). ln(10) is approximately 2.303 (this is enough
for most purposes I know, but if you need more digits, here they are:
2.3025850929940456840). In computer science people sometimes consider
2x whose derivative is 2x(ln(2)). ln(2) is
approximately .693 (again, enough information for most purposes I
know, but ln(2) is .69314718055994530942 [more or less!]). The nicest
and simplest ax for calculus purposes is one where the
derivative is simplest, where ln a is 1. And that occurs when
a=e. So
Of all the exponential functions,
ex is
best
because it is its own derivative. |
|---|
Finally I started on today's topic, related rates. This is
essentially applications of implicit differentiation and the chain
rule to geometric and physical situations. I just did a few problems.
Example I
Suppose the edge of a cube is growing so that at the time the
length of the edge is 2 cm, it is growing at .03cm/sec. How fast is
the volume of the cube changing at that time? Here we need to name
several variables: e will be the length of an edge of the cube, and V
will be the volume of the cube. And we need to "encode" in calculus
the further information given. That is something about the rate of
change of the volume with respect to time, t, measured in seconds. We
are told that de/dt|e=2=.03 (this
is read as the rate of change of edge length with respect to time
when the edge length is 2). We need to find dV/dt|e=2. Here we have a simple equation
relating e and V: V=e3. If we d/dt this equation, being
careful to pay respect to the chain rule, we get
dV/dt=3e2de/dt. When e=2, we get
dV/dt=3(22)(.03). By the way, what is the rate of change of
the surface area of the cube at this time? If S represents the surface
area, then since a cube has 6 square faces, S=6e2, and
dS/dt=12e(de/dt), so that (dS/dt)t|e=2=12·2·.03.
Example II
Here is a slightly more realistic example. A raindrop loses water
through evaporation at a rate which is directly proportional to
the surface area of the drop. Suppose a raindrop is spherical, and
that at the moment the drop has radius .02 cm, it is losing moisture
at the rate of -.003 cm3/sec. How fast is it losing
moisture when the radius is .005 cm? Here we need either some nice
intuition (to be discussed later) or some formulas. The needed
formulas are: S, the surface area of a sphere of radius R, is
4PiR2 (the area of 4 "great circles" -- this can be
verified using calculus). If V is the volume of a sphere of radius R,
then we have been told in the previous green
sentence that dV/dt=kS where k is a constant (presumably negative so
the raindrop is shrinking). Here we have when R=.02 that dV/dt=-.003,
and also kS is k(4Pi(.02)2), so that
k=-.003/(4Pi(.02)2). I didn't simplify for reasons which
will become apparent soon. We want to know dV/dt when R is .05. But
for this we just need
kS=-.003/(4Pi(.02)2)·4Pi(.005)2. Golly,
the 4 and the Pi cancel, and in fact all we get is
-.003(1/4)2. The original rate gets decreased by a factor
of 1/16. Probably we could have predicting this, since the rate is
directly proportional to the surface area, and the surface area is
directly proportional to the square of the radius, so
decreasing the radius by a factor of 1/4 causes the rate to change by
a factor of 1/16. The whole situation is just juggling various rates,
and the derivatives in this case seem almost to obscure the situation
instead of making it better.
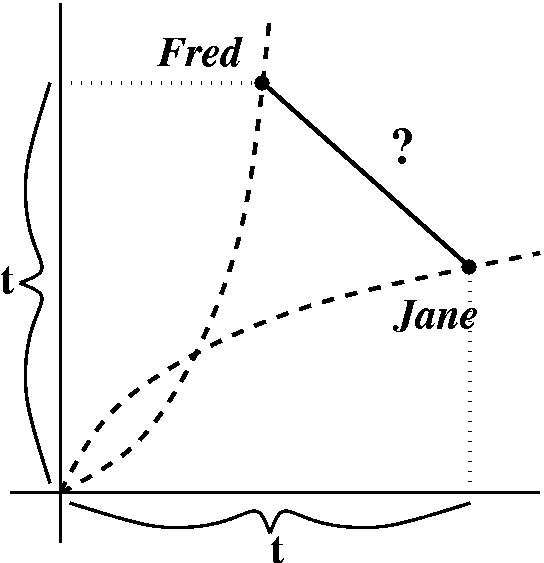
Example III [Different from what I did in class!]
Revisiting Fred and Jane, bugs. We had considered these bugs
earlier. Now here Jane will again travel on the curve y=sqrt(x) so
that at time t, her first coordinate will be t. And Fred travels so
that his second coordinate at time t will be t, but now Fred
travels on yx3 (in class I had Fred traveling on the right
half of the parabola y=x2 and this was a bit silly as one
student pointed out since it led to a rather simple limit). What
happens to the slope of the line connecting Fred and Jane as time gets
large? Jane's position is (t,sqrt(t)). Now Fred's position is a bit
more interesting. It is (something,t) where
something3=t in order for Fred to be on
y=x3. Therefore something=t1/3. so that
Fred's position is (t1/3,t). What is the slope of the line
joining Fred and Jane? It is
(t-t1/2)/(t1/3-t). What happens as t-->infinity?
Suppose we divide top and bottom by t. We get the equal fraction
(1-(1/t1/2))/(1/(t2/3-1). Now as t-->infinity,
the terms 1/t1/2 and 1/t2/3 both -->0 since
they have positive powers of t "underneath". So again the limiting
slope is -1.
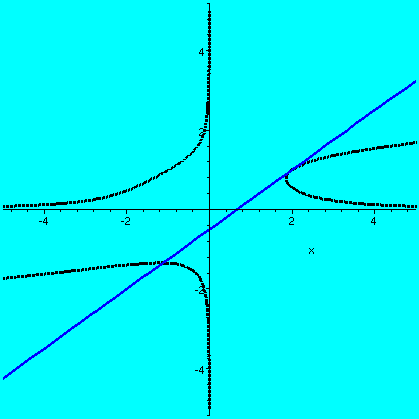 Example IV
Example IV
Here we consider a moving bug named Egbert. Egbert travels on the
curve x2y-xy4=2 and when
he (?) is at the point
(2,1) his horizontal velocity, dx/dt, is 1. What is dy/dt at that time?
This became the Question of the day. Indeed if we d/dt the
blue equation carefully (using the chain rule
and the product rule!) we get
2x(dx/dt)y+x2(dy/dt)-(1·y4+x·4y3(dy/dt))=0.
Now "insert" x=2 and y=1 and dx/dt=1. It is possible to solve for
dy/dt first, and then insert values, but I generally find it simpler
if the numbers are put in now. So we have:
2·2·1·1+22·dy/dt-(1·14+2·4·13·dy/dt)=0.
This leads to dy/dt=3/4. (I think!)
The graph that is displayed was generated by Maple and shows
x2y-xy4=2. We can almost (?) check the answer,
because on this curve as Egbert travels, dy/dx=(dy/dt)/(dx/dt)
(the chain rule again!), and so dy/dx=(3/4)/1=3/4. Egbert at
the point (2,1) should be traveling slightly tilted up, and indeed he
is (look at the graph). The line shown is y=(3/4)(x-2)+1, the tangent
line to the curve at the point (2,1).
The exams come back ...
I returned the exams. Here is a
discussion of the results. Please realize that there will be another
exam (100 points) and a final (200 points) and more points from the
QotD, textbook problems, and workshop problems. I urge students to study.
|
Sunday (!),
October 12 |
About 40 to 50 students showed up. I tried to outline the
course so far:
- "Review" of precalculus: functions, graphs, analytic geometry
- Limits: the definition, graphical interpretation, "intuition",
algebraic manipulation to detect limits.
- Continuity: definition, graphical interpretation, Intermediate
Value Theorem, continuity of familiar functions
- The derivative: a rate of change, slope of a tangent line. Formal
definition. The derivative as a function.
- Differentiation: the algorithms and the deriviatives of the common
functions.
I spent some time going over review problems and inventing "new"
problems. I hope the review session was helpful.
|
Wednesday,
October 8 |
I asked Ms. Brundage to do problem 21
in section 3.4: find an equation for a line tangent to y=tan(x) at the
point (Pi/4,1). We need to know the slope of the tangent line, and
that slope is the derivative of tan(x) at x=Pi/4. But tan's derivative
is (sec(x))2, so the slope needed is
(sec(Pi/4))2 which is equal to 2. You can check (and you
should know!) the wonderful special
triangles. Therefore the line desired is y-1=2(x-Pi/4).
Mr. Fredo and Mr. Lopes volunteered to do problem 13 of
section 3.5: find dy/dx if y=cos(a3+x3). Here
the trick and the difficulty is the inclusion of the symbol, a. The
conventional understanding, unless specifically advised otherwise, is
that unidentified letters represent constants relative to such
variables as x. Therefore the chain rule implies that
dy/dx=-sin(a3+x3)·3x2.
Mr. Cedeno happily did problem 19 of
section 3.5, which is a double use of the chain rule after a use of
the product rule. Here
y=(2x-5)4(8x2-5)-3. The outermost (?)
part of this formula is a product, so we use the product rule:
dy/dx=d/dx((2x-5)4)·(8x2-5)-3+(2x-5)4·d/dx((8x2-5)-3).
Now each "d/dx" uses the chain rule on a power function. The answer to
the whole problem will be:
dy/dx=4(2x-5)3(2)·(8x2-5)-3+(2x-5)4·-3(8x2-5)-2(16x).
It may be easy to get lost inside the maze of these derivatives.
Finally, Mr. Pankaj Bajaj did the
following problem: suppose y is implicitly defined as a function of x
by the equation y·cos(Pi·xy)=1/3. Find dy/dx at the
point where x=1/2 and y=1/3. In fact,
cos(Pi·(1/2)(1/3))=cos(Pi/6)=sqrt(3)/2. So I really should make
the right-hand side of that equation sqrt(3)/6. (Another error of the
lecturer!) The intent was to get the equation differentiated
implicitly, and that Mr. Bajaj did, using the product rule and then
the chain rule and then the product rule:
(dy/dx)·cos(Pi·xy)+y·(-sin(Pi·xy)[Pi·y+Pi·x(dy/dx)]=0.
We then insert the values of cosine and sine given by the
special
triangles which all students should know. We get:
(dy/dx)·sqrt(3)/2+(1/3)·(-1/2[Pi·(1/3)+Pi·(1/2)(dy/dx)]=0.
We can solve for dy/dx now.
I remarked:
- There would be a review session in our regular classroom on
Sunday, October 12, at 4:30 PM.
- There is a review sheet of problems which will be gone over in
workshop tomorrow.
- I would like to urge students to read the questions carefully, and
write their answers with some care. I would like to read answers to
the questions I actually ask, and not imaginary or invented
questions. I cannot read students' minds about what they would or
should have put on papers.
- I have now graded workshops for all three sections. Some students
are clearly getting the idea, and can write good narratives to
accompany their computations. Some do not write such statements, and
therefore might be at a disadvantage when I ask for sentences
describing an answer on the exam.
Some links to help preparing for the exam
Here are some pages which have practice problems with answers
completely worked out. You can glance at material you understand well,
and test yourself. You can look at worked-out problems in other
areas.
And now on to more, newer and possibly interesting material: well, it
is still fairly technical, enlarging the collection of functions we
can differentiate. Implicit differentiation lets us find derivatives
of lots of inverse functions.
arcsin
The text calls this function sin-1 and
some other sources call it asin. I find the "-1" superscript awkward,
and it sometimes confuses me when I compute since I get it confused
with "one over ...". So I will call the function inverse to sine,
arcsine, and abbreviate its value at x as arcsin(x).
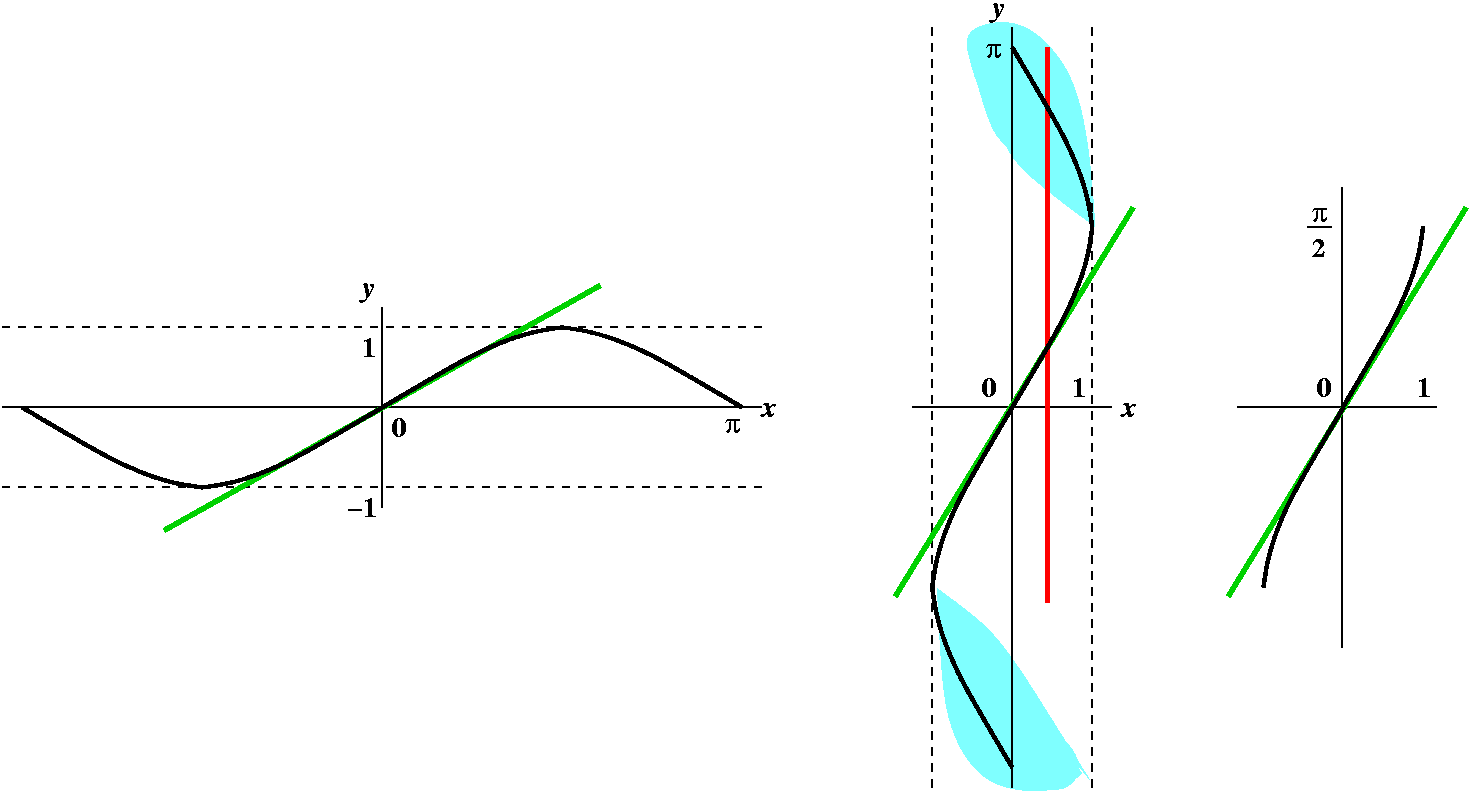
What's
happening in the pictures (left to right):
The first picture is
supposed to be a portion of the graph of sine. It is 2Pi periodic, and
its range is [-1,1]. The green line is the "main diagonal", y=x, which
also happens to be tangent to y=sin(x) at (0,0). This is because the
slope of the tangent line is the derivative of sine, which is cosine,
and cos(0)=1. To get the inverse function, we interchange inputs and
outputs. Geometrically we flip the graph over the main diagonal, and
get the second picture. The tangent line is still tangent, but now,
look at the red line. This demonstrates that the flipped graph is not
the graph of a function. It
fails the vertical line test to be a graph of a function. Thus
we need to cut away (!) part of the graph. The "clouds" in blue-green
(?) demonstrate what will be cut away. And what's left is shown in the
third picture. This is the official graph of y=arcsin(x): domain
[-1,1] and range [-Pi/2,Pi/2]. It has arcsin(0)=0, and the tangent
lines seem always to slope up, so the derivative should be
positive. And if we are ver careful to note it, the lines tangent to
sine at +/-Pi/2 are horizontal, so the lines tangent to the flipped
curve will be vertical and have no slope so there will be no
derivative at +/-1. Consider this process:
- y=arcsin(x) The inverse function
- sin(y)=sin(arcsin(x)) Using the inverseness
- sin(y)=x Recognition of inverseness
- cos(y)(dy/dx)=1 Implicit differentiation
- dy/dx=1/cos(y) Solving for dy/dx
- Since sin(y)=x, x2+(cos(y))2=1, and so
cos(y)=+/-sqrt(1-x2). Which sign to take? In the
range we are considering between -Pi/2 and Pi/2, cosine is
positive. Also the slope of the tangent line is positive for
arcsine. Thus we will take the + sign. And
cos(y)=sqrt(1-x2). Solving for dy/dx stuff in x
- Thus arcsin'(x)=1/sqrt(1-x2) Statement of
formula
We will go through this a few more times today. But in any case, the
derivative is 1/sqrt(1-x2). Notice that for -1<x<1,
this is positive, and that the derivative formula is not valid
at +/-1 as we predicted from the geometric evidence.
Example: The derivative of arcsin(5x3-ex) is
[1/sqrt(5x3-ex)](5·3x2-ex)
using the chain rule.
arctan
The text calls this function tan-1 and
some other sources call it atan. I will call the function inverse to tangent,
arcsine, and abbreviate its value at x as arctan(x).
What's
the picture supposed to show? The initial picture is y=tan(x). This
function is periodic with period Pi, and its domain does not
include odd multiples of Pi/2. The function is rather simple looking
(!), always tilted up, and has vertical asymptotes at odd multiples of
Pi/2. Flipping to get an attempted inverse function reveals lots of
problems (I omitted the red line here). The standard restriction is to
throw out the "branches" that don't intersect the horizontal axis, and
that's what I've attempted to suggest with the blue-green
"clouds". Again, y=x is a tangent line to both arctan and tan at
(0,0). Arctan is very useful. It "compresses" all of the real numbers
into the interval from -Pi/2 to Pi/2, so if you have lots of data and
you don't know ahead of time how big (+ or -) the data will be,
composing it with arctan will at least control it a bit. Now for the
derivative.
- y=arctan(x) The inverse function
- tan(y)=tan(arctan(x)) Using the inverseness
- tan(y)=x Recognition of inverseness
- (sec(y))2(dy/dx)=1 Implicit differentiation
- dy/dx=1/(sec(y))2 Solving for dy/dx
- Since tan(y)=x, x2+1=(sec(y))2 (much easier
than arcsine!). Solving for dy/dx stuff in x
- Thus arctan'(x)=1/(1+x2) Statement of
formula
Example: The derivative of arctan(e(5x4)) is
1/(1+(e(5x4))2·
e(5x4)·5·4x3: somewhat
of a mess, along with several uses of the chain rule.
The inverse function to exp
Should this be called arcexp? Well, it isn't. The exponential
function, ex, models exponential growth. It "takes" x and
multiplies e's x number of times (can you understand that
statement?). The inverse function to an exponential function is a
logarithmic function. This logarithm function is very
important. The log functions you may deal with include
log10 (used in the definition of pH, and for hand
calculation) and log2 (used in some computer science
applications). For reasons that will appear very soon, the log
function which identifies how many powers of e appear in a number is
called the natural log. Your text abbreviates it as ln, and
that's what I will use, but note that many sources call it just log.
What's ln? It is a function whose domain is all positive numbers and
whose range is all real numbers.
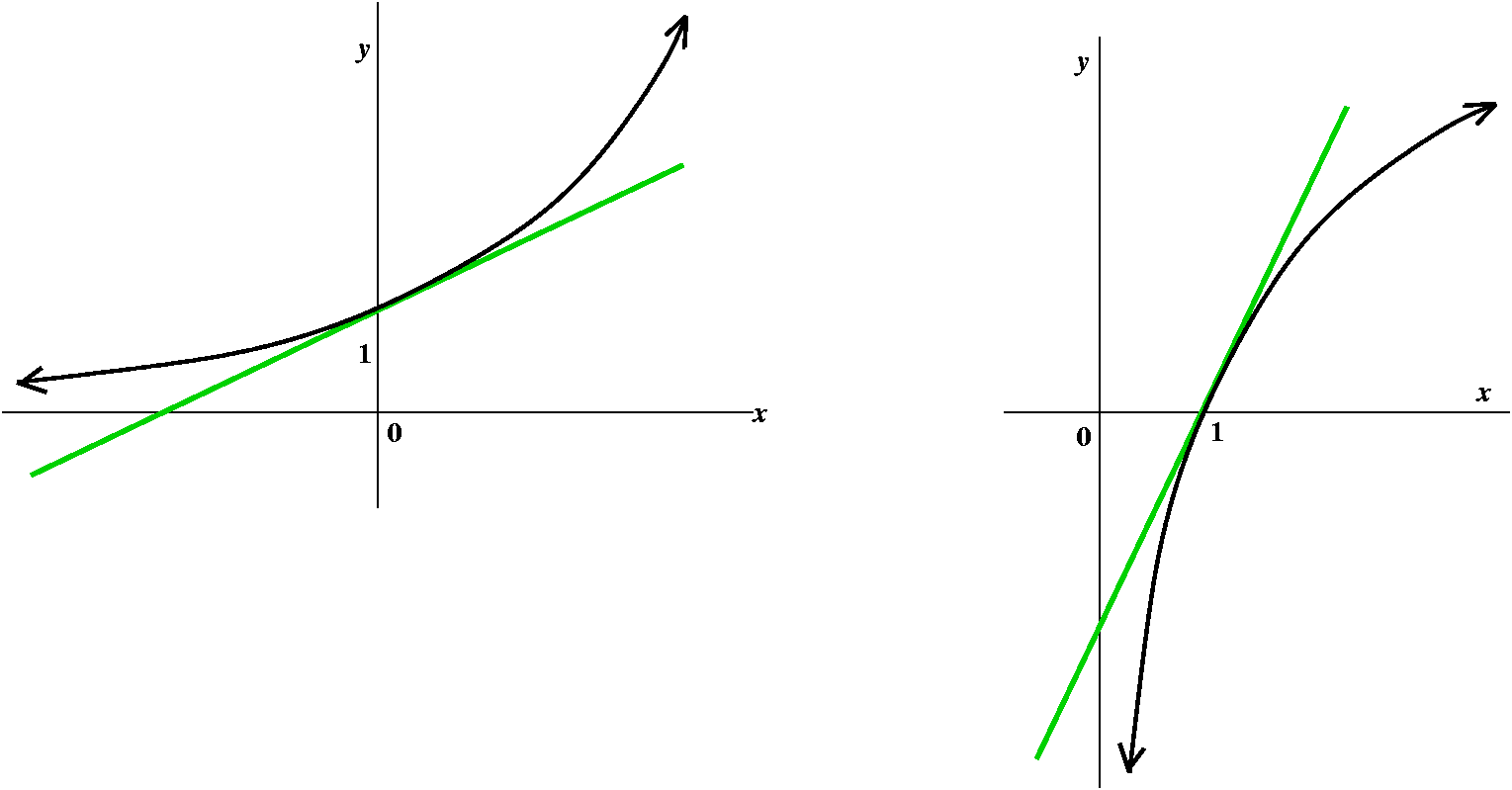
This
picture shows exp, the exponential function,
ex. Since this function is one-to-one, its inverse will be
a function: no more blue-green clouds! The green line is the tangent
at (0,1) which has slope=1. Then we flip it and get the graph of
ln. What about the derivative?
- y=ln(x) The inverse function
- exp(y)=exp(ln(x)) Using the inverseness
- exp(y)=x Recognition of inverseness
- exp(y)(dy/dx)=1 Implicit differentiation
- dy/dx=1/(exp(y))2 Solving for dy/dx
- Since exp(y)=x, we're done! This is even easier still Solving for dy/dx stuff in x
- Thus ln'(x)=1/x Statement of
formula
I then differentiated y=xsin(x) by doing this:
ln(y)=ln(xsin(x))=sin(x)ln(x), so that we can d/dx the
equation and get:
(1/y)(dy/dx)=(product rule!)cos(x)ln(x)+sin(x)/x, so that
dy/dx=y[cos(x)ln(x)+sin(x)/x]=xsin(x)[cos(x)ln(x)+sin(x)/x].
Next time: ax, and why e is the best of all possible a's.
The Question of
the day was extremely and painfully stupid. For the first time, I
think the majority of the students did not do the question
correctly.
I asked students to find dy/dx if
y=arcsin([ln(x+3)/arctan(ex)]). This was a terrible and
overelaborate concatenation of new functions, and I regret that I
asked something so complex.
Let me try to "disassemble" this function. For example, what is the
derivative of arctan(ex)? We must use the chain rule. The
"outer" function is arctan, and the inner function is
ex. Therefore the derivative of arctan(ex) is
1/[1+(ex)2]·ex.
Now what is the derivative of ln(x+3)? This is perhaps a simpler use
of the chain rule, and this derivative is 1/(x+3)·1.
What is the derivative of ln(x+3)/arctan(ex)? Here the
new ingredient is using the quotient rule. So the derivative of
this quotient is
[(1/(x+3))·arctan(ex)-1/[1+(ex)2]·ex·ln(x+3)]
(arctan(ex)2
Now continue to go backwards. We are asked for the derivative of
arcsin(ln(x+3)/arctan(ex)? We use the chain rule,
and place ln(x+3)/arctan(ex) into the argument of the
derivative of arcsin, and multiply by the expression we found above
for the derivative of the quotient. I think that the answer is:
(1/sqrt(1-[ln(x+3)/arctan(ex)]2))·([(1/(x+3))·arctan(ex)-1/[1+(ex)2]·ex·ln(x+3)])/(arctan(ex)2.
From the derivative of arcsine From the quotient rule
I hope this is comprehensible and again I apologize for throwing such
an absurd thing at people. See you Sunday, if you would like to be
there. Or else Monday for the first exam.
|



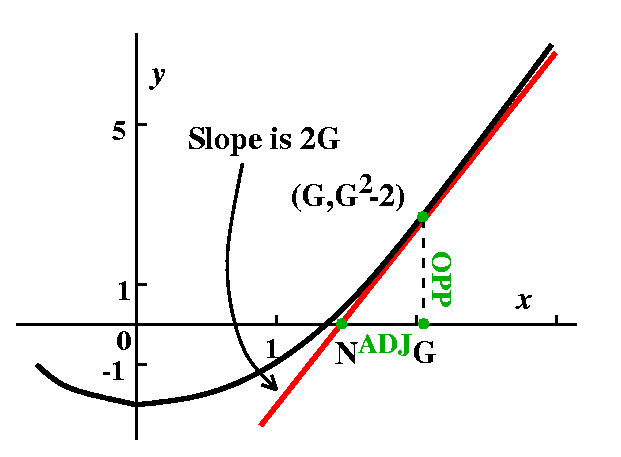
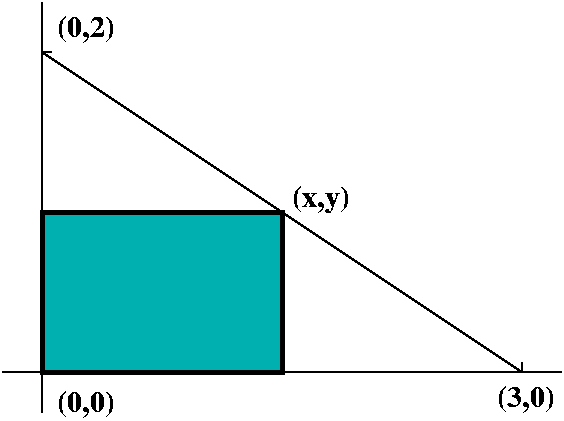 They sketched the picture shown. The rectangle has opposite corners
(x,y) and (0,0), with side lengths x and y. Its area is therefore
xy. What can we say about the relationship between x and y? The point
(x,y) is on the line connecting (0,2) and (3,0), and therefore if we
find an equation for this line, x and y must satisfy this equation,
and this will be a relationship between x and y. One equation
satisfied by both (0,2) and (3,0) is x/3+y/2=1. Therefore
y=2(1-x/3). The area becomes
A(x)=x·2(1-x/3)=2x-(2/3)x2. What x's will be
acceptable in this problem? If we look at the picture, x should be in
the interval [0,3]. So we need to maximize A(x)=2x-(2/3)x2
when x is in [0,3]. Some candidates can be found by looking for
critical numbers. A'(x)=2-(4/3)x, and the only x for which this is 0
is x=3/2. Then A(3/2)=3/2 seems to be the rectangle of largest
area.
They sketched the picture shown. The rectangle has opposite corners
(x,y) and (0,0), with side lengths x and y. Its area is therefore
xy. What can we say about the relationship between x and y? The point
(x,y) is on the line connecting (0,2) and (3,0), and therefore if we
find an equation for this line, x and y must satisfy this equation,
and this will be a relationship between x and y. One equation
satisfied by both (0,2) and (3,0) is x/3+y/2=1. Therefore
y=2(1-x/3). The area becomes
A(x)=x·2(1-x/3)=2x-(2/3)x2. What x's will be
acceptable in this problem? If we look at the picture, x should be in
the interval [0,3]. So we need to maximize A(x)=2x-(2/3)x2
when x is in [0,3]. Some candidates can be found by looking for
critical numbers. A'(x)=2-(4/3)x, and the only x for which this is 0
is x=3/2. Then A(3/2)=3/2 seems to be the rectangle of largest
area.  We begin with the picture shown. The triangle has height y and base
length x. Its area is therefore xy/2. Is there some relationship
between x and y? Look at the picture and see that (3,2) is on the same
line as (x,0) and (0,y). Well, the slope of the line between (3,2) and
(x,0) is -2/(x-3) and the slope of the line between (0,y) and (3,2) is
(y-2)/(-3). So these slopes must be equal, and we have (-2)/(x-3)=(y-2)/(-3).
Therefore y=[6/(x-3)]+2 and now A(x)=(1/2)x·([6/(x-3)]+2). What
is the domain of this function? Look at the picture: x must be greater
than 3.
We begin with the picture shown. The triangle has height y and base
length x. Its area is therefore xy/2. Is there some relationship
between x and y? Look at the picture and see that (3,2) is on the same
line as (x,0) and (0,y). Well, the slope of the line between (3,2) and
(x,0) is -2/(x-3) and the slope of the line between (0,y) and (3,2) is
(y-2)/(-3). So these slopes must be equal, and we have (-2)/(x-3)=(y-2)/(-3).
Therefore y=[6/(x-3)]+2 and now A(x)=(1/2)x·([6/(x-3)]+2). What
is the domain of this function? Look at the picture: x must be greater
than 3.
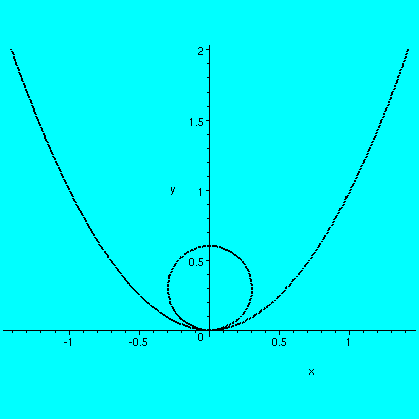
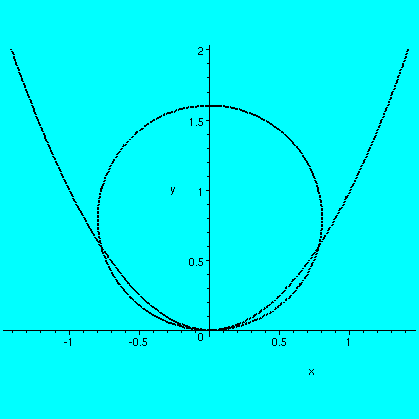
 Problem #1
Problem #1 Problem #2
Problem #2 This is different from the first problem. That was more
straightforward: a function to be maximized on a closed interval. Here
we need to worry about various things. For example, if we changed the
word "minimum" in this problem to "maximum" then we would have an
optimization problem with no solution!!! We'll see that
L(x) has no upper bound at all. For example, if x-->infinity, then the
length of the first subsegment, sqrt((x-3)2+4), gets very
large. The
other subsegment can't cancel this growth, since both of them are
postive. Therefore L(x) has no maximum in this domain. What happens at
x-->3+, that is, x is getting close to the other edge of
the domain? Now length of the second subsegment,
sqrt(9+9/(x-3)2), gets large (because (x-3)2 is
in the bottom of the fraction). So I now see that L(x) has some sort
of behavior looking like what is shown here (a not-so-accurate
sketch). Of course, we could use Maple or some other
computational tool to make a better sketch, but:
This is different from the first problem. That was more
straightforward: a function to be maximized on a closed interval. Here
we need to worry about various things. For example, if we changed the
word "minimum" in this problem to "maximum" then we would have an
optimization problem with no solution!!! We'll see that
L(x) has no upper bound at all. For example, if x-->infinity, then the
length of the first subsegment, sqrt((x-3)2+4), gets very
large. The
other subsegment can't cancel this growth, since both of them are
postive. Therefore L(x) has no maximum in this domain. What happens at
x-->3+, that is, x is getting close to the other edge of
the domain? Now length of the second subsegment,
sqrt(9+9/(x-3)2), gets large (because (x-3)2 is
in the bottom of the fraction). So I now see that L(x) has some sort
of behavior looking like what is shown here (a not-so-accurate
sketch). Of course, we could use Maple or some other
computational tool to make a better sketch, but:

 We sketched the graphs of a few more functions. We began with problem
#24 of section 4.5 which asked for a graph of y=ln(x4+27).
First I urged people to use a graphing calculator to get an
approximate idea of what the graph looks like. The result was
something like what's shown at the right. We can use derivatives to
confirm some of the aspects of the curve's shape.
We sketched the graphs of a few more functions. We began with problem
#24 of section 4.5 which asked for a graph of y=ln(x4+27).
First I urged people to use a graphing calculator to get an
approximate idea of what the graph looks like. The result was
something like what's shown at the right. We can use derivatives to
confirm some of the aspects of the curve's shape. 
 Then I tried to do problem #40 from section 4.5, to sketch a graph of
y=cos(x)/(2+sin(x)). I urged people to first graph the function in a
window of width 2Pi (the function has 2Pi periodicity). It looks like
what Maple gave me on the right. And we guessed that there
were two critical points, and (at least!) two inflection points. By
taking the first and second derivatives we verified these claims.
(More algebra and more simplification of the first and second
derivatives.) If f(x)= cos(x)/(2+sin(x)), then
f'(x)=[-sin(x)·(2+sin(x))-(cos(x)·cos(x))]/[(2+sin(x))2].
Again the bottom is always positive, and the top does simplify a bit:
-sin(x)·(2+sin(x))-(cos(x)·cos(x))=-2sin(x)-(sin(x))2-(cos(x))2=-2sin(x)-1.
(There are only a few trig identities that I keep in the top of my
brain, and (sin(x))2+(cos(x))2=1 is one of
them.) Now what can we say about the sign of -2sin(x)-1? I
class I actually sketched a graph of this function. To me this is the
simplest reasoning, because I tend to think in pictures. I learned
from the graph that -2sin(x)-1 is 0 at two places (where sin(x) is
-1/2) and is positive in a certain range and negative in a certain
range. After some thought, we found that the derivative is positive
between (7Pi)/6 and (11Pi)/6, and is 0 at both (7Pi)/6 and
(11Pi)/6. Elsewhere in the interval [0,2Pi] the derivative is
negative. Therefore our initial "feelings" about {in|de}crease and
local extrema are correct. Since
f'(x)=[-2sin(x)-1]/[(2+sin(x))2], we can compute the second
derivative:
f''(x)=[(-2cos(x)·(2+sin(x))2)-2(2+sin(x))(cos(x)))/[(2+sin(x))4].
This can be simplified by canceling just one power of 2+sin(x)
everywhere. Then
f''(x)=[(-2cos(x)·(2+sin(x)))-2(cos(x)))/[(2+sin(x))3].
The top is -2cos(x)(1+sin(x)), and the top is 0 at Pi/2 and 3Pi/2, and
further analysis here will confirm completely our initial "suspicions" about
inflection points and concavity. Please think about this:
Then I tried to do problem #40 from section 4.5, to sketch a graph of
y=cos(x)/(2+sin(x)). I urged people to first graph the function in a
window of width 2Pi (the function has 2Pi periodicity). It looks like
what Maple gave me on the right. And we guessed that there
were two critical points, and (at least!) two inflection points. By
taking the first and second derivatives we verified these claims.
(More algebra and more simplification of the first and second
derivatives.) If f(x)= cos(x)/(2+sin(x)), then
f'(x)=[-sin(x)·(2+sin(x))-(cos(x)·cos(x))]/[(2+sin(x))2].
Again the bottom is always positive, and the top does simplify a bit:
-sin(x)·(2+sin(x))-(cos(x)·cos(x))=-2sin(x)-(sin(x))2-(cos(x))2=-2sin(x)-1.
(There are only a few trig identities that I keep in the top of my
brain, and (sin(x))2+(cos(x))2=1 is one of
them.) Now what can we say about the sign of -2sin(x)-1? I
class I actually sketched a graph of this function. To me this is the
simplest reasoning, because I tend to think in pictures. I learned
from the graph that -2sin(x)-1 is 0 at two places (where sin(x) is
-1/2) and is positive in a certain range and negative in a certain
range. After some thought, we found that the derivative is positive
between (7Pi)/6 and (11Pi)/6, and is 0 at both (7Pi)/6 and
(11Pi)/6. Elsewhere in the interval [0,2Pi] the derivative is
negative. Therefore our initial "feelings" about {in|de}crease and
local extrema are correct. Since
f'(x)=[-2sin(x)-1]/[(2+sin(x))2], we can compute the second
derivative:
f''(x)=[(-2cos(x)·(2+sin(x))2)-2(2+sin(x))(cos(x)))/[(2+sin(x))4].
This can be simplified by canceling just one power of 2+sin(x)
everywhere. Then
f''(x)=[(-2cos(x)·(2+sin(x)))-2(cos(x)))/[(2+sin(x))3].
The top is -2cos(x)(1+sin(x)), and the top is 0 at Pi/2 and 3Pi/2, and
further analysis here will confirm completely our initial "suspicions" about
inflection points and concavity. Please think about this:

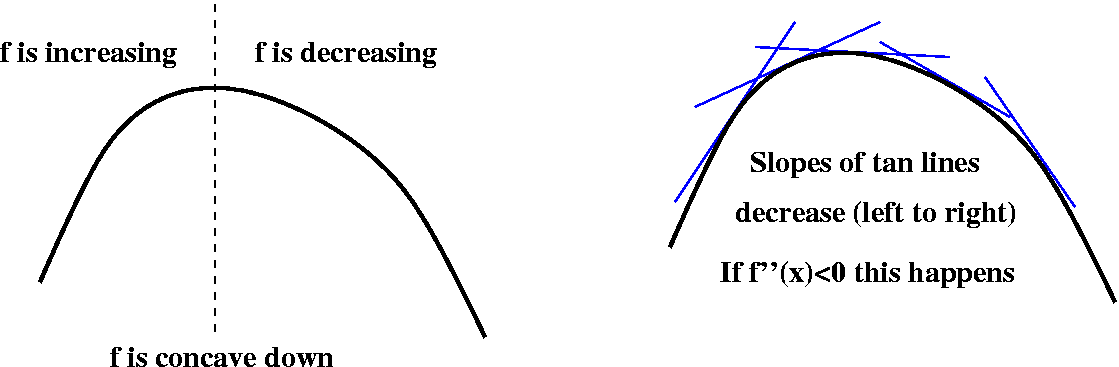


 Begin sincere sermon
Begin sincere sermon Then I discussed the following idea: graphing a polynomial. Of course
I had chose a rather non-random (!?) polynomial. I really started with
the polynomial x20(x-1)31, a polynomial of
degree 51, having only two roots, 0 and 1. I used Maple to
write an "expanded" form of this polynomial and called it H(x). Then I
had Maple antidifferentiate it (again, for a
polynomial, this is totally "mechanical") and got Q(x). I presented
this polynomial
to the class. I asked what its graph looked like. Notice that near,
say, 1, there will be things that are almost 0 computationally:
very difficult to keep track of using what is called "floating
point". In expanded form, Maple, even with 20 digit
precision which I requested, can't keep close enough track to
actually tell what the graph looks like. We got a mess from the
qualitative (and even quantitative!) point of view. The graph is
actually quite simple. If the derivative is
x20(x-1)31, there is no sign change passing 0
(this turns out to be a point of inflection of f) and there is a sign
change (in the derivative) passing x=1, so this is a local
extremum for f. In fact, checking signs, for x<1, f'(x)<0 (except for
x=0) and for x>0, f'(x)>0. Therefore f is decreasing to the left
of 1 (but has a horizontal tangent at x=0) and f is increasing to the
right of 1: f has a local minimum at x=1. It actually isn't even that complicated: to the right is a
glimpse of how the graph looks qualitatively. Follow
Then I discussed the following idea: graphing a polynomial. Of course
I had chose a rather non-random (!?) polynomial. I really started with
the polynomial x20(x-1)31, a polynomial of
degree 51, having only two roots, 0 and 1. I used Maple to
write an "expanded" form of this polynomial and called it H(x). Then I
had Maple antidifferentiate it (again, for a
polynomial, this is totally "mechanical") and got Q(x). I presented
this polynomial
to the class. I asked what its graph looked like. Notice that near,
say, 1, there will be things that are almost 0 computationally:
very difficult to keep track of using what is called "floating
point". In expanded form, Maple, even with 20 digit
precision which I requested, can't keep close enough track to
actually tell what the graph looks like. We got a mess from the
qualitative (and even quantitative!) point of view. The graph is
actually quite simple. If the derivative is
x20(x-1)31, there is no sign change passing 0
(this turns out to be a point of inflection of f) and there is a sign
change (in the derivative) passing x=1, so this is a local
extremum for f. In fact, checking signs, for x<1, f'(x)<0 (except for
x=0) and for x>0, f'(x)>0. Therefore f is decreasing to the left
of 1 (but has a horizontal tangent at x=0) and f is increasing to the
right of 1: f has a local minimum at x=1. It actually isn't even that complicated: to the right is a
glimpse of how the graph looks qualitatively. Follow 

 Rolle's Theorem
Rolle's Theorem
 We first met my pal Francine on
We first met my pal Francine on 


 Some more about Newton's method
Some more about Newton's method




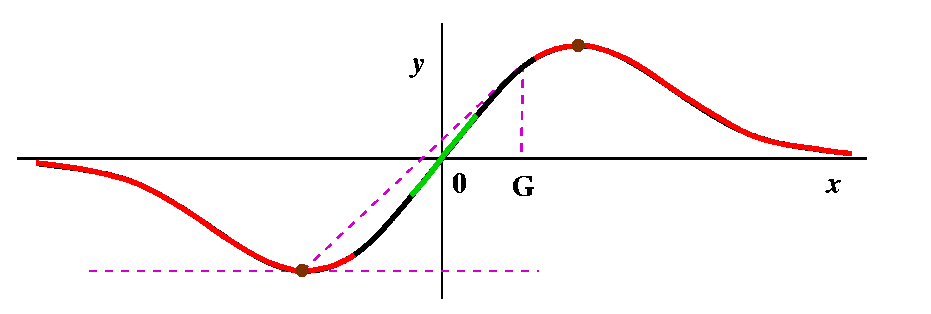




 An implicit function example
An implicit function example

 Example IV
Example IV