| A | B | C | DE | F | |
| G | H | I | J | K | L |
| M | N | O | P | Q In the diary |
R |
| S | T | U | V a) only |
W | X |
| Advice |
| Answers contributed by section | |||||
|---|---|---|---|---|---|
| 5 | 6 | 7 | 8 | 9 | 10 |
| 6 | 4 | 1 | 2 | 2.5 | 1 |
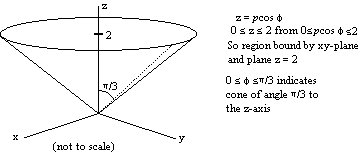
Sketch the region described in spherical coordinates by
0<=phi<=Pi/3 and 0<=rho cos(phi)<=2 and
0<=![]() <=2Pi.
<=2Pi.
B
Contributed by Chirag Walawalkar of Section 9:
Let f(x,y)=1/x+1/y+xy. True or
false? Explain BRIEFLY:
a) f has a local maximum at (1,1).
b) f has a saddle point at (1,-1).
a. (1, 1) is Local max?
First we take the first derivative with respect to x and then with
respect to y:
fx(x,y)=-1/x^2+y fx(1,1)=0
fy(x,y)=-1/y^2+x fy(1,1)=0
Therefore (1,1) is a critical point.
Now we do the second derivative test (S.D.T)
fxx(x,y)=2/x^3, fyy(x,y)=2/y^3 fxy(x,y)=1
H=fxx(1,1)fyy(1,1)-[fxy(1,1)^2]
H=(2)(2)-1
H=3
By S.D.T since H>0 and fxx(1,1)>0 f has a local min at (1,1)
therefore
the answer is False.
b) fx=-1/x2+y ==> fx(1,-1)=-1+-1=-2 not zero.
it is not a critical point therefore statement b) is also false.
C
Contributed by Shubha Sarode of Section 6:
Find the absolute max and min of f(x,y)=x2+2x+2y2 on the circle G(x,y)=x2+y2=4.
We use Lagrange multipliers to solve the equation ![]() F=
F=![]()
![]() G:
G:
Fx=2x+2, Gx=2x, Fy=4y, and Gy=2y
2x+2=![]() 2x
2x
4y=![]() 2y Note:
2y Note: ![]() can equal 2 or y=0
can equal 2 or y=0
If ![]() equals 2, then we plug this
value in the equation 2x+2=
equals 2, then we plug this
value in the equation 2x+2=![]() 2x
and we get 2x+2=4x. Solving this equation we get x=1.
If we plug this value into G(x,y)=4 we get y=+/-sqrt(3).
2x
and we get 2x+2=4x. Solving this equation we get x=1.
If we plug this value into G(x,y)=4 we get y=+/-sqrt(3).
Therefore possible max/min's could occur at (1,sqrt(3)) and (1,-sqrt(3)).
We need to evaluate these points in F(x,y) to see their values.
Plugging in both sets of points, we get the value of 9.
Now we need to see what the possible points could be if y=0.
Plugging in y=0 in the equation x2+y2=4 we get the x values of +2 and
-2. Therefore, possible points are (2,0) and (-2,0)
Evaluating F(x,y) at these points we get 8 and 0 respectively.
so:
(1,sqrt(3)) and (1,-sqrt(3)) gives F=9, This is the max.
(2,0) gives 8.
(-2,0) gives 0. This is the min.
b) To find the max and min on the disk x2+y2
less then or equal to 4 we just need to compare the values of F at the
critical points inside the disk with values at the points on the
boundary.
The critical points are:
Fx=2x+2 therefore x=-1;
Fy=2y therefore y=0.
The value of F(x,y) at (-1,0) is -1.
Therefore, -1 is going to be the absolute min and 9 (from above) is going to stay as the absolute max.
Comment Please note that in this solution, tracing down every alternative (including what happens if some variable is 0) was necessary to get the answer. You can't just assume all or any of the relevant variables and not 0.
D
Contributed by Jennifer Ng of
Section 22 in fall 2008:
please see here.
An error was found by S. Speights
(4/11/2010). The Jacobian for spherical coordinates should be
ρ2sin(φ), so the solution should have another power
of ρ and the final answer should therefore be (4/15)Π.
E
Contributed by Sonam Patel of Section 5:
Find all the critical points of F(x,y)=x^2-4xy+y^3-3y and describe the type of each critical point.
Fx=2x-4y and Fy=-4x+3y^2-3
Now, set both equations equal to zero in order to find the critical
points:
x=2y and -4x+3y^2-3=0 by substitution you get,
-4(2y)+3y^2-3=0 which can be also written as 3y^2-8y-3=0. When
factored, you get (3y+1)(y-3)=0 and
therefore y=-1/3 or y=3.
When y=3, x=6. So the first critical point is (6,3). When y=-1/3,x=-2/3,
and so the second critical point
is (-2/3,-1/3).
In order to classify them, take second partial derivatives.
Fxx=2 , Fxy=-4, Fyy=6y, Fyx=-4
D=D(a,b)=Fxx(a,b)Fyy(a,b)-[Fxy(a,b)]2=12y-16
so D(6,3)=20 and Fx(6,3)=2. When D(a,b)>0 and
Fx(a,b)>0, then F(a,b)
is a local minimum. Therefore
(6,3) is a local minimum of F.
D(-2/3,-1/3)=-20. D(-2/3,-1/3)<0 and therefore D(-2/3,-1/3) is a
saddle point.
Comment The solution by Sonam Patel arrived at Sat, 1 Apr 2006 15:24:14. A similar solution with the same answers by Demetri Koloseus-Gagnon arrived at Sat, 1 Apr 2006 15:34:33. The competition is heating up! Thanks to both of these people.
F
Contributed by Adam Skrzypczak of Section 10:
Find the maximum and minimum values of x-4y+2z subject to the constraint that (x,y,z) lies on the ellipsoid x2+y2+5z2=1.
F(x,y,z) =x-4y+2z and G(x,y,z)=x2+y2+5z2=1
![]() F=
F=![]()
![]() G (for diff. funct x, y, z) so you get 4 equations:
G (for diff. funct x, y, z) so you get 4 equations:
1. 1=![]() (2x)
(2x)
2. -4=![]() (2y)
(2y)
3. 2=![]() (10z)
(10z)
4. x2+y2+5z2=1
![]() cannot be 0
because the first equation would then be 1=0.
cannot be 0
because the first equation would then be 1=0.
Solve for each of the variables and insert into the constraint equation to get:
1/(4![]() 2)+4/(
2)+4/(![]() 2)+1/(5
2)+1/(5![]() 2)=1 so
2)=1 so ![]() =sqrt(89/20).
=sqrt(89/20).
Then plug back into eq's 1 through 3 and find values for x,y,z :
x=(+/-)1/[2sqrt(89/20)] and y=(+/-)-2/sqrt(89/20) and z=(+/-)1/[5sqrt(89/20)]
which gives you two points:
(1/2sqrt(89/20),-2/sqrt(89/20),1/5sqrt(89/20))
And
(-1/2sqrt(89/20),2/sqrt(89/20),-1/5sqrt(89/20))
Then plug back into F(x,y,z) and you find your max and min!
Max occurs at (1/2sqrt(89/20),-2/sqrt(89/20),1/5sqrt(89/20)) and is sqrt(89/20)([1/2]+8+[2/5]).
Min occurs at (-1/2sqrt(89/20),2/sqrt(89/20),-1/5sqrt(89/20)) and is -sqrt(89/20)([1/2]+8+[2/5]).
G
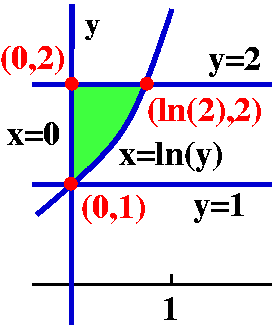
Contributed by Demetri Koloseus-Gagnon of Section 6:
Change the order of integration in ![]() 12
12![]() 0ln yf(x,y) dx dy.
0ln yf(x,y) dx dy.
![]() 0ln(2)
0ln(2)![]() ex2f(x,y) dy dx.
ex2f(x,y) dy dx.
Comment Certainly the answer is correct. I remark, though, that an answer alone may not receive full credit. In this case, some explanation is needed. Probably a picture together with some algebra is best. For example, one boundary curve of the problem statement is x=ln(y) which turns into y=ex. The picture to the right of the region of integration should show enough that a reader of the problem solution is convinced the student understands the problem.
H
Contributed by Robert J. Comito of
Section 5:
Change the integral
![]() 03
03![]() 0sqrt(9-y2)
0sqrt(9-y2)![]() sqrt(x2+y2)sqrt(18-x2-y2)(x2+y2+z2) dz dx dy
to spherical coordinates. DON'T EVALUATE THE INTEGRAL.
sqrt(x2+y2)sqrt(18-x2-y2)(x2+y2+z2) dz dx dy
to spherical coordinates. DON'T EVALUATE THE INTEGRAL.
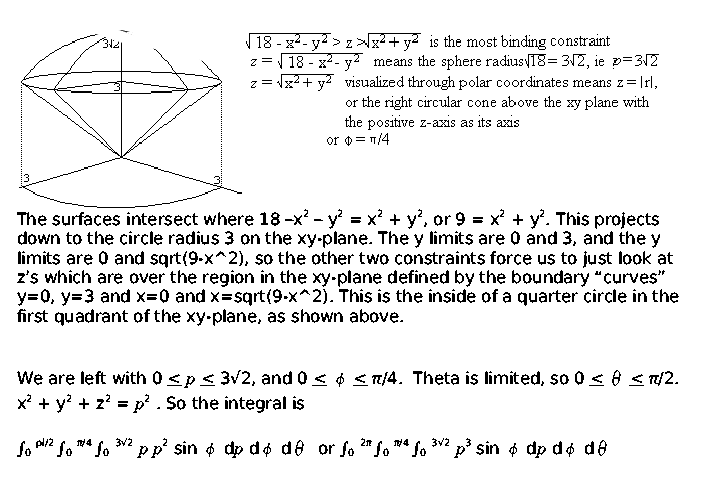
Comment This has been corrected today (4/5/2006) as a result of
e-mail from Karin Jensen of Section
6. One of the previous ![]() limits was incorrect. This "solid" only is in the first octant, above
a quarter circle (quarter disc!) in the first quadrant of the
xy-plane. I thank Ms. Jensen for her careful reading!
limits was incorrect. This "solid" only is in the first octant, above
a quarter circle (quarter disc!) in the first quadrant of the
xy-plane. I thank Ms. Jensen for her careful reading!
There;s also an error in the integrand, as Michael
Boxer of section 6 notices. Since
rho2=xs2+y2+z2, the
integrand should be rho4. I am sorry, and thank Mr. Boxer.
I
Contributed by Robert J. Comito of Section 5:
a) Compute
![]() 23
23![]() 1/xx2x2y-2x dy dx.
1/xx2x2y-2x dy dx.
b) Write this iterated integral in ``dx dy'' order. You may want to
begin by sketching the area over which the double integral is
evaluated. You are not asked to evaluate the dx dy result,
which may be one or more iterated integrals.
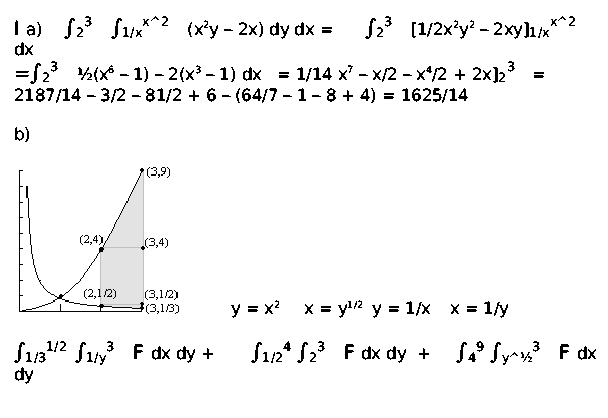
Comment Very neat answer. Thank you.
Of course we can compute the dx dy version and see if the answer
is the same as the answer to a), or we can type and read.
>int(int(x^2*y-2*x,x=1/y..3),y=1/3..1/2) + int(int(x^2*y-2*x,x=2..3),y=1/2..4) + int(int(x^2*y-2*x,x=sqrt(y)..3),y=4..9);
1625
----
14
K
Contributed by Sejalkumari Patel of Section 7:
Calculate ![]()
![]() Dy dA where D is
bounded by y=x-1 and y2=2x+6.
Dy dA where D is
bounded by y=x-1 and y2=2x+6.
The line y=x-1 intersects the curve y2=2x+6 at two places, so we can two points (-1,-2) and (5,4). You can find these two points by plugging in the value of x=y+1 into the formula y2=2x+6. This becomes y2=2(y+1)+6=2y+8, so y2-2y-2=0 and (y+2)(y-4)=0.
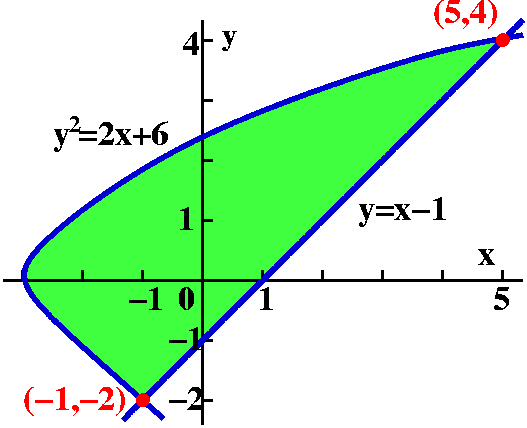 The limits of x and y are:
The limits of x and y are:
(y2-6)/2<=x<=y+1 and -2<=y<=4.
The double integral becomes the iterated integral:
![]() -24
-24![]() (y2-6)/2y+1y dx dy=
(y2-6)/2y+1y dx dy=![]() -24 xy](y2-6)/2y+1.
-24 xy](y2-6)/2y+1.
After some algebra, this is ![]() -24-2(y2-y3/2+4y)dy=
-2(y3/3-y4/8+2y2)]-24=18.
-24-2(y2-y3/2+4y)dy=
-2(y3/3-y4/8+2y2)]-24=18.
Comment Not out of disbelief, but sheerly because everyone should wear both suspenders and a belt, I present:
> int(int(y,x=(y^2-6)/2..y+1),y=-2..4);
18
L
Contributed by Qi Wen of Section 6:
Let
F(x,y)=e2yi+(1+2xe2yj. Find
a function f(x,y) such that ![]() f=F and use it to evaluate
f=F and use it to evaluate
![]() CF·dr where
r(t)=sqrt(t)i+(1+t3)j, and 0=<t<=1.
CF·dr where
r(t)=sqrt(t)i+(1+t3)j, and 0=<t<=1.
fx=e2y
![]() fxdx=
fxdx=![]() e2ydx=xe2y+g(y)
e2ydx=xe2y+g(y)
![]() [xe2y+g(y)]/
[xe2y+g(y)]/![]() y=2x e2y+g´(y).
y=2x e2y+g´(y).
The original function for the j component is
1+2x e2y,therefore the g'(y) is 1, then g(y)=y.
f(x,y)=xe2y+y
Because r(t)=sqrt(t)i+(1+t3)j and
0<=t<=1. Therefore the start and the end points are (0,1) and
(1,2).
![]() CF·dr=f(x2,y2)-f(x1,y1)
and
f(x2,y2)-f(x1,y1)=f(1,2)-f(0,1)
and f(1,2)-f(0,1)=e4+1.
CF·dr=f(x2,y2)-f(x1,y1)
and
f(x2,y2)-f(x1,y1)=f(1,2)-f(0,1)
and f(1,2)-f(0,1)=e4+1.
O
Contributed by Steve Swern of Section 8:
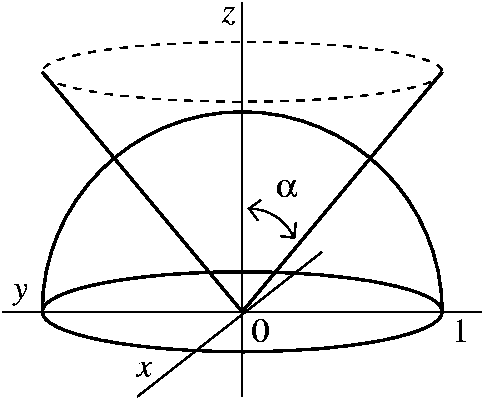 In this problem H is the upper half of the unit sphere in
R3: those (x,y,z) with
x2+y2+z2<=1 and z>=0. There is
a right circular cone whose vertex is (0,0,0) and whose axis of
symmetry is the positive z-axis which divides the volume of H into
two equal parts. Find the angle alpha that determines this
cone. The diagram defines alpha, which is the angle that the
positive z-axis makes with a line on the cone through the vertex.
In this problem H is the upper half of the unit sphere in
R3: those (x,y,z) with
x2+y2+z2<=1 and z>=0. There is
a right circular cone whose vertex is (0,0,0) and whose axis of
symmetry is the positive z-axis which divides the volume of H into
two equal parts. Find the angle alpha that determines this
cone. The diagram defines alpha, which is the angle that the
positive z-axis makes with a line on the cone through the vertex.

P
Contributed by Steve Swern of Section 8:
Suppose D is the path consisting of three straight line segments,
first from (1,2) to (4,-3), then from (4,-3) to (2,6), and then from
(2,6) to (3,4). Compute ![]() D(2xy3) dx+(3x2y2+4y3) dy.
D(2xy3) dx+(3x2y2+4y3) dy.
Since we're computing a work line integral for a vector field that is CLEARLY the gradient of another function. We can look at it and figure out what the potential was...
We'll use the dy side since it's more defining:
3(x2)y2+4y3dy ==> a little
antidifferentiation ==>
f(x,y)=x2(y3)+y4
this checks out for the dx side as well because
fx=2xy3.
given on the formula sheet is this :
"For V conservative with potential f (we were given V and i showed you
how to find f).. the integral for V .. blah blah blah... = f(THE END)
- f(THE START)"
the start was (1,2).. that danced around a couple points... and ended
at (3,4) ...f(3,4)-f(1,2)=832-24=808
Comment Mr. Swern's rather "breezy" approach is correct. You
might worry about the curve being defined in several pieces, but
things do work out. Certainly each line segment can use the potential,
so that the total integral is equal to this sum:
f(3,4)-f(2,6) (from the third line segment) +
f(2,6)-f(4,-3) (from the second line segment) +
f(4,-3)-f(1,2) (from the first line segment)
and the sum "telescopes" to give f(3,4)-f(1,2), even as asserted by
Mr. Swern.
R
Contributed by Robert J. Comito of Section 5:

S
Contributed by Jocelyn Alexander of Section 5:
Let C be the straight line segment from (0,1) to (4,3). Find ![]() Cx2y ds.
Cx2y ds.
Vector representation of line segment that starts at r0 and
ends at r1:
r(t)=(1-t)r0+t*r1
For the line segment given, r0=(0,1) and r1=(4,3)
r(t)=(1-t)<0,1>+t<4,3>=<0+4t,1-t+3t>=<4t,1+2t>.
Parametric representation:
x=4t so dx/dt=4
y=1+2t so dy/dt=2
(0<=t<=1)
ds=sqrt[(dx/dt)2+(dy/dt)2]dt=sqrt(42+22)dt=sqrt(16+4)dt=sqrt(20)dt
![]() Cx2y ds=
Cx2y ds=![]() t=0t=1(4t)2(1+2t)sqrt(20)dt=sqrt(20)
t=0t=1(4t)2(1+2t)sqrt(20)dt=sqrt(20)![]() 01(16t2+32t3)dt=sqrt(20)[16t3/3+8t4]01=([16/3]+8)2(sqrt(5))
01(16t2+32t3)dt=sqrt(20)[16t3/3+8t4]01=([16/3]+8)2(sqrt(5))
T
Contributed by Chirag Walawalkar of Section 9:
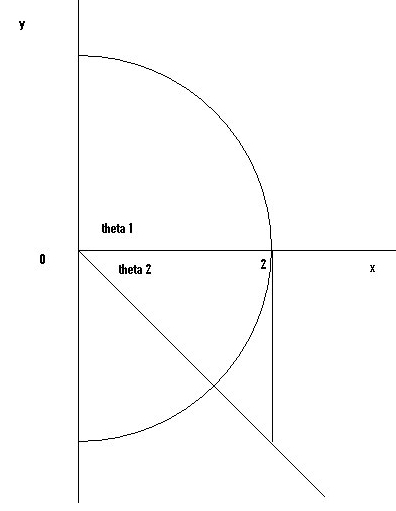 Compute
Compute ![]()
![]() Rx dA
where R is the region to the right
of the y-axis and bounded by the circle of radius 2 centered at the
origin, the positive part of the y-axis and the line y=-x.
Rx dA
where R is the region to the right
of the y-axis and bounded by the circle of radius 2 centered at the
origin, the positive part of the y-axis and the line y=-x.
R bounded by the positive y axis and the circle of radius 2 centered at
origin positive x axis and the line y=-x.
![]() 1
is the angle between the positive x-axis and the positive y-axis.
It is Pi/2.
1
is the angle between the positive x-axis and the positive y-axis.
It is Pi/2.
![]() 2 is the angle
between the positve x axis and the line y=-x. We can find this angle
using the picture and the fact that the line cuts the quarter
circle in half thus theta 2 will be half of Pi/2 or Pi/4.
2 is the angle
between the positve x axis and the line y=-x. We can find this angle
using the picture and the fact that the line cuts the quarter
circle in half thus theta 2 will be half of Pi/2 or Pi/4.
We can also find ![]() 2
using the fact that y=-x and when x=2, y must equal -2, and
2
using the fact that y=-x and when x=2, y must equal -2, and ![]() 2=arctan(-2/2)=-Pi/4.
The negative sign occurs because the angle is in the 4th quadrant (the
picture is better here).
r is simply between 0 and 2.
2=arctan(-2/2)=-Pi/4.
The negative sign occurs because the angle is in the 4th quadrant (the
picture is better here).
r is simply between 0 and 2.
x=r cos(![]() ) and
dA=r dr d
) and
dA=r dr d![]() so the integral becomes
so the integral becomes
![]() -Pi/4Pi/2
-Pi/4Pi/2![]() 02r cos(
02r cos(![]() ) r drd
) r drd![]() =(
=(![]() -Pi/4Pi/2cos(
-Pi/4Pi/2cos(![]() )d
)d![]() )(
)(![]() 02r2dr)=(r3/3]02)(sin(
02r2dr)=(r3/3]02)(sin(![]() )]-Pi/4Pi/2=(8/3)(1+sqrt(2)/2)
(
)]-Pi/4Pi/2=(8/3)(1+sqrt(2)/2)
(
U
Contributed by Tina Lee of Section 6:
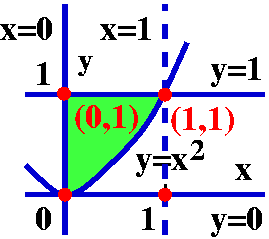 change x2<y<1 and 0<x<1 to 0<y<1 and
0<x<sqrt(y).
change x2<y<1 and 0<x<1 to 0<y<1 and
0<x<sqrt(y).
The graph is a parabola: x2=y in the 1st quadrant, x=0, y=1
and y=0 (just the lines). (0,0), (0,1), (1,0), and (1,1) are common
points.
The area above the parabola but under y=1 is the a
rea needed to be
integrated (in the
'square')
given: ![]() 01
01![]() x21x3sin(y3 dy dx
can be changed to
x21x3sin(y3 dy dx
can be changed to
![]() 01
01 ![]() 0sqrt(y)
x3sin(y3) dx dy
0sqrt(y)
x3sin(y3) dx dy
The integral inside: ![]() 0sqrt(y)
x3sin(y3) dx=(1/4)(x4)sin(y3)
]0sqrt(y)=(1/4)(y2-0)sin(y3)=(1/4)y2sin(y3).
0sqrt(y)
x3sin(y3) dx=(1/4)(x4)sin(y3)
]0sqrt(y)=(1/4)(y2-0)sin(y3)=(1/4)y2sin(y3).
Then the integral outside: ![]() 01(1/4)y2sin(y3) dy.
01(1/4)y2sin(y3) dy.
If y3=u then 3y2 dy=du
(y2dy=du/3) and 0<y^3<1 becomes 0<u<1 so the
integral above is (1/4)![]() 01sin(u)du/3=(1/12)( -cos (u))]01=-1/12(cos(1)-cos(0))=-1/12(cos1-1)=1/12(1-cos1).
01sin(u)du/3=(1/12)( -cos (u))]01=-1/12(cos(1)-cos(0))=-1/12(cos1-1)=1/12(1-cos1).
V
Contributed by Chirag Walawalkar of Section 9:
a) ![]() 01
01![]() 0x
0x![]() 0yint(0,y)xy2z3dz dy dx
0yint(0,y)xy2z3dz dy dx
The innermost integral: xy2![]() 0yz3dz=xy2z4/4]0y=xy4/4
0yz3dz=xy2z4/4]0y=xy4/4
Next: ![]() 0xxy6/4 dy=xy7/(7·4)]0x=x·x7/(28)=x8/28
0xxy6/4 dy=xy7/(7·4)]0x=x·x7/(28)=x8/28
Finally, ![]() 01x8/28 dx=x9/(28·9)]01=1/(28·9): lets
not simplify!!
01x8/28 dx=x9/(28·9)]01=1/(28·9): lets
not simplify!!
b) Write this as one or more integrals in dx dy dz order.
Comment A correct solution for part b) has not yet been
received. Perhaps the picture below can help "solve" b). Or perhaps not.
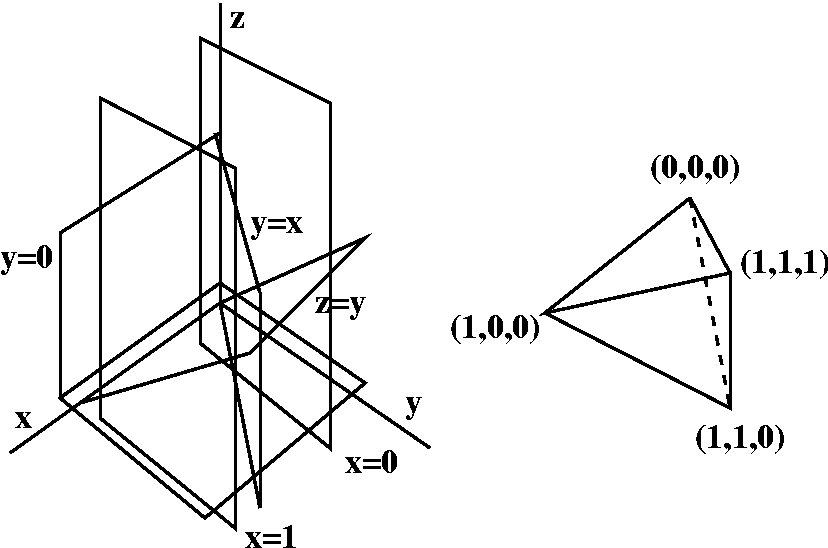
It is easy to test solutions for part b). For example, here is a
computation of the original integral in Maple:
> int(int(int(x*y^2*z^3,z=0..y),y=0..x),x=0..1);
1/252
So any suggested solution should be "robust" (strong) enough to have
the computed answer 1/252 with the integrand
xy2z3, Mr. Walawalkar suggested that "V is for
Vendetta."
| ... There have been many studies of elite performers -- concert violinists, chess grand masters, professional ice-skaters, mathematicians, and so forth -- and the biggest difference researchers find between them and lesser performers is the amount of deliberate practice they've accumulated. Indeed, the most important talent may be the talent for practice itself. K. Anders Ericsson, a cognitive psychologist and an expert on performance, notes that the most important role that innate factors play may be in a person's willingness to engage in sustained training. He has found, for example, that top performers dislike practicing just as much as others do. (That's why, for example, athletes and musicians usually quit practicing when they retire.) But, more than others, they have the will to keep at it anyway. |
| (From "The Learning Curve" by Atul Gawande, an article on the training of surgeons appearing on pages 52-61 of The New Yorker, January 28, 2002.) The article is also included in Complications, A Surgeon's Notes on an Imperfect Science, an interesting collection of Gawande's essays. |
Maintained by greenfie@math.rutgers.edu and last modified 9/5/2005.