I began this last time. Please see here to get a start. There are six different orders that are possible when converting a triple integral to an iterated integral. I did three of the six orders. Let's convert

Welcome, spring!
Happy birthday, Johann Sebastian Bach!
March 21, 1685 -- July 28, 1750.
Office hour shift this week
Tuesday office hours: from 3:30 to 4:30 or so.
Thursday office hours: from 9:30 to 11:30 or so.
A region in space
I began this last time. Please see here to get a
start. There are six different orders that are possible when
converting a triple integral to an iterated integral. I did three of
the six orders. Let's convert ![]()
![]()
![]() This regionSQUIRREL dV
into various iterated triple integrals.
This regionSQUIRREL dV
into various iterated triple integrals.
dx dy dz
I'll try this order first:
![]() (
(
![]()
![]() SQUIRREL dx dy)dz.
SQUIRREL dx dy)dz.
I've mentioned that my personal inclination in finding limits of
iterated integrals is working from the outside-most limit "in". There
are definitely people who are successful and do the exact opposite. I
would recommend that you find your own "natural" style and try to
follow that path. For me, I would look at the z limits first. For this
shape, I would try to find the highest and lowest z's in the spatial
region. This is not a complicated region, and we've already sketched it quite well. The highest and lowest
z's are, respectively, z=0 and z=3. So we've got ![]() z=0z=3(
z=0z=3(![]()
![]() SQUIRREL dx dy)dz.
SQUIRREL dx dy)dz.
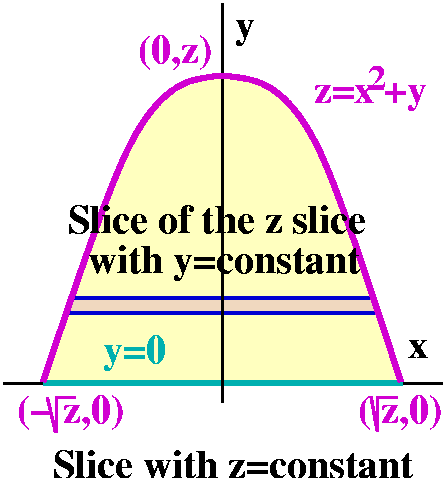 Now let's try slicing the region by z=CONSTANT, where the
CONSTANT is some unknown number between 0 and 3. This horizontal slice
of the original spatial region gets us something in the xy-plane. If
you were in class, you may recall that there was some effort involved
in sketching the slices that are shown here. But one boundary of the
sliced region is y=0, along the x-axis. The other, curved boundary, is
"inherited" from z=x2+y. Now z=CONSTANT so as a
curve in the xy-plane, if we write it in the standard
y=function of x format, we get
y=z-x2. Therefore this is a parabola (the square on x!)
opening down (the minus sign). The top of the parabola (the vertex)
occurs when x=0, and there y=z. The intersection(s) of the parabola
with the x axis occur when y=0, and there 0=z-x2, so that
x=+/-sqrt(z). The inner double integral is
Now let's try slicing the region by z=CONSTANT, where the
CONSTANT is some unknown number between 0 and 3. This horizontal slice
of the original spatial region gets us something in the xy-plane. If
you were in class, you may recall that there was some effort involved
in sketching the slices that are shown here. But one boundary of the
sliced region is y=0, along the x-axis. The other, curved boundary, is
"inherited" from z=x2+y. Now z=CONSTANT so as a
curve in the xy-plane, if we write it in the standard
y=function of x format, we get
y=z-x2. Therefore this is a parabola (the square on x!)
opening down (the minus sign). The top of the parabola (the vertex)
occurs when x=0, and there y=z. The intersection(s) of the parabola
with the x axis occur when y=0, and there 0=z-x2, so that
x=+/-sqrt(z). The inner double integral is ![]()
![]() SQUIRREL dx dy. What are the bounds on the
dy integral? We must look at the slice, and see what the highest and lowest values of y are on the slice. The lowest value is 0 and highest value is z: but on the slice, z is a CONSTANT. The highest value depends on z. Now we know:
SQUIRREL dx dy. What are the bounds on the
dy integral? We must look at the slice, and see what the highest and lowest values of y are on the slice. The lowest value is 0 and highest value is z: but on the slice, z is a CONSTANT. The highest value depends on z. Now we know:
![]() y=0y=z
y=0y=z![]() SQUIRREL dx dy
SQUIRREL dx dy
Now in the region pictured, I will slice with y=CONSTANT and see how
big and how small x can be. This is a slice of a slice (maybe
[slice]2?). So the boundary is given by z=x2+y,
and with both z and y CONSTANT, I get x2=z-y, so that
x=+/-sqrt(z-y). These will be the limits on the dx integral.
So the answer is:
![]() z=0z=3
z=0z=3![]() y=0y=z
y=0y=z![]() x=-sqrt(z-y)x=+sqrt(z-y)
SQUIRREL dx dy dz.
x=-sqrt(z-y)x=+sqrt(z-y)
SQUIRREL dx dy dz.
dy dz dx
Now
![]() (
(
![]()
![]() SQUIRREL dy dz)dx.
SQUIRREL dy dz)dx.
Examine the original picture and the limits on the
outermost variable, x, should be revealed. The largest and smallest
x's in this region are +/-sqrt(3), and therefore we get ![]() x=-sqrt(3)x=sqrt(3)(
x=-sqrt(3)x=sqrt(3)(
![]()
![]() SQUIRREL dy dz)dx. Our task is now to slice with x=CONSTANT and try
to get the other integrals' bounds.
SQUIRREL dy dz)dx. Our task is now to slice with x=CONSTANT and try
to get the other integrals' bounds.
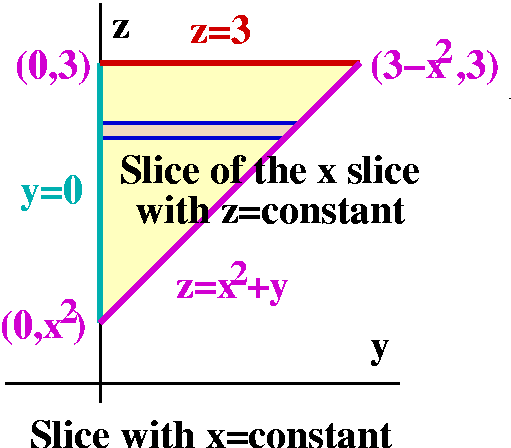
Again, once the "picture" is presented then much of the remainder of
the work is made much easier. We spent some time in class drawing this
picture. When x=CONSTANT, then certainly the slice goes through the
side (on the xz-axis) so that y=0 becomes the left boundary, if we
have z assigned to be the vertical coordinate and take y to be the
horizontal coordinate. Also the top of the region is still z=3. The
other edge is "inherited" again as the effect of the equation
z=x2+y. As I mentioned in class, it is this edge which
irritates my highly trained mathematical psychology (is there such a
thing?). Notice that x=CONSTANT, so that z=x2+y is a
straight line in the yz-plane. The slope of this line is 1. And, when
y=0, z must be x2.
The limits on the outside of the double iterated integral ![]()
![]() SQUIRREL dy dz can now be "read off" from
the picture, since the smallest value of z is x2 and the
largest value is 3. Therefore we have the limits on the outside of the
double iterated integral:
SQUIRREL dy dz can now be "read off" from
the picture, since the smallest value of z is x2 and the
largest value is 3. Therefore we have the limits on the outside of the
double iterated integral: ![]() z=x2z=3
z=x2z=3![]() SQUIRREL dy dz. Finally, the bounds on the
dy integral are obtained by slicing the slice. So now z=CONSTANT also,
and y goes from y=0 to the right side, which is a point on the line
(it still hurts to write this when there is a square in the equation!) z=x2+y, and therefore the upper bound is y=z-x2.
SQUIRREL dy dz. Finally, the bounds on the
dy integral are obtained by slicing the slice. So now z=CONSTANT also,
and y goes from y=0 to the right side, which is a point on the line
(it still hurts to write this when there is a square in the equation!) z=x2+y, and therefore the upper bound is y=z-x2.
So the answer is:
![]() x=-sqrt(3)x=sqrt(3)
x=-sqrt(3)x=sqrt(3)![]() z=x2z=3
z=x2z=3![]() y=0y=z-x2
SQUIRREL dy dz dx.
y=0y=z-x2
SQUIRREL dy dz dx.
dz dx dy
My last attempt:
![]() (
(
![]()
![]() SQUIRREL dz dx)dy.
SQUIRREL dz dx)dy.
Again, the picture shows that y in the solid region
varies from 0 to 3, and we've got 2 of the 6 limits (o.k., the easiest
of them): ![]() y=0y=3(
y=0y=3(
![]()
![]() SQUIRREL dz dx)dy. The y=CONSTANT slice should give the other information.
SQUIRREL dz dx)dy. The y=CONSTANT slice should give the other information.
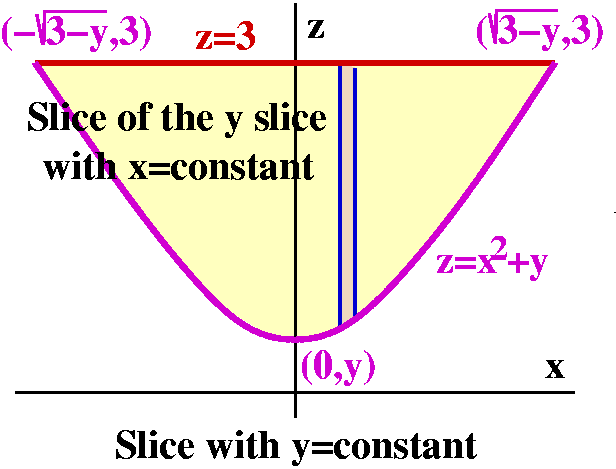
Again, the picture gives much of the information we need. Drawing the picture was some work. Here with y=CONSTANT, the top of the slice is caused by the plane z=3. The bottom of the slice is z=x2+y. Now since x is a variable, this is indeed a parabola. The parabola opens up (positive coefficient on the square term) and has vertex (0,y): the first coordinate is x and the second coordinate in this slice is z. The parabola intersects the line z=3 when 3=x2+y. Since y=CONSTANT, this occurs when x=+/-sqrt(3-y). The outer, x-limits, on the double integral will be x=-sqrt(3-y) and x=+sqrt(3-y). Now slice the slice, for make x=CONSTANT also. z will vary. The highest value of z will be 3 on the [slice]2. The lowest value of z is given by z=x2+y.
The final way the poor SQUIRREL is chopped up and then
summed is
![]() y=0y=3
y=0y=3![]() x=-sqrt(3-y)x=+sqrt(3-y)
x=-sqrt(3-y)x=+sqrt(3-y)![]() z=x2+yz=3SQUIRREL dz dx dy.
z=x2+yz=3SQUIRREL dz dx dy.
Comments
First, this is a classroom example. The solid region is actually not
very complicated. It is a convex region with boundaries given
by low-degree polynomials. The problem would be much more complicated
if the functions defining the boundary weren't so simple, or if some
of the slices weren't convex (then we'd need to split up the
integrals, etc.). I remarked in class and I'll repeat here that the
process of finding these limts seems to be difficult, and hard to
describe -- I don't know yet of a computer program which can do it
reliably.
Here are the "answers" again:
![]() z=0z=3
z=0z=3![]() y=0y=z
y=0y=z![]() x=-sqrt(z-y)x=+sqrt(z-y)
SQUIRREL dx dy dz
x=-sqrt(z-y)x=+sqrt(z-y)
SQUIRREL dx dy dz
![]() x=-sqrt(3)x=sqrt(3)
x=-sqrt(3)x=sqrt(3)![]() z=x2z=3
z=x2z=3![]() y=0y=z-x2
SQUIRREL dy dz dx.
y=0y=z-x2
SQUIRREL dy dz dx.
![]() y=0y=3
y=0y=3![]() x=-sqrt(3-y)x=+sqrt(3-y)
x=-sqrt(3-y)x=+sqrt(3-y)![]() z=x2+yz=3SQUIRREL dz dx dy.
z=x2+yz=3SQUIRREL dz dx dy.
I can't immediately see that the darn limits describe the same volume
in R3. Maybe you can. But you should see, just looking at
the patterns of the answers, what sorts of limits are "legal" and what
are not. You can only have variables in the limits if they haven't
been integrated yet. For example, in the last answer, the lower limit
of the innermost integral is z=x2+y, and the outside two
integrals are dx and dy. I could not have a limit in, say, the middle
integral of the form z=x2+y because there would be only one
variable left to be integrated, and there isn't any way to "kill" both
x and y. So there is a rough guide to the grammar (?) of the bounds on
iterated integrals.
How can you check this kind of "computation"?
Generally checking these things can be difficult and tedious. Luckily,
we are in the 21st century and I have powerful
friends. Well, I guess I can ask some electrons to run around. Look at
the following:
> W:=x^6*y^8*z^2;
6 8 2
W := x y z
> int(int(int(W,x=-sqrt(z-y)..sqrt(z-y)),y=0..z),z=0..3);
1/2
417942208512 3
-----------------
5763232475
> int(int(int(W,y=0..z-x^2),z=x^2..3),x=-sqrt(3)..sqrt(3));
1/2
417942208512 3
-----------------
5763232475
> int(int(int(W,z=x^2+y..3),x=-sqrt(3-y)..sqrt(3-y)),y=0..3);
1/2
417942208512 3
-----------------
5763232475
I specified a "random" function, W, to replace
SQUIRREL. I wanted the antiderivatives not to be a
problem, so I just specified some powers of x and y and z. I asked
Maple to compute the triple iterated integrals in all three
ways we found. The answers are shown. They are such large and silly
numbers, and they all agree exactly. I am fairly confident the bounds on
the iterated integrals are correct.
QotD
Choose one of the other three orders and write the triple iterated
integral for that order. You can't integrate
SQUIRREL without more specificity, so all you can do,
and what I wanted, was write the precise bounds. I think the answers
are (after reading many student answers):
![]() z=0z=3
z=0z=3![]() x=-sqrt(z)x=sqrt(z)
x=-sqrt(z)x=sqrt(z)![]() y=0y=z-x2
SQUIRREL dy dx dz
y=0y=z-x2
SQUIRREL dy dx dz
![]() x=-sqrt(3)x=sqrt(3)
x=-sqrt(3)x=sqrt(3)![]() y=0y=3-x2
y=0y=3-x2![]() z=x2+yz=3
SQUIRREL dz dy dx
z=x2+yz=3
SQUIRREL dz dy dx
![]() y=0y=3
y=0y=3![]() z=yz=3
z=yz=3![]() x=-sqrt(z-y)x=sqrt(z-y)
SQUIRREL dx dz dy
x=-sqrt(z-y)x=sqrt(z-y)
SQUIRREL dx dz dy
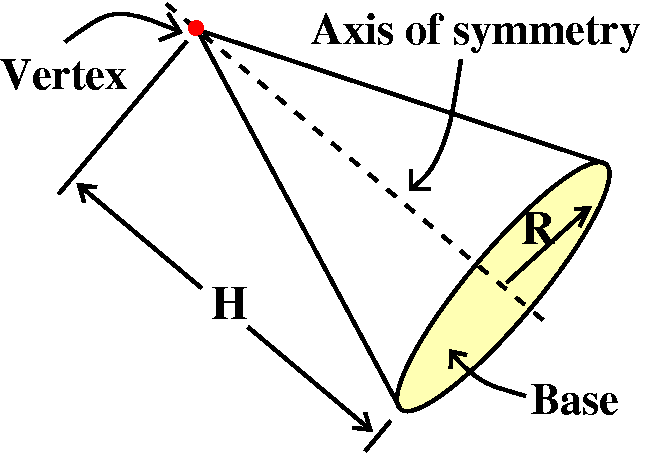 (Almost a real problem!) Moment of inertia of a cone
(Almost a real problem!) Moment of inertia of a cone
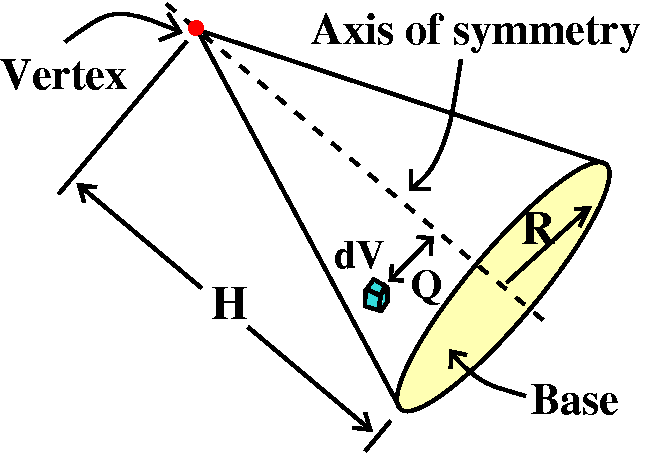
Suppose a right circular cone with base radius R and height H is
filled with a homogeneous substance with constant density, C. What is
the moment of inertia of the cone about its axis of symmetry?
Let me be more clear about some vocabulary.
Right circular cone Take a circle (to be called the base). Put
a line perpendicular to the plane of the circle through the circle's
center. Pick a point on this line which is not on the plane of the
circle. Connect that point (called the vertex) with the edge of the
circle. The solid interior to the collected line segments and the
circle is called a right circular cone. The "right" refers to the
right angle that the axis of symmetry makes with the base.
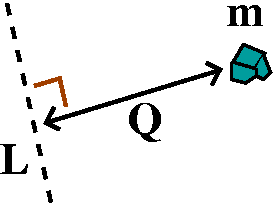
Moment of inertia Take a little piece of mass, m, external to a
line, L. The moment of inertia of m about L is defined to be
Q2m where Q is the distance from m to L.
There are many discussions of the moment of inertia on the web. One link
declares that it is the "inertia with respect to rotational motion"
and another
reads "... the rotational analog of mass for linear motion. It appears
in the relationships for the dynamics of rotational motion. The moment
of inertia must be specified with respect to a chosen axis of
rotation."
I think of a small merry-go-round in a playground, and trying to push
the seats around (with many noisy, small children on them). The moment
of inertia measures the resistance of the merry-go-round to being
pushed.
 Beginning the analysis
Beginning the analysis
Take a little piece of volume, dV, inside the cone. The mass of this
volume is C dV. Suppose Q is the distance of piece from the axis
of symmetry. Then the moment of inertia of this chunk of mass about
the axis of symmetry is Q2C dV. To get the moment of
intertia of the whole cone we need to add up the pieces of the moment
of intertia. So we need ![]()
![]()
![]() The whole coneQ2C dV.
The whole coneQ2C dV.
A major decision in this and many other geometric/physical problems is
where/how to put a coordinate system on the objects involved. Here
almost surely people would agree that the axis of symmetry should be
the z-axis. Sane human beings can disagree about where the origin
should be. Some would put it at the vertex of the cone, with the base
"up", and some would put the origin at the center of the base of the
cone, with the vertex "up". I'll do the first alternative because I
think some of the algebra will be simpler. As I mentioned in class, I
drew the cone in this awkward way because I wanted people to think
about how they would prefer to see it.
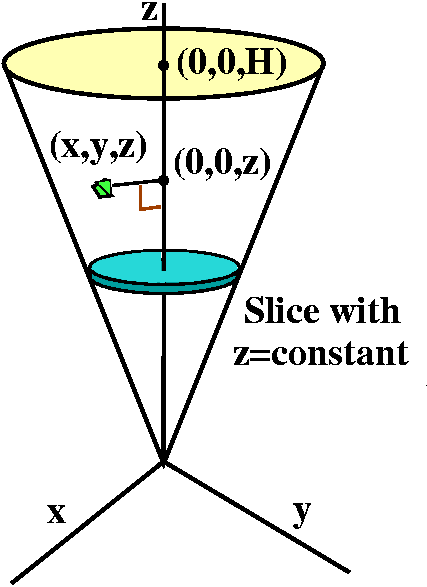 Coordinates?
Coordinates?
Now the cone is sitting correctly (?) in the picture. The chunk of
volume is at (x,y,z), and the closest point on the axis of symmetry is
(x,y,0). The distance between (x,y,z) and the axis must therefore be
sqrt(x2+y2. We should convert the triple
integral into an iterated integral. What should be the order?
Actually, it is possible to do this in any order, but the
simplest way has dz on the outside. Then the z limits are clear: from
0 to H, and the slices with z=CONSTANT are also simple shapes: circles.
The triple integral ![]()
![]()
![]() The whole coneQ2C dV
becomes the triply iterated integral
The whole coneQ2C dV
becomes the triply iterated integral
![]() z=0z=H(
z=0z=H(![]()
![]()
![]() (sqrt(x2+y2))2C dAxy)dz. I wrote dAxy to remind myself that the double integral is in the xy-plane.
(sqrt(x2+y2))2C dAxy)dz. I wrote dAxy to remind myself that the double integral is in the xy-plane.
The inside double integral is:
![]()
![]()
![]() (x2+y2)C dAxy.
(x2+y2)C dAxy.
Recognition: polar
Things are in red so that a bell will ring in your head and you will
think, polar!!!. Certainly
x2+y2=r2 and
dAxy=r dr d![]() . The limits on
. The limits on ![]() for a
whole circle are 0 and 2Pi. The limits on r are 0 (the center of the
circle) out to the radius of the circle, which I will cleverly call
RAD. The double integral is then
for a
whole circle are 0 and 2Pi. The limits on r are 0 (the center of the
circle) out to the radius of the circle, which I will cleverly call
RAD. The double integral is then
![]()
![]() =0
=0![]() =2Pi
=2Pi![]() r=0r=RAD(r2)C r dr d
r=0r=RAD(r2)C r dr d![]() .
.
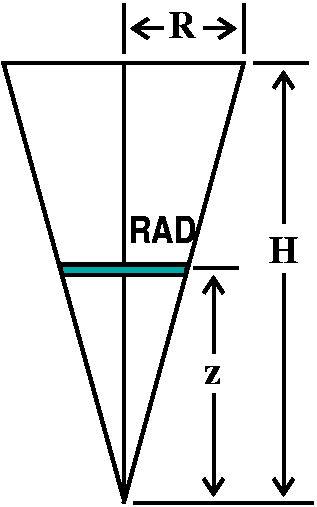
RADius
Look at the cone sideways and see some expected right triangles, so
RAD/z=R/H and RAD=(R/H)z. The double
integral becomes
![]()
![]() =0
=0![]() =2Pi
=2Pi![]() r=0r=(R/H)zC r3 dr d
r=0r=(R/H)zC r3 dr d![]() .
.
Computation
![]() r=0r=(R/H)zC r3 dr=(C/4)r4]r=0r=(R/H)z=(C/4)R4z4/H4.
r=0r=(R/H)zC r3 dr=(C/4)r4]r=0r=(R/H)z=(C/4)R4z4/H4.
![]()
![]() =0
=0![]() =2Pi(C/4)R4z4/H4d
=2Pi(C/4)R4z4/H4d![]() =[(Pi C)/2]R4z4/H4.
(Easy: no
=[(Pi C)/2]R4z4/H4.
(Easy: no ![]() in the integrand so
just multiply by 2Pi.)
in the integrand so
just multiply by 2Pi.)
![]() z=0z=H[(Pi C)/2]R4z4/H4dz=[(Pi C)/10]R4z5/H4]z=0z=H=[(Pi C)/10]R4H.
Is this correct?
z=0z=H[(Pi C)/2]R4z4/H4dz=[(Pi C)/10]R4z5/H4]z=0z=H=[(Pi C)/10]R4H.
Is this correct?
The units of moment of inertia should be
mass·(length)2. Since C is a density, C's units are
mass/(length)3. And R4H is length5 so
the units are correct. Sigh. What about the crazy constants (Pi and
10)? Here is help from an engineering student. Mr. Doig reports via e-mail:
|
Upon consultation with my statics text, I present to you: ... I_x = 3/10 * m * a^2 where a is the radius of the base of the cone. |
 Cylindrical coordinates
Cylindrical coordinates
This is a coordinate system that augments the r and ![]() of polar
coordinates with z. Any problem with an axis of symmetry may be easier
to understand in cylindrical coordinates. In words, the position of a
point in the cylindrical coordinate system is described by its height,
z, from the base coordinate plane. The foot of a perpendicular from
the point to the plane then has a description in terms of an angle,
of polar
coordinates with z. Any problem with an axis of symmetry may be easier
to understand in cylindrical coordinates. In words, the position of a
point in the cylindrical coordinate system is described by its height,
z, from the base coordinate plane. The foot of a perpendicular from
the point to the plane then has a description in terms of an angle,
![]() , from an initial ray (usually the positive x-axis) and a
distance, r, from the origin.
, from an initial ray (usually the positive x-axis) and a
distance, r, from the origin.
Here are some basic axially symmetric figures:
Cylinder Example: r=5.
Cone Example: z=7r.
Elliptical paraboloid Example: z=3r2.
The location of Piscataway
Where are we? I got several answers. But I enlightened students with
these facts:
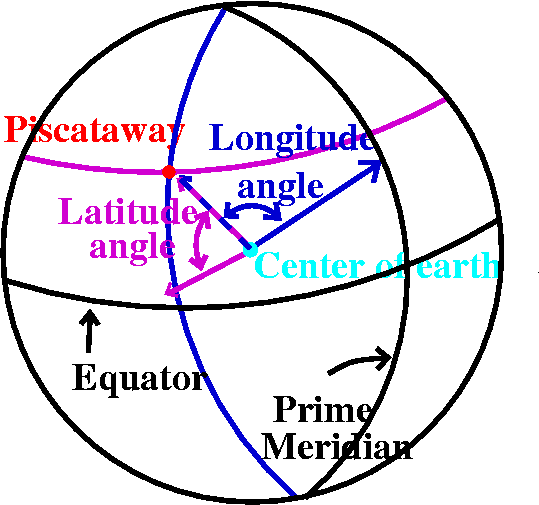 Pistcataway's latitude is 40.499oN
and Piscataway's longitude is 74.399oW.
Pistcataway's latitude is 40.499oN
and Piscataway's longitude is 74.399oW.
Or, in more antique fashion, the latitude is
40o32´39´´ and the longitude is
74o28´28´´.
Do not be as confused as I am. This is
not about stalagtites (the down-dropping things) and stalagmites (the
up-growing things).
We discussed what latitude and longitude are. The prime meridian is a
great circle (a circle whose center is the center of the earth) and it
goes through Greenwich, England and the north/south poles. The
longitude is the angle between that great circle and the great circle
connecting Piscataway and the north/south poles. The angle has vertex
at the center of the earth. W=west in the latitude, and it means the
the angle opens to the west of the prime meridian. Latitude is the
angle from the intersection of the great circle describing
Piscataway's longitude to Piscataway, again with the vertex at the
center of the earth. N=north means that we look in the northern
hemisphere. Constant latitude means a "small" circle. Constant
longitude means a great circle (actually semicircle). Piscataway is
located at the unique intersection on the surface of the earth of
these two curves.
I presume you know that the "23 and a half"
degree tilt of the axes (north/south pole line) from the ecliptic (the
plane of the earth's orbit about the sun) is responsible for seasonal
variation. Nature is terrific!
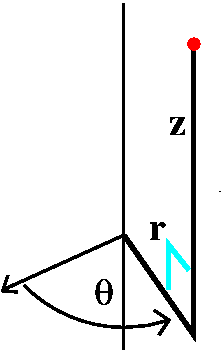
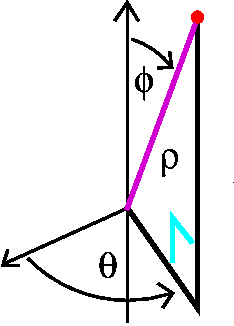
Spherical coordinates
Take a point in space. We describe its position with one length and
two angles. The length is the distance of the point to the origin: the
length of the radius vector. The first angle, phi, is the angle from
the positive z-axis to the radius vector. The second angle, ![]() , is
the angle from the positive x-axis to the projection of the radius
vector on the xy-plane. Spherical coordinates are very useful in
problems with central symmetry. I'll work a bit with them next
time.
, is
the angle from the positive x-axis to the projection of the radius
vector on the xy-plane. Spherical coordinates are very useful in
problems with central symmetry. I'll work a bit with them next
time.
HOMEWORK
Please read about triple integrals and cylindrical and spherical
coordinates: 15.7, 12.7, and 15.8
 Spring is coming!
Spring is coming!| Birders in the eastern United States and in many parts of the West are likely to see Fox Sparrows only during migration or winter, for this large sparrow nests in northern and western Canada and in mountainous areas in the western states. |
| Both the Fox Sparrow's common name and the Latin-specific epithet "iliaca" refer to the "foxy" rufous red color of eastern and northern Fox Sparrows. |
 dA in polar coordinates
dA in polar coordinates
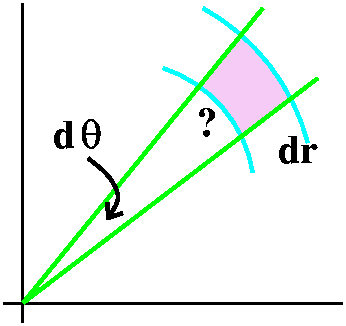
Here's a mostly emotional argument for how dA should be
described in polar coordinates. Later I will be able to give a more
precise derivation. Or you can look in the textbook (section 15.4) for
a more careful discussion.
Suppose I want to compute the area obtained by changing r to r+dr and
![]() to
to ![]() +d
+d![]() . The picture displays this area, dA, magnified a
lot. As mentioned, dA is an area and has dimensions
length2. If d
. The picture displays this area, dA, magnified a
lot. As mentioned, dA is an area and has dimensions
length2. If d![]() and dr are very small, the area dA is
approximately rectangular, and maybe the area is the product of the
length of its sides. Well, one side is dr but the other side is
not d
and dr are very small, the area dA is
approximately rectangular, and maybe the area is the product of the
length of its sides. Well, one side is dr but the other side is
not d![]() . Angles don't have dimensions (they are ratios!)
and, anyway, if you move circles centered at the origin in and out,
you can see that the intercepted arcs change in length. These arcs are
very short close to the origin and are longer as the radius of the
circle gets bigger. In fact, the length of the intercepted arc is
directly proportional to r. This length is also directly proportional
to d
. Angles don't have dimensions (they are ratios!)
and, anyway, if you move circles centered at the origin in and out,
you can see that the intercepted arcs change in length. These arcs are
very short close to the origin and are longer as the radius of the
circle gets bigger. In fact, the length of the intercepted arc is
directly proportional to r. This length is also directly proportional
to d![]() : if the angle at the origin is doubled, the length of the
intercepted arc is also doubled. Werll, "directly proportional means
that there is some constant, uhhh ..., let's call it K, so that the
length is K r d
: if the angle at the origin is doubled, the length of the
intercepted arc is also doubled. Werll, "directly proportional means
that there is some constant, uhhh ..., let's call it K, so that the
length is K r d![]() . What is K? In the nicest world, K
would be 1 because then I would not have to worry about it any
more. Well, golly, that is exactly why radian measure
was invented: so this darn constant would be 1 and would not
need attention.
. What is K? In the nicest world, K
would be 1 because then I would not have to worry about it any
more. Well, golly, that is exactly why radian measure
was invented: so this darn constant would be 1 and would not
need attention.
Comment: so what is K and what about those words?
Why is K=1 in radians? Well, the circumference of a circle of radius r
is 2Pi r. Here the d![]() is 2Pi. So apparantly the K is indeed
1. If you insisted on using degrees in all of calculus, then the angle
for a whole circle would be 360, and for Kr d
is 2Pi. So apparantly the K is indeed
1. If you insisted on using degrees in all of calculus, then the angle
for a whole circle would be 360, and for Kr d![]() =K(360)r to be
2Pi r, you would need K=2Pi/360, which is approximately the
obnoxious number .01745. I looked on the web, and the only other
candidate for angle measurement I found was the grad,
introduced in France as part of the metric system (my calculator
permits angle computations in grads). There are 400 grads in a circle
(I never knew that before today) and therefore the constant K, if we
used grads in calculus, would be 2Pi/400 which is approximately
.01571, also obnoxious. Yes, things would be better if Pi were equal
to 3.
=K(360)r to be
2Pi r, you would need K=2Pi/360, which is approximately the
obnoxious number .01745. I looked on the web, and the only other
candidate for angle measurement I found was the grad,
introduced in France as part of the metric system (my calculator
permits angle computations in grads). There are 400 grads in a circle
(I never knew that before today) and therefore the constant K, if we
used grads in calculus, would be 2Pi/400 which is approximately
.01571, also obnoxious. Yes, things would be better if Pi were equal
to 3.
Euphemism: The expression of an unpleasant or embarrassing notion
by a more inoffensive substitute
The word "golly" is a euphemism for "God" and the word "darn" is a
euphemism for "damn".
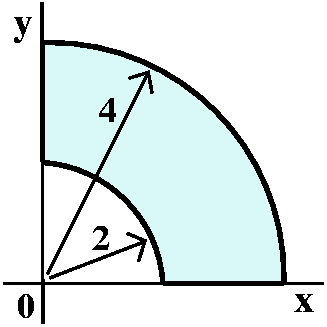 Computing the integral
Computing the integral
Let's return to computing ![]()
![]() Rx2+y2dA, if R is the region
shwon to the right (in the first quadrant, with the curves arcs of
circles centered at the origin).
Rx2+y2dA, if R is the region
shwon to the right (in the first quadrant, with the curves arcs of
circles centered at the origin).
How does one recogize that the integral is "polarish"? It is a
classroom example, but the integrand has central symmetry, and so does
the region. You may be helped if you recall the conversion formulas
From r,I've given the formulas the way I most often use them. In particular, the formula for gettingto x, y From x, y to r,
------------------- ------------------- x=r cos
r2=x2+y2 y=r sin
tan
=y/x
I recognize (primarily from the picture, but I can also use the
formulas) that R is described by 0<=![]() <=Pi/2 and by
2<=r<=4. We can convert the integral into polar coordinates:
<=Pi/2 and by
2<=r<=4. We can convert the integral into polar coordinates:
![]()
![]() Rx2+y2dA=
Rx2+y2dA=![]() 0Pi/2
0Pi/2![]() 24r2 r dr d
24r2 r dr d![]() =
=![]() 0Pi/2
0Pi/2![]() 24r3dr d
24r3dr d![]() =
=![]() 0Pi/2(1/4)r4]r=2r=4d
0Pi/2(1/4)r4]r=2r=4d![]() =60
=60![]() ]0Pi/2=30Pi.
]0Pi/2=30Pi.
Of course the computation is easy. It was arranged to that after
conversion to polar coordinates things would work out well. The
computation in rectangular coordinates, including finding the
boundaries of the integrals (there would have to be two of them) and
then computing the antiderivatives, would be very tedious. This is not
an entirely artificial example: it is the mathematics behind the
computation of the moment of inertia about the origin of a thin
homogeneous plate in the shape of the region R.
The earth is flat
So here I will try to convince you byu combining a valuable and
truthful computation with extremely dubious logic, that the earth is
flat. Please be reassured: the earth is probably not flat.
Newton's
Law of Universal Gravitation
Suppose I have two "point masses", m1 and m2,
which are a distance d apart. The magnitude of the force attracting
them together is directly proportional to the product of their masses
and inversely proportional to the square of the distance separating
them. The constant of proportionality is usually called G (alas, not
to recognize the lecturer!). Therefore the magnitude of the force is
G m1m2/d2.
Here's a quote from another
site:
|
... this constant [G] was worked out by Henry Cavendish in 1798. He
achieved this by measuring the gravitational attraction between two
1kg lead balls at a distance of 1 metre. I would guess that you would assume that this experiment must have found the attraction to be very small, in fact it was so small it was a stunning achievement to measure the tiny acceleration caused and to therefore calculate the gravitational attractive force (using Newton's second law). Cavendish found the force to be 6.67 x 10-11 Nm2/kg2 (or approximately 0.0000000000667 Nm2/kg2!). |
 The plate: from description to integral
The plate: from description to integral
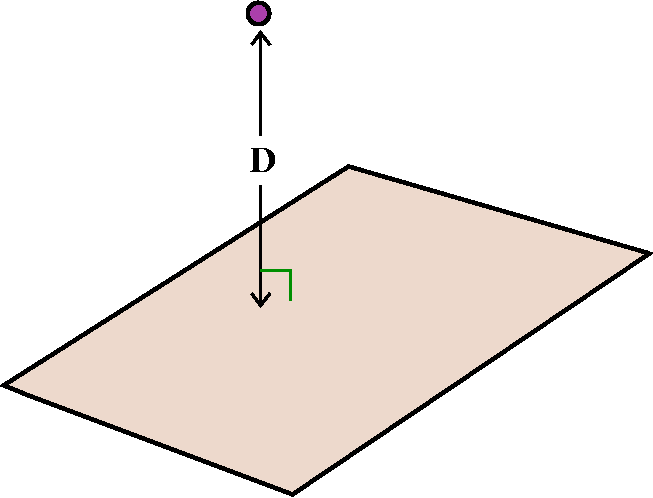
Let me assume that the "universe" consists of an infinite flat
homogeneous plate, and an external small object with a mass of m whose
distance to the plate is D. What is the gravitational attraction of
the object to the plate? A major part of such a problem is setting it
up. The correct location of the origin and the axes can make problems
much easier. In this case, I believe there are two reasonable
locations for the origin: the object, or the closest point on the
plane to the object. I'll use that closest point to be the origin. Of
course, the xy-plane with be the plate, and therefore the coordinates
of the object will be (0,0,D). The plate is homogeneous and thin. To
avoid having too many letters around, let me assume that the plate is
1 unit thick (otherwise I'll just have to carry around the thickness
in all of the computations, and I have a hard enough time with my own
thickness, both mental and physical). Since the plate is homogeneous
(the same at every point), it has a density, p (should be rho, but
html doesn't have Greek letters). A small chunk of the plate ("dA")
located at the point (x,y) will have mass equal to p dA (remember
the thickness is 1, and so it is already in the formula).
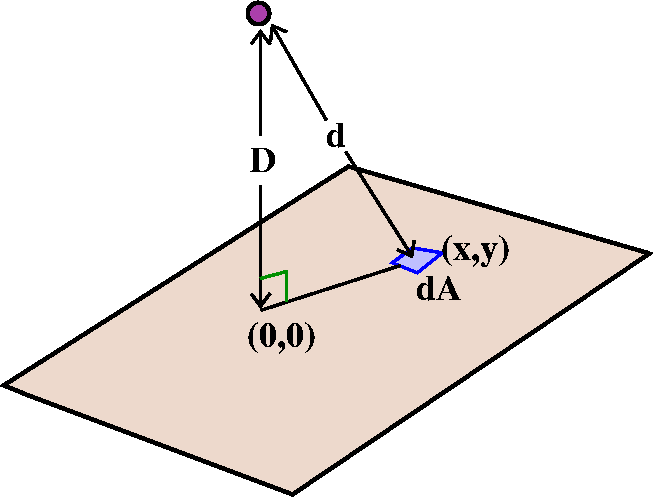
Now let us convert the ideas into more rigid "mathspeak". The magnitude of the force from the external mass to the dA piece of the plate is Gmp dA/d2. The piece is located at (x,y), and (x,y), (0,0), and the location of the external mass are at the vertices of a right triangle. The hypoteneuse of the right triangle is d, and the leg of the triangle from the external mass to (0,0) is D. The distance from (0,0) to (x,y) is sqrt(x2+y2). Therefore d2=D2+(sqrt(x2+y2)). The square root and the square cancel. The magnitude of the force is Gmp dA/(D2+x2+y2). Several students noticed a surprizing symmetry. Since we are dealing with the whole plane, R2, the chunk of dA at (x,y) has an antipodal chunk at (-x,-y), having the same mass and the same distance to the external object. Therefore the "lateral" parts of the forces (parallel to the plane) exactly cancel out. We only need to compute the vertical component of the force.
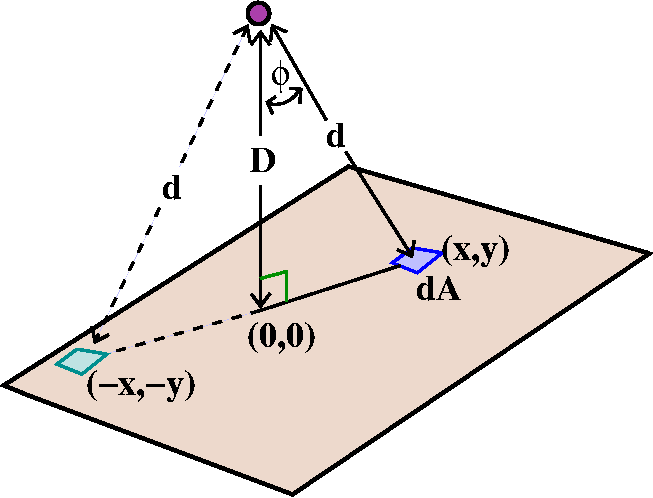 The vertical component of the force is the magnitude of the force
multiplied by the cosine of the angle, phi, between the vertical line
and the line connecting the external object to dA. But cos phi is
D/d, which is D/sqrt(D2+x2+y2). The
function to be integrated is the vertical component of the
gravitational attraction between the external object and dA. This is
GmpD dA/(D2+x2+y2)3/2. Since
the plate is infinite, we want
The vertical component of the force is the magnitude of the force
multiplied by the cosine of the angle, phi, between the vertical line
and the line connecting the external object to dA. But cos phi is
D/d, which is D/sqrt(D2+x2+y2). The
function to be integrated is the vertical component of the
gravitational attraction between the external object and dA. This is
GmpD dA/(D2+x2+y2)3/2. Since
the plate is infinite, we want ![]()
![]() R2Gmp dA/(D2+x2+y2)3/2.
R2Gmp dA/(D2+x2+y2)3/2.
Computing the integral
Many of the letters are constants: G and m and p and D. We can pull them out of the integral. We need to compute:
![]()
![]() R2dA/(D2+x2+y2)3/2.
R2dA/(D2+x2+y2)3/2.
Since this comes immediately after a discussion of polar coordinates, the student alert to pedagogical plans (how folks teach) will immediately think of converting to polar coordinates. Indeed, even those who are not so ... prescient might think: the region has symmetry around (0,0) and the integrand has that same x2+y2, so let's try polar coordinates!
Then dA=r dr d![]() , and
r2=x2+y2, and all we need are the
limits on the integral. For the whole plane, r should go from 0 to
infinity, and
, and
r2=x2+y2, and all we need are the
limits on the integral. For the whole plane, r should go from 0 to
infinity, and ![]() should go from 0 to 2Pi. The appearance of
infinity forces me to finally acknowledge that this is an improper
integral.
should go from 0 to 2Pi. The appearance of
infinity forces me to finally acknowledge that this is an improper
integral.
![]() 02Pi
02Pi![]() 0infinityr dr d
0infinityr dr d![]() /(D2+r2)3/2.
/(D2+r2)3/2.
The inner (improper) integral
I will be careful, since I am supposed to be teaching a math course.
![]() 0infinityr dr d
0infinityr dr d![]() /(D2+x2+y2)3/2=limB-->infinity
/(D2+x2+y2)3/2=limB-->infinity![]() 0Br dr d
0Br dr d![]() /(D2+r2)3/2
/(D2+r2)3/2
The r accompanying the dr is exactly what's needed to do the
substitution u=D2+r2 with du=2r dr. We sort out the constant by guessing (maybe).
![]() 0Br dr d
0Br dr d![]() /(D2+r2)3/2=-1/sqrt(D2+r2)]r=0r=B=
-1/sqrt(D2+B2)-{-1/sqrt(D2+02)}
/(D2+r2)3/2=-1/sqrt(D2+r2)]r=0r=B=
-1/sqrt(D2+B2)-{-1/sqrt(D2+02)}
As B-->infinity, the term
-1/sqrt(D2+B2)-->0. The other term has minus
signs which cancel, and (let's say D>0) square/sqrt which cancel,
so the limit is 1/D. But we need to multiply by the factors we pulled
out. The answer is:
GmpD(1/D)=Gmp.
And, therefore ...
There is no D in the answer!. The gravitational attraction of
a flat earth is constant! Now the lecturer discussed the fact that he
weighs the same standing on the floor and standing on a
table. Therefore ... therefore ... the earth is flat. (Similar
supporting logic: wouldn't people who wanted to lose weight climb
Mt. Everest, because they would lose weight when ...).
Discussion of the claim
Capacitor
This is still an interesting and useful computation. An electron is
very small. If we try to analyze the attraction an electron might have
to a small charged plate, even, say, 1/4 inch square, then, to the
electron, the plate might as well be infinite. That is, if the
electron in is near the center of the plate, the edge effect hardly
matters at all. And the force on the electron does not depend on
distance. Such considerations occur in the design of classical
capacitors, used in many devices.
The ocean
People who study the ocean (such as those affiliated with the Rutgers Institute of Marine &
Coastal Sciences are interested in such aspects as the temperature
and salinity and pressure and flow of the water. They employ remote
sensing devices to try to record data at various depths. Then analysis
of the data together with theory is used to try to predict interesting
things: the weather, fishing prospects, etc. I'm going to look at a
very simple model and try to link it up with things we study in this
course.
 The average temperature of a box of ocean
The average temperature of a box of ocean
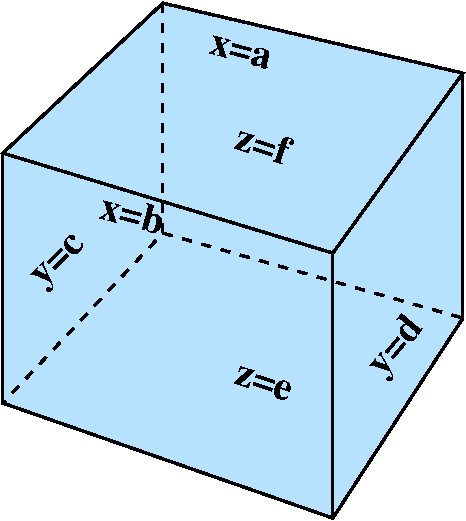
Consider a "box of ocean", say the region between x=a and x=b, y=c
and y=d, and z=e and z=f (here a<b, c<d, and e<f). We might
put some sort of measuring device at a point in this box and measure
the temperature of the water at that point. One or a few temperature
measurements are probably not going to give good information. If the
economics (!) and the equipment and time (!) are available, many
measurements should be made. One representation of the measurements might be the average: so the computation would be
SUM of all of the temperature measurements ------------------------------------------- The number of temperature measurementsConsiderations which might influence this "experiment" include the following:
Going abstract: the "limit"
Let me look at the average a bit more. The discussion that follows seems very clever to
me.
Suppose that I assume that the number of observations is
n3 where n is a large positive integer. Then I would have
something like this:
SUM of all of the temperature measurements
-------------------------------------------
n3
I will multiply the top and bottom of this fraction by
(b-a)(d-c)(f-e), so we would have:
SUM of all of the temperature measurements (b-a)(d-c)(f-e)
------------------------------------------- · ----------------
n3 (b-a)(d-c)(f-e)
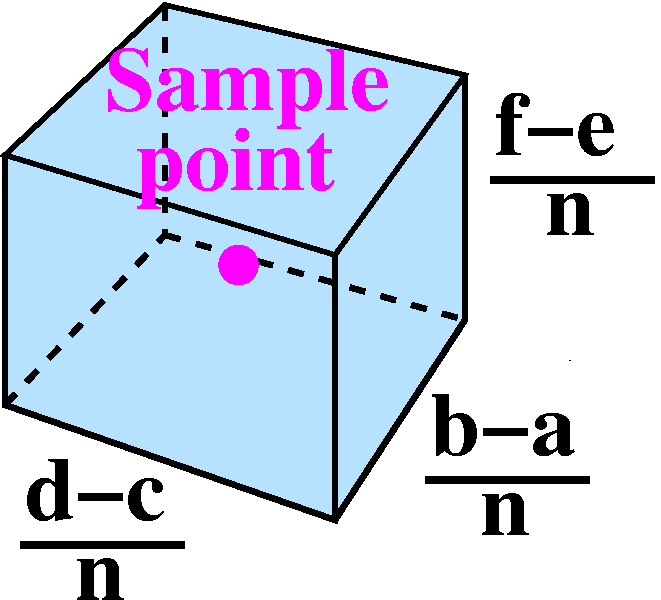 Just consider part of this, the fraction
(b-a)(d-c)(f-e)/n3. This is the same as
[(b-a)/n]·[(d-c)/n]·[(f-e)/n]. If n is large, this is
the same as splitting up each of the edges of the box into n equal
pieces, and what we have is a very small box of the ocean. Now if we
also want the points we measure to be well-distributed, then we might
expect that most of the boxes will contain exactly one sample point. We can think of
f(that sample point)·[(b-a)/n]·[(d-c)/n]·[(f-e)/n]
as f(that sample point)dx dy dz or as
f(that sample point)dV where dV is this very small box
inside the huge box of ocean. When we take the SUM we actually have an approximating Riemann
sum to
Just consider part of this, the fraction
(b-a)(d-c)(f-e)/n3. This is the same as
[(b-a)/n]·[(d-c)/n]·[(f-e)/n]. If n is large, this is
the same as splitting up each of the edges of the box into n equal
pieces, and what we have is a very small box of the ocean. Now if we
also want the points we measure to be well-distributed, then we might
expect that most of the boxes will contain exactly one sample point. We can think of
f(that sample point)·[(b-a)/n]·[(d-c)/n]·[(f-e)/n]
as f(that sample point)dx dy dz or as
f(that sample point)dV where dV is this very small box
inside the huge box of ocean. When we take the SUM we actually have an approximating Riemann
sum to box of oceanT(x,y,z) dV ------------------------- Volume of the box
A specific example
What if our box was bounded by x=0 and x=2, y=0 and y=3, and z=0 and
z=5, and the temperature at (x,y,z) was given by the formula
T(x,y,z)=x2+7yz. Then if we wanted to compute the average
temperature we would convert a triple integral into a (triply)
iterated integral. In this case, I see no advantage in any one of the
six possible orders, so:
![]() 02
02![]() 05
05![]() 03
x2+7yz dy dz dx
03
x2+7yz dy dz dx
Let's compute, from the inside out: ![]() 03
x2+7yz dy dz dx=yx2+(7/2)y2z]y=0y=3=3x2+(63/2)z.
03
x2+7yz dy dz dx=yx2+(7/2)y2z]y=0y=3=3x2+(63/2)z.
![]() 053x2+(63/2)z dz=3x2z+(63/4)z2]z=0z=5=15x2+(63/4)(25).
053x2+(63/2)z dz=3x2z+(63/4)z2]z=0z=5=15x2+(63/4)(25).
![]() 0215x2+(63/4)(25) dx=5x3+(63/4)(25)x]x=0x=2=40+(63/2)(25).
0215x2+(63/4)(25) dx=5x3+(63/4)(25)x]x=0x=2=40+(63/2)(25).
If this were the late 20th century, instead of 1872, we could type:
> int(int(int(x^2+7*y*z,y=0..3),z=0..5),x=0..2);
1655/2
Incidentally, I checked and 40+(63/2)(25) is the same as (1655)/2.
This isn't the average temperature. For that we need to divide by the volume of the box which is 2·3·5=30. The result is (331/6).
The "moral" of this: computation of triple iterated
integrals
I don't think that there are any essential new difficulties introduced
when we move from evaluating double iterated integrals to evaluated
triple iterated integrals. Yes, there are more opportunities for error
(50% more?) but they are not new in type. So I won't devote too much
time to actual evaluation.
Describing a volume in space
Since the difficulties involved in computation of a triple iterated
integral really are just those we've seen already with double
interated integrals, I want to illustrate something that definitely
seems more complicated to me: going from a description of a region in
space over which we want to compute a definite integral to the
corresponding iterated integrals (and there are 6=3! possible ordered
for the iterated integral). Let me "integrate" (convert to iterated
integrals) the function Bear over the region in space
(R3) defined by y=0, z=3, and z=x2+y.
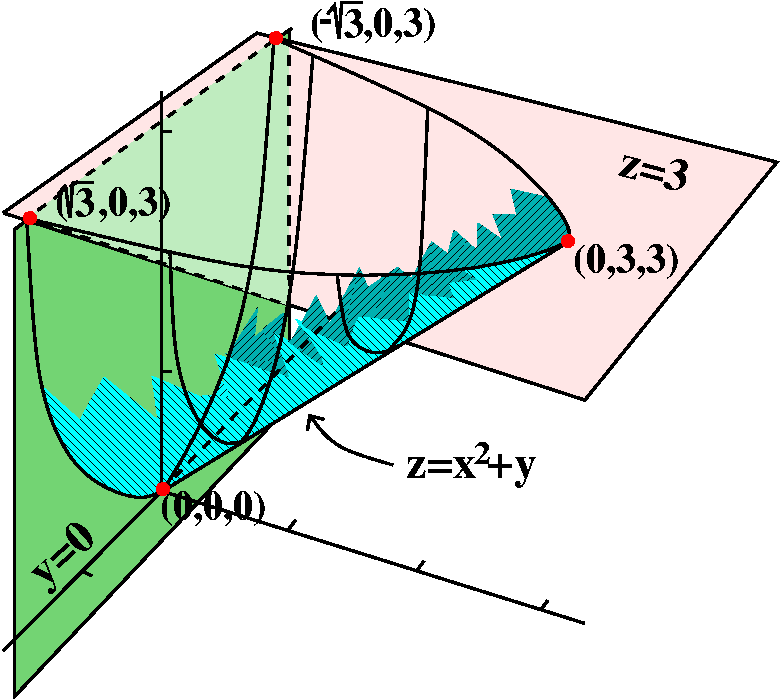 I want to
begin by sketching the region. The planes y=0 (the xz-plane) and z=3
(push the xy-pane up three units) are easy enough. The surface
z=x2+y cut by y=0 and z=3 is maybe not so obvious. When y=0
we get a parabolic arc cut off at z=3 in the xz-plane. As y increases,
the parabolic arc is translated up, but still cut off at z=3. In the
yz-plane, when x=0, the slice is a segment of the line z=y from (0,0)
(with the coordinates being y and z) to (3,3). The surface cuts the
plane z=3 with the parabola 3=x2+y or y=3-x2,
which opens "downward" (in the standard orientation of
xy-planes).
I want to
begin by sketching the region. The planes y=0 (the xz-plane) and z=3
(push the xy-pane up three units) are easy enough. The surface
z=x2+y cut by y=0 and z=3 is maybe not so obvious. When y=0
we get a parabolic arc cut off at z=3 in the xz-plane. As y increases,
the parabolic arc is translated up, but still cut off at z=3. In the
yz-plane, when x=0, the slice is a segment of the line z=y from (0,0)
(with the coordinates being y and z) to (3,3). The surface cuts the
plane z=3 with the parabola 3=x2+y or y=3-x2,
which opens "downward" (in the standard orientation of
xy-planes).
I've attempted to sketch the surface to the right of this description.
The colors are meant to show some of the curviness. There are some
extreme points which turn out to be
useful in setting up iterated integrals. Those are the points (0,0,0),
(0,3,3), (sqrt(3),0,3), and (-sqrt(3),0,3). These points are where
each of the coordinates (x and y and z) attain maximum and minimum
values on the solid region whose boundary curves were given.
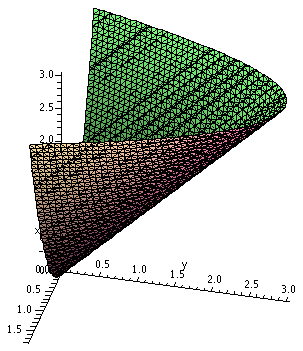 Nomenclature The surface z=x2+y is called a
tilted parabolic cylinder. It is a parabolic cylinder because
it results from a family of parallel lines in space which all meet the
parabola z=x2 in the xz-plane. It is "tilted" because these
lines are not perpendicular to the xz-plane.
Nomenclature The surface z=x2+y is called a
tilted parabolic cylinder. It is a parabolic cylinder because
it results from a family of parallel lines in space which all meet the
parabola z=x2 in the xz-plane. It is "tilted" because these
lines are not perpendicular to the xz-plane.
Now to the right is Maple's attempt to draw the tilted
parabolic cylinder in the region of interest to us. The picture to the
right is the result of using the command:
implicitplot3d(z=x^2+y,x=-1.75..1.75,y=0..3,z=0..3, grid=[40,40,40],axes=normal,labels=[x,y,z]);
This command did not display an immediate result on my home
computer. It requested that Maple to check a
three-dimensional grid of 403=64,000 points, and then
compute the light and the angle, etc. I rotated and chose lighting so
that I got the image displayed here. That's why "supercomputers" are
needed to draw the lighting effects for Pixar, etc.
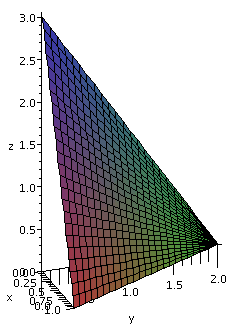 Maple can draw ...
Maple can draw ...
... some useful pictures for us when we want to look at double and
triple integrals. Last time we looked at the iterated integral
![]() 02
02![]() x=0x=1-(1/2)y3-3x-(3/2)y dx dy
x=0x=1-(1/2)y3-3x-(3/2)y dx dy
The command plot3d(3-3*x-(3/2)*y,x=0..1-(1/2)*y,y=0..2);
produces (after putting in the axes and making the view
constrained) the graph shown to the right. I did not know
until fairly recently that Maple had the capacity to show
only pictures corresponding to double integral limits. This could be
very helpful.
I also tried to experiment with the other problems I did in the last
class. For example, we discussed a textbook problem, #11 of section
15.3. The resulting double integral was
![]() 12
12![]() x=yx=y3ex/ydx dy
x=yx=y3ex/ydx dy
So I tried the Maple command
plot3d(exp(x/y),x=y..y^3,y=1..2). The first view I got is
shown below to the left. Notice, please, that the scales on the three
axes are all distinct and very different. The vertical axis is the
most squeezed. It goes from 0 to about 50. If you want to look at the
picture with all axes equal, the result is almost invisible (it
becomes tall and very, very thin). The second picture is the result of
my looking at the image unconstrained, but from directly above the
xy-axis, so that we can't see the z-axis at all. The result should be
the domain of integration. By the way, I had to magnify this picture
several times to get what is shown. You might want to compare the
picture shown on the right below to my picture of
the domain of integration. They should match, and they do, mostly.
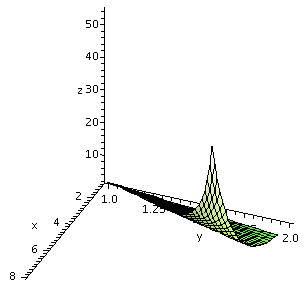
|
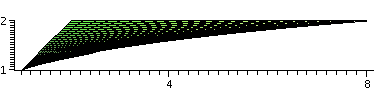
|
HOMEWORK
You have a workshop writeup to hand in. Please read about triple
integrals and do the suggested homework problems. Practice is most
important here: it will certainly improve the vague thing called
intuition. I will find some iterated integrals for the solid described above and the QotD will be for students do
write another iterated integral. You could also read ahead, and look
at cylindrical and spherical coordinates.
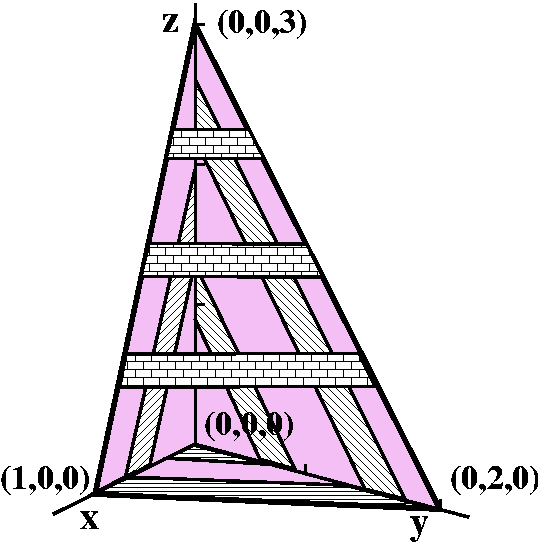 Volume of a tetrahedron
Volume of a tetrahedronHere we'll use a double integral to find the volume of the tetrahedron here. I think of this solid as lying over a triangle in the xy-plane. The triangle is determined by (0,0), (1,0), and (0,2).The height of the solid over this triangle is z=3-3x-(3/2)y, which I got from the equation for the titlted face, just by solving it for z.
As a double integral
So the volume is ![]()
![]() BaseHeight dA, and
this is
BaseHeight dA, and
this is ![]()
![]() The triangle3-3x-(3/2)y dA. I'll convert
this to an iterated integral to compute it.
The triangle3-3x-(3/2)y dA. I'll convert
this to an iterated integral to compute it.
47 second break for theory
Last time I was very careful to define the double integral as a limit
of Riemann sums, and the domain we integrated over was a
rectangle. Yet here I am apparently not even worrying about the
domain. Well, this is what we could do if we had another 30 minutes to
fritter away on details. I could define a function piecewise in this
way:
F(x,y)=3-3x-(3/2)y if (x,y) is in the triangle, and F(x,y)=0 if (x,y)
is not in the triangle. Suppose R is any rectangle in the xy-plane
which contains the triangle. The the volume of the tetrahedron would
be ![]()
![]() RF(x,y) dA. I hope that you will see this
double integral is the same as the double integral over the triangle
that I'll compute by looking at iterated integrals. The
discontinuities of the piecewise-defined function turn out to give a
perturbation of the Riemann sums which -->0 as the size of the peices
-->0.
RF(x,y) dA. I hope that you will see this
double integral is the same as the double integral over the triangle
that I'll compute by looking at iterated integrals. The
discontinuities of the piecewise-defined function turn out to give a
perturbation of the Riemann sums which -->0 as the size of the peices
-->0.
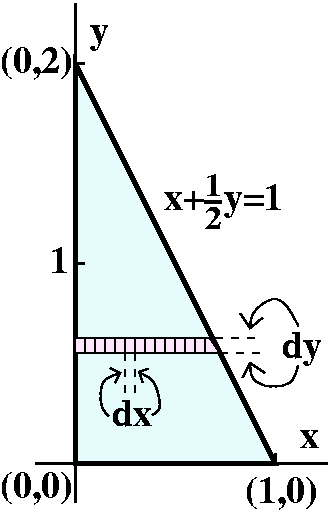 Converting to iterated integrals
Converting to iterated integrals
Let's write ![]()
![]() The triangle3-3x-(3/2)y dA as a
dx dy iterated integral. That means figuring out the bounds on
the integrals.
The triangle3-3x-(3/2)y dA as a
dx dy iterated integral. That means figuring out the bounds on
the integrals.
I will work from the outside in. So first I need to get the lowest and
highest values of y in the triangular base:
![]() Lowest yHighest y
Lowest yHighest y![]() ???3-3x-(3/2)y dx dy
???3-3x-(3/2)y dx dy
There's a sketch of the base to the right, and the sketch declares
that the Lowest y is 0 and the Highest y is 2. Now I
imagine (and frequently draw, as shown on the sketch!) a very thin
collection of dx by dy rectangles being added up in a row across the
region. It is so thin that y is almost constant and the x's range from
the leftmost edge to the rightmost edge. The left edge is certainly 0
always. But the right edge depends on y. When y is very near the
bottom (y=0), the right edge is very near 1. When y is near the top
(y=1), the right edge is near 0. What is the relationship between x
and y on this edge? Of course the edge reflects the tilted face of
the tetrahedron, which has the equation x+(y/2)+(z/3)=1. On the base,
z=0, so the equation giving the tilted side of the triangular base
must be x+(y/2)=1. Therefore x on the rightmost edge is given by
x=1-(1/2)y. Here is the resulting iterated integral:
![]() 02
02![]() x=0x=1-(1/2)y3-3x-(3/2)y dx dy
x=0x=1-(1/2)y3-3x-(3/2)y dx dy
Even thought it is not logically necessary (because the dx dy
notation does determine what variable is integrated first), I do tend
to write "x=" on the limits of the inner integrals. This may save me
from confusion and error as I compute.
Computing the iterated integral
I'll first compute the inner integral:
![]() x=0x=1-(1/2)y3-3x-(3/2)y dx=
(antidifferentiate with respect to x, so y is a constant here!)
3x-(3/2)x2-(3/2)yx]x=0x=1-(1/2)y=
3{1-(1/2)y}-(3/2){1-(1/2)y}2-(3/2)y(1-(1/2)y)-0. The -0 comes from the lower limit, x=0. I tend to expand and "simplify" here. So we get:
x=0x=1-(1/2)y3-3x-(3/2)y dx=
(antidifferentiate with respect to x, so y is a constant here!)
3x-(3/2)x2-(3/2)yx]x=0x=1-(1/2)y=
3{1-(1/2)y}-(3/2){1-(1/2)y}2-(3/2)y(1-(1/2)y)-0. The -0 comes from the lower limit, x=0. I tend to expand and "simplify" here. So we get:
3-(3/2)y-(3/2){1-(1/2)y}2-(3/2)y(1-(1/2)y)=3-(3/2)y-(3/2){1-y+(1/4)y2}-(3/2)y+(3/4)y2=
(3/2)-(3/2)y+(3/8)y2
Now the outer integral:
![]() 02(3/2)-(3/2)y+(3/8)y2dy=(3/2)y-(3/4)y2+(1/8)y3]02=(3/2)(2)-(3/4)(4)+(1/8)(8)=1.
02(3/2)-(3/2)y+(3/8)y2dy=(3/2)y-(3/4)y2+(1/8)y3]02=(3/2)(2)-(3/4)(4)+(1/8)(8)=1.
I remarked in class that, maybe it should be "clear" to me that the
volume is 1, but it isn't.
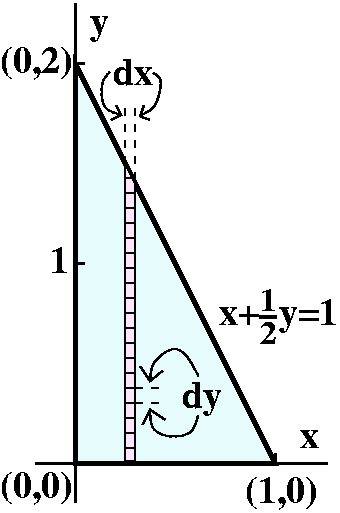 The other iterated integral
The other iterated integral
Now, just to practice, we'll write ![]()
![]() The triangle3-3x-(3/2)y dA as a
dy dx iterated integral.
The triangle3-3x-(3/2)y dA as a
dy dx iterated integral.
Again, I will work from the outside in. So first I need to get the
leftest (leftmost) and rightest (rightmost) values of x in the
triangular base:
![]() Leftmost xRightmost x
Leftmost xRightmost x![]() ???3-3x-(3/2)y dy dx
???3-3x-(3/2)y dy dx
Now the base triangle is again shown to the left, but with the kind of
"doodles" that I would make suitable to finding the limits of a
dy dx iterated integral. The leftmost value of x is 0 and the
rightmost value of x is 1. Now my dx by dy triangles form a vertical
strip where x is just about constant. For the inner limits on y I need
to know that the strip goes from the bottom, where y=0, to the
top. The top will vary, depending on x. The equation of the boundary
line for the top is the same: x+(y/2)=1. Now we need to know y as a
function of x. So solve for y and get y=2-2x. That's the upper limit
on the dx integral. Here is the resulting iterated integral:
![]() 01
01![]() y=0y=2-2x3-3x-(3/2)y dy dx.
y=0y=2-2x3-3x-(3/2)y dy dx.
Computing the iterated integral
I'll first compute the inner integral:
![]() y=0y=2-2x3-3x-(3/2)y dy=
(antidifferentiate with respect to y, so x is a constant here!)
3y-3xy-(3/4)y2]y=0y=2-2x=
3(2-2x)-3x(2-2x)-(3/4)(2-2x)2-0. Again, the -0 comes from the lower limit, y=0. Now expand and simplify:
y=0y=2-2x3-3x-(3/2)y dy=
(antidifferentiate with respect to y, so x is a constant here!)
3y-3xy-(3/4)y2]y=0y=2-2x=
3(2-2x)-3x(2-2x)-(3/4)(2-2x)2-0. Again, the -0 comes from the lower limit, y=0. Now expand and simplify:
6-6x-6x+6x2-(3/4){4-8x+4x2}=3-6x+3x2
The outer integral:
img src="gifstuff/is11.gif"
width=8>013-6x+3x2dx=3x-3x2+x3]01=3-3+1=1.
Thank goodness, we got 1 again.
Possible sources of error in these computations
I'm looking ahead a little bit here. We will discuss triple integrals
next time, and these are also usually computed by a transition to
triple iterated integrals. There are six possible orders for iterated
triple integrals. I make errors frequently. The prominent sources of
error include: antidifferentiating with respect to the wrong variable,
substituting for the wrong variable, and, well, general
confusion. Please try to guard against these. You may make these
errors, and just do the computation again, and try to keep your
composure intact ("Keep cool, y'know!").
By the way, although I wanted our first example to be as easy as
possible, when I was typing up the diary notes above, I ... made
several errors and had to go back and redo things. Oh well.
Another one
The base of a solid is the region in the first quadrant of the
xy-plane bounded by the curve y=x2 and the line y=3x. The
height over the xy-plane is given by
z=x6y7. Find the volume of this solid.
The double integral is ![]()
![]() BaseHeight dA, and
this is
BaseHeight dA, and
this is ![]()
![]() The shapex6y7 dA.
The shapex6y7 dA.
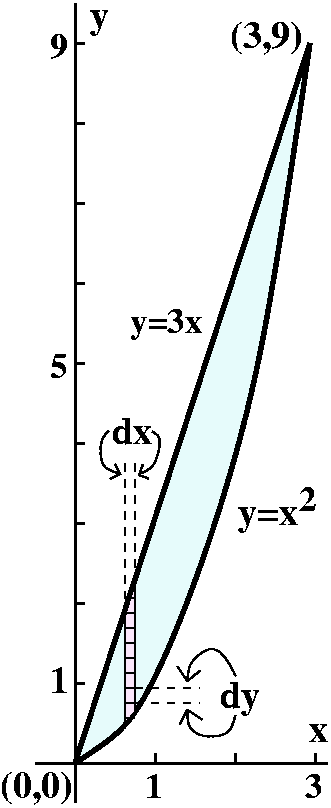
One iterated integral, with its computation
We will convert this first to a dy dx integral. The outside
limits come first. The most left x gets on the base is x=0. The most
right x gets is x=3. We know this because we graphed the base, and
found the intersection points of y=x2 and y=3x by solving
3x=x2, which has roots at x=0 and x=3. Therefore the
iterated integral looks like:
![]() 03
03![]() ???x6y7dy dx
???x6y7dy dx
What about the limits on y? Here the sketch of the base, together with
my doodles, may be useful. The vertical strip of boxes tells me that I
should add up things from y=x2, the lower bound, to y=3x,
the upper bound. Therefore this iterated integral is:
![]() 03
03![]() y=x2y=3xx6y7dy dx
y=x2y=3xx6y7dy dx
Now to compute the integral. The inner integral:
![]() y=x2y=3xx6y7dy=(1/8)x6y8]y=x2y=3x=(1/8)x6(3x)8-(1/8)x6(x2)8.
y=x2y=3xx6y7dy=(1/8)x6y8]y=x2y=3x=(1/8)x6(3x)8-(1/8)x6(x2)8.
This "simplifies" to
(1/8)38x14-(1/8)x22. (I am using the
powerful rules of exponential manipulation here!) And now the outer
integral:
![]() 03
(1/8)38x14-(1/8)x22dx=
(1/8)38(1/15)x15-(1/8)(1/23)x23]03=
(1/8)38(1/15)315-(1/8)(1/23)323=(1/8)323([1/15]-[1/23]). Wow!
03
(1/8)38x14-(1/8)x22dx=
(1/8)38(1/15)x15-(1/8)(1/23)x23]03=
(1/8)38(1/15)315-(1/8)(1/23)323=(1/8)323([1/15]-[1/23]). Wow!
The other iterated integral, with its computation
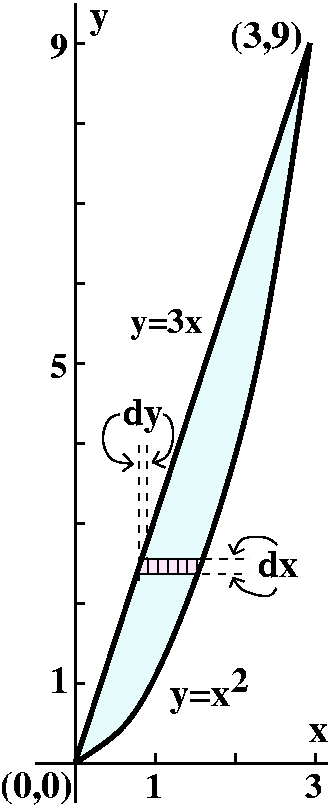 Now for the dx dy integral. The highest and lowest values for y
are 0 and 9. Therefore the integral must be:
Now for the dx dy integral. The highest and lowest values for y
are 0 and 9. Therefore the integral must be:
![]() 09
09![]() ???x6y7dx dy
???x6y7dx dy
Now we need to consider a (fixed) y slice through the base. The
left-hand side of that fixed y slice is determined by y=3x and the
right-hand side of the slice is determined by y=x2. We need
to know the limits on x in terms of y. So we need to know
x=Left(y) and x=Right(y). That means "solving for x" in the boundary
equations. This (here, in this classroom example!) is not too
hard. y=3x becomes x=(1/3)y on the left, and y=x2 becomes
x=sqrt(y) on the right. The positive square root gets used here
because (picture!) we're in the first quadrant. The iterated integral
is:
![]() 09
09![]() x=(1/3)yx=sqrt(y)x6y7dx dy
x=(1/3)yx=sqrt(y)x6y7dx dy
The computation begins with the inner integral.
![]() x=(1/3)yx=sqrt(y)x6y7dx=(1/7)x7y8]x=(1/3)yx=sqrt(y)=
(1/7){sqrt(y)}7y7-(1/7){(1/3)y}7y7=(1/7)y7/2y7-(1/7)(1/3)7y7y7
x=(1/3)yx=sqrt(y)x6y7dx=(1/7)x7y8]x=(1/3)yx=sqrt(y)=
(1/7){sqrt(y)}7y7-(1/7){(1/3)y}7y7=(1/7)y7/2y7-(1/7)(1/3)7y7y7
This now "simplifies" (what a silly word!) to
(1/7)y(21)/2-(1/7)(1/3)7y14> Now the
outside:
![]() 09(1/7)y(21)/2-(1/7)(1/3)7y14dy=
(1/7)(2/(23))y(23)/2-(1/7)(1/3)7(1/15)y15]09=
(1/7)(2/(23))9(23)/2-(1/7)(1/3)7(1/15)915=
(1/7)(2/(23))323-(1/7)(1/3)7(1/15)330=
(1/7)(2/(23))323-(1/7)(1/15)323=(1/7)323([2/(23)]-[1/15])
(1/7)(1/16)325-(1/7)(2/(25))325=
(1/7)325{(1/16)-2/(25))
Theorem
09(1/7)y(21)/2-(1/7)(1/3)7y14dy=
(1/7)(2/(23))y(23)/2-(1/7)(1/3)7(1/15)y15]09=
(1/7)(2/(23))9(23)/2-(1/7)(1/3)7(1/15)915=
(1/7)(2/(23))323-(1/7)(1/3)7(1/15)330=
(1/7)(2/(23))323-(1/7)(1/15)323=(1/7)323([2/(23)]-[1/15])
(1/7)(1/16)325-(1/7)(2/(25))325=
(1/7)325{(1/16)-2/(25))
Theorem
1 / 1 1 \ 1 / 1 2 \
--- · | ---- - ---- | = --- ·| ---- - ---- |
8 \ 15 23 / 7 \ 15 23 /
The proof consists of observing that the dx dy and
dy dx values of the double integral must be equal by the Fubini
result, and then dividing both values by 323. (The student
may, of course, verify this statement using the tools of third grade
arithmetic, but the prestige of double integrals is ... [priceless?].)
This "theorem" may be the silliest statement of the course.
Pi? The Bible??
Some students objected when I tried to write Pi instead of 3 as I was
assembling information for the computation above. I cited the Bible as
a reference. Here
is information about the "history of Pi" including specific biblical
citations. Since we are at a secular university, I give this not for
its religious value, but for ... uhhhh ... historical context. Also,
maybe ... uhhhh ... maybe the value of Pi has changed with time. Uhhhh
... also everyone should know a few digits of Pi. This
reference discusses how the computation of the first
trillion or so decimal digits was done. You can search the
first four billion bits (binary digits) of Pi for patterns here.
More on difficulties and on the psychology of the individual
Please don't panic. If you want to compute a double integral, you
don't need to do both iterated integrals -- just one of them. I
chose to do both to show you how (I hope!).
Notice that we needed to go from one description of the boundary
curves: {y=3x, y=x2}, to another: {x=(1/3)y,x=sqrt(y)},
when we did dx dy after dy dx. "Solving" (finding a
convenient form for inverse functions) may be difficult (or even
impossible in terms of familiar functions).
One last remark: I almost alway try to find the bounds on iterated
integrals going from the outside-most integral to the inside-most
integral. Some people may find the transition from inside to outside
more easy (this difference in approach will be more emphatic when we
do triple integrals). You should try a series of examples and settle
upon what you find most comfortable. And remember that you can always
"change" to the other way.
By the way ...
> int(int(x^6*y^7,x=(1/3)*y..sqrt(y)),y=0..9);
31381059609
-----------
115
> int(int(x^6*y^7,y=x^2..3*x),x=0..3);
31381059609
-----------
115
So Maple gets the same answer both ways, also.
 Integrating Frog over a region
Integrating Frog over a region
If the integrand (the function to be integrated) is not too weird,
then I hope you should be convinced that the actual
antidifferentiations probably aren't the essential difficulty. The
difficulty is more in setting up the iterated integrals:
finding the bounds. Here is a more complicated example.
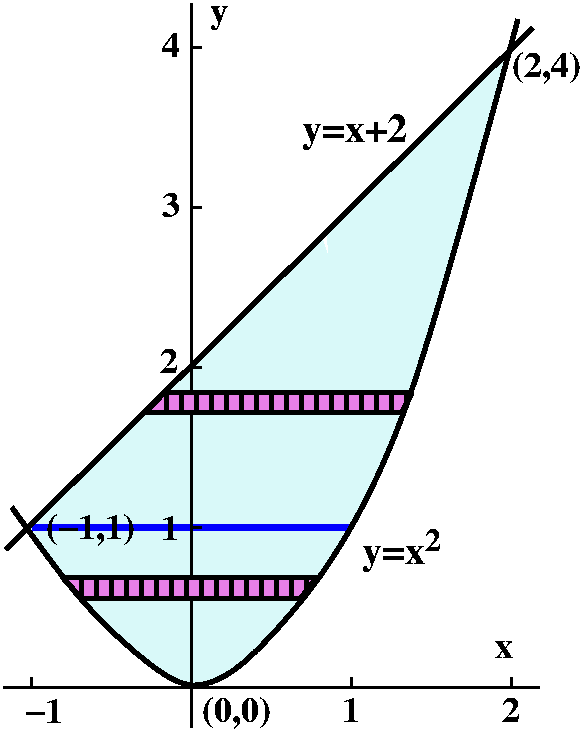
The region R is bounded by y=x+2 and y=x2. What does this
region look like? Well, this is a problem in a calculus course, so
solving x2=x+2 shouldn't be impossible. In fact, this leads
to x2-x-2=0 which is (x-2)(x+1)=0 so intersections occur
when x=-1 (so y=(-1)2=1) and when x=2 (so
y=22=4). I would like to integrate Frog over the region R:
![]()
![]() RFrog dA. More precisely,
I'd just like to set up the bounds of the iterated integrals which are
equal to this double integral.
RFrog dA. More precisely,
I'd just like to set up the bounds of the iterated integrals which are
equal to this double integral.
Totally randomly, dx dy first
This wasn't a random choice. The dx dy order introduces an
additional kind of complexity. Consider these limits:
![]() Bottom of yTop of
y
Bottom of yTop of
y![]() x=Left(y)x=Right(y)Frog dx dy.
x=Left(y)x=Right(y)Frog dx dy.
The Top of y and Bottom of y are easy enough. In the region R, the
smallest y value is 0 and the largest y value is 4. Now think about
x=Left(y) and x=Right(y). The thick horizontal
blue line in the sketch separates different formulas for
the Left limit of x as a function of y. Below it, the Left limit is
determined by the left-hand side of the parabola. Above it, the Left
limit is determined by the straight line. Theoretically this does not
cause any problems. But when you're actually trying to compute
everything, what people usually do is separate the pieces:
![]() 01
01![]() x=Left(y)x=Right(y)Frog dx dy +
x=Left(y)x=Right(y)Frog dx dy +![]() 14
14![]() x=Left(y)x=Right(y)Frog dx dy.
x=Left(y)x=Right(y)Frog dx dy.
In the first iterated integral, as y goes from 0 to 1, the left and
right boundaries are both given by formulas related to
y=x2. Here x=+/-sqrt(y), so Left(y)=-sqrt(x) and
Right(y)=+sqrt(x). In the second iterated integral, y goes from 1 to
4. Here also Right(y)=+sqrt(x), but Left(y) comes from y=x+2, so
Left(y)=y-2. So the dx dy iterated integrals which are
equal to the double integral are:
![]() 01
01![]() x=-sqrt(y)x=sqrt(y)Frog dx dy +
x=-sqrt(y)x=sqrt(y)Frog dx dy +![]() 14
14![]() x=y-2x=sqrt(y)Frog dx dy.
x=y-2x=sqrt(y)Frog dx dy.
Now dy dx
This one is much easier. I can read off the left and right extreme
values of x, and then the y boundary values are given by the equations
which already "present" the region R. I don't need to split up
things. Here it is:
![]() -12
-12![]() y=x2y=x+2Frog dy dx.
y=x2y=x+2Frog dy dx.
Almost surely, unless circumstances were very strange, I would set up
the iterated integral this way and no in the dx dy way.
The New
Jersey Chorus Frog, Pseudacris feriarum kalmi, is an
endangered species in some of its
range.
In my office ...
Hint
Problem #11 of section 15.3 in the textbook
But this should ring a bell: Polar
Coordinates! Why?
HOMEWORK
The initial setup is routine:
Solving these equations can be difficult. The aim is to find values
the variables which lead to the max and min of the objective
function. The analysis of the systems can be very idiosyncratic
(differing greatly for different systems). I generally try to solve
for
We can compare the various quantities that are equal to
Now C can be written only with x's,
and it becomes x2+10x2+(3x)2=1, and
x=+/-1/sqrt(20). We know 3x=z, so z=+/-3/sqrt(20). And
y2=10x2, so y2=10/20=1/2. y must be
+/-1/sqrt(2). Certainly it isn't vital in this simple classroom
example, but the +/- choices of x and z must be the same, and the +/-
choice of y is unlinked. We have identified 4 points in R3
as candidates for finding extreme values:
Although there are methods of identifying more specific max/min
behavior in Lagrange multipliers, I have never used them. I've just
"plugged" the values of the candidates into the objective
function. For example, I can look at xy+3yz and tell you that the
largest value will come from using
(1/sqrt(20),1/sqrt(2),3/sqrt(20)). And that value is
4/sqrt(40)=2/sqrt(20).
So the maximum value is 2/sqrt(20). I bet the minimum will be
-2/sqrt(20). The pciture displayed to the right shows the constrant
(the unit sphere) and the level surface of the objective function for
the maximum value. Isn't it pretty? Well, if not pretty, the
tangent behavior should again confirm the geometric nature of the
method.
I mentioned in class the work of Professor
Wilma Olson, Department of Chemistry and Chemical Biology, who
studies the structure of such molcules as DNA with mathematical and
computational tools. Since "nature" likes minimum energy arrangements,
much of her work consists of investigating minimization problems in
many variables. One of her collaborators is Professor Bernard
Coleman of the Department of Mechanics and Materials Science, who
has also done further work of his own. Similar problems arise for
mechanical engineers: the energy of a spring has kinetic and potential
pieces, so even a simple study of a construction with a half-dozen
springs immediately leads to energy minimization in 12 variables (I am
really simplifying here).
Quick review of the definite integral in calc 1
Theorem For any choices of sample points, as n-->infinity, the
Riemann sums-->a unique limit, the definite integral of f from a to b,
and written
Of course the integral sign and the dx's are notation to remind people
of the approximating sums. We could approximate the definite integral
with Riemann sums, and of course there are many other numerical
approximation schemes. But the champion method is:
FTC If F´=f, then
Defining the double integral
In fact the definition more or less parallels the single integral
definition. I'll follow the text closely here. We begin with a nice
function (say, continuous) defined on a rectangle R in R2
with bouindaries x=a, x=b, y=c, and y=d. Chop up the area of the
rectangle into a bunch of chunks. In each chunk, choose a sample
point. Compute the corresponding Riemann sum, the sum over all the
chunks of f's value at the sample point multiplied by the area of the
chunk. If f(x,y)>0 on R, then this Riemann sum approximates the
volume under z=f(x,y) and over R. Then it's true that as the maximum
size of the chunks-->0, the Riemann sums-->a unique limit. This limit
is the double integral over R of f(x,y):
Mass of a plate
Reality?
Well, you might work for Schlumberger and your sample points
might cost three to five million dollars each as you try to
investigate the oil or gas quantities of some region. You'd then
really think a bit about the whole process. And that's what they do.
Some very simple examples of double integrals
Example A The rectangle R is defined by x=3 and x=7 and y=5 and
y=8. The function is f(x,y)=700. Then
Basic properties
The basic properties of the double integral are exactly like those of
the 1-dimensional version.
How to compute?
Fubini's Theorem
Suppose f(x,y) is a continuous function in a rectangle R defined by
x=a, x=b, y=c, and y=d. Then
Example 1
Let me try to compute
I'll begin by computing the inner integral:
Now
My silicon buddy ...
Example 2
Let's try a random function: f(x,y)=sqrt(3x+8y). Well, this isn't so
random (as you'll see!). I just wish I had thought of it in class. The
rectangle I have in mind has these boundary lines: x=0 and x=3 and y=0
and y=2. In the previous example we converted the double integral into
a dx dy iterated integral. Let me try a dy dx order here. I
think that either order, again, is about the same amount of work.
So let's try:
The inner integral is
And now the outer integral:
Or, in the 21st century ...
QotD
Compute
The inner integral:
Course workload
I hope to have one more workshop problem (so that I can grade each
student's efforts at least once). There should also be two more
Maple labs, but I'd like them to be interesting and
useful. So we'll see.
HOMEWORK
Note I will submit formal warning
grades to students who got a D or an F on the first exam,
or who are registered for the course and did not take the exam.
Maintained by
greenfie@math.rutgers.edu and last modified 3/23/2006.
A student visited me and we did some more Frog-like problems (one with Toad and one with Lizard. Let me show you the Lizard problem. The region we looked at was
bounded by y=2-2x2 and y=x4-x2. A
Maple graph with these two functions is shown to the right.
Just as in the previous (Frog)
example, writing the dy dx integral is quite direct. My student
visitor and I wrote iterated integrals for the other
order:dx dy. You can try this problem. First, though, think a bit
and see how many iterated integrals will be necessary.
I think three pieces are needed. Notice that
y=x4-x2 is the same as
x4-x2-y=0 and this is
(x2)2-x2-y=0, a quadratic in
x2. So you can "solve" for x2 using the
quadratic formula, and then take square roots of the resulting answers
to get 4 possible values of x for each value of y. Certainly this is a
mess, but this is possible to do without extravagantly advanced
methods.
This problem shows one further "wrinkle" that can occur with double or
triple or any kind of "multiple" integral. Here's the statement:
Evaluate the double integral ![]()
![]() Dex/ydA, where D={(x,y)|1<=y<-2,
y<x<=y3}.
Dex/ydA, where D={(x,y)|1<=y<-2,
y<x<=y3}.
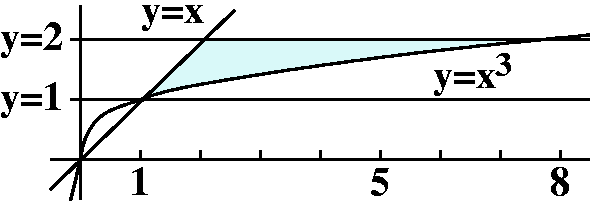 As to why this problem introduces a new kind of complexity, I invite
you to ask Maple to integrate ex/y both dx and dy.
That is, what are the respective antiderivatives? The x antiderivative
is yex/y but ... there is no y antiderivative in terms
of familiar functions. So if we want to get an answer to the
textbook's problem, we'd better first do dx and then leave dy until
later. The dx dy double integral is easy enough to write, because the region D is described suitably:
As to why this problem introduces a new kind of complexity, I invite
you to ask Maple to integrate ex/y both dx and dy.
That is, what are the respective antiderivatives? The x antiderivative
is yex/y but ... there is no y antiderivative in terms
of familiar functions. So if we want to get an answer to the
textbook's problem, we'd better first do dx and then leave dy until
later. The dx dy double integral is easy enough to write, because the region D is described suitably:
![]() 12
12![]() x=yx=y3ex/ydx dy
x=yx=y3ex/ydx dy
The inner antidifferentiation gives
![]() x=yx=y3ex/ydx=yex/y]x=yx=y3=yey3/y-ye1=yey2-ey
and then
x=yx=y3ex/ydx=yex/y]x=yx=y3=yey3/y-ye1=yey2-ey
and then ![]() 12yey2-ey dy is just
(1/2)ey2-(e/2)y2]12=(1/2)e4-2e.
12yey2-ey dy is just
(1/2)ey2-(e/2)y2]12=(1/2)e4-2e.
Comment I do know some examples, in "real" applications, not
textbooks, where looking at the order of the iterated integrals
changes something really nasty into a function which can be handled
routinely. So, although this is a textbook/class example, it does show
an idea which may be useful.
 Yet a different way ...
Yet a different way ...
What is ![]()
![]() Rx2+y2dA, if R is the region
shwon to the right (in the first quadrant, with the curves arcs of
circles centered at the origin)?
Rx2+y2dA, if R is the region
shwon to the right (in the first quadrant, with the curves arcs of
circles centered at the origin)?
The only part which may be difficult to understand is dA. Although we
changed dA to dx dy or dy dx, dA is not just the
product of d
![]() =0 and
=0 and
![]() =Pi/2 (for the first quadrant). In fact this region is actually
a polar rectangle.
=Pi/2 (for the first quadrant). In fact this region is actually
a polar rectangle.
![]() and dr. One way to see that is to realize that dA is
an area, so its dimensions are length2. dr is a length, but
d
and dr. One way to see that is to realize that dA is
an area, so its dimensions are length2. dr is a length, but
d![]() , an angle, is dimensionless. We'll see next time (or look in
the text) that dA=r dr d
, an angle, is dimensionless. We'll see next time (or look in
the text) that dA=r dr d![]() .
.
Please read about polar coordinates (15.4) and triple integrals
(15.7). I will deviate from the syllabus and cover the material
listed there for lecture 15 (15.5 and 15.9) later in the course.
![]() f=<2x,2y,2z>;
f=<2x,2y,2z>; ![]() g=<y,x+3z,3y>.
g=<y,x+3z,3y>.
The resulting system of four equations in four variables follows.
1 2x=![]() y
y
2 2y=![]() (x+3z)
(x+3z)
3 2z=![]() (3y)
(3y)
C x2+y2+z2=1
![]() in the equations 1 and 2 and 3 and
compare the results. Start with 1:
in the equations 1 and 2 and 3 and
compare the results. Start with 1:
![]() =2x/y.
=2x/y.
Already there is some difficulty. What if y is 0? You
can't ignore such alternatives, because the extreme values may be
hiding there. So if y=0 then 1 forces
x to be 0 and 3 shows that z must be 0
also. But (0,0,0) does not satisfy the constraint, C. So y can't be 0. Now 2 gives
![]() =2y/(x+3z).
=2y/(x+3z).
If x+3z=0 then y is 0 and that's not possible. And 3 gives
![]() =2z/(3y)
=2z/(3y)
![]() . So
2x/y=2z/3y and therefore 3x=z. And 2x/y=2y/(x+3z) so
2x2+6zx=2y2 but since 3x=z this is just
2x2+18x2=2y2 and
y2=10x2
. So
2x/y=2z/3y and therefore 3x=z. And 2x/y=2y/(x+3z) so
2x2+6zx=2y2 but since 3x=z this is just
2x2+18x2=2y2 and
y2=10x2
(1/sqrt(20),1/sqrt(2),3/sqrt(20)),
(-1/sqrt(20),1/sqrt(2),-3/sqrt(20)),
(1/sqrt(20),-1/sqrt(2),3/sqrt(20)),
(-1/sqrt(20),-1/sqrt(2),-3/sqrt(20)).

 Suppose we have a nice function f(x) of one variable defined on and
interval, [a,b]. We might want to find the area under y=f(x) on that
interval, althogh that is more of an excuse to define the definite
integral than a real ambition. Here is one approach to the
definition. Take a large positive integer n and divide [a,b] into n
equal parts each of width
Suppose we have a nice function f(x) of one variable defined on and
interval, [a,b]. We might want to find the area under y=f(x) on that
interval, althogh that is more of an excuse to define the definite
integral than a real ambition. Here is one approach to the
definition. Take a large positive integer n and divide [a,b] into n
equal parts each of width ![]() x=(b-a)/n. In each subinterval choose a sample point, say
qj in the jth subinterval. Compute the sum
SUMj=1nf(qj)
x=(b-a)/n. In each subinterval choose a sample point, say
qj in the jth subinterval. Compute the sum
SUMj=1nf(qj)![]() x. This is a Riemann sum
approximating the definite integral. As n-->infinity, any sequence of
sums is supposed to approach a unique limit, and that limit is the
definite integral. But there are many choices of sample points, and
maybe it isn't clear that the choices don't influence the limit. So
what if we take another point pj in the jth
subinterval as a sample point? Then since the width is
x. This is a Riemann sum
approximating the definite integral. As n-->infinity, any sequence of
sums is supposed to approach a unique limit, and that limit is the
definite integral. But there are many choices of sample points, and
maybe it isn't clear that the choices don't influence the limit. So
what if we take another point pj in the jth
subinterval as a sample point? Then since the width is ![]() x,
certainly |qj-pj|<=
x,
certainly |qj-pj|<=![]() x. The Mean Value
Theorem (let me assume that f is differentiable) then says there's
some constant, C, so that
|f(qj)-f(pj)|<=C
x. The Mean Value
Theorem (let me assume that f is differentiable) then says there's
some constant, C, so that
|f(qj)-f(pj)|<=C![]() x. (I'm not too
interested in the details here -- we're only skimming!) But we can estimate the difference when different choices of sample points are made:
x. (I'm not too
interested in the details here -- we're only skimming!) But we can estimate the difference when different choices of sample points are made:
|SUMj=1nf(qj)![]() x - SUMj=1nf(qj)
x - SUMj=1nf(qj)![]() x|<=nC
x|<=nC![]() x
x![]() x.
x.
The "n" comes because
there are n pieces in the sum. One of the ![]() x's occurs because
that's a common factor in both sums. The other comes from the MVT
estimate we just stated. But now, since
x's occurs because
that's a common factor in both sums. The other comes from the MVT
estimate we just stated. But now, since ![]() x=(b-a)/n, we see that
the estimate of the difference is C(b-a)2/n. Two of the n's
cancel. We are left with an n on the bottom, and this means that the
Riemann sums do get closer as n-->infinity, no matter what choice of
sample point is made.
x=(b-a)/n, we see that
the estimate of the difference is C(b-a)2/n. Two of the n's
cancel. We are left with an n on the bottom, and this means that the
Riemann sums do get closer as n-->infinity, no matter what choice of
sample point is made.
![]() abf(x) dx.
abf(x) dx.
![]() abf(x) dx=F(b)-F(a).
abf(x) dx=F(b)-F(a).
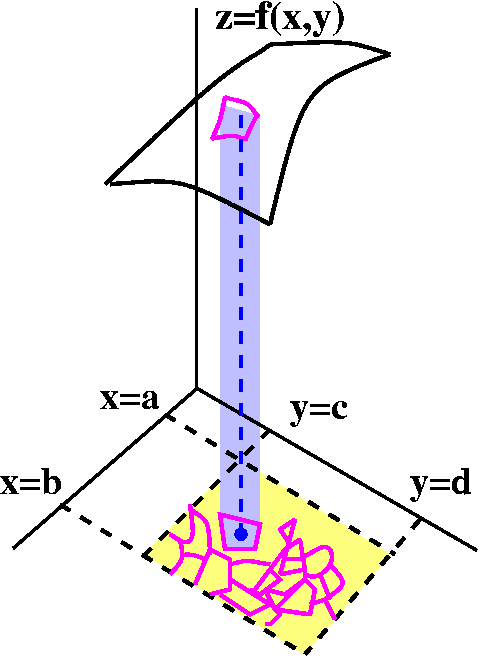
![]()
![]() Rf(x,y)dA. This is a mathematical abstraction of
the volume. The volumes computed as a result of formulas in earlier
calculus (solids of revolution, solids with simple cross-sections,
etc.) take advantage of symmetry. The theoretical tool defined here
allows us to compute volumes without any simple kinds of symmetry.
Rf(x,y)dA. This is a mathematical abstraction of
the volume. The volumes computed as a result of formulas in earlier
calculus (solids of revolution, solids with simple cross-sections,
etc.) take advantage of symmetry. The theoretical tool defined here
allows us to compute volumes without any simple kinds of symmetry.
Almost all the computations of volumes that I've made in my life have
occurred as a result of teaching third semester calculus. Maybe the
following is a bit more interesting.
 Maybe this is a more realistic "scenario". Suppose you are given a
thin rectangular metal plate with an unknown density
distribution. Therefore this is not necessarily a homogeneous
thin plate. The plate is too heavy or too unwieldy to weigh directly,
and you need to estimate the total mass. Also the mass distribution --
the density -- is not necessarily given by a simple formula. What
maybe could be done is tiny Samples taken at various parts of the
plate, according to some method (maybe depending on accessibility or
expense or ... anything). Then these samples could have their density
measured, and maybe then, after dividing the plate (thoughtwise!) into
pieces, the sample densities could be multiplied by the areas of the
pieces. The sum of these products would then be an estimate for the
mass in the plate. (It is a Riemann sum.) If a better (more accurate?)
estimate was wanted, maybe then use more sample points, smaller areas,
etc. The process is exactly the same mathematics as the definition of
the double integral.
Maybe this is a more realistic "scenario". Suppose you are given a
thin rectangular metal plate with an unknown density
distribution. Therefore this is not necessarily a homogeneous
thin plate. The plate is too heavy or too unwieldy to weigh directly,
and you need to estimate the total mass. Also the mass distribution --
the density -- is not necessarily given by a simple formula. What
maybe could be done is tiny Samples taken at various parts of the
plate, according to some method (maybe depending on accessibility or
expense or ... anything). Then these samples could have their density
measured, and maybe then, after dividing the plate (thoughtwise!) into
pieces, the sample densities could be multiplied by the areas of the
pieces. The sum of these products would then be an estimate for the
mass in the plate. (It is a Riemann sum.) If a better (more accurate?)
estimate was wanted, maybe then use more sample points, smaller areas,
etc. The process is exactly the same mathematics as the definition of
the double integral.
![]()
![]() Rf(x,y)dA is 700(7-3)(8-5). Of course, I am using the
fact that the volume described by the double integral is the volume of
a rectangular solid with edge dimensions 700 and 7-3 and 8-5.
Rf(x,y)dA is 700(7-3)(8-5). Of course, I am using the
fact that the volume described by the double integral is the volume of
a rectangular solid with edge dimensions 700 and 7-3 and 8-5.
Example B Here I took f(x,y) to be
5-x2+y2, definitely a more complicated function
than the previous example's. The rectangle I took was defined by x=-3,
x=3, y=-3, and y=3. Let's temporarily discard the 5 and concentrate on
-x2+y2. If I interchange x and y the sign of the
function's value changes. But the rectangular domain is symmetric
about (0,0), so the net value (+'s and -'s cancelling!) of the double
integral of -x2+y2 over the rectangle is 0
(!). Now I "integrate" the 5, and the result is 5(3-(-3))(3-(-3)). So
we did have a more complicated function but the choice of domain made
the hard part of the function drop out.
![]()
![]() Rf(x,y)+g(x,y)DA=
Rf(x,y)+g(x,y)DA=![]()
![]() Rf(x,y)dA+
Rf(x,y)dA+![]()
![]() Rg(x,y)dA; if k is a constant, then
Rg(x,y)dA; if k is a constant, then ![]()
![]() Rkf(x,y)dA=k
Rkf(x,y)dA=k![]()
![]() Rf(x,y)dA.
Rf(x,y)dA.
![]()
![]() Rf(x,y)dA<=
Rf(x,y)dA<=![]()
![]() Rg(x,y)dA.
Rg(x,y)dA. 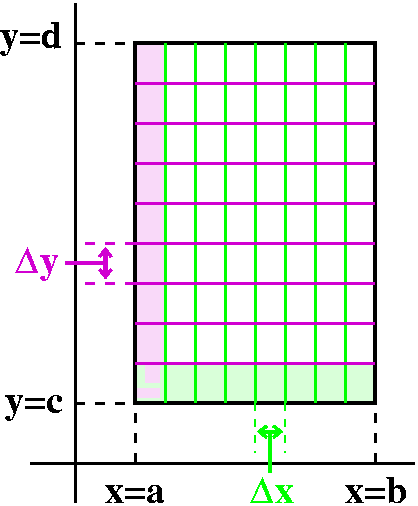 Maybe all this theory is very nice, but let me show you the way most
double integrals are computed. One method of chopping up a rectangle
is to use vertical and horizontal lines, parallel to the sides. So we
get a grid of subrectangles, each
Maybe all this theory is very nice, but let me show you the way most
double integrals are computed. One method of chopping up a rectangle
is to use vertical and horizontal lines, parallel to the sides. So we
get a grid of subrectangles, each ![]() x by
x by ![]() y, with both
y, with both
![]() 's very small. In addition to
choosing this special chopping strategy we could also decide to add up
the contributions (the f(sample point)
's very small. In addition to
choosing this special chopping strategy we could also decide to add up
the contributions (the f(sample point)![]() x
x![]() y) in an orderly manner. So, for example, we could add up the
contributions from the lowest "row" first. In that row, since
y) in an orderly manner. So, for example, we could add up the
contributions from the lowest "row" first. In that row, since ![]() y is small, y hardly varies at
all. The sum of a row sure looks like the definite integral with
respect to x only for "that" value of y. The same can be done for each
row. When the row sums are done, we now have the y's to worry
about. But this is a y integral. Of course, a completely symmetric
procedure can be used in the other order: first dy, with x held
constant, and then dx. Again what's here is not a "proof" but I hope
the discussion supports the following result.
y is small, y hardly varies at
all. The sum of a row sure looks like the definite integral with
respect to x only for "that" value of y. The same can be done for each
row. When the row sums are done, we now have the y's to worry
about. But this is a y integral. Of course, a completely symmetric
procedure can be used in the other order: first dy, with x held
constant, and then dx. Again what's here is not a "proof" but I hope
the discussion supports the following result.
![]()
![]() Rf(x,y)dA=
Rf(x,y)dA=![]() cd
cd![]() abf(x,y)dx dy=
abf(x,y)dx dy=![]() ab
ab![]() cdf(x,y)dy dx.
cdf(x,y)dy dx.
Comments The first "creature" in the equation above is called a
double integral. The two others are officially called
iterated integrals: iterated means "repeated". Technically and
precisely these integrals are different creatures. Also please note
that the outside integration limits go with the outside d-variable --
sometimes this can be confusing. When it is, I write things like "x=a"
instead of just "a" so I don't confuse myself.
![]()
![]() R x3y7dA where R is the
rectangle defined by x=1, x=4, y=2 and y=5. The Fubini Theorem allows
me to "trade in" the double integral for an iterated integral, either
dx dy or dy dx. There are some occasions where one order or
the other might be preferable (we'll see this later) but here I don't
think that happens. So:
R x3y7dA where R is the
rectangle defined by x=1, x=4, y=2 and y=5. The Fubini Theorem allows
me to "trade in" the double integral for an iterated integral, either
dx dy or dy dx. There are some occasions where one order or
the other might be preferable (we'll see this later) but here I don't
think that happens. So:
![]()
![]() Rx3y7dA=
Rx3y7dA=![]() 25
25![]() 14x3y7dx dy.
14x3y7dx dy.
![]() 14x3y7dx=(1/4)x4y7]14.
In this antidifferentiation, the y7 is a constant (this is,
not surprizingly, exactly the inverse of partial
differentiation). Then we evaluate and get
(1/4)44y7-(1/4)14y7=(255/4)y7.
I remarked in class that I sometimes lose my way in these
computations, and need to write
(1/4)x4y7]x=1x=4
to insure that I remember to substitute for the correct variable.
14x3y7dx=(1/4)x4y7]14.
In this antidifferentiation, the y7 is a constant (this is,
not surprizingly, exactly the inverse of partial
differentiation). Then we evaluate and get
(1/4)44y7-(1/4)14y7=(255/4)y7.
I remarked in class that I sometimes lose my way in these
computations, and need to write
(1/4)x4y7]x=1x=4
to insure that I remember to substitute for the correct variable.
![]() 25(255/4)y7dy=(255/4)(1/8)y8]25=(255/4)(1/8)58-(255/4)(1/8)28.
25(255/4)y7dy=(255/4)(1/8)y8]25=(255/4)(1/8)58-(255/4)(1/8)28.
A report from Maple:
> int(int(x^3*y^7,x=1..4),y=2..5);
99544095
--------
32
![]()
![]() Rsqrt(3x+8y)dA=
Rsqrt(3x+8y)dA=![]() 03
03![]() 02sqrt(3x+8y) dy dx.
02sqrt(3x+8y) dy dx.
![]() 02x3sqrt(3x+8y) dy. We
need a "dy" antiderivative of sqrt(3x+8y). Here we can really
get confused! To me writing the function as (3x+8y)1/2
makes the problem easier. I guess that the antiderivative will
be something close to (3x+8y)3/2. Well, but I need to
multiply by stuff to get rid of the various constants. For example, I
need to multiply by (2/3) because of the power. And I need to multiply
by (1/8) because of the coefficient of y that the chain rule will push
out. So the answer is (2/3)(1/8)(3x+8y)3/2, and we must
substitute:
02x3sqrt(3x+8y) dy. We
need a "dy" antiderivative of sqrt(3x+8y). Here we can really
get confused! To me writing the function as (3x+8y)1/2
makes the problem easier. I guess that the antiderivative will
be something close to (3x+8y)3/2. Well, but I need to
multiply by stuff to get rid of the various constants. For example, I
need to multiply by (2/3) because of the power. And I need to multiply
by (1/8) because of the coefficient of y that the chain rule will push
out. So the answer is (2/3)(1/8)(3x+8y)3/2, and we must
substitute:
(2/3)(1/8)(3x+8y)3/2]y=0y=2=
(2/3)(1/8)(3x+16)3/2-(2/3)(1/8)(3x+0)3/2, and
this is (1/12)(3x+16)3/2-(1/12)(3x)3/2.
![]() 03(1/12)(3x+16)3/2-(1/12)(3x)3/2dx=(1/12)(1/3)(2/5)(3x+16)5/2-(1/12)(1/3)(2/5)(3x)5/2]03=
{(1/90)(3·3+16)5/2-(1/90)(3·3)5/2}
-{(1/90)(3·0+16)5/2-(1/90)(3·0)5/2}=
(1/90)(255/2-95/2-165/2+0)=
(1/90)(55-35-45)=
(1/90)(3125-243-1024)=(1858/90)=(929/45).
03(1/12)(3x+16)3/2-(1/12)(3x)3/2dx=(1/12)(1/3)(2/5)(3x+16)5/2-(1/12)(1/3)(2/5)(3x)5/2]03=
{(1/90)(3·3+16)5/2-(1/90)(3·3)5/2}
-{(1/90)(3·0+16)5/2-(1/90)(3·0)5/2}=
(1/90)(255/2-95/2-165/2+0)=
(1/90)(55-35-45)=
(1/90)(3125-243-1024)=(1858/90)=(929/45).
Well, y'see, everything was chosen so
that the final answer would have no square roots. Isn't that
wonderful!
> int(int(sqrt(3*x+8*y),x=0..3),y=0..2);
929
---
45
![]() -21
-21![]() 12x2y-3xy2dy dx.
12x2y-3xy2dy dx.
![]() 12x2y-3xy2dy=(1/2)x2y2-xy3]y=1y=2={(1/2)x2·22-x·23}-{(1/2)x212-x·13}=(3/2)x2-7x.
12x2y-3xy2dy=(1/2)x2y2-xy3]y=1y=2={(1/2)x2·22-x·23}-{(1/2)x212-x·13}=(3/2)x2-7x.
The outer integral:
![]() -21(3/2)x2-7x dx=(1/2)x3-(7/2)x2]x=-2x=1={(1/2)-(7/2)}-{(1/2)(-2)3-(7/2)(-2)2}
-3-{-4-14}=18-3=15.
-21(3/2)x2-7x dx=(1/2)x3-(7/2)x2]x=-2x=1={(1/2)-(7/2)}-{(1/2)(-2)3-(7/2)(-2)2}
-3-{-4-14}=18-3=15.
As I sadly admitted in class, somehow I got the answer 6 for this. Oh well.
Please read the first sections of chapter 15. I'll discuss 15.3 and
probably 15.4 on Tuesday. Please hand in these problems at recitation
on Wednesday:
14.8: 6
15.2: 7, 15
15.3: 4, 11