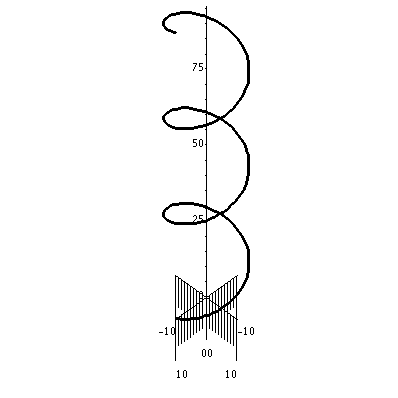
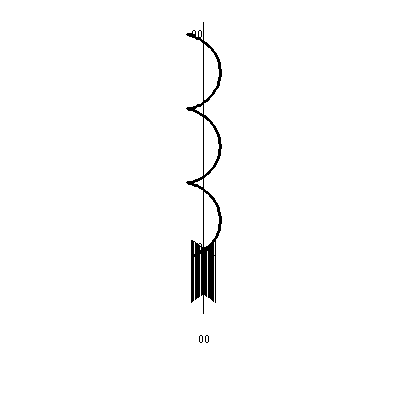
kappa=.01 & tau=.0005
kappa=.05 & tau=.05
kappa=.0005 & tau=.01
I'll carry along is a right circular helix as a basic example.
x(t)=a cos(t) y(t)=a sin(t) z(t)=b tThe quantities a and b are supposed to be positive real numbers. This helix has the z-axis as axis of symmetry. It lies "above" the circle with radius a and center (0,0) in the (x,y)-plane. The distance between two loops of the helix is 2Pi b.
If r(t)=x(t)i+y(t)j+z(t)k (the position vector), then r'(t)=x'(t)i+y'(t)j+z'(t)k=(ds/dt)T(t) is called the velocity vector. Here T(t) is called the unit tangent vector and is a unit vector in the direction of r'(t). ds/dt is the speed, and is sqrt(x'(t)2+y'(t)2+z'(t)2), the length of r'(t). We use ds/dt also to convert derivatives with respect to t to derivatives with respect to s, as last time (the Chain Rule).
Since T(t)·T(t)=1 differentiation together with commutativity of dot product gives 2T'(t)·T(t)=0, so T'(t) and T(t) are perpendicular. In fact, we are interested in dT/ds, which is the same as (1/(ds/dt))T'(t) (it is usually easier to compute T'(t) directly, however, and "compensate" by multiplying by the factor 1/(ds/dt)). Any non-zero(!) vector is equal to the product of its magnitude times a unit vector in its direction. For dT/ds, the magnitude is defined to be the curvature, and the unit vector is defined to be the unit normal N(t). This essentially coincides with what was done last time, when curvature was defined to be d(theta)/ds.
I remarked in one class that the two-dimensional version of curvature (the d(theta)/dt) could be negative. there could be problems if dT/ds is zero or if d(theta)/ds was negative (example: look at how T and N change for y=x3 as x goes from less than 0 to greater than 0). I will just ignore that here.
For the helix, we computed ds/dt=(sqrt(a2+b2)) and T(t)=(1/sqrt(a2+b2))(-a sint(t)i+a cos(t)j +bk) and also N(t)=-cos(t)i-sin(t)j. We noted that N(t) in this case always pointed directly towards the axis of symmetry. We also got a formula for curvature: kappa=a/(a2+b2). This is a constant, and partly you should be able to convince yourself that curvature is a constant in this case because each piece of this curve is congruent to each other piece of the curve: just move the helix along itself by sort of screwing it up or down as needed. We will also check the answer with some examples soon.
We "complete" T and N to what is called a 3-dimensional frame by defining the binormal B(t) to be the cross-product of T(t) and N(t). Since T(t) and N(t) are orthogonal unit vectors, B(t) is a unit vector orthogonal to both of them. This needs some thinking about, using properties of cross-product: certainly B(t) is perpendicular to each of its factors, and the size of B(t) is the area of the parellelogram determined by T(t) and N(t), and this parellelogram is a square one unit on each side.
How does B(t) change? Since B(t)·B(t)=1, differentiation results in 2B'(t)·B(t)=0, so B'(t) is orthogonal to B(t). But differentiation of B(t)=T(t)xN(T) results in B'(t)=T'(t)xN(t)+T(t)xN'(t). Since T'(t) is parallel to N(t) (because of our definition of N(t)!), the first product is 0 (another property of cross-product!) so that B'(t) is a cross-product of T(t) with something. Therefore B'(t) is also perpendicular to T(t). Well: B'(t) is perpendicular to both T(t) and B(t), and therefore, since only one direction is left, B'(t) must be a scalar multiple of N(t). The final important definition here for space curves is: dB/ds is a product of a scalar and N(t). The scalar is -tau. That is supposed to be the Greek letter tau, and the minus sign is put there so that examples (the most important is coming up!) will work out better. This quantity is called torsion, and is a measure of "twisting", how much a curve twists out of a plane (the particular plane is the plane determined by T and N).
If a space curve does lie in a plane, and if everything is nice and continuous, then B will always point in one direction (there are only two choices for B, "up" and "down" relative to the plane, and by continuity only one will be used) so that the torsion is 0 since B doesn't change. The converse implication (not verified here!) is also true: if torsion is always 0, then the curve must lie in a plane!
For our example, we computed B(t) by directly computing the cross-product of T(t) and N(t). We got (I think!) (1/(1/sqrt(a2+b2))(b sin(t)i-b cos(t)j+a k) for B(t). This can be "checked" in several ways. First, that the candidate for B(t) has unit length, and then, that B(t) is orthogonal to both T(t) and N(t). This candidate passes those tests. Then we took d/dt of this B(t) and multiplied it by 1/(ds/dt)=(1/sqrt(a2+b2)). The result was (b/(a2+b2))(cos(t)i+sin(t)j). Checking all the minus signs (one in the definition of torsion and one in the result of N(t)) shows that here torsion is (b/(a2+b2)).
Looking at the extreme values of a and b in this expression (a, b
separately big and small) is not as revealing and/or as useful as with
curvature, since a "feeling" for torsion isn't as immediate.
Then
I looked at dN/ds, using the expression N=BxT. The
result, after using the product rule carefully (remember that this
product is not commutative!) is
(dB/ds)xT+Bx(dT/ds) which, by the earlier
equations, is
-tauNxT+kappaBxN
which is tauB-kappaT. So we have the following
equations, called the Frenet-Serret equations (also called
the Darboux equations in mechanics):
dT/ds = 0 + kappaN + 0 dN/ds =-kappaT + 0 + tauB db/ds = 0 -tauN + 0This is a collection of 3 3-dimensional vector equations, so it is a collection of 9 scalar differential equations. The remarkable fact is that if an initial point is specified for the curve, and an initial "frame" for the Frenet frame of T, N, and B, and if the curvature and torsion are specified, then the solutions to the differential equations above give exactly one curve. All the information about the curve is contained in the equations. So, for example, the motion of an airplane or a robot arm or the (geometric) structure of a long molecule are, in some sense, completely specified by kappa and tau. Of course, this doesn't tell you really how to effectively control something so it moves or twists the way it is "supposed" to. The idea that the Frenet frame "evolves" in time, governed by the differential equations above, is useful.
Here are some pictures of various helices produced by Maple
(the plural of "helix" is "helices").
The pictures below were
produced using the command
spacecurve([a*cos(t),a*sin(t),b*t],t=0..6*Pi,axes=normal,color=black,thickness=2,scaling=constrained,numpoints=180);
The procedure
spacecurve is loaded as part of plots using the
command with(plots);. I used the option
scaling=constrained in order to "force" Maple to
display the three curves with similar spacing on the axes. Otherwise
the x and y variables would be much altered in each image. I hope that
these pictures give some idea of what the curvature and torsion
represent.
| Some helices: x=a cos(t) & y=a sin(t) & z=bt | ||
|---|---|---|
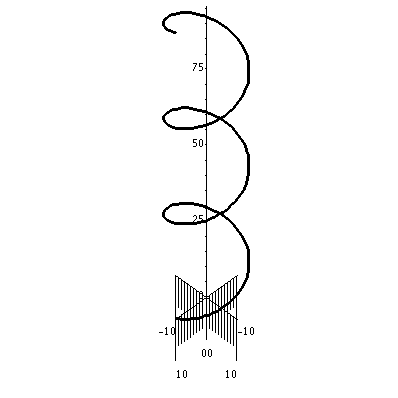| | | a=100 & b=5 kappa=.01 & tau=.0005 |
a=10 & b=10 kappa=.05 & tau=.05 |
a=5 & b=100 kappa=.0005 & tau=.01 |
QotD
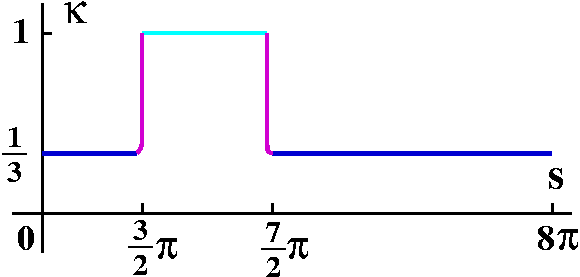I attempted to be "correct" both qualitatively and quantitatively in
this graph. The magenta curves are
my attempts to draw smooth transitions between the curvatures of the
circles.
HOMEWORK
Right now I am having "fun" trying to design an effective
Maple problem with curvature for the class.
Arc length
More realistically ...
There are some special test cases which I will want to keep in mind.
#1: a straight line
#2: a circle
#3: "the" parabola
The problem of understanding or defining curvature is to somehow
extract the geometric information from the parameterized curve. That
is, if a particle moves faster, say, along a curve, it might seem like
the same curve bends more. So what can we do? Somehow the
geometry of the curve should be separated from the dynamics
(kinetics?) of motion along the curve.
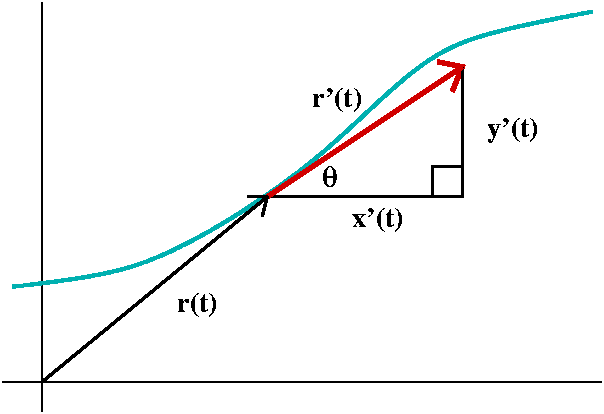
We looked at
theta, the angle that the velocity vector r´(t) makes with respect to
the x-axis. How does theta change? After some discussion it was
suggested that we look at the rate of change with respect to arclength
along the curve: that is the same as asking for the rate of change
with respect to travel along the curve at unit speed, and therefore
somehow the kinetic information will not intrude on the
geometry. This is the same as asking a bug to travel along the curve
at unit speed, and to describe the rate of change of theta (the
turning of r´(t), the velocity vector) as the bug strolls along
the curve.
The quantity s and the quantity t
By drawing a triangle we see that theta is arctan of y´/x´:
theta=arctan(y´/x´). We can find d(theta)/dt: it is
(y´´x´-x´´y´)/(x´2+y2)2. This uses
the formula for the derivative of arctan, the Chain Rule, and the
quotient rule. Then the previous results say that
Back to the test cases
I hope to have covered (note the tense!) sections 14.1 and 14.2 by the
end of Tuesday's lecture. Please
look at these sections.
Please prepare the following problems to hand in on
Wednesday: 13.3: 20, 39, 53; 13.4: 19; 14.1: 8; 14.2: 10, 19.
Of course you also have your wonderful workshop problem. I
strongly urge you to have some other student read it before you hand
it in. A student should be able to read your work without enormous
effort. Please also see this advisory about writeups.
Tuesday, January 31
A word from the management ...
The instructor gave a rather
terrible presentation Tuesday morning in front of the students of
sections 5, 6, and 7. An apology is due to them. He made at least one
serious conceptual error, and several pedagogical errors. The notes
below are mostly from the later lecture, given to students in sections
8, 9, and 10. While that lecture was not perfect, it went somewhat
better than the earlier lecture. The notes below are mostly,
therefore, from the second lecture.
If r(t)=<12t,8t3/2,3t2<, problem #6 of
section 13.2 asks for the length of the curve from t=0 to t=1. This is
a typical artificial problem in a textbook. We know that
r´(t)=<12,8(3/2)t1/2,6t< so that the
speed is
|r´(t)|=sqrt{122+122t+36t2}. Now
we "remember" that distance=rate·time, and that the magnitude
of the velocity vector is ds/dt, the speed. So the total distance
traveled is 
01sqrt{144+144t+36t2} dt.
Now look at the coincidences. We can pull out the 36 from under the
square root, and the result is 601sqrt{4+4t+t2} dt, and,
what a coincidence, 4+4t+t2 is (2+t)2 and the
integral becomes 601(2+t) dt=6(2t+(1/2)t2]01
and this is 6[2+(1/2)].
Almost every combination of two or three functions, even rather
"simple" functions that you try to use as a position vector, will
yield something that can't be antidifferentiated in terms of familiar
functions. For example, look at the following mess:
> a:=t->t^3;
3
a := t -> t
> b:=t->cos(t);
b := t -> cos(t)
> c:=t->exp(t);
c := t -> exp(t)
> int(sqrt(a(t)^2+b(t)^2+c(t)^2),t=0..1);
bytes used=4000036, alloc=3407248, time=0.14
bytes used=8007244, alloc=5241920, time=0.30
1
/
| 6 2 2 1/2
| (t + cos(t) + exp(t) ) dt
|
/
0
And that means Maple tried but can't figure out
anything useful to reply except to echo the integral back to the
questioner. My next step is
> evalf(%);
1.971185471
which asks for an approximate (numerical) evaluation of the
integral. That's almost always what's going to be necessary. Oh well:
the situation in textbook problems is much too nice.
Then I tried to analyze the idea of how a curve bends. Curvature will
be a measure of this bending.(Today a plane
curve, in R2, and tomorrow a space curve, in
R3.) I began an analysis that was apparently first done by
Euler in about 1750. A curve is a parametric curve, where a point's
position at "time" t is given by a pair of functions,
(x(t),y(t)). Equivalently, we study a position vector,
r(t)=x(t)i+y(t)j. Here x(t) and y(t) will be functions which I will
feel free to differentiate as much as I want.
A straight line does NOT bend, so it should have curvature 0.
A circle should have constant curvature, since
each little piece of a circle of radius R>0 is congruent to each
other little piece, and, in fact, the curvature should get large with
R gets small (R is positive), and should get small when R gets large
(and looks more like a line locally).
Even y=x2 might be a good test to keep in mind, since there
the curvature should be an even (symmetric with respect to the y-axis)
function of x, and should be bell-shaped, with max at 0 and limits 0
as x goes to +/- infinity.
Arc length, s, on a curve is computable with a definite integral:
sqrt(x´2+y´2) integrated from t0 to t
with dt is the arc length. This is rarely exactly computable with
antidifferentiation using the usual family of functions. But ds/dt is
just sqrt(x´2+y´2) by the Fundamental Theorem of
Calculus. And the Chain Rule suggests that d*/ds(ds/dt)=d*/dt if * is any quantity of
interest, such as theta. So to get d*/ds from d*/dt, multiply the
latter by 1/(ds/dt) which is 1/sqrt(x´2+y´2).
| The straight line We compute for some constants A and B and C and D: x(t)=At+B x´(t)=A x´´(t)=0 y(t)=Ct+D y´(t)=C y´´(t)=0so that the top of the curvature formula is 0. kappa=0 for any straight line. |
|
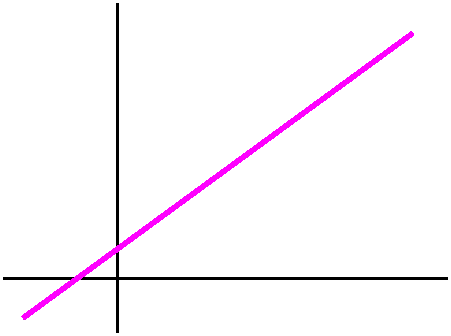
| A circle Suppose we have a circle of radius R centered at the origin. Then parametric equations are not too difficult to get: x(t)=Rcos(t) x´(t)=-Rsin(t) x´´(t)=-Rcos(t) y(t)=Rsin(t) y´(t)=Rcos(t) y´´(t)=-Rsin(t)Let me look first at the bottom of the curvature formula. This is (x´2+y´2)3/2. Notice that x´2+y´2=R2([-sin(t)]2+[cos(t)]2)=R2, so the 3/2´s power is R3. The top is y´´x´-x´´y´ and this is -Rcos(t)(-Rsin(t))--Rcos(t)Rcos(t)=R2·1. The whole curvature formula is then R2/R3 which is 1/R. When R is large, this is near 0. When R is close to 0 and positive, this is large positive. And the curvature is constant which it should be since the circle has the same local geometry at every point. |
|
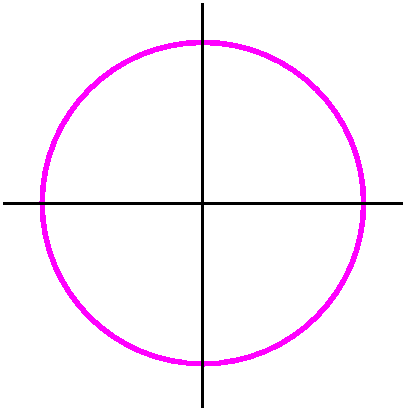
| A parabola Here I want to look at y=x2. A simple parameterization is good. So let's try: x(t)=t x´(t)=1 x´´(t)=0 y(t)=t2 y´(t)=2t y´´(t)=2Now the bottom of kappa, (x´2+y´2)3/2, becomes (1+4t2)3/2, and the top, y´´x´-x´´y´, is just 2. So k=2/(1+4t2)3/2. Here the "local geometry" definitely changes from point-to-point. The most curvy (?) part of the graph is at the origin. As x-->+/-infinity, although the graph gets steeper and steeper, the curve locally actually gets more and more flat: the curvature-->0. |
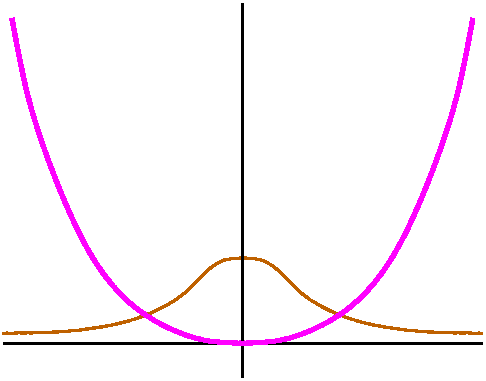 The smaller figure is supposed to be the cruvature of the parabla. |
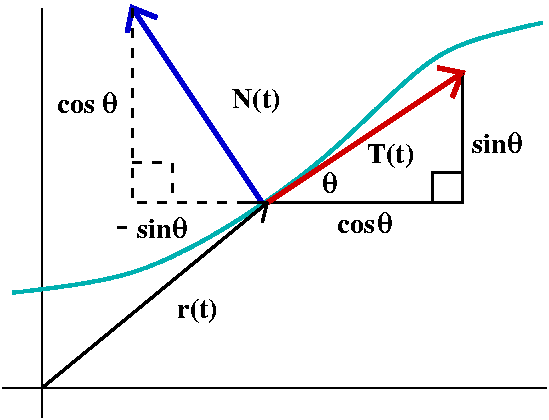I defined the unit
tangent vector, T, to be a unit vector in the direction of
r´(t). If theta is the angle that r´(t) makes with the positive
x-axis, then T must be cos(theta)i+sin(theta)j.
Also r´(t)=(ds/dt)T, where ds/dt is the length of r´(t),
the speed. Now differentiate the formula for r´(t) using
one of the product rules we had stated earlier. The result is
r´´(t)=(d2s/dt2)T+ (ds/dt)d/dt(T). But T is
cos(theta)i+sin(theta)j, and differentiation with respect to t is the
same as differentiation with respect to s multiplied by ds/dt. But
differentiation with respect to s gives (-sin(theta)i+cos(theta)j)
multiplied by the derivative of theta with respect to s, and this is
k. All this put together is:
We have decomposed acceleration into the normal and tangential directions. This can be significant physically. Here are two extreme situations.
Straight line motion: no transverse forces
I used this to show that motion in a straight line ( where
k= 0) had no normal component, and therefore a particle
moving in a straight line had no force needed transverse to its motion
(remember force and acceleration are vectors related by the scalar m,
according to Newton's second law).
Moving in a circle: always normal force
On the other hand, in our circular
situation, the curvature was a positive number, and as long as the
particle was moving (ds/dt not equal to 0) a force was needed
to keep it on the circle. This is because the curvature
k was non-zero, and so were the other terms. This is not
at all "intuitively clear" to me.
QotD
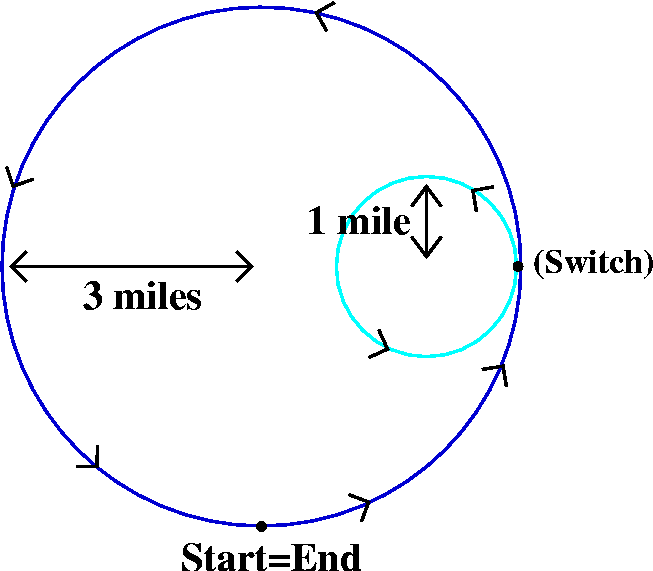
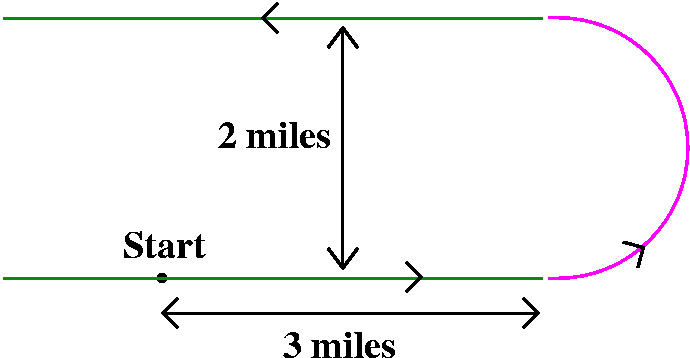
A racetrack: this racetrack consists, as nearly as possible, of two
straight line segments, each about 3 miles long, connected with a
semicircular track. Since the racetracks were specified to be 2 miles
apart, we "deduce" that the radius of the semicircle is 1 mile. The
racetracks certainly have curvature=0, and the semicircle, which is Pi
units long, has curvature 1. I asked that people try to draw
the curvature of this racetrack. I remarked at the next class that
students seem to have neglected the precise quantitative information
that they were given.
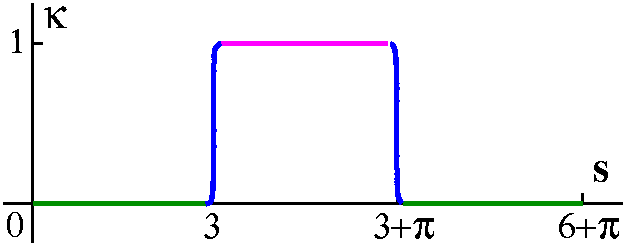
I attempted to be "correct" both qualitatively and quantitatively in this graph. The blue curves are my attempts to draw smooth transitions between the curvatures of the circles.
Parametric curves: a nuisance?
So I began with some irritating examples.
Distinguishing between geometric aspects of the path of a particle and the dynamic aspects of the particle will take up most of our next class. This won't be obvious.
Pictures of a point in motion
Twisted cubic
The twisted cubic is the curve
r(t)=<t,t2,t3>. It is one of the beginning
curves shown to students in this subject, with the warning that here
is how pictures can be deceptive. Here is a Maple command I
used, and then I rotated the image and exported the pictures
below.
spacecurve(<t,t^2,t^3>,t=-5..5,color=black,axes=normal,thickness=2);
| |
| |
| |
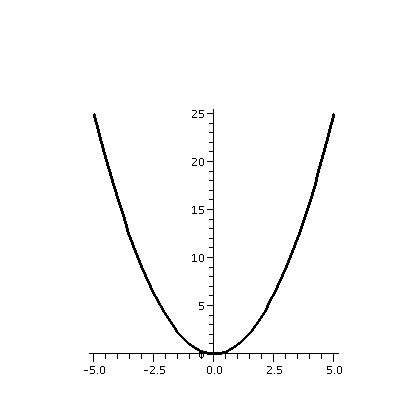
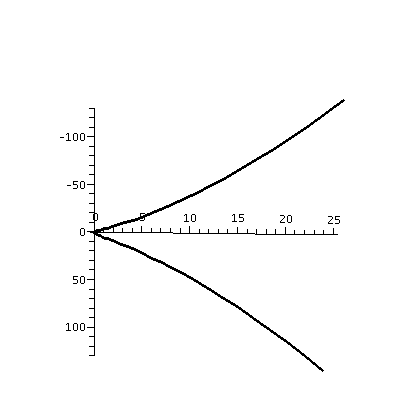
Frequently, similar difficulties have occurred in dissections, when slides of different cells are prepared. Depending on the angles of the slices, very different pictures are seen. |
|
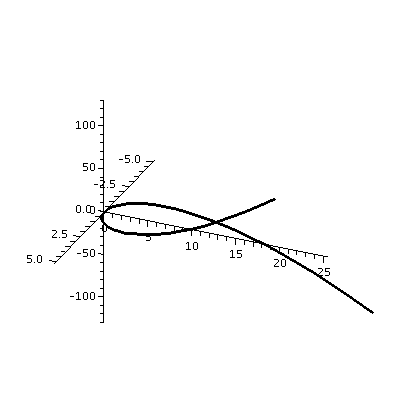
Robots and molecules
I remarked that people who wanted to understand the conformation of
biologically active macromolecules nned to learn how to look at curves
in R3. Also, people who want to describe motion of robot
arms are necessarily interesting in this subject.
The derivative
If r(t)=<a(t),b(t),c(t)> is a vector function of t, we can
consider (1/h){r(t+h)-r(t)}. Inside the {} is a difference of vectors,
and that's therefore a vector. Then multiplying by 1/h: that's a
scalar multiple. So the result is a vector. It may happen that the
limit as h-->0 of this quotient may or may not exist. If it does,
we'll say that r(t) is differentiable and that the limit, which is
labeled r´(t), will be called the derivative. It is also called the
velocity vector.
It doesn't take many examples to convince yourself that the (vector) derivative will exist exactly when all of the scalar functions a(t) and b(t) and c(t) are differentiable, and that the components of the resulting vector derivative will be the derivatives of these functions.
Various formulas, especially product formulas
The derivative of u(t)·v(t) is u´(t)·v(t)+u(t)·v´(t). The
derivative of u(t)xv(t) is u´(t)xv(t)+u(t)xv´(t). And
there's even another product rule (multiplying a vector function by a
scalar function and then differentiating). Since the cross product is
not commutative, the order is important (we'll see an example next
time).
Computations
I did some examples using leftovers from the textbook problems.
Meaning of the derivative
The derivative balances out a large scalar, 1/h (when h is small),
with a very small secant vector, r(t+h)-r(t). That the limit
exists is rather neat, and one should really not expect it!
The magnitude: speed
The magnitude of the velocity vector, |r´(t)|, is the speed.
The direction: unit tangent vector
The direction of r´(t)is gotten by taking r´(t) and dividing
by its norm, |r´(t)|. This is a unit vector, called the unit
tangent vecotr, and usually written T(t).
Velocity vector, tangent vector
So the direction of the velocity vector to tangent to the path of the
particle, and its length represents the speed of the particle.
Tangent line to a helix
Look at the curve r(t)=<3cos(2t),3sin(2t),8t>. What is this?
The first two variables describe uniform circular motion. The radius
of the circle is 3, and that's the distance from the central axis of
this curve, which turns out to be a helix. The 2 changes the angular
velocity of the curve, and doubles it. The 8 affects the "pitch", the
angle of the helix, and also the distance between "loops". When 2t
changes by 2Pi, the curve passes around one loop. That means the
change in t is Pi, so the change in z is 8Pi.
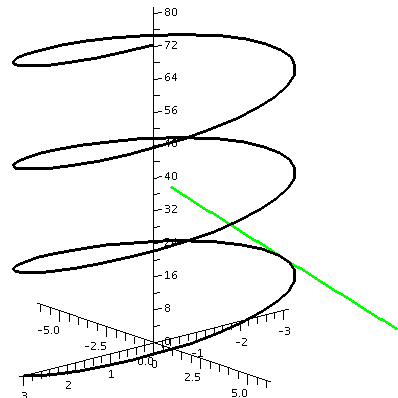Let's find the parametric equations of a line tangent to this helix
when t=Pi/2. The line must pass through
r(2)=<3cos(2[pi/2]),3sin(2[Pi/2]),8[Pi/2]>=<-3,0,4Pi>. A
vector in the tangent direction can be gotten from the velocity
vector. So: r´(t)=<-6sin(2t),6cos(2t),8> which, when
t=Pi/2, gives <0,-6,8>. Therefore the parametric equations for
the line are:
x=-3+0t
y=0-6t
z=4Pi+8t
To the right is a picture of both the helix and the tangent line just
specified. And I only had to do it twice because I made a mistake.
Question of the day
I asked students to find the parametric equations of a line tangent to
r(t)=<t2,1/t2,-4> when t=2.
HOMEWORK
Please read 13.1-13.4. You should hand in the following problems at
the Wednesday, February 1, recitation. Two of them will be graded.
Hand in: 13.1: 34, 13.2: 17, 26, 13.3: 2, 14.
Tuesday, January 24
101o Fahrenheit is about the same as 30.67o
Réaumur. This is another temperature scale. See here,
for example.
Old QotD
I looked at last week's QotD's and then I computed a dot product and a
cross product.
v=(1/sqrt{3})i-(2/sqrt{3})j+(5/sqrt{3})k and w=7sqrt{3}i-4sqrt{3}j+sqrt{3}k.
| i j k |
Then vxw=det| 1/sqrt{3} -2/sqrt{3} 5/sqrt{3} |
| 7sqrt{3} -4sqrt{3} sqrt{3} | This is:
Maple information
I then remarked that everyone who was a registered student and who had
filled out a student information
form should have gotten information about the
first Maple assignment. Students who did not get that
information should send me e-mail immediately. The due date for
this assignment is Wednesday, February 1 and late work will not
be accepted.
I will have office hours probably Tuesday and Thursday afternoons, but not today, since I need to go home and go to bed with my cold. You can see me in my office (Hill 542) on Thursday afternoon from 2:30 to 4:30. By then I might be healthier.
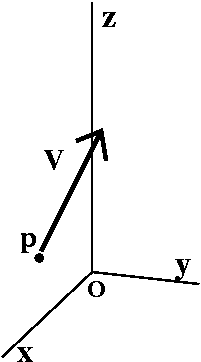Specifying a line
The following information will usually be the most convenient way to
specify a line in this course:
Example
Other parametric representations
There is a plethora of different parameterizations for the same
straight line.
Symmetric equations
Two points determine a line
Example
What condition(s) on x and y and z will guarantee that q=(x,y,z) is on
the plane? Well, the vector pq should be perpendicular to n. We can
check perpendicularity easily with dot product. An example may help.
Example
Again, there are many equivalent equations for one geometric plane
since there are lots of vectors normal to one plane, and lots of
points on one plane. And we can do the reverse:
Reversing ...
Three points determine a plane
Another way ...
QotD
The following material was not done in class, maybe due to the
instructor barely being alive.
Parallel lines
Skew lines
Intersection of two planes
The planes are not parallel because the normal vectors (<3,-1,0> and
<2,-2,1>, respectively) are not scalar multiples of one another. A
vector in the direction of the line will be perpendicular to both of
these normal vectors. The cross product gives us such a vector:
<3,-1,0>x<2,-2,1> is -i-3j+4k. We also
need a point on both planes. Well, if z=0 then we must find x and y
which satisfy both 3x-y=4 and 2x-2y+0=1. I can do this: double the
first equation and subtract the second equation. The result is 4x=7,
so x=7/4 and then the first equation becomes 3(7/4)-y=4 so y=5/4. And
(7/4,5/4,0) is a point on the line. Therefore a set of parametric
equations for the line is
Parametric equations for a plane
HOMEWORK
What's on the web and why?
Really the squares of the lengths
The obstacle to making it work
The dot product and its basic properties
Example with a little table
The law of cosines lurks ...
The geometry of the dot product
Determining an angle
Resolving a vector into perpendicular and parallel parts
How long is vpar? If you look at the picture, the
vpar is part of a right triangle. It is the adjacent leg
and v is the hypoteneuse. Theta is the angle between them. Therefore
|vpar|=|v|cos(theta)=v·w/|w|. We did some of these
computations just above, so |vpar|=13/sqrt(65). How can we
get the correct direct? So we want a vector whose length is
13/sqrt(65) and whose direction is the direction of w. Well, we can
create a unit vector (a vector of length 1) in the direction of
w: that will be w/|w| which is <5,2,6>/sqrt(65). And now we adjust
this unit vector by stretching it, to get
[13/sqrt(65)]<5,2,6>/sqrt(65). This is about all I did in class, but
let me finish things here. The vector is
(13/65)<5,2,6>=<1,26/65,78/65>. Since
v=vpar+vperp, we know that
vperp=v-vpar=<3,2,-1>-<1,26/65,78/65>=<2,104/65,-143/65>.
Checking the answer
Another product, introduced geometrically
Direction of vxw
The only reason that such a weird product would be considered is that
it is useful. We will see some geometric uses of it in this course and
most of you will see uses in mechanics (torque), eletromagnetism, etc.
The i,j,k multiplication table
Weird stuff
Then the cross product in terms of components is ...
This last formula can be expressed in a very neat way if you know about determinants.
It turns out that
Why is what I've done correct?
QotD
HOMEWORK
Torpor
Who am I?
Who are you?
What will we study?
Then we went on to "review" analytic geometry of one and two and even
three dimensions. I put the word in quotes because most students who
have taken courses in applied science and engineering have already
seen the material we will discuss in 3 or 4 other courses.
R1
R2
R3
{Levero|dextro}
Here is a short
discussion of parity in chemistry and physics. And here is a Wikipedia
article on enantiomers, which are compounds that are
non-superimposable mirror images of one another. This article is a bit
more technical, but has many examples of pharmaceutical products which
are mirror images.
The Euclidean distance
A bunch of comments
A sphere of radius 3
Completing the square to "recognize" a sphere
Vectors
Vectors are used to do algebra in more than one dimension. This is
because algebra has really been successful, and the interaction
between algebra and geometry has paid off well in both
directions. Therefore we'll need to add and multiply vectors. Efforts
to multiply run into serious difficulties, as we will see next
time. Addition is neat and "everything" works well. As I mentioned in
class, the generally accepted definition for vector addition models
some situations which can be experienced and measured in "real life"
with forces, velocities, etc. The word resultant is sometimes
used in connection with this definition.
Definition of vector addition
Zero and minus
Then v+(-v)=0, and v+0=0 etc. for all vectors.
Scalar multiplication
If c is a scalar and v is a vector, then the vector cv is defined by
the following:
The head and the tail produce the vector (algebraically)
How long is a vector?
NO! NO, NO, NO!!!
Next time I will explore how the differences can be explained,
as we discuss multiplication of vectors.
QotD
HOMEWORK Maintained by
greenfie@math.rutgers.edu and last modified 1/19/2006.
If p=(3,9,5) and v=<4,-7,6>, then the vector pq will be
x=3+4t
y=9+-7t
z=5+6t
So these are parametric equations for the straight line
determined by the data p and v. Notice where the 3 chunks of p's
information go (no t's!) and where the 3 chunks of v's information
(the direction) go (with the t's).
I then played with these equations for a while. For example, the
equations
x=3+12t
y=9+-21t
z=5+18t
represent the same line. I just multiplied the direction v by 3. This doesn't
change the actual geometric line which is parameterized by the equations: every
point in "this" line is in the other line, and, similarly, the other way
around. And
x=3-4t
y=9+7t
z=5-6t
represents also the same line: I multiplied the direction by -1 but still
we will get the same total collection of points: the same straight line. And,
perhaps more complicated:
x=7+4t
y=-2+-7t
z=11+6t
This is also the same line. Notice, please, that the direction vector
is the same, but what I have changed is the "base point",
(7,-2,11). But if you consider the original parameterization, and put
t=1 in those equations, we will get (7,2,11). So, in fact, the
descriptions sort of "overlay" one another: the v's are the same, and
the we've just happened to start the parameterizations at different
points on the same line.
Plethora officially means "A superabundance; an excess."
Some manipulation gives another way to represent the line.
x=3+4t becomes t=(x-3)/4
y=9+-7t becomes t=(y-9)/(-7)
z=5+6t becomes t=(z-5)/6
so that we have (x-3)/4=(y-9)/(-7)=(z-5)/6. Such a collection of
equations is called the symmetric form of the line. As far as I know,
we won't describe lines this way in this course.
The original work of Euclid is available, translated and illustrated,
for free on the web. You may see here.
This work has been done by Professor Joyce of Clark
University. So, way back, thousands of years ago, Euclid decided
that a line would be determined by two points. How can we use such
information to get an algebraic description?
Suppose p=(3,3,-9) and q=(-5,2,1). What are parametric equations for
the line through the points p and q?
The vector pq=<-5-3,2-3,-5-(-9)>=<-8,-1,4> is a vector in the direction of the line. We could use
either p or q (I'll use p here) for a "base point"
for the line. So we get the following parametric equations for the
line:
x=3+(-8)t
y=3+(-1)t
z=-9+(4)t
The colors are an effort to show where to put the data in the
parametric formulas.
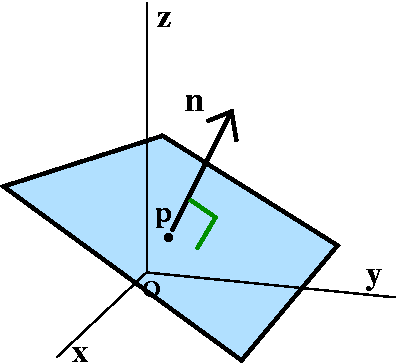Specifying a plane
In this course, the data specifying a plane will also turn out to be a
point and a vector. What I'm about to describe may not look
immediately useful, but it will be, really. So what we will need is
I hope that a picture can be persuasive. There are many planes which
pass through the point p. But if you add on the requirement that, at
the point p, the vector n be perpendicular, exactly one geometric
"candidate" persists, and that's the plane I'd like to describe
algebraically.
Suppose p=(4,5,-7) and n is the vector <11,2,31>. The vector pq is
11(x-4)+2(y-5)+31(z+7)=0
This is a fine equation. You don't need to "clean it up". Of
course, it can be rewritten (if you must!) as
11x+2y+31z=44+10-217=163.
6x+-3y+7z=20 is the equation of a plane.
What is a vector normal to this plane? If you
followed the previous discussion, I hope you can see that the
components of such a vector are the coefficients of x and y and z in
order. So n=<6,-3,7> is a vector normal to this plane.
What are all (non-zero) vectors normal to this plane? These vectors
are the non-zero scalar multiples of <6,-3,7>.
What are the coordinates of a point on the plane 6x-3y+7z=20?
Part of the problem in answer this question is that there are so
many possibly answers! For example, (0,0,20/7) is one answer, and
so is (1,-7/3,1), and so is .... uhhh ... (1,000, -1,000,
-8,980/7). There are many points on the plane.
Again, Euclid declared that 3 points in space should determine a
plane. So can we find an algebraic description of a plane through
the points p=(3,3,-9) and q=(-5,2,1) and r=(4,2,2)? We need to find a
vector n normal to the plane. Well, the vectors pq and (say) qr are in
the plane's direction. The cross-product of these two vectors will be
perpendicular to the plane. So: pq=<-8,-1,4> and qr=<9,0,1>, and
| i j k |
det|-8 -1 4 |=-i-(-8-36)j-(-9)k=-i+44j+9k
| 9 0 1 |
is a normal vector. So -1(x-3)+44(y-3)+9(z-(-9))=0 is an equation of this
plane. (We would get equivalent equations if we used q or r instead of p, or
if we computed with pqxpr instead of pqxqr.)
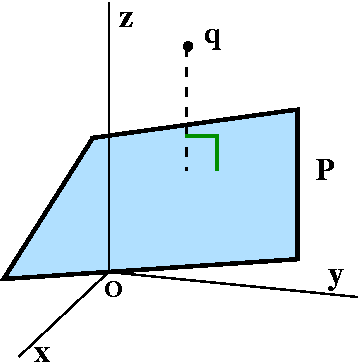Distance of a point to a plane
Suppose the point q is not on a plane, P. How can we find the
distance from q to P? I did this in a rather clumsy way in class,
mostly because I wanted to practice how to use line and plane
equations. Let me start with specific information:
Suppose
q=(2,1,3) and P is the plane specified by the equation
5x-7y+6z=10.
First, is q on the plane, P? Well, we can check this by substituting
the coordinats of q into the equation presented for P:
5·2-7·1+6·3=10-7+18=21, and 21 is not 10, so q is
not on P.
My strategy for finding the distance was to write the parametric
equations for a line through q perpendicular to P, see where the line
intersected P, and then compute the distance from q to that point. So
let me try to carry this out.
x=2+5t
y=1-7t
z=3+6t
are parametric equations for the desired line.
5x-7y+6z=10 becomes 5(2+5t)-7(1-7t)+6(3+6t)=10 which is
(25+49+36)t=10-10+7-18 and this is 110t=-11 so t=-11/110=-1/10.
What does this value of t mean? It is the value of t which, when
substituted in the parametric equations, gives the intersection
point. So:
x=2+5(-1/10)=15/10
y=1-7(-1/10)=17/10
z=3+6(-1/10)=24/10
The intersection point is (15/10,17/10,24/10).
Several students had much better suggestions than the computation
above. So here is another way: (2,1,3) is not on the plane
5x-7y+6z=10. I can find a point on the plane just by "guess" (as I did
earlier, and I will guess for something convenient!): r=(2,0,0). Then
the vector rq=<0,1,3> points from the plane to q. ow if I project rq
onto the normal vector I will get a vector whose length is the
distance from the plane to the point. This "projection" is just what I
did last time when I found the parallel part of a
vector. So n=<5,-7,6> is still a vector normal to the plane. So we
just compute rq·n/|n|=(-7+18)/sqrt{110}=11/sqrt{110},
which is the same answer. This is more direct and more efficient.
Given a point and a vector, I asked students for parametric equations
of a line in the direction of the vector, and for the equation of a
plane through the point normal to the vector.
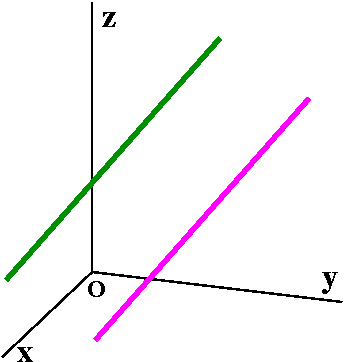I guess two lines are parallel if they are distinct (that is,
separate lines!) and if their directions are non-zero multiples of one
another. So, for example, the lines
Line A Line B
x=5+t x=30+t
y=3+2t y=-9+2t
z=-1+3t z=-1+3t
are parallel. Well, certainly their directions are multiples of one
another (the multiple is 1). But why are they "distinct"? The point
(5,3,-1) is on the first line. For it to be on the second line, uhhh ...
30+t=5, so t=-25. The second equation is then y=-9-(2)25=-59, and this is
not 3. So (5,3,-1) is not on the other line.
These are parallel lines.
Parallel planes
Two planes are parallel if they are distinct (that is, separate
planes!) and their normal vectors are non-zero multiples of one
another. For example, 2x+3y-z=56 and 4x+6y-2z=10 are parallel. Double
the first equation and get the right-hand side of the second: that
shows their normal vectors are non-zero multiples (the multiple is
2). But since twice 56=112 is not the same as 10, these planes are
definitely distinct: different.
As dimensions increase, generally geometry gets more complicated. One
phenomenon which does not occur in two dimensions is skew
lines. A pair of lines is skew if they are not parallel and
also do not intersect. So look at, say, the x-axis (where parametric
equations could be x=t,y=0,z=0) and a line through (0,1,0) which is
tilted with respect to the x-axis: x=t,y=1,z=t. These lines don't
intersect since no point with second corrdinate 0 is on the second
line. They aren't parallel since <1,0,0>, the direction of the first
line, is not a non-zero scalar multiple of <1,0,1>. So they are skew.
Things get even worse as n, the dimension, increases. For example, it
is possible to have pairs of skew planes (two dimensional
objects) in R4.
The two planes 3x-y=4 and 2x-2y+z=1 are not parallel. They intersect
in a line. How can we get parametric equations for this line?
x=7/4+-t
y=5/4+-3t
z=0+4t.
Another way to describe a plane is parametrically. Pick a point
on the plane, and pick two vectors with distinct directions pointing
in the plane. Wait: let's look at an example. Suppose the plane
contains the point p=(9,-5,1) and the vectors u=<3,-2,5> and v=<6,5,4>
point along the plane. Then for all numbers s and t, the points described by
(9,-5,1)+su+tv describe a plane. I can break this up into components:
x=9+3s+6t
y=-5-2s+5t
z=1+5s+4t
We will deal with this alternative algebraic description of planes
later when we discuss parametric surfaces. We can get back a
vector normal to the plane by taking the cross product of u and v.
Read more of chapter 12. Work on the Maple assignment.
Friday, January 19
I thanked the students who had shown up for the Maple labs. I don't think you need to fall in love
with Maple, but you should see it as
another tool you can use to learn.
I discussed the material I would place on the web for this course. I
called attention to the list of
students. I urged in class and I urge readers now to consider
forming a study group for Math 251: do homework problems together,
prepare for exams, etc. There is considerable evidence that
students who work in study groups learn more and get higher grades.
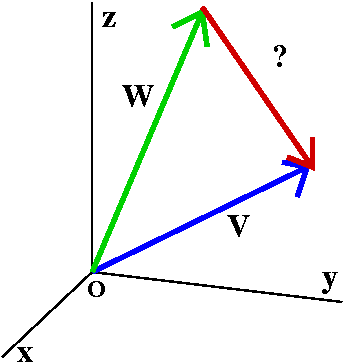Looking at lengths again
I started with v=ai+bj+ck so that
|v|=srqt{a2+b2+c2}. If w=di+ej+fk,
then |w|=srqt{d2+e2+f2}. If I draw
the vectors v and w with their tails on the origin, then a vector,
identified in the picture with "?", completes a triangle, going from
the head of w to the head of v. Well, that vector isn't too
mysterious. I know that w+?=v, so ?=v-w. In terms of components, we
can write v-w=(a-d)i+(b-e)j+(c-f)k. The length of v-w is
sqrt{(a-d)2+(b-e)2+c-f)2}. We saw last
time that the sum of the lengths is not the length of the sum.
With all the square roots, maybe we should be looking at the squares
of the lengths. Also the algebra will be easier!
Then |v|2=a2+b2+c2
and |w|2=d2+e2+f2
and |v-w|2=(a-d)2+(b-e)2+c-f)2.
We can "expand" the last term to get
|v-w|2=a2-2ad+d2+b2-2be+e2+c2-2cd+e2.
Well, if you compare terms, the sum |v|2+|w|2 is
the same as |v-w|2 except for -2ad-2be-2cf=-2(ad+be+cf). So
computations with lengths and squares of lengths will have to include
that "mess". Let me forget the -2, which isn't that essential.
Here we'll define the dot product. This is also called the scalar or inner product.
If v=ai+bj+ck and w=di+ej+fk, then v·w=ad+be+cf. In some places, v·w
is written <v,w>.
The dot product obeys the following rules.
Suppose we have four rambunctious ("Boisterous and disorderly"
vectors: v1 and v2 and w1 and
w2. I also have this little multiplication table for their
dot products:
· | w1 | w2
--------------
v1 | 3 | 7
--------------
v2 | 4 | -2
I asked students to compute something like
(4v1-3v2)·(5w1-2w2).
Here I expected people to distribute or take advantage of linearity on
both the left- and right-had sides. So here is how the process might
go:
(4v1)·(5w1-2w2)+(-3v2)·(5w1-2w2)
(4v1)·(5w1)+(4v1)·(-2w2)+(-3v2)·(5w1)+(-3v2)·(-2w2)
(4·5)v1·w1+(4·-2)v1·w2+(-3·5)v2·w1+(-3·-2)v2·w2
(4·5)(3)+(4·-2)7+(-3·5)(4)+(-3·-2)(-2)
And the answer seems to be .... 60-56-60-12=-68. I think this is
correct. I make more errors in such computations when no one is
watching me.
There's a formula which generalizes the Pythagorean Theorem's
formula. For the triangle shown, here it is:
|v-w|2=|v|2+|w|2-2|v| |w|cos(theta)
Here theta is the angle opposite the side v-w. If theta is Pi/2, the
cosine term is 0 and we get back Pythagoras. Here is the geometric view
of the areas of the squares on the sides of a triangle.
Since we know that
|v-w|2=|v|2+|w|2-2|v| |w|cos(theta)
and we know that
|v-w|2=a2-2ad+d2+b2-2be+e2+c2-2cd+e2=|v|2+|w|2-2v·w. We
see that (cancelling the -2's)
v·w=|v| |w|cos(theta) where theta is the angle between v and w.
Notice that we can now see if v and w are not 0, then v and w are
orthogonal (perpendicular, normal) exactly when v·w=0.
Suppose v=<3,2,-1> and w=<5,2,6>. What is the angle between v and w?
Well, v·w=15+4-6=13, |v|=sqrt(14), and |w|=sqrt(65). Therefore
cos(theta)=13/[sqrt(14)sqrt(65)]. This gives approximately
(calculator-assisted computation here!) 64.55 degrees or (better, I
guess) 1.126 radians.
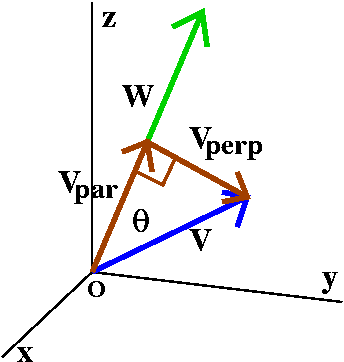Let me continue using the v=<3,2,-1> and w=<5,2,6> from the previous
question. I'd like to show you how to write v as a sum of two
vectors, vpar and vperp where vperp
is perpendicular to w and vpar is parallel to w. This will
be useful several times in the course, and is also important in
physics.
Well, vperp should be perpendicular to w. So let's
compute vperp·w=<2,104/65,-143/65>·<5,2,6>=10+(208/65)-(859/65)=(650+208-858)/65=(858-858)/65=0,
so these vectors are indeed orthogonal.
Comment I admit (informative to you and irritating to me) that
I did all these computations by hand, and I had to do them three
times to get them to come out correctly.
I defined the dot product by a rather simple algebraic formula. The
cross product has a complicated algebraic formula, and maybe it is
easier to beguin by defining it geometrically.
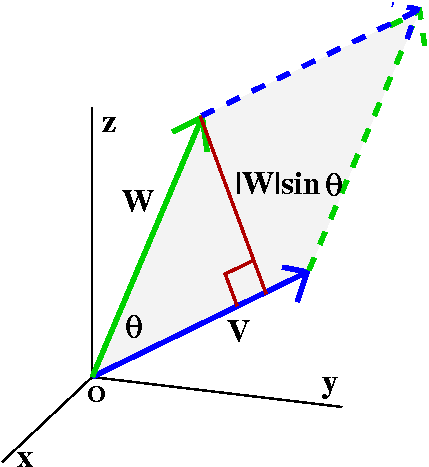The cross product (also called the vector or outer product) takes two
vectors, v and w, and produces vxw, another vector. Since this is a
vector, it is specified by its magnitude and direction.
Magnitude of vxw
Look at the the vectors v and w. There is a parallelogram which has
sides v and w. The area (a non-negative quantity) of that
parallelogram is the magnitude of vxw.
I forgot to say in class that there is an easy formula for the area in
terms of the lengths of the vectors and the angle between them. The
area is |v| |w|sin(theta). You get this by mulitplying the base
by the altitude in the plane of the parellelogram.
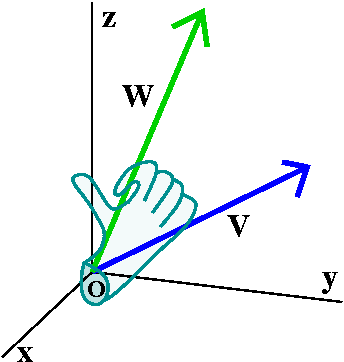Take your right hand and extend your
thumb. Curl up your fingers. Insert your hand (I guess by though, not
physically) so that your fingers go from v to w. Then
your thumb will be (sort of) pointed perpendicular to the plane
containing v and w. That perpendicular direction is the direction of
vxw.
So before anyone could yell too much I computed the cross product
"multiplication table" for i and j and k. This wasn't too hard,
although getting the directions correct involved some thought
and some physical contortions. These are unit vectors and all mutually
perpendicular. If the vectors in the product are the same, then the
parallelogram involved collapses to a line segment and has no area. If
the vectors are different, then the parallelgram is a square with 1
unit sides, and has area 1. The important thing is the sign of the
answer and its direction. I tried to get that correct. If you were not
in class or you were confused, I urge you to try to get some of the
entries in this table yourself. x | i | j | k
--------------------
i | 0 | k | -j
--------------------
j | -k | 0 | i
--------------------
k | j | -i | 0
Things to notice:
ixj=k and jxi=-k. The cross product is not necessarily commutative.
(ixj)xj=kxj=-1 and ix(jxj)=ix0=0. The cross product is not
necessarily associative.
This means that you can't necessarily rearrange or regroup cross
products. This is annoying. The cross product does not resemble many
other products you have seen.
I then did the following awful computation, which you should never do:
If v=ai+bj+ck and w=di+ej+fk, then vxw=
(ai+bj+ck)x(di+ej+fk)=ad(ixi)+ae(ixj)+af(ixk)+bd(jxi)+be(jxj)+bf(jxk)+cd(kxi)+ce(kxj)+cf(kxk).
I filled in all the values from the multiplication table above and got
the following mess:
vxw=ad(0)+ae(k)+af(-j)+bd(-k)+be(0)+bf(i)+cd(j)+ce(-i)+cf(0)=(bf-ce)i+(cd-af)j+(ae-bd)k
| i j k |
vxw=det| a b c |
| d e f |
There's a very brief discussion of determinants in the textbook. I
will probably evaluate this determinant most of the time by "expanding
along the first row" but you may use any valid method.
The definition I gave for cross product was geometric. Some of the
properties of cross product are easy from the geometric
definition. But I've just used linearity (or distributed the sum over
the cross product), something like this:
(v1+v2)xw=(v1xw)+(v2xw). Why
is this true? This is not clear (!)
to me at all from the geometric definition. Here
is a paper which shows why you can distribute using geometry. Figure 6
on page 8 of this paper is a picture which should convince you that
cross product does have the desired algebraic property. I hope you
will find it convincing.
I gave two vectors (something like v=<3,1,-2> and w=<1,-2,4>
and asked people to compute the dot and cross products of these vectors.
Please read 12.1-12.4, and begin reading 12.5. You should hand in the following problems at the Wednesday, January 25, recitation. Two of them will be graded. You will also have a short quiz. The quiz problem will be similar to a homework problem.
Hand in: 12.1: 12, 12.2: 26, 12.3: 51, 12.4: 27, 12.5: 23
Torque
Tuesday, January 17
This is Math 251. The lectures are done by me, and I will attempt to
give lectures with the same approximate content on first and third
periods each Tuesday and Friday. The first period perhaps will be more
spontaneous but also will have more errors both in content and in
presentation. The third period is likely to be a bit more organized,
but perhaps less lively. Sigh.
I'm a faculty member in the Rutgers Math Department. Much of my
professional work has involved differential equations involving
functions of more than one variable. I actually like the
content of this course, and I may get almost incoherent with
excitement and pleasure when describing some of the subject matter. I
haven't taught this course in almost a decade. I have taught Math 421
several times in the last few years. Math 421 is required for several
engineering degrees (Mechanical, Chemical, Biochem), and almost
everything done in that course builds directly on the material of this
course.
Most of the students in these sections are
engineering students. Others are from such disciplines as chemistry,
computer science, mathematics, meteorology, and physics.
I tried to briefly discuss the background of the
course. The link indicated has more information.
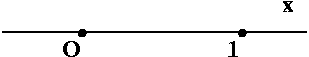This is supposed to be the real line. There's an origin and a
unit length, and the conventional choice is to make the positive
direction go off to the right. Each point on the line corresponds to a
real number. The distance between points on the line which correspond
to the real numbers a and b is defined to be |a-b|.
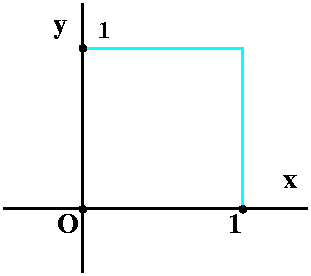And here is the plane (I don't think I've ever heard anyone
call it the "real plane"). The simplest situation is what's shown
here. Two straight lines as axes, perpendicular to each. Every point
corresponds to a unique ordered pair of real numbers. There is a set
unit length on each coordinate axis, and almost always right is
positive and up is positive. Later in the course we will consider
situations where the coordinate axes are not necessarily
perpendicular. And even where what corresponds to the axes are not
straight. I hope that tilted axes could make sense if, for
example, you were interested in looking at crystals which did not have
rectangular symmetry.
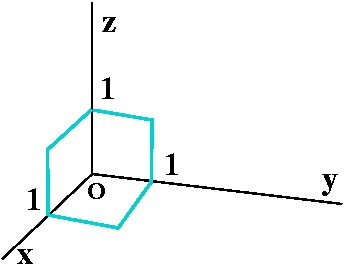In three dimensions, the geometric situation is specified by three
mutually perpendicular lines. Points will correspond to ordered
triples of real numbers. In almost every situation you are likely to
encounter, these axes will be right-handed. Right-handed means
... means ... means ... well, it means what I sketched to the right
(heh heh). The three dimensional world is complicated, and you will
see that the choice of right-handedness has some interesting
consequences.
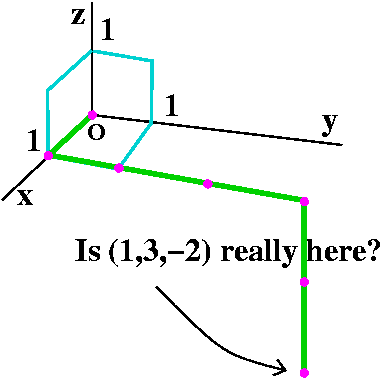Perilous pictures
Here is my attempt to draw the point with coordinates (3,2,-1).
The green "path" with 
's sort of tells how to find the
point. I walk (?) from (0,0,0) to (1,0,0), then to (1,3,0), and
finally to (1,3,-2). Each is
supposed to represent one unit of the path. I think that the
complications of perspective and reducing the "object" from three
dimensions to a two-dimensional representation may make even such a
simple picture difficult to understand. If you weren't told that the
point was supposed to be (1,3,-2), would you have guessed those were
the coordinates? Sigh.
I will try to draw good pictures, but I won't always
succeed. And even if I draw pictures which I believe are suitable, you
may well not agree. Pictures are complicated.
A brick
in space
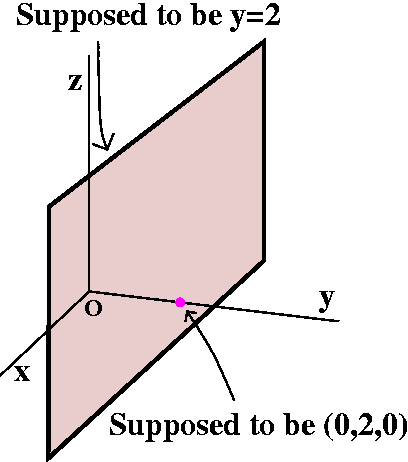
Some simple geometry and equations
What points in R3 have y=2? Certainly (0,2,0), on
the y-axis, is the only point on the y-axis with y=2. We can move up
and down (changing z-coordinate) and sideways (changing
x-coordinate). We can even change both. The collection of points we
get is a plane, perpendicular to the y-axis through the point
(0,2,0). An attempt at a picture is to the right. The words "Supposed"
refer to the possibility that you don't agree it is a good picture!
I mentioned that in this course I would probably regard the following
as synonyms (the words mean the same) most of the time:
perpendicular
orthogonal normal
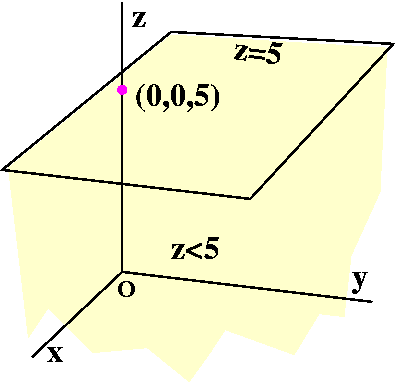
What points in R3 have z<5? As one student
observed, this is a half-space. The plane z=5 is the boundary
of this region. It is a plane normal to the z-axis through the point
(0,0,5). The plane, however, is not included in the region
specified by z<5. The region does not include its boundary. A
region which does not include its boundary is called an open region
(we'll go into more detail later). So what I've attempted to show in the picture is an open half-space.
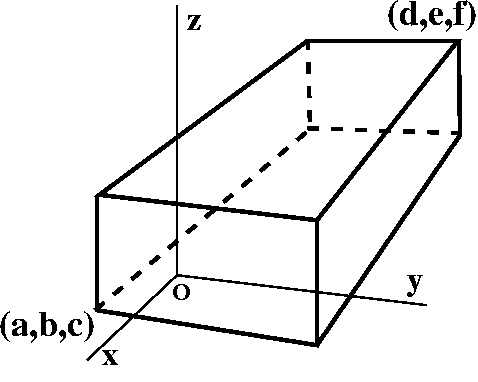
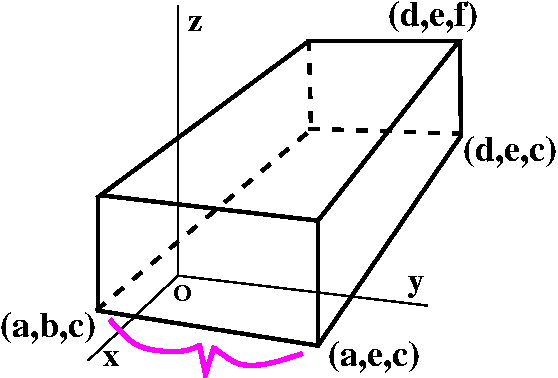
Let's imagine a brick in R3 with its
sides parallel to the xy and yz and xz planes. Maybe this could be
called a right-angled parallelopiped. Suppose one corner (also called
a vertex) has coordinates (a,b,c) and the diagonally opposite corner
has coordinates (d,e,f).
Suppose now we look at the corner displayed in the
accompanying picture, the corner illustrated with
. What are the coordinates of that
point?
If you can "see" what the picture is supposed to show, then the
designated corner is just moved "out" parallel to the direction of the
y-axis. The x-coordinate doesn't change at all, and the height from
the xy-plane (which is the z-coordinate) also doesn't change.
Therefore the coordinates of are
certainly (a,?,c). What about the second coordinate of the
point? If you look at the picture with me, you can see that the entire
face or side of the solid between and the point (d,e,f) has constant y-value: it is
perpendicular to the y-axis. Therefore the mystery middle coordinate
must be the same as the middle coordinate of (d,e,f), and so
=(a,e,c).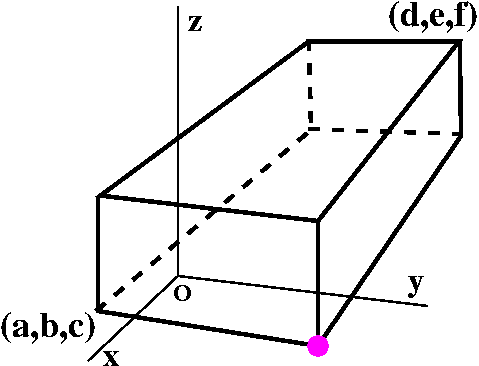 
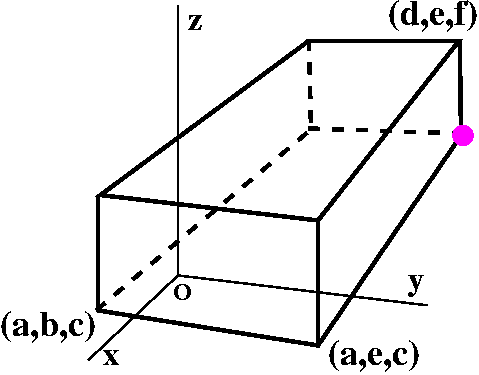
Now let us play the same game with another vertex (or
corner). So the designation of
has been moved to the corner shown. What are the coordinates of this
point? This point is on the same face or side of the solid so it
certainly shares the second or y-coordinate with both (d,e,f) and
(a,e,c), so =(?1,e,?2). Well, the
third coordinate, ?2, must be c since the point
we're looking at is certainly on the bottom face of the solid. The
first coordinate might be the most puzzling, but both (d,e,f) and are on the "back" face (that is part
of the plane x=d) of the solid, so the x-coordinate we're looking for
is d. Therefore this is (d,e,c).
A good exercise for you is to figure out the coordinates of
some of the other corners of the brick.
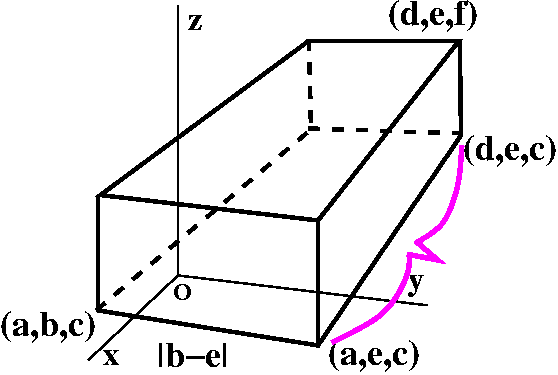
Now I'd like to compute the length of some of the edges of the
brick. For example, what is the length of the line segment connecting
(a,b,c) and (a,e,c)? This is the distance between these two
points. Notice that the only coordinate which is varying is the middle
one. This side is a line segment which is parallel to the y-axis. We
can measure length along it only by thinking about the
one-dimensional distance between b and e. That distance is |b-e|. The
reason for the absolute value signs is that distance is supposed to be
non-negative.
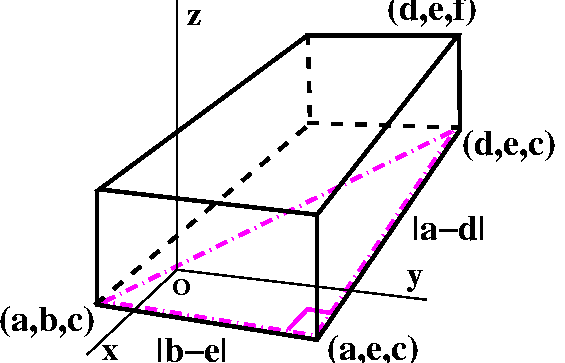
We can try to do the same thing with the edge connecting the
points with coordinates (a,e,c) and (d,e,c). Here the only coordinate
difference is in the first, x-, coordinate. So distances again should
be measured as if they were in one dimension, along the parallel
x-axes. The distance we want is |a-d|.
Now we can be even more bold. (Well, bold for a math class.)
We can find the distance from (a,b,c) to (d,e,c). Well, look carefully
and see that there is a right triangle whose hypotenuse is the
distance wanted, and whose "legs" have distances we already know. Then
Pythagoras declares that the length of the hypotenuse is
I'm not going to try to put that formula in the picture. I
will just label the distance Blah. Now I want the distance
along one of the main diagonals of the brick, from (a,b,c) to
(d,e,f). There is, as shown, another right triangle. The hypotenuse is
the distance I want, and the two legs have distances we know: one is
Blah and the other is ... the other is: well, the same ideas as
before (since the endpoints differ in only one coordinate) tell me
that the distance is |c-f|. Therefore (again Pythagorus) the
distance between the farthest apart corners is
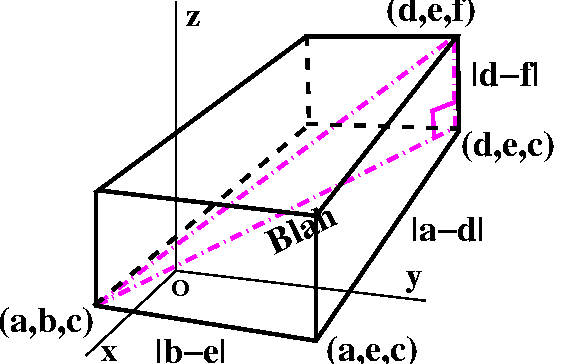
The (Euclidean) distance between (a,b,c) and (d,e,f) is sqrt((a-d)2+(b-e)2+(c-f)2).
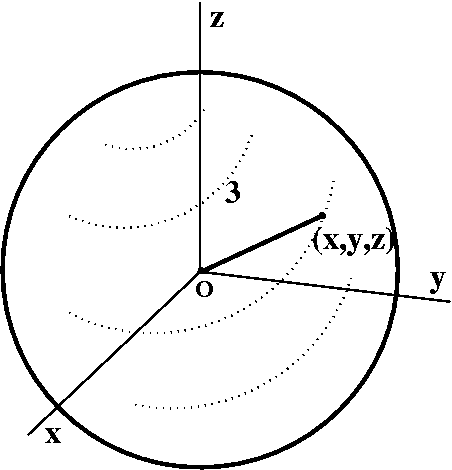
What algebraic condition on a point (x,y,z) is equivalent to the
geometric statement that the point lies on a sphere of radius 3
centered at (0,0,0)? This means that the distance from (x,y,z) to
(0,0,0) should be 3, or
sqrt((x-0)2+(y-0)2+(z-0)2)=3 which of
course is the same as x2+y2+z2=9.
We could of course "reverse" the process if we're given an equation
(or at least an equation of the correct form). For example, the equation
x2-3x+y2+4y+z2-7=0
represents a sphere. What is its center and its radius? The key
algebraic maneuver here is completing the square, and
everything works very much as in two dimensions.
x2-3x -->
x2+2(-3/2)x -->
x2+2(-3/2)x+(-3/2)2-(-3/2)2 -->
(x-3/2)2-(-3/2)2
y2+4y -->
y2+2(2y) -->
y2+2(2y)+22-22 -->
(y+2)2-22
We don't have any term with z to the first power. So the equation
becomes:
(x-3/2)2-(-3/2)2+(y+2)2-22+z2-7=0
which is the same as
(x-3/2)2+(y+2)2+(z-0)2=(-3/2)2+22+7
and we can "read off" that the center is (3/2,-2,0) and the radius is
sqrt((-3/2)2+22+7). It is easy to make mistakes
with minus signs when identifying the center. It is also easy to
forget to take the square root when identifying the radius. Oh well.
If we had different (but positive) numbers in front of the squares
(x2 and y2 and z2) then we'd get an
egg-shaped object, an ellipsoid. We'll see more about this
later.
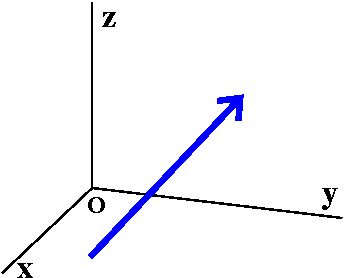
A vector is a directed line segment. It is used as a
mathematical model for any quantity which has both magnitude and
direction. For example, some of the following quantities are vectors
and some are not:
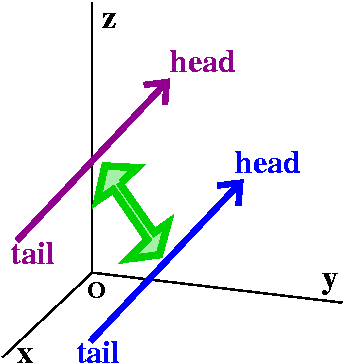Equal vectors
A vector can also be specified by its head and tail.
Two vectors will be called equal (maybe the official word is
equivalent) if when the tail of one of them is moved to the tail of
the other, then their heads are in the same place.
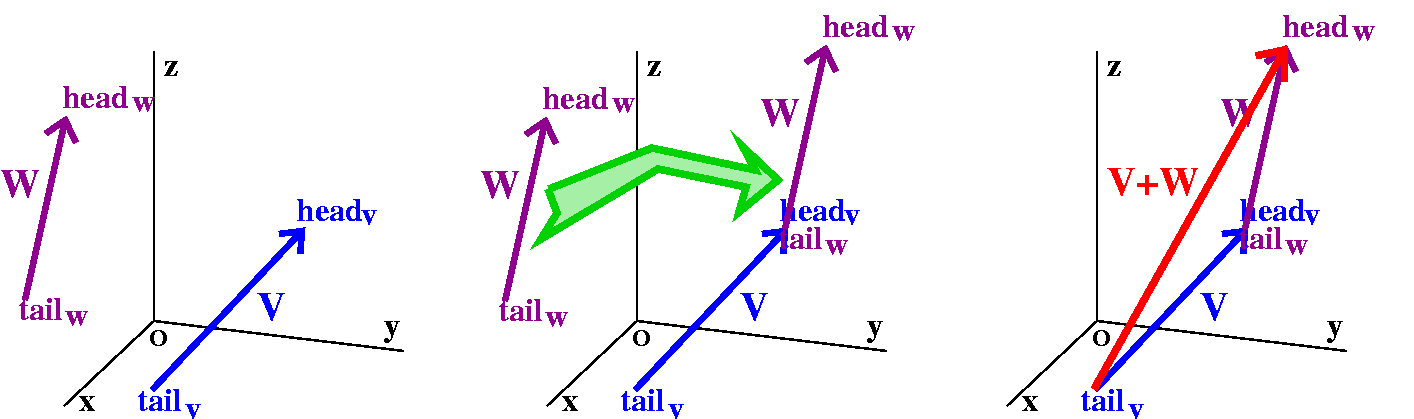
Properties of vector addition
First suppose there are two vectors, v and w, which are
roaming, free and happy in R3.
We take the vector w and drag it so that the tail of w is at
the same point as the head of v.
The vector v+w is now defined using the geometric display we just
arranged. v+w the vector whose tail is at the tail of v and whose head
is at the head of w.
This can be proved from the geometric definition by drawing a
parallelogram which has one pair of sides translates of v and the
other pair of sides translates of w. Anyway, the order in which you
add vectors doesn't matter.
I think this can be proved by drawing some
parallelopided (three-dimensional analogue of a parallelogram) with
sides gotten form v and w and u: but the diagram would almost be more
annoying than just thinking about it. The important consequence is
that you can group adding vectors in any way you want, and the result
will be the same.
The zero vector has its head equal to its tail. If v is a vector, then
-v is the vector whose length is v's but whose direction is the
reverse: so the head of -v is the tail of v and the tail of -v is the
head of v. Huh. Say that fast.
I am especially proud of the image of the zero vector in the picture
to the right. I wanted to show the special beauty of the zero
vector. I tried several different angles. (This is a joke!)
In this course the scalars will be real numbers. Scalars are
things that multiply vectors. Many of the students in the course will
see later situations where the scalars are complex numbers. In the
case of the RGB vectors above (and other situations which arise in
computer science and electrical engineering) the scalars are much less
familiar.
If c>0 the direction of the vector cv is the same as the
direction of v, and the length of cv is the length of v multiplied by
c.
If c=0 then cv is the zero vector.
If c<0 the direction of the vector cv is the same as the
direction of -v and the length of cv is the length of v
multiplied by |c|. (The absolute value makes sure that lengths stay
positive.)
Here are pictures of v and -v and 3v and -2v.
Vector addition in terms of components
Important vectors
Some vectors are more important than others, especially if you have a
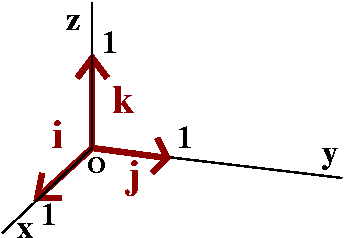
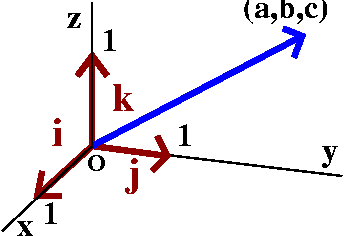
coordinate system. The vectors i and j and k are vectors of length 1
(such vectors are called unit vectors) which are parallel to
the coordinate axes x and y and z, respectively.
Now take any vector v and move it so that the tail of v is at the
origin, (0,0,0). Then the head of v will be at some point, (a,b,c). If
you think about the geometry I hope you can convince yourself that
v=ai+bj+ck. We have written v as a sum of its components.
The textbook also uses the notation v=<a,b,c> for this.
Since vector addition is commutative and associative, and certainly
(c1+c2)(any vector)=(c1)(that vector)+(c2)(that vector),
we see clearly that if v=ai+bj+ck
and w=di+ej+fk, then v+w=(a+d)i+(b+e)j+(c+f)k.
The components of the sum are the sum of the respective components.
If you know the components, it is easy to compute vector sums and
scalar multiples of vectors.
Suppose the point P has coordinates
(x1,y1,z1) and the point Q has
coordinates (x2,y2,z2). Then the
vector from P to Q (so P is the tail and Q is the head) is just
(x2-x1)i+(y2-y1)j+(z2-z1)k.
I hope that you can draw a picture convincing yourself of that,
or you can look in the text.
Example The vector from P=(1,2,-3) to Q=(-5,6,2) is
(-5-1)i+(6-2)j+(2-[-3])k=-6i+4j+5k. It is easy to make mistakes with
signs in this computation.
I will use length and norm and magnitude to mean
the same thing about a vector: its length. If v=ai+bj+ck, then we can
think of the tail of v as sitting at (0,0,0) and the head of v, at
(a,b,c). The length formula we got then says that the length must be
sqrt(a2+b2+c2). So if you know the
components, the magnitude can be computed. In the textbook we are
using the magnitude is written |v|. Please note that in some books and
some situations, this quantity is written ||v|| (with double "absolute
value" bars).
Suppose that v=<1,2,3> and w=<-2,3,2>. Then v+w=<-1,1,5>. And
|v|=sqrt(14) (approximately 3.74), |w|=sqrt(17) (approximately 4.12),
and |v+w|=sqrt(27) (approximately 5.19). In general, these numbers are
not related at all. Please realize this.
The Question of the Day asked: if v=<5,2,3> and w=3j-2k, what
is 3v+2w?
Start reading chapter 12, please.