The Risk-Averseness Graph for the St. Petersburg Gamble with 7 rounds and entrance fee 7
Suppose that you are given the following gamble.
-
With prob. 1/2 you win 2 dollars and exit the casino.
-
If you are still here, you toss a fair coin and if it lends Heads you win 4 dollars, and exit. Hence
With prob. 1/2*1/2=1/4 you win 4 dollars.
-
If you are still here, you toss a fair coin and if it lends Heads you win 8 dollars, and exit. Hence
With prob. (1/2)3=1/8 you win 8 dollars.
-
If you are still here, you toss a fair coin and if it lends Heads you win 16 dollars, and exit. Hence
With prob. (1/2)4=1/16 you win 16 dollars.
-
If you are still here, you toss a fair coin and if it lends Heads you win 32 dollars, and exit. Hence
With prob. (1/2)5=1/32 you win 32 dollars.
-
If you are still here, you toss a fair coin and if it lends Heads you win 64 dollars, and exit. Hence
With prob. (1/2)6=1/64 you win 64 dollars.
-
If you are still here, you toss a fair coin and if it lends Heads you win 128 dollars, and exit. Hence
With prob. (1/2)7=1/64 you win 128 dollars.
-
If you are made it so far (i.e. all the coin tosses landed Tails, you also win 128 dollars.
With prob. (1/2)7=1/64 you win (again) 128 dollars.
The expected gain of this gamble is 8 dollars, hence you should be willing to pay 7 dollars entrance fee, and still come out ahead, or do you?
The probability table is now:
[[-5, 1/2], [-3, 1/4], [1, 1/8], [9, 1/16], [25, 1/32], [57, 1/64], [121, 1/128], [121, 1/128]]
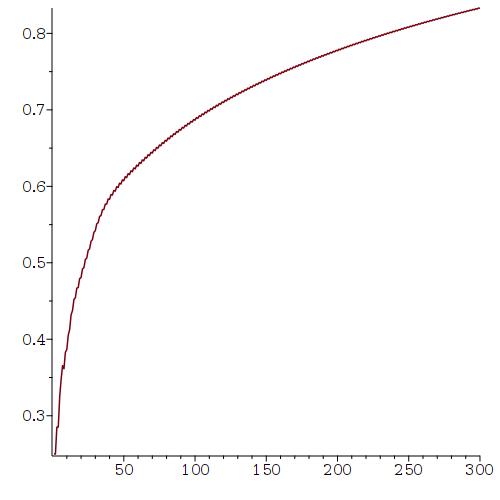
Here is the graph of the probability of not losing money if you insist on playing n times, for n from 1 to 300.
back to
article's front-page

