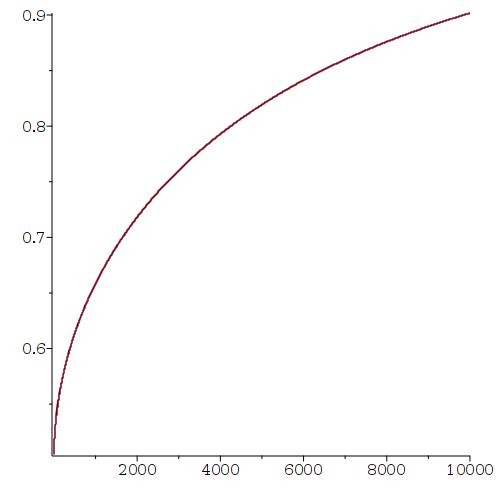
The Approximate Risk-Averseness Graph for the St. Petersburg Gamble with 11 rounds and entrance fee 11, using the Central Limit Theorem Approximation

The Approximate Risk-Averseness Graph for the St. Petersburg Gamble with 7 rounds and entrance fee 7, using the Central Limit Theorem Approximation

Suppose that you are given the following gamble.

With prob. 1/2 you win 2 dollars and exit the casino.
If you are still here, you toss a fair coin and if it lends Heads you win 4 dollars, and exit. Hence With prob. 1/2*1/2=1/4 you win 4 dollars.
If you are still here, you toss a fair coin and if it lends Heads you win 8 dollars, and exit. Hence With prob. (1/2)³=1/8 you win 8 dollars.
... If you are still here after 11 rounds , you toss a fair coin and if it lends Heads you win 2048 dollars, and exit. Hence With prob. (1/2)¹¹=1/2048 you win 2048 dollars.
If you are made it so far (i.e. all the coin tosses landed Tails, you also win 2048 dollars.

The expected gain of this gamble is 12 dollars, hence you should be willing to pay 11 dollars entrance fee, and still come out ahead, or do you?

The probability table is now:

[[-9, 1/2], [-7, 1/4], [-3, 1/8], [5, 1/16], [21, 1/32], [53, 1/64], [117, 1/128], [245, 1/256], [501, 1/512], [1013, 1/1024], [2037, 1/2048], [2037, 1/2048]]

So the expected gain is one dollar, but the standard-deviation is 77.44675590 . Using the Central Limit Approximation, we get much faster, the graph of the approximate probability of not losing money if you insist on playing n times, for n from 1 to 2000.

back to article's front-page