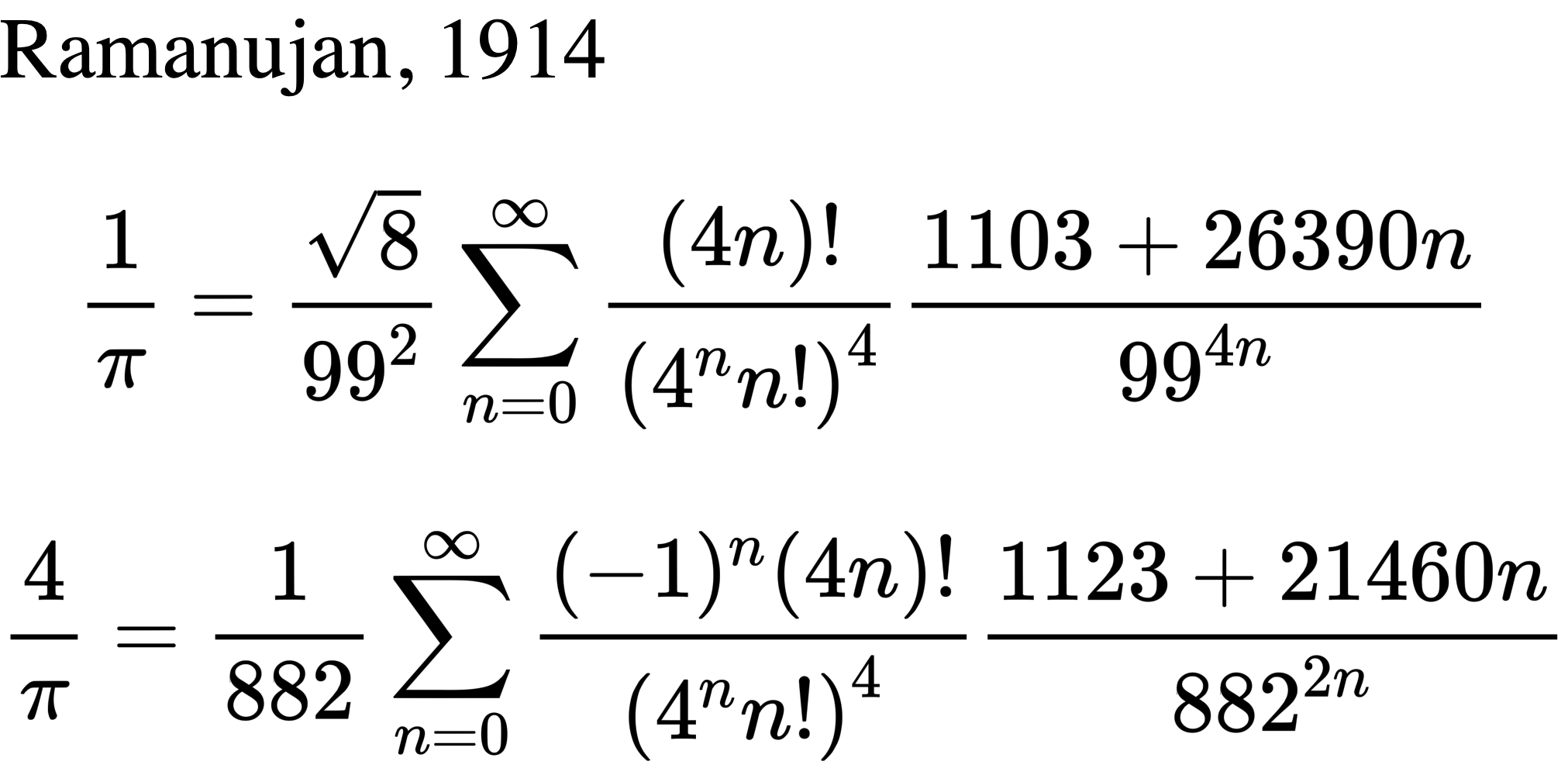Srinivasa Ramanujan
Biography


Complete Works
\hr
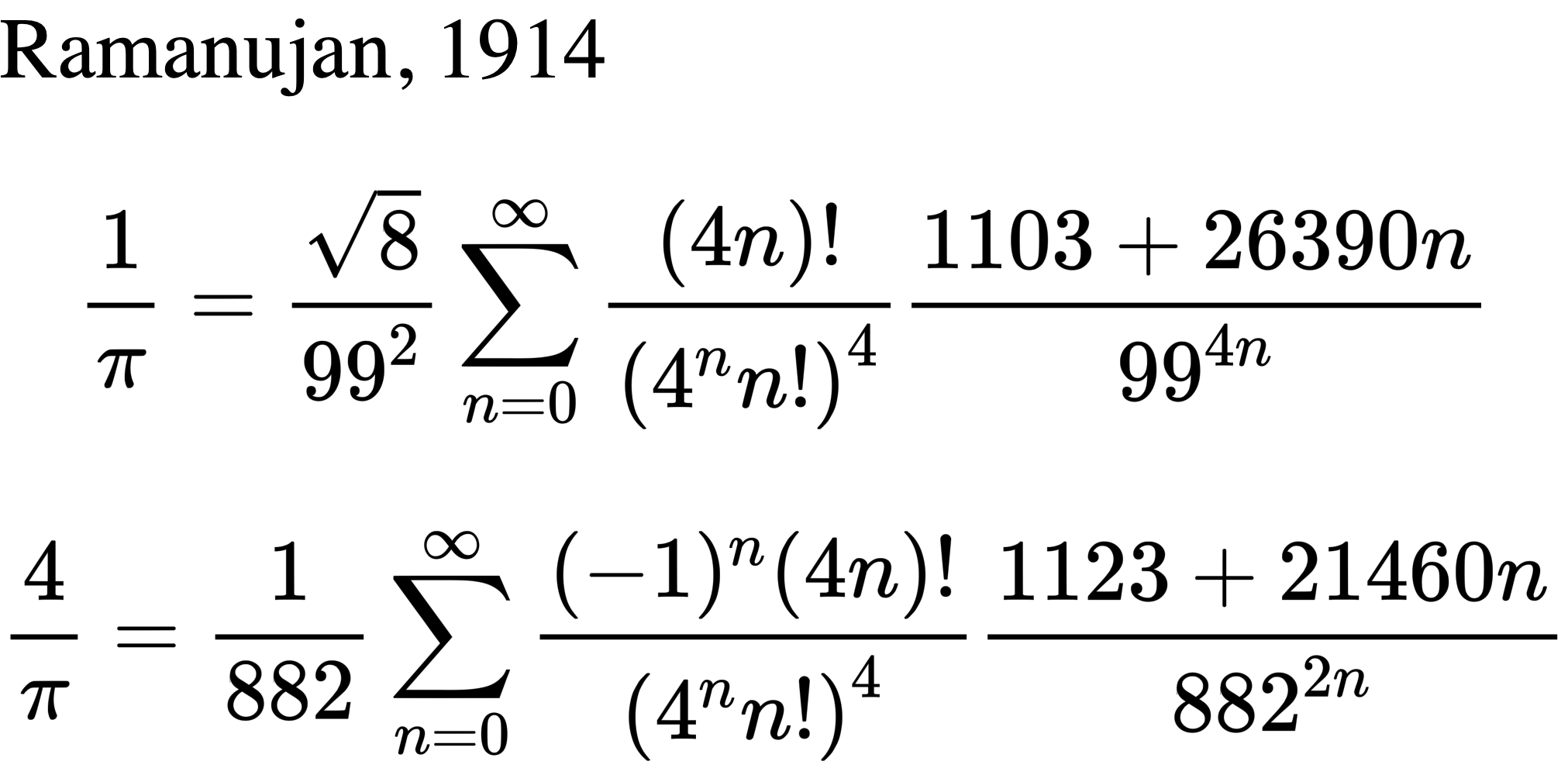
Taxicab number 1729

I remember once going to see him when he was ill at Putney. I had ridden in taxi cab number 1729 and remarked that the number seemed to me rather a dull one, and that I hoped it was not an unfavorable omen. "No", he replied, "it is a very interesting number; it is the smallest number expressible as the sum of two cubes in two different ways."
Complete cubic parametrization of the Fermat cubic surface, Elkies
Carr's Synopsis
G.S. Carr’s: A Synopsis of Elementary Results, a book on Pure
Mathematics

4865 formulae without proofs, in algebra,
trigonometry, analytical geometry and calculus.
"It was this book which awakened his genius. He set himself to establish the formulae
given therein. As he was without the aid of other books, each solution was a piece of
research so far as he was concerned.}" -P.V. Seshu Aiyar, R. Ramachandra Rao
References
Ramanujan Obituary by Hardy
Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work (AMS Chelsea Publishing), GH Hardy
Michael D. Hirschhorn (1995) An Amazing Identity of Ramanujan, Mathematics Magazine, 68:3, 199-201, DOI: 10.1080/0025570X.1995.11996312
Berndt, B.C. (2002). The Influence of Carr’s Synopsis on Ramanujan.
Books
Videos/ Documentaries
Websites
Letters and Papers, Cambridge Archive