Variational inequalities and their applications in designs

The mathematical theory of varational inequalities has by and large been established in the last century, see e.g., textbook of Kinderlehrer and Stampacchia (1980) and Friedman (1982). The latest applications of variational inequalities in solid mechanics is (i) to construct optimal microstructures for composites, and (ii) to construct structures for any desirable physically possible fields. Moreover, it enables us to systematically define or construct special geometries which we name as "polynomial inclusions". Polynomial inclusions of degree two are precisely ellipsoids and an example of polynomial inlcusions of degree three is illustrated below.

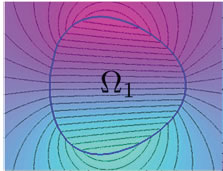
Figure 1. A polynomial inclusion of degree three.

We can use polynomial inclusions to construct structures generating any desirable local fields. For example, upon overlapping two polynomial inclusions of degree three, we obtain a perfect quadrupole field in the bore region, as shown below.

Figure 2. The blue regions has magnetization point up and red regions point down. The magnetic field inside the bore area is a perfect quadrupole field.

Applications of variational inequalities in designing arbrary magnetic field is presented in our publication Liumagnetdesign2011. Current project in this direction is to use currents as sources and to design magnets with desirable field so as to manipulate nanoparticles or for imaging in MRI applications.