Dynamic modeling of heterogeneous structures/media

It may sound surprising that it is still unknown whether free surface waves exist for any anisotropic media, though Barnett and Lothe in 1970's have resolved the existence of subsonic free surface waves. The technical difficulty lies in characterizing whether the stable solutions to an algebraic Riccati equation overlaps a fixed subspace when a real parameter v (phase-speed of the surface wave) varies from zero to the largest bulk wave phase speed.

However, by energy method we can show the existence of free surfaces in periodic heterogeneous media. The argument is to first derive a lower bound on the continuous spectrum, and then construct a test function with Rayleigh quotient smaller than this bound. This method can only be used to prove the existence of subsonic waves, as explained in HuLiuBhatt2011.

Another dynamic problem we have work on concerned sandwich plates for their applications in naval structures. The lowest branch wave modes changes significantly as wavelength decreases (or frequency increases) as illustrated in the following figure and explained in LiuBhatta2009.

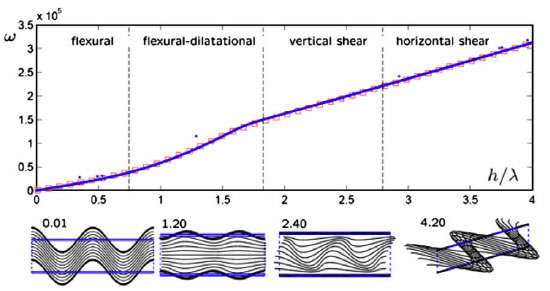
Figure 1. The top figure shows the lowest branch of the dispersion relation of the sandwich structure. The horizontal axis is roughly divided into four regimes labeled by ''flexural", ''flexural-dilatational", ''vertical shear" and ''horizontal shear". The corresponding typical mode shapes are shown in the bottom.