Optimal bounds and optimal microstructures for multiphase composites

A central problem in the study of composite materials is to characterize the effective properties of a composite based on the observed microstructure of the constituent phases. The effective properties, however, depend on the detailed microstructure, and finding the effective properties of a composite requires solutions to partial differential equations which are generally impractical for realistic microstructures.

This problem can be addressed by a classic method of first deriving microstructure-independent bounds and then constructing microstructures for composites. The best-known rigorous bounds are obtained by Hashin-Shtrikman bounds in 1960's. It is also known that Hashin-Shtrikman bounds are attainable for two-phase composites, at least for some effective modulus, e.g., conductivity and bulk modulus. On the other hand, Hashin-Shtrikman bounds are not optimal for three or more phase composite, not even for the conductivity, and hencforth cannot be used to completely characterize the possible effective behaivors of composites of more than two constituent phases.

Improving against Hashin-Shtrikman bounds appears to be extremely difficult for multiphase composites, not to mention the optimality. Nevertheless, there are other mathematically and physically interesting problems in this area as follows.

1. Characterizing the optimality of Hashin-Shtrikman bounds for multiphase composites. An easier problem than improving Hashin-Shtrikman bounds is to find precisely when the Hashin-Shtrikman bounds are attainable and when they are unattainable. This problem can be solved for three-phase conductivity problem and partially solved for four and more-phase composites. The necessary conditions for attainability follows from the a property of Null Lagrangian and the Maximum principle; the sufficient condition follows from a new type of microstructure:three-phase coated spheres with variable effective properties on the shell, as illustrated below

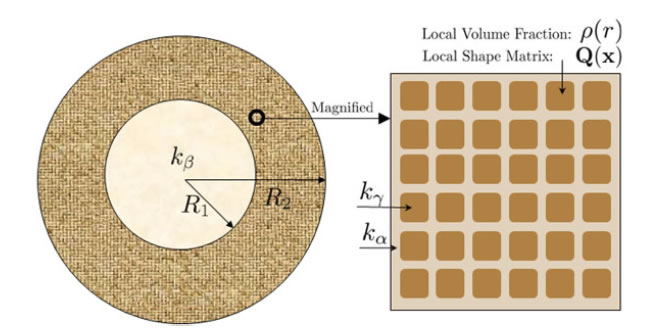
Figure 1. A three-phase coated sphere: the core sphere is occupied by phase-alpha; the shell is occupied by two-phase composites of phases beta and gamma. The microstructure of the composite is a periodic E-inclusion with local shape matrix Q(x) and local volume fraction rho(r).

Figure 2. The assembled composites (Hashin's construction) by three-phase coated sphere.

Upon combining the necessary condition and sufficient condition, we can plot the attainable, unattainalbe and unknown regions of the Hashin-Shtrikman bounds in the parameters space which are typically chosen as the volume fractions of contituent phases. As an example, in the following figure we show the attainable, unattainalbe and unknown regions for four-phase composites.

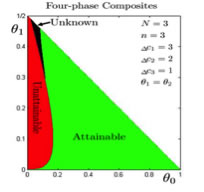
Figure 3. The attainability of the lower HS bounds for four-phase composites. Various parameters are specified on the top-right of each panel; all intermediate phases have the same volume fraction. The horizontal axis represents the volume fraction of worst conductor whereas the vertical axis represents the volume fraction of best conductor. The plane is divided into three regions of Hashin-Shtrikman bounds: attainable (green), unattainable (red) and unknown (black).

The details for the above results are presented in our publications: LiuMultiphase2010, LiuAttainability2011.

Along the above line of argument, on-going or open project problems include:

a) Characterizing the G-closure for multiphase composites;

b) Attainability of shear modulus bounds for two or more phase composites.

2. Improving the Hashin-Shtrikman bounds for multiphase composites. As mentioned above, this problem is difficult but still worth being examed from time to time.

3. An easier but practically important problem is to derive and improve microstructure-dependent bounds. Of course, the additional microstructure information used in deriving bounds shall be judiciously chosen so that the bounds are informative and simple.