Here are appropriate textbook homework problems for some of the content of the last few meetings of the course:

3.1: 10, 11, 12, 14, 18, 20; 3.3 4 a), b), d); 5 a), b), c); 7a), b), d).

The Riemann sphere and stereographic projection
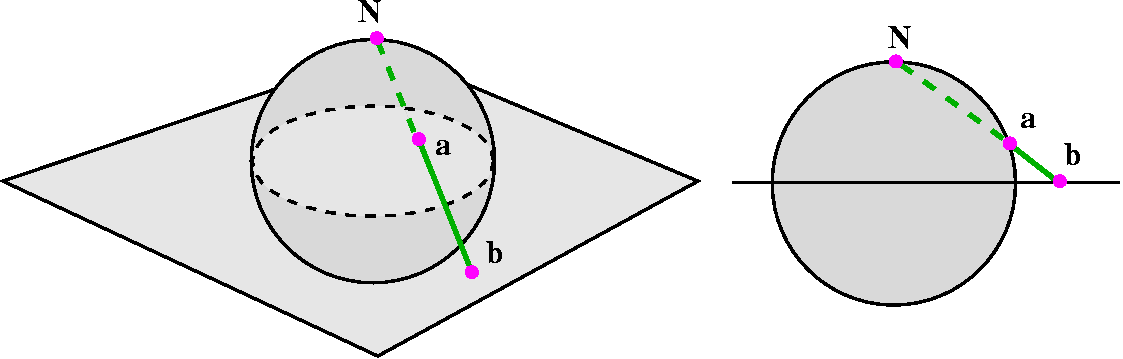One geometric method which helps understand certain conformal mappings is to visualize what is going on using stereographic projection. Put the complex plane into space (R³) as the xy-plane, with third coordinate equal to 0. Draw a sphere with radius 1 and center the origin, (0,0,0). Let N, the North Pole, be located at (0,0,1). Then every point a on the sphere which isn't N corresponds to a unique point b on the complex plane. The correspondance is by drawing a line from N to a and extending it until it intersects the plane. The intersection point is called b. Of course, we could start with b on the complex plane, and connect it with N, and the line would always hit the sphere in some other point, a. This "correspondance" is a useful thing to keep in the back of your mind (?) throughout your study of the subject. Of course you can write lots and lots of equations describing everything, but right now I just want the idea, without proofs or whatever. In fact, it turns out that stereographic project also "preserves angles" between corresponding curves (this is not immediately obvious at all).

Comment The stereographic project shown here is what's usually done now. But there is another common variant, where the sphere is "balanced" on top of the plane, so its center is at (0,0,1/2) and the North Pole is at (0,0,1). This is what's done in the video by Arnold and Rogness.

Now back to D₁(0) and H
We then struggled to see what happens to the unit disc. It corresponds under stereographic projection to the lower half of the sphere. We could then rotate the sphere and make the lower half into the "back" half. This then corresponds to H, the upper half plane. So: we see that D₁(0) and H are the same. We had previously shown that z⇒(z–i)/(z+i) maps H to D₁ in a 1-1, onto, conformal fashion.

Linear fractional transformations

And 2-by-2 matrices Triple transitivity

Circles and lines

Examples
From a past exam and from class examples.

Diangles