Several weeks ago we asked when a vector field could be a gradient
vector field. That is, given F=Pi+Qj+Rk,
when is there φ so that ∇φ=F? Although we can
integrate and compare the various descriptions, integration is
frequently tedious and difficult. I mentioned that a quick check can
be gotten by looking at the "cross second derivatives". The resulting
equations are also callled "compatibility conditions". Here is a
way of encoding this idea.
The curl
If F(x,y,z)=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k,
then the curl of F is another vector field, ∇xF. It is a cross-product, and can be
evaluated by taking the determinant:
( i j k )
det ( ∂/∂x ∂/∂y ∂/∂z )
( P(x,y,z) Q(x,y,z) R(x,y,z) )
It turns out this is equal to (if I don't foul up the signs!) the
following vector field:
(Ry–Qz)i–(Rx–Pz)j+(Qx–Py)k.
F satisfies the compatibility conditions above if
curl F=∇xF is 0. This isn't an accident. Hamilton
invented the del so that it would be useful!
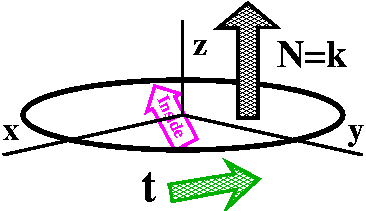
If a vector field is a gradient, its curl is 0
A way of testing if a vector field is a gradient vector field: take
the curl: the result should be 0. Hamilton would want you to remember
this by writing ∇x∇f=0 since a vector crossed with
itself is 0.
The formula for curl is horrible, and difficult to remember but the
notation (especially the cross product and ∇) is supposed to
help. Suppose we ∂/∂x the i component of curl
F, ∂/∂y the
j component, and ∂/∂z the k component. Here in
this 21st century (!) math course, I may be doing this for
fun. The people who actually invented these results had the
computations forced on them (really!) because they wanted
descriptions of certain aspects of reality involving fluid flow and
electromagnetism. These are the three results we get for the
differentiations:
(Qzx–Ryx) (Pzy–Rxy) (Pyz–Qxz).
A number of students observed that if we added them, the
result would be 0! This is weird and wonderful (or weird and
remarkable, a phrase which might
be used either positively or negatively about many parts of this
course).
If a vector field is a curl, its divergence is 0
Our conclusion is that a vector field G for which
∇·G is not 0 cannot be the curl of another
vector field. This is a "compatibility condition" for being a
curl. Hamilton would want you to remember this by writing
∇·∇xF=0 since a vector dotted with
something which is a cross product with itself must be zero!
The ingredients for Stokes' Theorem
Stokes' Theorem was developed in response to ideas of electromagnetism
and fluid dynamics. Just like Green, Stokes was interested in both
mathematics and physics, and he attempted to construct mathematical
models for rapidly evolving fields of physics. I will attempt to list
the ingredients for a (relatively!) straightforward version of Stokes'
Theorem.
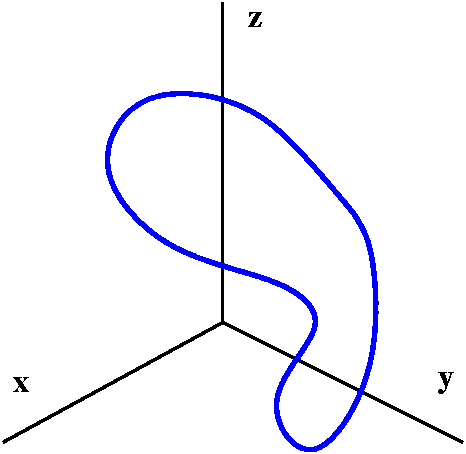
A simple closed curve
So this is a curve in space (R3) with START=END
and which has no other self-intersections.
|
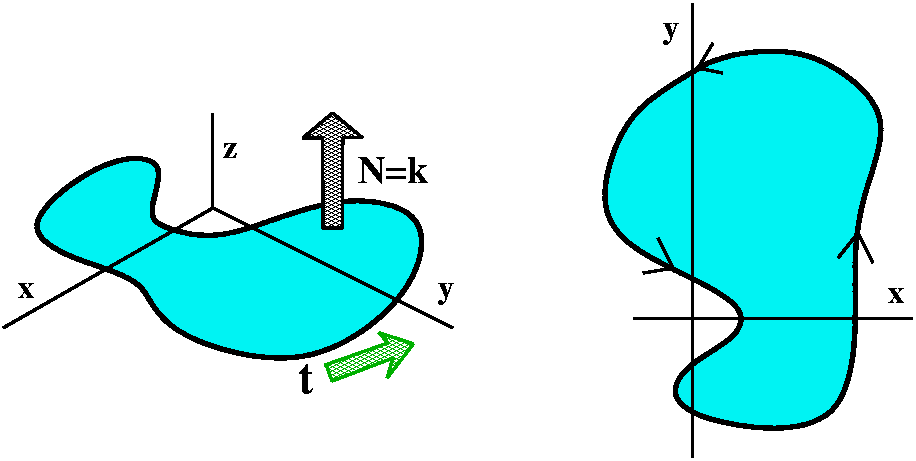
A piece of surface
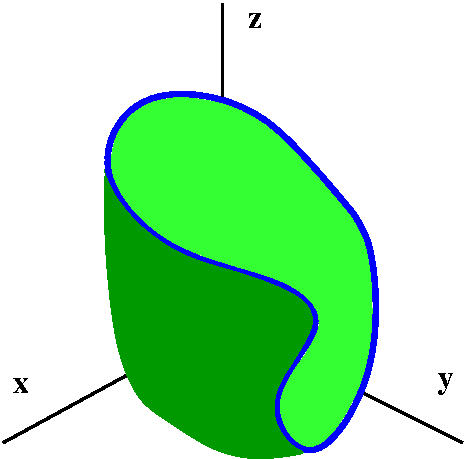 This should be a piece of a surface, all of whose boundary is the
curve mentioned above. As several students remarked, specifying the
boundary curve does not mean there's only one surface. In fact,
there are many really neat and clever computations which depend on
changing the surfaces involved. I'll show you one of these in a few
minutes.
This should be a piece of a surface, all of whose boundary is the
curve mentioned above. As several students remarked, specifying the
boundary curve does not mean there's only one surface. In fact,
there are many really neat and clever computations which depend on
changing the surfaces involved. I'll show you one of these in a few
minutes.
|
Work and flux
Stokes' Theorem connects the work of a vector field around a closed
curve with the flux of a related vector field over a surface. So
this means that we need to have a direction on the curve (how we push
things around) and we also need to make a selection of normal vector
on the surface. These choices need to be made together.
The textbook interprets the work in the fluid dynamics sense, as a
circulation. We didn't have enough time in class to consider
circulation. There is discussion of this in sections 17.1 (on page
1010) and 17.2 (see page 1025).
|
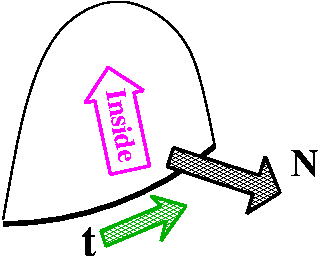
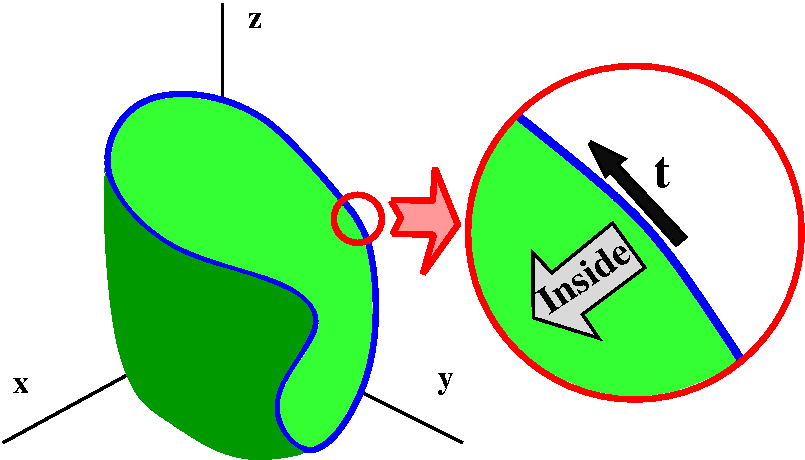 • How the surface and curve interact (by their orientations)
• How the surface and curve interact (by their orientations)
The word "orientation" here means how to select t, the unit
tangent vector on the boundary curve, and N, the unit normal on
the surface. The boundary curve will be a parameterized curve. It has
a unit tangent vector, t, pointing in the direction of
increasing parameter value. If we "walk" along the boundary curve in
this direction, the surface should be to our left. Now we have
t and a direction to the left. Complete this to a right-handed
coordinate system. The selection of N, the unit normal vector
to the surface, is made so N points in the direction of the
last entry of a right-handed coordinate system which begins with
t and the inside surface direction. I think in the accompanying
picture to the right, the N would point "out" of the page, and
towards the "inside" of the cup-shaped surface.
Under these conditions, then the Stokes Theorem Equation is
true:
∫The boundary curveF·t ds=∫∫The surfacecurl F·N dS
Pretty darn embarrassing that I forgot the
"curl" the first time I wrote the statement of the theorem. I kept
telling myself on the way to Hill Center this morning, "Don't screw up
the statement of Stokes' Theorem. Don't screw up the statement of ..."
so of course what did I do? I am so darn sorry.
The textbook writes this in a slightly different way as
∫The boundary curveF·ds=∫∫The surfacecurl F·dS
So the work or circulation of F around the boundary is equal to
the flux through the surface of the curl F. This is a
well-known complicated theorem. If the curve is in R2 and
the surface is the inside of the curve, then the result is "just"
Green's Theorem, which is already quite complicated. I'd like to spend
most of the time in this lecture just checking both sides of the
Stokes' Theorem equation, and getting some familiarity with it that
way.
A textbook problem
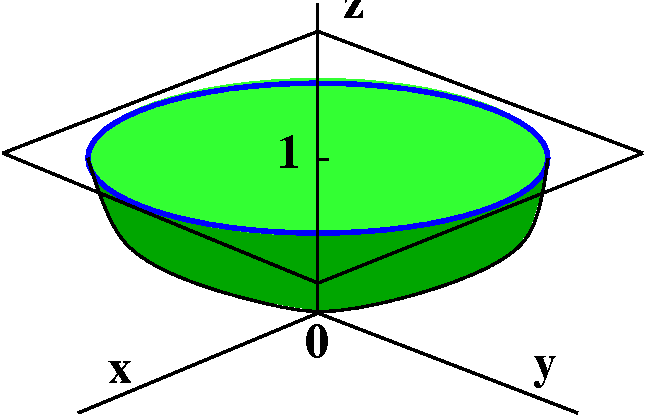 Here is a problem from a calculus textbook:
Here is a problem from a calculus textbook:
Verify that Stokes' Theorem is true for the vector field
F(x,y,z)=y2i+xj+z2k
and the surface is the part of the paraboloid
z=x2+y2 that lies below the plane z=1, oriented
upward.
Some discussion
The plane z=1 intersects the paraboloid in a circle. This is a circle
of radius 1 centered at (0,0,1). The paraboloid "overlays" a region
inside a circle of radius 1 centered at the origin in the xy-plane. We
will compute both integrals in Stokes' Theorem and (I hope!) get the
same answers. If the paraboloid is "oriented upward" then I presume
that the N points up. Going around the blue circle in the
standard (counterclockwise/positive) direction will orient the
boundary curve "compatibly": the t, the leftish piece of
surface next to the boundary curve, and the up N form a
right-handed triple. This took some time to see in class.
The work integral
So I need to compute ∫The curvey2dx+x dy+z2dz.
The curve is a circle, and can be parameterized as:
x=1cos(t) dx=–sin(t)dt
y=1sin(t) dy=cos(t)dt
z=1 dz=0
and the
parameterization interval for the whole circle is [0,2Π]. Then ∫The curvey2dx+x dy+z2dz
becomes
∫t=0t=2Π–[sin(t)]3+[cos(t)]2dt.
I can "compute" this integral with tricks. It can also be
computed using the things done in Calc 2. But we're near the end of
the term, and tricks make the computations flow faster.
First, look at sine on the interval [0,Π/2], and then look at
[sin(x)]3. Both the curves go up from 0 to 1. The
appearance is flipped left/right on [Π/2,Π], and then the
appearance on [0,Π] is flipped down|up on [Π,2Π]. The total
integral from 0 to 2Π must be 0 because of the cancellation. The
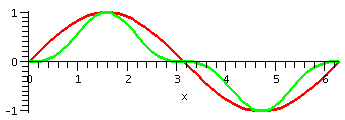
first picture below shows my drawings of sine and the cube of
sine. The red/green picture with two curves shows a Maple graph of the two curves. Consequence:
∫t=0t=2Π[sin(t)]3dt=0.
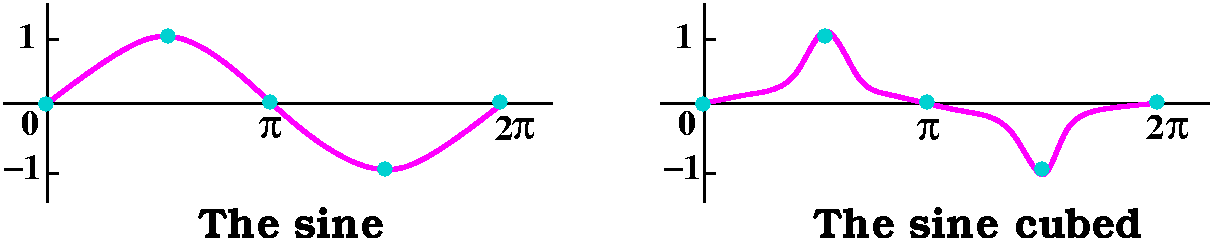
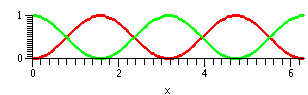
How about the integral of [cos(t)]2 on [0,2Π]? The value
should certainly be the same as the integral of [sin(t)]2
on the same interval since the shapes are the same, just one quarter
period out of phase. The sum of these curves is 1
(sin2+cos2) which on [0,2Π] has integral
2Π. So ∫t=0t=2Π[cos(t)]2dt must be
half of that and it equals Π.
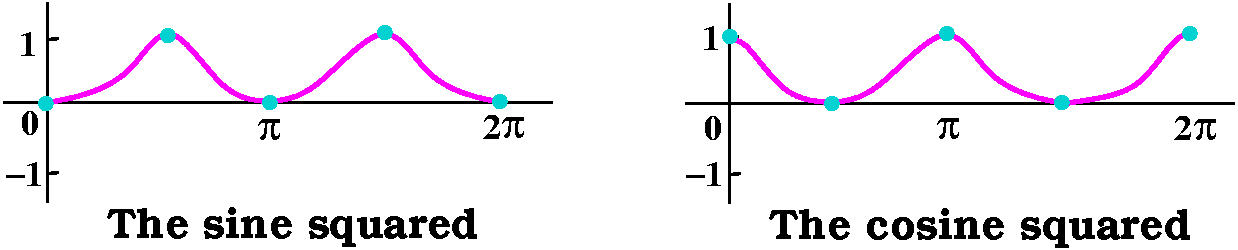
The line integral side of Stokes' Theorem is Π.
The surface integral
Now we need to compute
∫∫The paraboloidcurl F·N dS.
The curl
This is ∇xF, so:
( i j k )
det( ∂/∂x ∂/∂y ∂/∂z )=0i–0j+(1–2y)k
( y2 x z2 )
Parameterizing the surface, etc.
Since the surface is presented as a graph, try the graph function
itself as a parameterization:
r(u,v)=ui+vj+(u2+v2)k so
ru(u,v)=1i+2uk and
rv(u,v)=1j+2vk.
Then ruxrv= ( i j k )
det( 1 0 2u )=–2ui–2vk+1k
( 0 1 2v )
We discussed the magical cancellation a few
lectures ago. V·N dS became
V·(ruxrv) dAu,v.
curl F here is (1–2y)k=(1–2v)k so that
curl F·N dS=(1–2v)k·(–2ui–2vk+1k)dAu,v=(1–2v)dAu,v.
Computation of the surface integral
We need to identify the domain in the uv-plane which parameterizes our
little cup. The uv-plane is the xy-plane in different clothing, but
the cup is the graph over the region inside the unit circle:
u2+v2≤1. So we need
∫∫Inside the unit circle(1–2v)dAu,v
But the 2v integrates to 0, since the region is symmetric in v and 2v is "odd" (the + and – cancels totally). The 1 in the integrand just gives the area, and the area inside the unit circle is Π(12), and this is Π.
This instantiation (?) of Stokes' Theorem is verified: Π=Π.
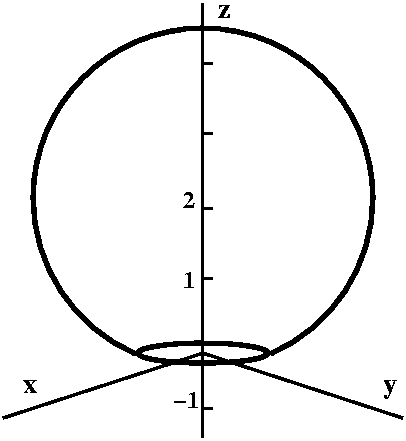 Another textbook problem
Another textbook problem
Here is a slightly more vicious (viscous?) problem from the Stokes'
Theorem section of a calculus text by Robert A. Adams:
Find ∫∫The surfacecurl F·N dS where the surface is that part of
the sphere x2+y2+(z–2)2=8 which lies
above the xy-plane, and N is the outward unit normal on the
surface, and F is
y2cos(xz)i+x3eyzj–e–xyzk.
Since the problem occurs in the Stokes' Theorem section of the text we
should probably use Stokes' Theorem. The region of the sphere is shown
to the right. The sphere is centered at (0,0,2) and its radius is
sqrt(8)=2sqrt(2). So a portion of the sphere extends below the
xy-plane.
 The boundary of the top portion occurs if z=0 in the
equation
x2+y2+(z–2)2=8. Then
x2+y2+(–2)2=8 and
x2+y2=4. This is a circle of radius 2 centered
at the origin in the xy-plane. We should establish the orientation of
this circle. If we look closely at a small piece of the surface near
the boundary curve, the outward unit normal points slightly down. We
must "walk" along the curve so that the surface is to the left. The
t direction is the standard counterclockwise direction on the
boundary circle. I hope the local picture to the right helps to
convince you of that. Again, the problem of deciding the resulting
orientation of one chunk (surface, boundary curve) from the other
(boundary curve, surface) seemed in class to be the most complicated
qualitative aspect of this problem.
The boundary of the top portion occurs if z=0 in the
equation
x2+y2+(z–2)2=8. Then
x2+y2+(–2)2=8 and
x2+y2=4. This is a circle of radius 2 centered
at the origin in the xy-plane. We should establish the orientation of
this circle. If we look closely at a small piece of the surface near
the boundary curve, the outward unit normal points slightly down. We
must "walk" along the curve so that the surface is to the left. The
t direction is the standard counterclockwise direction on the
boundary circle. I hope the local picture to the right helps to
convince you of that. Again, the problem of deciding the resulting
orientation of one chunk (surface, boundary curve) from the other
(boundary curve, surface) seemed in class to be the most complicated
qualitative aspect of this problem.
I think I also made a mistake about
this is class. I think what's written here is correct and what I've
written here is correct.
Now Stokes' Theorem applies:
∫∫The spherical surfacecurl F·N dS=∫The boundary circleF·t ds.
 But notice:
this circle is also the correctly oriented boundary of the disc of
radius 2 centered at the origin in the xy-plane. So I can use Stokes'
Theorem a second time to change the line integral to a much
simpler surface integral:
But notice:
this circle is also the correctly oriented boundary of the disc of
radius 2 centered at the origin in the xy-plane. So I can use Stokes'
Theorem a second time to change the line integral to a much
simpler surface integral:
∫The boundary circleF·t ds=∫∫The disccurl F·N dS
This is simpler for several reasons. The region over which we're
integrating is flat, a disc in the xy-plane. The correctly oriented
normal, N, is just k. I hope the picture convinces you
of that.
We should compute curl F. Wait, we just need to compute
the k part of curl F:
( i j k )
det ( ∂/∂x ∂/∂y ∂/∂z )=Blah!i–Blah, blah!j+[3x2eyz–2ycos(xz)]k
( y2cos(xz) x3eyz –e–xyz)
A further simplification occurs. We're on the xy-plane, where z=0. So
the k component, 3x2eyz–2ycos(xz), becomes
3x2–2y because cos(0)=1 and e0=1.
So we need ∫∫The disc3x2–2y dAu,v. Just
as in the previous problem, the –2y integral over the disc is 0,
because there is cancellation of the positive and negative
contributions of y. I see no clever way to compute the 3x2
integral and will do this using polar coordinates (with
x=rcos(θ)):
∫∫The disc3x2dAu,v=3∫θ=0θ=2Π∫r=0r=2r2[cos(θ)]2r dr dθ=
3∫θ=0θ=2Π[cos(θ)]2dθ∫r=0r=2r3dr. The θ
integral is Π (a trick used before) and the r integral is 16/4. So
the flux is 12Π.
Comment
I did this problem because using the same boundary
curve to switch surfaces is a very common "trick" done in
electromagnetism and fluid flow. If two surfaces have the same
boundary and if the vector field is nice, then the flux of the curls
of the vector fields through the two surfaces must be the same. This
is weird and wonderful, and people use it. See the discussions on page
1024 and 1026-1027.
Also since the divergence of a curl is 0, the flux of a curl vector
field on a closed surface must be 0 (the Divergence Theorem) so again
the previous result is verified.
 Green's Theorem
Green's Theorem
If the boundary curve is in R2 and the "surface" is a
region in R2 then Stokes' Theorem is Green's
Theorem. Why is this true? If the simple closed curve is oriented
counterclockwise as usual, then the normal will be +k. So if the vector field is
Pi+Qj+Rk, the normal N is k and the
k component of the curl of the vector field is
Qx–Py. The Stokes' Theorem equation declares
that the integral of Pdx+Qdy over the boundary curve (with the usual
orientation) equals the double integral of Qx–Py
over the interior.
FTC through the ages ...
The three
semesters of calculus are a tour of results originating around 1630 or
so to around 1870 or so. We go through, therefore, 250 years of
mathematical development, and certainly this semester, multivariable
calculus, has had its share of really clever ideas. The Fundamental
Theorem of Calculus appeared in the first semester. This semester had
a 2-dimensional version (Green's Theorem), a 3-dimensional version,
the Divergence Theorem, and even today a 2.5-dimensional version
(Stokes' Theorem). Wow! And now we are all the way up to the late
Nineteenth Century! Imagine if you took a series of
chemistry or physics or bio courses which would have left you at that
time of the discipline. Just think ...
|

 This should be a piece of a surface, all of whose boundary is the
curve mentioned above. As several students remarked, specifying the
boundary curve does not mean there's only one surface. In fact,
there are many really neat and clever computations which depend on
changing the surfaces involved. I'll show you one of these in a few
minutes.
This should be a piece of a surface, all of whose boundary is the
curve mentioned above. As several students remarked, specifying the
boundary curve does not mean there's only one surface. In fact,
there are many really neat and clever computations which depend on
changing the surfaces involved. I'll show you one of these in a few
minutes.
 • How the surface and curve interact (by their orientations)
• How the surface and curve interact (by their orientations) Here is a problem from a calculus textbook:
Here is a problem from a calculus textbook:
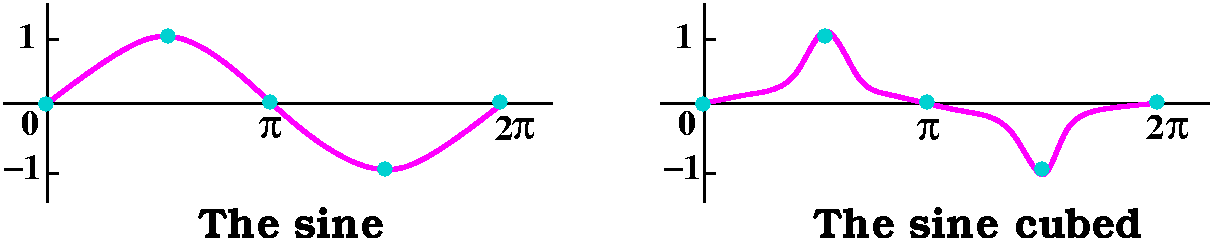


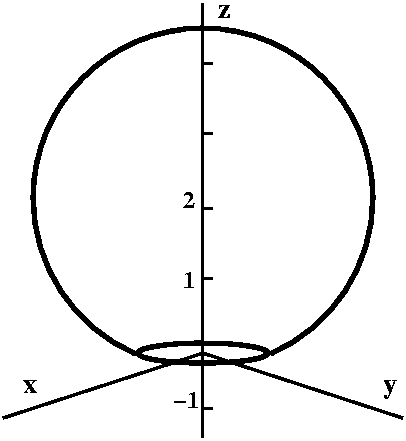 Another textbook problem
Another textbook problem The boundary of the top portion occurs if z=0 in the
equation
x2+y2+(z–2)2=8. Then
x2+y2+(–2)2=8 and
x2+y2=4. This is a circle of radius 2 centered
at the origin in the xy-plane. We should establish the orientation of
this circle. If we look closely at a small piece of the surface near
the boundary curve, the outward unit normal points slightly down. We
must "walk" along the curve so that the surface is to the left. The
t direction is the standard counterclockwise direction on the
boundary circle. I hope the local picture to the right helps to
convince you of that. Again, the problem of deciding the resulting
orientation of one chunk (surface, boundary curve) from the other
(boundary curve, surface) seemed in class to be the most complicated
qualitative aspect of this problem.
The boundary of the top portion occurs if z=0 in the
equation
x2+y2+(z–2)2=8. Then
x2+y2+(–2)2=8 and
x2+y2=4. This is a circle of radius 2 centered
at the origin in the xy-plane. We should establish the orientation of
this circle. If we look closely at a small piece of the surface near
the boundary curve, the outward unit normal points slightly down. We
must "walk" along the curve so that the surface is to the left. The
t direction is the standard counterclockwise direction on the
boundary circle. I hope the local picture to the right helps to
convince you of that. Again, the problem of deciding the resulting
orientation of one chunk (surface, boundary curve) from the other
(boundary curve, surface) seemed in class to be the most complicated
qualitative aspect of this problem.
 But notice:
this circle is also the correctly oriented boundary of the disc of
radius 2 centered at the origin in the xy-plane. So I can use Stokes'
Theorem a second time to change the line integral to a much
simpler surface integral:
But notice:
this circle is also the correctly oriented boundary of the disc of
radius 2 centered at the origin in the xy-plane. So I can use Stokes'
Theorem a second time to change the line integral to a much
simpler surface integral: