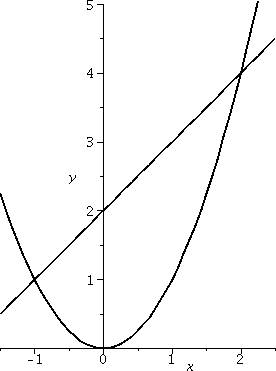
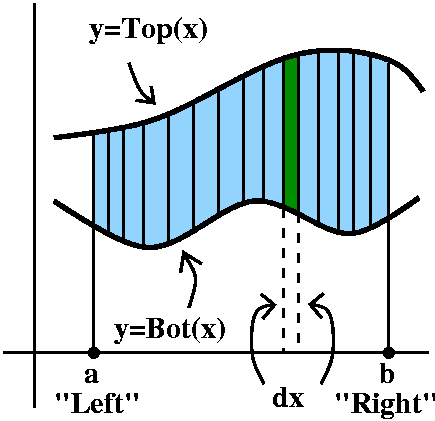
Area between two curves
Here's the final topic of the semester, which is a simple introduction to the uses of the definite integral. The definite integral has hundreds of important applications in science and engineering.

Suppose we are given two functions defined on an interval, Top(x) and Bot(x) ("Bot" is an abbreviation for "Bottom") and we know on that interval that Top(x)>Bot(x). How can we compute the area enclosed by the two curves and by vertical lines on the sides of the interval?

I always imagine that the interval is chopped into lots of little pieces, each of length dx. Then these pieces chop up the area, as shown in the picture to the right. Each little slice of area is almost a rectangle (if we ignore the possible tilts at the top and bottom). The area of the approximate rectangle is [Top(x)–Bot(x)] (the length of the vertical side, the difference in the heights of the graphs) multiplied by dx, the width. Now I need to take the Sum of these approximating slices, and add them up from a to b, or, as I think, from Left to Right. Therefore I believe that the area between these curves on this interval is
∫_Left^Right[Top(x)–Bot(x)]dx.

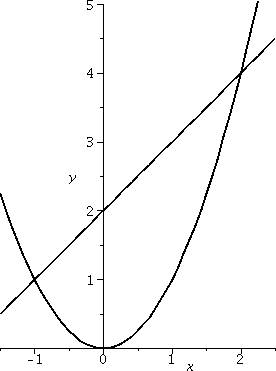
Random example #1
This example is not random, but it is constructed so I could do it easily in class. I would like to find the area of the region enclosed by the line y=x+2 and the parabola y=x². I would probably try to begin almost any problem of this type by sketching the region first. The picture to the left is such a sketch. Where do these curves intersect? Well, we need to find x's which give the same y, so we solve x²=x+2 so that x²–x–2=0 and this is (wow! Oh, hold on, he made it so it would work out) x²–x–2=0 so that (x–2)(x+1)=0. The roots are x=2 and x=–1.
I honestly think that the phrase "the region enclosed by the line y=x+2 and the parabola y=x²" specifies exactly one piece of the plane. You can argue with me -- I discuss this a bit more in the example below. Here I think we have Left=–1 and Right=2 and Top(x)=x+2 and Bot(x)=x². So let's compute:
∫_Left^Right[Top(x)–Bot(x)]dx=∫_–1²[{x+2}–{x²}]dx=
(1/2)x²+2x–(1/3)x³|_–1²=[(2²/2)+2·2–(8/3)]–[((–1)²/2)+2·(–1)–(–8/3)].
This turns out to be 9/2. I hope. And, by the way, if you look at the picture, I hope you can see that the region fits inside a box with height 4 and width 3, so the area should be less than 3·4=12, which it is. Getting some approximate idea of the answer is useful, if you, like me, make sign errors and ... well, other kinds of errors.

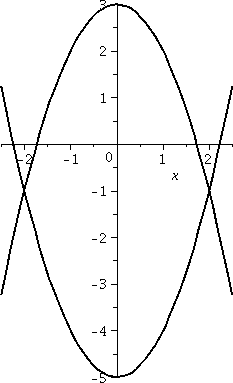Random example #2
Again, this is an arranged example and everything will work out neatly. Real problems are rarely like this. I'd like to compute the area of the part of the plane which is between the parabolas y=x²–5 and y=3–x². The first curve opens up and has its bottom at (5,0). The second opens down, with its top at (3,0). A picture of the two curves is shown to the right.

I mentioned in class that it is certainly possible to "misunderstand" the statement of this problem, if you work at it. The plane is actually divided into five different regions by these two curves. And maybe someone could maybe declare that there's more than one candidate for the region between the parabolas (maybe all five are candidates, or maybe only three of them are?). I guess maybe I might agree if you really argue with me about it, but if the discussion is just a way to get out of computing the area of the only region with finite area then I would not agree. Please compute the area of that region, and then, later, argue about it.

The curves intersect where x²–5=3–x². Since this is a problem in a math class, let's see: that's 2x²=8 or x²=4 so that x=+/–2. I think that Left=–2 and Right=+2.

Something new!?
There is a little bit that's new here. Notice that if Top(x)=3–x² and Bot(x)=x²–5, then actually Bot(x) is always negative in the interval [–2,2]. Even so, the quantity Top(x)–Bot(x) gives the geometric length of the vertical side of a (dx) thin slice of area. Top(x)–Bot(x) will be positive. In fact, if you look really carefully at the picture, you'll see that there are two pieces of [–2,2] where both Top(x) and Bot(x) are negative. But Top(x) is still bigger than Bot(x), so Top(x)–Bot(x) will be positive, even though both of them are negative. The geometric length is still Top(x)–Bot(x).

The computation
∫_Left^Right[Top(x)–Bot(x)]dx=∫_–2²[{3–x²}–{x²–5}]dx=
∫_–2²[{8–2x²]dx=8x–(2/3)x³|_–2²=[(8·2)–(2/3)2³]–[(8·–2)–(2/3)(–2)³]=64/3.
This is less than a box which is 8 units high and 4 units wide (such a box would enclose the entire area). Also, several students remarked that we could have computed the integral from 0 to 2 and doubled the result, to take advantage of symmetry.

Random example #3
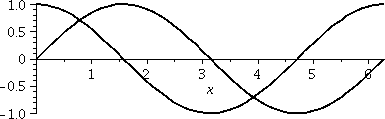I would like to find the geometric area between the sine and cosine curves over one period of these functions. So I drew a picture similar to what's shown to the right. Again, it may be possible to misunderstand the question since this situation is more complicated than previous ones. But "one period" is 2Π here, and the word "between" in this situation refers, in fact, to three specific regions in the picture.

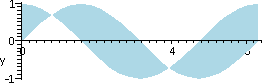So the area which I wanted to compute is shown to the right. Here is what I thought that I needed to do (clear evidence that the brain was not totally functional!). I thought that I would need to split the area computation into three pieces, and compute three different integrals, and then add them up. The idea would be as shown to the left 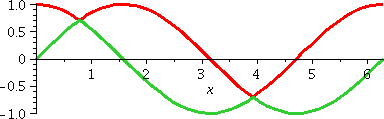where first one formula then the other, and then the other again, is on top. Well, this could be done but it would actually be much more work than is needed.

A student (who?) kindly pointed out that the left-most region and the right-most region when put together are congruent to the central region: so the sum of the areas of these two regions must be equal to the area of the region in the middle. Thank you!

The curves intersect where sin(x)=cos(x). This is at x=Π/4 and x=5Π/4. So Left=Π/4 and Right=Π/4 and between these numbers, the sine curve will be Top(x) and the cosine curve will be Bot(x). So I need to compute twice the definite integral over this interval to get the total area requested. Here we go (and be careful with minus signs!):
    2∫_Π/4^5Π/4(sin(x)–cos(x))dx=–cos(x)–sin(x)|_Π/4^5Π/4=[–cos(5Π/4)–sin(5Π/4)]–[–cos(Π/4)–sin(Π/4)]=
    [–{–sqrt(2)/2}–{–sqrt(2)/2}]–[–{sqrt(2)/2}–{sqrt{2}/2}]=4sqrt(2)
There were only SEVEN minus signs in the next-to-last expression. Mistakes are easy!

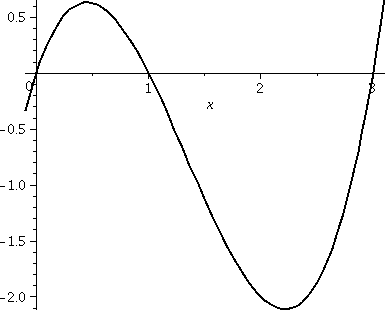
Another ...
How much geometric area is enclosed by y=x(x–1)(x–3) and the x-axis? Again, a graph is shown to the right, and these bumps definitely have different sizes. But my patience (?) is running out. In a spare tenth of a second, we get:

> int(x*(x-1)*(x-3),x=0..1);
            5/12

> int(x*(x-1)*(x-3),x=1..3);
            -8/3

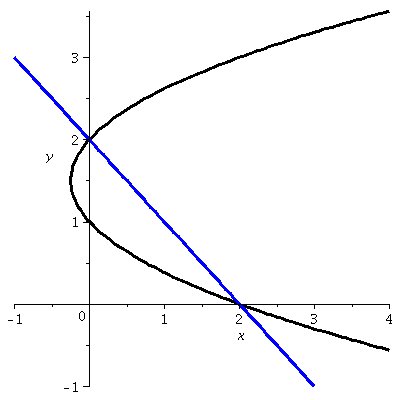
Sideways?
I asked what does the curve defined by the equation (y–1)(y–2)=x look like? With a bit of thought, we decided that it was a parabola with axis of symmetry parallel to the x-axis, and that it was opening to the right. A graph is shown to the right.

Notice, please, that the point (2,0) is on the graph, as well as the point (0,2). Therefore there's a (exactly one!) straight line through these two points. Its equation is x+y=2 (Admission: I sort of guessed at the equation, since the sum of each pair of coordinates is 2, that must be the equation!). What's the area of the region bounded by the line and the parabola?

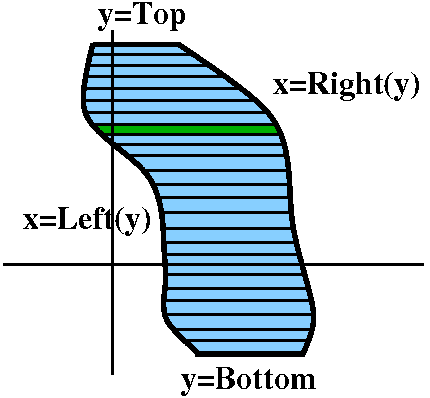
The dy method
If we have a region in the plane bounded by two curves, x=Left(y) and x=Right(y) (where Left(y)<Right(y) for the y's of interest here) and also bounded by lines y=Bottom and y=Top, then we could imagine slicing this area by lots of horizontal lines dy apart. The region would be divided into lots of pieces, and each piece would approximately be retangular. The height of the (almost) rectangle would be dy, and the width would be Right(y)–Left(y). So the area would be (Right(y)–Left(y))dy. Since this is the area of a slice, we would get the total area by taking the Sum of the areas of the slices, from the Bottom to the Top: ∫_y=Bottom^y=Top(Right(y)–Left(y))dy.

In our case ...
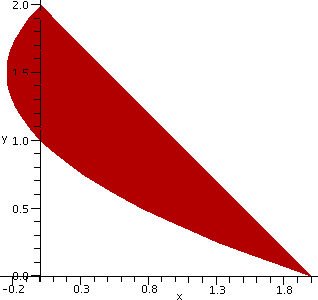Top is 2 and Bottom is 0. Left(y) is (y–1)(y–2)=y²–3y+2 (you should multiply/distribute/expand/foil whatever! before integrating) and Right(y) is 2–y. Thus the area can be computed by
∫_y=Bottom^y=Top(Right(y)–Left(y))dy=
∫_y=0^y=2([2–y]–[y²–3y+2])dy= ∫_y=0^y=2([2y–y²])dy=y²–(1/3)y³|₀²=4–8/3=4/3.

Comments
Certainly this is not the only method of getting this area. You could possibly imagine dissecting the area dx, and chopping it up somehow so the computation could be done. You would need to solve for x in terms of y, which is possible in this case but maybe not too easy if the equation were more complicated. Also that would be much more work, I think. Or maybe you just interchange x and y, and then redraw the graph, and do it dx. That's certainly possible. I just report, though, that for many students in the class (physics students, engineering students) many other geometric and physical quantities will occur (moment of inertia, center of gravity, etc.) which can be computed more naturally dy, and therefore "chopping up" regions in this way will be useful.

Winding up ...
Please study for the final exam.