One solution to a possible QotD for 10/29/2009

Solution to a possible QotD for 10/29/2009
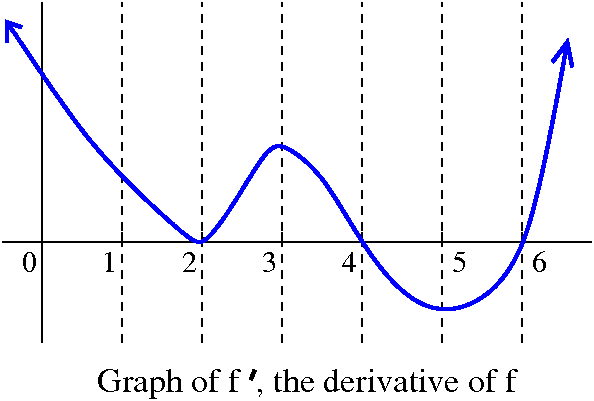
I've given a picture of the original graph to the right. This may help you understand the discussion that follows.

  1. What are the critical points of f?
    Since f´ has domain all of R, certainly the derivative exists at every point. So critical points will occur exactly where f´(x)=0. I look at the graph and read off x=2 and x=4 and x=5.
  2. In what intervals is f decreasing?
    f is decreasing in intervals where f´(x)<0. The only interval which qualifies is 4<x<6.
  3. In what intervals is f increasing?
    f is increasing in intervals where f´(x)>0. Several intervals qualify: (–∞,2) and (2,4) and (5,∞). It actually turns out that f is increasing in the entire interval (–∞,4) because just one point with a horizontal tangent line doesn't "hurt" such behavior, but either answer would be accepted by me as correct on an exam.
  4. For each critical point: is it a local max or a local min or neither?
    First, x=2: to the left, f is increasing since f´>0, and to the right, f is increasing since f´>0. Therefore x=2 is neither a local max nor a local min.
    Now x=4: to the left, f is increasing since f´>0, and to the right, f is decreasing since f´<0. Therefore x=4 is a local max.
    Finally, x=6: to the left, f is decreasing since f´<0, and to the right, f is increasing since f´>0. Therefore x=4 is a local min.
  5. Where is the graph of f concave up?
    The graph of f is concave up in intervals where f´´>0. If we consider the graph of f´ which is given, the "tilt" of the tangent lines is up (so f´´>0) in the intervals (2,3) and (5,∞). These are intervals where f´ is increasing.
  6. Where is the graph of f concave down?
    The graph of f is concave down in intervals where f´´<0. If we consider the graph of f´ which is given, the "tilt" of the tangent lines is down (so f´´<0) in the intervals (-∞,2) and (3,5). These are intervals where f´ is decreasing.
  7. Where are the inflection points of f?
    There are changes in concavity at x=2 and x=3 and x=5 so this is where the inflection points are located.
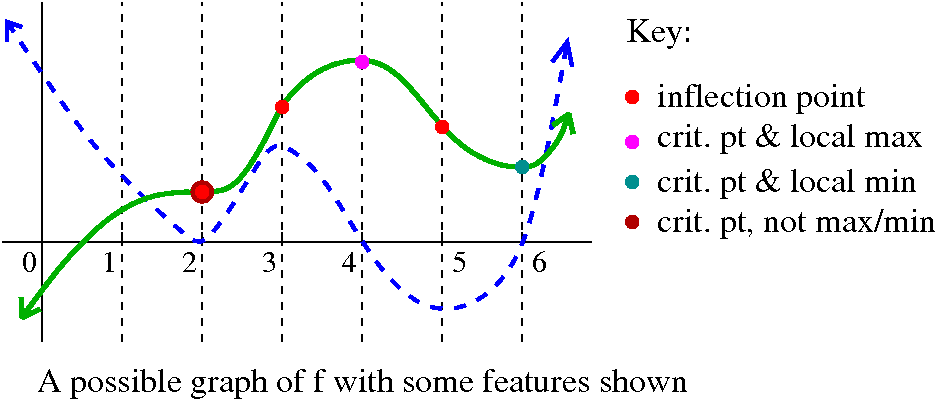
Here is one possible graph of f. As I mentioned, there are many correct answers to this question. They all should present correct {in|de}creasing behavior, correct concavity, correct local behavior at critical points, and also correct inflection points.

Maintained by greenfie@math.rutgers.edu and last modified 10/30/2009.