Part b) brings up the function defined by the expression max(1,x). Here is a graph of this function on the interval [0,5].
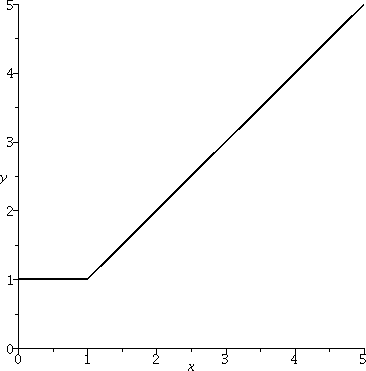
| Thursday, December 10 | (Lecture #28 sort of) |
|---|
History: the Basel problem
This problem was stated by Pietro Mengoli in 1644, and was solved by
Euler almost a century later, in 1735. There is some question about
the validity of his solution of the problem (or, at least, the
validity of the solution we'll look at as presented by him!), and I'll
address that later. The problem is to find some "analytical
expression" or precise value for
∑n=1∞1/n2. The Wikipedia
article discusses the problem and supplies several solutions. The
problem is notorious, and has attracted many solutions. Robin
Chapman, an English mathematician, has assembled fourteen
different proofs. You can also look at the very large
number of references here.
Leonhard Euler
Euler was
one of the greatest known mathematicians, and almost certainly the
most prolific, writing incredible numbers of papers and books
(including, as I mentioned, the first systematic calculus book).
Here is a quote from another source:
Euler devises some clever approximations to get the [sum of the series] to six decimal places, 1.644934. Euler notes that to achieve such accuracy using direct calculation requires more than 1000 terms, so his estimate of the solution to the Basel problem was far more accurate than any available to his competitors. He later improved his estimate to 17 decimal places. Moreover, Euler was a genius at arithmetic, so he probably recognized this value as what will turn out to be the exact solution to the Basel problem, &Pi2/6. Euler didn't share this with the world, so he had a valuable advantage as he raced to solve the problem; he knew the answer.It is amazing to me that Euler could have done this, but he was quite remarkable. These days, smart people have constructing a web page called the Inverse Symbolic Calculator which can help people less gifted than Euler to recognize numbers. For example, when I enter 1.644934 in the ISC search bar one of the first suggestions I get is &zeta(2) (the Greek letter zeta), which is a standard notation for ∑n=1∞1/n2. The ISC and the previously mentioned Encyclopedia of Integer Sequences are wonderful sources of amazing information.
The Vatter problems
39. Find all the roots of f(x)=sin(sqrt(x))/sqrt(x), i.e.,
values of x for which f(x)=0.
40. If a polynomial of degree 3 has roots r1,
r2, and r3, then it is given by
p(x)=c(x–r1)(x–r2)(x–r3) for some
constant c. By expanding this product, verify that
41. Assume, as Euler did, that Exercise 40 holds for infinite
series to show that
42. The function f(x)=2–{1/(1–x)} has a single root,
x=1/2. Derive its Maclaurin series and conclude that, contrary to
Euler's assumption, Exercise 40 cannot be applied to infinite series.
By an amazing coincidence, Dr. Vincent Vatter, a
former Rutgers math graduate student now at Dartmouth, visited me the
morning before today's class. He asked me what I was teaching and when
I told him today's topic he remarked that the topic was a collection of
problems in his calculus book, still in manuscript form. He kindly
allowed me to print the page containing the problems and then the
class and I solved the problems. Here they are.
38. Derive the Maclaurin series for
f(x)=sin(sqrt(x))/sqrt(x).
[1/r1}+[1/r2]+[1/r3]=–{coefficient of x}/{constant term}.
(This fact is true for polynomials of any degree.)
[1/r1}+[1/r2]+[1/r3]+...=1/6
where r1, r2, r3, ... are the roots
from Exercise 39.
Conclude that
∑n=1∞1/n2=Π2/6.
I mentioned that Euler used similar techniques to find explicit values of ∑n=1∞1/nEVEN, where EVEN is any even integer (the values have the form (rational number)·ΠEVEN, so that, for example, ∑n=1∞1/n12=(691/{638,512,875})Π12). There is no known nice form for the sum of ∑n=1∞1/n3, even though a lot of people have thought about it for a long time. I tried for while with no success.
So it was wrong, wasn't it?
So the proof we just "toured" was certainly incorrect. This is interesting. But
the historical
source I quoted earlier noted that Euler gave at least three other
solutions of the Basel Problem, and the "proof" we just discussed is
the one most remembered. Several of Euler's other proofs use
techniques familiar to all 152 students, but the proofs are definitely
much more intricate although quite ingenious, and they are not very
appealing (although undoubtedly correct even by today's
standards). It is interesting that an incorrect but
insightful proof is the one which most people remember!
Further, Euler was sort of correct although power series are not "exactly" like long polynomials. There are ways of relating the roots of a power series to the coefficients of the power series. About 150 years later, another mathematician named Weierstrass fixed up Euler's proof using a factorization theorem for power series. One of the key assumptions made in Weierstrass's result rules out an example like the one given in problem 42 above (thank goodness!). Weierstrass, a great and famous mathematician, is less well known for being one of the lecturer's mathematical ancestors.
Rearranging a series
There are some other strange things that happen with series. Many of these
were known to Euler, and he mostly disregarded them. For example, we
know that the Alternating Harmonic Series,
1–1/2+1/3–1/4+1/5–1/6+1/7...
converges since it satisfies all of the
hypotheses of the Alternating Series Test. Call its sum, S (actually
its sum is ln(2) but we don't need this here). Now let's
rearrange it.
Write a positive term followed by two negative terms, and keep doing
this. So the rearranged series begins
1–1/2–1/4+1/3–1/6–1/8... and notice that we'll never run out of either
positive or negative terms since there are infinitely many of both of
them. Now put parentheses around the results in this way:
(1–1/2)–1/4+(1/3–1/6)–1/8...
and realize that the numbers inside pairs of parentheses can be
simplified:
1/2–1/4+1/6–1/8...
And then further realize that we could factor out 1/2:
(1/2)(1–1/2+1/3–1/4 ....)
which certainly shows that this series converges and its sum is (1/2)S.
Most people find this startling and at least moderately unpleasant. In fact, absolutely convergent series can be rearranged in any way, and rearrangement won't change the sum -- the resulting series will have the same sum as the original series. But any conditionally convergent series can be rearranged so that the sequence of partial sums does almost anything you want. For example, it can be rearranged so that the rearrangement converges to any selected number. (This is because that positive and negative parts of the series separately diverge, but a proof of all this is not really a part of this course.)
Convergence and infinite series can be rather subtle. But now we need to turn to preparing for the final exam.
Using series instead of L'H
I asked people to use Maclaurin series to compute
(sin(3x)–3x)2 lim --------------- x→0 (e2x–1–2x)3We did this by using the known series for the sine and the exponential functions and then factoring out and canceling as many powers of x as we could (6) from the top and bottom. Solution using L'H would need 6 differentiations of the top and bottom functions, and that's quite unappealing.
Finding some terms of a Taylor series
I asked for the first four non-zero terms of the Maclaurin series for
cos(3x)/(1+x4). This can be obtained by using series for
cos(3x) (easy to get from the cosine series) and by realizing the
1/(1+x4) is the sum of a geometric series with first term 1
and ratio x4.
|
An integral Here's a problem from the textbook: write ∫0xln(1+t2)dt as a power series in x assuming |x|<1. How many terms of this series would be needed to get the value of the integral when x=1/3 to an accuracy of .001? (Of course, I can find an antiderivative of ln(1+t2) using integration by parts fairly easily.) |
If you want to come to the review session ...
On Monday afternoon, I'll have a review session from 3 to 5 PM in Hill
525. You could prepare for it by filling out this neat quiz written by
Dr. Julia Wolf. She gave it to her class and allowed half an hour. So
give yourself half an hour, and then come to the review session with
your results.
| Wednesday, December 9 | (Lecture #27 sort of) |
|---|
| Monday, December 7 | (Lecture #26 sort of) |
|---|
I don't want to kill the problems (from my pedagogical point of view!) by writing solutions to them in this diary. But I will give some amplification of the classroom discussions by displaying some appropriate graphs.
|
Problem 1 b) Part b) brings up the function defined by the expression max(1,x). Here is a graph of this function on the interval [0,5]. | 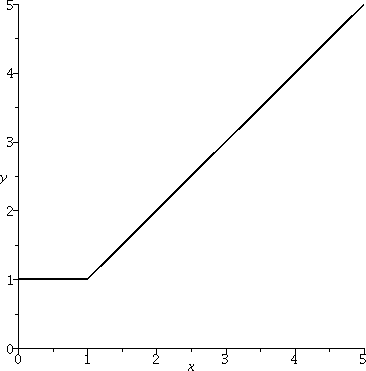 |
|
Problem 1 a) And the answer to part a) makes me think of the two-variable function f(x,y)=max(x,y). Here is a graph (in three dimensions -- you'll appreciate it more next semester) of the function z=f(x,y) for x and y both between 0 and 2. | 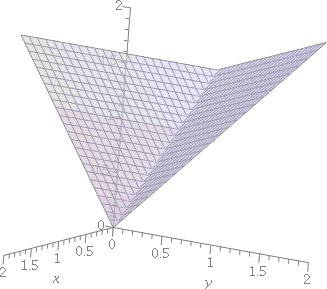 |
|
Problem 2 So here is a graph showning two curves on the interval [1,100]. One of them is ln(x) and the other is 210(x(1/210)–1). They overlay one another so closely that, to me, only one "curve" is consistently visible. | 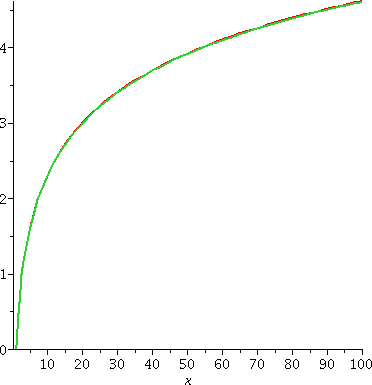 |
|
Problem 2 (another picture) Here are the same two functions on the interval [90,100]. The functions get separated more as the distance to 1 increases (similar to partial sums of most Taylor series). Now you can "see" the two curves and also maybe understand why the separation could not be seen on the scale of the graph above. | 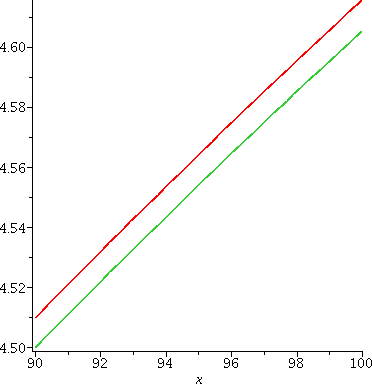 |
|
Problem 5 Here is a graph of the function e2cos(x)(cos(2sin(x)) on the interval [0,20]. You can compare this with the partial sum given in the problem statement. If this graph doesn't convince you that complex numbers exist (at least as much as the numbers sqrt(2) and Π "exist") then I don't know what argument would. | 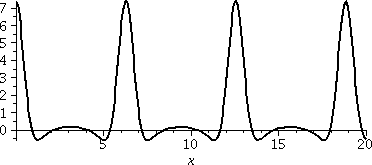 |
|
Problem 7 Here is a graph of J0, a Bessel function of the first kind on the interval [0,10]. | 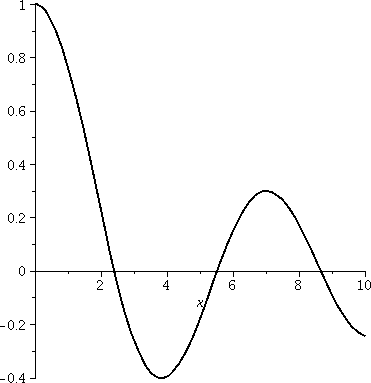 |
Preparation for the final exam
Please see this file. I'll discuss
whether you want a formal review session or office hours or
whatever. The balance of class time this week will be devoted to
further observations about power series.
| Thursday, December 3 | (Lecture #25) |
|---|
A familiar series
We know 1/(1–x). It is the sum of a geometric series with first term 1
and ratio equal to x. So
1/(1–x)=∑n=0∞xn. This
equation is valid when |x|<1, or –1<x<1. Some remarkable
things can be done with this series.
Logarithm
What the Maclaurin series of ln(x)? This is a trick question because
y=ln(x) looks like this ![]() and the
limit of ln(x) as x→0+ is –∞ so ln(x)
can't have a Taylor series centered at 0. What's a good place
to consider? Since ln(1)=0, we could center the series at 1. Most
people would still like to compute near 0, though, so usually the
function is moved instead! That is, consider ln(1+x) whose graph now
behaves nicely at 0
and the
limit of ln(x) as x→0+ is –∞ so ln(x)
can't have a Taylor series centered at 0. What's a good place
to consider? Since ln(1)=0, we could center the series at 1. Most
people would still like to compute near 0, though, so usually the
function is moved instead! That is, consider ln(1+x) whose graph now
behaves nicely at 0 ![]() so we can
analyze it there.
so we can
analyze it there.
If f(x)=ln(1+x), I want to "find" ∑n=0&infin[f(n)(0)/n!]xn. Well, f(0)=ln(1+0)=ln(1)=0, so we know the first term. Now f´(x)=1/(1+x) so that ... wait, wait: remember to try to be LAZY.
Look at
1 --- 1+xThis sort of resembles the sum of a geometric series. We have two "parameters" to play with, c, which is the first term, and r, which is the ratio between successive terms. The sum is c/(1–r). If we take c=1 and r=–x then 1/(1+x)=1/(1–{–x}) is the sum of a geometric series. So
Computing with ln
What if x=–1/2 in the previous equation? Then ln(1–1/2)=ln(1/2)=–ln(2)
and this is approximately –69314. A friend of mine has just computed
&sumn=110[(–1)n+1(–.5)n/n]
and this turns out to be –.69306. We only get 3 decimal places of
accuracy. It turns out that this series converges relatively slowly
compared to the others we've already seen, which have the advantage of
factorials in the denominator. So this series is usually not directly
used for numerical computation, but other series related to it are used.
Book problem: 10.7, #9
Find the Maclaurin series of ln(1–x2).
Be LAZY. We know that
ln(1+x)=x–[x2/2]+[x3/3]–[x4/4]+[x5/5]+...=&sumn=1∞[(–1)n+1xn/n]. This
so we can substitute –x2 for x and get
ln(1–x2)=–x2–[(–x2)2/2]+[(–x2)3/3]–[(–x2)4/4]+[(–x2)5/5]+...=&sumn=1∞[(–1)n+1(–x2)n/n] and further
ln(1–x2)=–x2–[x4/2]–[x6/3]–[x8/4]–[x10/5]+...=–&sumn=1∞[(–1)n+1x2n/n] (valid for |x|<1).
Computing a value of a derivative
I know that the degree 8 term in the Maclaurin series for
ln(1–x2) is –[x8/4]. But it is also supposed to
be (by abstract "theory") [f(8)(0)/8!]x8. This means "clearly" (!!!) that
–1/4=[f(8)(0)/8!] and therefore f(8)(0)=–8!/4.
That's if you desperately wanted to know the value of the derivative. An alternate strategy would be to compute the 8th derivative and evaluate it at x=0. Here is that derivative:
6 8 4
10080 (28 x + x + 70 x + 28 x + 1)
- --------------------------------------
2 8
(-1 + x )
Sp the derivative at 0 is –10,080, and this is the same as
–40,320/8. Wonderful!
arctan
Let me try to find a Taylor series centered at 0 (a Maclaurin series)
for arctan. Well, the general Maclaurin series is
∑n=0∞[f(n)(0)/n!]xn
so we can just try to compute some derivatives and evaluate them at
0. Let's see:
n=0 f(x)=arctan(x) so f(0)=arctan(0)=0.
n=1 f´(x)=1/(1+x2) so
f´(0)=Stop this right now! Why?
Because this way is madness. Here is the 7th derivative of
arctan(x):
6 4 2
720 (7 x - 35 x + 21 x - 1)
------------------------------
2 7
(1 + x )
Does this look like something you want to compute?
Instead look at
1 ---- 1+x2This sort of resembles the sum of a geometric series. We have two "parameters" to play with, c, which is the first term, and r, which is the ratio between successive terms. The sum is c/(1–r). If c=1 and r = –x2 then 1/(1+x2)=1/(1–{–x2}) is the sum of a geometric series. So
|
Computing π This series has been used to compute decimal approximations of π. For example, if x=1, arctan(1)=π/4, so this must be 1–1/3+1/5–1/7+... but the series converges very slowly (for example, the 1000th partial sum multiplied by 4 gives the approximation 3.1406 for π which is not so good for all that arithmetic!) . Here is a history of some of the classical efforts to compute decimal digits of π. You can search some of the known decimal digits of π here. There are more than a trillion (I think that is 1012) digits of π's decimal expansion known. Onward! The methods used for such computations are much more elaborate than what we have discussed. |
In physics they say ...
Many of the force "laws" stated in physics are quadratic (second
degree) and therefore it is not surprising that squares and square
roots need to be computed frequently. What does sqrt(1+x) "look like"
near 0? Well, in this case I will try a direct computation. If
f(x)=sqrt(1+x) then ...
| Function | Value at x=0 |
|---|---|
| f(x)=(1+x)1/2 | 1 |
| f´(x)=(1/2)(1+x)–1/2 | 1/2 |
| f´´(x)=(1/2)(–1/2)(1+x)–3/2 | (1/2)(–1/2) |
| f(3)(x)=(1/2)(–1/2)(–3/2)(1+x)–5/2 | (1/2)(–1/2)(–3/2) |
| I forget but look at the pattern. | (1/2)(–1/2)(–3/2)(–5/2) |
So this Taylor series looks like
(1+x)1/2=1+(1/2)x+[(1/2)(–1/2)/2]x2+[(1/2)(–1/2)(–3/2)/6]x3+[(1/2)(–1/2)(–3/2)(–5/2)/24]x4+...
where those other strange numbers come from the factorials, of
course. Well, how might this be used in physics. Suppose you are
trying to analyze sqrt(1+w). If |w| is very small, well then I bet
that sqrt(1+w) is quite close to sqrt(1+0) which is 1. But the value
will not equal 1 if w is not 0. What sort of "first order" estimate
would I believe in? I bet that sqrt(1+w) is approximately 1+(1/2)w for
small w. I also believe that the error will be (roughly) proportional
to the size of w2 (that's the Error Bound again). For many
applications, knowing this is enough. But what if I wanted more
accuracy, and I wanted an estimate which was correct to "second order
terms". I bet this would take sqrt(1+w) and then the estimate would be
1+(1/2)w–(1/8)w2, with an error which would be (roughly)
proportional to w3. Depending on the application you were
interested in, the estimate would be a bigger and bigger partial sum
of the Taylor series.
Why do I insist on writing the coefficients of the series in the silly
way done above? Why not just multiply out and write that? Well, if I
do the result may be rather deceptive. It would be
1+(1/2)w–[1/8]w2+[1/16]w3–[5/128]w4+...
(I think we got the coefficient of the fourth degree term wrong in
class when we "simplified" -- I'm sorry!)
so if I accidentally saw only the first 4 terms I might think there is
some obvious pattern to the series. Actually, the pattern is more
complicated, as the coefficient of w4 showns. There is an
abbreviation which is used (binomial coefficients) but the numbers are
complicated.
Binomial series with m=1/3
One of Newton's most acclaimed accomplishments was the description of
the Maclaurin series for (1+x)m. Here is more
information. Here I'll specialize by analyzing what happens when
m=1/3. (In class we looked at 1/2.) We'll use a direct approach by
taking lots of derivatives and trying to understand
∑n=0∞[f(n)(0)/n!]xn.
1+(1/3)x+[(1/3)(–2/3)/2]x2+[(1/3)(–2/3)(–5/3)/2·3]x3+[(1/3)(–2/3)(–5/3)(–8/3)/2·3·4]x4+...
I'll come back to the general ideas later, but let's see how to use this in various ways.
Naive numerical use
So you want to compute (1.05)1/3? This is a doubtful
assumption, and anyway wouldn't you do a few button pushes on a
calculator? But let's see:
Suppose we use the first two terms of the series and let x=.05:
(1+.05)1/3=1+(1/3)(.05)+Error
What's interesting to me is how big the Error is. Of course, we
have the Error Bound, which states that
|Error|≤[K/(n+1)!]|x–a|n+1. Here, since the top
term in the approximation is the linear term, we have n=1. And a, the
center of the series, is 0, and x, where we are approximating, is
.05. Fine, but the most complicated part still needs some work. K is
an overestimate of the absolute value of the second derivative of f on
the interval connecting 0 and .05. Well (look above!) we know that
f(2)(x)=(1/3)(–2/3)(1+x)–5/3. We strip away the
signs (not the sign in the exponent, since that means something
else!). We'd like some estimate of the size of (2/9)(1+x)–5/3
on [0,.05]. Well, it is exactly because of the minus sign in
the exponent that we decide the second derivative is decreasing
on the interval [0,.05] and therefore the largest value will be at the
left-hand endpoint, where x=0. So plug in 0 and get
1/9(1+0)–5/3=2/9. This is our K. So the Error Bound
gives us [(2/9)/2!](.05)2, which is about .00027. We have
three (and a half!) decimal digits of accuracy in the simple
1+(1/3)(.05) estimate.
What if we wanted to improve this estimate? Well, we can try another term. By this I mean use 1+(1/3)(.05)+[(1/3)(–2/3)/2](.05)2 as an estimate of (1.05)1/3. How good is this estimate? Again, we use the Error Bound: |Error|≤[K/(n+1)!]|x–a|n+1. Now n=2 and a=0 and x=.05, and K comes from considering f(3)(x)=(1/3)(–2/3)(–5/3)(1+x)–8/3. We need to look at (10/27)(1+x)–8/3 on [0,.05]. The exponent is again negative (what an accident not -- these methods are actually used and things should be fairly simple!) and therefore the function is again decreasing and an overestimate is gotten by looking at the value when x=0, so (10/27)(1+x)–8/3 becomes (10/27)(1+0)–8/3=(10/27). Hey, [K/(n+1)!]|x–a|n+1 in turn becomes [(10/27)/3!](.05)3, about .000008, even better.
Approximating a function on an interval
People usually use the partial sums considered above in a more
sophisticated way. For example, consider replacing (1+x)1/3
by
T2(x)=1+(1/3)x+[(1/3)(–2/3)/2!]x2=1+(x/3)–(x2/9)
anywhere on the interval [0,.05]. I like polynomials, because
they can be computed just by adding and multiplying. The function
(1+x)1/3 has this irritating and weird exponent, that I, at
least, can't readily estimate. What about the error? The Error
Bound declares that an overestimate of the error is
[K/3!]|x–0|3. Now if 0<x<.05, then the largest
x3 can be is (.05)3. What about K? Again, we
look at the third derivative with the signs (not the exponent
sign!) dropped. This is (10/27)(1+x)–8/3 which we are
supposed to estimate for any x in [0,.05]. But since the third
derivative is still decreasing (–1/3<0) again the K is gotten by
plugging in x=0. Hey: the estimate is the same as what we had before,
about .000008. Below are some pictures illustrating what's going on.
| (1+x)1/3 & T2(x) on [0,.05] | (1+x)1/3 & T2(x) on [0,2] |
|---|---|
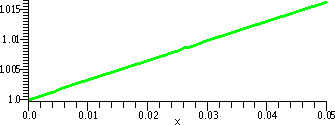 |
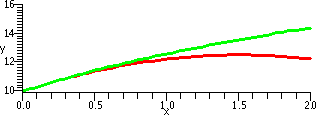 |
| Comments Yes, there really really are two curves here. One, (1+x)1/3, is green and one, T2(x)=1+(x/3)–(x2/9), is red. But the pixels in the image overlay each other a lot, because the error, .000008, makes the graphs coincide on the [0,.05] interval. There are only a finite number of positions which can be colored, after all! | Comments This graph perhaps shows more about what's going on. The domain interval has been changed to [0,2]. The K in the Error Estimate is not changed, but the x's now range up to 2. So [K/3!]x3 becomes as a worst case estimate [(10/27)/3!]23, which is about .49. You can see T2(x) revealed (!) as just a parabola opening downward (hey, 1+(x/3)–(x2/9) has –1/9 as x2 coefficient!). The two curves are close near x=0, and then begin to separate as x grows larger. |
Improving the approximation
The whole idea is maybe by increasing the partial sum (going to
Tn(x)'s with higher n's) we will get better
approximations. This is only usable if the approximations are easy to
compute (nice polynomials with simple coefficients) and if the error
estimates are fairly easy to do. This actually occurs so that people
use these ideas every day.
Binomial series in general
Suppose m is any number (yes: any
number). Then
The list ...
Pascal's triangle
I very rapidly discussed the magical assembly of numbers called
Pascal's triangle. There's a long wikipedia article about it,
of course, and here's
another link which has pictures of more old documents mentioning
the triangle. I tried to explain some of the uses of the numbers which
occur, and how the Taylor expansion above generalizes the result for
(1+x)INTEGER POWER.
1/(1+x)2
More a part of this course was my effort to compute that Taylor series
for 1/(1+x)2 using as many different techniques as we could
imagine. I think we discussed the methods that follow.
The Binomial Theorem Take m=–2 and try to understand the
binomial coefficients which result. Well:
The –2 over 0 binomial coefficient has 0! downstairs, and this is
1. On the top we have zero terms multiplied together, and (by special
understanding, to make the notation work!) this is defined also to be
1 ("the empty product is 1" is the what people say). The result is 1.
The –2 over 1 binomial coefficient has 1!=1 downstairs, and on top has
just –2. So the result is –2.
The –2 over 2 binomial coefficient has 2!=2 downstairs, and on top has
just –2 multiplied by –2–1=–3. So the result is 6 divided by 2, or 3.
The –2 over 3 binomial coefficient has 3!=6 downstairs, and on top has
–2 multiplied by –2–1=–3 multiplied by –2–2=–4. So the result is –24
divided by 6, or –4.
By now people mostly saw the pattern, and therefore 1/(1+x)2=1–2x+3x2–4x3+...
Multiply two series I know from the geometric series result that 1/(1+x) is the same as 1–x+x2–x3+... because the first term is 1 and the common ratio is –x. The sum is therefore 1/(1–{–x})=1/(1+x). So then 1/(1+x)2 should be the same as (1–x+x2–x3+...)2. Now we tried to discuss how to think about the multiplication. The only way to get a constant term is to multiply 1 times 1. There are two ways to get a degree 1 in x term: multiply 1 times x and also multiply x by 1. Both of these have a negative sign, so the result is –2x. How about x3? We can multiply 1 times x2, and also x2 times 1, and also –x times –x. The result is 3x2. We also even computed the x3 term, and we got –4x3. Etc. (!!) Therefore 1/(1+x)2 must be 1–2x+3x2–4x3+... again.
Differentiate That is, the original geometric series for 1/(1+x) is 1–x+x2–x3+... and we can differentiate. The derivative of 1/(1+x) is –1/(1+x)2, and the derivative of the series is 0–1+2x–3x2+... and we get our result again if we multiply by 1. Wow.
| Wednesday, December 2 | (Lecture #24) |
|---|
Hypothesis Suppose the power series ∑n=0∞an (x–x0)n has some positive radius of convergence, R, and suppose that f(x) is the sum of this series inside its radius of convergence.These results are not obvious at all, and they take some effort to verify, even in more advanced math courses. The results declare that for calculus purposes, a power series inside its radius of convergence can be treated just like a polynomial of infinite degree. You just differentiate and integrate the terms and the sums are the derivative and antiderivative of the original sum function.Differentiation The series ∑n=0∞n an (x–x0)n–1 has radius of convergence R, and for the x's where that series converges, the function f(x) can be differentiated, and f´(x) is equal to the sum of that series.
Integration The series ∑n=0∞[an/(n+1)] (x–x0)n+1 has radius of convergence R, and for the x's where that series converges, the sum of that series is equal to an indefinite integral of f(x), that is ∫f(x)dx.
And algebraically ...
It is also true that inside the radius of convergence, power series
can be manipulated just like l-o-n-g polynomials so terms can be
interchanged in any fashion, etc. So everything works inside the
radius of convergence where power series converge absolutely.
Please note that other kinds of series many of you will likely see in applications later (such as Fourier series or wavelet series) do not behave as simply and nicely as power series.
If a function has a power series then ...
Suppose I know that f(x) is equal to a sum like
A+B(x–x0)+C(x–x0)2+D(x–x0)3+E(x–x0)4+...
and I would like to understand how the coefficients A and B and C and
D etc. relate to f(x). Here is what we can do.
Step 0 Since
f(x)=A+B(x–x0)+C(x–x0)2+D(x–x0)3+E(x–x0)4+...
if we change x to x0 we get f(x0)=A. All the
other terms, which have powers of x–x0, are 0.
Step 1a Differentiate (or, as I said in class, d/dx) the
previous equation which has x's, not x0's. Then we have
f´(x)=0+B+2C(x–x0)1+3D(x–x0)2+4E(x–x0)3+...
Step 1b Plug in x0 for x and get
f´(x0)=B. All the
other terms, which have powers of x–x0, are 0.
Step 2a Differentiate (or, as I said in class, d/dx) the
previous equation which has x's, not x0's. Then we have
f´´(x)=0+0+2C+3·2D(x–x0)1+4·3E(x–x0)2+...
Step 2b Plug in x0 for x and get
f´´(x0)=2C, so
C=[1/2!]f(2)(x0). All the other terms,
which have powers of x–x0, are 0.
Step 3a Differentiate (or, as I said in class, d/dx) the
previous equation which has x's, not x0's. Then we have
f(3)(x)=0+0+0+3·2·1D+4·3·2E(x–x0)1+...
Step 3b Plug in x0 for x and get
f(3))(x0)=3·2·1D=3!C
so D=[1/3!]f(3)(x0). All the other terms,
which have powers of x–x0, are 0.
ETC. Continue as long as you like. What we
get is the following fact: if
f(x)=∑n=0∞an(x–x0)n
then an=[f(n)(x0)/n!]. This is
valid for all non-negative integers, n. Actually, this formula is one
of the reasons that 0! is 1 and the zeroth derivative of f is f
itself. With these understandings, the formula works for n=0.
What this means is
If a function is equal to a power series, that power series must be the Taylor series of the function.
I hope you notice, please please please, that the partial sums of the Taylor series are just the Taylor polynomials, which we studied earlier.
Usually I'll take x0=0, as I mentioned so that (x-x0)n becomes just xn. Then the textbook and some other sources call the series the Maclaurin series but I am too lazy to remember another name. A useful consequence of this result (it will seem sort of silly!) is that if a function has a power series expansion, then it has exactly one power series expansion (because any two such series expansions are both equal to the Taylor series, so they must be equal). This means if we can get a series expansion using any sort of tricks, then that series expansion is the "correct one" -- there is only one series expansion. I'll show you some tricks, but in this class I think I will just try some standard examples which will work relatively easily.
ex
I'll take x0=0. Then all of the derivatives of
ex are ex, and the values of these at 0 are all
1. So the coefficients of the Taylor series, an, are
[f(n)(x0)/n!]=1/n!. The Taylor series for
ex is therefore
∑n=0∞[1/n!]xn.
e–.3
Let's consider the Taylor series for ex when
x=–.3. This is
∑n=0∞[1/n!](–.3)n. What
can I tell you about this? Well, for example, my "pal" could compute a
partial sum, say
∑n=010[1/n!](–.3)n. The
result is 0.7408182206. That's nice. But what else do we know? Well,
this partial sum is T10(–.3), the tenth Taylor
polynomial for ex centered at x0=0, and
evaluated at –.3. The Error Bound gives an estimation of
|T10(–.3)–e–.3|. This Error
Bound asserts that this difference is at most
[K–|.3–0|11/11!], where K is some overestimate
of the absolute value of the 11th derivative of
ex on the interval between –.3 and 0. Well, that
11th derivative is also ex. And we know that
ex is increasing (exponential growth after all!) so
that for x's in the interval [–.3,0], ex is at most
e0=1, and we can take that for K. So the Error Bound is
1|–.3–0|11/11!. Now let's look at some numbers:
|–.3|11=0.00000177147 and 11!=39,916,800, and their
quotient is about 4·10–14.
This means that e–.3 and T10(–.3) agree at least
to 13 decimal places. Indeed, to 10 decimal places, e–.3 is
reported as 0.7408182206, the same number we had before. Wow? Wow!
Let's change 10 to n and 11 to n+1. Then |Tn(–.3)–e–.3| is bounded by K|–.3–0|n+1/(n+1)!. Here K=1 again because all of the derivatives are the same, ex. Since 1|–.3–0|n+1/(n+1)!→0 as n→∞ what do we know?
I think that the sequence {Tn(–.3)} converges, and
its limit is e–.3. Since this sequence of Taylor polynomial
values is also the sequence of partial sums of the series
∑n=0∞[1/n!](–.3)n, I
think that the series converges, and its sum is
e–.3. Therefore
e–.3=∑n=0∞[1/n!](–.3)n.
|
e.7 We could try the same sequence of ideas with x=.7. First examine T10(.7). This is ∑n=010[1/n!](.7)n. To 10 decimal places, this is 2.0137527069. We have information from the Error Bound. It declares that |T10(.7)–e.7| is no larger than K|.7–0|11/11!. Here K is an overestimate of the 11th derivative, which is ex, on the interval [0,.7]. The exponential function is (still!) increasing, so the largest value is at x=.7. But I don't know e.7. I do know it is less than e1 which I hardly know also. I will guess that e<3. So a nice simple K to take is 3. Let me try that. The Error Bound is less than 3|.7–0|11/11!. Let's do the numbers here. 11!=39,916,800 (again) but .711=0.0197732674 (small, but not as small as |–.3|11). The Error Bound 3|.7–0|11/11! is about 2·10–9, not quite as small. Now e.7, to 10 decimal places, is 2.0137527074 and this is close enough to the sum value quoted before.
Again, go to n and n+1: |Tn(.7)–e.7| is less
than 3|.7–0|n+1/(n+1)!, and again, as n→∞ this
goes to 0. Our conclusion is: |
e50
Just one more example partly because we'll see some strange
numbers. Let's look at T10(50)
which is
∑n=010[1/n!]50n.
This turns out to be (approximately!) 33,442,143,496.7672, a big
number. The Error Bound says that |T10(50)–e50|
is less than K|50–0|11/11! where K is the largest
ex can be on [0,50]. That largest number is e50
because ex is increasing. I guess e50 is less
than, say, 350, which is about
7·1023. I'll take that for K. Now how big is that Error?
K|50–0|11/11! still has 11! underneath but now the top is
growing also. This is approximately 9·1034, a sort
of big number.
The situation for x=50 may look hopeless, but it isn't really. To
analyze |Tn(50)–e50| we need to look at
K[(50)n+1/(n+1)!]. Here the fraction has power growth on
the top and factorial growth on the bottom. Well, we considered this before. I called it a
"rather sophisticated example". Factorial growth is faster eventually
than power growth. So this sequence will →0 as
n→∞. A similar conclusion occurs:
e50=∑n=0∞[1/n!](50)n.
In fact, e50 is 5.18470552858707·1021 while the partial sum with n=100, ∑n=0100[1/n!](50)n has value 5.18470552777323·1021: the agreement is not too bad, relatively.
And generally for exp ...
It turns out that
∑n=0∞[1/n!]xn converges
for all x and its sum is always ex. The way
to verify this is what we just discussed. Most actual computation of
values of the exponential function relies on partial sums of this
series. There are lots of computational tricks to speed things up,
but the heart of the matter is the Taylor series for the exponential
function.
Sine
We analyzed sine's Taylor polynomials, taking advantage of the cyclic
(repetitive) nature of the derivatives of cosine:
sine→cosine→–sine→–cosine then back to sine. At
x0=0, this gets us a cycle of numbers:
0→1→0→–1→0 etc. The Taylor series for sine
centered at 0 leads off like this:
x–[x3/3!]+[x5/5!]–[x7/7!]+[x9/9!]–...
It alternates in sign, it has only terms of odd degree, and each term has the reciprocal of an "appropriate" factorial (same as the degree) as the size of its coefficient. Using summation notation, which is convenient and compact, this series is ∑n=0∞[(–1)n/(2n+1)!]x2n+1.
What happens to the error bound?
This is similar to what we did with exp. There are two claims: the
series
∑n=0∞[(–1)n/(2n+1)!]x2n+1
converges and the sum of the series is sin(x). Well, to see that this
is true we investigate the difference between sin(x) and
SN, the Nth partial sum of the series. But
SN is the same as TN(x), the Nth
Taylor polynomial. And the error bound tells us that
|sin(x)–TN(x)|≤[K/(N+1)!]|x–0|n+1. Just as
before, [|x|N+1/(N+1)!]→0 as N→∞. What about
the K's? If they misbehave (get very big) that could make the whole
estimate lousy. But in fact in this specific case, |K| is an
overestimate on the size of some derivative of sine. But all of the
derivatives of sine are +/–sine and +/–cosine, and these all are ≤1
in their absolute values. So, in fact, we're done. We have verified
that the series converges and that sin(x) is its sum.
Cosine
We could duplicate this work for cosine, or, as I mentioned in class,
be a bit cleverer. Since we know that
sin(x)=∑n=0∞[(–1)n/(2n+1)!]x2n+1
is true for all x, we could differentiate this equation. The result is
cos(x)=∑n=0∞[(–1)n/(2n+1)!](2n+1)x2n.
In fact, most people realize that (2n+1)/(2n+1)! is 1/(2n)! so that we
have verified the equation
cos(x)=∑n=0∞[(–1)n/(2n)!]x2n
for all x. This is two facts: the series converges, and the sum of the
series (the limit of the sequence of partial sums) is cos(x) for all
x's.
|
A numerical example: cos(1/3) How close is 1–[(1/3)2/2!]+[(1/3)4/4!]–[(1/3)6/6!]+[(1/3)8/8!]–[(1/3)10/10!] to cos(1/3)? Here we sort of have two candidates because T10(1/3) is the same as T11(1/3) since the 11th degree term is 0. Error bound, n=10 So we have K|(1/3)–0|11/11!, where K is a bound on the size of the 11th derivative of cosine. Hey: I don't care much in this example, because I know that this derivative is +/–cosine or +/–sine, so that I can take K to be 1. Now it turns out that (1/3)11/11! is about 1.4·10–14. This is tiny, but ... Error bound, n=11 This is even better. So we have K|(1/3)–0|12/12!, where K can again be taken as 1 (this is easier than exp!) So (1/3)12/12! is about 4·10–15, even tinier. Hey, cos(1/3)=0.944956946314738 and T10(1/3)=0.944956946314734. |
Cosine and sine estimates
For both cosine and sine, the estimates are easy because K for both
can be taken to be 1.
Is success guaranteed?
The material in this lecture showed that exp and sine and cosine have
Taylor series and their Taylor series converge everywhere and the sum
of each Taylor series is always equal to the original function. This
is a wonderful situation, and, for example, is essentially used to
compute values of exp and sine and cosine using partial sums of the
series (as I wrote above, there are some other "computational tricks
to speed things up, but the heart of the matter is the Taylor
series").
But these are the first and nicest and simplest examples. The situation is not always so easy. We will see a few functions where things don't work out. I can even think about one of them with you now. Consider tangent. Certainly if we take x0 to be 0, we can differentiate tangent lots of times and "get" a Taylor series for tangent centered at 0. The reason I wrote "get" with quotes is that the coefficients of the Taylor series for tangent are well-known in the math world to be rather, well, rather irritating and difficult to predict and understand. So already there's a problem. How about convergence? Things also don't go well there because, if you remember tangent's graph, vertical asymptotes occur at odd multiples of Π/2. You can't expect that the series will converge, for example, at +/–Π/2 and, in fact, the radius of convergence turns out to be only Π/2 (this is not so obvious, actually). Most calculators I know compute values of tangent by computing values of sine and cosine and then dividing. This is easier than direct computation of tangent.
I asked a pal to compute tan(j)(0) for j running from 0 to 20. My pal produced these numbers:
0, 1, 0, 2, 0, 16, 0, 272, 0, 7936, 0, 353792, 0, 22368256, 0, 1903757312, 0, 209865342976, 0, 29088885112832, 0There are 0's for even j's because tangent is an odd (tan(-x)=–tan(x), symmetric with respect to the origin) function.
This is a very peculiar sequence. Here is a very abbreviated description of what's known about it. Incidentally, anyone with any mathematical curiosity (or even anyone who can count!) should go to that website and spend some wonderful time, like a kid in a toy store. Fun, fun, fun ...
|
A series for cos(x3) We can use the series we know to "bootstrap" and get other series. That is, we build on known results. For example, since we know that cos(x)=1–[x2/2!]+[x4/4!]–[x6/6!]+[x8/8!]–[x10/10!]... for all x, I bet cos(x3)=1–[(x3)2/2!]+[(x3)4/4!]–[(x3)6/6!]+[(x3)8/8!]–[(x3)10/10!]... which is 1–[x6/2!]+[x12/4!]–[x18/6!]+[x24/8!]–[x30/10!]... and this is much easier than trying to compute derivatives of cos(x3) which we would have to do to plug in the values of the derivatives in the Taylor series. The Chain Rule makes things horrible. For example, the fifth derivative of cos(x3) is –243sin(x3)x10+1620cos(x3)x7+2160sin(x3)x4–360cos(x3)x and that's fairly horrible.
How about x2cos(x3)? A question and its answer
What are the first four non–zero terms of the Taylor series for
x3e–2x centered at 0?
|
What do we know?
If a function f(x) has a power series expansion centered at a, then
f(x)=∑n=0∞[f(n)(a)/n!](x–a)n.
The partial sums of this series are Taylor polynomials, and this is
called a Taylor series.
Almost all the time we and other people in the world take a to be
0. Then the series is also called a Maclaurin series. Examples so far include:
As I mentioned in class, I am not allowed to tell you why these series resemble each other because your heads might explode. eix=cos(x)+isin(x) The not-accidential resemblance will be discussed in your differential equation course. This can be verified, at least on some sort of symbolic level, by plugging ix into the Taylor series for exp, and then realizing that powers of i are periodic with period 4 (how curious -- where did we ever see than before?): i, i2=–1, i3=–i, i4=1, and then reorganizing the result to "find" cos(x)+isin(x).Book problem: 10.7, #21
I mentioned the logical difficulty of the request to "find the first four terms in the Maclaurin series" since maybe 0+x+x2+[x3/3] answers that question. Usually people want the first four non-zero terms and that was the question I answered.
Of course, in class I messed up this computation because I can't think standing up. (Well, I can't think sitting either but ...)
In honor of Mr. Gretzmacher I added a
part b) to this question:
b) If f(x)=exsin(x), what is f(5)(0)?
There are several ways to answer this question. One would be to
compute the fifth derivative. This is actually not too difficult, but
let me be a little slick. I know that f(x) has one and only one power
series centered at 0, and that series must be its Taylor
series. Therefore the coefficient of x5 must be
f(5)(0)/5!. But we know that coefficient. It is
–1/30. So f(5)(0)/5!=–1/30 and
f(5)(0)=–5!/30=–4. Isn't that cute?
Of course Mr. Levi nearly ruined this magical moment by exclaiming something about a workshop problem. Sigh. It turns out that this trick, used for nothing really too interesting here, has actually some more profound uses in such areas as probability (when studying what's called the moment generating function).
Book problem: 10.7, #14
Find the Maclaurin series of cos(sqrt(x)).
Since
cos(x)=1–[x2/2!]+[x4/4!]–[x6/6!]+[x8/8!]–[x10/10!]...=∑n=0∞(–1)n+1x2n/(2n)!
I know that
cos(sqrt(x))=1–[(sqrt(x))2/2!]+[(sqrt(x))4/4!]–[(sqrt(x))6/6!]+[(sqrt(x))8/8!]–[(sqrt(x))10/10!]...=∑n=0∞(–1)n+1(sqrt(x))2n/(2n)!
and so
cos(sqrt(x))=1–[x/2!]+[x2/4!]–[x3/6!]+[x4/8!]–[x5/10!]...=∑n=0∞(–1)n+1xn/(2n)!,
and please be LAZY.
Book problem: 10.7, #19
Find the Maclaurin series of (1–cos(x2))/x.
Since
cos(x)=1–[x2/2!]+[x4/4!]–[x6/6!]+...
I know that
cos(x2)=1–[x4/2!]+[x8/4!]–[x12/6!]+...
and
1–cos(x2)=[x4/2!]–[x8/4!]+[x12/6!]+...
so that
(1–cos(x2))/x=[x3/2!]–[x7/4!]+[x11/6!]+...
If we had to, we could write this in summation form (I hope I get this
correct!)
(1–cos(x2))/x=∑n=0∞(–1)n+1x4n+3/(2(n+1))!
Note, please, that at least initially the "function" given, (1–cos(x2))/x, looks like it has bad behavior at 0 since it looks like division by 0. But the series approach just wipes that out. Many computations done using L'Hôpital's Rule also can be easily accomplished with Taylor series manipulation.
An integral
The function e–x2 is extremely important in
probability. Its integral is called the error
function.
Suppose we want to compute
∫x=0.5e–x2dx. It can
be proved that e–x2 has no
antiderivative which can be written in terms of familiar
functions. How could we then compute this definite integral?
Its value, a pal of mine tells me, is approximately 0.461281. Well, I
could use the Trapezoid Rule or Simpson's Rule or ... Look at this:
ex=∑n=0∞xn/n!
Substitute –x2 for x.
e–x2=∑n=0∞(–x2)n/n!=∑n=0∞(–1)nx2n/n!
Integrate.
∫x=0x=.5e–x2dx=∫x=0x=.5∑n=0∞(–1)nx2n/n! dx=∑n=0∞∫x=0x=.5(–1)nx2n/n!=∑n=0∞(–1)nx2n+1/([2n+1]n!)|x=0x=.5
Evaluate.
The integral is∑n=0∞(–1)n(1/2)2n+1/([2n+1]n!)
 This series is alternating, and satisfies all the hypotheses of the
Alternating Series Test. Any partial sum is within the accuracy of the
first omitted term (look in the textbook or think about with the help
of the
This series is alternating, and satisfies all the hypotheses of the
Alternating Series Test. Any partial sum is within the accuracy of the
first omitted term (look in the textbook or think about with the help
of the Xmas tree picture to the right). Well, if I want 5 digit
accuracy, I just need to find n so that
(1/2)2n+1/([2n+1]n!) is less than .00001, which is
1/(100,000).
If n=4, then (1/2)9/[9·24] is {1/(512)}·[1/(216)] which is 110,592. The sum from n=0 to 3, that is, S3, is 0.461272 (accurate to +/–.00001 as desired).
| Monday, November 30 | (Lecture #23) |
|---|
Statement of the Root Test
The Root Test Consider the series ∑n=0∞an, and the limit limn→∞|an|1/n. Suppose that this limit exists, and call its value, L. (L is what's used in our textbook.)
If L<1, the series converges absolutely and therefore must converge. If L>1, the series diverges. If L=1, the Root Test supplies no information.
Ludicrous example
Let's consider the series ∑n=1∞((5n+7)/(6n+8))n which
I invented specifically to use the Root Test. I don't know any
application where I've ever seen anything like this series which seems
fairly elaborate and silly to me. Well, anyway, the terms are all
positive, so I can "forget" the absolute value signs. We take the
nth root and remember that repeated exponentiations
multiply:
[((5n+7)/(6n+8))n]1/n=((5n+7)/(6n+8))n·(1/n)=((5n+7)/(6n+8))1=((5n+7)/(6n+8)).
Now we need to discover the limit (if it exists!) of ((5n+7)/(6n+8)). But
(L'Hôpital) this limit is 5/6. Since L=5/6<1, the series
converges absolutely and must converge.
I don't know what the sum is. Oh well.
Less silly (maybe) example
This may look almost as ludicrous, but it turns out to be more
significant. Again, though, this example is chosen to work well with
the Root Test.
For which x's does the series
∑n=1∞nnxn converge?
The powers of n signal to me that probably I should try the Root
Test. Here an is nnxn. We can't just
discard the absolute value here, but we can push it through to the x
because everything is multiplied. So:
|nnxn|1/n=(nn|x|n)1/n=nn·(1/n)|x|n·(1/n)=n|x|.
 As I mentioned in class, as n→∞ jumping to the
"conclusion" may be unwise. There are actually two cases. If x=0, the
limit is 0, If x≠0, the limit does not exist (it is "∞"). So we
can conclude that the series
∑n=1∞nnxn
converges exactly when x=0.
As I mentioned in class, as n→∞ jumping to the
"conclusion" may be unwise. There are actually two cases. If x=0, the
limit is 0, If x≠0, the limit does not exist (it is "∞"). So we
can conclude that the series
∑n=1∞nnxn
converges exactly when x=0.
Even less silly example
Let's try this: for which x's does
∑n=1∞xn/nn
converge? I hope you will see the resemblance and contrast with the
previous computation:
|xn/nn|1/n=(|x|n/nn)1/n=|x|n·(1/n)nn·(1/n)=|x|/n.
 In this example, there aren't any special cases. For any x,
limn→∞|x|/n=0=L. Since L<1 always, the series
∑n=1∞xn/nn
converges absolutely for all x's and therefore converges for all x's.
In this example, there aren't any special cases. For any x,
limn→∞|x|/n=0=L. Since L<1 always, the series
∑n=1∞xn/nn
converges absolutely for all x's and therefore converges for all x's.
Comment: Root vs. Ratio
As I mentioned in class, I have an emotional preference for the Ratio
Test that I can't explain. But I will admit that analyzing the two
previous examples with the Ratio Test would be very
difficult. However, the Ratio Test works exceptionally well when
series have factorials (you'll see why there are lots of series with
factorials in the next lecture). So series with similar results to the
two previous examples which I'd examine with the Ratio Test would be
∑n=0∞n!xn and
∑n=0∞xn/n!.
|
The next few examples were tedious to do in class, and I thank
students for the patience they mostly displayed, since the reasons for
doing them were not at all clear.
Example 76
Example 77
|
|
Because I have the brains of a toad, I forgot to do this example,
which is logically necessary. This example shows that we can have
divergence at both ends of the interval of convergence.
Example 78
|
A challenge example
I asked students to give me an interval and to tell me whether to
include or exclude endpoints. I was given (4,8]. I then declared that
this interval was the collection of x's for which the series
∑n=1∞(-1)n(x-6)n/(2nn)
converged, and that it would diverge at all other x's. At the
suggestion of Mr. Oakes we used the
(sigh) Root Test where L=|x-6|/2. It worked but I think the Ratio Test
would also have worked. We separately examined the endpoints x=4 and
x=8 and got the correct answers.
The reason for my going through all of these examples is that there basically aren't any others. Well, what I mean is that, qualitatively, there are no further types of behavior possible for this sort of series. So let me tell you the accepted vocabulary for what we are studying, and then describe the result.
What is a power series?
A power series centered at x0 (a fixed number) is an
infinite series of the form
∑n=0∞cn(x–x0)n
where the x is a variable and the cn are some collection of
coefficients. It is sort of like an infinite degree
polynomial. Usually I (and most people) like to take x0 to
be 0 because this just makes thinking easier.
Convergence and divergence of power series
It turns out that the collection of examples we looked is a complete
qualitative catalog of what can happen to the convergence and
divergence of a power series. This isn't obvious, but it also isn't
totally hard (it just involves comparing series to geometric series
and needs no theoretical equipment beyond what we've already
done). Here is the result:
A power series centered at x0 always has an interval of
convergence with the center of that interval equal to
x0. Inside the interval of convergence, the power series
converges absolutely and therefore converges. Outside the interval,
the power series diverges. The power series may or may not converge on
the two boundary points of the interval. The interval may have any
length between 0 and ∞. Half the length of the interval is
called the radius of convergence.
Why is this true?
Here is an indication of what's going on. Let me take x0 to
be 0, since I am lazy and the logic is the same. So we will consider a
power series centered at 0:
∑n=0∞cnxn. The
series will always converge when x=0 (not much news!). But suppose
this series converges for a number v which is not 0. Let me
explore the consequences. (This will involve the innermost source of
the "strength" of power series, and why they are used so much.)
We assume that ∑n=0∞cnvn converges. If an infinite series converges, the terms must go to 0 as n→∞. So limn→∞cnvn=0. In particular, I bet that the sequence of the individual terms, {cnvn}, is bounded. For n large enough, these all cluster "near" 0. More explicitly, There is some M>0, maybe a really large M, so that |cnvn|<M.
Now take any number w with |w|<|v|. I want to analyze the
{con|di}vergence of
∑n=0∞cnwn. I
will do this by comparing the individual terms with the same series
with v instead of w (there isn't much else to do!). I'll take absolute
values because I like absolute convergence. Signs make things more
delicate and maybe a simple approach will work. Certainly since
|w|<|v| we know
|cnwn|<|cnvn|<M. Well, look at this:
|cnwn|=|cnwn(v/w)n|=|cnwn||v/w|n=Mrn.
Here r=|v/w| is a number which is less than 1. But this means if we consider the series ∑n=0∞cnwn and take absolute values, the terms will all be less than ∑n=0∞Mrn, a convergent geometric series (since r<1). So convergence must "spread inward" for power series.
Going back to the examples
| The series | converges for x in | and has
radius of con- vergence equal to | Pictures: convergence in red and divergence in green |
|---|---|---|---|
| ∑n=1∞nnxn | [0] | 0 |  |
| ∑n=1∞xn/nn | (–∞,+∞) | ∞ |  |
| ∑n=1∞xn/n | [–1,1) | 1 | 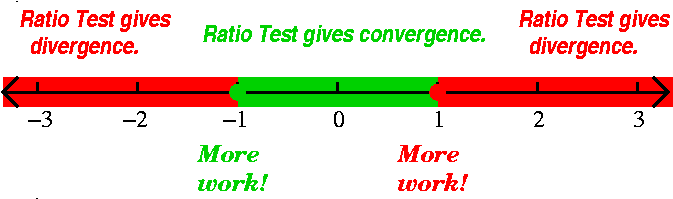 |
| ∑n=1∞xn/n2 | [–1,1] | 1 | 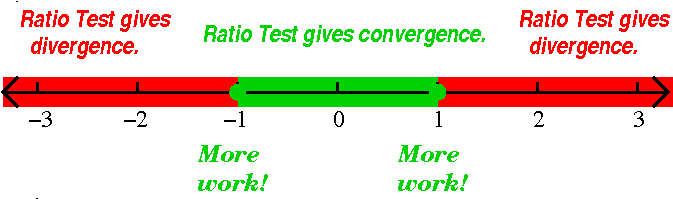 |
| ∑n=1∞n xn | (–1,1) | 1 | 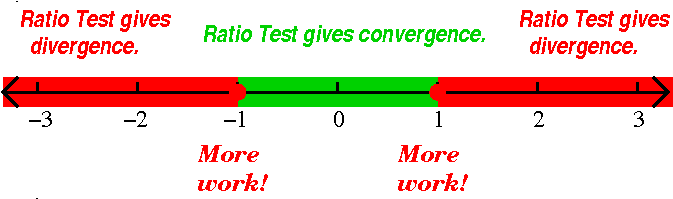 |
These examples show that the interval of convergence of a power
series may or may not include one or both of the endpoints of the
interval. The reason for the number of examples was to show you,
explicitly, that it is possible for the series to converge on neither
or one or both of the boundary points. I wanted to show a "complete"
collection of examples.
It turns out that behavior on the edge of the interval is probably
only interesting (sigh) as an exam question in calc 2 (where it
is frequently asked!) because of some results you'll be told
about in a few lines.
A suspiciously simple question ... (the "IQ" test in class)
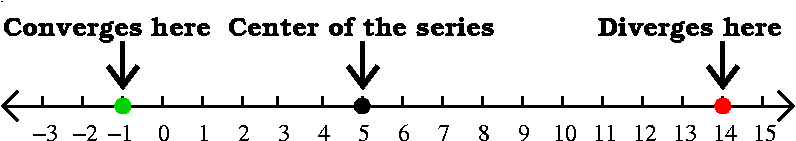 Suppose that you have a power series
∑n=0∞an (x–5)n
centered at x0=5. You are told that the series converges
when x=–1 and diverges when x=14. What can you say about the
radius of convergence? For which x's must this series converge
and for which x's must this series diverge? You are given no
other information.
Suppose that you have a power series
∑n=0∞an (x–5)n
centered at x0=5. You are told that the series converges
when x=–1 and diverges when x=14. What can you say about the
radius of convergence? For which x's must this series converge
and for which x's must this series diverge? You are given no
other information.
Answer The general theory, quoted above, states that a power
series converges in an interval, and the center of the series, here
x0=5, must be in the center of the interval. If the series
converges at x=–1, then, since the distance from –1 to 5
is 6, the series must (by the general theory) converge at every
number x whose distance to 5 is less than 6. I think to myself that
"convergence spreads inward". What about divergence? Actually,
"divergence spreads outward." The distance from 5 to 14, where we're
told that the series diverges, is 9. Therefore any x whose distance to
5 is greater than 9 (left or right!) must be a place where the series
diverges (because if it converged then the series would converge at
14, also, by the contagious (?) nature of convergence, and this isn't
true).

What we can conclude from this information is the following:
I hope you note that if I had told you this information:
The series, centered at 5,
diverged at –1 and converged at 14.
Then I would be lying (or "I misspoke" as a politician might
declare). There is no such series. Convergence at 14 with center at 5
would immediately imply that the series converged at –1.
But what are the qualitative properties of a function which happens
to be the sum of a power series?
Suppose I know that
f(x)=∑n=0∞cnxn,
wherever the series converges. I want to study f(x). What follows is
not in the textbook.
Let's look just a little bit more at the abstract setup discussed
above, with v and w. So
∑n=0∞cnvn
converges, and |w|<|v| means that
∑n=0∞cnwn. But
we actually got a bit more. We saw that
∑n=0∞cnwn can be
compared to a geometric series,
∑n=0∞Mrn with
r=|w/v|<1. Now this series can be split into a partial sum and an
infinite tail:
∑n=0∞Mrn=∑n=0NMrn+∑n=N+1∞Mrn.
Because geometric series are so simple, I can actually compute the sum
of the infinite tail. It has first term MrN+1 and ratio r,
so that the sum is MrN+1/(1-r) or (M/(1-r))rN+1. The only
place that N appears is as part of the exponent of r. Well, as N
increases, we know that rN+1→0. In fact, if you give
me some positive number ε (sorry: the Greek letter
epsilon is what's customarily used here) then I can find N so
that the tail will have sum less than ε. People actually make
these quantitative estimes in "real life" but here I'm just outlining
the process. So I can select N so that
MrN+1/(1-r)<ε. Also, "notice" (this all took
about 150 years to "notice"!) that once N is selected for |w| the same
N works for any number whose absolute value is at most |w|. Well, for
example, if w1 and w2 are any numbers with
absolute value at most |w|, then f(w1) and f(w2)
are (with error at most ε) the same as the finite sums
∑n=0Ncnw1n
and
∑n=0Ncnw2n.
These are values of the polynomial
P(x)=∑n=0Ncnxn. I know
from long ago (calc 1) that polynomials are continuous, so I know that
if |w1–w2| is small, then I can make
|P(w1)–P(w2)|<ε. So look
carefully:
If |w1–w2|
is small, then |f(w1)–f(w2)| is small
since we can "forget" the infinite tails in each case (committing a
possible error of ε twice) and since polynomials are
continuous.
Any f(x) which is the sum of a power series must be continuous inside the interval of convergence. What we just went through was a proof, and, even more, it actually gives a way of making numerical estimates for how the values of f can change. The method is very involved, but it does work.
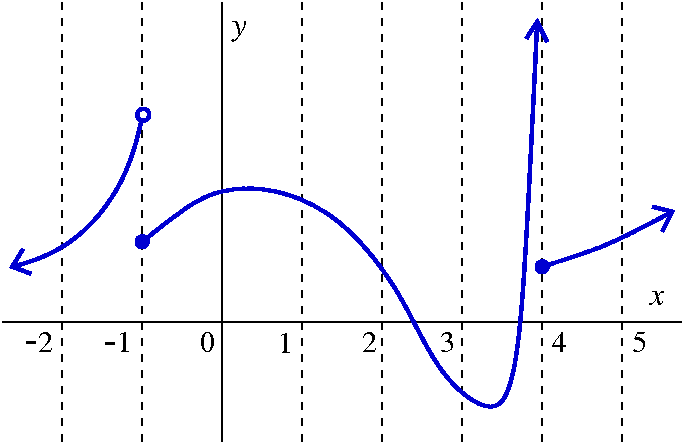 Let me give a consequence here in a rather silly form. (I tried a
version of this rapidly at the end of the lecture.) Suppose we have a
function f whose graph is shown to the right. The graph is supposed to
be part of the graph of a function whose domain is all real
numbers. From the calculus point of view, there are several things
that spoil (?) the graph. First, there's a "jump discontinuity" at
–1 (I'm using the standard solid point/empty point graph model
to indicate behavior of limits and values). Also, there is a vertical
asymptote from the left at 4 (from the right the behavior is "nice").
Let me give a consequence here in a rather silly form. (I tried a
version of this rapidly at the end of the lecture.) Suppose we have a
function f whose graph is shown to the right. The graph is supposed to
be part of the graph of a function whose domain is all real
numbers. From the calculus point of view, there are several things
that spoil (?) the graph. First, there's a "jump discontinuity" at
–1 (I'm using the standard solid point/empty point graph model
to indicate behavior of limits and values). Also, there is a vertical
asymptote from the left at 4 (from the right the behavior is "nice").
Suppose f(x) is equal to the sum of a power series centered at 0. I claim that the largest radius of convergence for that power series is 1. If the power series converges for a radius Q more than 1, then the graph of f would have to be continuous inside the interval (0–Q,0+Q). But –1 can't be in that interval since f is not continuous at 1, so Q is at most 1. Suppose f(x) is equal to the sum of a power series centered at 2. I claim that the largest radius of convergence for that power series is 2. If the power series converges for a radius Q more than 2, then the graph of f would have to be continuous inside the interval (2–Q,2+Q). But 4 can't be in that interval since f is not continuous at 4, so Q is at most 2. |
| Monday, November 23 | (Lecture #22) |
|---|
Given a series, take absolute valuesThe scheduled subject for today's lecture is Ratio and Root Tests, and for the next lecture, the subject is Power Series. Today I will definitely motivate and state the Ratio Test, and probably won't get to the Root Test (added, after class: I did sort of get to it -- at least I suggested what the Root Test might involve). I will, however, show an application to a power series. On Monday, I will continue with a statement of the Root Test, and then formally define and state the principal properties of power series, and use both of the "tests" to analyze power series.
The result just stated is a very powerful and easily used method. If you "give" me a series with random signs, the first thing I will do is strip off or discard the signs and try to decide if the series of positive (non-negative, really) terms converges.
Two neat Tests for convergence
The last lecture discussed the relationship between absolute
convergence and conditional convergence. Today we will begin to study
the two standard "tests" which are used to diagnose absolute
convergence. Both of these tests rely on some relationship with
geometric series. Let me begin with an example.
∑n=0∞(50)n/n!
We met the sequence of individual terms
{(50)n/n!} earlier. We showed that this
specific sequence converges to 0. We did this by looking at what
happens after the 100th term. Then each later sequence term is
less than half the size of the term immediately before it. Eventually
the terms squeeze down and their limit is 0.
But what about the series? Just knowing that the sequence of
individual terms →0 is not enough information to guarantee that
the series, the sum of the terms, is convergent. (That's what the
harmonic series shows!) But look here:
∑n=0∞(50)n/n!=∑n=0100(50)n/n!+∑n=101∞(50)n/n!.
Let's ignore the first big lump -- I don't care how big it is. It
actually doesn't influence whether the series converges or not. The
convergence of the series depends on whether the infinite tail
converges. Look at what can we say here:
50101/(101!)+50102/(102!)+50103/(103!)+...<50101/(101!)+50101/(101!)[1/2]+50101/(101!)[1/2]2+...
We can compare this infinite tail to a certain geometric series which
is larger than it, and this geometric series must converge
because it is a series with ratio 1/2 and 1/2<1.
Why -- what's happening?
The Ratio Test is a way of using the sort of logic that we considered
above. It systematically checks if there is a valid comparison to a
convergent or to a divergent geometric series. Here is the idea.
If we are studying a series ∑an, then we may hope
that somehow an resembles crn, a term of a
geometric series. We further hope that an+1 will
resemble crn+1. But then if the "resemblance" is good
enough, we might hope that the quotient,
an+1/an, will be like
(crn+1)/(crn), and this would be r. This is only
a resemblance, so the textbook actually uses a different letter in its
statement of the Ratio Test. And we put on absolute value signs, since
whether or not a geometric series converges only depends on whether
|r|, the absolute value of the ratio, is less than
1. Etc. So here is a formal statement:
The Ratio Test Consider the series ∑n=0∞an, and the limit limn→∞|an+1/an|. Suppose that this limit exists, and call its value, ρ. (That's supposed to be the Greek letter rho.) Then:
If ρ<1, the series converges absolutely and therefore must converge. If ρ>1, the series diverges. If ρ=1, the Ratio Test supplies no information
Applied to this problem
Let's see what happens when we try to apply this "Test" to the series
∑n=0∞(50)n/n!. Since
an=(50)n/n!, the next term, an+1,
will be (50)n+1/(n+1)!. Try to avoid possibly invalid
shortcuts: just plug in n+1 everywhere that n appears. Then let's consider the absolute value of the ratio:
| 50n+1| 50n+1 | ----- | ----- | (n+1)!| (n+1)! (50n+1)n! 50(n!) 50(n!) 50 |-------| = ------- = ----------- = ------- = ------- = ---- | 50n | 50n (50n)(n+1)! (n+1)! (n+1)n! n+1 | ----- | ----- | n! | n! Step A Step B Step C Step D Step E Step FLet me try to describe sort of carefully the various steps. This is the first example, and I chose it not because it is especially difficult, but because the sequence of things to do is typical of many applications of the Ratio Test.
Step A Write |an+1/an|. I really try to
avoid "premature simplification" here. That is, I try to just insert
n+1 for n correctly, and then write things.
Step B In this case, the absolute value signs are not needed
because everything involved is a positive number. This is not always
going to be true!
Step C We have a compound fraction in Step B. I find them
difficult to understand. Life is easier if we convert the compound
fraction into a simple fraction, with one indicated division. So if
you were in class you may have heard me mumbling, "The top of the
bottom times the bottom of the bottom" which is the top of the simple
fraction, and "The bottom of the top times the top of the bottom"
which is the bottom of the simple fraction. O.k.: if you want, use
numerator and denominator instead of top and bottom.
Step D Now I'll start the simplification. Since
50n+1=50n·50, we can cancel
50n from the top and bottom.
Step E Here is possibly the most novel part, algebraically, of
this mess. We need to confront the factorials. (n+1)! is the product
of all the positive integers from n+1 down to 1. Therefore it is the
same as n+1 multiplied by the product of all the positive integers
from n down to 1. Algebraically, this statement is the equation
(n+1)!=(n+1)n!. I want to rewrite (n+1)! so that we can realize the
cancellation of the n!'s.
Step F And here is the result which can be used to compute ρ.
The Ratio Test for ∑n=0∞(50)n/n! leads us to consider limn→∞|an+1/an|=limn→∞50/(n+1)=0. So for this series, ρ=0. Since 0<1, the series converges absolutely and (using what we did last time) it converges.
I can identify the sum (and you will be able to also after a few more classes). It is e50. Partial sums of series of this type are exactly what your calculators use to compute values of the exponential function.
Another example
Let's consider
∑n=1∞n2/5n. Again,
this is not a casual example. This sort of series occurs in the study
of the statistical properties of certain types of component failures
(it is involved with computing the standard deviation). Here
an is n2/5n and
an+1=(n+1)2/5n+1. So:
| (n+1)2| (n+1)2 | ----- | ----- | 5n+1 | 5n+1 (n+1)25n (n+1)2 |-------| = ------- = --------- = ------ | n2 | n2 n25n+1 n25 | ----- | ----- | 5n | 5n
Well, again I just forget the absolute value signs because the terms are all positive. I rearrange from a compound fraction to a simple fraction. I cancel powers of 5. The result I need to consider is [(n+1)/n]2·(1/5). The core of this is what happens to (n+1)/n as n→∞. We can use L'Hôpital's Rule since this is an ∞/∞ case, and get 1/1, so the limit is 1. Or we can just rewrite, as some students suggested: (n+1)/n=1+(1/n), and this also →1 as n→∞. In any case, for the series ∑n=1∞n2/5n, we can compute limn→∞|an+1/an|= limn→∞[(n+1)/n]2·(1/5)=1/5=ρ. Since 1/5 is less than 1, the Ratio Test implies that the series converges absolutely and therefore converges.
| The sum can actually be computed and it is 15/32 (really!). I will show you how to compute this in a few more classes. |
In all of these examples the terms are quotients, and essentially we are trying to compare the rates of growth of the top and the bottom. Exponentials (with a base>1) grow faster than any polynomial. For example, we could consider the infinite series ∑n=1∞n20/(1.01)n. The 20th term in this series is about 2.6·1019. That's B-I-G. Does this series converge? Well, the Ratio Test applies. If similar algebra is done, then |an+1/an| becomes [(n+1)/n]15/1.01 and, when n→∞, the limit is ρ=1/1.01 which is less than 1, so the series converges absolutely and therefore converges! I don't think this is obvious: {con|di}vergence all depends on the infinite tail -- you can't think about the "first few" terms. Here is a little more numerical information. If an=n20/(1.01)n, then a1,000=4.7·1040 (approximately and this is even bigger) and a10,000=6.1·1016 and a100,000=7.3·10–358. The last term is quite small, and the exponential growth has definitely surpassed the polynomial growth by then.
And another
We consider
∑n=0∞72n/(n!)2. In
this series we contrast the exponential growth on top with factorial
growth on the bottom. Factorials increase faster (they are
"superexponential"). In this case, some care is needed with the
algebra using the Ratio Test. If
an=72n/(n!)2 then
an+1=72(n+1)/((n+1)!)2. Parentheses
are your friends so use many of them in computations and you likely
will make fewer errors!
| 72(n+1) | 72(n+1) | -------- | -------- | ((n+1)!)2 | ((n+1)!)2 72(n+1)(n!)2 |-----------| = ---------- = ------------ | 72n | 72n 72n((n+1)!)2 | ------- | ------- | (n!)2 | (n!)2But 72(n+1)=72n+2=72n72 and so part of that cancels with 72n. Analysis of the factorials can be more confusing, but here it is:
Again, this is not a "random" series. The sum of ∑n=0∞72n/(n!)2 is close to a value of a Bessel function, J0(14). The series for J0(14) is actually ∑n=0∞(–1)n72n/(n!)2. It has an alternating sign, also. One simple place such functions occur is in the description of vibrations of circular drums (really!). The series with alternating signs must also converge, since we just verified that the series without signs converges since absolute convergence implies convergence.
Textbook example
The textbook analyzes (Example 4, page 591, section 10.5) what the
Ratio Test tells about the series
∑n=1∞1/n and the series
∑n=1∞1/n2. Please see the
textbook (I did this in detail in class). In both cases the resulting
value of ρ is 1. Notice that one series (the harmonic series, a
p-series with p=1) diverges and the other series (a p-series with
p=2>1) converges. So truly if ρ=1 you can conclude
nothing about the convergence or divergence of the original
series.
It is certainly possible to have series where the limit of |an+1/an| doesn't even exist, so there isn't even any ρ to consider. I don't want to give such an example right now, but you should know that things can be very strange.
For which x's does ...
Here's the question. For which x's does the series
∑n=1∞xn/(3n+n)
converge?
The Ratio Test does work here, but we need to be careful. First, the bottom is more complicated. And second, certainly the signs of the terms will vary because x can be negative.
Important facts about absolute value
|A·B|=|A|·|B| but |A|+|B| and |A+B| are not the same if the signs of
A and B differ.
Look: |(–3)7|=|–21|=21 and |–3|·|7|=3·7=21 but
|(–3)+7|=|4|=4 and |–3|+|7|=3+7=10. 10 and 4 are not the same.
If an=xn/(3n+n), then |an|=|x|n/(n+3n) because the bottom is always positive (so the signs agree) and the top is an absolute value of a product of x's, so it becomes a product of absolute values of x's. And |an+1| is similarly |x|n+1/(n+1+3n+1). Now we need to analyze the quotient. I am getting exhausted with all of this typing. I'll skip the compound fraction and just write the simple fraction which results:
|x|n+1(n+3n) (n+3n) -------------- = |x|·--------- |x|n(n+1+3n+1) (n+1+3n+1)We need to analyze the behavior of the somewhat complicated quotient (n+3n)/(n+1+3n+1) as n→∞. When we're done, we need to multiply by |x| in order to get ρ.
Informal analysis Well, as n increases, the polynomial growth doesn't matter at all. It is negligible compared to the exponential growth. So really we've got (approximately) just 3n/3n+1, and this is 1/3.
Formal analysis Look at (n+3n)/(n+1+3n+1) and divide the top and bottom by 3n. The result is ([n/3n]+1)/([n/3n]+[1/3n]+[3n+1/3n]) which is ([n/3n]+1)/([n/3n]+[1/3n]+3). What about [n/3n] as n→∞? We will use L'Hôpital's Rule since this is again ∞/∞. Remember that AB=eB ln(A), so that the quotient [n/3n]=[n/en ln(3)]. The derivative of the top (with respect to n) is 1, and the derivative of the bottom with respect to n is en ln(3)ln(3) (what's in the exponent is just a constant multiplying n, so the Chain Rule works easily. Therefore by L'H, limn→∞[n/3n]= limn→∞[1/en ln(3)ln(3)]= limn→∞[1/3nln(3)]=0. So (wow!) limn→∞(n+3n)/(n+1+3n+1)=limn→∞([n/3n]+1)/([n/3n]+[1/3n]+3)=1/3.
 What about the Ratio Test limit? We need to multiply by |x| since we
discarded it to get the fraction we just studied. So in this
complicated case, ρ=|x|(1/3). We get convergence (actually
absolute convergence) when ρ<1, which means that |x|<3. The
x's which satisfy this are an interval from –3 to 3 (not including the
endpoints). We get divergence when |x|>3. So for those x's
satisfying either –∞<x<–3 or 3<x<∞ there is
divergence. The Ratio Test doesn't work if x=3 or if x=–3. It turns
out that this situation is typical, and we will look at more examples
and more detail next time.
What about the Ratio Test limit? We need to multiply by |x| since we
discarded it to get the fraction we just studied. So in this
complicated case, ρ=|x|(1/3). We get convergence (actually
absolute convergence) when ρ<1, which means that |x|<3. The
x's which satisfy this are an interval from –3 to 3 (not including the
endpoints). We get divergence when |x|>3. So for those x's
satisfying either –∞<x<–3 or 3<x<∞ there is
divergence. The Ratio Test doesn't work if x=3 or if x=–3. It turns
out that this situation is typical, and we will look at more examples
and more detail next time.
The Root Test is another result which relies on how a series resembles a geometric series. We'll discuss this next time.
What happens at the "edges"?
We saw that the Ratio Test doesn't give any information when x=3 or
x=–3. So if we really needed to know what happens, we will need more
work. Look at
∑n=1∞xn/(3n+n)
when x=3. This is
∑n=1∞3n/(3n+n). The
nth term is 3n/(3n+n) and if we
divide the top and bottom by 3n we see that the
nth term is 1/(1+[n/3n]). But we saw that as
n→∞, n/3n→0 so that
an→1. Any series which converges must have its
nth term go to 0. Since this one doesn't, the series must
diverges when x=3. Similarly, if you insert the value –3 for x in the
series, you'll see that the terms do not→0, so the series must
also diverge when x=3.
Return of the second exam
I returned the second exam. Information about grading and statistics
concerning the results are here.
Was the exam too long? Were the last two problems (parametric curves, polar coords) too novel? I am sorry. As I mentioned in class, I will try to be sure that students are not "penalized" for being in the H section. Therefore the final exam results will be used to calibrate or measure or compare performance of the H section with the overall 152 group's work, and I will adjust (I hope favorably!) course grades appropriately. I mean that the group achievement will be considered, so it is in the interest of individual members of the class that the whole class do as well as possible!
I also distributed a last workshop. So, for the last time: Please hand in N problem solutions written by teams of N students, where 1≤N≤3.
| Wednesday, November 18 | (Lecture #21) |
|---|
| Monday, November 16 | (Lecture #20) |
|---|
And now, where and what?
So we discussed series with positive (actually all we needed was
non-negative) terms. The textbook has clean and coherent
statements of the results: the dichotomy, the Comparison Test,
the Limit Comparison Test, and the Integral Test.
The technical meanings of
these terms have been discussed: infinite series; sequence of partial
sums; infinite tails; convergence of an infinite series.
I will repeat the fundamental dichotomy, one of this week's
notable vocabulary words. (And dichotomy means, briefly, "a
division into two, esp. a sharply defined one." As I mentioned in
class, this will be very valuable to you when you repeat your whole
life and must take SAT's again.).
Series with terms of varying signs
So now we will complicate things a bit, and look at series whose signs
vary. Let me start really easily but things will get more intricate
rapidly.
( Varying
stop
signs) (These are varying
signs, hah hah hah.)
1–1+1–1+1–...
This is just about the simplest example I could show. We got a formula
for the nth term. We need the sign to alternate, and that
will be given by (–1)something here. The sign will
alternate if the "something here" is either n or n+1. The first
term will be +1 and the second term will be –1 if we use n+1. So an
explicit formula is an=(–1)n+1. Next I asked
about convergences of the series
∑n=1∞(–1)n+1. For this
we must consider the sequence of partial sums.
S1=1; S2=1–1=0;
S3=1–1+1=1; S4=0, etc.
It isn't too difficult to see that Seven integer=0 and
Sodd integer=1. The partial sums flip back and
forth. This is exactly the kind of behavior we did not get when
we considered series with all positive terms. There the partial sums
just traveled "up", to the right. Well, this particular infinite
series does not converge, since the partial sums do not
approach a unique limit.
∑n=1∞(–1)n+1 diverges
even though the sequence of partial sums is bounded.
2–(1{1/2})+(1{1/3})–(1{1/4})-(1{1/5})+...
This is a more complicated series. I suggested that we try to "guess"
a formula by first getting a formula for the sign, and then a formula
for the absolute value (the direction and magnitude, thinking about
numbers as sort of one-dimensional vectors). In this case, the sign is
surely given by (–1)n+1, just as before. The magnitude
or absolute value is
1+{1/n}. The formula {n+1}/n was also suggested, another a good
answer. So putting these together,
an=(–1)n(1+{1/n}). And now we looked at the
{con|di}vergence of ∑n=1∞(–1)n+1(1+{1/n}).
The partial sums are more complicated and more interesting.
S1=2; S2=2–(1{1/2})–{1/2}=.5; S3=2–(1{1/2})+{1{1/3})=11/6=1.8333; S4=2–(1{1/2})+(1{1/3})–(1{1/4})={7/12}=.58333This is where I stopped in class, but, golly, I have a friend who could compute S17 either exactly ({4218925/2450448}) or approximately (1.72169). This is nearly silly. Richard Hamming, one of the twentieth century's greatest applied mathematicians, remarked that
From S1 to S2, we move left since the
second term in the series is negative. From S2 to
S3 we move right, because the third term in the series is
positive. But notice that we don't get to S1. because the
jump right has magnitude 1{1/3} and this is less than 1{1/2}, the
magnitude of the previous jump left.
I hope you are willing to believe that what's described persists in general.
Does this series converge? Students had varied opinions about this,
but the question was definitively settled by the observations of
several clever students. The distance between any odd partial sum and
any even partial sum will be at least 1, since the magnitude of the
nth term is 1{1/n}, which is certainly >1. The
successive partial sums can't get close to each other! But the
collection of partial sums does not approach a unique limit.
∑n=1∞(–1)n+1(1+{1/n})
diverges.
1–1/2+1/3–1/4+1/5–...
Here an has sign (–1)n+1 again, and the absolute
value or magnitude is 1/n. Does ∑n=1∞(–1)n+1(1/n) converge?
The partial sums are more complicated and more interesting.
s1=1; s2=1–(1/2)–1/2=.5; s3=1–(1/2)+{1/3)=5/6=.8333; s4=1–(1/2)+(1/3)–(1/4)=7/12=.58333Here's a picture of these partial sums. Things are a bit more crowded (that's good for convergence!) than in the previous picture.
The previous three qualitative properties still hold. Since the signs
alternate, the partial sums wiggle left and right. Since the absolute
values decrease, the odd sums are less than the even sums, and all of
the even sums are less than all of the odd sums. But now the distance
between the odd and even sums→0 since the magnitude of the terms is
1/n, and this→0. So here is a rather subtle phenomenon:
∑n=1∞(–1)n+1(1/n) converges.
The theorem on alternating series (Alternating Series Test)
The following is a major result of section 10.4 of the text, where it
is called the Leibniz Test for Alternating Series.
Hypotheses Suppose thatThis is a cute result and useful to analyze some special series. The most famous example is the alternating harmonic series, ∑j=1∞(–1)n+1(1/n), which we just saw. There are other examples in the textbook.The terms of a series alternate in sign (+ to – to + etc.). The absolute value or magnitude of the terms decreases. The limit of the absolute values of these terms is 0.
Conclusion The series converges.
The sum of the alternating harmonic series is ln(2). But the convergence is actually incredibly slow. The one millionth partial sum (which took almost 8 seconds for a moderately fast PC to compute) only has 5 accurate decimal digits. This is not the best and fastest way to compute things -- we will see much faster methods. |
But what if ...
The sign distribution
of terms in an infinite series could be more
complicated. I suggested that we consider something like
7cos(36n7–2n2)+2sin(55n+88)
∑n=1∞ ---------------------------
2n
Here the sign distribution of the top of the fraction defining
an is quite complicated. These are the first 20 signs:Does this series converge?
Please notice that with a few modifications, the corresponding question can be answered very easily. Look at:
7|cos(36n7–2n2)|+2|sin(55n+88)|
∑n=1∞ --------------------------------
2n
Absolute values signs have been put around the cosine and sine
functions. Now the series has all non-negative terms and we can use
our comparison ideas. How big is the top? Since the values of both
sine and cosince are in [–1,1], the top can't be any bigger than
9. The bottom is 2n. Therefore each term of this series is
at most 9/2n. But this larger series is a geometric series
with ratio 1/2<1 and so it must converge.
Proof via manipulative
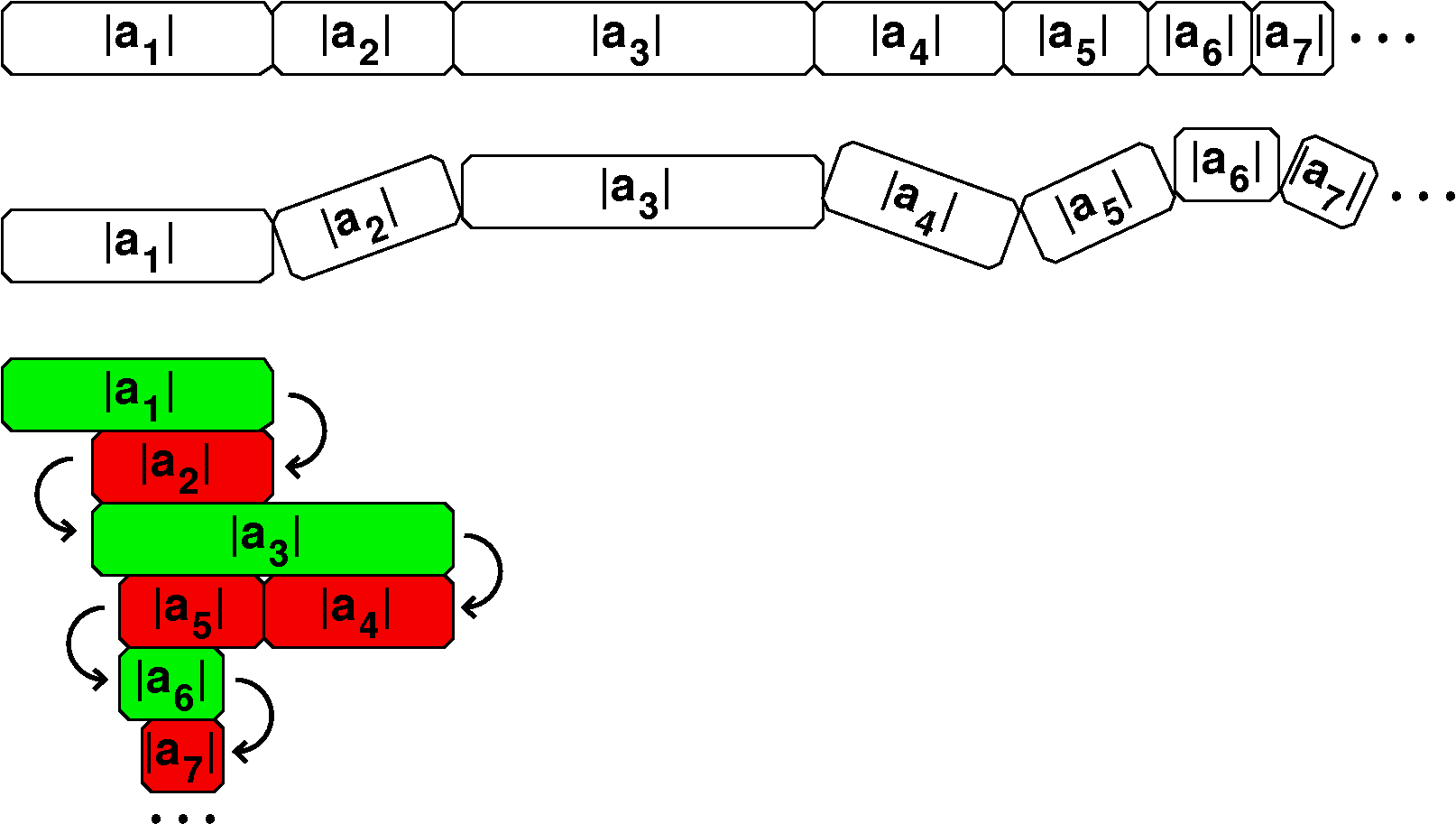 One definition of manipulative (as a noun) is: "In teaching or
learning arithmetic: a physical object which may be manipulated to
help demonstrate a concept or practise an operation."
There was a spectacular demonstration in
class! It was inspired by thinking about old-fashioned folding
carpenter's rulers. If we have an infinite series ∑n=1∞an, we could
consider the associated series ∑n=1∞|an|,
where we have stripped off the signs of the terms, and are just
adding up the magnitudes. This is sort of like an unfolded carpenter's
rule, stretched out as long as possible. It may happen that the series
of absolute values, a series of positive terms, may converge. So when
"the ruler" is stretched out as long as possible, it has finite
length. Well, if we then fold up the ruler, so some segments point
left (negative) and some point right (positive) then the resulting
length will also be finite.
One definition of manipulative (as a noun) is: "In teaching or
learning arithmetic: a physical object which may be manipulated to
help demonstrate a concept or practise an operation."
There was a spectacular demonstration in
class! It was inspired by thinking about old-fashioned folding
carpenter's rulers. If we have an infinite series ∑n=1∞an, we could
consider the associated series ∑n=1∞|an|,
where we have stripped off the signs of the terms, and are just
adding up the magnitudes. This is sort of like an unfolded carpenter's
rule, stretched out as long as possible. It may happen that the series
of absolute values, a series of positive terms, may converge. So when
"the ruler" is stretched out as long as possible, it has finite
length. Well, if we then fold up the ruler, so some segments point
left (negative) and some point right (positive) then the resulting
length will also be finite.
The picture here is an attempt to support this statement and to duplicate the physical effect of what I displayed in class. The top has the segments stretched out as far as possible. The next picture shows some of the segments rotating, aimed backwards (negatively). The last segment shows in red segments which are negative and in green the other segments, oriented postively. I hope this makes sense, and justifies the following:
The "folded" series compared to the "unfolded"
series
If ∑n=1∞|an|
converges, then ∑n=1∞an must converge
also (and, actually, |∑n=1∞an|≤∑n=1∞|an|).
Proof via algebra
There is a verification of these statements in the textbook, using
algebra, on p.584, Theorem 1, in section 10.4, if you would like to
read it. Sigh.
And conversely?
Notice that the converse of
the assertion about absolute values and series may not be
correct. That is, a series may converge, and the series of absolute
values of its terms may not. The simplest example, already verified,
used the alternating harmonic series, covergent, and the harmonic
series, divergent.
Vocabulary
A series ∑n=1∞an which has ∑n=1∞|an|
converging is called absolutely convergent. Then the correct
implication above is:
If a series is absolutely convergent, then it is a convergent series.A series for which ∑n=1∞an converges and ∑n=1∞|an| diverges is called conditionally convergent. The alternating harmonic series is conditionally convergent.
Another example
Consider ∑n=1∞{sin(5n+8)}37/n5. I
don't know very much about {sin(5n+8)}37 except that, for
any n, this is a number inside the interval [–1,1]. Therefore ∑n=1∞|{sin(5n+8)}37/n5| has terms which are all smaller than ∑n=1∞1/n5 (a p-series
with p=5>1, so it must converge). The comparison test asserts that
∑n=1∞|(sin(5n+8)37/n5| converges, and therefore ∑n=1∞{sin(5n+8)}37/n5
itself must be a convergent series.
|
How to use these ideas quantitatively What is I actually wanted to find ∑n=1∞{sin(5n+8)}37/n5, say to an accuracy of +/-.00001? Well, I could split this series up into SN+TN, a partial sum plus an infinite tail, and try to select N so that |TN|<.00001. Once I do that, well then I just (have a computer) compute the corresponding SN. So how can I get N with |TN|<.00001? Here is a way. I know that TN=∑n=N+1∞{sin(5n+8)}37/n5. This is an infinite series. I bet (using the result of a preceding paragraph that |TN|=|∑n=N+1∞{sin(5n+8)}37/n5|≤∑n=N+1∞1/n5 again since the biggest that sine can be absolute value is 1, and 137=1. We looked at an integral comparison technique for this series in the last lecture. There we learned that this infinite series was less than ∫x=N&infin[1/x5]dx and we can evaluate the improper integral. It is (see the link for computations!) exactly 1/[4N4]. If we want this to be less than .00001=1/105 I guess we could take N to be 13 (I cheated -- I used a computer). Then the value of the sum, to 5 decimal place accuracy, is S13=∑n=113{sin(5n+8)}37/n5 which is .00317. Maybe this specific example isn't too impressive, but the whole thing really does work in a large number of cases! |
Given a series, take absolute values
The result just stated is a very powerful and easily used method. If
you "give" me a series with random signs, the first thing I will do is
strip off or discard the signs and try to decide if the series of
positive (non-negative, really) terms converges. For example, I
mentioned rapidly and casually that
∑n=1∞{sin(nx)}/n2 converged
absolutely for all x's, and therefore converged for all x's O (no
matter what the signs of the sines are) since |sin(nx)|≤1 always,
and the denominators make up a p-series for p=2>1. This series does
come up in practice, and the logic just used is used very commonly
when considering Fourier series.
Maintained by greenfie@math.rutgers.edu and last modified 11/16/2009.