Thursday, July 6
Homework problems
Ms. Atkins kindly put her correct solutions of the two homework
problems on the board. These are the problems:
Compute the derivatives of the following functions, using only the definition of derivative:For example, I think her solution of problem 6 went like this:
6. g(t)=1/(t2+1)
8. p(t)=sqrt(4t-2).
1 1
------ - ---
(t+h)2 t2
----------------
h
t2-(t+h)2 t2-(t2+2th+h2)
---------- -----------------
(t+h)2t2 (t+h)2t2
-------------- = ---------------------
h h
This whole business is very vulnerable to errors. The fractions on top
must be combined, then the (t+h)2 "expanded", and don't
lose the darn minus sign! Here you have to hope that the subject makes
sense -- you need faith that the computation will come to a good end.
t2-(t2+2th+h2) -2th+h2
-------------- ----------
(t+h)2t2 (t+h)2t2 -2th+h2
--------------- = -------------- = ----------------
h h h((t+h)2t2)
One of my favorite movies ("Shakespeare in Love") has the following
line: "Strangely enough , it all turns out well." Here, too, it all
turns out well. The darn h's cancel. (If they didn't cancel, there
would be, for most purposes, no calculus!)
-2t+h ---------- (t+h)2t2
Algebra, ugly; pictures, pretty
Well, the title above represents my own "esthetic" but like much
opinion, it can be overdone. I wrote it in response to the crawly
scrawl which covered the board solving the two homework problems. But
in thinking about the homework, I decided that you should have a
chance to work with some pictures and maybe learn from them. So I
prepared this handout.
Patterns of thought
I asked students to sketch y=f´(x) on page 1 of the handout, and
then to sketch y=g(x) on page 2 of the handout. I emphasized that I
was interested in the qualitative behavior of the sketches, and the
absence of numerical indications on the axes showed that I wasn't
giving very definite information, only "relative" information. In
particular, I don't think that either request had any particular single
sketch as a correct answer.
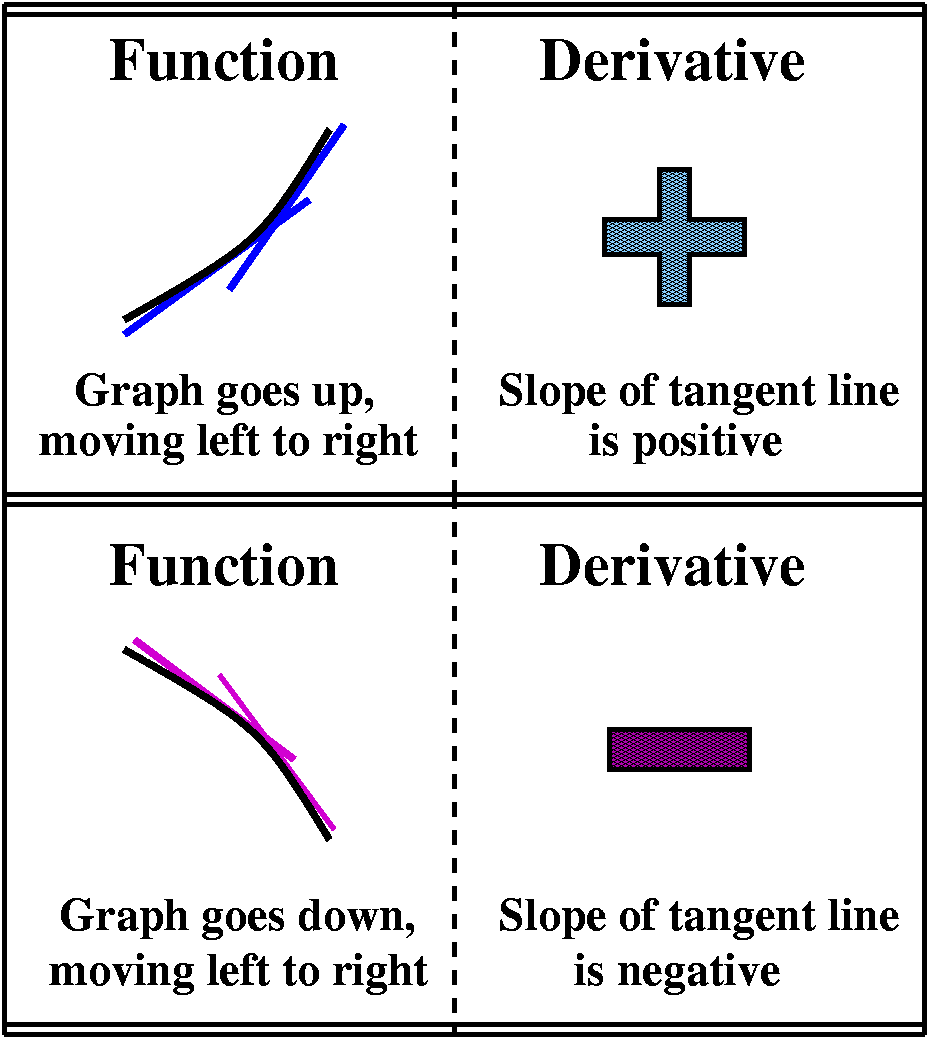
| Here are the ideas I wanted to discuss when we considered the handout: first, that when the graph of a function goes up (y-values increasing) as we consider "movement" along the graph from left to right (the x-values are increasing), then the slope of tangent lines will be tilted up also: that is, the slopes will be positive. Since one interpretation of the value of the derivative is the slope of the tangent line, I would expect that a "going up" function would have a positive derivative, and a "going down" function would have a negative derivative. |
 |
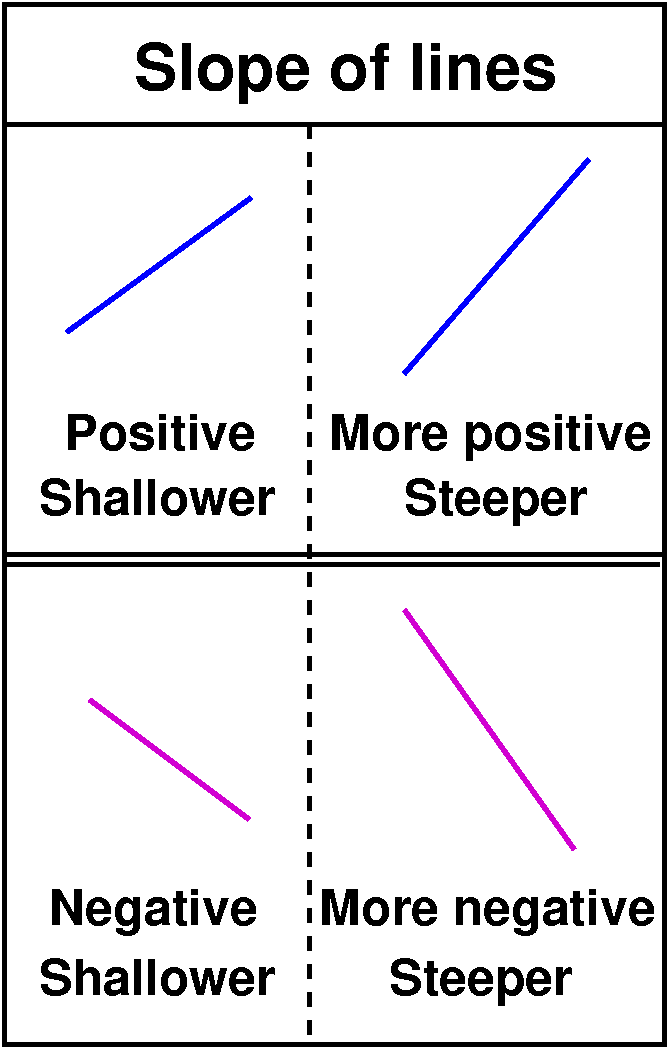
| We did run into some linguistic problems in our discussion. We needed to talk about lines whose slope was bigger/smaller than other lines. In our discussion, we sometimes confused magnitude with order. So maybe some people might think that -7 and 16 were "larger" than -3 or 5. Other people might state something the other way. But, in fact, -7<-3 and -3<3 and 5<16. This is not "too obvious" because language can be imprecise. Steeper lines have greater magnitude (that is what's left after taking the sign away!). "Shallower" lines have smaller magnitude. So -7 is steeper than -3, but -3>-7: -3 is greater than -7. This can be confusing, so be alert! | 
|
Getting a graph of f´(x) from a graph of f(x)
| So here's the initial graph of y=f(x). Let me describe one approach to getting a graph of the derivative. This is certainly not the only approach -- one of the reasons I tried the handout was so that people would get their own ways of describing and understanding what's going on. |
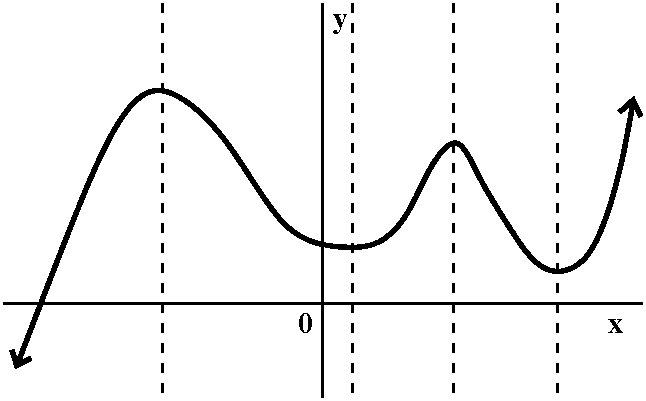 |
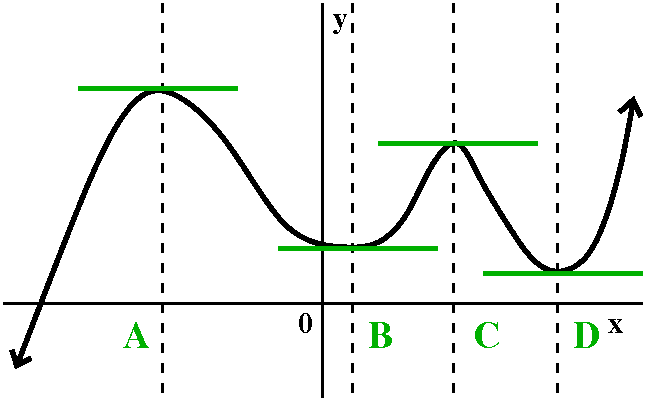
| I think I would first find where the tangent lines are horizontal. In this case, the bumps up and down (we will call them local or relative maxima and minima in more pedantic language) provide points on the graph where the tangent lines are horizontal. Just by accident (nah!) these happen to be where the vertical lines are. The vertical lines go down to the empty axes where we're supposed to draw the graph of y=f´(x). For those values of x, I know that f´(x)=0. So the derivative of f(x) has x-intercepts for those values of x. In order to be able to discuss the graphs more easily, I labeled the four values of x: A, B, C, and D, in increasing order. |
 |
|
Now let me concentrate on just two "chunks" of the graph of f(x), one
chunk between x=B and x=C, and one chunk between x=C and x=D. The
"logic" is sort of the same, just with signs flipped. Let me try.
At x=B the tangent line is horizontal. For x's a bit to the right of
x=B. the tangent line has positive slope. Move x more to the right,
and the slope tilts "up": the line gets steeper. So the slope, a
positive number, gets bigger. But as x gets closer to x=C, another
value of x where the tangent line is horizontal, the slope
decreases. It is still positive, but it gets less steep, and becomes
more shallow. Finally the slope returns to 0 at x=C.
The description of the slope transition on the interval from x=C to
x=D is similar, only with a sign change. So near and to the left of
x=C, the sign of the slope of the tangent line is negative. As x
travels more right, the tangent line gets steeper. The magnitude of
the slope gets bigger, and the slope itself gets more negative. I am
trying to be careful with language here. Even farther to the right, as
we get closer to x=D, the tangent line begins to flatten out (?). The
slope is still negative, but it is small in magnitude and
negative. Finally, the slope comes back to 0 at x=D. |
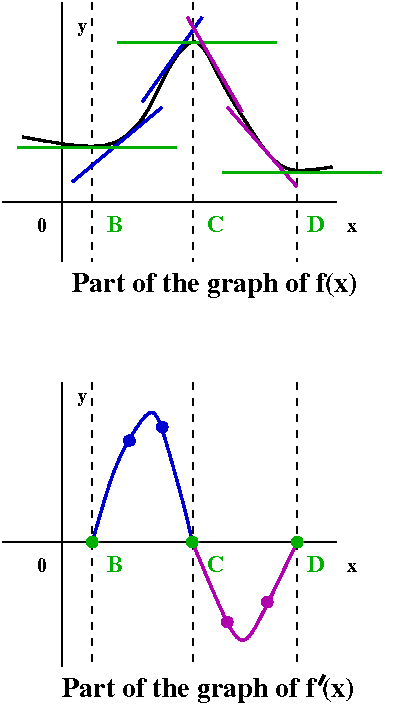 |
|
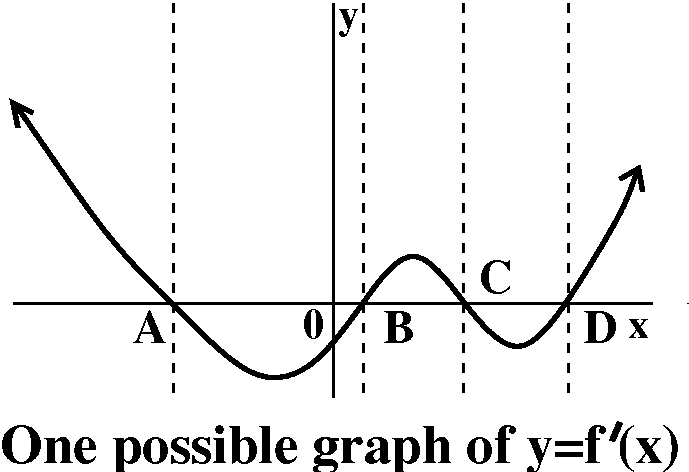
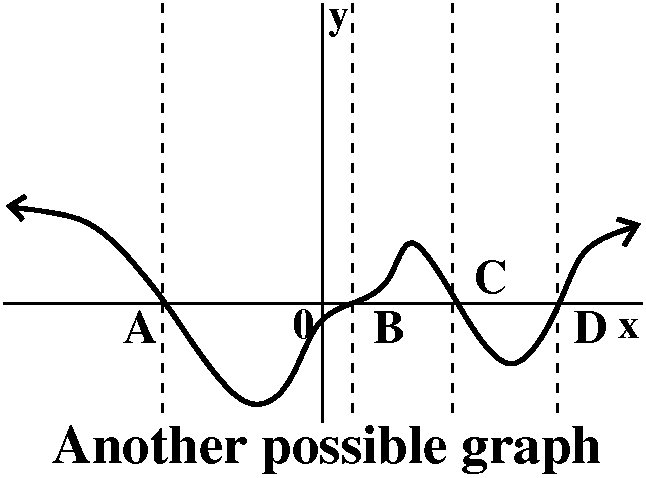
The top graph to the right is the graph of f(x). The graph in the middle is a simple "realization" of the graph of f´(x). It has the correct positive and negative portions separating the places where it should be 0. The graph on the bottom is another possible picture of y=f´(x). It has some details noted by Mr. Wientraub. In particular to the right of x=A he noted that the graph of y=f(x) seems to be almost like a straight line. Therefore the graph of the derivative should, as x goes to the left, become almost constant. It should still be positive, because f(x) is still increasing, going up, but the rate of increase, the slope of the tangent line, is just about the same. He observed something similar about the derivative to the right of x=D. The graph of y=f(x) seems to get straighter, almost like a line, so that the derivative again should get more like a constant. Again, the derivative in this region (x>D) is still positive, but the derivative may be sort of constant. (Huh? "sort of"?) Also notice please that maybe something is happening around x=B. The graph of y=f(x) certainly has a horizontal tangent at x=B, but to the left and to the right the slope is horizontalish (not a word to be tried in a Scrabble game!). If we wanted to be fanatical about drawing the derivative maybe I might try to indicate this by flattening the graph of f´(x) near x=B more than at other x-intercepts of the derivative. All this is certainly finer structure than I would expect of a first attempt at drawing the derivative and I congratulate him for his observations. | 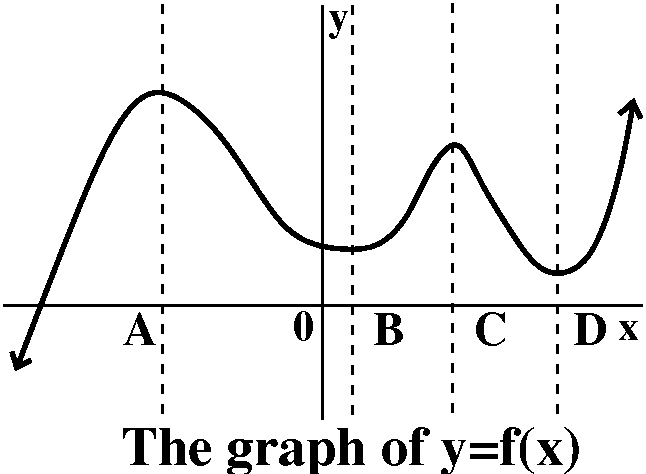 |
 | |
 | |
Getting a graph of g(x) from a graph of g´(x)
|
Page 2 of the handout had a related question. A graph of a derivative
was given. It was labeled a graph of y=g´(x). That is what's shown
here. What was requested was a graph of the original function. In
addition, a large, fat point was given, with the information that the
graph of g(x) should pass through this point. To the right is the graph. I've labeled the x-intercepts of y=g´(x) with A and B and C and D. (Darn it, I know that there won't always be four such points, but in the two examples considered in class, there were.) Also, I labeled the "other" possibly interesting x value (which connected with the fat point) with x0. I'll ignore x0 temporarily. | 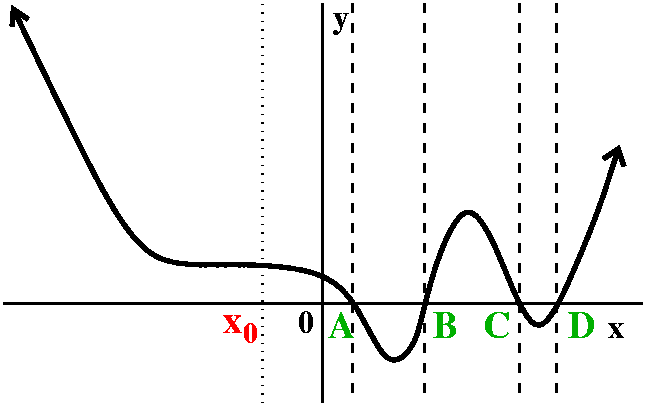 | ||
| |||
|
What I've just described is a major difference from the
previous analysis of the transition from the graph of y=f(x) to the
graph of y=f´(x). Here, going "backwards" from g´(x) to g(x),
the information given only permits us to make a relative placement of
the points on the graph of y=g(x). So from x=B to x=C the graph should
go "up". But there is not enough information in the graph of
y=g´(x) to tell me where it should go up "from"!
On the algebraic side, this is reflected in the fact that all horizontal lines have slope 0. Therefore the lines y=234 and y=-117 both have slope 0. So the functions whose graphs are those lines (say, h(x)=234 and k(x)=117) are both functions so that h´(x)=0 for all x and k´(x)=0 for all x. If you just give me the derivative, you can't tell me where the graph of the function is.
One mathematical model
Another mathematical model I agree that this is partly linguistic and partly logical, but such precision really might be necessary. Especially if you are thinking of buying the business ... heh, heh, heh. | |||
| Back to the graphs Well, the purpose of the fat point should be clearer now. At x0, the graph goes through the fat point. Now let me try to "draw" a possible graph of y=g(x) consistent with the fat point (sigh: o.k., the mathematic term is "initial value"). I'll start at x0 and move right first.
Moving right from x0
Moving left from x0 | 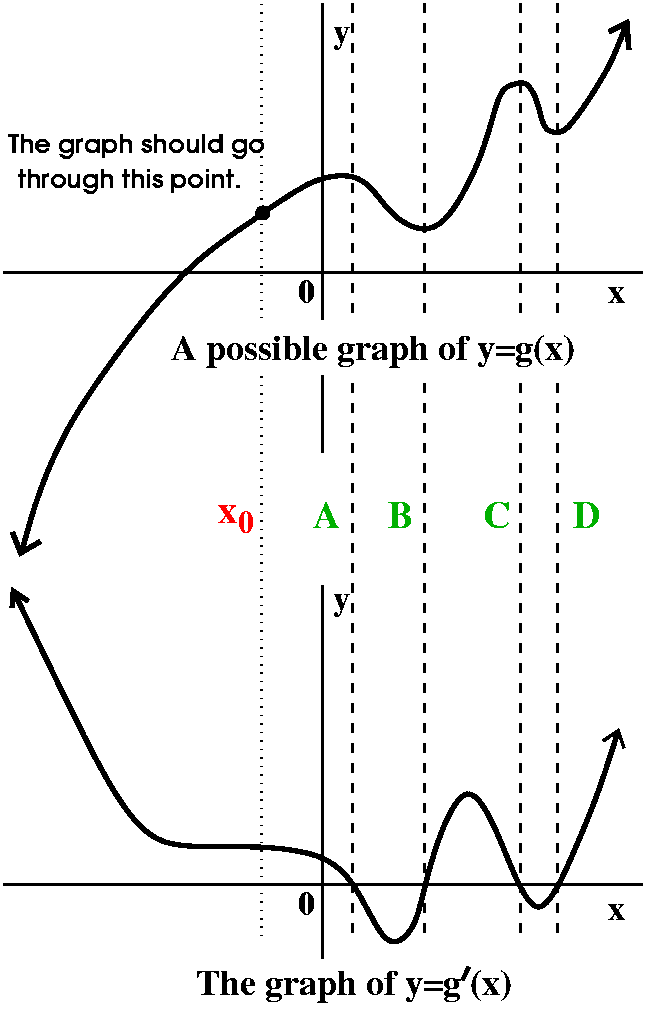 | ||
| I'd like to emphasize again that these graphs are only qualitative. I have not inserted any numbers or reasoned using anything except where numbers are zero or positive or negative. This means that there could be many answers to the question -- many different valid sketches of y=g(x). In particular, Ms. Smookler asked the following prescient (prescience means "foreknowledge of events") question: look at the interval between x=A and x=C. The graph of y=g(x) dips down and then up. How do we know (or not know!) that the bump in y=g(x) is above (below?) the x-axis? I remarked that we really don't know. All that we can deduce is the correctness of the relative positions of the heights on the graph of y=g(x). I have no good, reliable feeling about exactly where or how high any specific point on the graph is. Later in the course, I hope to show you how to get such information, but we'll need to develop a bit more "technique" than we have now. | |||

The derivative of sine is cosine.
In a calculus textbook, something like the following is done when f(x)=sin(x):
sin(x+h)-sin(x) sin(x)cos(h)+sin(h)cos(x)-sin(x)
----------------- = ---------------------------------- = PIECE #1 + PIECE #2
h h
where
sin(h)
PIECE #1 = cos(x) --------
h
and as h-->0 this --> cos(x)·1 because we arranged it this
way when we decided to use radian measure! Also,
cos(h)-1
PIECE #2 = sin(x) ----------
h
If we multiply this top and bottom by cos(h)+1, the result on top is
[cos(h)]2-1 which is [sin(h)]2. Then
[sin(h)]2 sin(h) 1
PIECE #2 = sin(x) ------------- = sin(x) -------- sin(h) ------------
h [cos(h)+1] h [cos(h)+1]
Now as h-->0, I claim:
sin(h) 1
sin(x)-->sin(x); ------ -->1; sin(h)-->0; ----------- --> 1/2.
Nothing happens! h [cos(h)+1]
So the result is sin(x)·1·0·1/2=0.
Cosine You can play the same game with cosine as with sine. Here is an impression of what the picture of the derivative of cosine might look like:

If you look closely at the picture, there is a loose minus sign around. This we can't get rid of: I'm sorry.
The derivative of cosine is -sine.
Some practice
If f(x)=-7x3+23sin(x)+56, then
f´(x)=(-7)3x2+23cos(x)+0. And
if f(x)=88x2-2x+Pi*cos(x)-56, then
f´(x)=(88)2x1-2+Pi*{-sin(x)}+0.
Building a table of Func's and Func´'s
So we have some ways of computing derivatives of functions which are
defined by formulas:
| Function | Derivative |
|---|---|
| xn | nxn-1 |
| sin(x) | cos(x) |
| cos(x) | -sin(x) |
| Constant | 0 |
| c f(x) if c is a constant | c f´(x) |
| f(x)+g(x) | f´(x)+g´(x) |
Valery and Fred: how they grow
 Here are two mythical adolescents. I tell you the following
"facts" (this means, "Please make the following assumptions."):
Here are two mythical adolescents. I tell you the following
"facts" (this means, "Please make the following assumptions."):
Valery is 14 years old, 60 inches tall, and grows
1/2 inch per year.
Fred is 16 years old, 66 inches tall, and grows 1
inch per year.
![]() Valery stands on top of Fred
Valery stands on top of Fred
Suppose Valery stands on top of Fred. The assembled object seems to be
60+66=126 inches tall. How much does it grow in a year? I think it
grows (1/2)+1=3/2 inches a year.
Valery and Fred lay decorously on the lawn
Huh: one definition of decorous begins with the phrase
characterized by propriety and dignity and good taste in manners
and conduct
so you should keep your impure thoughts
buried. Anyway, they decide to recline on a lawn. Their feet are in
contact and they are perpendicular to each other. Together they form
two sides of a rectangle. What is the area of the rectangle?
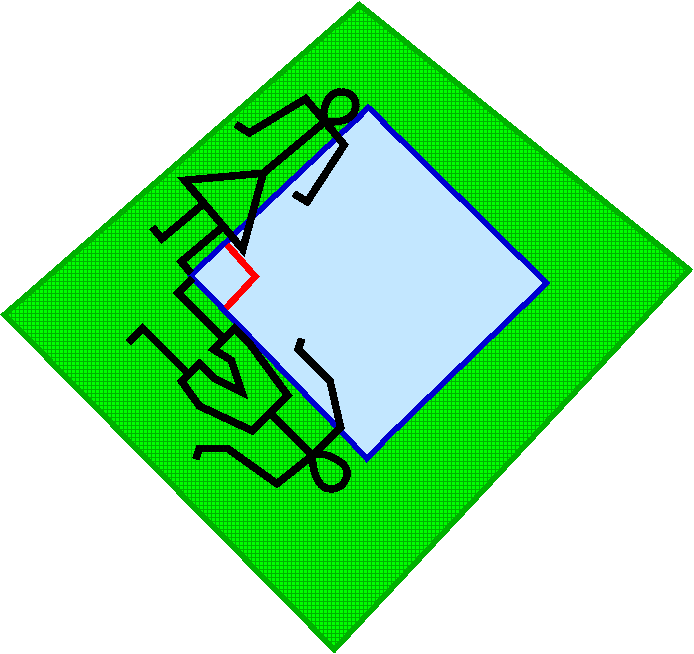
Well, Arearect is the product of the heights of the two people. So Arearect is 60·66=3,960 square inches (in2, I guess). How much is the area in a year? (These are extremely patient, persistent people, who will do anything to help the progress of mathematics.) Well, let's look at the heights and the product of the heights: (60+{1/2})·(66+1)=60·66+(1/2)(66)+(60)(1)+{1/2}(1). I don't want to "simplify" because in this case any messing around with the numbers might disturb the structure in the answer. How much does the area change in a year? That's certainly 60·66+(1/2)(66)+(60)(1)+{1/2}(1)-60·66=(1/2)(66)+(60)(1)+{1/2}(1). The area change is related to the change of the factors in a complicated way.
I can follow the suggestion of Ms. Smookler and look at the grow rate of the area. Suppose we assume that Valery and Fred grow steadily. Of course this is not correct in any "real" situation but, heck, this whole story is totally silly. Well, if h represents that amount of a year which has occurred, then Valery is 60+{1/2}h inches tall and Fred is 66+1h inches tall. The area increase at time h is 60·66+(1/2)h(66)+(60)(1h)+{1/2}h(1)h-60·66=(1/2)h(66)+(60)(1)h+{1/2}(1)h2. The average rate of increase of the area over the time period, h, is [(1/2)h(66)+(60)(1)h+{1/2}(1)h2]h=(1/2)(66)+(60)(1)+{1/2}(1)h. Of course if we wanted the totally mythical instantaneous rate of increase of the area (with units of in2 per year), we'd let h-->0. The result would be (1/2)(66)+(60)(1). I hope that this discussion is a sufficient justification of the following result.
The Product Rule
| Function | Derivative |
|---|---|
| f(x)·g(x) | f´(x)·g(x)+f(x)·g´(x) |
Some examples
The derivative of
(5x7-19x3+44)(-8x4+23x2+8x)
is
({5}7x6+{-19}3x2+0)(-8x4+23x2+8x)+(5x7-19x3+44)({-8}4x3+{23}2x1+8x0).
Here the template for the product rule has the following
entries:
f(x)=5x7-19x3+44
g(x)=-8x4+23x2+8x
Another one:
The derivative of
(44sin(x)-66x8)
(x100+23cos(x)) is
(44cos(x)+{-66}8x7)(x100+23cos(x))+(44sin(x)-66x8)(100x99+23{-sin(x)}).
Here the functions in the product rule are:
f(x)=44sin(x)-66x8
g(x)=x100+23cos(x)
A homework problem again
I then did something tricky which I probably should not have done. I
looked at a problem that Ms. Atkins had
put on the board earlier.
So let's consider g(t)=1/(t2+1). Then
(t2+1)g(t)=1. If I differentiate this equation, the
right-hand side has derivative equal to 0 and the left-hand side's
derivative can be gotten with the product rule:
(2t)g(t)+(t2+1)g´(t)=0.
Now I rewrite:
(t2+1)g´(t)=-(2t)g(t).
And solve:
g´(t)=-[(2t)g(t)]/(t2+1).
Sigh. If you plug in the original definition of g(t), you'll get
g´(t)=-(2t)/(t2+1)2.
This was the solution gotten with lots of algebra earlier. In fact,
there's a better way to do this.
The Quotient Rule
| Function | Derivative |
|---|---|
| f(x)/g(x) | [f´(x)·g(x)-f(x)·g´(x)]/(g(x))2 |
Example
x
Suppose we need to compute the derivative of the function defined by
the formula
4x7-5sin(x) -------------- 6x3-19cos(x)Here the top, f(x), is given by f(x)=4x7-5sin(x) and the bottom, g(x), in the Quotient Rule, is given by g(x)=6x3-19cos(x). The derivative is then:
[(4)7x6-5cos(x)][ 6x3-19cos(x)]-[4x7-5sin(x)][(6)3x2+(-19){-sin(x)}]
------------------------------------------------------------------------
[6x3-19cos(x)]2And, yeah, even if you're "in the business", this is all fairly ludicrous. In its
favor, though, is that fact that the formulas are specific and
the process is "straightforward".
Example
I'll do one last random no example. If
F(x)=sin(x)/cos(x). In the template for the Quotient Rule, the top,
f(x), is f(x)=sin(x), and the bottom, g(x), is g(x)=cos(x).
Then the Quotient Rule reports that the answer is:
cos(x)cos(x)-[sin(x)][-sin(x)]
------------------------------
[cos(x)]2
The quotient, F(x), occurs often enough in practice (it is tan(x),
notice!) that the result is usually simplified. The top is
cos2+sin2, and that's 1. Another entry in the
table of derivatives is the result:
| Function | Derivative |
|---|---|
| tan(x) | 1/{cos(x)}2 or {sec(x)}2 |
Wednesday, July 5
A function f(x) is continuous at w if limx-->wf(x) exists
and is equal to f(w). So the limit exists, and we can evaluate the
limit by "plugging in". This is a very nice situation. If we're told
that a function is continuous, then we don't need to do any (possibly
tricky) algebraic manipulation and things like sin(h)/h won't
occur. We just "plug in" (we decided that "substitute" is the polite
word).
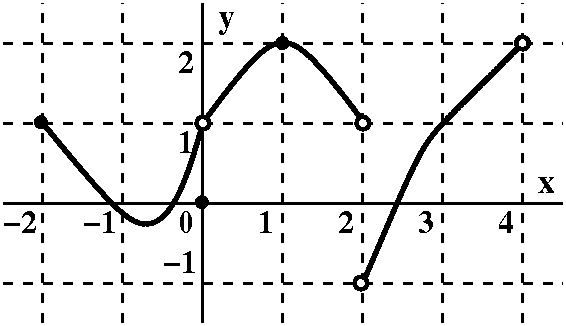 To the right is a graph which accompanied review problem 7. The
"standard" notation is used with an empty circle and a full circle. On
Monday I tried to illustrate the definition of continuous by looking
at the behavior near and at various points on this graph.
To the right is a graph which accompanied review problem 7. The
"standard" notation is used with an empty circle and a full circle. On
Monday I tried to illustrate the definition of continuous by looking
at the behavior near and at various points on this graph.
The most interesting consequence of continuity is a result called the Intermediate Value Theorem. I introduced this result with a call on my friend Francine.
The Garden State Parkway, from Cape May to Montvale
and my friend Francine ...
 The
Garden State Parkway runs most of the length of New Jersey. Mile
0 is at Cape May, while the other end, mile 172, seems to be close to
Montvale. Suppose that my friend Francine leaves Cape May at 7 AM one
morning, and drives north on the Garden State Parkway. Further,
suppose she arrives at mile 172, the northern end, at, say, 10
AM. Must Francine at some time be at mile 135 (fairly near Busch
campus)? The parkway seal here was "borrowed" from a State of New
Jersey webpage.
The
Garden State Parkway runs most of the length of New Jersey. Mile
0 is at Cape May, while the other end, mile 172, seems to be close to
Montvale. Suppose that my friend Francine leaves Cape May at 7 AM one
morning, and drives north on the Garden State Parkway. Further,
suppose she arrives at mile 172, the northern end, at, say, 10
AM. Must Francine at some time be at mile 135 (fairly near Busch
campus)? The parkway seal here was "borrowed" from a State of New
Jersey webpage.
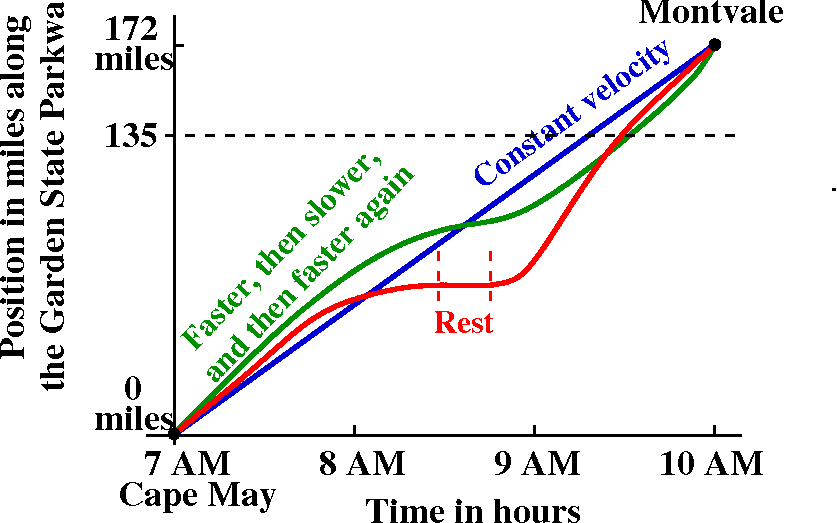 We discussed various curves which could represent the position of
Francine on the parkway in terms of miles from the start of the
parkway at time t, in terms of hours elapsed from 7 AM. I tried to
show that our everyday intuition lead to the graph being
increasing (as you travel from left to right, the points on
the graph go up). The graph can have level spots, where Francine pulls
over for a rest stop. Legally Francine isn't supposed to drive
backwards, though.
We discussed various curves which could represent the position of
Francine on the parkway in terms of miles from the start of the
parkway at time t, in terms of hours elapsed from 7 AM. I tried to
show that our everyday intuition lead to the graph being
increasing (as you travel from left to right, the points on
the graph go up). The graph can have level spots, where Francine pulls
over for a rest stop. Legally Francine isn't supposed to drive
backwards, though.
If we believe that motion is continuous (so Francine does not have a Star Trek transporter or other device) then the graph of Francine's position goes from (7 AM, 0 miles) to (10 AM, 172 miles) and therefore the graph must have on it at least one point with coordinate description (*,135). All of this, by the way, rests on some complicated assumptions, some of them philosophical (why should motion be continuous?). Today, though, I believe that motion is continuous, and therefore at sometime Francine must be at Mile 135. By the way, I will retain this information for later, when we analyze the rate of change of position (velocity) so that we can see whether Francine deserves a speeding ticket.
The Intermediate Value Theorem
Suppose that the function f is
defined and continuous on the interval [a,b]. Then the equation f(x)=y
has at least one solution for every y which is between f(a) and f(b).
One application is root finding. If we were desperate to compute sqrt(2) (that is, really, desperate to approximate sqrt(2)), for example, we could look at f(x)=x2-2 on the interval [0,2]. This f(x) is certainly continuous. (We already observed that we could "plug in" values to evaluate limits for polynomials. I know that f(0)=-2<0 and f(2)=+2>0. Therefore according to the Intermediate Value Theorem there will be at least one x inside the interval [0,2] so that f(x)=0: x2-2=0. This is a positive number whose square is 2, which we call sqrt(2). Now we have "trapped" sqrt(2) inside the interval [0,2]. If we compute f(1)=12-2=-1, we know that a root must be inside [1,2] since the signs of f(x) at the two endpoints differ. We can continue this "game", each time halving the interval, and chosing a half-subinterval so that the signs of f(x) differ on the endpoints. The graph of f(x) on the first few subintervals is shown below.
| Interval: [0,2] | Interval: [1,2] | Interval: [1,1.5] | Interval: [1.25,1.5] | Interval: [1.375,1.5] |
|---|---|---|---|---|
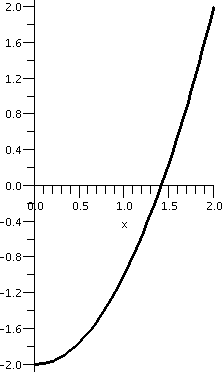 |
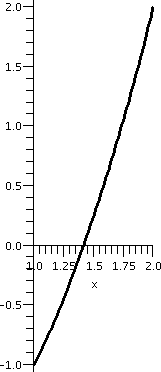 |
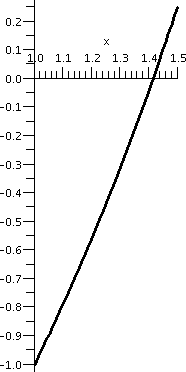 |
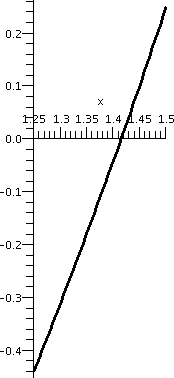 |
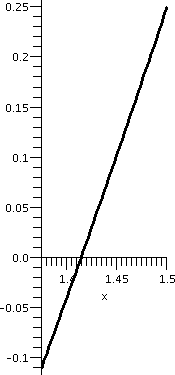 |
Another example
We realized that polynomials may not have real roots. I think one
example was x4+78.
I tried to give an example that looked like this:
12-8x+15x3+166x12+800x55
I asked if this polynomial had a real root.
The trick here is to think in terms of pictures, but sort of pictures without details. Weird pictures.
| The picture I'm thinking of is not like this, which is a nice tame picture of part of the graph. | I'm interested in what happens when x is really large, both positive and negative. There the "dominant" term in the polynomial will be the highest degree term, 800x55. Since the exponent is an odd integer and the coefficient is a positive number, this term and the whole polynomial will be positive for x large positive (this one term will "overwhelm" the other terms) and this term and the whole polynomial will be negative for x large negative (this one term will "overwhelm" the other terms). So the Intermediate Value Theorem states that the graph must cross the x-axis somewhere. |
 |
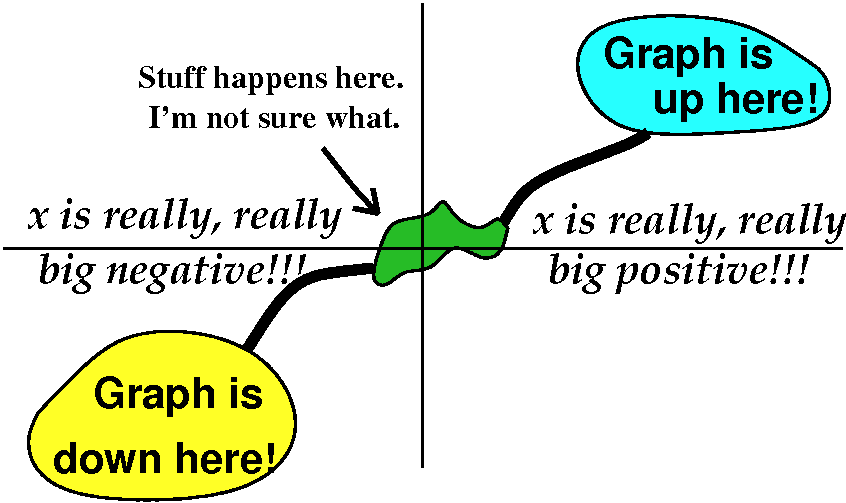 |
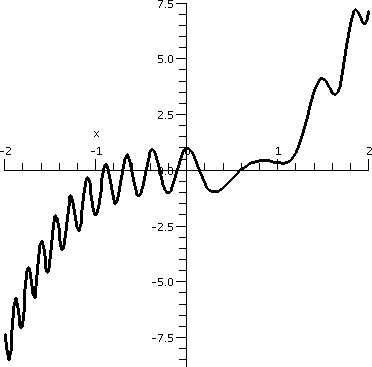 A computer program found a 20 digit approximate root of this
polynomial (-.96533812077786645838) in less than a fifth of a second,
mostly using the ideas we just learned.
A computer program found a 20 digit approximate root of this
polynomial (-.96533812077786645838) in less than a fifth of a second,
mostly using the ideas we just learned.
Here is maybe a simpler example, maybe. Look at f(x)=x3+cos(13x-9x2). This is a continuous function. What can be said about the sign of f(2), say? Since 23=8 and the most/least any value of cosine can be is +1/-1, I bet that f(2) is at least 7. Similarly, f(-2) can differ by at most 1 from (-2)3=-8, so I bet that f(-2) must be at most -7. Hey: on the interval [-2,2] f(x) changes sign. Since it is continuous it must have at least one root.
To the right is a graph of f(x) on the interval [-2,2]. It actually has lots of roots. Well, "lots" and "at least one" are logically consistent.
Major definition A function f(x) is differentiable if the limit limh-->0[f(x+h)-f(x)]/h exists. If this limit exists, it is the derivative of f(x), and written f´(x). This is read as "eff-prime of x".
The absolute value function
I looked at f(x)=|x|. Here a piecewise linear definition of |x| reads
as follows:
/ x if x≥0
|x|=<
\ -x if x<0
f(x) is continuous.
f(x) is not differentiable at 0.
I am supposed to look at the limit defining f´(0). This is
limh-->0[f(0+h)-f(0)]/h. I'll look at the two one-sided
limits separately.
limh-->0-[f(0+h)-f(0)]/h
f(0+h)=f(h), and
since h<0 (the left-hand limit) f(h)=-h. Also f(0)=|0|=0. Therefore
limh-->0-[f(0+h)-f(0)]/h=
limh-->0--h/h=-1.
limh-->0+[f(0+h)-f(0)]/h
f(0+h)=f(h), and
since h>0 (the right-hand limit) f(h)=h. Also f(0)=|0|=0. Therefore
limh-->0-[f(0+h)-f(0)]/h=
limh-->0-h/h=1.
Since -1 and 1 aren't the same (!) the derivative of f(x) at 0 does
not exist.
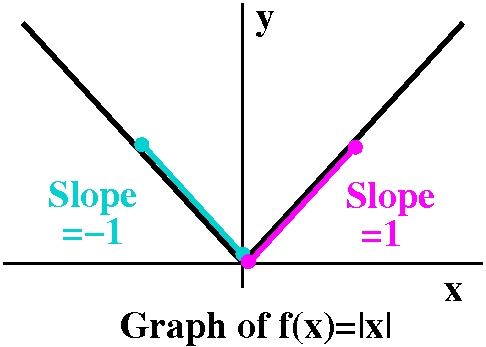
In pictures, please!
I'm more of a picture person than an algebra person, so let me show
you on a graph what was computed above. Here's a graph of
f(x)=|x|. The graph is unbroken, no jumps or breaks, providing
evidence that the function is continuous. Near 0, if we look at the
slopes of secant lines from the left and from the right, we get
completely different pictures. The secant lines from
the left all have slope -1, while those
from the right all have slope +1. There's no agreement or "approach"
of the slopes as the points on the ends of the line segments travel
towards 0. This means there is not a unique tangent line, and there is
no good unique candidate for the slope of the tangent line. Since that
is supposed to be the derivative, there's no f´(0).
Of course as I mentioned in class you are welcome to look at the more complicated but certainly real-world function, the U.S. individual rate schedule for 2006. As a matter of public policy, the function involved is continuous. Due to the progressive and piecewise linear nature of the function there, the function is not differentiable at 5 income values.
If a function is differentiable, then we know that limh-->0[f(x+h)-f(x)]/h=f´(x). This statement may no longer be precisely correct if "limh-->0" is omitted. I tried to illustrate this by looking at f(x)=x2, so f(x+h)=(x+h)2=x2+2xh+h2. Then the fraction [f(x+h)-f(x)]/h becomes exactly
(x2+2xh+h2)-x2 2xh+h2
------------- = ------ = 2x+h.
h hBut f´(x) is 2x, so there's an
"error".
In fact, generally there will be an error. So what we have is
[f(x+h)-f(x)]/h=f´(x)+Err(h)
where Err(h) is some sort of error function which -->0 as h-->0.
We could then multiply the equation by h and get
f(x+h)-f(x)=f´(x)h+Err(h)h
and add f(x) to both sides and
get
f(x+h)=f(x)+f´(x)h+Err(h)h
Certainly you should see, I hope, I hope, again something which was
mentioned repeatedly last week. If we kick or perturb the input to
f(x) and if we know that f(x) is differentiable, then the kicked or
perturbed output will be the old output plus a term directly
proportional to the disturbance (this is what's called in economics
the marginal response) plus, well, Err(h)h. Since I think of h as
small and Err(h) is also small, well, the product is even smaller
still. That's the important idea.
Look at f(x+h)=f(x)+f´(x)h+Err(h)h and make h-->0. On the right-hand side, f(x) doesn't change, but both f´(x)h and Err(h)h go to 0. So the right-hand side -->f(x). Goodness, this means the left-hand side, f(x+h), also -->f(x) as h-->0.
A differentiable function must be continuous. BUT there are continuous functions which are not differentiable (such as |x| and the U.S. tax function).
The converse of a statement is not necessarily true even if the statement is true. All frogs are green, but not all green things are frogs (I rarely see grass hop, for example).
Now we can start a feast of computational methods for derivatives or I can tell you about the ideas. Most books begin by computing everything in sight and so will I.
f(x)=x80
Now [f(x+h)-f(x)]/h==[(x+h)80=x80]/h. Now I
ain't gonna multiply out
(x+h)(x+h)(x+h)(x+h)····(x+h)
(there
are 80 factors) because, realizing that there are 2 choices to make
inside each parentheses pair, there would be a total of
280=12089 25819 61462 91747 06176
terms. This is too many even for maniacs. So let's organize things a
bit.
We can see what happens if we always choose x's. There will be 80 x's
multiplied together: x80.
We could choose h in the first term and x's in all the others. The
result will be hx79 (there always will be 80 "things"
multiplied together. Or we could choose an x in the first term, then
an h, and then all x's. This gets xhx78 which is the same
as
hx79. In fact, if you think it through, you can choose one
h exactly one time from each factor with all the rest x's. There are
80 factors, so there will be a total of 80 terms with one h and 79
x's: 80hx79.
All of the other terms have at least two h's.
Here is how I want to organize (x+h)80:
Terms with Terms with Terms with
no h's one h at least two h's
(x+h)80 = 1x80 + 80hx79 + h2(JUNK)
If the terms have at least two h's then I can certainly "factor
out" h2. I don't really care about the JUNK, and you will
see why shortly.
f(x+h)-f(x) x80+80hx79+h2JUNK-x80
----------- = ----------------------
h hNow the x80's cancel. And we
can factor h's out of the top and bottom and cancel, and the result is
80x79+h(JUNK) and as h-->0, the JUNK term drops out.
The function f(x)=x80 is differentiable, and its
derivative is f´(x)=80x79.
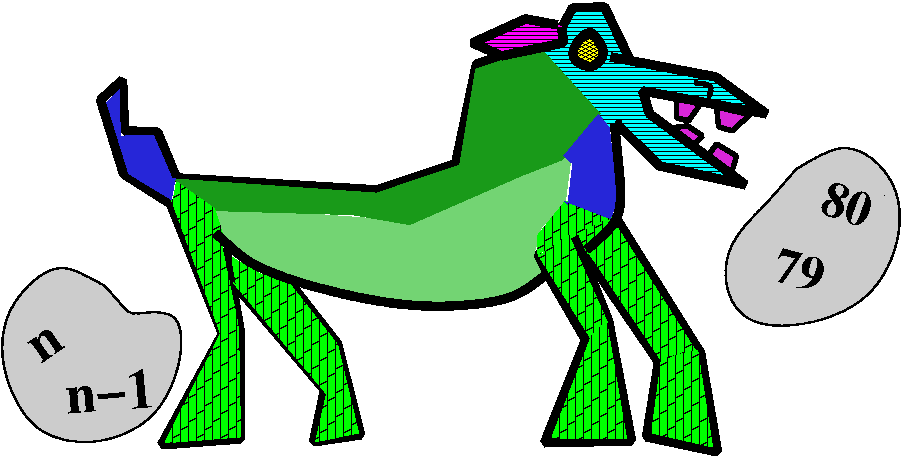
Well, now let's (metaphorically!) go out into the woods. Please imagine we meet yet another pattern beast (mostly green -- it must be a frog). This beast would eat 79's and 80's and excrete n-1's and n's. If we let the beast munch on what was just written, it would become a verification of the following:
The function f(x)=xn is differentiable, and its
derivative is f´(x)=nxn-1.
This is amazing, and gives us a very nice template to compute bunches
of derivatives.
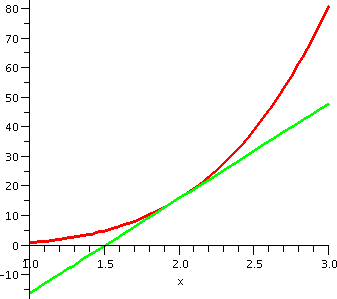 Write an equation for a line tangent to y=x4 when
x=2
Write an equation for a line tangent to y=x4 when
x=2
I can write such an equation if I know a point the line goes through
and if I know the slope of such a line. Well, if x=2, then y will be
24=16. And now you should remember that one
"interpretation" of f´(x) is as the slope of the tangent line to
y=f(x) at x. If
f(x)=x4, then f´(x)=4x3. When x=2, this is
4·23=32. So an equation for the tangent line is
y-16=32(x-2). If you want the equation in slope-intercept form, I
guess the answer becomes y=32x-48.
To the right is a picture of part of the curve y=x4 and part of the line y=32x-48. The line certainly seems to be tangent to the curve.
We further deduced two more rules for differentiation. Here they are:
Multiplication by a constant
If c is a constant and f(x) is a differentiable function and its
derivative is f´(x), then the function F(x)=cf(x) (this is f(x)
multiplied by the constant c) is differentiable, and
F´(x)=cf´(x).
Sum of differentiable functions
If f(x) is a differentiable function and its derivative is f´(x),
and if g(x) is a differentiable function and its derivative is
g´(x), then F(x)=f(x)+g(x), the function defined by taking the sum
of f(x) and g(x), is also a differentiable function, and
F´(x)=f´(x)+g´(x)
These "rules" allow us to find the derivatives of any polynomial. For
example, the derivative of
12-8x+15x3+166x12+800x55 (a polynomial
we met earlier today) is
0-8x0+15(3x2+166(12x11)+800(55x54).
I inserted a "zinger" here: the derivative of 12 is 0. In fact, the
derivative of any constant is 0. The graph is a horizontal line, and
horizontal lines have slope 0, and slopes are values of
derivatives. Also I should remark that I am lazy and I wouldn't
compute 166·12 or 800·55 unless I needed to.
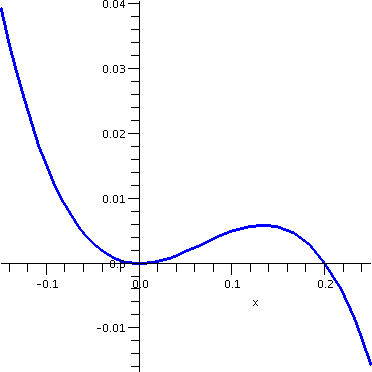
One last "reward"
To the right is a graph of y=x2-5x3 for x
between -.15 and .25. There is a quite delicate little bump. Where is
the delicate bump? Well, the delicate bump (a local maximum, not an
absolute maximum because there are points on the curve which have
larger y values) occurs where the derivative is 0: that's where the
tangent line is horizontal. The derivative of
x2-5x3 is 2x-15x2=x(2-15x). One root
is x=0 and the other comes from 2-15x=0 or 2=15x or 2/[15]=x. And so
the delicate bump is at
(2/[15],(2/[15])2-5(2/[15])3). I can honestly
declare that I don't know any faster or simpler way to locate this
point.
Monday, July 3
I defined continuous. We went over the review problems. The
semiexam was given.
|
|
|
Limits: our obligation to math culture
I would like to display part of the culture of mathematics: the
deduction of examples for collections of results. The structure of
deductions is an important ingredient of mathematics (not the only
one, certainly, but rather important). This is what makes the
transition from heuristic to accepted knowledge valid.
In any case, part of taking a math course is to learn how a
mathematician "thinks", just as in a history course students should
expect some exposure to certain methods of historians. So let's
go.
Logic? We don't need no steenkin' badges logic ... Let's just
guess!
Algebraic rules
Here are some statements about how limits interact with algebra:
A1 Suppose that limx-->cf(x) exists and equals L1 and that limx-->cg(x) exists and equals L2 then limx-->cf(x)+g(x) exists and equals L1+L2.
A2 Suppose that limx-->cf(x) exists and equals L1 and that limx-->cg(x) exists and equals L2 then limx-->cf(x)·g(x) exists and equals L1·L2.
A3 Suppose that limx-->cf(x) exists and equals L1 and that limx-->cg(x) exists and equals L2 . Also suppose L2 IS NOT 0 then limx-->cf(x)/g(x) exists and equals L1/L2.
These results are true. They can be given detailed proofs using a carefully formulated definition of limit. I don't believe that such detailed proofs are a proper part of Math 135, but there are a number of math courses which do have such discussions. I hope that you are willing to believe if two functions have limits as x approaches c, so they each get close to their limits, then their sum gets close to the limits of the sums. The restriction on L2 in A3 is needed because I don't want to worry about division by 0!
"Doing" the homework problem
One of our homework problems (#2 from chapter 3) asks for the limit of
x2+4 divided by x+8 as x-->2. If I wanted to be rather
formal I could begin with the observations that
limx-->2x=2 (as x gets close to 2, then x gets close to 2
[!]) and limx-->24=4 (the function whose output is always
4 is always close to 4 [11]). Then:
By A2,
limx-->2x2=(limx-->2x)·(limx-->2x)=2·2=4.
By A1,
limx-->2x2+4=(limx-->2x2)+(limx-->24)=4+4=8.
Again by A1,
limx-->2x+8=(limx-->2x)+(limx-->28)=2+8=10.
Finally, by
A3, limx-->2(x2+4)/(x+8=(limx-->2x2+4)/(limx-->2x+8)=8/(10).
The citation of A3 is valid since 10 is not 0.
This sort of approach is maybe interesting, but (to me) it is hardly
interesting more than once. Heh, heh.
Polynomials and "plugging in"
Well, suppose p(x) is a polynomial function of x. What is this? This
means that p(x) is a (finite) sum of (integer) powers of x possibly
multiplied by real coefficients. Then repeated use of A1 and
A2 implies limx-->wp(x)=p(w). That is, a limit of a
polynomial can always be obtained by just "plugging in" the target
value of the limit.
Example If p(x)=33x47-18x12+13.046, then
limx-->79p(x)=33(7947)-18(7912)+13.046.
(I don't want to "simplify", please!)
Rational functions and "plugging in"
A rational function is a quotient of polynomials. So a rational
function, r(x), is p(x)/q(x) where p(x) and q(x) are
polynomials. Suppose that w is a number so that q(w) is not
0. Then limx-->wr(x)=p(w)/q(w). Of course we need the
restriction that q(w) not be 0 in order to use A3.
Example If
r(x)=(3x4-5x+777)/(44x12+88). I chose the bottom
because 12 is even and 88 is positive, so there is no way that the
bottom can be 0 for any value of x. Then
limx-->-211r(x)=(3({-211}4)-5{-211}+777)/(44({-211}12)+88).
A first strategy: "plugging in"
To me this implies a first strategy for limits. I look at
limx-->wf(x), for almost any kind of x, and I try to see
what happens if I "plug in" w for x in f(x). What is f(w)? Does it
make sense (in math language, is w in the domain of f(x)?)? Then I'd
try to convince myself that f(w) is "obviously" ("clearly"?) somehow
connected with the f(x) values for x close to w. All this doesn't
necessarily need to be true, but it is one strategy, a first strategy.
Well, but how about ...
Let's look at limh-->0{sqrt(5+h)-sqrt(5)}/h. If I just try
to generalize the plug in strategy recommended previously, well, then
I'll get 0/0, and we'd better not divide by 0.
An apparently intractable problem is tamed
So look at {sqrt(5+h)-sqrt(5)}/h. We want to see what happens when h
gets small. Maybe some algebraic "stuff" can help. You may vaguely
remember can candidates for action here. The top is the difference of
square roots, and maybe the sum of square roots can help. That is,
consider
(A-B) (A-B) (A+B) A2-B2 ----- = ----- · ----- = ------ C C (A+B) C(A+B)If we apply this "template" to our situation, here is what happens:
{sqrt(5+h)-sqrt(5)} {sqrt(5+h)-sqrt(5)} {sqrt(5+h)+sqrt(5)} (sqrt(5+h))2-(sqrt(5))2
------------------- = ------------------- · ------------------ = -----------------------
h h {sqrt(5+h)+sqrt(5)} h{sqrt(5+h)+sqrt(5)}
The square roots and the squares cancel, so the result is
(5+h)-5 h 1
--------------------- = -------------------- = -------------------
-h{sqrt(5+h)+sqrt(5)} h{sqrt(5+h)+sqrt(5)} {sqrt(5+h)+sqrt(5)}and the horrible h in the bottom cancels with the h remaining on the top.
What happens to 1/{sqrt(5+h)+sqrt(5)} as h-->0? Well, here I think that algebraic results like A1, A2, etc. help. The result is that we can just plug in, and the limit is 1/{sqrt(5)+sqrt(5)}=1/{2sqrt{5}}.
Limit strategies, part II
First try to "plug in". If that doesn't work, try to use algebraic
methods of rewriting things in order to get some equivalent form which
allows the limit to be recognized easily (by "plugging in"!).
So, what about the patterns (another part of math culture)
So far what you may have seen in Math 135 about the culture of
mathematics includes logical deduction and drawing pictures (I am a
picture person, actually). But a good deal of mathematics consists of
computing examples, sometimes in an almost drearily repetitive way,
and then looking at the results and trying to discern patterns.
Here we know that
sqrt(5+h)-sqrt(5) 1
lim ----------------- = --------
h-->0 h 2sqrt(5)
 What if we wanted to know the limit of {sqrt(3+h)-sqrt(3)}/h as h-->0?
What if we wanted to know the limit of {sqrt(3+h)-sqrt(3)}/h as h-->0?
This is a metaphor, darn it! Actually the large animals roaming the woods on the Busch campus are mostly deer, too many deer.
Now suppose we allow this animal to browse on our previous collection of formulas. This is what it would eat:
{sqrt(5+h)-sqrt(5)} {sqrt(5+h)-sqrt(5)} {sqrt(5+h)+sqrt(5)} (sqrt(5+h))2-(sqrt(5))2
------------------- = ------------------- · ------------------ = -----------------------
h h {sqrt(5+h)+sqrt(5)} h{sqrt(5+h)+sqrt(5)}
(5+h)-5 h 1
--------------------- = -------------------- = -------------------
-h{sqrt(5+h)+sqrt(5)} h{sqrt(5+h)+sqrt(5)} {sqrt(5+h)+sqrt(5)}
sqrt(5+h)-sqrt(5) 1
lim ----------------- = --------
h-->0 h 2sqrt(5)
And this is what it would excrete:
{sqrt(3+h)-sqrt(3)} {sqrt(3+h)-sqrt(3)} {sqrt(3+h)+sqrt(3)} (sqrt(3+h))2-(sqrt(3))2
------------------- = ------------------- · ------------------ = -----------------------
h h {sqrt(3+h)+sqrt(3)} h{sqrt(3+h)+sqrt(3)}
(3+h)-3 h 1
--------------------- = -------------------- = -------------------
-h{sqrt(3+h)+sqrt(3)} h{sqrt(3+h)+sqrt(3)} {sqrt(3+h)+sqrt(3)}
sqrt(3+h)-sqrt(3) 1
lim ----------------- = --------
h-->0 h 2sqrt(3)
Another animal
We could imagine another animal eating the same formulas and changing
the 5's to 11's. Etc.
A fairly general animal and a result
The pattern recognition is most interesting. What about the animal
that would take in formulas with 5's and excrete formulas with x's,
say? It would prove (oops!) the following result:
If x is a positive number, then
sqrt(x+h)-sqrt(x) 1
lim ----------------- = --------
h-->0 h 2sqrt(x)
and we would have verified that if f(x)=sqrt(x), then
f´(x)=1/{2sqrt(x)}. Later, later, later.
Order rules and limits
In this case the word "order" doesn't refer to "command" but to "less
than ... greater than" type of order. Here is one generally recognized limit rule:
L Suppose that f(x)<g(x) for all x's near (but not
necessarily equal to) c, and that limx-->cf(x) exists and
equals L1 and that limx-->cg(x) exists and
equals L2. Then L1<L2.
People actually use this sort of result frequently in daily reasoning. Rates (as derivatives) are certain kinds of limits. If one faucet and hose arrangement takes 10 minutes to fill a container, and another takes 10 minutes, then I bet the rate of water flow through the first is less than the flow rate through the second. I admit that this observation isn't profound, but ... it is used. Somewhere in your brain there is a mental arrangement, a framework, comparing rates, and this is essentially L. We will use L at various times in the course to get some approximate information about rates.
Example Suppose I know that the values of f(x) are all between
-17 and 504. Suppose I also know that, for example,
limx-->32f(x) exists. Then that limit must be between -17
and 504.
Please notice that there are functions whose values are between -17 and 504 for which the limit does not exist, such as the piecewise defined function
/ -5 for x<32
f(x)= < 12 for x=32
\ 22 for x>33
So you can't conclude anything quantitative about
limx-->32f(x) using L because one of the hypotheses
of L is not ture or valid or fulfilled: the limit doesn't
exist.
The squeeze theorem, a very special result
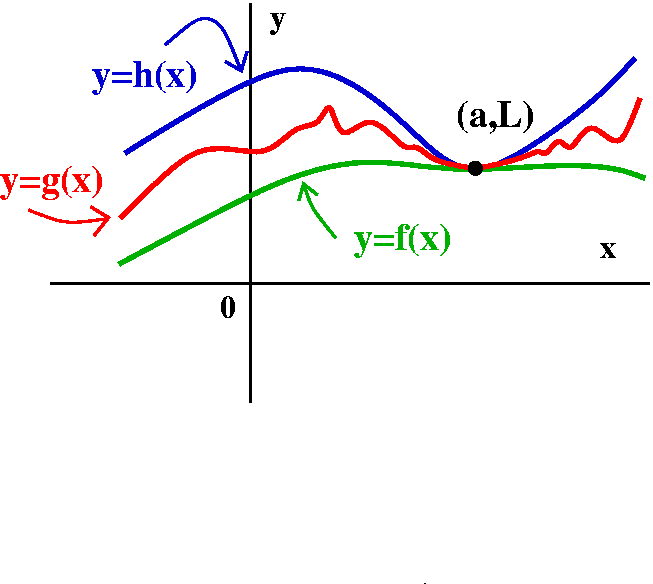 The squeeze
theorem is a very special result which is vital to the success (!) of
calculus. It will look quite weird if you have not seen it before.
The hypotheses require information about three functions.
The squeeze
theorem is a very special result which is vital to the success (!) of
calculus. It will look quite weird if you have not seen it before.
The hypotheses require information about three functions.
The Squeeze Theorem
Hypotheses
The limit of the function f(x) as x-->a exists and
is the number L.
The limit of the function h(x) as x-->a exists and
is the number L.
These two limits agree.
For x's which are not equal to a, we know that
f(x)≤g(x)≤h(x).
Conclusion
The limit of the function g(x) as x-->a also exists, and is also equal
to L.
You'll have to see how this is used in several important
applications. Here, though, is a rather contrived
Example Suppose I know that the function Q(x) is always between
-5 and +8. What can I say about the limit as x-->4 of Q(x)? What about
the limit as x-->4 of 33+(x-4)Q(x)?
Well, there is not much which can be said, based on the information
given, about the limit of Q(x) as x-->4. For example, to the left of
4, Q(x) could be -2 and to the right of 4, it could be +2 (since both
-2 and +2 are between -5 and +8, this is a possible example). In this
case, the limit of Q(x) as x-->4 certainly does not exist.
What happens to 33+(x-4)Q(x)? Well the largest it could be is
33+|x-4|8, and the smallest it could be is 33+|x-4|(-5). Those are the
top and bottom possibilities for the values of Q(x). But examine the
top, 33+|x-4|8, as x-->4. This must go to 33. The bottom,
33+|x-4|(-5), as x-->4, also approaches 33. So 33+(x-4)Q(x) is
squeezed or sandwiched between two functions which both approach 33 as
x-->4. Therefore according to the squeeze theorem, the limit of
33+(x-4)Q(x) as x-->4 must also exist, and it must be 33.
The factor of (x-4) as x-->4 goes to 0. When it multiplies Q(x), since
we know Q(x) doesn't get very big either positive or negative, the
result also goes to 33. So the 33 remains alone.
Sine
We will eventually want to find the derivative of sin(x). In order to
do this, we'll need to handle the limit as h-->0 of
{sin(x+h)-sin(x)}/h. Here is, I think, just about the only time in the
course where we need the addition formula for sine. It turns out that
sin(x+h)=sin(x)cos(h)+sin(h)cos(x). Therefore
sin(x+h)-sin(x) sin(x)cos(h)+sin(h)cos(x)-sin(x)
--------------- = --------------------------------
h h
The top of the fraction is sin(x)cos(h)+sin(h)cos(x)-sin(x) which is
supposed to help you "organize" the fraction. The fraction is equal
to
( cos(h)-1) (sin(h))
sin(x)(---------) + cos(x)(------)
( h ) ( h )
Honestly it isn't supposed to be "clear" why the fraction is rewritten
or reorganized like this. One advantage, easy to say, is that writing
the fraction this way sort of "separates" (decouples!) the h and x
parts of the fraction. We can study them separately.
I'll concentrate right now on the behavior of sin(h)/h as h-->0. I had student volunteers show some graphs produced by their graphing calculators of sin(h)/h for h between -5 and 5. Here are the graphs similar to what they got:
| sin(h)/h in radians, -5≤h≤5 | sin(h)/h in degrees, -5≤h≤5 |
|---|---|
|
|
A sine limit
It is true that limh-->0 sin(h)/h exists and equals
1 if angles are measured in radians. The numerical simplicity of this
result is the chief reason that everyone who studies how things
change measures angles in radians rather than in degrees, wombats, or
glinkas. (The last two are angle measures for extinct civilizations.)
I did not go further in class, but here is further discussion of the
limit, including geometric reasoning supporting the statement.
A vote on angle measurement
We voted, 14 to 1, to use radian measure for angles in this
course. Sigh: there's alway someone.
Some more limits
sin(h) ( 1 ) (sin(h)) ------ = (---) · -------- --> (1/5)(1) 5h ( 5 ) has h-->0. So this limit exists and is 1/5.
But if h is very small, 7h is also very small. So I am willing to believe that the ratio sin(7h)/(7h) is close to 1. Therefore I write the following:
sin(7h) ( ? ) (sin(7h)) ( 7 ) (sin(7h)) ------- = (----) · --------- = (---) ·--------- --> (7/1)(1) h ( ?? ) (7h) ( 1 ) 7has h-->0. So the limit exists and is 7: limh-->0(sin(7h)/h=7.
Left- and right-hand limits
Real functions in real life have different behavior on the two sides
of a point. Look at the income tax function. To the left of $15,1000,
the tax rate is 10% and to the right it is 15%. There is mathematical
language to describe this sort of behavior. The language is left- and
right- hand limits.
Each of these has the geometric and algebraic definition of limit but
restricted to one side or the other. The left-hand limit of f(x) as
x approaches c is usually denoted
limx-->c-f(x). For consideration of this limit,
we are supposed to restrict our attention to x's on the left
(negative) side of c . Dually,
the right-hand limit of f(x) as
x approaches c is usually denoted
limx-->c+f(x). For consideration of this limit,
we are supposed to restrict our attention to x's on the right
(positive) side of c.
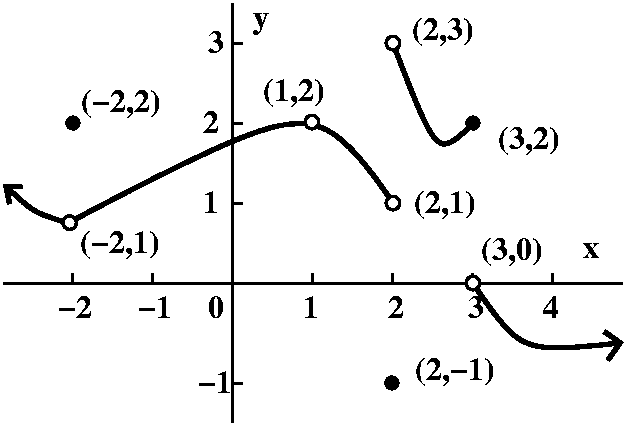
A graphical example
Let's look at f(x), a function whose graph is shown to the right. The
graphical "notation" which is commonly used is an empty circle
where there is no point of the graph (but where, perhaps, your
intuition (?) might want there to be one. A solid circle (maybe a
thickened-up point) shows a value on the graph. I'm particularly
interested in describing what happens at and nearby to -2, 1, 2, and
3. Some of what is describe is "delicate" behavior. In the table
below, the entry DNE abbreviates "Does Not Exist." So either the
function value doesn't exist (the domain does not include that value
of x) or the limit doesn't exist.
| c= | f(c) | Left-hand limit limx-->c-f(x) |
Right-hand limit limx-->c+f(x) |
Two-sided limit limx-->cf(x) |
Comments |
|---|---|---|---|---|---|
| -2 | 2 | 1 | 1 | 1 | The graph approaches the point (-2,1) from both sides, but the function value is in the "wrong" place! |
| 1 | DNE | 2 | 2 | 2 | There doesn't seem to be a value for the function at 1, but the limits are go to 2 there. |
| 2 | -1 | 1 | 3 | DNE | From the left the limit is 1 and from the right the limit is 3. The two values don't agree, so the two-sided limit which we originally considered doesn't exist. |
| 3 | 2 | 2 | 0 | DNE | The two-sided limit doesn't exist since the two one-sided limits disagree. |
Prescribing behavior
We could also go the other way. That is, we could "prescribe" various
one- and two- sided limits and ask for graphs.
Wednesday, June 28
Some discussion of the homework
Another example
We could imagine that s(t) is the position on the x-axis at time
time. Wait, better: we drive along the highway, and s(t) is the
distance we've driven on the highway at time t. If we assume we don't
drive backwards, then the distance we've driven is actually equal to
our position (displacement) on the highway.
Average rate of change to instantaneous rate of change
The average rate of change between the times t and t+h is
{s(t+h)-s(t)}/h. Then as h-->0, this approaches the instantaneous rate
of change.
Average speed/velocity to instantaneous velocity
The quantity {s(t+h)-s(t)}/h is called, in this physical context, the
average speed (or, more correctly, velocity) over time interval
[t,t+h]. The limit as h-->0 is called the instantaneous velocity at
time t. Interestingly, the speedometer in cars measures average
velocity for very small h's, using either a mechanical or an
electronic device. This measurement is supposed to approximate the
ideal quantity, instantaneous velocity.
Definition of derivative
The derivative of a function, f(x), is another function, f´(x),
which is defined by the equation
f´(x)=limh-->0{f(x+h)-f(x)}/h.
This is our first view of one of the major "objects" (ideas?) of the
course, and I believe some familiarity is needed to internalize the
definition and really use it.
Discussion
Let's see: there are three parts.
f´(x) This is just more mysterious mathematical
notation. It is read as "eff prime of ecks". It is intended to
represent what is on the other side of the equation.
{f(x+h)-f(x)}/h This is what I called "the average rate of
change of f(x) over the interval whose end points are x and x+h". It
can represent all sorts of real quantities of interest. It is my job
to try to convince you of this with more examples.
limh-->0 Well, this represents ... this represents
... uh, the "instantaneous rate of change of f(x) at x": that just
names the thing. It doesn't really tell me what is going on. But maybe
I should first discuss an example of the derivative in a bit more
detail. And I also would like to discuss it from several different
points of view.
f(x)=1/x; f´(3) algebraically
According to the definition (can't argue with a definition, except to
suggest that it be modified or replaced, and after about three
centuries and millions and millions of people using the definition,
replacement seems unlikely!)
f´(3)=limh-->0{f(3+h)-f(3)}/h.
In order to analyze this further, we write f(3+h)=1/(3+h), and then
f(3+h)-f(3)={1/(3+h)-1/3}. I can combine fractions and get
f(3+h)-f(3)={[3-(3+h)]/[(3+h)3]}. Please: it is very easy to mess up
signs in this computation. I like to use lots of parentheses. There is
some simplification which can be done:
{[3-(3+h)]/[(3+h)3]}={-h/[(3+h)3]} (the 3's cancel in the top).
Now we will need to handle a compound fraction. The scheme looks like
this:
A
--- A 1 A
B = --- · --- = ----
------- B C BC
C
So
-h
--------
f(x+h)-f(x) (3+h)3 -h
----------- = ------------ = ------------
h h h·(3+h)3
Now the h's top and bottom cancel, and we know
{f(3+h)-f(3)}/h=-1/[(3+h)3].
As h-->0, the only thing that changes is on the bottom. I bet that
3+h-->3. Therefore, as h-->0, {f(3+h)-f(3)}/h-->-1/(3·3)=-1/9.
The derivative of f(x) at x=3 is -1/9 (for this function).
Intellectually curious people can ask many questions about this algebraic feast (too much: a mental stomachache!). Why do it? (Answer: yes, there are easier "ways" but more sophistication is needed.) A more interesting question, to me, is why is the answer -1/9? Here there are a variety of answers. One answer is, well, dummy, I just showed you. I transformed the original definition using various algebraic "tricks" until I could get a formula where the limit was more easily recognized. That's a sort of ground floor answer. But what is the significance of the minus sign (if any!) and what about the size (1/9). Well, here are some pictures.
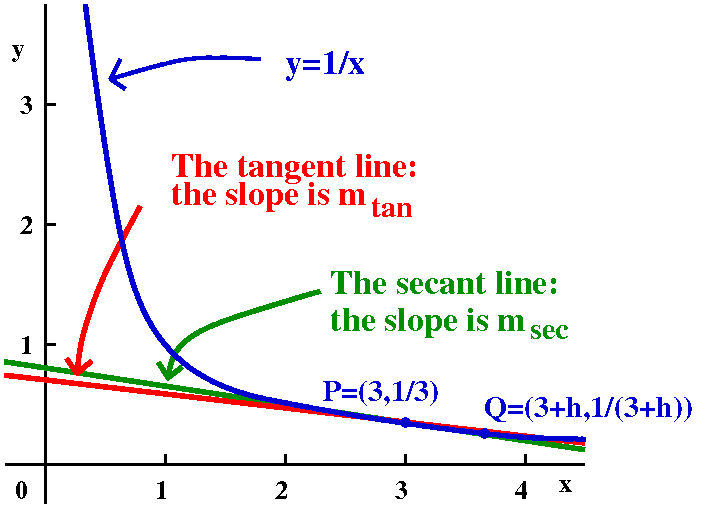 f(x)=1/x; f´(3) geometrically
f(x)=1/x; f´(3) geometrically
Here is part of the graph of y=1/x. Suppose P is the point (3,1/3),
and Q is the point (3=h,1/(3+h)). Both P and Q are on the graph. I
want to think of h as small and positive, maybe h very small (!). The
straight line through P and Q is called a secant line of this
graph. I'll call its slope msec. I can write this slope in
terms of the coordinates of P and Q: it is the difference in the
second coordinates divided by the difference in the first
coordinates. This turns out to be (no: there aren't any accidents here
-- several centuries have gone by with clever people working to make
sure that seeming coincidences really happen)
1 1
----- - ---
3+h 3
-----------------
(3+h) - 3
This fraction is the same as the average rate of f(x) over the
interval [3,3+h]. Now look closely at the picture, because to me, what
I am about to describe is difficult to see. When h "gets" smaller and
smaller (positive, say) then the point Q "travels" on the curve y=1/x
closer and closer to the point P. The QP line seems to more and more
look like the line tangent to y=1/x at P. If this is so, then the
slope of the secant line, msec, should get closer and
closer to the slope of the tangent line, mtan. The
limit of msec should be mtan. What we did
before should convince you that mtan is actually -1/9.
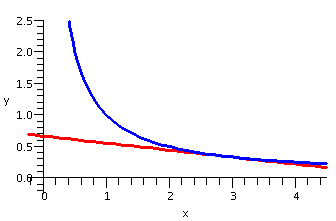 We can actually write the equation of the line tangent to y=1/x at the
point P. We just need some "data": say, a point on the line, and the
slope of the line. We've got this:
We can actually write the equation of the line tangent to y=1/x at the
point P. We just need some "data": say, a point on the line, and the
slope of the line. We've got this:
Point: (3,1/3). Slope: -1/9.
(x,y) will be on the line when [y-(1/3)]/[x-3]=-1/9. so that
y-1/3=-1/9(x-3) or y-1/3=-(1/9)x+1/3 or y=-(1/9)x+2/3.
The graph to the right was done by Maple. It shows a portion of y=1/x and the line y=-(1/9)x+2/3. They are not intended to "prove" anything, but rather to help support the preceding discussion. I hope the line does look tangent to the curve at the point where x=3, though. The minus sign in -1/9 occurs because the curve is decreasing as x is increasing. The magnitude of -1/9, that is, 1/9, is not so big: the curve is fairly "flat" around (3,1/3).
f(x)=1/x; f´(3) numerically
Some people like pictures (me!), and some might not like algebra (also
me!), but some people do like lots and lots of numbers. So let me try
to tell you a numerical interpretation of f´(3).
I tried to convince you that linear functions (functions whose graphs
are straight lines) take input differences and multiply them by a
fixed number (which happens to be m, the slope). NONlinear functions
aren't as nice. The "local multiplier" is {output difference} divided
by {input difference}. If h is small, the input difference is x+h
minus x, or h. The output difference is f(x+h)-f(x). And, goodness!,
the local multiplier is the quotient {f(x+h)-f(x)}/h (this should look
familiar!). If h is small, if f(x) is 1/x, if x is 3, then this local
multiplier is pretty darn near -1/9. This means f(3+h) should be
"close" to (1/3)+(local multiplier)(h), which is (1/3)+(-1/9)h.
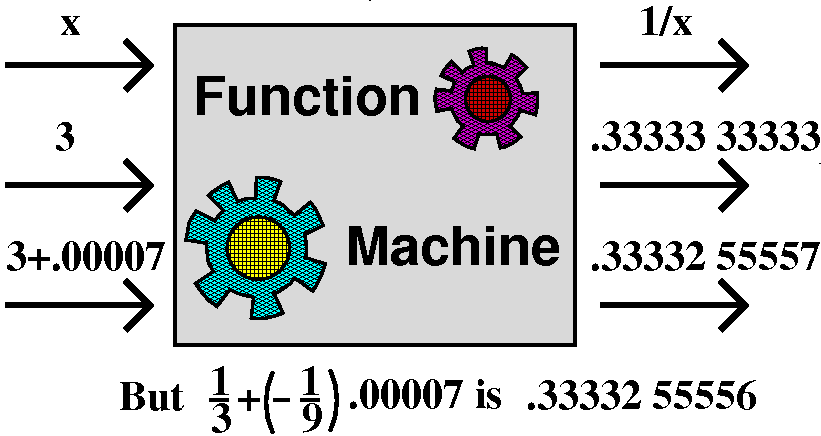
Here I show the function machine for f(x)=1/x. (The machine has gears inside, of course! A few of them are showing.) As an example, I computed f(3+.00007). This is 0.33332 55557 to 10 decimal place accuracy. (The purpose of the space is just to help you "see" the darn numbers better.) And (1/3)+(-1/9).00007 is 0.33332 55556. So there is agreement up to one digit in the tenth decimal place (a discrepancy of 10-10). Whether this is interesting or not to you is certainly a matter of personal taste. But it should indicate that maybe for more complicated functions we will be able to compute small perturbations "easily" if we understand f´(x).
This is not enough!
Although these three explanations (?) of f´(x) are a beginning, I
still do not believe that I've even begun to approach some sort of
realistic payoff for Math 135. I still need to do this.
What's a limit?
The part of the definition of derivative which
Here is the definition written by Gootman.
The expression limx-->cf(x)=L means that as x gets closer and closer to c, through values both smaller and larger than c, but not equal to c, then the values of f(x) get closer and closer to the real number L.This is a version of the definition which took more than 100 years to be generally accepted. I would like to investigate the meaning of the definition by considering a numbers of examples. By the way, the phrase " limx-->cf(x)=L" is usually read as "The limit of f(x) as x approaches c is L."
Easy
I bet limx-->3x2=9. I think this should be
emotionally (?) correct. If x is very close to 3 (though not
exactly 3) then x2 will be very close to 9. The "=9" in the
preceding line of algebra really doesn't just represent equality: it
really represents a more complicated logical situation, that the
assertion in the definition is fulfilled. You get the range variable,
x2, close to 9, by taking x close to 3. Any output
tolerance can be obtained by selecting the input close enough.
Another step
In fact, I bet that limx-->6x2=36 and
limx-->-5x2=25 and ... This function is maybe
too easy.
 Change it a bit
Change it a bit
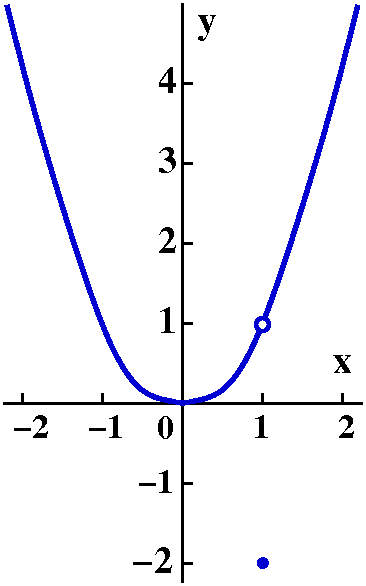
Let me define f(x) in a piecewise fashion. Here f(x)=x2 if
x is not equal to 1, and f(1)=-2. (Don't complain -- the income
tax function is much more complicated!) A chunk of the graph of f(x)
is shown to the right. It is a parabola with a hole in it, and the
value for x=1 moved to (1,-2). The conventional way to show a "missing
value" (hole?) is to draw a circle (an empty circle?) at the
point. The conventional way to show a point that is on the
graph and otherwise might be missed is to draw a sort of fat point (a
filled circle?).
Well, what is limx-->3f(x)? Let's look at values of x close to 3. The definition declares we should examine x's which are "closer and closer to c [c is 3 here], through values both smaller and larger than c [c is 3 here] ..." For close x's, f(x) is actually x2. That means we could just consider x2 in the limit statement, and then the limit statement (as x-->3, x2-->9) is correct if we write limx-->3f(x)=9. O.k.: that seems good. I hope.
What is limx-->1f(x)? Here we have the whole, and the
"moved" value of x2. But the definition declares we should
look at " values both smaller and larger than c [c is 1 here], but
not equal to c [c is 1 here] ..." In this limit statement, we
should not consider f(1). Therefore f(x) will be x2! And
our limx-->1f(x) is logically the same as
limx-->1x2. That value is 1.
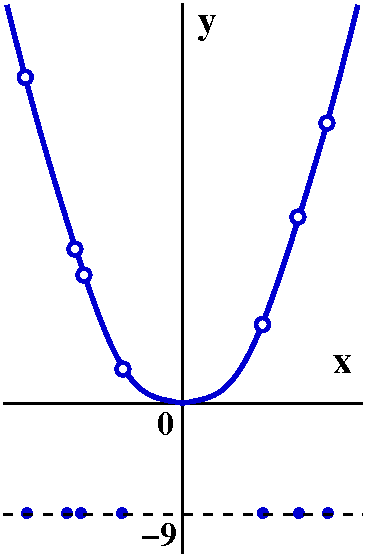
The aliens attack ...
The aliens attack (Babylonians?) and they strike at one of the great
prizes of the human race, the squaring function:
f(x)=x2. Here is what they do: they take 318 different
values of x, and for those values of x (as inputs to their version of
f(x)) they change the outputs to -9. I will call this alien version of
the squaring function, A(x). Notice that I haven't told you
which values of x the aliens have changed. Weird, huh? Not very much
information. The graph shown maybe gives you some idea, but I have
intentionally removed horizontal axis scaling, because we don't know
where the holes are.
What can we say about limx-->3A(x)? Well, let me give two arguments.
Limits may not "exist"
| Of course graphs may be more complicated. For example, the limiting behavior on two sides may not agree. This can be illustrated with something as simple as the piecewise defined function f(x) which is 0 for x<0 and 1 for x>0. Then the two pieces won't meet up. | 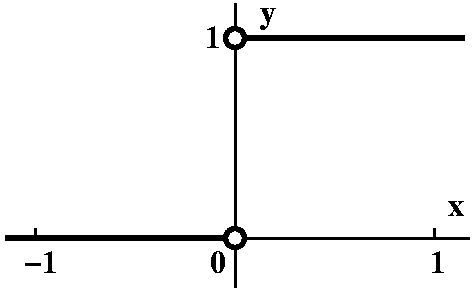 | |
| But in fact situations without limits may be considerably more bizarre. The function pictured is a piecewise linear function which jumps infinitely often between 1 and 0. I don't think I want to describe this with too much precision, but you should appreciate that such things "exist". We won't meet functions with infinitely oscillatory behavior on finite intervals in Math 135, but they do occur in certain applications. |
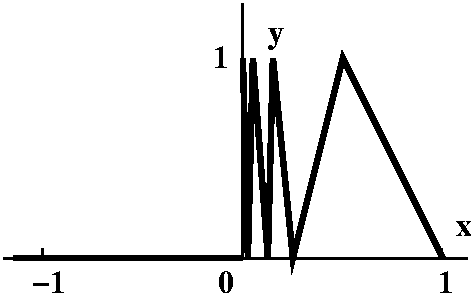
| |
| h | f(2+h) | h |
|---|---|---|
| .1 | 9.261 | 12.61 |
| .01 | 8.120601 | 12.0601 |
| .001 | 8.012006001 | 12.006001 |
| .0001 | 8.001200060001 | 12.00060001 |
| .00001 | 8.000120000600001 | 12.0000600001 |
| .000001 | 8.000012000006000001 | 12.000006000001 |
| .0000001 | 8.00000120000006 | 12.0000006 |
| .00000001 | 8.0000001200000006 | 12.00000006 |
| .000000001 | 8.000000012000000006 | 12.000000006 |
| .0000000001 | 8.0000000012000000001 | 12.0000000006 |
These computations were done to 30 digit accuracy and then truncated to 20 digit accuracy. If all computations were done with "only" 20 digit accuracy, the last entry would have been 12.0000000001, not 12.0000000006, because even 20 digit accuracy errors accumulate. Amusing, but not very amusing.
Average and instantaneous
So what do we learn? Well, the second column tells me that
f(2+h)=(2+h)3 is darn close to f(2)=23=8 when h
is small. This maybe is not too surprising, although we'll talk a bit
more about it in a day or so. But it is the changes that are more
interesting.
We seem to see that the average rate of change of f(x)=x3 in the interval [2,2+h] gets really close to 12. So for this f(x) and for this value of x (that is, x=2), we seem to see that f(2+h) is approximately 8+12h for h very small.
The ugly algebra
Let me show another way to look at what we're doing. The average rate
of change of f(x)=x3 on the interval [2,2+h] is
[(2+h)3-23]/h. I will actually compute out
(2+h)3=(2+h)(2+h)(2+h) in order to really, really see what
is happening. Let's begin.
I compute
(2+h)(2+h)=22+2·2·h+h2=4+4h+h2.
This maybe is not too bad. Now I need to multiple the result by
2+h. So I first multiply by 2:
2·(4+4h+h2)=8+8h+2h2.
Now multiply by h:
h·(4+4h+h2)=4h+4h2+h3.
Now add these results, making sure to keep track of all the powers of
h:
(2+h)3=8+12h+6h2+h3.
Finally, the algebraic form of the average rate of change:
[(2+h)3-23]/h=(8+12h+6h2+h3-8)/h.
Stay calm. Stay very, very calm. Notice that the 8's cancel on
top:
(12h+6h2+h3)/h.
Now the h on the bottom lowers the degree of the h's in all the terms on the top:
12+6h+h2
The result is that the average rate of
change of f(x)=x3 on the interval [2,2+h] is
12+6h+h2. So therefore (!!!) when h is very very small,
this is close to 12. Hey, our observation with the numerical data is
confirmed.
Pictures?
Here are some pictures of y=x3. The pictures need to be
considered carefully. The software which produces these pictures (a
program called Maple) automatically tries to fill up a square
box. This means that the vertical or horizontal scale is adjusted
(squeezed or expanded) to show the graph without "wasting" any space.
For example, in the first picture, the width of the base is 3, but the
height goes from 03=0 to 33=27. The "square"
should actually be almost a 1-to-10 thin rectangle.
In each graph, the green dot is supposed to be the point (2,8).
| x3 in [0,3] | x3 in [1.5,2.5] | x3 in [1.95,2.05] |
|---|---|---|
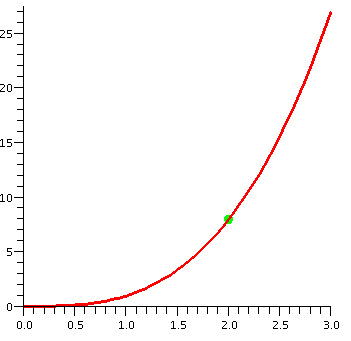 |
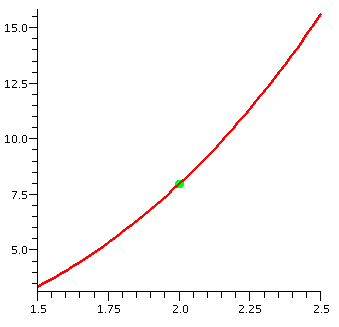 |
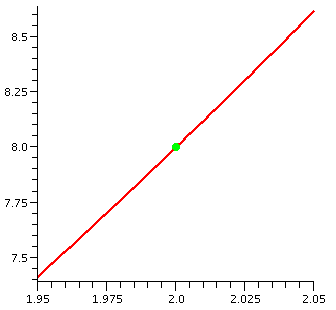 |
 What you should see in these pictures is that as we get closer and
closer to (2,8) the curve seems to resemble more and more a straight
line. This is the geometric version of the numerical computations
above: smaller and smaller changes in the input will get more and more
like the output responses to a suitable linear function. In this case,
the "linear function" is 8+12h. The 8 comes from 23, and is
shown at (2,8), the green dot. Where the heck is the the 12?
Well, if I force my last picture above (the third, on the interval
for x's in [1.95,2.05]) to be displayed with correct, real
proportion, the result is to the right. Hey: if we could measure this
graph, an almost line-looking graph, you would see that its slope is
12!
What you should see in these pictures is that as we get closer and
closer to (2,8) the curve seems to resemble more and more a straight
line. This is the geometric version of the numerical computations
above: smaller and smaller changes in the input will get more and more
like the output responses to a suitable linear function. In this case,
the "linear function" is 8+12h. The 8 comes from 23, and is
shown at (2,8), the green dot. Where the heck is the the 12?
Well, if I force my last picture above (the third, on the interval
for x's in [1.95,2.05]) to be displayed with correct, real
proportion, the result is to the right. Hey: if we could measure this
graph, an almost line-looking graph, you would see that its slope is
12!
Monday, June 26
I discussed the course and this specific section of the course. What I
said is here along with other
information. I handed out student
information forms.
I asked students to work on some starter problems, and discussed solutions.
1. A sign at the track near the Werblin recreation center declares
that 9 laps is 4 miles. What is the length in miles of 7 laps?
If x is the length in miles of 7 laps, we set up a proportion, so
4/9=x/7 and x=(28)/9 or three and one-ninth miles.
I mentioned that
people should be comfortable with arithmetic, and mentioned another
problem I could have asked:
Suppose that A=1010 and
B=10-10 and C=-1010 and D=-10-10. Can
we "order" these numbers on the number line?
There was some early misunderstanding. Exponentiation is usually
supposed to be done "first" before subtraction, so -1010 is
-(1010), and so -1010 is a negative
number. It is the number -100000 00000: this is minus ten
billion. Well we saw that C and D were negative numbers and A and B
were positive numbers. A is ten billion, and B is .00000 00001,
one ten-billionth.
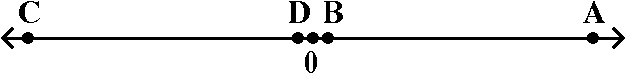
| 2. The graph to the right is taken from a webpage of the Financial Forecast Center. It records and predicts the Dow Jones Industrial Average (DJIA) for the period indicated.(The graph was copied on 6/22/2006 from http://www.forecasts.org/djia.htm.) |
 |
|
a) What is the (approximate) highest value of the DJIA shown? What
date does it occur on? Also answer the corresponding questions for the
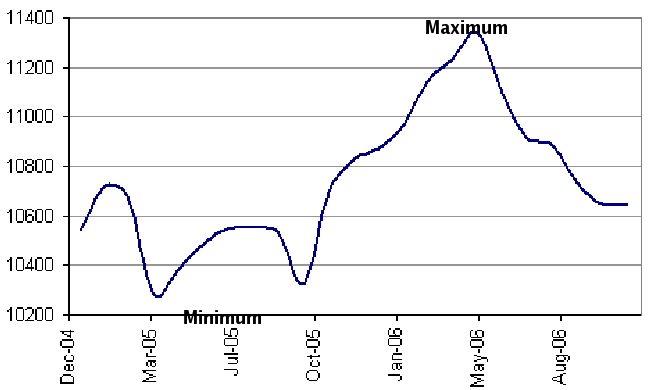
lowest value. The highest value seems to occur on about the beginning of May 06 and the value is about 11350. The lowest value is near the beginning of March 04 and the value is about 10280. The top is technically called a maximum and the bottom is called a minimum. There is other "local" tops (at about late January 04 and about July-August 05): these are called local maxima and there is a "local" bottom around October 05: this is a local mimimum. We will discuss these terms later. |
 |
|
b) What (approximately) is the length of the longest period of time
shown when the DJIA seems to be increasing? What are the beginning
values (date, DJIA amount) and ending values for this period of
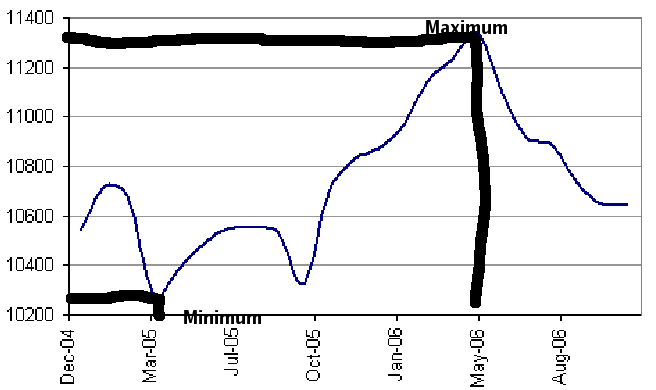
time? This seems to be the period from October 05 to May 06. The DJIA increases from about 10350 to 11350. The function shown is increasing. This means, specifically, that for any two time values, say t1 and t2 in this interval, with t1<t2, then the DJIA at t1 is less than the DJIA at t2. The logic here is important: we need to be able to check this for any pair of time values. |
 |
3. The Body Mass Index (BMI) is computed by taking a person's
weight (in kilograms), and dividing by the person's height (in meters)
squared.
a) Write a formula for BMI using the variables W for weight and H
for height. Your formula should begin BMI(W,H)=....
Here BMI(W,H)=W/H2.
b) Describe how the BMI changes if weight increases and height stays
the same. What happens exactly to BMI if the weight is doubled and the
height is fixed? Verify your assertion algebraically.
I think that if W increases and H stays the same, then BMI(W,H) will
increase. This is because (??) W is on top and H2 is on the
bottom. If the weight is doubled while the height is fixed, then the
BMI will double. Here is algebraic verification:
BMI(2W,H)=(2W)/H2=2(W/H2)=2BMI(W,H).
c) Describe how the BMI changes if height increases and weight stays
the same. What happens exactly to BMI if the height is doubled and the
weight is fixed? Verify your assertion algebraically.
If W is fixed and H increases, then the BMI will decrease. Again, this
is because the H stuff is on "the bottom" and the W stuff is on "the
top". If the height is doubled while the weight is fixed, then the
BMI will be divided by four. Here is algebraic verification:
BMI(W,2H)=W/(2H)2=W/(4H2)=(1/4)(W/H2)=(1/4)BMI(W,H).
A big chunk of this course will be devoted to understanding increasing and decreasing, both graphically and algebraically.
 Here is my "tribute" to standard geometrical problems.
Here is my "tribute" to standard geometrical problems.
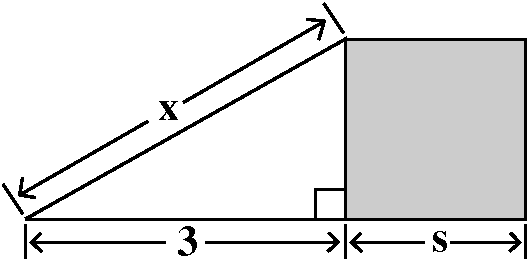
4. A right triangle and a square share sides, as
shown in the diagram to the right. The hypotenuse of the right
triangle has length x, and one "leg" of triangle (not shared with
the square) has length 3.
a) What is the side length, s, of the square? (Find this by computing
the length of the other leg of the triangle.)
In a right triangle, the square of the hypotenuse is the sum of
the squares of the two "legs" (Theorem of Pythaogoras) so that
x2=s2+32. We solve for s:
s2=x2-9, and then ... well, there can be two
square roots of numbers (the square of both 5 and -5 is 25). So s is
the square root (I'll abbreviate this as sqrt!) of
x2-9. But which one? Well, we'd better take the one that is
not negative. A triangle whose side length is negative doesn't
feel good. So s=sqrt(x2-9).
b) What is the area of the square? What is the area of the
triangle?
The area of the square is s2=(sqrt(x2-9))=x2-9. The area of the triangle is half the
base multiplied by the height. The base is 3 and the height is s, so
the area of the triangle is (3/2)s=(3/2)sqrt(x2-9).
c) Define a function, f(x), to be the sum of the areas of the square
and the triangle. Write an algebraic formula for f(x). What is the
"natural domain" of this function?
f(x)=x2-9+(3/2)sqrt(x2-9). This function is
defined if x2-9 is at least 0 (we can't take square roots
of negative numbers in this course). This means that x should be at
least 3 (greater than or equal to 3) or (actually!) at most -3 (less
than or equal to -3).
Please notice that the geometrically "meaningful" part of f(x)'s
domain is x>=3.
d) Find x so that the sums of the areas of the square and rectangle
is 7. (One way is to write f(x) in terms of s, find s so
that the total area is 7, and then compute x.)
We did not do solve this in class since I wanted to have a break. If
we put s=sqrt(x2-9) then
f(x)=x2-9+(3/2)sqrt(x2-9)=s2+(3/2)s.
To get s2+(3/2)s=7 we multiply by 2: 2s2+3s=14
and then change this to 2s2+3s-14=0. But amazingly (!!)
2s2+3s-14=(2s+7)(s-2). (Not too amazing, this is a problem
in a math course. In real life, nothing as nice as this happens!)
Now if (2s+7)(s-2)=0 either s=-7/2 or s=2. The side length of the
square should be positive, so take s=2. Since
s=sqrt(x2-9), we know that 2=sqrt(x2-9) and
4=x2-9. This means x2=13, so that x is either
-sqrt(13) or sqrt(13). I think the length of the hypotenuse should not
be negative, so x=sqrt(13).
More to come!!!
 Function
A function is a rule transforming (real) numbers to (real) numbers.
I frequently think of functions in terms of "boxes". This metaphor (?)
can help organize my thoughts.
Function
A function is a rule transforming (real) numbers to (real) numbers.
I frequently think of functions in terms of "boxes". This metaphor (?)
can help organize my thoughts.
The collection of all inputs is called the domain of
the function, and the collection of all possible outputs is
called the range of the function.
In the DJIA example above (#2) the domain seems to be dates from from about Dec 04 to Dec 06. The range, the collection of possible values, goes from 10280 to 11350. In interval notation, the range is [10280,11350]. The square brackets indicate that the numbers on the boundary are included. Otherwise, round brackets are used.
Natural domain of a function defined by a formula Many of the functions we'll consider will be defined by simple algebraic formulas. For example, f(x)=x2. Here the input is a number x, and the output is x2. When we have such a function, the domain will usually be the natural domain implied by the formula. This is all numbers for which the formula gives a real answer. In our course, the obstacles we will encounter to "a real answer" are created by division and square root. We can't divide by 0 and we can't take the square root of a negative number.
Example
If f(x)=(1/{x-2})+sqrt(6-x), what is the natural domain of f(x)? Since
we can't divide by 0, the first part of the formula implies that x
should not equal 2. But the input to sqrt must be non-negative, so we
need 6-x>=0, which means 6>l;=x. Therefore the domain of the
function f(x) defined by this formula is all numbers less than or
equal to 6 except for 0.
An even sillier example
What if we wanted a function whose domain was the following collection
of numbers:
all numbers greater than 5 except for the numbers 7 and 8.
This is the sort of weird question which I believe that none of you
will ever see again outside of Math 135. Well, we can get rid of 7 and
8 by somehow making sure that pieces of the function involve dividing
by x-7 and also x-8. How about excluding numbers less than 5? Well, a
suitably shifted square root can do that: sqrt(x-5) excludes
everything to the left of 5. So one possible function whose domain is
as requested is f(x)=(1/{x-7})+(1/{x-8})+sqrt(x-8).
Please notice that this is not the only f(x). For example, the even
more silly formula
f(x)=(1/{x-7}19)+(1/{x-8}84)+sqrt(x-8) has the
same domain. Sigh.
Graph of a function If f(x) is a function, the collection of points in the plane whose coordinates are the order pairs (Input,Output) for all choices of Inputs is called the graph of the function. So if f(x)=x2, then (2,4) and (-2,4) and (3,9) are on the graph of f(x).
Condition for a collection of points in the plane to be a graph (the
Vertical Line Test)
A bunch of points in the plane will be the graph of a function exactly
when each vertical line hits the points at most one time. This is
because inputs are supposed to have only one output. So if the point
with coordinates (64,221) is on the graph of a function, the point
(64,-117) cannot be on the graph of that function. If the input 64
produces 221 as its output, it can't also produce -117. So the line
x=64 only intersects the graph at y=221.
Therefore if we want to "study" circles, for example, we'd better
think carefully, because a circle is not the graph of a function.
Some graphs Student should be familiar with the graph of f(x)=x2. This is a parabola. It touches 0 at 0 (I mean that (0,0) is on the graph and nothing else on the x axis is on the graph.) Also it is symmetric with respect to the y-axis. This is because f(x)=f(-x).
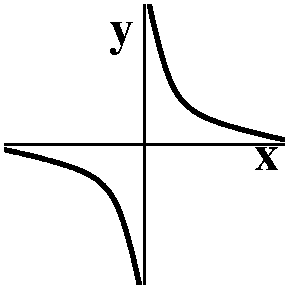 Another useful function is f(x)=1/x. When x is large positive, f(x) is
small positive. And when x is small and positive, f(x) is large and
positive. Since f(-x)=-f(x), what happens in quadrant I is flipped
into quadrant III.
Another useful function is f(x)=1/x. When x is large positive, f(x) is
small positive. And when x is small and positive, f(x) is large and
positive. Since f(-x)=-f(x), what happens in quadrant I is flipped
into quadrant III.
Straight lines
We will study rates of change a great deal, and those functions whose
graphs are straight lines have the simplest rates of change to analyze.
Vertical and horizontal lines
x=3 is a vertical line, and it is
not the graph of a function (because it hits itself more than once!).
Horizontal lines are the graphs of functions, although as functions
they aren't too interesting (the range of a horizontal line function
is just one number!). y=2 is a
horizontal line,
Lines given in slope-intercept form: these are graphs of functions. Functions defined by formulas such as f(x)=mx+b have graphs in the xy-plane defined by y=mx=b. This is called the slope-intercept form. The b refers to the point (0,b) on the y-axis where the line intersects the y-axis. The m refers to the amount of tilt in the function.
How functions related to lines change when inputs change
| If f(x)=mx+b, then the point (x,mx+b) is on the line y=mx+b. If we increase x to x+h, the corresponding point is (x+h,f(x+h)). The formula for f(x) makes this equal to (x+h,m(x+h)+b). This is (x+h,mx+b+mh). The change in the height is mh. This means that the change in x (from x to x+h) becomes a change in y of mh: the change in y is directly proportional to the change in x, and the constant of proportionality is m. |
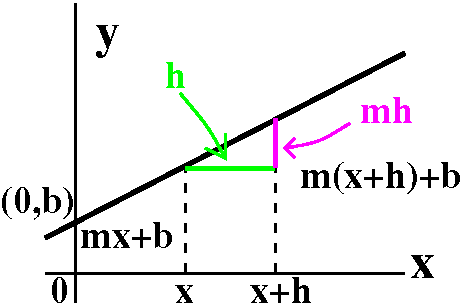
|
| Here is another way of looking at this computation. Think of the function as a box with various inputs. One input/output pair (x,mx+b). If we "kick" the input by h, then the corresponding pair is (x,m(x+h)+b). The output changes in a particularly simple way. |
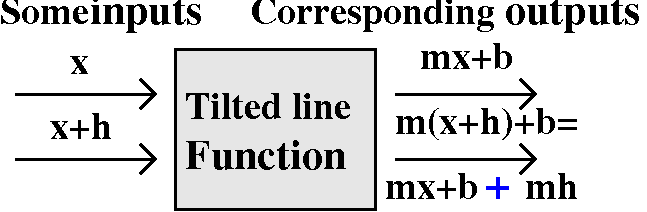
|
Let's look at some numbers ...
Maintained by greenfie@math.rutgers.edu and last modified 7/9/2006.