 The one integral you'll need ...
The one integral you'll need ...We know that
 The one integral you'll need ...
The one integral you'll need ...
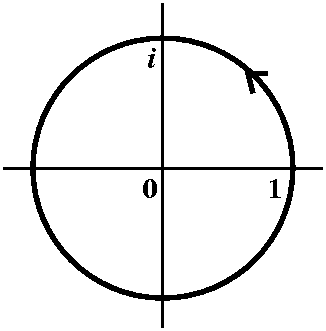
We know that ![]() |z|=1(1/z)dz=2Pi i. This is a vital fact.
|z|=1(1/z)dz=2Pi i. This is a vital fact.
And almost all the others are 0, anyway!
Well, here is a version of Cauchy's Theorem which relies totally on
Green's Theorem for its verification.
Cauchy's Theorem Suppose f(z) is analytic on and inside a
simple closed curve C. Then ![]() Cf(z) dz=0.
Cf(z) dz=0.
Proof Suppose that f(z)=u(x,y)+iv(x,y) where u and v are
real-valued functions (the real and imaginary parts of f). Then
f(z) dz=[u(x,y)+iv(x,y)][dx+idy]=[u(x,y)dx-v(x,y)dy]+i[v(x,y)dx+u(x,y)dy]. The
statement of Green's Theorem we will use is that ![]() Cpdx+qdy=
Cpdx+qdy=![]()
![]() Rqx-pydA where R is the
region bounded by C, dA means area (dxdy, if you would rather) and
both p and q are continuously differentiable everywhere in C and R
(even one point with a problem might make the equation invalid!).
Rqx-pydA where R is the
region bounded by C, dA means area (dxdy, if you would rather) and
both p and q are continuously differentiable everywhere in C and R
(even one point with a problem might make the equation invalid!).
 Let's look at
Let's look at ![]() C[u(x,y)dx-v(x,y)dy] with p=u and q=-v. Then
qx-py is -vx-uy. But one
of the Cauchy-Riemann equations is uy=-vx, so
the integrand in the double integral over R is 0.
C[u(x,y)dx-v(x,y)dy] with p=u and q=-v. Then
qx-py is -vx-uy. But one
of the Cauchy-Riemann equations is uy=-vx, so
the integrand in the double integral over R is 0.
Let's look at ![]() C[v(x,y)dx+u(x,y)dy] with p=v and q=u. Then
qx-py is ux-vy. The other
Cauchy-Riemann equation is ux=vy, so the
integrand in this use of Green's Theorem is 0 also.
C[v(x,y)dx+u(x,y)dy] with p=v and q=u. Then
qx-py is ux-vy. The other
Cauchy-Riemann equation is ux=vy, so the
integrand in this use of Green's Theorem is 0 also.
Both the real and imaginary parts are 0, so the integral is 0. We're done.
A note about Goursat
The key hypothesis in Cauchy's Theorem is that u and v are
continuously differentiable and satisfy the Cauchy-Riemann equations
in the appropriate region. But Goursat, late in the 19th
century, showed that that if f´(z) exists, then the conclusion of
Cauchy's Theorem follows. The continuity of the derivative is
unnecessary. The proof is in the text, and is quite clever. I won't
give it here, because to my knowledge the techniques of the proof are
rarely used in most of complex analysis.
 Deforming curves, not changing integrals
Deforming curves, not changing integrals
Here is a more complicated corollary of Cauchy's Theorem. It will allow
us to compute many more integrals by comparing them with one another.
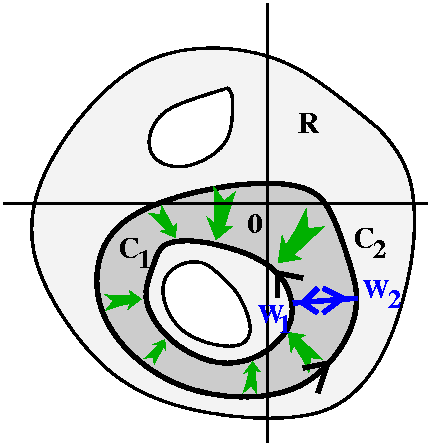
Corollary Suppose that f(z) is analytic in a region R, and that
C1 and C2 are simple closed curves in R. Suppose
also that the curves can be deformed, one into the other, all
inside the region R. Then ![]() C1f(z) dz=
C1f(z) dz=![]() C2f(z) dz.
C2f(z) dz.
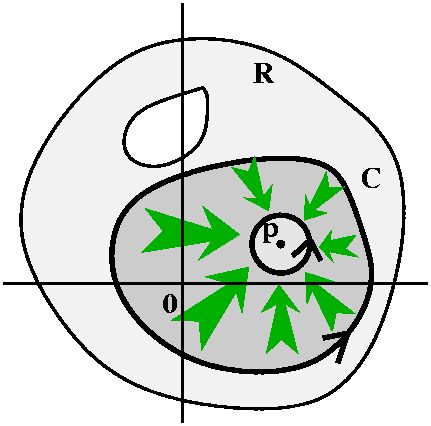
About the picture The picture attempts to illustrate the
situation described in the corollary. The region R is a connected open
set. The green arrows show how the curve
C2 is deformed into C1 through part of R
(but not through any of the holes!). If we picked a point
w2 on C2, the deformation would move it along a curve to a point w1 on
C1: let's call that curve B.
Proof Look at this curve, which is a sum of curves: start at
w2 and move along C2 until we get to
w2 again. Then move on B until we arrive at
w1. Now move backwards on C1, returning
to w1. Finish by moving backwards on B. The curve described
is C2+B-C1-B. We apply Cauchy's Theorem to that
curve, because f(z) is analytic on and inside the curve. The integral
is 0, but that means 0=![]() C2+B-C1-Bf(z) dz=
C2+B-C1-Bf(z) dz=![]() C2f(z) dz+
C2f(z) dz+![]() Bf(z) dz-
Bf(z) dz-![]() C1f(z) dz-
C1f(z) dz-![]() Bf(z) dz, so (since the B integrals cancel) we get
Bf(z) dz, so (since the B integrals cancel) we get
![]() C1f(z) dz=
C1f(z) dz=![]() C2f(z) dz.
C2f(z) dz.
Comment Here is some (negative) discussion about this
"proof". What do I mean precisely by "deformation"? I haven't
described this. Well, the notion can be described precisely, but I
won't do it in this course, and any situation I use this result in
this course will be one where a picture verifying the proof can be
explicitly drawn. Another objection can be applying Cauchy's Theorem
to the curve C2+B-C1-B. This really isn't a
simple closed curve. Again, this is true, but it is a limit of
simple closed curves (think of twin B's slightly separated, with
accompanying twin w2's and w1's). Each of those
curves would be simple closed curves, and each would have integral
equal to 0. The limiting curve with limiting integral would then also
have integral equal to 0. The idea is what I'm showing here, and I am
willing to admit that I've given up some precision!
A strange choice of function
 What I'm describing is a somewhat complicated setup. I don't think
I'll make it better by declaring that the whole procedure is one which
is used repeatedly in many areas of applied mathematics, engineering,
and physics. I will try, though, to describe the simplest incarnation
of the situation. So here are the ingredients:
What I'm describing is a somewhat complicated setup. I don't think
I'll make it better by declaring that the whole procedure is one which
is used repeatedly in many areas of applied mathematics, engineering,
and physics. I will try, though, to describe the simplest incarnation
of the situation. So here are the ingredients:
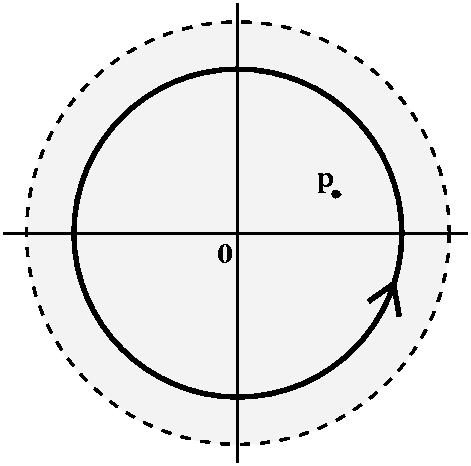
The Cauchy Integral Formula
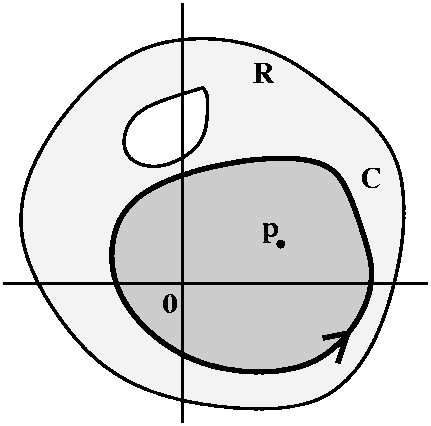
Suppose R is a connected open set, C is a simple closed curve whose
inside is contained entirely in R, p is a point inside C, and f is
analytic in R. Then f(p)={1/[2Pi i]}![]() C[f(z)]/[z-p]dz.
C[f(z)]/[z-p]dz.
Comment This is a fundamental and remarkable
result. Differentiability, that is, complex differentiability,
has the consequence that knowing the values of f on C determines the
values of f inside C. We need to sort of "average" the values
properly with weights determined by 1/[z-p] but everything is
determined by the boundary values. This has no counterpart in real
calculus. Certainly a differentiable function's value inside an
interval is not determined by what happens at the endpoints of the
interval.
 Expanding the Cauchy kernel
Expanding the Cauchy kernel
The Cauchy kernel is the function 1/[z-p]. It can be
manipulated algebraically in a variety of ways to give properties of
analytic functions. I'll do a basic example of this manipulation
here. Later we will do others.
I will suppose f(z) is analytic in some big disc centered at 0. For my
simple closed curve I will take a circle of radius R centered at
0. The radius will be smaller than the radius of the "big disc". Also
p will be some point inside the circle of radius R. Then I know
f(p)={1/[2Pi i]}![]() |z|=R[f(z)]/[z-p]dz. Consider 1/[z-p]. Since z is
on |z|=R and p is inside the circle, |p|<R=|z|. |p/z| is less than
1. So do this:
|z|=R[f(z)]/[z-p]dz. Consider 1/[z-p]. Since z is
on |z|=R and p is inside the circle, |p|<R=|z|. |p/z| is less than
1. So do this:
1/[z-p]=[1/z]/[1-{p/z}]: this is supposed to make you think of the
formula for the sum of a geometric series, a/[1-r], since we have
arranged for r to be p/z, a complex number of modulus less than 1. We
could write the whole infinite series, or just stop after a few
terms. Let me show you.
[1/z]/[1-{p/z}]=![]() n=0
n=0![]() pn/zn+1=
pn/zn+1= ![]() n=0Npn/zn+1+
n=0Npn/zn+1+![]() n=N+1
n=N+1![]() pn/zn+1=
pn/zn+1=![]() n=0Npn/zn+1+[pN+1/zN+2]/[1-{p/z}].
n=0Npn/zn+1+[pN+1/zN+2]/[1-{p/z}].
Here the error, the difference between
the partial sum and the whole series, is
[pN+1/zN+2]/[1-{p/z}]. The modulus of this is at
most (for any z on the circle)
[|p|N+1/RN+2]/[1-{|p|/R}] and since |p|/R<1,
this will go to 0 as N increases.
Now let's stuff the preceding stuff into the integral:
![]() |z|=R[f(z)]/[z-p]dz=
|z|=R[f(z)]/[z-p]dz=![]() |z|=R[f(z)](
|z|=R[f(z)](![]() n=0Npn/zn+1+error)dz
n=0Npn/zn+1+error)dz
The finite sum is really
![]() n=0N
n=0N![]() |z|=R[f(z)]
pn/zn+1dz=
|z|=R[f(z)]
pn/zn+1dz= ![]() n=0N(
n=0N(![]() |z|=R[f(z)]/zn+1dz)pn.
|z|=R[f(z)]/zn+1dz)pn.
The other term can be estimated by ML: the length is 2Pi R while the M is the maximum of |f| on the circle |z|=R multiplied by [|p|N+1/RN+2]/[1-{|p|/R}]. Since
|p|/R<1,
this will go to 0 as N increases. But put everything together. We have just shown that a certain infinite series converges, and since we know the Cauchy integral formula, we also know the sum of the infinite series.
f(p)=![]() n=0
n=0![]() anpn where
an=[1/{2Pi i}]
anpn where
an=[1/{2Pi i}]![]() |z|=R[f(z)]/zn+1dz.
|z|=R[f(z)]/zn+1dz.
Complex differentiability implies power series
Here is a general statement of the preceding result.
Theorem Suppose f(z) is analytic in a connected open set which
includes some disc centered at a point z0. Then there are
complex numbers {an}n=0![]() so that the series
so that the series ![]() n=0
n=0![]() an(z-z0)n converges at
least for all z in that disc centered at z0. Additionally,
the coefficients an are given by the formula
an=[1/{2Pi i}]
an(z-z0)n converges at
least for all z in that disc centered at z0. Additionally,
the coefficients an are given by the formula
an=[1/{2Pi i}]![]() |z-z0|=R[f(w)]/(w-z0)n+1dw
where R is any positive number less than the radius of the disc.
|z-z0|=R[f(w)]/(w-z0)n+1dw
where R is any positive number less than the radius of the disc.
Consequences
First, since power series can be differentiated inside their
radius of convergence, we see that a complex differentiable function
has a derivative which is itself a complex differentiable function!
This is totally unlike real calculus. For example, we know that |x|
can't be differentiated at 0. It has an antiderivative, let's call it
h(x), given piecewise by x2/2 for x>=0 and by
-x2/2 for z<0. The function h(x) has a derivative (just
|x|) and it does not have a second derivative. In the complex "realm",
functions always have more derivatives! There aren't any problems like
|x|. One derivative implies having infinitely many derivatives!
Second, we saw when we studied power series that a function can
have only one power series representation centered at a point. That
is, if f(z)=![]() n=0
n=0![]() an(z-z0)n and
f(z)=
an(z-z0)n and
f(z)=![]() n=0
n=0![]() bn(z-z0)n, both
converging near z0, then each an is equal to the
corresponding bn. In fact, since we can differentiate power
series, the power series must be a Taylor series:
an=(1/n!)f(n)(z0). But we can compare
the two descriptions of the coefficients an we have to
deduce the following result.
bn(z-z0)n, both
converging near z0, then each an is equal to the
corresponding bn. In fact, since we can differentiate power
series, the power series must be a Taylor series:
an=(1/n!)f(n)(z0). But we can compare
the two descriptions of the coefficients an we have to
deduce the following result.
The Cauchy Integral Formula for Derivatives
Suppose R is a connected open set, C is a simple closed curve whose
inside is contained entirely in R, p is a point inside C, and f is
analytic in R. Then for any positive integer n, f is n times
differentiable, and f(n)(p)={n!/[2Pi i]}![]() C[f(z)]/[(z-p)n+1]dz.
C[f(z)]/[(z-p)n+1]dz.
I think I proved this only for a circle which has p inside it, but any
C described in the theorem can be deformed to such a circle, so the
result is true also.
Maintained by greenfie@math.rutgers.edu and last modified 2/21/2008.