blob implies maximum modulus principle. harmonic function is locally the real part of an analytic function, so get maximum principle

Diary entry in progress! More to come.

Another point of view
If sqrt(z) has a removable singularity at 0, then we have an analytic function f(z) defined in a disc centered at 0 so that f(z)²=z. But then we can differentiate, and get 2f(z)f´(z)=1 for |z|<1. What if z=0? Well, as z-->0, I think that sqrt(z)-->0, so f(0)=0. But: 2·0·SOMETHING=1. This can't be true. So where is the contradiction?

Isolated singularity?
sqrt(z) does not have an isolated singularity at 0. There is no r>0 so that sqrt(z) is analytic in all of 0<|z|<r.In fact, if you look at sqrt(z) as it travels "around" a circle, you will see that when you get back to where you started, the arguments do not match up (one-half of 2Pi is not the same as 0, mod 2Pi). So there is a need to be a bit careful.

A Laurent series from the textbook
z/[sin(z)]².

Is residue additive?

Is residue multiplicative?

A residue e^z+(1/z)

A version of the grown-up Residue Theorem

A real integral

Goals

Exam?

Diary entry in progress! More to come.

Examples

The child's residue theorem

HOMEWORK

Diary entry in progress! More to come.

A return to the snowball
A few lectures ago we analyzed a problem about the melting of a snowball. I felt somewhat dissatisfied with the statement of the problem, because I didn't think the statement gave enough background. Let's look again at the problem. The setup is certainly simplified from "real life". The snowball is a sphere of radius r, with surface area S=4Pi r² and with volume V=[4/3]Pi r³. Put the snowball in a warm environment. The snowball will melt, of course. But how does it melt? If you think about it, the volume, V, will decrease, but more precisely it will decrease as the snowball absorbs heat. Heat is absorbed through the surface of the snowball. (I don't think in this model that we should imagine a little machine in the middle of the snowball radiating heat!) So I think that the rate of change of the snowball's volume should be directly proportional to the surface area. That is, there is a constant k so that dV/dt=kS. What happens to the radius of the snowball? Well, since V=[4/3]Pi r³, then (r varies!) dV/dt=[4/3]Pi 3r²[dr/dt]. Match this with dV/dt=kS, and, wow!, we see that dr/dt=k. So if we believe this model, then (as the original problem statement specifies) the radius of the snowball is constantly decreasing.

The surface area of a baby?
The snowball problem is quite relevant to certain aspects of biology. There are approximate formulas for the surface area of a baby. Such formulas can be useful if estimations of fluid balance (sweat) or temperature change are needed. Babies are smaller than adults, and such balances may be very unstable. If the balances are not maintained, illness and even death can result.

So how does the radius change?
What is (7.3)²?
What is (50)²?
The chip company
Biological systems are complicated
Prozac etc. Animal tranquilizers. The formula and a picture
But the ERROR
QotD
What is the approximate value of (7.98)^1/3? here I asked that people not use calculators, and use the linear approximation scheme discussed above Here's the whole story
Multiple names: linear approximation, differfential, etc. Bob Roundy Having little better to do this morning while at the car dealer's waiting room (car being serviced) I looked at the recent SI swimsuit issue, and of course paid the most attention to the masthead, and there you were, a MANAGER. Have you been a manager for long? I am confused. But it was good to see you there. I think it took about 45 to 50 minutes driving from Douglass to Busch yesterday afternoon, which at that time usually takes about 5 to 7 minutes. Driving was yucky.

Order of a zero
I should have mentioned, darn it, that there is an alternate characterization of the order of a zero. If f(z₀)=0, then either f(z) is always 0 everywhere, or if we look at the power series for f(z) centered at z₀, it will look lik SUM_n=0^infinity[f⁽ⁿ⁾(z₀)/n!](z-z₀)ⁿ. But if f does have a zero of order k, the first k terms (starting counting from the n=0 term!) are 0, so in fact, "locally" f(z)=SUM_n=k^infinity[f⁽ⁿ⁾(z₀)/n!](z-z₀)ⁿ with f^(k)(z₀) not 0. I can factor out (z-z₀)^k, and the power series will still converge. Let me call the sum g(z). Since g(z) is the sum of a convergent power series, g(z) is an analytic function, and g(z₀) is not 0 (because it is actually f^(k)0)/k!). Therefore, if f has a zero of order k at z₀ then we can write f(z)=(z-z₀)^kg(z), where g(z) is analytic, and g(z₀) is not 0 (so g(z) is not 0 near z₀, actually). The converse is true also. That is, if we can write f(z) as (z-z₀)^kg(z), where g(z) is analytic, and g(z₀) is not 0, we look at the power series for g(z) and reverse the procedure to see that the needed derivatives of f(z) are 0 until the k^th derivative.

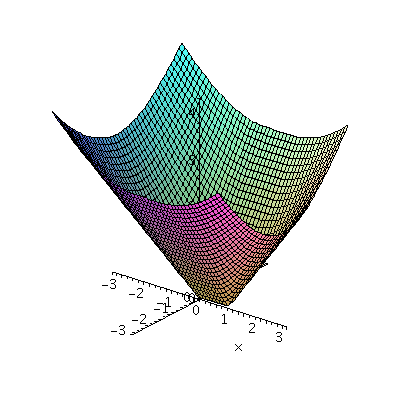
THIS  IS  NOT  COMPLEX  ANALYSIS  SO  YOU  CAN  DISREGARD  IT! In general, if one studies continuous functions on R2 very complicated things can happen. For example, consider the function which assigns to a point (x,y) its distance to the unit interval (the set of points (x,0) where x is between 0 and 1. Then the function is complicated. To the right is a Maple picture of its graph. It sticks to the bottom (it is equal to 0) on the whole interval. You will never, never, never, see such a function in a complex analysis course. Our functions are either 0 everywhere or they are zero at isolated points. The picture was produced using these commands: f:=(x,y)->piecewise(x<0,sqrt(x^2+y^2),x<1,abs(y),sqrt((x-1)^2+y^2)); plot3d(f(x,y),x=-3..3,y=-3..3,grid=[50,50]);

Isolated singularities
Examples If f(z) is not the zero function, and if f(z₀)=0, then the function Names Properties Reasons the pow RRST POLE C-W 2.4 20 24 do any 1 of these! 2.5 1 6 7 10 12 14 22b 2.6

Diary entry in progress! More to come.