I also mentioned that the word mantissa is currently used in computer architecture. As used there, it refers to the fractional part of a floating point number.

Another aspect of substitution was addressed. Suppose a definite integral is given. Should the limits in x also be changed to limits in u, or should the "return to x-land" always be done and then x limits used? I tried to give a number of examples in order to illustrate the two possibilities. I usually go back to x-land and use the original limits because I make mistakes, sometimes many mistakes, and the return to x means I don't need to change the limits. Other people have other opinions.

I computed some areas between two curves. I used the general formulation of _x=Left^y=RightTop(x)-Bottom(x) dx and illustrated this using examples where Top and Bottom have different signs.

I did a very few examples where the area is computed dy, so the formula above becomes _y=Bottom^y=TopRight(y)-Left(y) dy. This is discussed in section 6.1.

Mantissa n. [L., an addition, makeweight; of Tuscan origin.] (Math.) The decimal part of a logarithm, as distinguished from the integral part, or characteristic.

Does it necessarily follow that logarithms themselves are obsolete? While at first glance this may seem to be true, I "analyzed" the following function:
L(x)=_t=1^t=x(1/T)DT.

We showed that L´(x)=1/x using FTC. Then we used the Chain Rule and FTC to see that if A is some fixed positive number, and W(x)=L(Ax), then W´(x)=1/x also (almost a miracle in that the effect of the A's cancel!). Then the Mean Value Theorem states that W(x)-L(x)=a constant since the derivatives of L and W are identical. If we put x=1, L(1)=0 and W(1)=L(A). Therefore the constant is L(A), and we see that since W(x)=L(Ax)BB,
L(Ax)=L(A)+L(x)
The "profile" function used to define L (that is, 1/t) is not a very complicated function. So if we are interested in computing definite integrals, we'd better be able to compute L, and the equation above may be used to simplify computations of L.

Indeed, if we use the following Maple instruction:

> f:=n->evalf(add((1/(1+(j/n)))*(1/n),j=1..n));

Number of subdivisions	Approximate value of the sum
10	0.6687714032
100	0.6906534305
1,000	0.6928972431
10,000	0.6931221812
100,000	0.6931446806

Of course, as I mentioned in class, these are approximations to ln(2), whose 10-digit value is 0.6931471806. By the way, even the computer gets tired computing Riemann sums and the last entry in the table above takes about three-quarters of a second on a moderately fast PC. Next semester we'll see numerical methods which give much better accuracy with much less computation. But the point I was trying to make here was that the conceptual idea of logs was useful, even though the computational need for logs may be obsolete.

There are many other integrals which must be computed, and which satisfy quite weird equations that come from the Chain Rule and FTC. So this whole development is something you will likely see again.

The remainder of the lecture was devoted to a certain method for obtaining indefinite integrals: substitution.

We began by studying (x³+5)⁴⁰⁰ x² dx.
This is not a random integral, at all. If I omitted the x² or changed it much, the integral would be quite difficult to do "by hand". The integrand (the function to be integrated) is "just" a polynomial, so there is no great theoretical obstacle to computing it. The practical difficulty of obtaining a formula for the antiderivative is what I wish to address.

One way of computing the indefinite integral is to "unfold" or "expand" (x³+5)⁴⁰⁰. By hand (even by computer!) this takes a bit of time and storage space! In fact, we recognized that we could do this by sort of guessing and reversing the Chain Rule. It is important to remember, though, that the derivative of a product of two functions is NOT equal to the product of the derivatives!

So we guesses. I wrote the Chain Rule and we identified the pieces of the computation. Then I introduced the Substitution Method, which is essentially a "bookkeeping" strategy to keep track of constants as we go from "x-land" to "u-land".

Here (x³+5)⁴⁰⁰ x² dx is in x-land. If u=x³+5, then du/dx=3x² and du=3x²dx and (1/3)du=x²dx. The entire integral, translated into u-land, is then u⁴⁰⁰(1/3)du. This is easy to compute in u-land, and the result is (1/401)u⁴⁰¹(1/3)+C. Now we go back to x-land, and the final answer is (1/401)(x³+5)⁴⁰¹(1/3)+C.

I computed some other indefinite integrals with this method:

1. x sqrt(4-x²) dx (use u=4-x²)
2. cos(3x-7) dx (use u=3x-7)
3. [(x+1)/(x²+2x+117)] dx (use u=x²+2x+117).

We then computed the indefinite integral of tan(x). Since tan(x)=sin(x)/cos(x), the substitution u=cos(x) leads us to the answer -ln(cos(x))+C. Like any other indefinite integral, this can be checked using differentiation. And this indefinite integral again shows that logs will be needed in calculus!

Then I "discussed" two problems from section 5.5 of the text:
#58, which was ₀¹x e^-x2dx. The antiderivative can be computed with u=-x².
#56, which was ₀²dx/(2x-3)². I remarked that this was an error in the text (a misprint!). 2x-3=0 when x=3/2, and therefore a simple graph should convince you that the definite integral (the "area") must be infinite. If the upper bound of the integral is changed from 2 to 1, then the substitution u=2x-3 will allow us to compute the value of this definite integral.

Number of subdivisions	Approximate value of the sum
10	0.7105093416
100	0.6714629470
1,000	0.6671601350
10,000	0.6667164623
100,000	0.6666716592

Maybe these results which I computed with Maple make the assertion that the limit of the Riemann sums exists and equals 2/3 more believable.

Numbers are numbers are numbers

₃⁵[x³]/[3+cos(x²)]dx     ₃⁵[u³]/[3+cos(u²)]du     ₃⁵[t³]/[3+cos(t²)]dt     ₃⁵[v³]/[3+cos(v²)]dv     ₃⁵[s³]/[3+cos(s²)]ds

I then tried to do some simple exercises with part of the FTC. It was something like this: if f(x)=₂^x cos(t⁷)dt, then f'(x)=cos(x⁷). And then if f(x)=₂^x cos(s⁷)ds, then f'(x)=cos(x⁷). The "dummy variable" strikes again!

How about if f(x)=_x³ cos(s⁷)ds? Here we need to think a bit about definite integrals. Here's a fact:
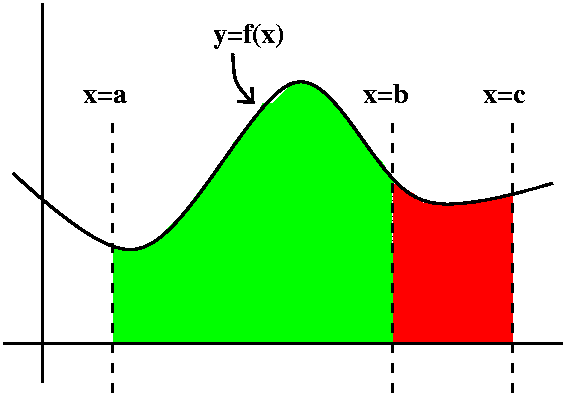
Adding areas fact
If a<b<c, and if f is continuous on the interval from a to c, then _a^bf+ _b^cf= _a^cf.
So adjoining areas can be added up (something many of us learn as infants, and it is a rather subtle fact!). But we also agree that _a^a=0: that is, a region with 0 width should have 0 area. Suppose we make some changes in the adding areas fact, and transform c into a. Then the right-hand side becomes 0, and we see that _a^bf+ _b^af=0, which is the same as _a^bf=-_b^af. Therefore if we want to be able to add areas and if we want to recognize that lines have area=0, we must also acknowledge that interchanging limits causes a - sign to prefix the integral. Therefore we can do this:
if f(x)=_x³ cos(s⁷)ds, then f(x)=-₃^xcos(s⁷)ds so that f'(x) must be -cos(x⁷). Amazing! (Well, not really, but ...)

We can even do one further variation. Suppose F(x)=_-2^xsqrt(1+w⁶)dw. Then we know that F'(x)=sqrt(1+x⁶) by FTC. What if I ask the following ludicrous question:
Suppose G(x)=_-2^cos(x)sqrt(1+w⁶)dw. What is G'(x)?
How can we think about this? Since we know F'(x), and G(x)=F(cos(x)), this is just (!?) an application of the Chain Rule (!): G'(x)=F'(cos(x))·(the derivative of cos)=sqrt(1+(cos(x))⁶)·(-sin(x)). Whew! This takes some getting used to.

A paradigm shift
Several cultures invented approaches similar to what we've done here to compute quantities such as area and volume and mass and moments. These cultures (which were located in areas corresponding to present day China, India, Egypt, and Greece) all used the same general approach: chop up the quantity into smaller pieces, approximate the pieces, take the sum, and then "compute" the limit. Of course the notation was different, but the ideas were fundamentally the same. Very clever algebraic and numerical techniques were used. See section 5.2 for information about this. It turns out that studying what seems to be a harder problem (!) earns both conceptual and computational advantages. So I attempted to do that for the specific case of f(x)=(3/2)x²+(1/2)x. I wanted to compute the area "under" this curve from 1 to 2. This is the area of the region bounded by x=1, x=2, the x-axis, and y=f(x). A direct approach is possible, but instead I studied the following problem:

Suppose A(r) is the area bounded by x=1, x=R, y=f(x), and the x-axis. What can we learn about A(r)?

The Fundamental Theorem of Calculus
I stated and commented on the Fundamental Theorem of Calculus (FTC). Then I applied it to about half a dozen problems in section 5.3 of the textbook.

Maple data and its construction
I also gave some data which I had computed using Maple. Maple is a program which is available on the Eden system and on many other computer systems around campus, since Rutgers has a site license. It is quite useful.

> f:=x->(3/2)*x^2+(1/2)*x;
                                          2
                           f := x -> 3/2 x  + 1/2 x

> f(1);A
                                       2

> f(2);
                                       7

> add(f(1+(j/50))*(1/50),j=1..50);
                                     43001
                                     -----
                                     10000

> evalf(%);
                                  4.300100000

Number of subdivisions	Approximate answer	Predicted error
50	4.300100000	<.1
500	4.255001000	<.01
5,000	4.250500100	<.001
50,000	4.250050000	<.0001
500,000	4.250005000	<.00001

We used FTC to see that the "true" value of the definite integral was 4.25 (maybe not too much of a surprise). I mentioned that the last number (which involved a half-million subdivisions!) took about 16 seconds to compute. I consider that a lot of time.

Given a function f(x) defined on an interval [a,b], I wanted to compute the area "enclosed" by y=f(x), x=a, x=b, and the x-axis. I discussed these technical words and phrases:

1. Partition of [a,b].
2. Sample points.
3. Riemann sum.

I analyzed Riemann sums for a piecewise defined function, something like f(x)=2 if x<4 and f(x)=5 for x>=4, on the interval from 2 to 6. We were able to understand "any" Riemann sum, and we showed that if the length of the largest subinterval in the partition was small, then the Riemann sums would approach what we naively might call the area "under" the curve.

I then moved on to (3/2)x³+(1/2)x on the interval [1,2]. First we looked at a Riemann sum which divided the interval into 50 equal parts, and we showed by a rather simple (but clever!) geometric argument that we could estimate the "error" of that specific sum from the "true value" of the area. Then I turned things around, and asked if we could find a Riemann sum which was within 1/100,000 of the true value. We did this.

I then defined the definite integral. This is all in section 5.2 of the text.

A homily
Before I returned the second exam, I made some remarks which I attempt to record here. I apologize if these comments are too direct and too personal, but I believe they are truthful and may be necessary.

1. The exam
   With the possible exception of the last problem, all of the problems on this exam were routine. Students should have looked at the problems and realized that they had done ten problems just like them (or should have done ten such problems!). Most of the problems were copied directly from the textbook or review material. I graded 6 of the 8 problems on the exam. Here are some specific remarks.
   The first problem was the most routine. When I looked at a solution to that problem, I could tell instantly if a student knew what to do. The problem asks for the max/min values of a function on an interval. The function, a low-degree polynomial, is simple. So: differentiate the polynomial, find the critical points, compare the value of the function at the endpoints and the critical points in the interval. This is perhaps 4 or 5 lines of computation. Anything else is overwork and misunderstanding.
   The seventh problem, a graphing problem, was worth the most points and was the most intricate. It is analogous to an essay in a composition course. The solutions written by many students contained contradictory ideas, which I found very difficult to understand. The problem asks for coherent, deductive reasoning and achieving this should be possible.
2. Personal
   I repeat what I said in class. I don't think any law forces students to learn calculus. So perhaps there's little reason to attend lectures or recitations. The recitations are likely to be the most helpful part of class attendance. The instructor is very approachable. But many students don't come to these classes and this is likely to be an important reason for their lack of success.
   At the beginning of the semester, I declared that this course is different from a high school class chiefly in that it requires much more effort and responsibility from students. For example, I would expect that in a high school class, perhaps 30 to 40 optimization problems could be discussed in class, either by the instructor or with students working in groups. There was time to discuss only 4 or 5 of these problems during the lectures. This difference must be made up by student effort: you can't learn this material by sitting and watching the lecturer and/or the recitation instructor only, no matter how sympathetic or learned they are. An exaggerated metaphor: would you learn to play the trumpet by watching and listening to Wynton Marsalis?
   Students who want to study and successfully understand almost any scientific, engineering or technical subject must learn basic calculus. If you don't learn this stuff, you won't be able to learn that stuff: very simple! Effort and practice are most important. Yes, intelligence and talent are good, but I really believe that almost all students have sufficient intelligence and talent. Persistence is the most important factor in learning mathematics.
3. Competitiveness
   One reason to learn this material, aside from what I think is its intrinsic beauty and interest, is that such knowledge qualifies people for good jobs. The initial salary and benefits package for many engineering jobs requiring a bachelor's degree is quite good. On the other hand, look at the deal from the company or employer side: why should a person be hired if they can't do the job? Please realize that in a few countries I can name, there are more than a quarter million people graduating each year who can write solutions to the problems on the second exam quite well. You should be worried if you're going to compete with them.
   Does Math 151 give sufficient support for learning? My part is chiefly to give prepared lectures and to write appropriate exams. I try to support student learning in other ways, also. But much -- most! -- of the learning will follow from student effort. As you go through life you'll need to take more and more responsibility for your own learning.
   Suppose a person knew how to program in, say, Visual Basic 20 or 30 years ago. That was good. But if that person insisted, for a whole career, on only doing what always was done, that career wouldn't have been very rewarding. Much of the time you'll need to learn new things, new ideas, new methods. Sometimes this will involve lots of work. I know, even in my own teaching "racket", that I've had to learn new ways of thought and new methods, even for subjects which I would hope I understood fairly well by now. You will need to periodically reinvent yourself.
4. Exam grades
   The exam grades were quite low. You can improve your grade. In recitations on Thursday, November 30, students will have 30 minutes to earn 30 points, which will be added to their second exam grades. The topics will be the same as those tested by the second exam, along with antiderivatives. Good luck, really, seriously. I will succeed as a teacher if you succeed as a student.

• Technical computations:
  • The chain rule
  • Implicit differentiation
• Consequences of the tangent line
  • Linear approximation, tangent line approximation, linearization, "differentials"
  • Newton's method
  • L'Hopital's rule
• The Mean Value Theorem. The theory:
  • If f´=0 in an interval, then f=a constant in that interval (so two functions with the same derivative must differ by a constant)
  • If f´>0 in an interval, then f is increasing in that interval.
  • If f´<0 in an interval, then f is decreasing in that interval.
• Graphing a function
  • The first derivative: its sign indicates {in|de}creasing behavior.
  • The second derivative: its sign indicates concave {up|down} on the graph.
  • Critical points; local and global max and min; inflection points
• "Stories"
  • Related rates
  • Optimizing a function (max/min in an interval)

Again ...
I discussed how to "solve" the initial value problem f´(x)=sqrt(1+x³) with f(0)=2. From the qualitative aspect (using direction fields) I knew that f(1)>f(0)=2. What if we wanted more precise information? I showed how we can do "simple arithmetic" motivated by the Mean Value Theorem, and approximate f(1) as closely as we wished.

I began with

The problem of area

We will try to be a bit more indirect, more sneaky, and learn properties of area which will let us approximate what we want. What properties does "area" have?

1. Area should assign a region in the plane a non-negative number.
   Comment This certainly seems reasonable. But there are things in the plane which have zero area: one point, or a line both should have area equal to 0.
2. If one region, R₁, is inside another region, R₂, then the area of R₁ is less than or equal to the area of R₂.
   Comment The areas could actually be equal. For example, R₁ could be R₂ with just 1 point taken out!
3. Two regions which are congruent must have the same area.
   Comment Again, this seems reasonable, but then the word "congruent" needs to be dealt with. The on-line dictionary I use says "congruent" means "coinciding exactly when superimposed" and if clarity is wanted, then the words there need to be explained further. In the plane, two shapes or blobs are congruent if we can move them one onto the other. Sometimes "flips" are allowed.
4. If a region R is made up of two regions R₁ and R₂ which don't overlap, then the area of R is equal to the sum of the area of R₁ and the area of R₂.
   Comment In fact, as was pointed out, we can weaken the hypothesis a bit here. The two regions R₁ and R₂ can overlap as long as the overlapping takes place only on the boundary.
5. The area of a rectangle is its length multiplied by its width.
   Comment Without this assertion, assigning area to be 0 to every region would obey all the previous rules! Of course that's a silly example, but it does show that some reference must be made to "normalize" area, to give it units or something.

With RULES A THROUGH E we can begin an organized campaign to compute or approximate areas. For example, here is how we could compute the area of a typical blob. I will use the RULES in the analysis that follows. I would first slice the blob by line segments to get something which had at most one curvy side. I will be done if I describe to you how to compute the area of each of the pieces. I will specialize to one of the pieces, and assert that similar things can be done to all of the other pieces. So:

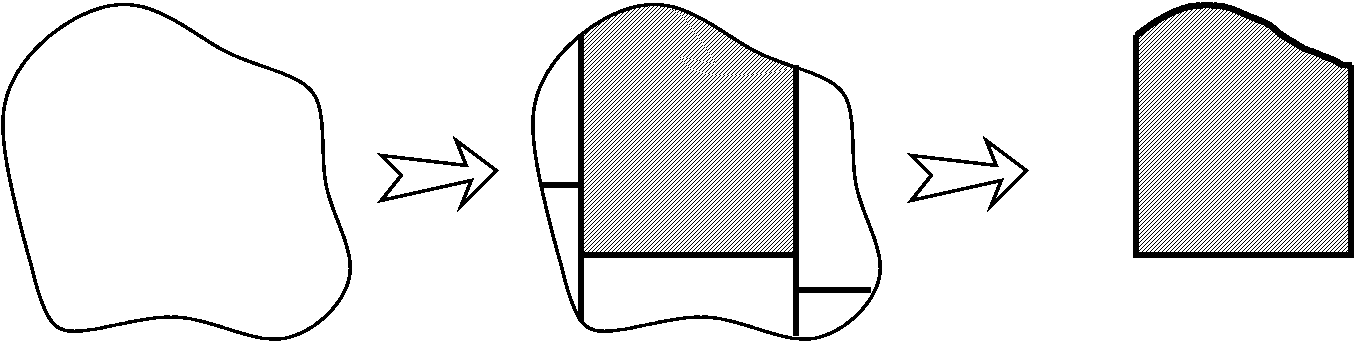
Now I can approximate inside this piece of the blob and outside the blob by rectangles, and since I know the area of a rectangle, I can get some estimate of the area of the piece of the blob.

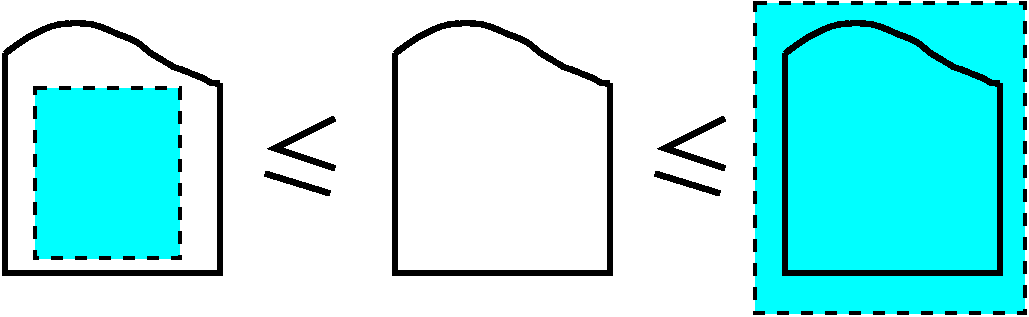
Of course this estimate is not so good, but we could improve it with some sort of scheme like this:

So we can get a collection of approximations which get closer and closer and closer to the true value of the area, and maybe that's good enough. (It is, in many cases.)

As I remarked, another instructor told me of a wonderful way of bringing home the idea of area: look at your hand and ask, what is its area? Giving a "good" answer to this may be difficult and involve quite a lot of approximation.

Maintained by greenfie@math.rutgers.edu and last modified 10/16/2006.