Mr. Rowland's presence and guidance were extremely valuable during this meeting.  

Rice
Problem statement: Rice
Search for positive integer solutions to the equation x2+y2+z2=w2. Are there any? 0Eliminate any duplicates and solutions that are not primitive. What can you say about these solutions? In particular, which variables must be odd and which must be even?
I think that Ms. Kalia reported for Rice. A procedure was shown and some results were displayed. We had quite a debate about why there seemed to be no solutions to the equation x2+y2+z2=w2 having w an even integer. There were actually lots of solutions, but none of the solutions found had an even w. Why? The only way we could get an even w, since ODD2 is ODD and EVEN2 is EVEN always (look at (2n+1)2 which is 4n2+4n+1 and (2n)2 which is 4n2) is if all of x, y, and z are even (not allowed since then all of x, y, z, and w would be even, and they would have a common factor and not be primitive) of if two of x, y, z were odd, and one was even. Well, we settled this, but it took some effort. We needed to think about multiples of 4. Consider:
     (4n)2=16n2
     (4n+1)2=(4n)2+8n+1=16n2+8n+1
     (4n+2)2=(4n)2+16n+4=16n2+8n+4
     (4n+3)2=(4n)2+24n+9=16n2+24n+8+1
So this means that odd squares have remainders of 1 when divided by 4, and the sum of two of them must have remainder of 2 when divided by 4. But even numbers have remainders of 0 when divided by 4. Therefore the sum of two ODD squares and one EVEN square can't be equal to an EVEN square.

 

Wheat
Problem statement: Wheat
We looked at the equations x2+y2=z2 and x2+y2=2z2 and x2+y2=3z2. The number of positive integer solutions seems to change based on the multiplier of z2. Begin to check systematically. That is, look at x2+y2=Qz2 when Q=4, Q=5, and so on. For some Q's, the equation has solutions, and for other Q's it doesn't seem to have solutions. Accumulate some evidence. You may then want to consult the The On-Line Encyclopedia of Integer Sequences and see if you can get some insight.
Here the initial report was given by Who, please?. The collection of Q's for which x2+y2=Qz2 was investigated using a procedure which was displayed. The numbers which seemed to have solutions were 1, 2, 5, 10, 13, 17, ... the numbers are the starting part of integer sequence A008784. We discussed the characterization(s) given there of these numbers. Here is part of one of the phrases describing the entries in the sequence: "Numbers whose prime divisors all congruent to 1 mod 4, with the exception of at most a single factor of 2." Mr. Rowland and I attempted to explain the phrase "congruent to 1 mod 4" This is the following: if N is a positive integer, then we can attempt to divide N by 4. The result will be a quotient, Q, and a remainder, R. The remainder will be 0, 1, 2, or 3. So we have N=4Q+R, and we also say that N is congruent to R mod 4, meaning that the difference between N and r is evenly divisible by 4. I noted that the relevance of this description to the solvability of the original equation was not at all obvious, and would take about half of a semester of number theory, an upper-level math course, to verify.

Jointly Mr. Rowland and I noted a wonderful and difficult to state fact: suppose we have some sort of equation which involves integers. There may or may not be integer solutions to this equation. There is no general method ("decision procedure" or algorithm) which tells if there are integer solutions. This fact is difficult to state precisely and it is quite difficult to understand. But it is true.

 

Corn
Problem statement: Corn
There certainly seem to be lots of Pythagorean triples. What if we start putting extra conditions on them?
  • y close to z
    Suppose we want positive integer solutions to x2+y2=z2 but look for y's which are close to the corresponding z's. You can search for ...
         Solutions with y=z-1;
         solutions with y=z-2;
         solutions with y=z-3;
         etc.
  • x close to y
    Suppose we want positive integer solutions to x2+y2=z2 but look for x's which are close to the corresponding y's. You can search for
         Solutions with x=y+1;
         solutions with x=y+2;
         solutions with x=y+3;
         etc.
    • Here I think the report was given by Mr. Shah. There are many (primitive) Pythagorean triples which are:
    Almost isoceles: so there are integers x and z with x2+(x+1)2=z2. Although there seem to be a lot of them, they aren't very common. Indeed, there just seemed to be only one or two new ones each time we increased the "search space" by a power of 10 (from 10 to 100 to 1,000 to 10,000 to ... etc.). The equation x2+(x+1)2=z2 turns out to be a form of Pell's equation which was studied in Europe about 250 years ago. In fact, individuals in India had found methods of solution a thousand years before that, and special cases had been investigated in Greece and India even two thousand years ago. There have been smart (and crazy!) people around for quite a while. (This was going to be part of my presentation in meeting #8!)

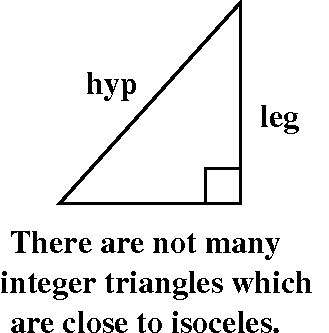
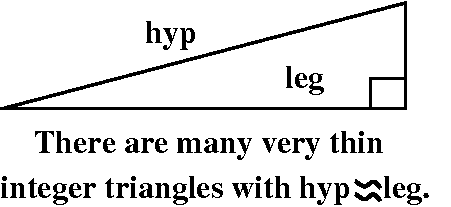
    There turn out to be many, many long thin Pythagorean triangles. That is, x2+y2=(x+1)2 has many solutions. This equation (square things out) is just y2=2x+1. And, yes, there are many many odd numbers which are squares.

     

    Barley
    Problem statement: Barley
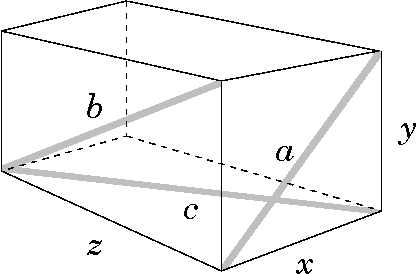
    Suppose we have a rectangular box with positive integer side lengths x, y, and z. The sides of this box have many different diagonals but they only come in 3 different lengths, say a, b, and c. A drawing of such a box is shown to the right. Can all of the six values (x, y, z, a, b, and c) be positive integers? So we want positive integer solutions to these equations:
    x2+y2=a2;   y2+z2=b2;   z2+x2=c2.
    Solutions to this system are called Euler bricks. Please search for solutions.
    Comment If we also want the box's main diagonal (the "space diagonal" connecting the most distant corners) to be an integer -- that is, x2+y2+z2=d2 where d is an integer -- then no solution is known. It's not known if there is any solution, even one not yet found!
    I think this group was the first to report, and I think Mr. Hard for his presentation. He described how to search for these Euler bricks. (Mr. Rowland knew this reference, which allowed us to cheat a bit, so we knew that a search would be successful in a certain range.) A direct search, with, say, x, y, and z all running from 1 to 300 would take examination of 27,000,000 cases. Even for a computer this is a big number. So first the Barley team searched for x and y so that sqrt(x2+y2) was an integer, and then they looked for a suitable z. Even with this method, which considerably pruned the "search tree", the Maple program took about 160 seconds to find several Euler edge lengths. Mr. Hard also used Matlab to do a similar search, and this search was done in a bit more than 3 seconds. This difference was rather surprising to both Mr. Rowland and me. After class, I think that Mr. Esmet showed us a similar search program in Java which took one-tenth the time taken by Matlab! All of this is a very interesting contrast.

    Further comments So Mr. Rowland tried this search in Mathematica, which is another sort of general purpose symbolic/numerical/graphical program. There the search took about 1 second, but also he tried Maple and his version of a similar program took about half a second. This seemed very different from what Mr. Hard had reported. Indeed, Mr. Hard told us that his program had not done the pruning above, so maybe Maple and Mathematica are not so different from Matlab. Still the Java implementation is better, which is not surprising if you know about the designs and purposes of all of these languages. This is still all interesting if one is a fanatic about efficiency. And efficiency matters, because it determines whether certain computations are truly realistic or merely hypothetical!

    Maintained by greenfie@math.rutgers.edu and last modified 10/28/2008.