Let's call this surface A: x^3+5zy^2-4z^2=3 and this one B: y^4-7z-2x^2 =5.
It is very difficult to find out the exact equation for where A and B intersect, but it is not necessary. Your original intuition could follow that this line tangent to C (lets call it T) is a line that is tangent to both A and B. Therefore, this line is going to reside in the tangent planes to A and B, and go through the point (3,2,-1). Unless both tangent planes are equal, there will be 1 distinct line through tangent planes to A and B at (3,2,-1).
We start by finding each tangent plane. The book says that a tangent plane to a curve S through (X_0,Y_0,Z_0) is Z-Z_0=(dz/dx)(X-X_0)+(dz/dy)(Y-Y_0).
A: (we must do implicit differentiation of x^3+5zy^2-4z^2=3)
dz/dx:
3x^2+5y^2(dz/dx)-8z(dz/dx)=0 so dz/dx=3x^2)/(8z-5y^2) and at (3,2,-1),
dz/dx=-27/28.
dz/dy:
10yz + 5y^2(dz/dy)-8z(dz/dy)=0 so dz/dy=(10yz)/(8z-5y^2) and at (3,2,-1),
dz/dy=20/28.
B: (regular partial differentiation from y^4-7z-2x^2=5)
So dz/dx=(-4/7)x and at (3,2,-1), dz/dx=-12/7.
And dz/dy=(2/7)y and at (3,2,-1), dz/dy=4/7.
The normal vector for the tangent plane to A at (3,2,-1) is
<-(27/28),(20/28),-1>.
The normal vector for the tangent plane to B at (3,2,-1) is
<-(12/7),(4/7),-1>.
Well all lines in the tangent plane are perpendicular to the normal vector, so our tangent line T must be perpendicular to both normal vectors of the planes A and B. The cross product of these normal vectors will be a vector in the direction of T.
The cross product is <9/7,3/4,33/49>. We can use <3/7,1/4,11/49> (just divided by common factor of 3 which does not affect the direction).
Sent by Matt Brown on Fri, 7 Mar 2003 04:03:57
I might have just taken the gradient of the left-hand sides of each of
the equations x^3+5y^2z-4z^2=3 and y^4-7z-2x^2=5, remembering that
gradient vectors are perpendicular to level "sets" (curves in two
dimensions, surfaces in three dimensions, etc.). Then I would "plug
in"
(3,2,-1). That way I have to think and remember less.
You can try these Maple
commands:
Now we have
The answer(I hope I didn't make any mistakes):
x=3+(3/7)t
y=2+(1/4)t
z=-1+(11/49)t
 Message from the management
Message from the management
with(plots):
F:=(x,y,z)->x^3+5*y^2*z-4*z^2;
G:=(x,y,z)->y^4-7*z-2*x^2;
RED:=implicitplot3d(F(x,y,z)=3,x=1..5,y=0..4,z=-3..1,axes=normal,color=red,grid=[20,20,20]):
BLUE:=implicitplot3d(G(x,y,z)=5,x=1..5,y=0..4,z=-3..1,axes=normal,color=blue,grid=[20,20,20]):
display3d({RED,BLUE});
A view of what is produced is included here, so you perhaps can "see"
the two surfaces and the intersection curve. It is remarkable to me
that the tangent line can be described so easily. The curve itself is
difficult to describe algebraically.
 Message from the management
Message from the management
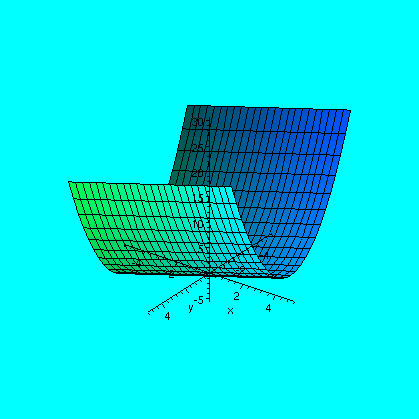 Message from the management
Message from the management