• What is the coefficient of x⁶y⁴z² in (x+y+z)¹²?

• What is an approximation to the only root of 3x+cos(2x²)=0?

• What do the points (x,y,z) which satisfy the equation z²+(x²+y²-1)(x²+y²-2)=0 look like?

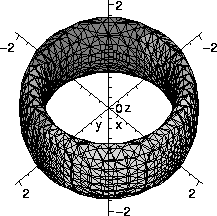
The freedom to work with "exact" symbolic computation, with numerical approximation (with specified accuracy), and with visual display of data (humans learn much more from pictures than from lists of numbers!) is very useful.

Almost all of my teaching and research is now improved by access to powerful programs which allow me to experiment. I can get examples which are useful for instruction. I've also used these programs to try to understand complicated phenomena which I could not easily explain (specific examples are available!).

Computer help
Many students have graphing calculators. These are useful, but are limited by speed and memory size. Simple errors may occur. There are large computer programs with powerful numerical, symbolic, and graphical capabilities. These still may have the potential for errors, but much effort has gone into their programming. The most widely distributed programs are Maple, Mathematica, and Derive. In this course Maple will be favored, since almost every large computer system at Rutgers has Maple installed. These programs are not infallible but they can be very helpful. Other programs available with special capabilities. For example, Matlab, a program originally directed at problems of linear algebra, is installed on systems of the Engineering School.

Also, I usually use Maple because I have a copy at home. Students should learn how to use such programs.

Maple in Math 291 on eden
Please become familiar with the capabilities of Maple. Most students have accounts on the eden system. In order to effectively use Maple with the xmaple interface students need to get out of the menu system which they may have with their default eden login. To do this they need to find the command revert on their menu system, enable this command, and then logoff and logon again. They will then get a unix prompt and will be able to begin the sequence of exercises described here. Students who want the menu system back will need to remove the file .nolush and the menu system will return at their next login.

A year ago Professor Costin wrote a nice sequence of "labs" to teach students about the capabilities of Maple. You may want to work though them: see the paragraph labeled Maple. I hope to have a sequence of exercises introducing Maple to students in a week or so. Also I very much would like students to use Maple (and/or their graphing calculators) when this is appropriate.

The Maple field trip
The class will meet in the instructional computer lab ARC 116 (an X-term "lab" inside the Busch Campus Computing Center) on Thursday, January 30, from 4:30 to 5:50 PM. I hope that students will work through the following sequence of exercises (copies will be provided). Here are links to PDF files. These are slightly changed (and, I hope, improved!) versions of the handouts used last semester.

The last question asked on the fourth handout is difficult. I've written a complete solution which is quite long, but verifying clear (!) geometric facts is often tedious.

How to get those answers
The answers to the questions above were obtained with the following Maple instructions. Please: this is not an effort to impress you, but rather to show you how easy is is to get the answers.

• coeff(coeff(coeff((x+y+z)^12,x^6),y^4),z^2);
  The command coeff(P,monomial) finds the coefficient of the monomial in the expression P. Layering three repetitions of coeff finds the desired coefficient.

• fsolve(3*x+cos(2*x^2)=0,x);
  fsolve is a general "floating point" approximate equation solver. Care must be used if there's more than one root. There are also symbolic solvers, useful when there is a nice formula for the solution.

• with(plots):
  V:=((x^2+y^2)-1):
  W:=((x^2+y^2)-2):
  implicitplot3d(-V*W=z^2,x=-2..2,y=-2..2,z=-2..2,grid=[30,30,30],axes=normal);
  The implicitplot3d command allows implicit equations to be sketched. Since Maple has so many functions and libraries available, many need to be specifically loaded before use. The command with(plots) loads a variety of plotting commands. The implicitplot3d command has a wide variety of options. The grid option gives control over the spacing of sample points. Of course increasing the number of sample points "costs" computational time.

Programming in Maple
Maple is also a programming environment. Maple programs are known as procedures. The language has many statements supporting program flow such as if ...then and while and do etc., and also has a variety of data types. There's no time in this course to teach this material, but students should know that programmng is possible.

I have several books on Maple programming. My current favorite is Maple A comprehensive introduction by Roy Nicolaides and Noel Walkington, Cambridge University Press ($55, 466 pages). There are also many web pages which discuss programming in Maple. For example, here's an online tutorial. Warning: such pages are only for the enthusiast!