The answers ...
Please read these answers after
you work on the problems. Reading the answers without working on the
problems is not a useful strategy!
Notation exp(Frog) will denote eFrog. sqrt(Toad)
will denote the square root of Toad (so sqrt(4) is 2).
Problem 1 You should draw a picture! The candidate rectangles
have corners at the points (-x,0) and (x,0) and (-x,4-x2)
and (x,4-x2). The lengths of the sides of the rectangle are
2x and 4-x2, so its area A is 8x2
-2x3. Here x must be between 0 and 2 to get a "real"
rectangle. Note that A is 0 when x is 0 or when x is 2, so a positive
maximum will occur at a critical number between 0 and 2. A´ is
16x-6x2. A's critical numbers are 0 and sqrt(8/3). We want
the positive cricial number since it will supply the maximum because
of the reasons stated before. From this you can
get the length of the sides (one side has length 2sqrt(8/3) and the
other has length 4/3) and area, which is (8/3)sqrt(8/3).
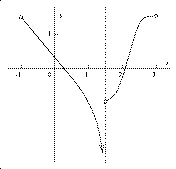 Problem 2
The information given in this problem is graphical, so what you can
answer is principally qualitative, not quantitative. Here is a graph
of h´. We can see that h seems to have two critical
numbers. There's one critical number at x=.2 or maybe .3 and there's
another at x=2. Also h has a relative maximum at the left-hand
critical number and h has a relative minimum at the right-hand
critical number. h does not seem to have any inflection
points, although to the left of 1.5 the graph is concave down and to
the right of 1.5 the graph is concave up, 1.5 itself is not in the
domain of h, so h can't have an inflection point with x=1.5 (tricky!).
Problem 2
The information given in this problem is graphical, so what you can
answer is principally qualitative, not quantitative. Here is a graph
of h´. We can see that h seems to have two critical
numbers. There's one critical number at x=.2 or maybe .3 and there's
another at x=2. Also h has a relative maximum at the left-hand
critical number and h has a relative minimum at the right-hand
critical number. h does not seem to have any inflection
points, although to the left of 1.5 the graph is concave down and to
the right of 1.5 the graph is concave up, 1.5 itself is not in the
domain of h, so h can't have an inflection point with x=1.5 (tricky!).
Problem 3 Suppose the numbers are a and b. Then a+b=P. We are
supposed to maximize a3b2: make it largest. We
convert this to a problem in calculus of one variable using the
constraint a+b=P, or b=P-a. We need to maximize
a3(P-a)2 with 0 < a < P. Of course near the
endpoints this function gets close to 0. So the maximum will occur
where the derivative is 0. The derivative is
3a2(P-a)2 - a32(P-a)1 (the
- sign is from the chain rule!). Some simplification is useful and we
can factor so the derivative becomes: a2(P-a) (3(P-a)-
2a). The first factor tells us there's vanishing at a and at P (we
don't care about these!). The other factor tells us that the
derivative is 0 also vanishes at (3/5)P. This gives us a maximum. The
endpoint conditions tell us it is a maximum, and this can be checked
with the first or second derivative. Select the numbers so that the
one to be cubed is three-fifths of the sum, and the one to be squared
is two-fifths of the sum.
Problem 4 a) As x->infinity, the largest part is exp(4x).
Divide the top and bottom by this, and get on top exp(-2x). The bottom
is 3exp(-4x)+1. The limit of the bottom is 1 and the limit of the
top is 0 as x->infinity, so the quotient has limit 0. As x->-infinity,
the bottom approaches 3 and the top approaches 0. Therefore the limit
is 0.
b) Again divide the top and bottom by exp(4x). Now as
x->infinity, the top ->1 but the bottom (which is 3exp(-4x)+exp(-2x))
->0 and is positive. So the quotient ->+infinity. Another way to
analyze the behavior is by dividing by exp(2x). As x->-infinity, the
limit will be 0 (same reason as in a)).
c) Divide the top and bottom by x2. The top leads off with x,
and the bottom leads off with 1 (the non-leading terms are lower order
when x->+infinity or -infinity). So the limit as x->+infinity is
+infinity and the limit as x->-infinity is -infinity.
d) This one is tricky. The top looks like "x" and a quick glance
at the bottom says, well, there's a square root of x2, so
it is "x" also (again, neglecting lower order terms). There will be no
problem when x->+infinity: the limit is 1. But look again at the
bottom, and now algebra snarls at us: remember that the square root of
a number squared is the absolute value of the number. Therefore, when
x is large NEGATIVE, the bottom is approximately -x, not x! So
the quotient is close to -1, and the limit is -1 as x->-infinity. I
advise you to graph this function (and also the others) to verify that
the claims made here are correct.
Problem 5 You should draw a picture! Here are some variables:
the rectangle will have length L and width W and area A and length of
a diagonal (they are both equal!) D. Then we know A=LW and
D2=L2+W2 (Pythagoras). Yes, we could
take the square root, but maybe this is easier to handle.
We also know that at "at certain time" L=3, W=5, L´=+.4
and W´=-.5 (all derivatives are with respect to time). Now
let's get to work!
a) The product rule tells us that A´=L´W + LW´ so
that at the "certain time" A´ is (.4)5+3(.-5)=.5 and we see that the
area is increasing.
b) Implicit differentiation (the chain rule) tells us 2DD´ =
2LL´+2W W´ and at the "certain time" the equation becomes
2DD´=2(3)(.4)+2(5)(-.5)=-2.6: therefore I already know
that D is decreasing. The exact amount can only be found if I discover
what D is, and for that I use the original equation
D2=L2+W2which becomes
D2=32+52=34 so D=sqrt(34) and finally
D´=-2.6/(2sqrt(34)).
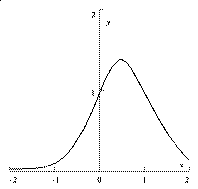 Problem 6
a) A graph is presented at the right. Please note the difference in
horizontal and vertical scales.
Problem 6
a) A graph is presented at the right. Please note the difference in
horizontal and vertical scales.
b) f´(x)=exp(x-x2) (1-2x). The only root is
x=1/2. f´ is positive to the left of 1/2 and negative to the
right of 1/2. Therefore f is increasing in the interval [-2,.5] and
decreasing in the interval [.5, 2].
c) f´´(x)=exp(x-x2) (1-2x)2 +
exp(s-x2)(-2)=exp(x-x2)(1 -4x+4x2
-2). Since the exponential function is never 0, any roots of
f´´(x)=0 are where 1-4x+4x2-2=0 or where
4x2-4x-1=0. The quadratic formula says that these roots
are at (+4 +\-sqrt(32))/8=(approximately) 1.21 and -.21 . These turn
out to be inflection points of f, because f is concave up between -2
and -.21, concave down between -.21 and 1.21 and finally concave up
again between 1.21 and 2.
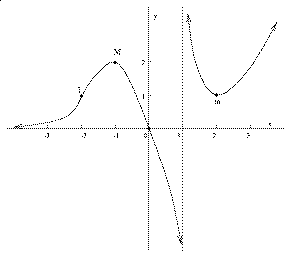 Problem 7 There is one relative maximum, indicated by M on the
picture. There is one relative maximum, indicated by m on the
picture. There is one inflection point, indicated by I on the
picture. The x-axis whose equation is y=0 is a horizontal asymptote
and the line x=1/2 is a vertical asymptote.
Problem 7 There is one relative maximum, indicated by M on the
picture. There is one relative maximum, indicated by m on the
picture. There is one inflection point, indicated by I on the
picture. The x-axis whose equation is y=0 is a horizontal asymptote
and the line x=1/2 is a vertical asymptote.
Problem 8 Suppose the radius is r and the area is a. Then
a=(PI)r2. Taking derivatives with respect to time, we see
that a´=2(PI)rr´ (don't forget the chain rule!). At "a
certain time" we know r´=.3 and a=25. So 25=(PI)r2
at that time, and we can solve for r, which turns out to be
sqrt(PI/25). Therefore since a´=2(PI)rr´ we get
a´=2(PI)sqrt(PI/25)(.3) (wow!).
Problem 9 We will need Q´(x)=3x2+4(x-4). The
critical numbers of Q are 4/3 and -2.
a) The easiest way to find the max and min of Q on the interval [-4,4]
is to test Q's values at the endpoints and the critical numbers in the
interval. So:
Q(-4)=0; Q(4)=64; Q(4/3)=(256)/(27) (approximately 9.48);
Q(-2)=28
The max value of Q on this interval is 64 and its min value is 0.
b) Here we need only test Q's values at 0 and 4/3 and 4. Q(0)=16, and
the other values are above. So the max value of Q on this interval is
64 and its min value is approximately 9.48.
Check this computation by looking at a graph of Q, please.
Problem 10 a) The only way a quotient can be 0 is if the top is
0. sin(x) is 0 only at integer multiples of PI.
b) Recognition that the function in this part of the problem is the
derivative of the function in the first part of the problem is most
important. Once you do that, an application of Rolle's Theorem tells
you that the derivative must be zero at least once between at
two roots of the function. There are at least 6 roots of the function
in an interval of length 20, so the derivative must be 0 at least 5
distinct times. There are actually 6 times the derivative is 0,
because we're "lucky" - the function is 0 at 0 and the function has 7
roots in [0,20].
Problem 11 If the square bottom has side length S and the
height of the box is H (both measured in feet), then the volume is
S2H. The constraint is 10=S2H. The "objective
function" to be minimized is the cost. The sides have area 4SH and
cost $20 per square foot, so their cost is 80SH. The bottom has area
S2 and costs $10 per square foot, so its cost is
10S2. The total cost is C=80SH+10S2. We use the
constraint to reduce this to a problem involving one variable. So we
try H=10/(S2) and get
C=80S(10/(S2))+10S2=800/S+10S2. Note
that when S->0+ or when S->infinity, C gets very large. We
have just shown that the minimum cost must occur at a critical
point. You could also see this using the first or second derivatives.
What are the critical point(s) of C? C´=-800/S2+20S.
We can find out where C´=0 easily, and this happens when
S=(40)1/3 which is approximately 3.42 and for this S,
the cost is approximately $351.
Problem 12 Repeated from a discussion of an earlier problem:
"The information given in this problem is graphical, so what you can
answer is principally qualitative, not quantitative."
Q is continuous everywhere except 0, where the left- and right-hand
limits emphatically do not coincide. Q seems to be differentiable
everywhere except 0. Q seems to have three critical numbers: there are
two places where the derivative exists and is 0 (horizontal tangent
lines), at about -2 and 1, and one place where the derivative does not
exist, 0. The y-axis (whose equation is x=0) seems to be a vertical
asymptote, and there seem to be two horizontal asymptotes, the x-axis
with equation y=0 and the line y=1. Q seems to be increasing in the
intervals [-2,0] and (0, 1]. Note that Q is NOT increasing in the
whole interval [-2,1]. This is a bit delicate! Q is decreasing in the
intervals (-infinity,-2] and [1,infinity). Q seems to be concave up in
[-2, -.75] and in [1.6, infinity) (your answers may differ - I'm just
looking at the graph!) and is concave down in (-infinity, -2] and in
[-.75,0] and in (0, 1.6). There are three points of inflection: -2 and
-.75 and 1.6. The limit at -infinity seems to be +1, the limit at
0- seems to be 1.5, the limit at 0+ seems to be
-infinity, and the limit at +infinity seems to be 0,
Problem 13 We know 10x+2y+2xy´+4yy´=0 by implicit
differentiation from the original equation. So
y´=-(10x+2y)/((2x+4y).
a) Horizontal tangent lines occur where y´ is 0. That is where
10+2y=0 or where y=-5x. The original equation is 5x2+2xy +
2y2=7, so we know that
5x2+2x(-5x)+2(-5x)2=7 at points where the
tangent lines are horizontal. This is just 45x2=7 whose
roots are approximately +/-.394. y is then -5 times each of those, or
approximately -/+ 1.97. So the points desired are (.394,-1.97) and
(-.394, 1.97).
b) Vertical tangent lines have "no slope". So these occur where
2x+4y=0 or where x=-2y. Then 5x2+2xy+2y2=7
becomes 5(-2y)2+2(-2y)y+2y2=7 which gives
18y2=7, whose roots are approximately +/-.623, so that x
must be approximately -/+1.246. The points here are about
(-1.246,.623) and (1.246,-.623).
c) If you really believe in the hint, the box "clearly" has corners
(1.246,1.97) and (-1.246,1.97 ) and (1.246,-1.97) and (-1.246,-1.97).
Problem 14 Suppose E(t) is the enzyme activity at time t.
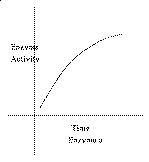 a) Here we know E´ (t) > 0 but E´´ <0. The graph is
increasing and concave down.
a) Here we know E´ (t) > 0 but E´´ <0. The graph is
increasing and concave down.
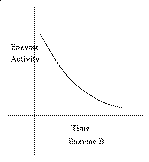 b) Here we know E´ (t) < 0 but E´´ > 0 (the rate of
decrease is slowing!). The graph is decreasing and concave up.
b) Here we know E´ (t) < 0 but E´´ > 0 (the rate of
decrease is slowing!). The graph is decreasing and concave up.
Problem 15 The two parts of V are each positive. The exp(-2x)
part goes to +infinity when x->-infinity, and the exp(3x) part goes to
+infinity when x->+infinity. Therefore it seems likely the function
has a minimum value (let me call it "v"), and that the range of the
function is [v,+infinity).
V´(x)=-2(exp(-2x))+3(exp(3x)). This is equal to 0 when -2
e+3 +3e3x=0. Multiply this equation by
e2x and use properties of exponentials. Then it becomes -2
+3 e5x=0 which is equal to 0 when e5x= 2/3 or
when 5x= ln(2/3) or when x=(1/5)ln(2/3). This is the minimum of V
because we already know what happens to V(x) when x gets large
positive or large negative. What is v=V((1/5)ln(2/3))? Some work with
exponentials (a healthy activity!) can give it exactly.
v=(exp(-2(1/5)ln(2/3)))+(exp(3(1/5)ln(2/3)))=(2/3)-2/5+(2/3)3/5=
(5/6)32/523/5. Another wow! The last
"simplification" is recommended only to those who are very desperate
or who enjoy algebraic suffering! I tried graphing V(x) and found a
"good" graph difficult to get because the exponentials increase quite
rapidly: you try to see what it looks like from -3 to 3. The minimum
occurs approximately at (-.081,1.960). This is not obvious!
Problem 16 We know that W(x+h) is approximately
W(x)+W´(x)h and here x will be 3 and h will first be +.03 and
then -.02. So W(3.03) is approximately 4+2(.03) which is 4.06 and
W(2.98) is approximately 4+2(-.02) which is 3.96.
Since W´´(3) is negative, it is likely that the graph of
y=W(x) is concave down near 3. The linear approximation used above
depends on replacing the "true" value of the function by its value on
the tangent line. When the graph is concave down, the tangent line is
above the graph. It is therefore likely that the approximate values
given above are more than the true values of W.
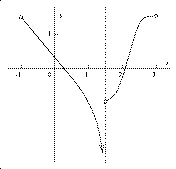 Problem 2
The information given in this problem is graphical, so what you can
answer is principally qualitative, not quantitative. Here is a graph
of h´. We can see that h seems to have two critical
numbers. There's one critical number at x=.2 or maybe .3 and there's
another at x=2. Also h has a relative maximum at the left-hand
critical number and h has a relative minimum at the right-hand
critical number. h does not seem to have any inflection
points, although to the left of 1.5 the graph is concave down and to
the right of 1.5 the graph is concave up, 1.5 itself is not in the
domain of h, so h can't have an inflection point with x=1.5 (tricky!).
Problem 2
The information given in this problem is graphical, so what you can
answer is principally qualitative, not quantitative. Here is a graph
of h´. We can see that h seems to have two critical
numbers. There's one critical number at x=.2 or maybe .3 and there's
another at x=2. Also h has a relative maximum at the left-hand
critical number and h has a relative minimum at the right-hand
critical number. h does not seem to have any inflection
points, although to the left of 1.5 the graph is concave down and to
the right of 1.5 the graph is concave up, 1.5 itself is not in the
domain of h, so h can't have an inflection point with x=1.5 (tricky!).
 Problem 6
a) A graph is presented at the right. Please note the difference in
horizontal and vertical scales.
Problem 6
a) A graph is presented at the right. Please note the difference in
horizontal and vertical scales.
 Problem 7 There is one relative maximum, indicated by M on the
picture. There is one relative maximum, indicated by m on the
picture. There is one inflection point, indicated by I on the
picture. The x-axis whose equation is y=0 is a horizontal asymptote
and the line x=1/2 is a vertical asymptote.
Problem 7 There is one relative maximum, indicated by M on the
picture. There is one relative maximum, indicated by m on the
picture. There is one inflection point, indicated by I on the
picture. The x-axis whose equation is y=0 is a horizontal asymptote
and the line x=1/2 is a vertical asymptote.
 a) Here we know E´ (t) > 0 but E´´ <0. The graph is
increasing and concave down.
a) Here we know E´ (t) > 0 but E´´ <0. The graph is
increasing and concave down.
 b) Here we know E´ (t) < 0 but E´´ > 0 (the rate of
decrease is slowing!). The graph is decreasing and concave up.
b) Here we know E´ (t) < 0 but E´´ > 0 (the rate of
decrease is slowing!). The graph is decreasing and concave up.