Celestial Mechanics

J. Massimino
History of Mathematics
Rutgers, Spring 2000

Throughout the history of mathematics, branches of scientific study have regularly used mathematical methods to explain natural phenomena. This is very true in the field of astronomy, and particularly in the case of celestial mechanics. Celestial mechanics is defined as the branch of astronomy dealing with the mathematical theory of the motions of celestial bodies. The curiosities of celestial mechanics date back in to ancient times. The ancient Greeks, for instance, gave divine status to the cosmos, and therefore felt the need for further exploration. At this time, astrology established itself and became a part of everyday life. The principle that stars could influence man's life "...received some kind of justification from the notion of cosmos, a cosmos which is so well arranged that no part is independent of the other parts and of the whole. Was this not proved by the tides, caused by Moon and Sun, by the menstruation of women, by the farmers' moonlore... (Sarton, 165)." During the third century BC, Aristarchos of Samos combined Euclidean geometry with the assumption that the Sun is the center of the "universe" rather than the Earth1. In his model the planets circle the Sun, the Moon orbits the Earth, and the stars are fixed, while their apparent "rotation" is an illusion caused by the Earth's rotation. This heliocentric model was later reaffirmed by Nicholas Copernicus (c. 1520).

In the late 17th century, a new age of thinking, now called the Enlightenment, began. During this Age of Reason, intellectuals looked for a single principle that would join together the concepts of nature, God, and reason2. Sir Isaac Newton (1642-1727) of Great Britain made a major contribution to the scientific world during this time with the publication of his greatest work, Philosophiae Naturalis Principia Mathematica, later referred to simply as Principia. In this great work Newton discussed many influential ideas, including his famous Laws of Motion, which dramatically affected the understanding of celestial mechanics. These laws are:

  1. That every body continues in its state of resting or of moving uniformly in a straight line, except insofar as it is driven by impressed forces to alter its state.
  2. That the change of motion is proportional to the motive force impressed, and takes place following the straight line in which that force is impressed.
  3. That to an action there is always a contrary and equal reaction; or, that the mutual actions of two bodies upon each other are always equal and directed to contrary parts.
These laws became essential in the study of mechanics of bodies in space. These laws were combined with the law of gravity, which was an essential factor for further discoveries in celestial mechanics. The gravitational factor established in this law was an important component of the works of a key 18th century mathematician, Joseph-Louis Lagrange.

The Life of Joseph-Louis Lagrange4

Joseph-Louis Lagrange was born on January 25, 1736 in Turin to an influential family. At the age of fourteen, Lagrange was sent to the University of Turin to study law, after his father went bankrupt after poor financial speculation. Although he was to study law, his interests and abilities quickly showed to favor mathematics, especially math analysis. Justly so, Lagrange was appointed substitute professor at the Royal Artillery School in Turin in 1755, and only two years later established the Royal T urin Academy of Sciences with his colleagues, chemist Count Saluzzo di Monesiglio (1734-1810) and anatomist Giovanni Cigna (1734-1790). However, in 1766, Lagrange grew unhappy with the limited research resources available in Turin, and so, moved to Berl in where he was installed as Director of Mathematics in the Berlin Academy. His years in Berlin proved to be the most fruitful period of his life. "During this time, he wrote on all branches of mathematics and intensively studied mechanics. The majorit y of his memoirs during this period deal with celestial mechanics (Lagrange, xix)." The writings from these memoirs were submitted to the Académie des Sciences de Paris, whose major scientific questions during the Enlightenment focused around:

  1. describing mathematically the motion of the Moon,
  2. accounting for the apparently secular inequality in the motions of Jupiter and Saturn,
  3. determining the precise shape of the Earth.
    4. Lagrange's writings on these topics won competitions held by the Académie five times, which helped to further establish him as a prominent mathematician of the time.

    With political changes occurring in Berlin in 1786, Lagrange again became unhappy and dissatisfied and so accepted the position of pensionaire vétéran of the Académie des Sciences, causing him to move to Paris. In less than a year later, the first e dition of Lagrange's most famous work, Mécanique Analytique, was published. This book dealt with his findings about principles of statics and dynamics and eventually laid the groundwork for further studies in mechanics. Lagrange continued his studies in Paris, despite the fact that the French Revolution (c. 1789) was all around him, even through to his death in 1813. Just prior to his death, Lagrange summarized his life with these words:

    " Death is not to be dreaded and when it comes without pain, it is a last function which is not unpleasant. I have had my career; I have gained some celebrity in mathematics. I never hated anyone, I have done nothing bad, and it would be well to end (Kramer 220)." The second edition of Mécanique Analytique, which expands upon the works of the first, was published posthumously in 1815.

    The Works of Joseph-Louis Lagrange5

    In the second edition of Mécanique Analytique, Lagrange's work focused more on celestial mechanics than the previous edition had. In this edition, Lagrange produced equations6 aiding the understanding of celestial mechanics, including those dealing with:

    1. Orbital Shapes
    2. Planetary Periods
    3. Changes in Orbits when a Planet is subjected to an Arbitrary Impulse
    4. Perturbations
    5. Orbital Shapes7

    In the world system, according to Lagrange, the force of attraction is inversely proportional to the square of the distance.

    R= g/r2 => 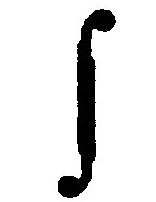Integral R dr=-g/r

    Using the equation between F and r, the substitution becomes

    R dr = 2H + (2g/r) - (D2/r2). Then the polar equation of the conic section with parameter b and eccentricity e is r = b/(1+ ecosF given that b = D2/g , and e = [1+ (2HD2/g2)]1/2. Lagrange calls the average distance a, so that a = b/(1-e2). Using simplification and substitution with D and H, the new relationship is 1/a = (1-e2)/b = -2H/2g, where the constant H must be negative in order to produce an elliptical orbit. If H were zero, the orbit would be parabolic, and if H were positive, the orbit would be hyperbolic.

    Planetary Periods

    In order to compute the period of a planet, Lagrange began with the equation

    dt = dr/ [(2H-(2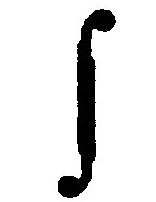IntegralR dr) - D2/r2)]1/2 Using the substitution dt = (r dr) / ([ga]1/2 [e2-(1-r/a)2]1/2), and r = a(1-e cosq ), we have dt = [a3/g]1/2 (1-ecosq dq After integration, t-c = [a3/g]1/2 (q-e sin q), thus giving q as a function of t, and therefore, r as a function of t. Lagrange then made a substitution into dt using F. This became: dF = dq (1-e2)/ (1- ecosq) => F= sin-1 (sinq[(1-e2)]1/2/(1-ecosq)) + constant. Through a comparison of the expressions for r, F as functions of q, b/(1+ecosF) = a (1-ecosq). Because b=a(1-e2), Lagrange concluded cosF = (cosq - e)/ (1 - e cosq), sinF=(sinq) [(1-e2)]1/2/(1-ecosq), and thus, tan (F/2) = [((1+e)/(1-e))]1/2tan (q/2). Lagrange concludes, "It is clear from these formulas that when the angle qis increased by 360 degrees, the radius r remains the same but the angle F is also increased by 360 degrees. Therefore, the planet returns to the same point after having completed an entire revolution. But since the angle q has increased by 360 degrees, the time t will increase by 360(a3/g)1/2. This is the time required for the planet to return to the same point in its orbit. Hence, this amount of time is called the planet's period ... ." (Lagrange, 325)

    Expressing Orbits in Terms of x, y, z

    Recalling that r(1+ecosq)=b and r=a(1-ecosq), Lagrange substituted in X=a(cosq - e), so that X= (b-r)/e = (a(1-e2)-r)/e. Therefore, X=a(cosq - e) and 2)]1/2sinq. Using these expressions for X and Y, Lagrange concluded that it was possible to substitute these expressions in the general expressions for x,y,z, for which he claimed,

    " Thus, it will only be a question of substituting the expression for ? as a function of t, obtained from the equation given in Article 169 in order to obtain the three coordinates as functions of time (Lagrange, 326)", yet he never demonstrates this substitution.

    Changes in Orbital Elements When a Planet is Subjected to an Arbitrary Impulse

    Up to this point, Lagrange had shown how to express the elements of elliptical orbits using the functions of x,y,z and of their differentials dx/dt, dy/dt, and dz/dt. However, it was observed that planets were subject to impulses which affected the veloci ties. This, Lagrange concluded, could be accounted for by the following adjustments:
    dx/dt --> dx/dt + x.
    dy/dt --> dy/dt + y.
    dz/dt --> dz/dt + z.
    This gave the new elements of the planetary orbit after the impulse. Then using the radius vector r, y, and r Lagrange rewrote the elements of the orbits as:

    1/a = 2/r -( r2(cos2y dr2 + dy2) + dr2)/ g dt2
    b = r4(cos2ydr2 + dy2)/gdt2
    tan h = (sinrdy - sinycosycosrdr)/ (cosrdy - sinycosysinrdr)
    tan i = [(dy2 +sin2&#cos2ydr2)/(cos2ydr)     where "dr/dt, rdr/dt, and rdy/dt are velocities in the direction of the radius r, in a direction perpendicular to this radius and parallel to the plane of projection, and in a direction perpendicular to this same plane (Lagrange, 361)."

    Elements of Motion Produced by Perturbing Forces

    Although the previous equations worked for arbitrary, momentary impulses, Lagrange realized that it was necessary to compensate for impulses that are infinitesimal and continuous, or perturbation forces.

    His work on perturbation forces begins:

    "Let X,Y,Z, be the perturbing forces resolved in the directions of the rectangular coordinates x,y,z and having a tendency to increase the coordinates. These forces will create during the instant dt the small velocities Xdt, Ydt, Zdt which should be adde d to the velocities dx/dt, dy/dt, dz/dt in the expression for each of the elements... because the added velocities are infinitesimal they will only produce in the elements infinitesimal variations which can be determined by the differential calculus (Lagr ange, 367)."

    Allowing the following definitions, dx/dt = x', dy/dt = y', dz/dt = z', Lagrange concluded that each of the elements of the orbit could be expressed using x, y, z, x', y', z'. If a is one of these elements, then it "... will have its variation da by augmenting x', y', z' of the infinitesimal quantities Xdt, Ydt, Zdt. Thus one will have da = (da/dx' X + da/dy' Y + da/dz' Z) dt and similar equations will be obtained for the other elements ... (Lagrange, 367)."

    This work on the perturbation theory became a significant part of the future of celestial mechanics.

    Conclusion

    With the development of Lagrange's equations for perturbations, significant developments have occurred. It was through the use of perturbation theory that Neptune was discovered. When astronomers of the mid-nineteenth century observed a perturbed orbit of Uranus, "astronomers Adams and Leverrier independently came to the conclusion that the perturbation must be due to a planet as yet unknown to astronomers (Kramer, 221)." This planet was soon discovered and named Neptune. The discovery of Pluto in th e twentieth century was similar.

    Celestial mechanics has developed greatly throughout many centuries of observation. From a time where the cosmos were used to explain daily activity to the time of the Enlightenment when knowledge of how the universe worked was desired, it is an ever re levant field. The work of Joseph-Louis Lagrange, during the Enlightenment, proved to be a prominent and fruitful assets to our current understanding of the world.

    Bibliography

    Table of Variables

    Notes

    1. As shown below
    2. From Translator's Introduction to Mécanique Analytique.
    3. As translated from Principia.
    4. The biographical information used here is taken from the Translator's Remarks of Mécanique Analytique and from the work of Edna Kramer.
    5. As translated from Mécanique Analytique.
    6. Lagrange does not provide diagrams with his work, because he felt that algebra was more appropriate than Euclidean geometry in these computations.
    7. Please refer to the table of variables given above when following the computations.
    8. Lagrange, pages 322-324.
    9. This is the equation t-c = [a3/g]1/2 (q -e sin q)