
Alexandrian Algebra according to Diophantus
Marni Kirschenbaum
History of Mathematics
Spring 2000
Alexandrian Algebra can best be viewed through the work of Diophantus of Alexandria. Diophantus of Alexandria had a great impact in the world of mathematics. He is often referred to as the father of Algebra. He produced only a few works, but their influence on mathematics was far reaching. He is known for considering only rational solutions to equations: a negative or irrational solution was considered preposterous. Moreover , he usually obtained only one such rational solution. Numerous scholars have analyzed the methods of Diophantus in detail. It is these styles and methods of solving equations that are most interesting to those who study him, and most difficult to understand, since Diophantus rarely recorded general formulas. The interpretations of his work by Nesselmann and Heath will be examined here, and we will attempt to determine which of these interpretations reflects his work more accurately.
The exact time of Diophantus's life is very uncertain. James Gow estimates that Diophantus lived in the first half of the fourth century, while Thomas Heath's estimation falls at approximately 250 AD, which is relatively close to Gow's estimate. A third mathematical historian, Wilbur Knorr, cautiously estimates Diophantus's dates to have been in the first half of the third century (187), which matches Heath's estimation more closely than Gow's. Gow's estimation was derived from an epigram concerning Diophantus' age which placed him before 330 AD (Gow 100). He also used the work of later scholars, like Theon and Theon's daughter Hypatia, to show that Diophantus' dates did not go beyond this time. However, he also considers the possibility that Diophantus may have lived much earlier (Gow 101). So, Gow only has an upper bound of Diophantus' dates. Heath, on the other hand, first considered 150 BC as a lower bound to Diophantus' dates, based on Diophantus' reference to work by Hypsicles who preceded him (Heath D 2), then raised that lower bound to about 250 AD after considering a letter which showed that Diophantus and Anatolius once worked together when writing on "the Egyptian method of reckoning." (Heath D 2) Furthermore, Wilbur Knorr concluded Diophantus' dates to be approximately 240 AD, also based on his relationship to Anatolius (187). However, Knorr also allows the possibility of a different Diophantus being associated with Anatolius, which could permit our Diophantus to be placed as early as the first century AD, as a contemporary of Hero (Knorr 184). Ultimately, Knorr concludes that more chronological research is needed to resolve this issue (187). In addition, both Gow and Heath refer to a problem in the form of an epigram presumed to be written about Diophantus after his death, indicating that he was eighty four years old when he died. This epigram, which was composed by Metrodorus, reads as follows:

The most interesting work of Diophantus is his Arithmetica, which originally contained thirteen books, of which, unfortunately, only six survived, though Diophantus stated in the first book of Arithmetica that it would include thirteen books. Other evidence to support the assumption that additional books had in fact been written is the fact that certain propositions and concepts are left unproved and unexplained in the text as we have it. Gow notes that historians do not think that the propositions of Arithmetica are now found in the order in which they were originally written, and that essential discussions of determinate quadratic equations and indeterminate simple equations are excluded (102). Gow and Heath both refer to another work by Diophantus on Polygonal Numbers that was significantly altered from its original state, so that many proofs are now incomplete. A third work by Diophantus is called Porisms, which consists of a series of propositions.
A critic and historian of mathematics from the latter part of the nineteenth century by the name of Hankel describes the Arithmetica as having included one hundred and thirty problems each of which could be classified into fifty different types (Heath D 54). Hankel divided these problems into two categories: determinate and indeterminate. Determinate problems have one specific solution, while indeterminate problems offer general solutions. In modern terms, for example, a determinate problem could be 5x = 10, so x = 2, and an indeterminate solution could be x + 4 where x is any integer. It should also be noted that Hankel's distinction between determinate and indeterminate problems is standard. Heath classifies them this way as well. Hankel's more detailed classification is the following: Book I contains determinate algebraic problems, Book II, III, IV, and V contain indeterminate problems, and Book VI contains problems of right-angled triangles described only arithmetically (qtd. in Heath D 54).
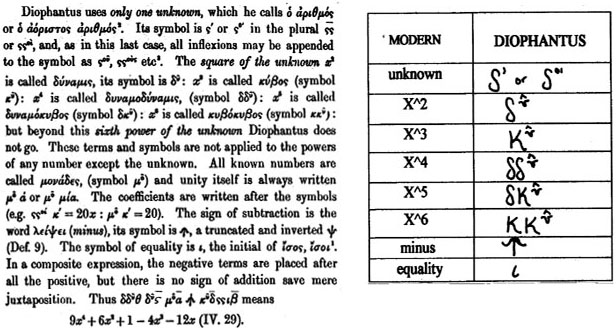
Gow interprets the Arithmetica as dealing predominantly with algebra and algebraic symbols in an analytical way. These elements, however, did not originate with Diophantus. For example, both Heath and Gow assert that the concept of unknowns came from the Egyptians, who used the term "Hau" or "heap" (Gow 105). Also, the concept of an analytic proof was gotten from Plato (Gow 105). Gow brought attention to the fact that Diophantus laid no claim to the invention of algebraic symbolism, so other unknown scholars may have utilized this concept (108). However, since there is no evidence to prove otherwise, it is said that Diophantus "invented" Algebraic symbolism (Gow 108). The following is an excerpt from A Short History of Greek Mathematics, by Gow, describing Diophantus' notation.
Overall, Gow believes that the purpose of Arithmetica was to discover general solutions to problems, but Diophantus does not do that. His equations often possess only one or a couple of solutions. Furthermore, he says that Diophantus only gave one roo t to quadratic equations that have two positive roots. So, it is difficult to find general solutions given the work of Diophantus that is available. Gow describes Diophantus as the engineer of two facets of Algebra. First, setting up an equation and ma nipulating it into an equation he can solve, and second, actually solving the problem (Gow 113). In addressing Diophantus' methods of solving equations Gow quotes Hankel as having said, "In 130 indeterminate equations, which Diophantus treats, there are more than fifty different classes...Almost more various than the problems are their solutions...Each calls for a quite distinct method, which is often useless for the most closely-related problems. It is therefore difficult for a modern, after studying 100 Diophantic equations, to solve the 101st" (qtd. in Gow 115). Thus, it is Gow's opinion that "the extraordinary ability of Diophantus appears rather in the other department of his art, namely the ingenuity with which he reduces every problem to an equation which he is competent to solve" (115). So, to study Diophantus' greatest work is to study his methods of simplifying an equation to find its solution.
Heath describes the views of three men Hankel, Nesselmann and Euler, and offers his own assessment of their views concerning the nature of Diophantus' work. Hankel is of the opinion that Diophantus is incomplete in his work. He describes Diophantus as "...shrewd, clever, quick-sighted, indefatigable, but [who] does not penetrate thoroughly or deeply into the root of the matter. As his problems seem framed in obedience to no obvious scientific necessity, but often only for the sake of the solution, the solution itself also lacks completeness and deeper signification" (qtd. in Heath D 55). Diophantus was not thorough in his investigation of his equations and solutions, and this disturbed Hankel. Nesselmann believes that Diophantus' focus was on tho roughly explaining the method of solution. This supports Gow's view of Diophantus' purpose in writing Arithmetica. Moreover, Euler also believed that Diophantus' goal was not in simply finding various solutions but in the method. He supports this opinion by making note of the fact that the idea of using letters to represent numbers to achieve general solutions did not exist at that time. So he says, "...the actual methods which he uses for solving any of his problems are as general as those in use today;..."(qtd. in Heath D 56). Therefore, Euler is of the opinion that even though he uses actual numerical values, Diophantus' methods still elicit general solutions. Overall, there seem to be opposing views as to the significance of Diophantus' work. The opinion that the methods used by Diophantus for solving equations was his most significant contribution to Algebra appears to be the best supported opinion. Therefore, these methods must be thoroughly explored. The methods that Diophantus used to solve numerous equations are interpreted differently by various scholars, including Nesselmann and Heath. Nesselmann describes eight methods Diophantus used in solving determinate and indeterminate equations. In contrast, Heath describes Diophantus' style by dividing it into three parts, the first of which can be subdivided into seven smaller parts. Both Nesselmann's and Heath's interpretations will be examined here accompanied by examples which will clarify their content. Modern notation is used to ensure understanding. Each example is inspired by the suggestion of Gow and they are extracted from Heath's book Diophantus of Alexandria that contains a translated copy of Arithmetica. It is also interesting to note here that as Gow suggests certain problems from Arithmetica to illustrate Nesselmann's methods, his reference to the problem number and book number are not consistent with the translated copy in Heath's book. Sometimes the problem Gow refers to lies near the referenced place and at other times the exact problem cannot be found. Frequently, only questions worded similarly can be found. As Gow was writing before Heath's work had appeared, that could explain some of these discrepancies. That is, later revised translations could have resulted in some changes of the position of problems. Nesselmann divides Diophantus' "methods" of solutions of determinate and indeterminate equations into eight different styles. Gow describes each of these methods with a supporting example. The first is "The adroit assumption of unknowns," meaning he had a very clever way of choosing his unknowns. An example of this is found in problem 16, Book I of the Arithmetica, and it reads as follows:
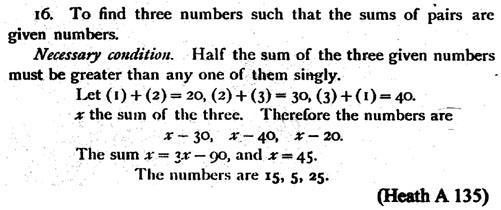
The problem is to find three numbers given the sum of any two of them. Gow describes Diophantus' method in modern terms as "...the three given sums being a,b,c he takes the sum of all three numbers together = x. The num bers therefore are x-a, x-b, and x-c. Whence 3x - (a + b + c) = x: and x = (a + b + c)/ 2" (Gow 116). Moreover, an additional question remains. Is Diophantus' "necessary condition" really necessary? Imagine taking the three given numbers x + y, y + z , and x + z as the sums of any two of the three numbers x, y, and z we are searching for. Then, the "necessary condition" says that ((x + y) + (y + z) + (x + z)) / 2 = (2x + 2y + 2z) / 2 ==> x + y + z > x +y. Given that Diophantus did not accep t zero or negative numbers, his "necessary condition" is absolutely necessary. So, Diophantus chose particular unknowns to easily simplify equations. In this case he wrote his three numbers in terms of one unknown so they could be easily solved. The second method is "Method of reckoning backwards and auxiliary questions" meaning he picked unknowns that do not satisfy all the necessary conditions and in their inaccuracy the necessary unknowns emerged (Gow 116). The third method is "Use of the sym bol for the unknown in different significations" meaning he used his symbol for unknowns when needed. An example of these last two methods, is found in problem 9, Book IV of the Arithmetica, and it reads as follows:

This problem is asking to add a single number to two numbers, of which the first is the cube of the second, so that the two resulting sums consist of a number and its cube root. After several creative steps a solution was found. Diophantus gave the cube a value of 125/343, the cube root the value 5/7, and the added number 267/343. So, 125/343 + 267/343 = 392/343 = 8/7 = the cube root, and 5/7 + 267/343 = 512/343 = the cube. Then (512/343)1/3 = 8/7 is true. A detailed analysis of this pr oof can bring great insight into the work of Diophantus. He began by choosing a cube, its root, and the number to be added. He preformed the given operations and arrived at 35x2 = 5, which according to Diophantus is not a solution since it is not rational. But, he noticed how he got the values 35 and 5. 35x3 came from adding 27x3 and 8x3 and 5x came from adding 3x and 2x. So, he noticed that 35 = 27 + 8 is the sum of the cubes and 5 = 3 +2 is the sum of the cube roots. Then he simplified the pro blem to adhere to the condition found in line 7 of the proof. It states that to solve this problem one needs to find two cubes (the original cube and the cube found in the number being added) such that their sum and the sum of their cube roots form a rat io of a square to a square. Imagine the cube is a3x3 with the cube root 'ax' and the number to be added is b3x3 - ax. Following the initial problem a3x3 + b3x3 - ax is to be the cube root and ax + b3x3 - ax is to be the cube. Then (b3x 3)1/3 = a3x3 + b3x3 - ax ==> bx + ax = a3x3 + b3x3 ==> x(a + b) = x3(a3 + b3) ==> (a + b)/(a3 + b3) = x2 or x2 = (a3 + b3)/(a + b). In either case the condition is satisfied, and this is necessary in order to find rational solutions.
Next he chose the sum of the sides to be 2 and calls one side z. So the other cube has side (2- z). He changes variables here to denote that this portion of the solution is separate from the other. His goal was to find the numbers that gave the ratio o f the sums of cubes to the sums of cube roots to be a square. The symbol Diophantus may have used here instead of 'z' is unknown. Given this information one cube is z3 and the other is (2 - z)3. Thus the sum of the cubes is 6z2 - 12z + 8 which he re duced to 3z2 - 6z + 4. According to the condition of line 7 he wanted this to be a square. He claimed this square was equal to (2 - 4z)2. It can be assumed that he used the 2 to cancel out the 4, but the origin of 4 as the coefficient to 'z' is not a s obvious. Imagine that we do not know that the coefficient is 4. Let us call it 'a'. So, 3z2 - 6z + 4 = (2 - az)2 ==> (a2 - 3)z2 + (6 - 4a)z = 0 ==> (a2 - 3)z + (6 - 4a) = 0 ==> z = (-6 + 4a)/(a2 - 3). If z = 10/13 then a = 4. So it is convincing that 3z2 - 6z + 4 = (2 - 4z)2 when z = 10/13. It follows that the sides are 10/13 and 16/13. Using these solutions Diophantus noticed that if the denominators are ignored and the numerators are simplified by a factor of two the values of 5 and 8 are left for the sides or cube roots. He took this information and reverted back to the original prob lem. Except this time he took one cube to be 125x3, its cube root to be 5x, and the number to be added as 512x3 - 5x. He could do this since from the previous calculation it was determined that these values, 5 and 8, when cubed will result in a ration al solution. So he preformed the original operation, 125x3 + 512x3 - 5x = the sum of the cube and the number and 5x + 512x3 - 5x = the sum of the cube root and the number. Then 637x3 - 5x = (512x3)1/3 ==> 637x3 - 5x = 8x ==> 635x3 = 13x ==> x2 = 13/635 ==> x = 1/7. So, the cube root or side = 5(1/7) = 5/7, the cube = (5/7)3 = 125/343 and the number added is 512(5/7)3 - 5(1/7) = 267/343. This problem is an illustration of method two in that he used his incorrect solution of 35x2 = 5 to help him find the correct rational solution. Method three was used when he used his symbol for an unknown to solve the problem. For example, he used a s ymbol for 'x' to represent the factor of the side of the cube and another symbol for 'z' to represent the side of a new cube to help find the rational solutions. The fourth is "The Method of Limits" meaning he used upper and lower boundaries to narrow down the solution set until a valid solution was found. An illustration of this method is found in problem 31, Book IV of the Arithmetica, and it reads as follows:

The problem presented here is to divide a whole into two parts such that if given numbers are added to each respectively, the product of the two sums gives a square. Although Diophantus' first solution is difficult to follow, his second solution is more explicitly stated. Diophantus began by choosing 3 and 5 to be the given numbers to be added, one part to be (x - 3) and the other part to be (4 - x). Notice 4 - x + x - 3 = 1. So, the sum of (x - 3) + 3 = x and the sum of (4 - x) + 5 = 9 - x. Its pro duct is x(9 - x). Diophantus wanted this to be a square and chose it to be 4x2. Then x = 9/5, which is not possible since 3 < x < 4 because x - 3 > 0 and 4 - x > 0. He continued to explain that the value of 'x' came from dividing nine by a square numb er plus one, and since x > 3 the value of the square number plus one must be less than three. Subtracting both by one it is clear that the square number must be less than two. Also, since x < 4 the value of the square number plus one must be greater tha n 9/4. Again subtracting one, it is clear that the square number must be greater than 5/4. So now the goal was to find a square number between 5/4 and 2. Then he changed the denominators to 64, which is a perfect square, and then chose the number 100 f or the perfect square in the numerator. So, after reducing, 25/16 was his coefficient of x2 and he used this to find the values of (x - 3) and (4 - x). Method four was used here when Diophantus created boundaries for x such that 3< x < 4, and used these boundaries to find his solution. The fifth method is "Solution by mere reflection," meaning he put the solution together by combining its parts. An example of this is found in problem 29, Book IV of the Arithmetica, and it reads as follows:

The question being asked is fairly easy to understand as translated. The sum of Diophantus' four square solutions added to the sum of their sides does result in the given number 12. How Diophantus arrives at this solution is difficult to understan d and will not be analyzed at this time. Method five was used here since he began with a number and found the solution by finding its parts. The sixth method "Solution in general expressions," meaning he found some general solutions. An example of this is found in problem 19, Book IV of the Arithmetica, and it reads as follows:

The problem is to find three numbers such that the product of any two of them plus one gives a square. This example has been inserted purely to display the fact that some of Diophantus' problems were indeterminate, meaning they had general solutions . An analysis of his work on this problem will not be provided. Furthermore, Heath points out in the footnote, that Diophantus' solution can easily be written as a general solution. The seventh method is "Arbitrary determinations and assumptions," meaning sometimes he gave unknowns determinate values, or introduced new conditions into the problem in order to make the solution more apparent (Gow 120). For example, in problem 14, Book I of the Arithmetica, he chose a given ratio as well as a second value for x, thus creating a rather simple problem to solve (Gow 120). It reads as follows:
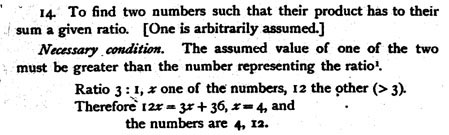
Diophantus' solution is quite clear and can be followed easily. However, the necessity of his "necessary condition" must be explored. To test its validity, assume that both values of the two numbers are less than the number representing the given ratio. Say the ratio is 5:1. Choose x = 1 to be one of the numbers and four to be the other number. Then 4x/(x + 4) = 5 ==> 4x = 5x + 20 ==> x = -20. Thus, Diophantus included this "necessary condition" to keep the value of the numbe rs positive. The last method described by Nesselmann is "Use of the right angled triangle," and Book VI of the Arithmetica is filled with a plethora of examples of this style of solving equations. Although Nesselmann's idea of the distinct style Diophantus used to so lve equations is well supported by numerous examples from Arithmetica, scholars like Heath did not agree with his analysis. Heath disagreed with Nesselmann's dissection of Diophantus' solution style. Rather than cite all of Heath's disagreements with Nesselmann's approach, a description of Heath's analysis will be provided instead. Heath notices that Diophantus did on occa sion give a method for the formulation of a conclusion. So instead of assigning methods to the numerous problems in Arithmetica as Nesselmann did, Heath extracts the methods that Diophantus recorded in his work. Heath categorizes these methods as three different types; "Treatment of Equations," "Method of Limits," and "Method of Approximation to Limits." "Treatment of Equations" is subdivided into "Determinate equations of different degrees" and "Indeterminate equations," and each of these is divided f urther. Diophantus solved pure determinate equations in the following familiar method. "If a problem leads to an equation in which any terms are equal to the same terms but have different coefficients, we must take like from like on both sides, until we get one term equal to one term. But, if there are on one side or on both sides any negative terms, the deficient terms must be added on both sides until all the terms on both sides are positive. Then we must take like from like until one term is left on each si de" (qtd. in Heath D 59). This popular method of solving equations is familiar to anyone who learns algebra today. Mixed quadratic equations had three different cases, according to Diophantus, each with a different method of solution.
"Case I: mx2 + px = q the root is [-1/2p + (1/4p2 + mq)]/m.
Case II: mx2 = px + q then x = [1/2p + (1/4p2 + mq)]/m.
Case III: mx2 + q = px with root [1/2p + (1/4p2 - mq)]/m"
(qtd. in Heath D 64-65).
To solve simultaneous equations involving quadratics Diophantus simplified the equation into a "pure" quadratic equation which he already had a method for solving (He ath D 66). The last type of determinate equation Diophantus acknowledged was the cubic equation for which he had no specific rule (Heath D 67). Next, Heath addresses the way in which Diophantus treated indeterminate equations. Diophantus divided these equations into two categories. The first was indeterminate equations of the second degree, which were subdivided into single equations and double equations. When dealing with single equations Heath finds that Diophantus manipulated the equations in various ways and said "is equal to a square," or "makes a square" (qtd. in Heath D 68). He used the concepts and facts about squares to solve various single equation problems. To solve the latter, double equations, one method was written by Diophantus to be, "Observing the difference, seek two numbers such that their products equal to this difference; then either equate the square of half the differe nce of the two factors to the lesser of the expressions or the square of half the sum to be the greater" (qtd. in Heath D 73). Heath continues to illustrate higher order double equations by citing examples from Arithmetica, and he must make conjectures a bout what he perceives to be Diophantus' intended method, since they "lack generality" (Heath D 93). He continues in this way when describing Diophantus' probable "Methods of Limits" and "Methods of Approximation to Limits." The "Method of Limits" required multiplying the given numbers by 2n, 3n ... until the wanted value, say xn, lies between the products of the two given numbers (Heath D 94). This creates boundaries for the value that is being sought. The last method, "Approximation to Limits" is described by Heath as follows: "The object of this is to solve such problems as that of finding two, or three, square numbers the sum of which is a given number, while each of them approximates as closely as possible to one and the same number" (Heath D 95).
Both scholars interpret Diophantus and his methods in clear concise ways. Nesselmann provided a list of possible methods that Diophantus used to solve equations. Similarly, Heath attempts to provide his readers with the methods he believed Diophantus use d in solving his equations by extracting problems from Arithmetica where Diophantus stated a general formula or where his work implies certain generalities. Certain methods involving finding general solutions and using limits to approximate a solution we re common in both Nesselmann's and Heath's analysis of Diophantus' work. However, Nesselmann seems to offer a more obvious analysis, since generalities are hard to find in Diophantus' work. Thus, it is essential to reflect on Diophantus' work by exam ining his style of solving different problems since his general methods were rarely explicitly stated.
Although much information about Diophantus appears to be conjecture, the remnant of the Arithmetica that is available to us reflects the indisputable fact that his work had a great impact on mathematics. The interpretations of Diophantus' methods for s olving problems vary. Unfortunately, from the information available it is obvious that Diophantus did not concern himself with general formulas, but rather, with finding specific solutions to problems. He has left the analysis of his work to later schol ars. Nesselmann is most successful at identifying the methods that were probably used by Diophantus. Diophantus' lack of general solutions makes it difficult for Heath's analysis to be straightforward. Thus, from these interpretations of Diophantus' s methods, one would like to choose the one that might accurately reflect his intentions. It is clear, however, that Alexandrian Algebra reached a high point, unsurpassed for centuries, in the work of Diophantus.