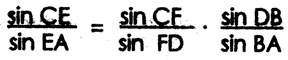
The Beginnings of Trigonometry
Joseph Hunt
History of Mathematics
Rutgers, Spring 2000
The ancient Greeks transformed trigonometry into an ordered science. Astronomy was the driving force behind advancements in trigonometry. Most of the early advancements in trigonometry were in spherical trigonometry mostly because of its application to astronomy. The three main figures that we know of in the development of Greek trigonometry are Hipparchus, Menelaus, and Ptolomy. There were likely other contributors but over time their works have been loss and their names have been forgotten.
"Even if he did not invent it, Hipparchus is the first person of whose systematic use of trigonometry we have documentary evidence." (Heath 257) Some historians go as far as to say that he invented trigonometry. Not much is known about the life of Hipp archus. It is believed that he was born at Nicaea in Bithynia. (Sarton 285) The town of Nicaea is now called Iznik and is situated in northwestern Turkey. Founded in the 4th century BC, Nicaea lies on the eastern shore of Lake Iznik. He is one of the g reatest astronomers of all time. We know from Ptolemy's references that he made astronomical observations from 161 to 127 BC. (Sarton 285) Unfortunately, nearly all of his works are lost, and all that remains is his commentary on the Phainomena of Eudoxos of Cnidos, and a commentary on an astronomical poem by Aratos of Soloi. (Sarton 285) Most of what we know about Hipparchus comes from Ptolemy's Almagest and a few remarks by other writers. The sole trigonometric function used by the ancient Greeks is the chord, which is closely related to the sine function (Toomer 7). What is known from Ptolemy is that Hipparchus produced a table of chords, which were an essential tool in the early development of trigonometry. According to Theon of Alexandria, who worked in Alexandria as a teacher of mathematics and astronomy, Hipparchus wrote a treatise in twelve books on chords in a circle, which has been lost (Sarton 286) . It is believed that this treatise contained some general trigonometric theory together with some tables.
Hipparchus is believed to be the first person to determine exactly the times of the rising and setting of the zodiacal signs. Pappus of Alexandria, who was a teacher of mathema tics in the fourth century, observed that "Hipparchus in his book on the rising of the twelve signs of the zodiac shows by means of numerical calculations that equal arcs of the semicircle beginning with Cancer which set in times having a certain relation to one another do not everywhere show the same relation between the times in which they rise."(Heath 257) Other mathematicians and astronomers of the time including Euclid, Autolycus, and Theodosius could only prove that the times are greater or less in relation to one another; they could not calculate the actual times. (Heath 257-258). "As Hipparchus proved corresponding propositions by means of numbers, we can only conclude that he used propositions in spherical trigonometry, calculating arcs from ot hers which are given, by means of tables."(Heath 258).
For his astronomical work Hipparchus needed a table of trigonometric ratios. It is believed that he computed the first table of chords for this purpose. He considered every triangle as being inscribed in a circle, so that each side became a chord. While chords were easy to calculate in some special cases with Euclidean knowledge, in order to complete his table Hipparchus would have needed to know many formulas of plane trigonometry that he either derived himself or borrowed from elsewhere. Hipparchus is credited as generalizing Hypsicles' idea of dividing the ecliptic into 360 degrees, an idea borrowed from the Babylonian astronomers, by dividing every circle into 360 degrees (Sarton 287). He divided the diameter into 120 units and expressed quantities smaller than degrees as sexagesimal fractions (Sarton 287), in the Babylonian style.
After Hipparchus the next Greek mathematician known to have made a contribution to trigonometry was Menelaus. We know very little about the life of Menelaus. Ptolemy mentions that Menelaus observed in Rome in the year 98 AD (Toomer). Thus it is believed that he was born around 70 AD (History of Mathematics). Both Pappus and Proclus call him Menelaus of Alexandria (Heath 260), so we may assume that he spent some of his time in Rome, and much of his time in Alexandria. He wrote a six-book treatise on chords, which was mentioned by Theon of Alexandria, but those books have all been lost. (Heath 260) His only surviving work is a three-book work called Sphaerica, whose third book contains some excellent information about the development of trigonometry and is the earliest surviving work on spherical trigonometry. Unfortunately the Greek version of this text is lost, and all that remains is an Arabic version translated a thousand years after the original was written. To make matters worse, various translators over the years have had their commentary included in the work, and it becomes difficult to separate the original from the commentators. Nevertheless, this work still provides a good source for the development of Greek trigonometry.
In the first book of the Sphaerica, there is the first known conception and definition of a spherical triangle (Heath 262). Menelaus describes a spherical triangle as the area included by arcs of great circles on the surface of a sphere subject to the restriction that each of the sides or legs of the triangle is an arc less then a semicircle. He then goes on to give the main propositions about spherical triangles corresponding to Euclid's propositions about plane triangles. (Heath 263). The second book has astronomical interest only. The third book contains trigonometric ratios. The first proposition in the third book is Menelaus's theorem with reference to a spherical triangle and any transversal (great circle) cutting the sides of a triangle. R ather than using a spherical triangle he expresses his proposition in terms of two intersecting great circles. "Between two arcs ADB, AEC of great circles are two other arcs of great circles DFC and BFE which intersect them and also intersect each other in F. All the arcs are less than a semicircle."(Heath 266). He then goes on to prove
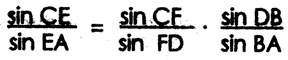
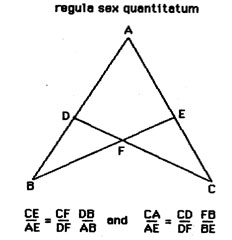
The rest of the third book consists of trigonometric propositions that were necessary for astronomical work. The last great contributor to trigonometry in the Greek period is Ptolomy. Very little is known about Ptolemy's actual life. He made astronomical observations from Alexandria in Egypt during the years AD 127-41. The first observation which we can date ex actly was made by Ptolemy on 26 March 127 while the last was made on 2 February 141. There is no evidence that Ptolemy was anywhere other than Alexandria. Heath says "it is evident that no part of the trigonometry, or of the matter preliminary to it, in Ptolemy was new. What he did was to abstract from earlier treatises, and to condense into the smallest possible space, the minimum of propositions necessary to establish the methods and formulas used." (276) Other math historians believe that Ptolemy com pleted the work started by Hipparchus that he worked out some necessary details and compiled new tables. It is difficult to tell what additions and modifications Ptolemy made to already existing works. Toomer calls the Almagest a masterpiece of clarity and method, superior to any ancient scientific textbook and with few peers from any period. But it is much more than that. Far from being a mere compilation of earlier Greek astronomy, as it is sometimes described, it is in many respects an original work.
Whatever the case, Ptolemy's Almagest is our main source of information on Hipparchus and on Alexandrian trigonometry. "The encyclopedic nature of the Almagest, its superior value, and its formal perfection were probably the main causes of the loss of Hipparchus' original writings. The early copyists must have felt that the Almagest rendered previous writings obsolete and superfluous." (Sarton 286). The use of the Sine, cosine, and tangent functions lay several hundred years in the future. However, the table of chords can be used in formulas that are equivalent to present day formulas for the trigonometric functions. The table of chords in the Alma gest is likely the same as Hipparchus' table or an expansion of it but we cannot be sure since we don't have a copy of Hipparchus' table to compare it with. (Heath 259) Ptolemy's table of chords is completed for arcs subtending angles increasing from 1/2 degrees to 180 degrees by steps of 1/2 degrees. In order to have calculated is table of chords Ptolemy must have been aware of the equivalents of several trigonometric identities and formulas. Ptolemy was aware of the of the formula, (chord 2x) + (chord (180x - 2x)) = 4r, which is equivalent to sin x + cos x = 1 . Ptolemy also used a formula that later became known as Ptolemy's theorem. That formula is chord (a-b) = 1/2 (chord a chord (180-b)) - (chord b chord (180-a)) where a and b are angles. "Pt olemy must have carried out his calculations to five sexagesimal places to achieve the accuracy he does in the third place."(Toomer 57-58). Ptolemy's calculations are accurate enough to be useful today. Here is a partial table of Ptolemy's chords taken from Toomer:
Ptolemy's Table of Chords
|
|
The table of chords is equivalent to a table of sines for all central angles 0 degrees to 90 degrees at 15' intervals and thus can be used to solve any planar triangle, provided that at least one side is known. The function sin x is equivalent to 1/2 (chord 2x), and cos x is equivalent to 1/2 chord(180-2x). The Almagest also contains trigonometric theorems equivalent to the present day law of sines and the compound-angle and half-angle identities. The assumption is that Hipparchus also must have known of these and possibly invented them.
Both Heath and Neugebauer have suggested that the beginnings of trigonometry as an ordered science go back a few years before Hipparchus. "The earliest preserved evidence for the approach to specifically trigonometric problems is found in the treatise, On the Sizes and Distances of the Sun and the Moon by Aristarchus, written about 250 BC"(Neugebauer 773). Aristarchus made use of one important inequality, which is the equivalent of the inequalities Sin x < x < tan x
With the help of such inequalities Aristarchus estimated the numerical values of trigonometric functions in some specific cases of small angles. A few decades later, Archimedes made use of the same formula. al-Biruni has preserved a Lemma of Archimedes, which shows that he had an equivalent version of Ptolemy's Theorem at his disposal (Neugebauer 773). In Menelaus' work there is a remark that suggests that one of the trigonometric propositions can be attributed to Apollonius, who lived a few years before Hipparchus (Heath 253). "Tannery (from his Recherches sur l'hist. De l'astronomic ancienne, p. 64) ... suggested that not only Apollonius but Archimedes before him may have compiled a table of chords or at the least shown the way to such a compilation." (Heath 253)
As we have seen, the beginnings of trigonometry can be traced far back into history. Hipparchus, in the middle of the first century BC, was the first person known to have treated trigonometry as an applied science, and the first person to compile a table of chords. Menelaus greatly advanced the field of spherical trigonometry. "By the second century A.D. trigonometry had reached its final form before Islamic developments in Book I of the Almagest" (Neugebauer, p. 772).