
Views of
Euclid's Parallel Postulate
in Ancient Greece and in Medieval
Islam
Michelle Eder History of Mathematics Rutgers, Spring 2000
Throughout the course of history there have been many remarkable advances, both intellectual and physical, which have changed our conceptual framework. One area in which this is apparent is Mathematics. In some cases mathematicians have spent years of their lives trying to solve a single problem. Such are Euclid, Proclus, John Wallis, N.I. Lobachevsky and Abu' Ali Ibn al-Haytham, who will be considered here in connection with the history of Euclid's parallel postulate.
Little or nothing is reliably known about Euclid's life. It is believed that he lived in Alexandria, Greece around 300 B.C. (Varadarajan, page 3). Some say that he was the most successful textbook writer the world has ever known, whose manuscripts dominat E the teaching of the subject (Smith, page 103). In the writing of his Elements, Euclid "successfully incorporated all the essential parts of the accumulated mathematical knowledge of his time" (Sarton, page 104). And although he was no t the first of Greek mathematicians to consolidate the materials of geometry into a text, he did so so "perfectly" that it came to replace the works of his predecessors (Morrow, page xxii). Every step to the proofs of his theorems was justified by referring back to a previous definition, axiom, theorem or proof of a theorem. However, though Euclid's Elements became the "tool-box" for Greek mathematics, his Parallel Postulate, postulate V, raises a great deal of controversy within the mathematical field. Euclid's formulation of the parallel postulate was as follows:

(Heath, page 202)
This states: That, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the tw o right angles. (Heath, page 202). This postulate, one of the most controversial topics in the history of mathematics, is one that geometers have tried to eliminate for more than two thousand years.
Among the first to explore other options to the parallel postulate were the Greeks. The Greek geometers of the 7th to 3rd centuries B.C. helped to enrich the science with new facts and took important steps toward the formulation of a "rigorou s logical sequence " (Pogorelov, page 186). They saw the parallel postulate as a theorem involving many difficulties whose proof required a number of definitions and theorems. In comparison to Euclid's other postulates the parallel postulate was com plicated and unclear. In addition, some found it difficult to accept on an intuitive basis. Even Euclid himself must have been displeased with it, for he made an effort to prove some of his other propositions without the use of the parallel postulate an D only began using it when it became absolutely necessary (Varadarajan, page 5). From his view, "there was no way out but to accept it as a postulate and go ahead. " (Sarton, page 39).
In the course of many failed attempts to modify this postulate, mathematicians have tried desperately to find an easier way to deal with the parallel postulate. a person of average intelligence might say that the proposition is evident and needs no proof (Sarton, page 39). However, from a more sophisticated mathematical viewpoint one would realize the need of a proof and attempt to give it (Sarton, page 39). In the attempt to clarify the status of this postulate some mathematicians tried to eliminate it altogether by replacing it with a simpler, more convincing axiom, while others tried to deduce it from other axioms. In these attempts, all these people proved that the fifth postulate is not necessary if one accepts another postulate "rendering the same service "; however, the use of them would seem "artificial " (Sarton, page 40). It is because of this that Euclid, seeing the necessity of the postulate, selected what he apparently found to be the simplest form of it as his fifth postulate (Sarton, page 40).
Among those who attempted a proof of the parallel postulate was Proclus, who lived 410 to 485 A.D. (Heath, page 29), receiving his training in Alexandria, Greece and afterwards Athens, where he became a "prolific writer " (Smith, page 139). His works, a valuable source of information on the history of Greek geometry, included a commentary on Book I of Euclid's Elements. This commentary may not have been written with the intention of correcting or improving upon Euclid, but there is one instance in which he attempts to alter a "difficulty " he finds in Euclid's Elements (Heath, page 31). This difficulty is what we commonly refer to as the "parallel postulate ".
The statement Proclus proves instead of the parallel postulate is,
"Given
a
+
b
<
2d , prove that the straight lines g'
and g''
meet at a certain point C."
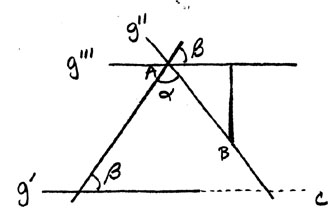
In his proof of this, Proclus draws a straight line, g''' through a given point a parallel to g'. Then taking a point B on g '' he drops a perpendicular to g ''' from it. From this he reasons that since the distance from g ''' increases without limit as the distance between a and B grows and the distance between g' and g''' is constant then there must be a point C on g'' belonging to g'. And it is this point where g' and g'' meet, thus completing his proof. However, as with most of the other alternatives to the parallel postulate, this one had faults. It is observed by Pogorelov that the parallel straight lines this proof relies on are not explicitly contained in the other postulates or axioms and therefore cannot be deduced from them. (Pogorelov, page 188).
Another person who attempted a proof to the parallel postulate was John Wallis. Wallis studied at Emmanuel College in Cambridge where he earned both a B.A. and a M.A in Theology in 1637 and 1640, respectively (Smith, page 407). Although his degre es were in theology, his "taste " was in the line of physics and mathematics (Smith, page 407). In 1649 he was elected to the Savilian professorship of geometry at Oxford (Smith, page 407). In his interest in Mathematics, Wallis was one of the first to recognize the "significance of the generalization of exponents to include negative and fractional, as well as positive and integral, numbers. " (Smith, page 408).
In addition to Wallis' recognition of the significance of exponents, he also attempted a proof to the parallel postulate. However, instead of proving the theorem directly with neutral geometry, he proposed a new axiom. This postulate expressed the idea was that one could either magnify or shrink a triangle as much as one likes without distortion. Using this, Wallis proves the parallel postulate as follows.
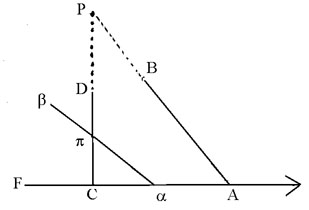
He begins with two straight lines making, with a third infinite straight line, two interior angles, less than two right angles. He then "slides " one angle down the line AF until it reaches a designated position ab, cutting the first line at p Then using his first postulate, he claims that the two triangles aC b and ACP are similar, thus showing that AB and CD meet at a point P, and proving the theorem. However, this too had a fault. In fact, the original postulate that he based the proof on was logically equivalent to Euclid's fifth postulate. (Heath, page 210). Therefore, he had assumed what he was trying to prove, which makes his proof invalid.
In addition to Proclus' and Wallis' proofs, in 1826 another mathematician's replacement of the parallel postulate lead to the discovery of Non-Euclidean geometry. This mathematician was N.I. Lobachevsky. Lobachevsky was a Russian mathematician wh o lived 1792 to 1856. For his proof to the parallel postulate, Lobachevsky proved that "Atleast two straight lines not intersecting a given one pass through an outside point. " In proving this he hoped to find a contradiction in the "Eucli dean corollary system ". However, in the development of his theory, Lobachevsky, instead, saw that the system was "non-contradictory ". From this he drew the conclusion that there existed a geometry, different from Euclidean, with the fifth postulate not holding. This geometry became known as "Non-Euclidean " geometry (Pogorelov, page 190).
Another group to comment on Euclid's parallel postulate was the Medieval Islams. From the ninth to the fifteenth centuries, extensive mathematical activity revived only in the large cosmopolitan cities in Islam. Arabic thinkers cultivated mathema tics in at least two ways. The first was by "the preservation and transmission of older knowledge " (Calinger, page 166). And the second was by original contributions to arithmetic, algebra and geometry. In Islam, society became more firmly es tablished and they began to focus their energies more toward educational developments in Mathematics. To them mathematics was closely linked to astronomy, astrology, cosmology, geography, natural philosophy, and optics (Calinger, page 169). From this, Islamic society shifted its interest to Greek thought. The first of the Greek texts to be translated, Euclid's Elements, brought the issues involved in the parallel postulate to the attention of Islamic mathematicians, and they, too, as the Greeks before them, began exploring the possibility of proving this postulate.
One mathematician from this time who contributed to clarification of
Euclid's
parallel postulate was Abu' Ali Ibn al-Haytham,
an Arabic physicist, mathematician, and astronomer.
He begins his proof by first addressing Euclid's definition
of parallel lines:
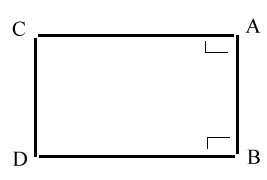 then begins his proof. First, he begins with a given vertical line
AB. Then from an endpoint A he constructs a line AC,
forming a right angle with AB.
Similarly, he constructs a line BD, meeting at
endpoint D.
In this figure al-Haytham claims that
CD is equal to AB. To prove this,
he uses a proof by contradiction.
He first supposes that CD is
greater than AB. He then
extends the line CA through A to form AE.
Similarly, he forms the
line BF through B.
Next al-Haytham cuts the line AE so that AE is
equal in length to AC, after which he drops a perpendicular
from E
to F. Finally he draws the lines CB and BE.
then begins his proof. First, he begins with a given vertical line
AB. Then from an endpoint A he constructs a line AC,
forming a right angle with AB.
Similarly, he constructs a line BD, meeting at
endpoint D.
In this figure al-Haytham claims that
CD is equal to AB. To prove this,
he uses a proof by contradiction.
He first supposes that CD is
greater than AB. He then
extends the line CA through A to form AE.
Similarly, he forms the
line BF through B.
Next al-Haytham cuts the line AE so that AE is
equal in length to AC, after which he drops a perpendicular
from E
to F. Finally he draws the lines CB and BE.
To
continue his proof, al-Haytham needs to show that line CD is equal to
EF, and that both are greater than AB.
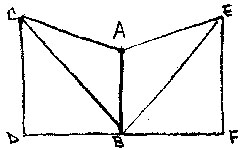 Using what we now refer to as
the Side-Angle-Side Theorem,
he says that since CA is
equal to AE, angle CAB is equal to angle EAB
(right angles), and the side
AB is common, therefore the triangles CAB and
EAB must also be equal. Thus
line CB is equal to EB
and the two remaining angles must also be
equal. al-Haytham continues that angle CBA and angle EBA
are equal,
and since angles ABD and ABF are equal, therefore
the angles CBD and EBF must
also be equal. Next, by what we now refer to as the Side-Angle-Side
Theorem, he claims that since the angles CDB and EFB
are equal and sides DB and BF are equal,
therefore the triangles CDB and EFB must be equal.
Therefore, CD and EF are also equal. Then, since CD
is greater than AB (by assumption) EF must also be greater than AB. Next in
al-Haytham's proof, he says to imagine EF moving along FB
so that the angle EFB
remains a right angle throughout the motion, with EF remaining
perpendicular to FB.
Then when point F coincides with point B, line
EF will be "superposed" onto AB.
But he claims that since
the magnitude of EF is greater than that of AB,
point E will lie
outside AB (on the same side with A).
Thus at this point EF is equal to HB.
Using what we now refer to as
the Side-Angle-Side Theorem,
he says that since CA is
equal to AE, angle CAB is equal to angle EAB
(right angles), and the side
AB is common, therefore the triangles CAB and
EAB must also be equal. Thus
line CB is equal to EB
and the two remaining angles must also be
equal. al-Haytham continues that angle CBA and angle EBA
are equal,
and since angles ABD and ABF are equal, therefore
the angles CBD and EBF must
also be equal. Next, by what we now refer to as the Side-Angle-Side
Theorem, he claims that since the angles CDB and EFB
are equal and sides DB and BF are equal,
therefore the triangles CDB and EFB must be equal.
Therefore, CD and EF are also equal. Then, since CD
is greater than AB (by assumption) EF must also be greater than AB. Next in
al-Haytham's proof, he says to imagine EF moving along FB
so that the angle EFB
remains a right angle throughout the motion, with EF remaining
perpendicular to FB.
Then when point F coincides with point B, line
EF will be "superposed" onto AB.
But he claims that since
the magnitude of EF is greater than that of AB,
point E will lie
outside AB (on the same side with A).
Thus at this point EF is equal to HB.
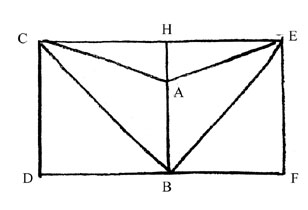 Next al-Haytham slides line BH along BD. If
in this process point B coincides with point D then BH
will be "superposed" on DC (because angles HBF and CDB
are equal). Then
since BH =
EF = CD,
al-Haytham claims that H
coincides with C. Thus al-Haytham has showed that if EF
is put in motion along FD, then the points E and F
will coincide with C and D,
respectively. Next he notes that if any straight line moves in this
way then it's ends will describe a straight line. Thus the point E
describes the straight line EHC. al-Haytham concludes that since H
does not lie on AB it can not coincide with point a and therefore
there must exist a surface bound by two straight lines which he finds
to be &q uot;absurd ", therefore proving that CD is neither
greater nor less than A. Thus al-Haytham has showed that CD
and all other perpendicular lines dropped from AC to BD
are equal to AB.
(Rosenfield, pages 59-62).
Next al-Haytham slides line BH along BD. If
in this process point B coincides with point D then BH
will be "superposed" on DC (because angles HBF and CDB
are equal). Then
since BH =
EF = CD,
al-Haytham claims that H
coincides with C. Thus al-Haytham has showed that if EF
is put in motion along FD, then the points E and F
will coincide with C and D,
respectively. Next he notes that if any straight line moves in this
way then it's ends will describe a straight line. Thus the point E
describes the straight line EHC. al-Haytham concludes that since H
does not lie on AB it can not coincide with point a and therefore
there must exist a surface bound by two straight lines which he finds
to be &q uot;absurd ", therefore proving that CD is neither
greater nor less than A. Thus al-Haytham has showed that CD
and all other perpendicular lines dropped from AC to BD
are equal to AB.
(Rosenfield, pages 59-62).
In conclusion, throughout the past 2300 years of mathematical history many mathematicians from all around the world have unsuccessfully been trying to prove Euclid's parallel postulate. Although these attempted proofs did not lead to the desired result, they did play a part in the development of geometry, enriching it with new theorems that were not based on the fifth postulate, as well as leading to the construction of a new geometry, Non-Euclidean geometry, not based on the parallel postulate.
Works Cited